Deformation Behavior of 3D Printed Auxetic Structures of Thermoplastic Polymers: PLA, PBAT, and Blends
Abstract
:1. Introduction
2. Materials and Methods
2.1. Compounding of Materials and Filament Extrusion
2.1.1. Materials
2.1.2. Compounding
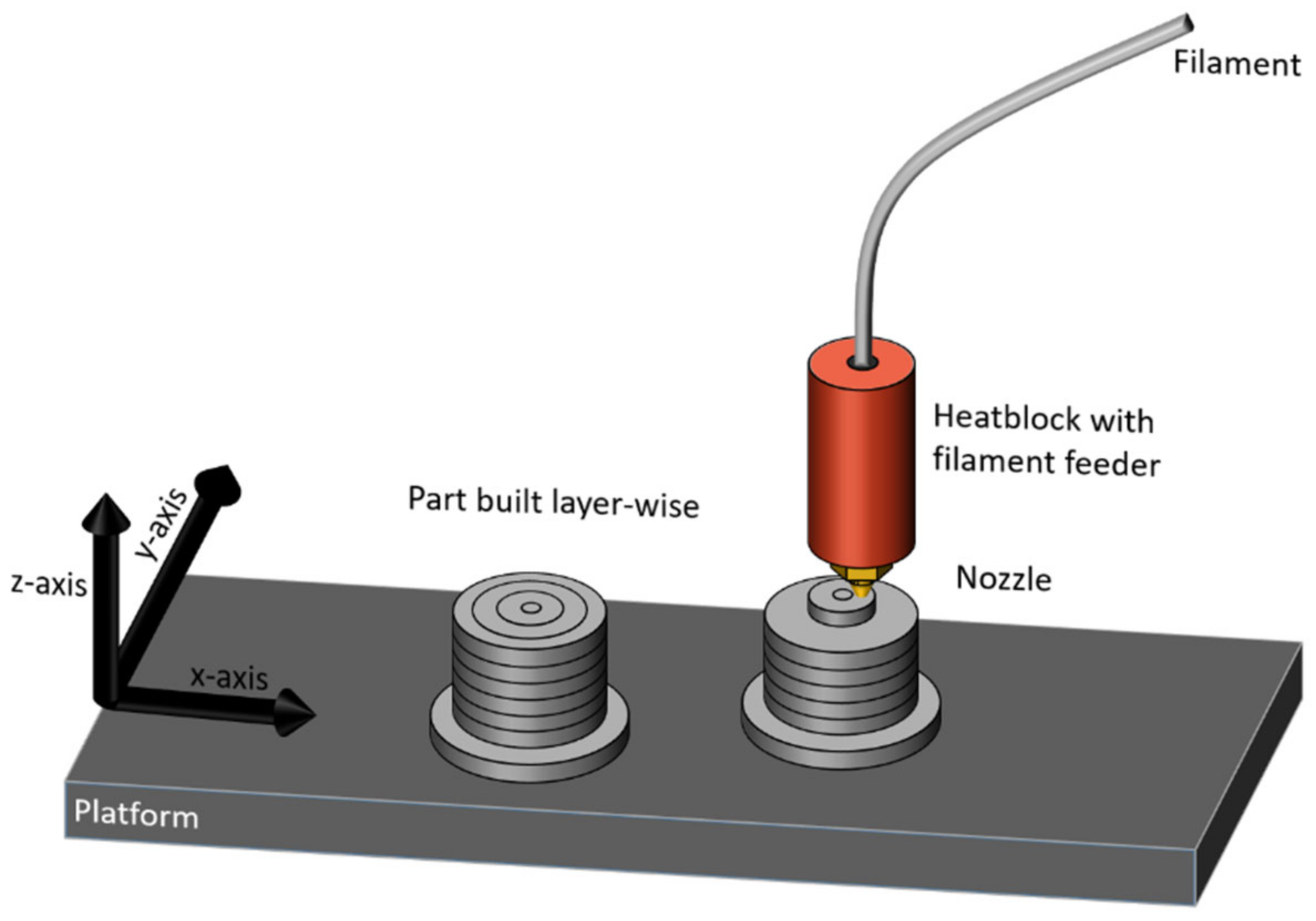
2.1.3. Filament Extrusion
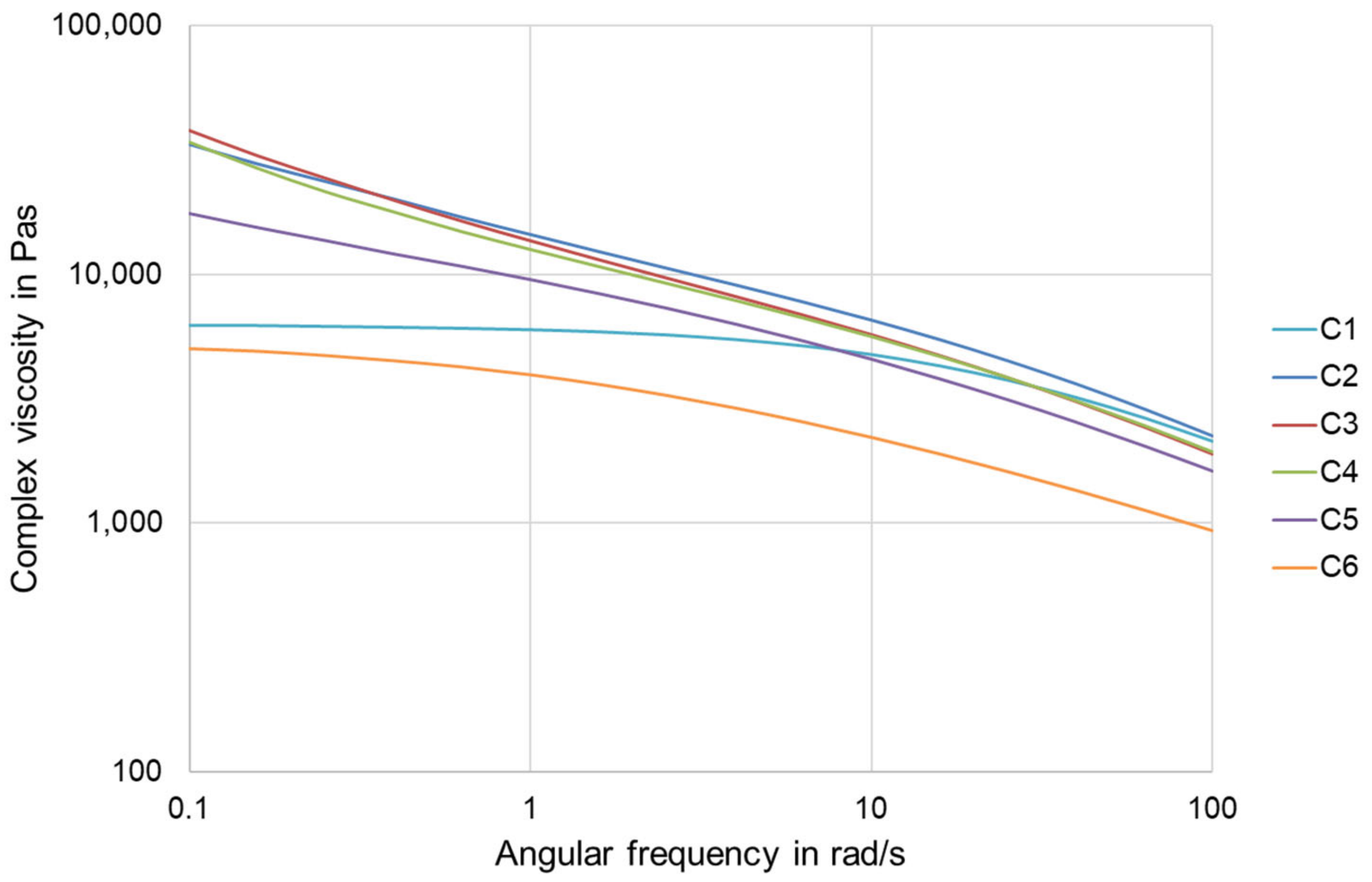
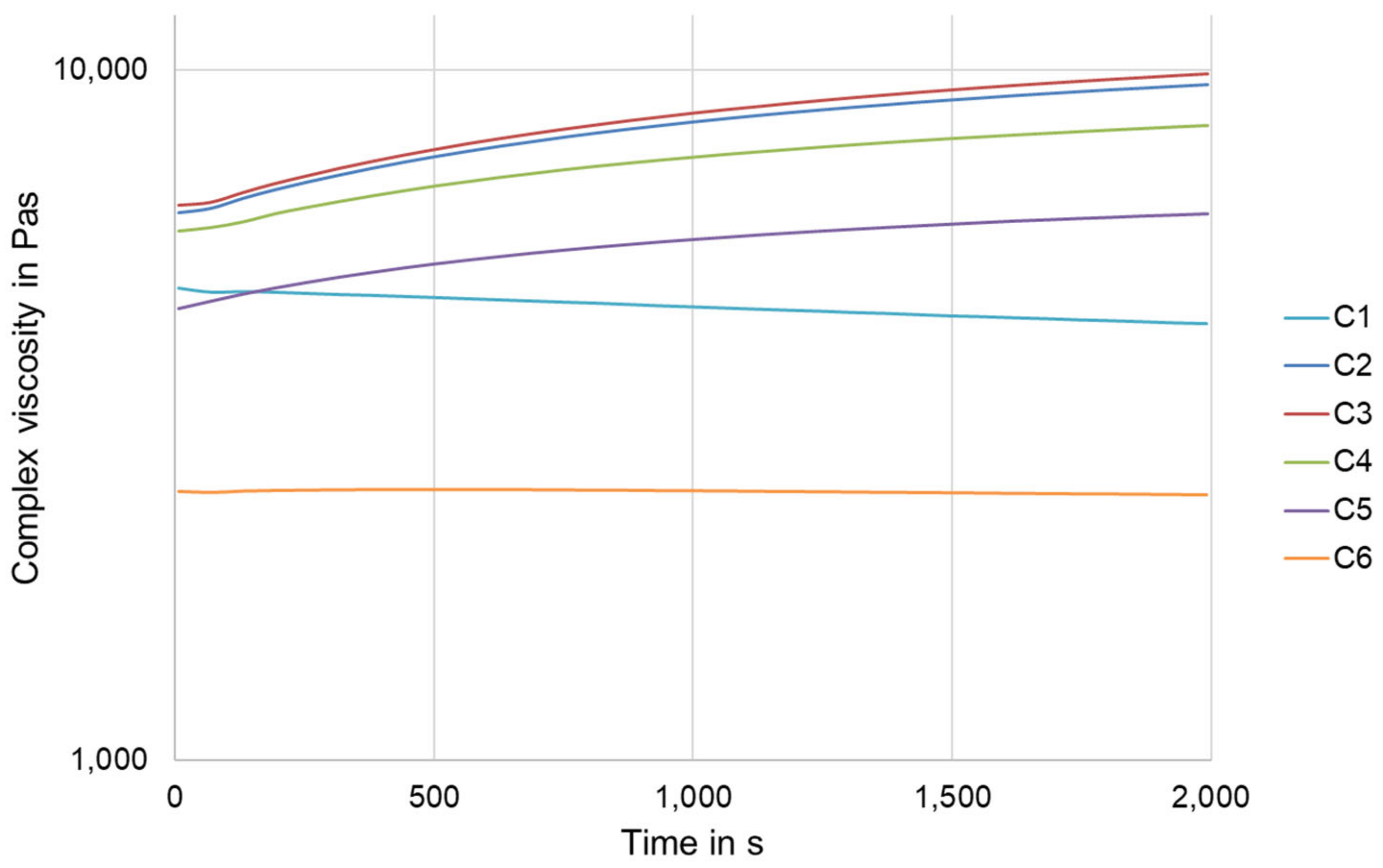
2.2. Characterization of the Materials
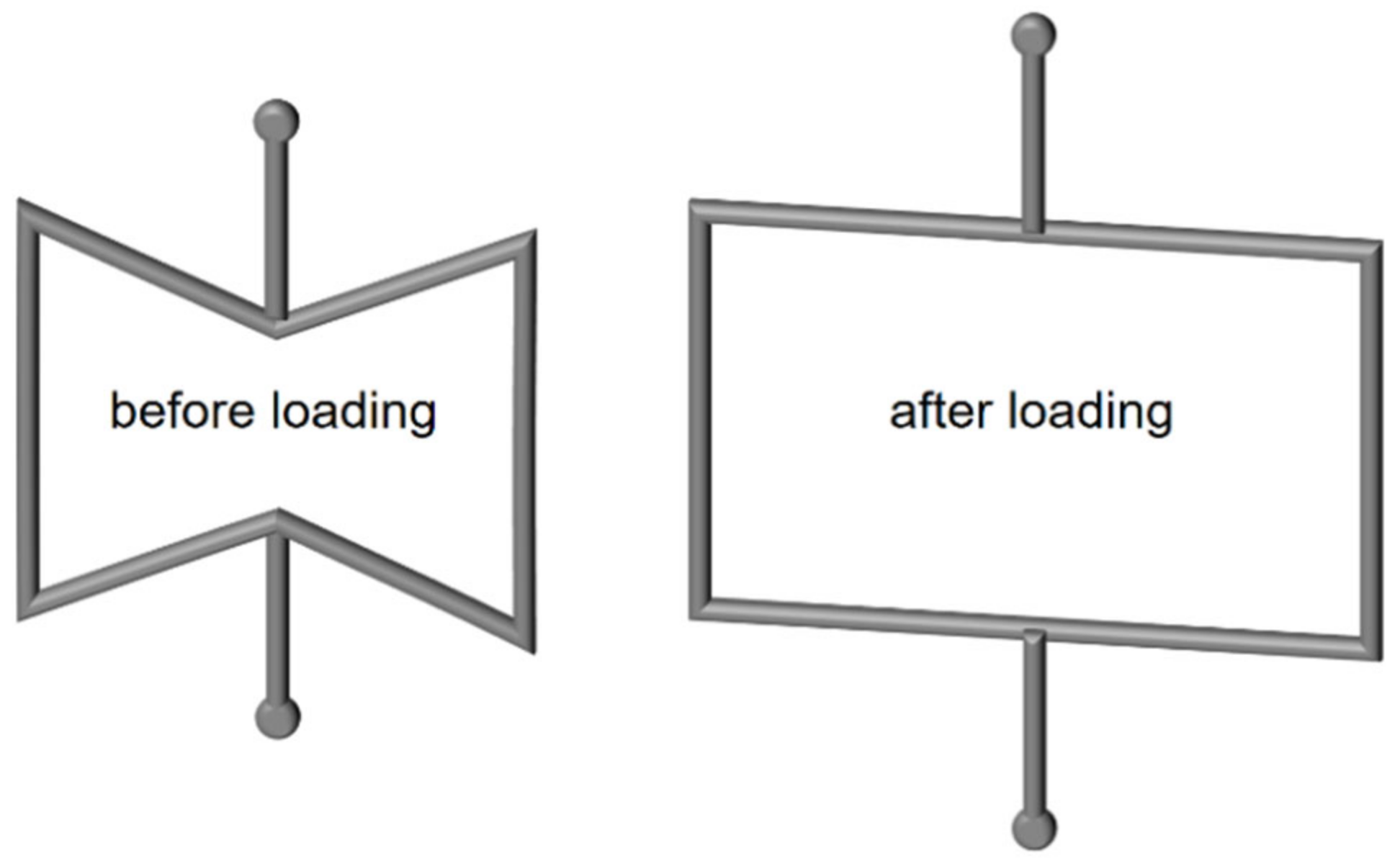
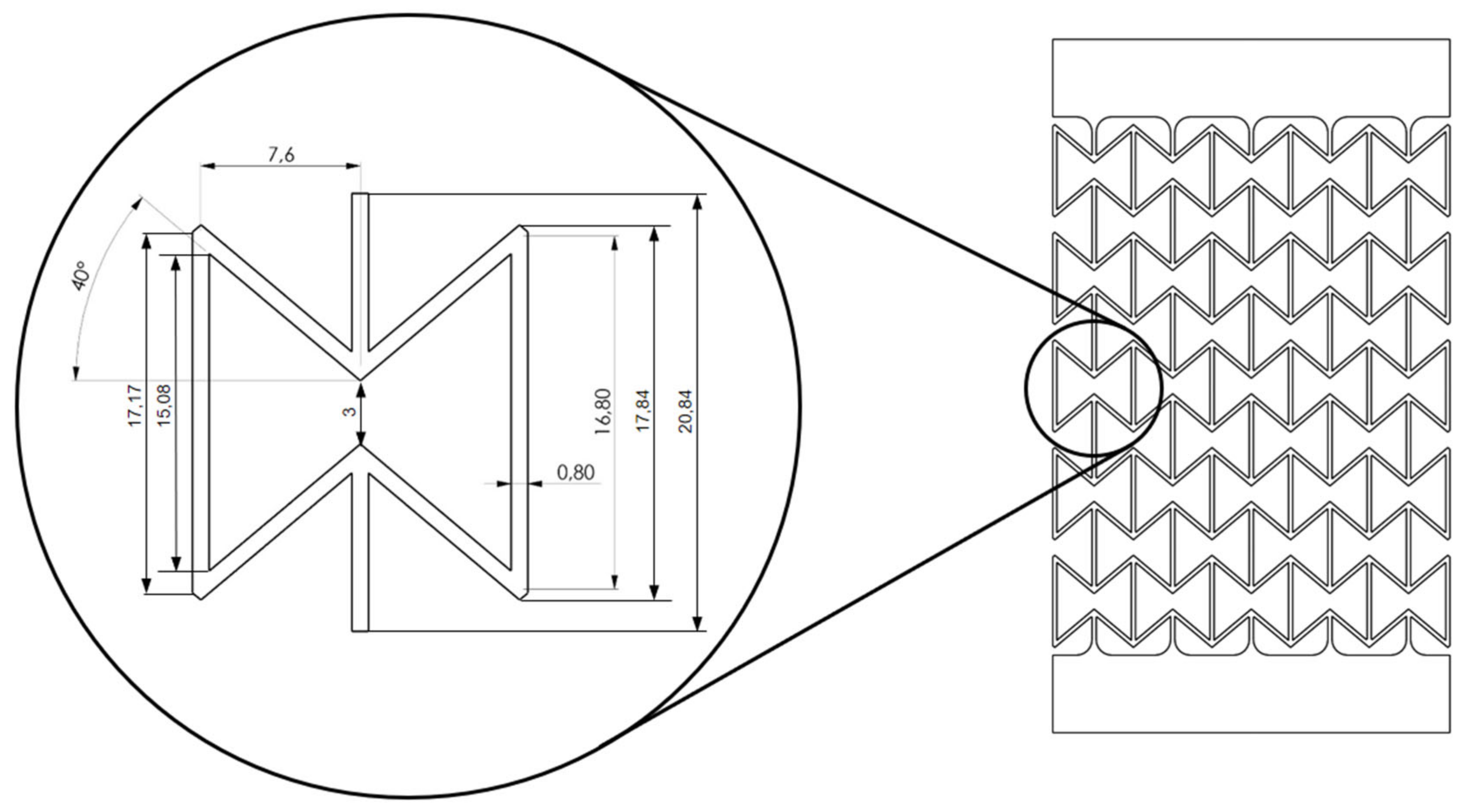
2.3. Fabrication of Auxetic Structures
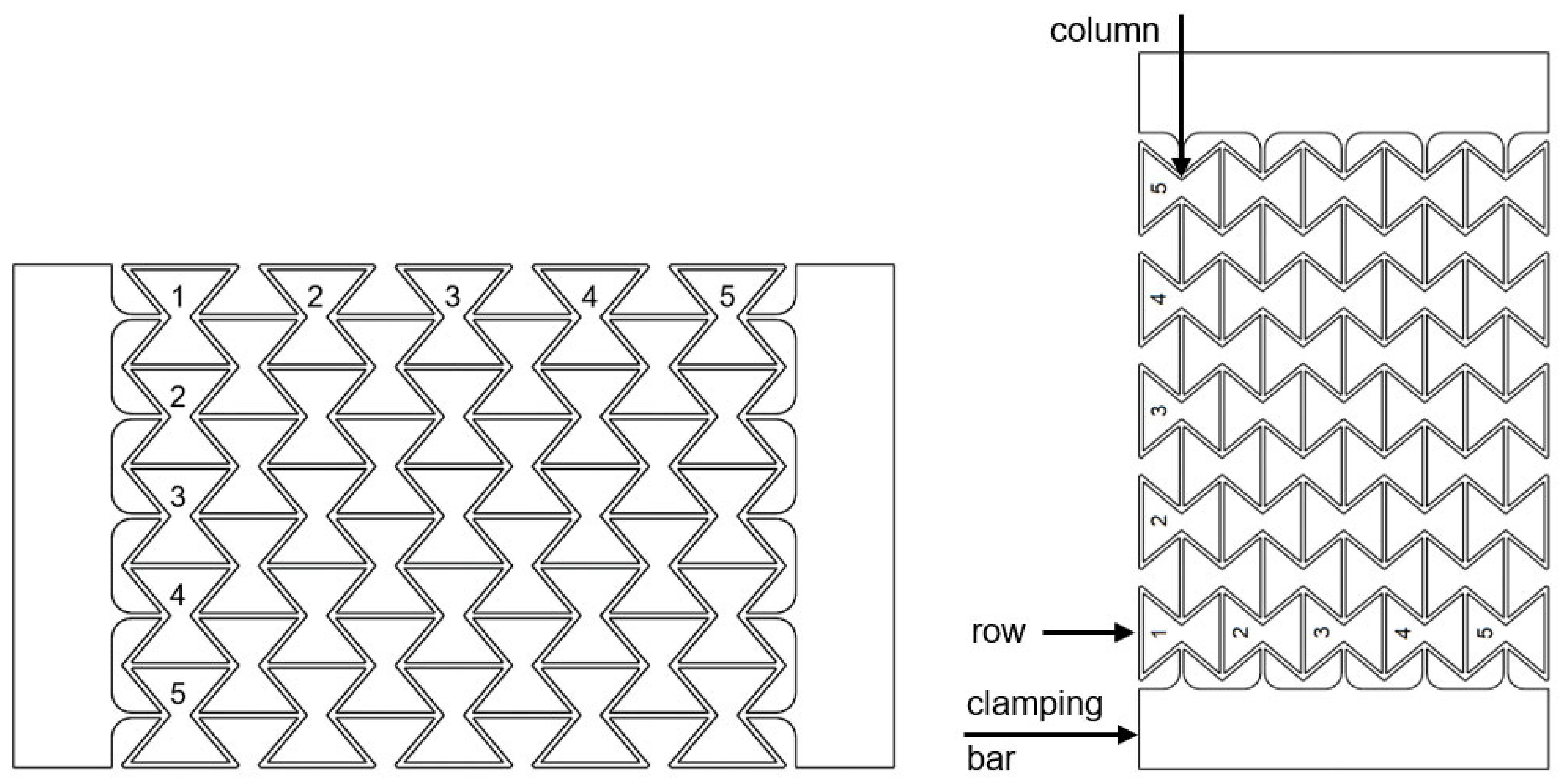
2.4. Determination of the Poisson’s Ratio
2.5. In-Situ Computed Tomography (CT) Test
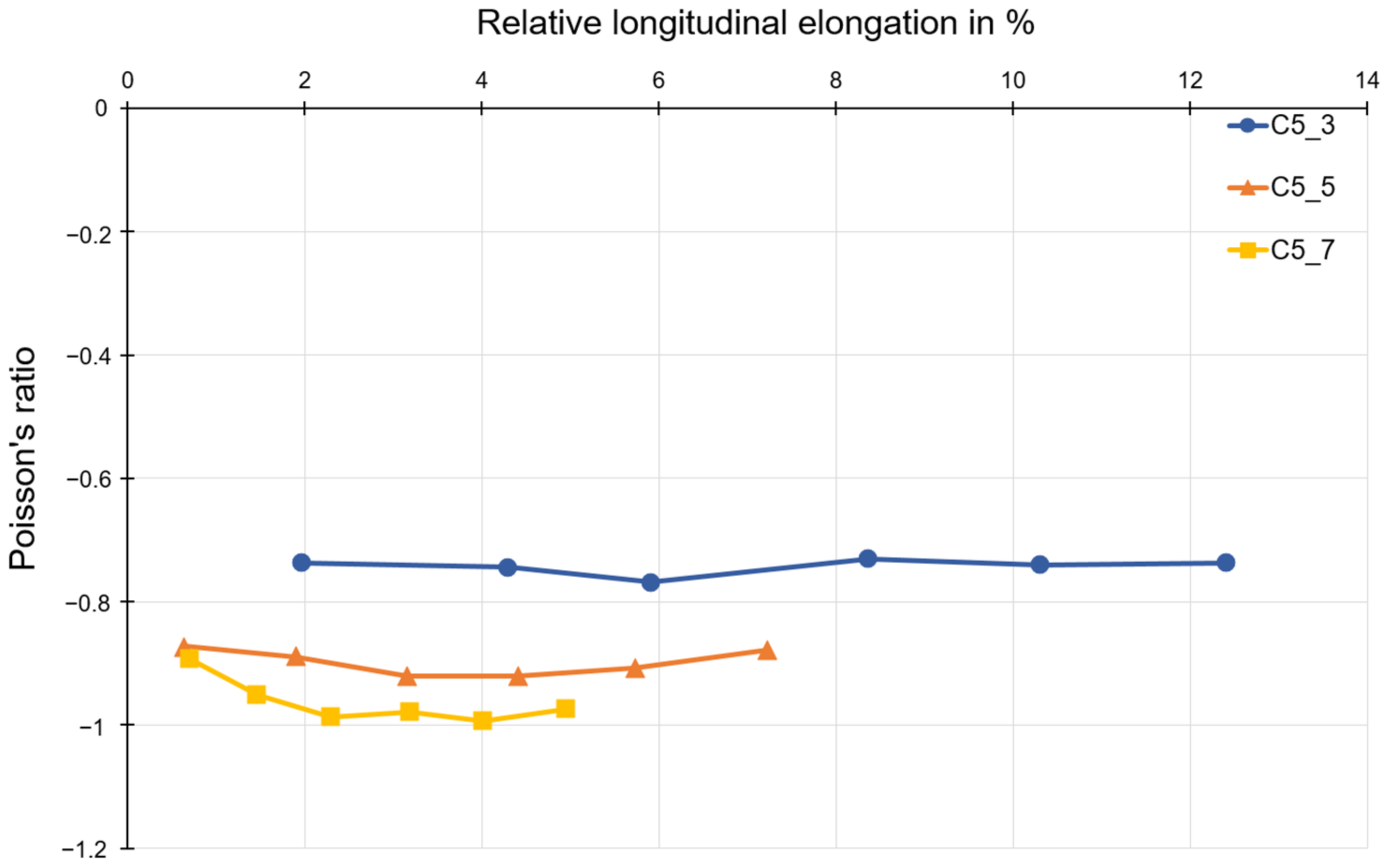
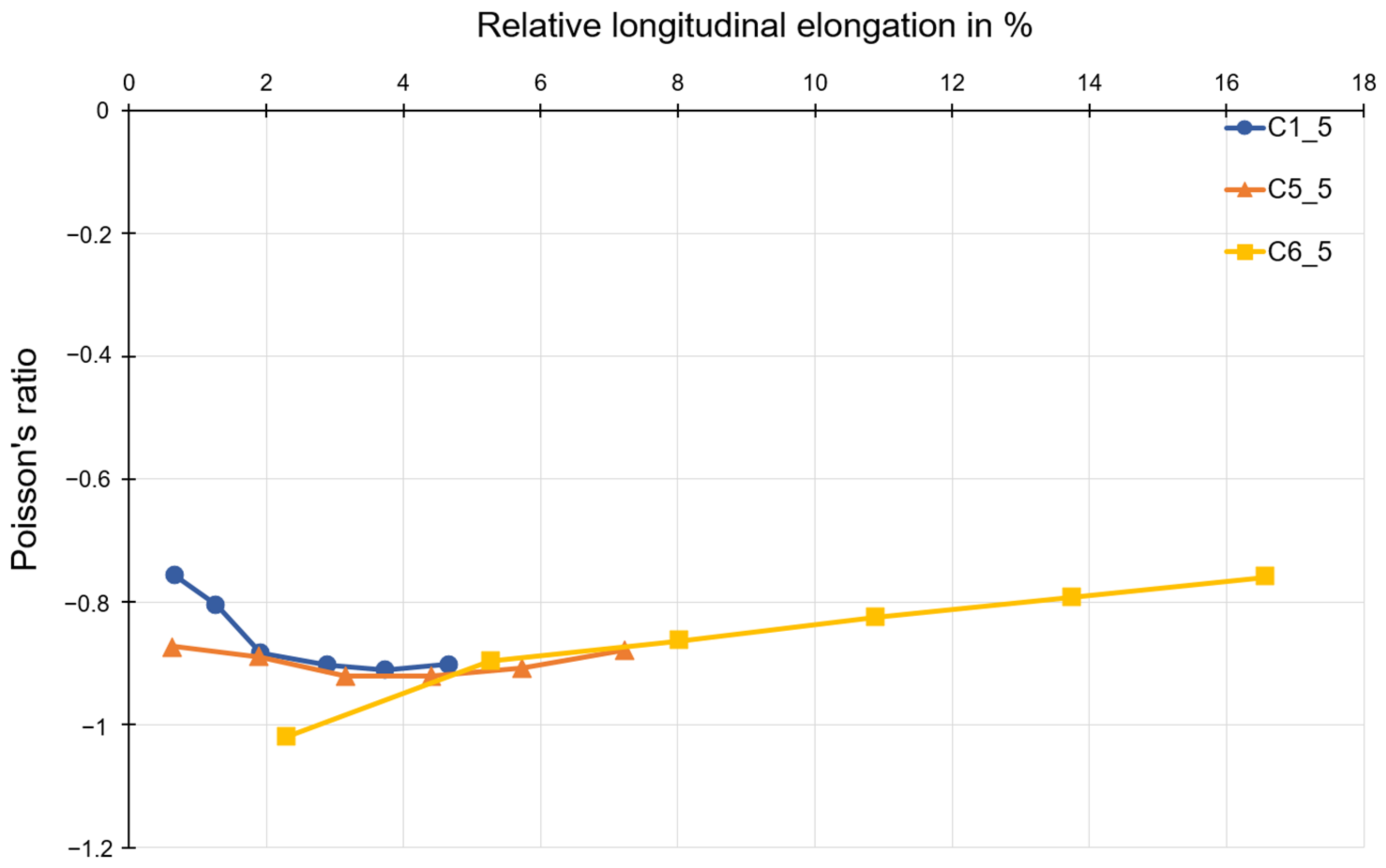
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Evans, K. Auxetic polymers: A new range of materials. Endeavour 1991, 15, 170–174. [Google Scholar] [CrossRef]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity; Courier Corporation: North Chelmsford, MA, USA, 1892; Volume 1, p. 75. [Google Scholar]
- DIN EN ISO 527-1; Kunststoffe–Bestimmung der Zugeigenschaften––Teil 1: Allgemeine Grundsätze. Beuth: Berlin, Germany, 2019.
- Obrecht, H.; Reinicke, U.; Walkowiak, M. Neue Wege zu gewichtseffizienten Konstruktionen. Light. Des. 2011, 4, 37–42. [Google Scholar] [CrossRef]
- Kolken, H.M.A.; Zadpoor, A.A. Auxetic mechanical metamaterials. RSC Adv. 2017, 7, 5111–5129. [Google Scholar] [CrossRef] [Green Version]
- Alderson, K.; Webber, R.; Kettle, A.; Evans, K. Novel fabrication route for auxetic polyethylene. Part 1. Processing and microstructure. Polym. Eng. Sci. 2005, 45, 568–578. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, H. Auxetic materials and their potential applications in textiles. Text. Res. J. 2014, 84, 1600–1611. [Google Scholar] [CrossRef]
- Yeganeh-Haeri, A.; Weidner, D.J.; Parise, J.B. Elasticity of α-Cristobalite: A Silicon Dioxide with a Negative Poisson’s Ratio. Science 1992, 257, 650–652. [Google Scholar] [CrossRef]
- Lim, T.-C. Auxetic Materials and Structures; Springer Science + Business Media: Singapore, 2015; pp. 6–7. ISBN 978-981-287-274-6. [Google Scholar]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 2000, 19, 1563–1565. [Google Scholar] [CrossRef]
- Prall, D.; Lakes, R. Properties of a chiral honeycomb with a poisson’s ratio of—1. Int. J. Mech. Sci. 1997, 39, 305–314. [Google Scholar] [CrossRef]
- Masters, I.; Evans, K. Models for the elastic deformation of honeycombs. Compos. Struct. 1996, 35, 403–422. [Google Scholar] [CrossRef]
- Attaran, M. The rise of 3-D printing: The advantages of additive manufacturing over traditional manufacturing. Bus. Horiz. 2017, 60, 677–688. [Google Scholar] [CrossRef]
- Mehrpouya, M.; Dehghanghadikolaei, A.; Fotovvati, B.; Vosooghnia, A.; Emamian, S.S.; Gisario, A. The Potential of Additive Manufacturing in the Smart Factory Industrial 4.0: A Review. Appl. Sci. 2019, 9, 3865. [Google Scholar] [CrossRef] [Green Version]
- Bonten, C. Plastics Technology–Introduction and Fundamentals; Carl Hanser Verlag GmbH & Co. KG: Munich, Germany, 2019; pp. 413–414. ISBN 978-1-56990-767-2. [Google Scholar]
- Kattinger, J.; Ebinger, T.; Kurz, R.; Bonten, C. Numerical simulation of the complex flow during material extrusion in fused filament fabrication. Addit. Manuf. 2021, 49, 102476. [Google Scholar] [CrossRef]
- Lim, L.-T.; Auras, R.; Rubino, M. Processing technologies for poly(lactic acid). Prog. Polym. Sci. 2008, 33, 820–852. [Google Scholar] [CrossRef]
- Chacón, J.M.; Caminero, M.A.; García-Plaza, E.; Núñez, P.J. Additive manufacturing of PLA structures using fused deposition modelling: Effect of process parameters on mechanical properties and their optimal selection. Mater. Des. 2017, 124, 143–157. [Google Scholar] [CrossRef]
- Jian, J.; Xiangbin, Z.; Xianbo, H. An overview on synthesis, properties and applications of poly(butylene-adipate-co-terephthalate)–PBAT. Adv. Ind. Eng. Polym. Res. 2020, 3, 19–26. [Google Scholar] [CrossRef]
- Weng, Y.-X.; Jin, Y.-J.; Meng, Q.-Y.; Wang, L.; Zhang, M.; Wang, Y.-Z. Biodegradation behavior of poly(butylene adipate-co-terephthalate) (PBAT), poly (lactic acid) (PLA), and their blend under soil conditions. Polym. Test. 2013, 32, 918–926. [Google Scholar] [CrossRef]
- Al-Itry, R.; Lamnawar, K.; Maazouz, A. Rheological, morphological, and interfacial properties of compatibilized PLA/PBAT blends. Rheol. Acta 2014, 53, 501–517. [Google Scholar] [CrossRef]
- Wang, B.; Jin, Y.; Kang, K.; Yang, N.; Weng, Y.; Huang, Z.; Men, S. Investigation on compatibility of PLA/PBAT blends modified by epoxy-terminated branched polymers through chemical micro-crosslinking. e-Polymers 2020, 20, 39–54. [Google Scholar] [CrossRef] [Green Version]
- Cardoso, P.H.M.; Coutinho, R.R.T.P.; Drummond, F.R.; Da Conceição, M.D.N.; Thiré, R.M.D.S.M. Evaluation of Printing Parameters on Porosity and Mechanical Properties of 3D Printed PLA/PBAT Blend Parts. Macromol. Symp. 2020, 394, 2000157. [Google Scholar] [CrossRef]
- Nature Works LLC Ingeo™ Biopolymer 4032D Technical Data, Sheet Minnetonka USA. Available online: https://www.natureworksllc.com/~/media/Technical_Resources/Technical_Data_Sheets/TechnicalDataSheet_4032D_films_pdf.pdf (accessed on 10 November 2022).
- BASF Ecoflex® F Blend C1200 Product Data Sheet, Ludwigshafen Germany. Available online: https://download.basf.com/p1/8a8082587fd4b608017fd63230bf39c4/en/ecoflex%3Csup%3E%C2%AE%3Csup%3E_F_Blend_C1200_Product_Data_Sheet_English.pdf (accessed on 10 November 2022).
- BASF Joncryl® ADR 4468 Data Sheet, Ludwigshafen Germany. Available online: https://pic.dginfo.com/upfile/file/2020/01/07/10/ori/6371399111773954075835672.pdf (accessed on 10 November 2022).
- Yared, W.; Chen, C.-Y.; Sievers, N.; Tillmann, W.; Zielke, R.; Schimpfermann, M. Void distribution in a brazed cemented carbide steel joint analyzed by X-ray microscopy. Measurement 2019, 141, 250–257. [Google Scholar] [CrossRef]
- Tillmann, W.; Hagen, L.; Schaak, C.; Zielke, R.; Schaper, M.; Aydinöz, M.E. Pretreatment and coatability of additive manufactured components made by means of selective laser melting. Weld. Cut. 2018, 3, 208–214. [Google Scholar]
- Hoppe, K.; Maricanov, M.; Schaldach, G.; Zielke, R.; Renschen, D.; Tillmann, W.; Thommes, M.; Pieloth, D. Modeling the separation performance of depth filter considering tomographic data. Environ. Prog. Sustain. Energy 2020, 39, 5. [Google Scholar] [CrossRef] [Green Version]
- Schneider, Y.; Zielke, R.; Xu, C.; Tayyab, M.; Weber, U.; Schmauder, S.; Tillmann, W. Experimental Investigations of Micro-Meso Damage Evolution for a Co/WC-Type Tool Material with Application of Digital Image Correlation and Machine Learning. Materials 2021, 14, 3562. [Google Scholar] [CrossRef] [PubMed]














| Compound | PLA wt% | PBAT wt% |
|---|---|---|
| C1 | 100 | 0 |
| C2 | 80 | 20 |
| C3 | 70 | 30 |
| C4 | 60 | 40 |
| C5 | 40 | 60 |
| C6 | 0 | 100 |
| Compound | Zone | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1, C2, C3, C4 | Temperature in °C | 30 | 80 | 120 | 160 | 185 | 185 | 185 | 185 | 185 | 195 | 210 |
| C5, C6 | 30 | 80 | 120 | 160 | 185 | 185 | 185 | 185 | 185 | 195 | 200 |
| Compound | Zone | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| C1, C2, C3, C4, C5 | Temperature in °C | 160 | 190 | 205 | 205 | 190 |
| C6 | 160 | 180 | 185 | 185 | 185 |
| Name | Young’s Modulus in MPa | Tensile Strength in MPa | Elongation at Break in % |
|---|---|---|---|
| C1 | 3813 ± 192 | 63 ± 3 | 3.5 ± 1.3 |
| C2 | 2682 ± 139 | 49 ± 3 | 20 ± 16 |
| C3 | 1883 ± 189 | 29 ± 3 | 182 ± 45 |
| C4 | 1459 ± 75 | 28 ± 1 | 160 ± 17 |
| C5 | 485 ± 46 | 20 ± 1 | 176 ± 9 |
| C6 | 86 ± 2 | 15 ± 1 | >350 |
| Compound | C1 | C5 | C6 |
|---|---|---|---|
| Layer height in mm | 0.20 | 0.20 | 0.20 |
| Extrusion width in mm | 0.40 | 0.44 | 0.44 |
| Extruder temperature in °C | 210 | 220 | 200 |
| Printing speed in mm/s | 45 | 35 | 35 |
| Printing speed first layer in mm/s | 13 | 17 | 17 |
| Heated bed temperature in °C | 50 | 50 | 60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hufert, J.; Grebhardt, A.; Schneider, Y.; Bonten, C.; Schmauder, S. Deformation Behavior of 3D Printed Auxetic Structures of Thermoplastic Polymers: PLA, PBAT, and Blends. Polymers 2023, 15, 389. https://doi.org/10.3390/polym15020389
Hufert J, Grebhardt A, Schneider Y, Bonten C, Schmauder S. Deformation Behavior of 3D Printed Auxetic Structures of Thermoplastic Polymers: PLA, PBAT, and Blends. Polymers. 2023; 15(2):389. https://doi.org/10.3390/polym15020389
Chicago/Turabian StyleHufert, Jonas, Axel Grebhardt, Yanling Schneider, Christian Bonten, and Siegfried Schmauder. 2023. "Deformation Behavior of 3D Printed Auxetic Structures of Thermoplastic Polymers: PLA, PBAT, and Blends" Polymers 15, no. 2: 389. https://doi.org/10.3390/polym15020389
APA StyleHufert, J., Grebhardt, A., Schneider, Y., Bonten, C., & Schmauder, S. (2023). Deformation Behavior of 3D Printed Auxetic Structures of Thermoplastic Polymers: PLA, PBAT, and Blends. Polymers, 15(2), 389. https://doi.org/10.3390/polym15020389






