Mechanical Anisotropy of Injection-Molded PP/PS Polymer Blends and Correlation with Morphology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation
2.3. Mechanical Anisotropy Determination via Short-Beam Shear Testing [24]
2.4. Morphology Observation
3. Results and Discussions
3.1. Relation of Morphology and Mechanical Anisotropy of Injection-Molded PP-Rich Polymer Blends
3.2. Relation of Morphology and Mechanical Anisotropy of Injection-Molded PS-Rich Polymer Blends
3.3. Yield Conditions for PP/PS Polymer Blends
4. Conclusions
- When PP is a continuous phase, the phase structure forms a sea-island structure. The yield condition under uniaxial tensile loading was interface debonding.
- When PS is a continuous phase, the phase structure has a dispersed phase that is elongated in the flow direction. This structure was changed by the addition of SEBS. The yielding condition under uniaxial tensile loading was shear yielding.
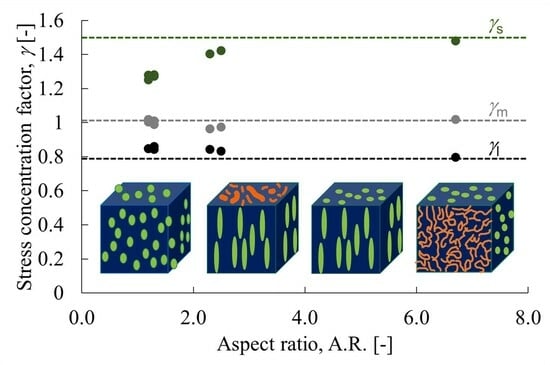
- The aspect ratio of the dispersed phase was correlated with the stress concentration factor.
- When the PP forming the sea-island structure is a continuous phase, the shear yield initiation stress is explainable by the log-complex law without considering the interfacial interaction stress.
- When the PS forming the structure with stretched dispersed phase is a continuous phase, the shear yield initiation stress is explainable by the shear yield initiation stress considering the interfacial interaction force.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- McCrum, N.G.; Buckley, C.P.; Bucknall, C.B. Principles of Polymer Engineering; Oxford University Press: New York, NY, USA, 1988. [Google Scholar]
- Juster, H.; Aar, B.; Brouwer, H. A Review on Microfabrication of Thermoplastic Polymer-Based Microneedle Arrays. Polym. Eng. Sci. 2019, 59, 877–890. [Google Scholar] [CrossRef]
- Chaudhary, B.; Li, H.; Matos, H. Long-term mechanical performance of 3D printed thermoplastics in seawater environments. Results Mater. 2023, 17, 100381. [Google Scholar] [CrossRef]
- Ge, J.; Luo, M.; Catalanotti, G.; Falzon, B.G.; Higgins, C.; McClory, C.; Thiebot, J.-A.; Zhang, L.; He, M.; Zhang, D.; et al. Process characteristics, damage mechanisms and challenges in machining of fibre reinforced thermoplastic polymer (FRTP) composites: A review. China Plast. 2023, 36, 140–149. [Google Scholar]
- Thakkar, R.; Thakkar, R.; Pillai, A.; Ashour, E.A.; Repka, M.A. Systematic screening of pharmaceutical polymers for hot melt extrusion processing: A comprehensive review. Int. J. Pharm. 2020, 576, 118989. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Yu, F.; Deng, H.; Huang, Y.; Li, G.; Fu, Q. Morphology evolution of polymer blends under intense shear during high speed thin-wall injection molding. J. Phys. Chem. B 2017, 8, 6257–6270. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Xiao, Y.; Zhang, Q.; Gao, X.-L.; Fu, Q. The morphology and mechanical properties of dynamic packing injection molded PP/PS blends. Polymer 2003, 44, 1469–1480. [Google Scholar] [CrossRef]
- Omonov, T.S.; Harrats, C.; Groeninckx, G.; Moldenaers, P. Anisotropy and instability of the co-continuous phase morphology in uncompatibilized and reactively compatibilized polypropylene/polystyrene blends. Polymer 2007, 48, 5289–5302. [Google Scholar] [CrossRef]
- Mao, Z.; Zhang, X.; Jiang, G.; Zhang, J. Fabricating sea-island structure and co-continuous structure in PMMA/ASA and PMMA/CPE blends: Correlation between impact property and phase morphology. Polym. Test. 2019, 73, 21–30. [Google Scholar] [CrossRef]
- Li, Z.-M.; Yang, W.; Yang, S.; Huang, R.; Yang, M.-B. Morphology-tensile behavior relationship in injection molded poly(ethylene terephthalate)/polyethylene and polycarbonate/polyethylene blends (I). J. Mater. Sci. 2004, 39, 413–431. [Google Scholar] [CrossRef]
- Friedrich, K.; Evstatiev, M.; Fakirov, S.; Evstatiev, O.; Ishii, M.; Harrass, M. Microfibrillar reinforced composites from PET/PP blends: Processing, morphology and mechanical properties. Compos. Sci. Technol. 2005, 65, 107–116. [Google Scholar] [CrossRef]
- Sajjadi, S.A.; Ghasemi, F.A.; Rajaee, P.; Fasihi, M. Evaluation of fracture properties of 3D printed high impact polystyrene according to essential work of fracture: Effect of raster angle. Addit. Manuf. 2022, 59, 103191. [Google Scholar] [CrossRef]
- Haile, L. Study of Recycling of Waste High Impact Polystyrene (PS-HI) and Polystyrene with Flame Retardant Additives (PS-FR) Co-Polymers. J. Text. Sci. Fash. Technol. 2021, 7, 1–11. [Google Scholar] [CrossRef]
- Nishino, K.; Shindo, Y.; Takayama, T.; Ito, H. Improvement of impact strength and hydrolytic stability of PC/ABS blend using reactive polymer. J. Appl. Polym. Sci. 2017, 134, 44550. [Google Scholar] [CrossRef]
- Kannan, S.; Ramamoorthy, M. Mechanical characterization and experimental modal analysis of 3D Printed ABS, PC and PC-ABS materials. Mater. Res. Express 2020, 7, 015341. [Google Scholar] [CrossRef]
- Krache, R.; Debbah, I. Some Mechanical and Thermal Properties of PC/ABS Blends. Mater. Sci. Appl. 2011, 2, 404–410. [Google Scholar] [CrossRef]
- Tan, Z.Y.; Xu, X.F.; Sun, S.L.; Zhou, C.; Ao, Y.H.; Zhang, H.X.; Han, Y. Influence of rubber content in ABS in wide range on the mechanical properties and morphology of PC/ABS blends with different composition. Polym. Eng. Sci. 2006, 46, 1476–1484. [Google Scholar] [CrossRef]
- Macosko, C.W. Morphology development and control in immiscible polymer blends. Macromol. Symp. 2000, 149, 171–184. [Google Scholar] [CrossRef]
- Li, S.; Tian, H.; Hu, G.-H.; Ning, N.; Tian, M.; Zhang, L. Effects of shear during injection molding on the anisotropic microstructure and properties of EPDM/PP TPV containing rubber nanoparticle agglomerates. Polymer 2021, 229, 124008. [Google Scholar] [CrossRef]
- Hammani, S.; Moulai-Mostefa, N.; Samyn, P.; Bechelany, M.; Dufresne, A.; Barhoum, A. Morphology, Rheology and Crystallization in Relation to the Viscosity Ratio of Polystyrene/Polypropylene Polymer Blends. Materials 2020, 13, 926. [Google Scholar] [CrossRef]
- Guevara-Morales, A.; Figueroa-López, U. Residual stresses in injection molded products. J. Mater. Sci. 2014, 49, 4399–4415. [Google Scholar] [CrossRef]
- Sargent, P.M.; Page, T.F. Factors affecting the measurement of hardness and hardness anisotropy. J. Mater. Sci. 1985, 20, 2388–2398. [Google Scholar] [CrossRef]
- Jiang, Q.; Takayama, T. Relationship between interfacial shear strength and impact strength of injection molded short glass fiber-reinforced thermoplastics. Procedia Struct. Integr. 2023, 45, 117–124. [Google Scholar] [CrossRef]
- Takayama, T.; Shibazaki, R. Evaluating Mechanical Anisotropy of Injection Molded Polymer Products using Short Beam Shear Testing. Results Mater. 2023, 19, 100434. [Google Scholar] [CrossRef]
- Fukunaga, S. Propylene-Based Resin Composition, Propylene-Based Resin Mixture and Molded Body. JP2015193695A, 5 November 2015. [Google Scholar]
- Kim, Y.; Park, O.O. Effect of Fiber Length on Mechanical Properties of Injection Molded Long-Fiber-Reinforced Thermoplastics. Macromol. Res. 2020, 28, 433–444. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, M.; Zheng, S.; Xie, Y.; Jin, Z. Effect of process parameters on the mechanical properties of fiber-reinforced thermoplastics fabricated by direct fiber feeding injection molding. Polym. Eng. Sci. 2023, 63, 2457–2467. [Google Scholar] [CrossRef]
- Cathelin, J. Through-Process Modelling for Accurate Prediction of Long Term Anisotropic Mechanics in Fibre Reinforced Thermoplastics. MATEC Web Conf. 2018, 165, 17002. [Google Scholar] [CrossRef]
- Takayama, T.; Motoyama, Y. Injection molding temperature dependence of elastic coefficients obtained using three-point bending tests to ascertain thermoplastic polymer coefficients. Mech. Eng. J. 2021, 8, 20–00414. [Google Scholar] [CrossRef]
- Gray, R.W.; McCrum, N.G. Origin of the γ relaxations in polyethylene and polytetrafluoroethylene. J. Polym. Sci. Part A-2 Polym. Phys. 1969, 7, 1329–1355. [Google Scholar] [CrossRef]
- Spreeman, M.E.; Stretz, H.A.; Dadmun, M.D. Role of compatibilizer in 3D printing of polymer blends. Addit. Manuf. 2019, 27, 267–277. [Google Scholar] [CrossRef]









| Material | Code | Manufacturer | Name | MFR (g/10 min) |
|---|---|---|---|---|
| PP | H-PP | Japan Polypropylene Corp., Tokyo, Japan | Novatec-PP MA1B | 21@230 °C, 2.160 kgf |
| B-PP | Japan Polypropylene Corp., Tokyo, Japan | Novatec-PP BC03B | 30@230 °C, 2.160 kgf | |
| PS | PS | Toyo Styrene Co., Ltd., Tokyo, Japan | Toyo styrene G210C | 10@230 °C, 2.160 kgf |
| SEBS | L-SEBS | Asahi Kasei Corp., Tokyo, Japan | Tuftec H1052 | 13@230 °C, 2.160 kgf |
| H-SEBS | Asahi Kasei Corp., Tokyo, Japan | Tuftec H1043 | 2@230 °C, 2.160 kgf |
| H-PP (vol.%) | B-PP (vol.%) | PS (vol.%) | L-SEBS (vol.%) | H-SEBS (vol.%) |
|---|---|---|---|---|
| 100.0 | ||||
| 77.0 | 23.0 | |||
| 69.2 | 25.2 | 4.0 | 1.6 | |
| 33.3 | 66.7 | |||
| 31.4 | 63.4 | 1.7 | 3.5 | |
| 100.0 | ||||
| 100.0 | ||||
| 77.0 | 23.0 | |||
| 69.2 | 25.2 | 4.0 | 1.6 | |
| 33.3 | 66.7 | |||
| 31.4 | 63.4 | 1.7 | 3.5 | |
| 100.0 |
| H-PP (vol.%) | B-PP (vol.%) | PS (vol.%) | L-SEBS (vol.%) | H-SEBS (vol.%) | Tinj (°C) | Tmold (°C) | Vinj (mm/s) | Phold (MPa) | Tinj (s) | Tcool (s) |
|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 230 | 50 | 30 | 46 | 10 | 15 | ||||
| 77.0 | 23.0 | 230 | 50 | 30 | 46 | 10 | 15 | |||
| 69.2 | 25.2 | 4.0 | 1.6 | 230 | 50 | 30 | 49 | 10 | 15 | |
| 33.3 | 66.7 | 230 | 50 | 30 | 56 | 10 | 15 | |||
| 31.4 | 63.4 | 1.7 | 3.5 | 230 | 50 | 30 | 56 | 10 | 15 | |
| 100.0 | 230 | 50 | 30 | 46 | 10 | 15 | ||||
| 100.0 | 225 | 50 | 30 | 46 | 10 | 15 | ||||
| 77.0 | 23.0 | 230 | 50 | 30 | 46 | 10 | 15 | |||
| 69.2 | 25.2 | 4.0 | 1.6 | 230 | 50 | 30 | 49 | 10 | 15 | |
| 33.3 | 66.7 | 230 | 50 | 30 | 56 | 10 | 15 | |||
| 31.4 | 63.4 | 1.7 | 3.5 | 230 | 50 | 30 | 56 | 10 | 15 | |
| 100.0 | 230 | 50 | 30 | 46 | 10 | 15 |
| (a) Mechanical Anisotropy Factor | ||||||||||
| H-PP (vol.%) | B-PP (vol.%) | PS (vol.%) | L-SEBS (vol.%) | H-SEBS (vol.%) | τs (MPa) | τm (MPa) | τl (MPa) | As (-) | Am (-) | Al (-) |
| 100 | 4.2 | 6.1 | 8.1 | 0.25 | 0.31 | 0.48 | ||||
| 77.0 | 23.0 | 5.5 | 7.0 | 8.3 | 0.16 | 0.21 | 0.34 | |||
| 69.2 | 25.2 | 4.0 | 1.6 | 5.2 | 6.7 | 7.7 | 0.13 | 0.22 | 0.32 | |
| 100 | 4.5 | 5.6 | 6.6 | 0.15 | 0.20 | 0.32 | ||||
| 77.0 | 23.0 | 5.2 | 6.6 | 7.9 | 0.16 | 0.21 | 0.34 | |||
| 69.2 | 25.2 | 1.7 | 3.5 | 4.4 | 5.4 | 6.5 | 0.17 | 0.19 | 0.32 | |
| 100.0 | 13.1 | 16.2 | 18.8 | 0.14 | 0.19 | 0.30 | ||||
| (b) Stress concentration factor and aspect ratio | ||||||||||
| H-PP (vol.%) | B-PP (vol.%) | PS (vol.%) | L-SEBS (vol.%) | H-SEBS (vol.%) | γs (-) | γm (-) | γl (-) | A.R. (-) | ||
| 100 | 1.51 | 1.04 | 0.78 | - | ||||||
| 77.0 | 23.0 | 1.28 | 1.00 | 0.85 | 1.2 | |||||
| 69.2 | 25.2 | 4.0 | 1.6 | 1.27 | 0.99 | 0.86 | 1.3 | |||
| 100 | 1.25 | 1.01 | 0.85 | - | ||||||
| 77.0 | 23.0 | 1.28 | 1.01 | 0.84 | 1.3 | |||||
| 69.2 | 25.2 | 4.0 | 1.6 | 1.25 | 1.02 | 0.85 | 1.2 | |||
| 100.0 | 1.24 | 1.00 | 0.86 | - | ||||||
| (a) Mechanical Anisotropy Factor | ||||||||||
| H-PP (vol.%) | B-PP (vol.%) | PS (vol.%) | L-SEBS (vol.%) | H-SEBS (vol.%) | τs (MPa) | τm (MPa) | τl (MPa) | As (-) | Am (-) | Al (-) |
| 100.0 | 4.5 | 5.6 | 6.6 | 0.15 | 0.20 | 0.32 | ||||
| 33.3 | 66.7 | 5.2 | 7.6 | 8.9 | 0.15 | 0.32 | 0.42 | |||
| 31.4 | 63.4 | 1.7 | 3.5 | 6.4 | 9.3 | 11.9 | 0.22 | 0.31 | 0.46 | |
| 100.0 | 4.5 | 5.6 | 6.6 | 0.15 | 0.20 | 0.32 | ||||
| 33.3 | 66.7 | 4.8 | 7.0 | 8.0 | 0.13 | 0.31 | 0.40 | |||
| 31.4 | 63.4 | 1.7 | 3.5 | 5.6 | 8.2 | 10.5 | 0.22 | 0.32 | 0.47 | |
| 100.0 | 13.1 | 16.2 | 18.8 | 0.14 | 0.19 | 0.30 | ||||
| (b) Stress concentration factor and aspect ratio | ||||||||||
| H-PP (vol.%) | B-PP (vol.%) | PS (vol.%) | L-SEBS (vol.%) | H-SEBS (vol.%) | γs (-) | γm (-) | γl (-) | A.R. (-) | ||
| 100.0 | 1.25 | 1.01 | 0.85 | - | ||||||
| 33.3 | 66.7 | 1.42 | 0.97 | 0.83 | 2.5 | |||||
| 31.4 | 63.4 | 1.7 | 3.5 | 1.48 | 1.02 | 0.80 | 6.7 | |||
| 100.0 | 1.25 | 1.01 | 0.85 | - | ||||||
| 33.3 | 66.7 | 1.40 | 0.96 | 0.84 | 2.3 | |||||
| 31.4 | 63.4 | 1.7 | 3.5 | 1.49 | 1.02 | 0.79 | ∞ | |||
| 100.0 | 1.24 | 1.00 | 0.86 | - | ||||||
| H-PP (vol.%) | B-PP (vol.%) | PS (vol.%) | L-SEBS (vol.%) | H-SEBS (vol.%) | τs (MPa) | γs (-) | σy,MD (MPa) | σfy,exp (MPa) | υ (-) | σy,exp (MPa) |
|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 4.2 | 1.51 | 19.0 | 28.0 | 0.407 | 19.9 | ||||
| 77.0 | 23.0 | 5.5 | 1.28 | 21.1 | 25.5 | 0.392 | 18.3 | |||
| 69.2 | 25.2 | 4.0 | 1.6 | 5.2 | 1.27 | 19.8 | 23.6 | 0.393 | 16.9 | |
| 33.3 | 66.7 | 5.2 | 1.42 | 22.2 | 31.5 | 0.363 | 23.1 | |||
| 31.4 | 63.4 | 1.7 | 3.5 | 6.4 | 1.48 | 28.4 | 38.0 | 0.366 | 27.8 | |
| 100.0 | 4.5 | 1.25 | 16.9 | 24.1 | 0.413 | 17.1 | ||||
| 77.0 | 23.0 | 5.2 | 1.28 | 20.0 | 22.2 | 0.398 | 15.9 | |||
| 69.2 | 25.2 | 4.0 | 1.6 | 4.4 | 1.25 | 16.5 | 19.9 | 0.398 | 14.3 | |
| 33.3 | 66.7 | 4.8 | 1.40 | 20.2 | 28.0 | 0.366 | 20.5 | |||
| 31.4 | 63.4 | 1.7 | 3.5 | 5.6 | 1.49 | 25.0 | 32.2 | 0.368 | 23.5 | |
| 100.0 | 13.1 | 1.24 | 48.6 | 65.5 | 0.342 | 48.8 |
| H-PP (vol.%) | B-PP (vol.%) | PS (vol.%) | L-SEBS (vol.%) | H-SEBS (vol.%) | σy,MD (MPa) | σy,exp (MPa) | YCMD |
|---|---|---|---|---|---|---|---|
| 77.0 | 23.0 | 21.1 | 18.3 | Debonding | |||
| 69.2 | 25.2 | 4.0 | 1.6 | 19.8 | 16.9 | Debonding | |
| 33.3 | 66.7 | 22.2 | 23.1 | Shear yield | |||
| 31.4 | 63.4 | 1.7 | 3.5 | 28.4 | 27.8 | Shear yield | |
| 77.0 | 23.0 | 20.0 | 15.9 | Debonding | |||
| 69.2 | 25.2 | 4.0 | 1.6 | 16.5 | 14.3 | Debonding | |
| 33.3 | 66.7 | 20.2 | 20.5 | Shear yield | |||
| 31.4 | 63.4 | 1.7 | 3.5 | 25.0 | 23.5 | Shear yield |
| FS (MPa) | FM (MPa) | α (10−5/K) | υ (-) | E (MPa) | K (MPa) | ρ (g/cm3) | |
|---|---|---|---|---|---|---|---|
| H-PP | 42.1 | 1728 | 9 | 0.407 | 767 | 1374 | 0.9 |
| B-PP | 36.3 | 1469 | 10 | 0.412 | 623 | 1181 | 0.9 |
| PS | 98.2 | 3237 | 7 | 0.342 | 2100 | 2215 | 1.04 |
| L-SEBS | 1.6 | 40 | 61 | 0.481 | 4 | 38 | 0.89 |
| H-SEBS | 46 | 1200 | 11 | 0.367 | 693 | 868 | 0.97 |
| H-PP (vol.%) | B-PP (vol.%) | PS (vol.%) | L-SEBS (vol.%) | H-SEBS (vol.%) | YCMD | σy,exp (MPa) | K (MPa) | σd (MPa) | σi (MPa) |
|---|---|---|---|---|---|---|---|---|---|
| 77.0 | 23.0 | Debonding | 18.3 | 1567 | 163.8 | −48.5 | |||
| 69.2 | 25.2 | 4.0 | 1.6 | Debonding | 16.9 | 1524 | 198.9 | −60.6 | |
| 77.0 | 23.0 | Debonding | 15.9 | 1419 | 164.3 | −49.5 | |||
| 69.2 | 25.2 | 4.0 | 1.6 | Debonding | 14.3 | 1375 | 193.4 | −59.7 |
| H-PP (vol.%) | B-PP (vol.%) | PS (vol.%) | L-SEBS (vol.%) | H-SEBS (vol.%) | σy,MD (MPa) | σy,p or σy,s (MPa) | σi (MPa) | Structure |
|---|---|---|---|---|---|---|---|---|
| 77.0 | 23.0 | 21.1 | 23.6 | −48.5 | Sea-island | |||
| 69.2 | 25.2 | 4.0 | 1.6 | 19.8 | 21.0 | −60.6 | Sea-island | |
| 33.3 | 66.7 | 22.2 | 36.4 | −9.5 | Elongated Disc | |||
| 31.4 | 63.4 | 1.7 | 3.5 | 28.4 | 38.0 | −7.3 | Cylinder | |
| 77.0 | 23.0 | 20.0 | 21.4 | −49.5 | Sea-island | |||
| 69.2 | 25.2 | 4.0 | 1.6 | 16.5 | 19.2 | −59.7 | Sea-island | |
| 33.3 | 66.7 | 20.2 | 34.5 | −10.0 | Elongated Disc | |||
| 31.4 | 63.4 | 1.7 | 3.5 | 25.0 | 36.1 | −9.0 | 2D network |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takayama, T.; Shibazaki, R. Mechanical Anisotropy of Injection-Molded PP/PS Polymer Blends and Correlation with Morphology. Polymers 2023, 15, 4167. https://doi.org/10.3390/polym15204167
Takayama T, Shibazaki R. Mechanical Anisotropy of Injection-Molded PP/PS Polymer Blends and Correlation with Morphology. Polymers. 2023; 15(20):4167. https://doi.org/10.3390/polym15204167
Chicago/Turabian StyleTakayama, Tetsuo, and Rin Shibazaki. 2023. "Mechanical Anisotropy of Injection-Molded PP/PS Polymer Blends and Correlation with Morphology" Polymers 15, no. 20: 4167. https://doi.org/10.3390/polym15204167
APA StyleTakayama, T., & Shibazaki, R. (2023). Mechanical Anisotropy of Injection-Molded PP/PS Polymer Blends and Correlation with Morphology. Polymers, 15(20), 4167. https://doi.org/10.3390/polym15204167