Artificial Neural Networks for Predicting Mechanical Properties of Crystalline Polyamide12 via Molecular Dynamics Simulations
Abstract
:1. Introduction
2. Molecular Dynamics Simulations
2.1. System Setup
2.2. Force Field Selection
2.3. Simulation Details and Preliminary Analysis
3. Artificial Neural Network for Constitutive Law
3.1. Data Collection and Processing
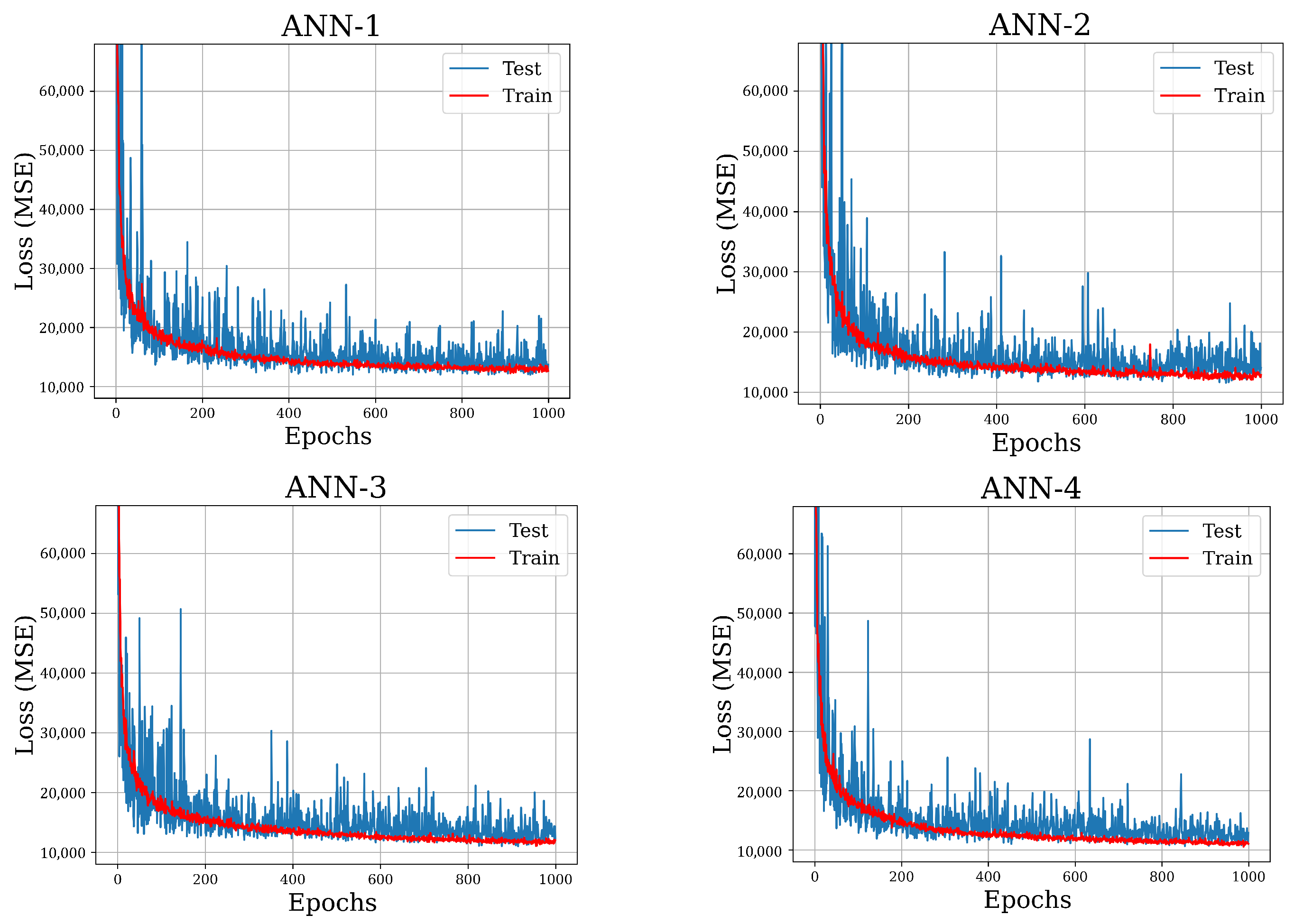
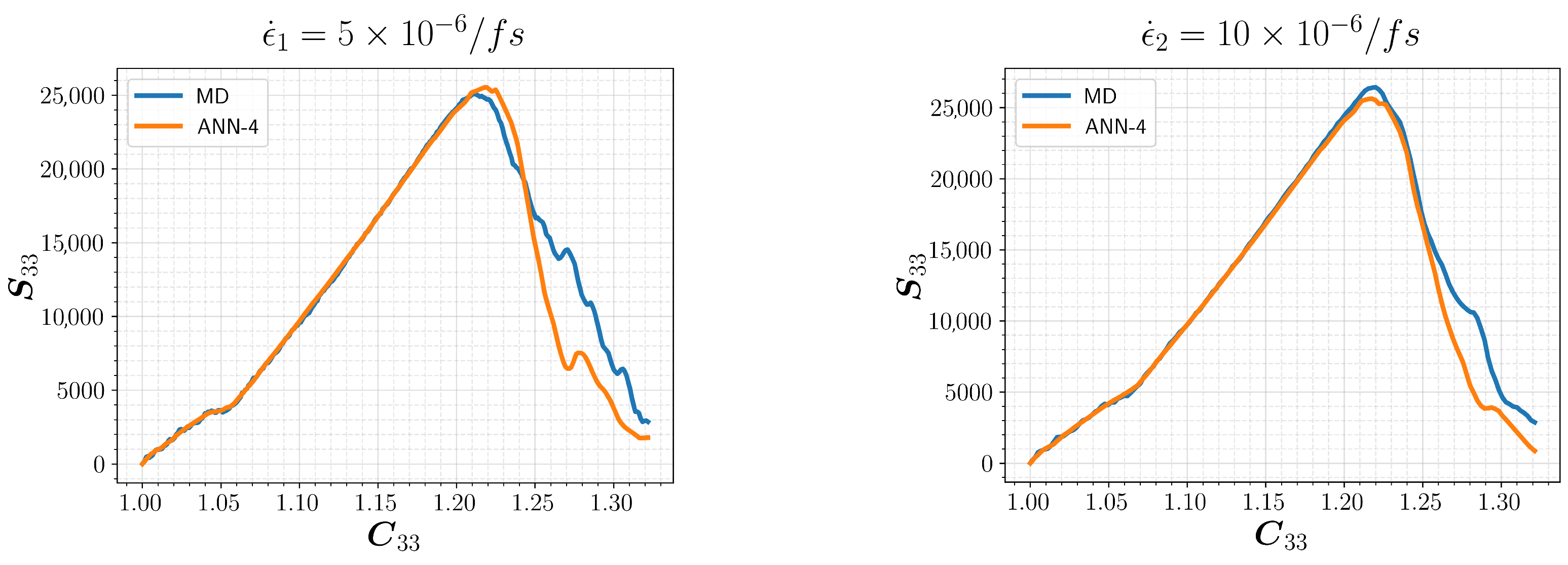
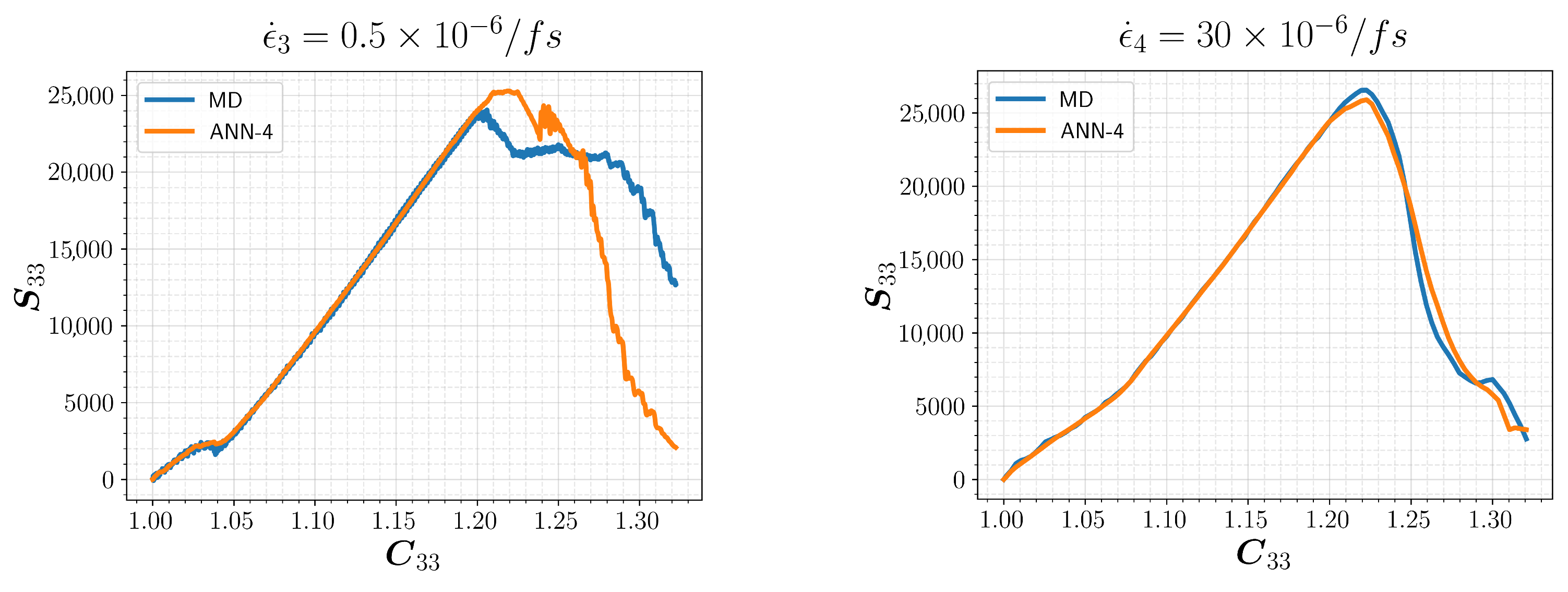
3.2. Model Selection and Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- López Barreiro, D.; Yeo, J.; Tarakanova, A.; Martin-Martinez, F.; Buehler, M. Multiscale Modeling of Silk and Silk-Based Biomaterials A Review. Macromol. Biosci. 2019, 19, 1800253. [Google Scholar] [CrossRef]
- Sharafi, S.; Santare, M.; Gerdes, J.; Advani, S. A multiscale modeling approach of the Fused Filament Fabrication process to predict the mechanical response of 3D printed parts. Addit. Manuf. 2022, 51, 102597. [Google Scholar] [CrossRef]
- Jamshidian, M.; Boddeti, N.; Rosen, D.; Weeger, O. Multiscale modelling of soft lattice metamaterials: Micromechanical nonlinear buckling analysis, experimental verification, and macroscale constitutive behaviour. Int. J. Mech. Sci. 2020, 188, 105956. [Google Scholar] [CrossRef]
- Urata, S.; Li, S. Higher order Cauchy Born rule based multiscale cohesive zone model and prediction of fracture toughness of silicon thin films. Int. J. Fract. 2017, 203, 159–181. [Google Scholar] [CrossRef]
- Bishara, D.; Li, S. A machine-learning aided multiscale homogenization model for crystal plasticity: Application for face-centered cubic single crystals. Comput. Mech. 2023, 72, 77–93. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, K.; Zhang, H.; Tian, X.; Jiang, Q.; Murugadoss, V.; Hou, H. Dislocation motion in plastic deformation of nano polycrystalline metal materials: A phase field crystal method study. Adv. Compos. Hybrid Mater. 2022, 5, 2546–2556. [Google Scholar] [CrossRef]
- Saidi, W.A.; Shadid, W.; Castelli, I.E. Machine-learning structural and electronic properties of metal halide perovskites using a hierarchical convolutional neural network. Npj Comput. Mater. 2020, 6, 36. [Google Scholar] [CrossRef]
- Saidi, W.A. Emergence of local scaling relations in adsorption energies on high-entropy alloys. Npj Comput. Mater. 2022, 8, 86. [Google Scholar] [CrossRef]
- Wang, J.; Pan, Z.; Wang, Y.; Wang, L.; Su, L.; Cuiuri, D.; Zhao, Y.; Li, H. Evolution of crystallographic orientation, precipitation, phase transformation and mechanical properties realized by enhancing deposition current for dual-wire arc additive manufactured Ni-rich NiTi alloy. Addit. Manuf. 2020, 34, 101240. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, F.; Zhai, W.; Cheng, S.; Li, J.; Wang, Y. Unraveling of advances in 3D-printed polymer-based bone scaffolds. Polymers 2022, 14, 566. [Google Scholar] [CrossRef]
- Wang, Y.; Zhai, W.; Li, J.; Liu, H.; Li, C.; Li, J. Friction behavior of biodegradable electrospun polyester nanofibrous membranes. Tribol. Int. 2023, 188, 108891. [Google Scholar] [CrossRef]
- Khorshidi, H.; Zhang, C.; Najafi, E.; Ghasemi, M. Fresh, mechanical and microstructural properties of alkali-activated composites incorporating nanomaterials: A comprehensive review. J. Clean. Prod. 2022, 384, 135390. [Google Scholar]
- Cojazzi, G.; Fichera, A.; Garbuglio, C.; Malta, V.; Zannetti, R. The crystal structure of polylauryllactam (nylon 12). Die Makromol. Chemie Macromol. Chem. Phys. 1973, 168, 289–301. [Google Scholar] [CrossRef]
- Inoue, K.; Hoshino, S. Crystal structure of nylon 12. J. Polym. Sci. Polym. Phys. Ed. 1973, 11, 1077–1089. [Google Scholar] [CrossRef]
- Mathias, L.J.; Johnson, C.G. Solid-state NMR investigation of nylon 12. Macromolecules 1991, 24, 6114–6122. [Google Scholar] [CrossRef]
- Krishna, S.; Sreedhar, I.; Patel, C.M. Molecular dynamics simulation of polyamide-based materials–A review. Comput. Mater. Sci. 2021, 200, 110853. [Google Scholar] [CrossRef]
- Pinheiro, L.A.; Chinelatto, M.A.; Canevarolo, S.V. The role of chain scission and chain branching in high density polyethylene during thermo-mechanical degradation. Polym. Degrad. Stab. 2004, 86, 445–453. [Google Scholar] [CrossRef]
- Awaja, F.; Zhang, S.; Tripathi, M.; Nikiforov, A.; Pugno, N. Cracks, microcracks and fracture in polymer structures: Formation, detection, autonomic repair. Prog. Mater. Sci. 2016, 83, 536–573. [Google Scholar] [CrossRef]
- Van Duin, A.C.; Dasgupta, S.; Lorant, F.; Goddard, W.A. ReaxFF: A reactive force field for hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef]
- Chenoweth, K.; Van Duin, A.C.; Goddard, W.A. ReaxFF reactive force field for molecular dynamics simulations of hydrocarbon oxidation. J. Phys. Chem. A 2008, 112, 1040–1053. [Google Scholar] [CrossRef]
- Senftle, T.; Hong, S.; Islam, M.M.; Kylasa, S.B.; Zheng, Y.; Shin, Y.K.; Junkermeier, C.; Engel-Herbert, R.; Janik, M.J.; Aktulga, H.M.; et al. The ReaxFF reactive force-field: Development, applications and future directions. Npj Comput. Mater. 2016, 2, 1–14. [Google Scholar] [CrossRef]
- Yang, Q.; Li, W.; Stober, S.T.; Burns, A.B.; Gopinadhan, M.; Martini, A. Molecular Dynamics Simulation of the Stress–Strain Behavior of Polyamide Crystals. Macromolecules 2021, 54, 8289–8302. [Google Scholar] [CrossRef]
- Kowalik, M.; Ashraf, C.; Damirchi, B.; Akbarian, D.; Rajabpour, S.; Van Duin, A.C. Atomistic scale analysis of the carbonization process for C/H/O/N-based polymers with the ReaxFF reactive force field. J. Phys. Chem. B 2019, 123, 5357–5367. [Google Scholar] [CrossRef] [PubMed]
- Mattsson, T.R.; Lane, J.M.D.; Cochrane, K.R.; Desjarlais, M.P.; Thompson, A.P.; Pierce, F.; Grest, G.S. First-principles and classical molecular dynamics simulation of shocked polymers. Phys. Rev. B 2010, 81, 054103. [Google Scholar] [CrossRef]
- Zhang, W.; Van Duin, A.C. Improvement of the ReaxFF description for functionalized hydrocarbon/water weak interactions in the condensed phase. J. Phys. Chem. B 2018, 122, 4083–4092. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Evans, D.J.; Holian, B.L. The nose–hoover thermostat. J. Chem. Phys. 1985, 83, 4069–4074. [Google Scholar] [CrossRef]
- Yilmaz, D.E.; van Duin, A.C. Investigating structure property relations of poly (p-phenylene terephthalamide) fibers via reactive molecular dynamics simulations. Polymer 2018, 154, 172–181. [Google Scholar] [CrossRef]
- Subramaniyan, A.K.; Sun, C. Continuum interpretation of virial stress in molecular simulations. Int. J. Solids Struct. 2008, 45, 4340–4346. [Google Scholar] [CrossRef]
- As’ ad, F.; Avery, P.; Farhat, C. A mechanics-informed artificial neural network approach in data-driven constitutive modeling. Int. J. Numer. Methods Eng. 2022, 123, 2738–2759. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Orr, G.B.; Müller, K. Efficient backprop. In Neural networks: Tricks of the trade; Springer: Berlin/Heidelberg, Germany, 2002; pp. 9–50. [Google Scholar]
- Sola, J.; Sevilla, J. Importance of input data normalization for the application of neural networks to complex industrial problems. IEEE Trans. Nucl. Sci. 1997, 44, 1464–1468. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 15 April 2023).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: https://www.tensorflow.org/ (accessed on 15 April 2023).
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 2017, 18, 6765–6816. [Google Scholar]
- O’Malley, T.; Bursztein, E.; Long, J.; Chollet, F.; Jin, H.; Invernizzi, L. KerasTuner. 2019. Available online: https://github.com/keras-team/keras-tuner (accessed on 15 April 2023).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- LeNail, A. NN-SVG: Publication-Ready Neural Network Architecture Schematics. J. Open Source Softw. 2019, 4, 747. [Google Scholar] [CrossRef]


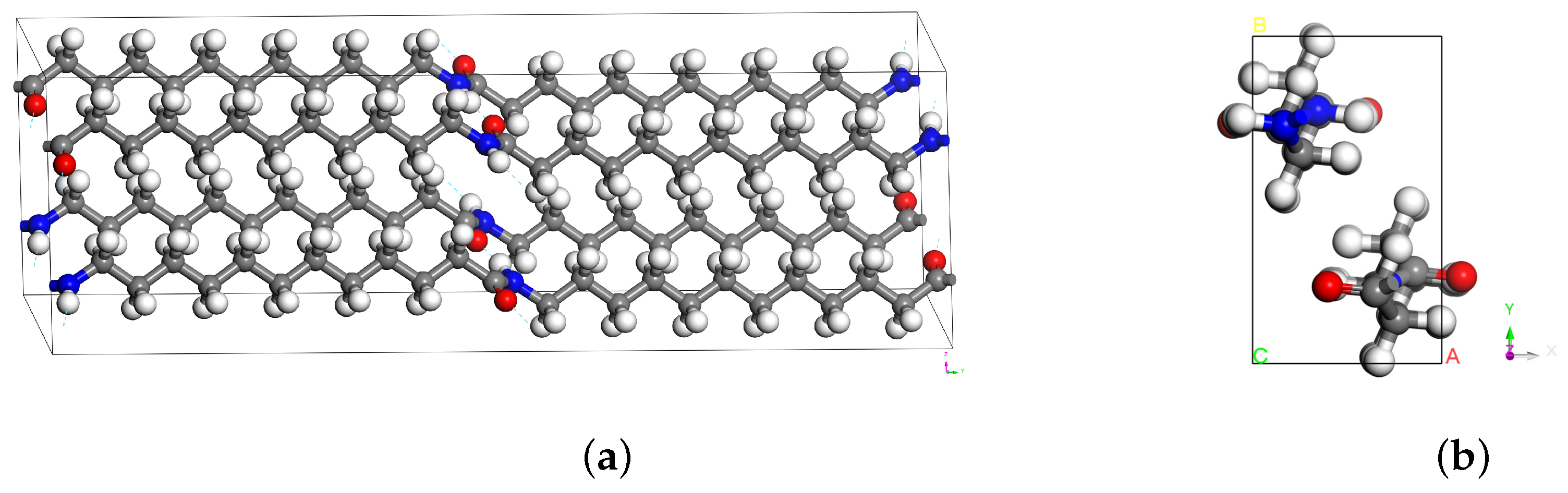




| Lattice Parameters | |
|---|---|
| a | 4.79 Å |
| b | 31.90 Å |
| c | 9.58 Å |
| 120 | |
| Space Group | P21/C |
| Deformation Direction | |||
|---|---|---|---|
| x | y | z | |
| Ultimate Strain | 0.5 | 0.6 | 0.15 |
| Strain Rate () | |||
| Hyperparameters | |||
|---|---|---|---|
| Hidden Layers | Neurons | Activation Function | Learning Rate |
| {ReLu, Softplus} | |||
| Hyperband (1) | Bayesian (2) | Hyperband (3) | Bayesian (4) | |
|---|---|---|---|---|
| Input Layer | 6 | 6 | 6 | 6 |
| Hidden Layer 1 | 192 × ReLu | 64 × ReLu | 160 × ReLu | 224 × ReLu |
| Hidden Layer 2 | 32 × Softplus | 32 × Softplus | 64 × Softplus | 96 × Softplus |
| Hidden Layer 3 | 32 × ReLu | 256 × Softplus | 32 × ReLu | 64 × ReLu |
| Hidden Layer 4 | 64 × ReLu | 32 × ReLu | 128 Softplus | 96 × Softplus |
| Hidden Layer 5 | 128 × ReLu | 64 × ReLu | - | - |
| Output Layer | 6 × Linear | 6 ×Linear | 6 × Linear | 6 ×Linear |
| Validation Loss | 15,630 | 15,026 | 14,109 | 13,538 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamur, C.; Li, S.; Zeng, D. Artificial Neural Networks for Predicting Mechanical Properties of Crystalline Polyamide12 via Molecular Dynamics Simulations. Polymers 2023, 15, 4254. https://doi.org/10.3390/polym15214254
Tamur C, Li S, Zeng D. Artificial Neural Networks for Predicting Mechanical Properties of Crystalline Polyamide12 via Molecular Dynamics Simulations. Polymers. 2023; 15(21):4254. https://doi.org/10.3390/polym15214254
Chicago/Turabian StyleTamur, Caglar, Shaofan Li, and Danielle Zeng. 2023. "Artificial Neural Networks for Predicting Mechanical Properties of Crystalline Polyamide12 via Molecular Dynamics Simulations" Polymers 15, no. 21: 4254. https://doi.org/10.3390/polym15214254
APA StyleTamur, C., Li, S., & Zeng, D. (2023). Artificial Neural Networks for Predicting Mechanical Properties of Crystalline Polyamide12 via Molecular Dynamics Simulations. Polymers, 15(21), 4254. https://doi.org/10.3390/polym15214254







