Numerical Study on the Damage of a Carbon Woven Composite Panel Subjected to Blast Loading
Abstract
:1. Introduction
2. Materials and Methods
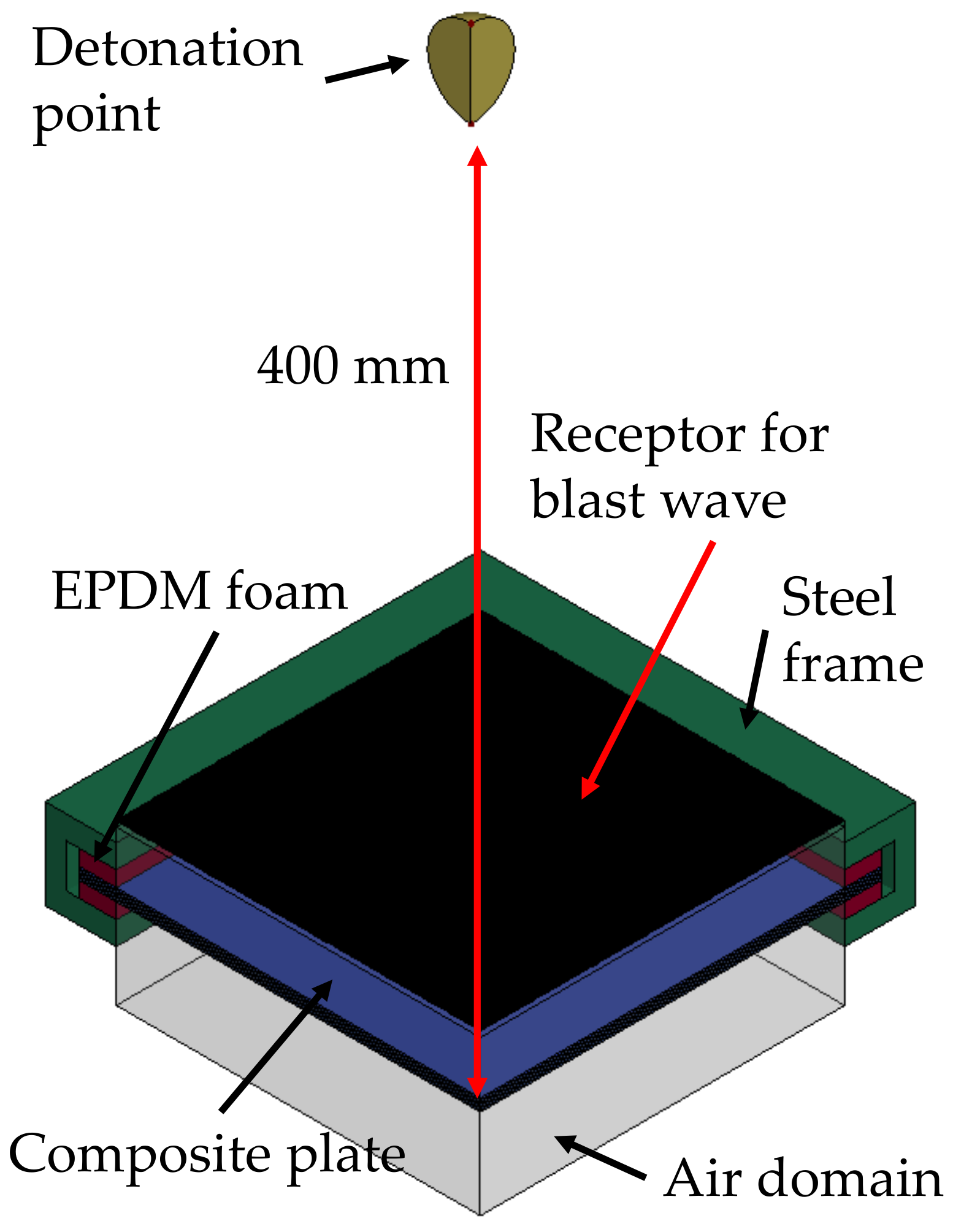
2.1. Validation Case Study
2.2. Uncoupled Approach
2.3. Coupled Eulerian–Lagrangian Approach
2.4. Structural Components
| Failure Mode | Criteria |
|---|---|
| Tensile failure | |
| Compressive failure | |
| Shear failure |
| Failure Mode | Criteria |
|---|---|
| Tension–shear fiber mode | |
| Compression fiber mode | |
| Crush mode | |
| In-plane matrix failure mode | |
| Parallel matrix failure mode |
3. Results
4. Discussion
5. Conclusions
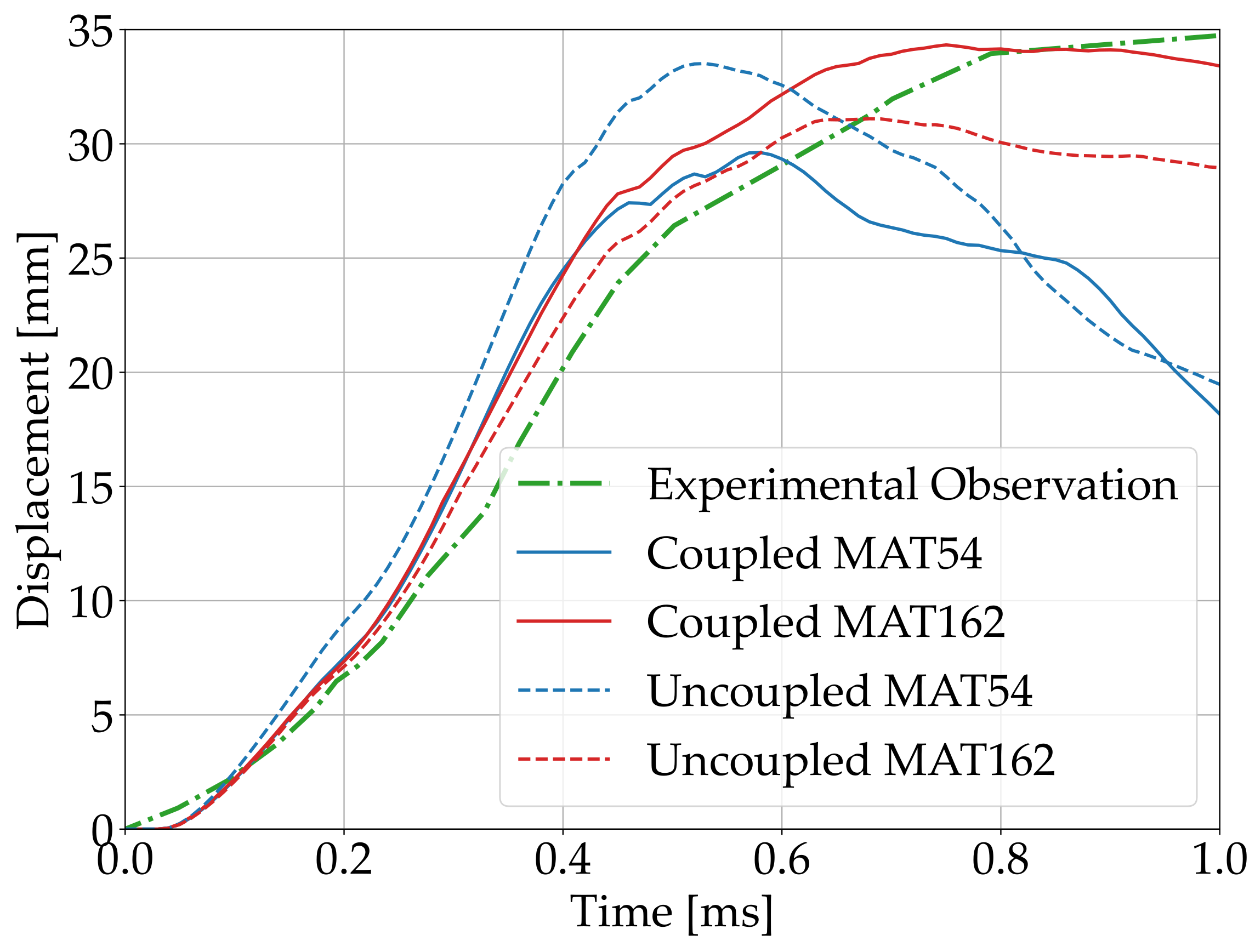
- The exerted pressure and the resulting maximum deflection predicted in the simulations adhered to the experimental observations.
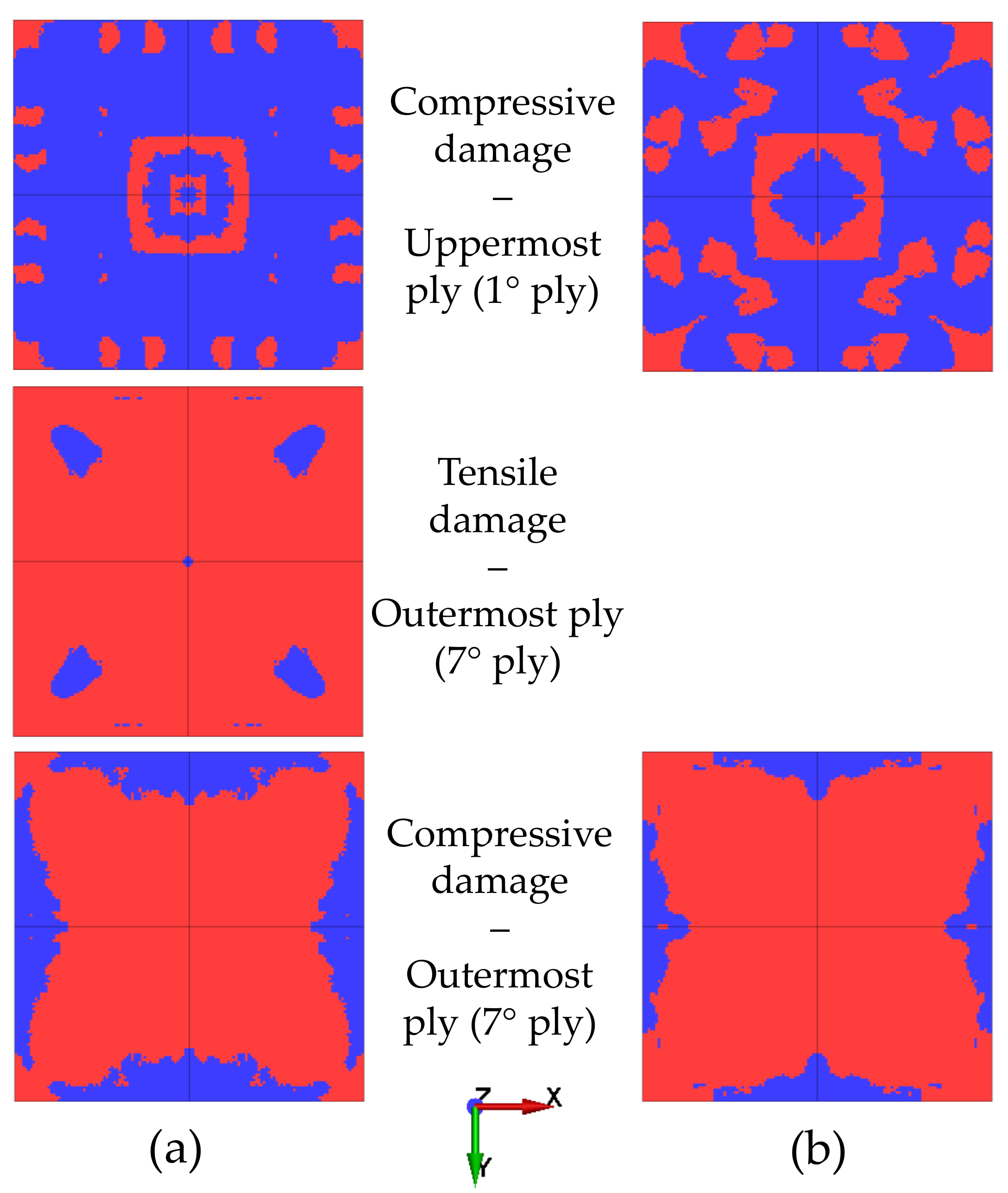
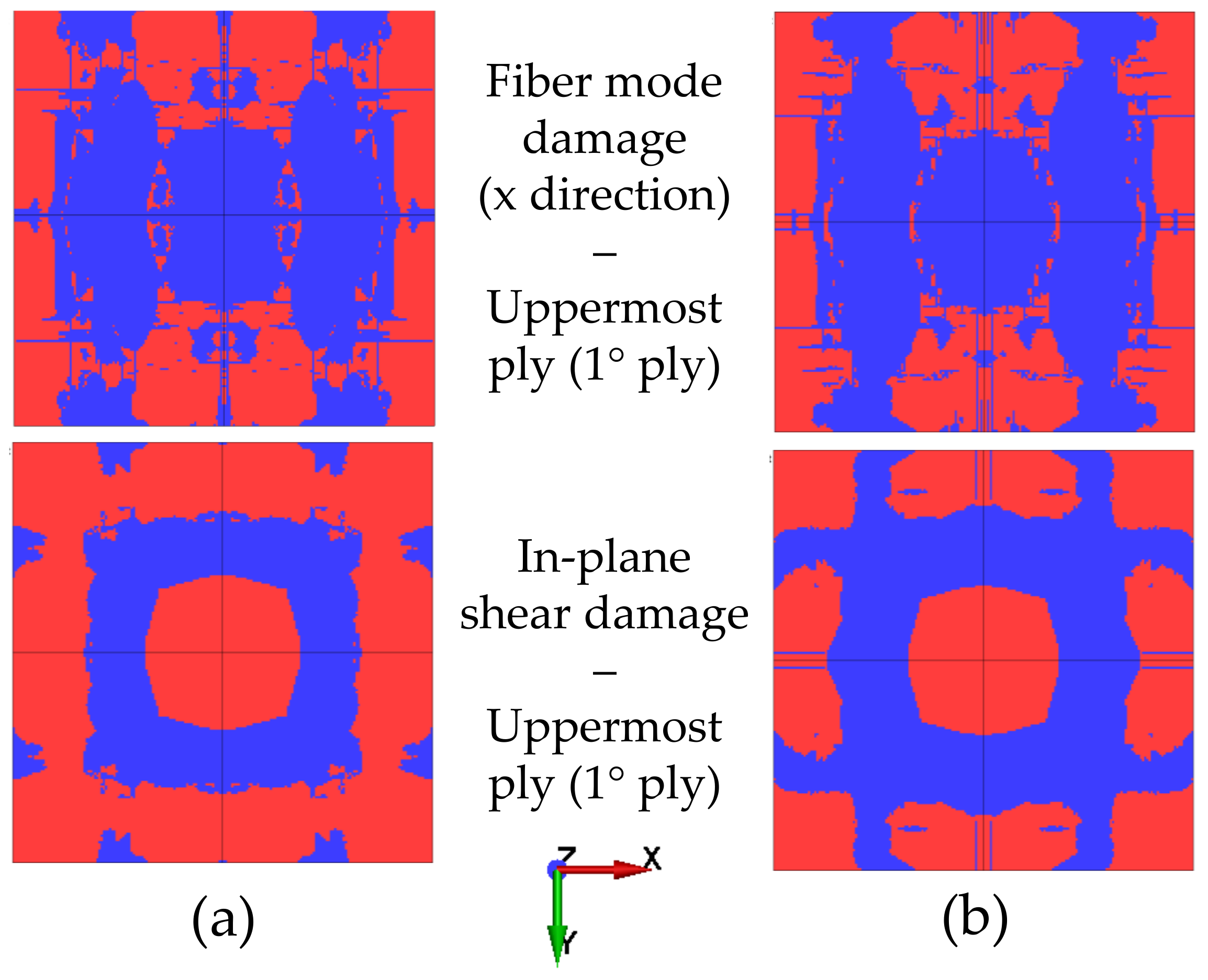
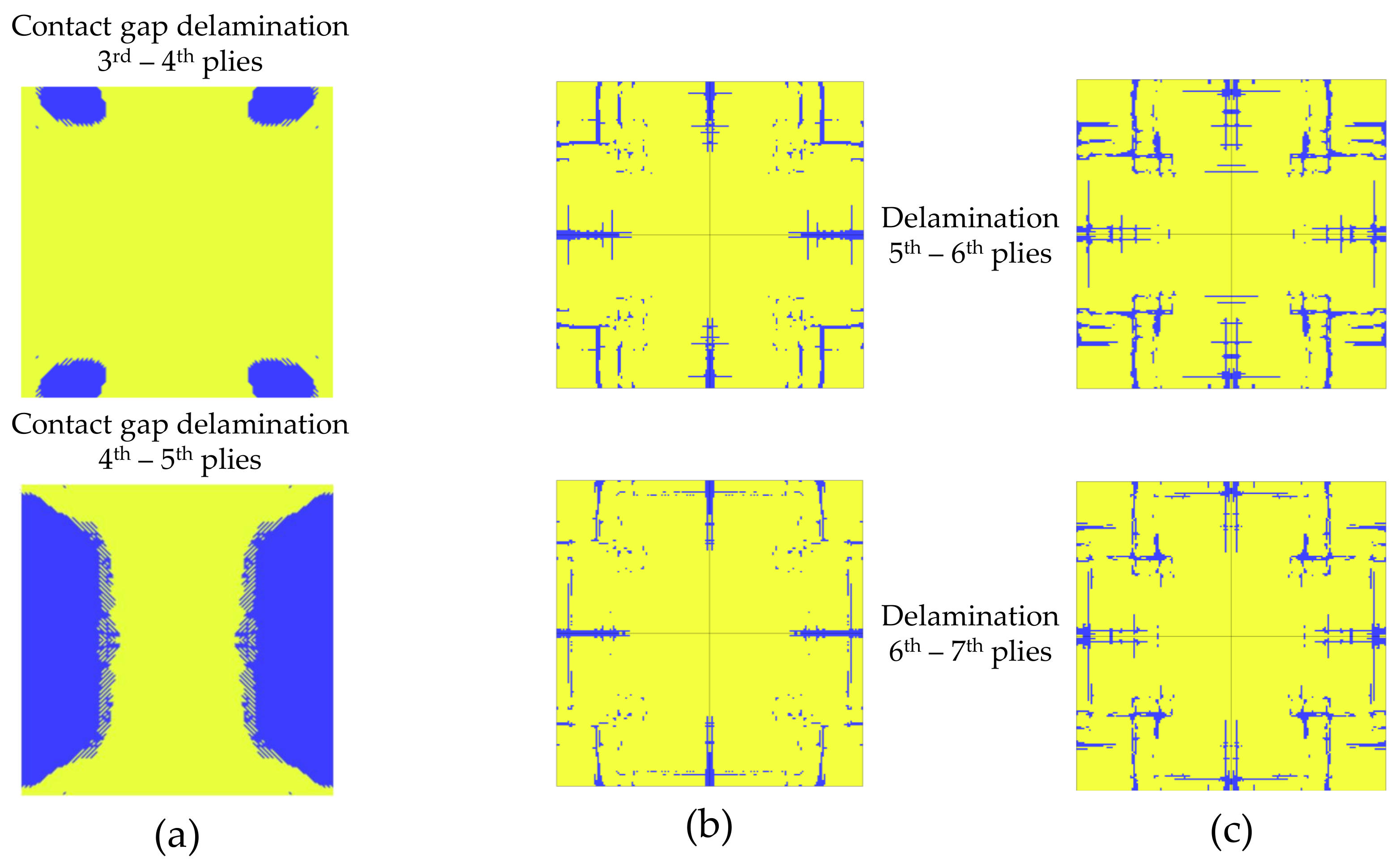
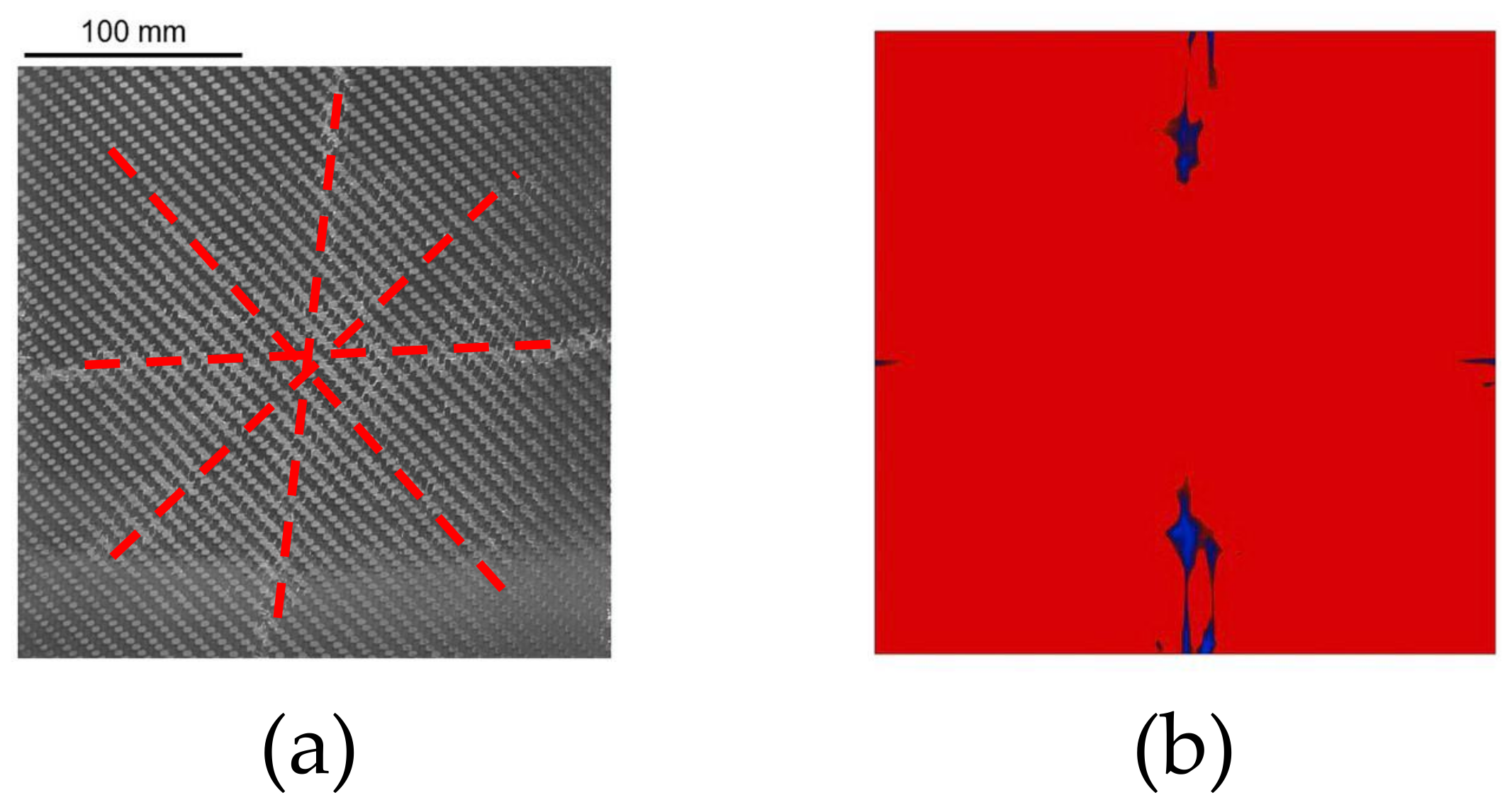
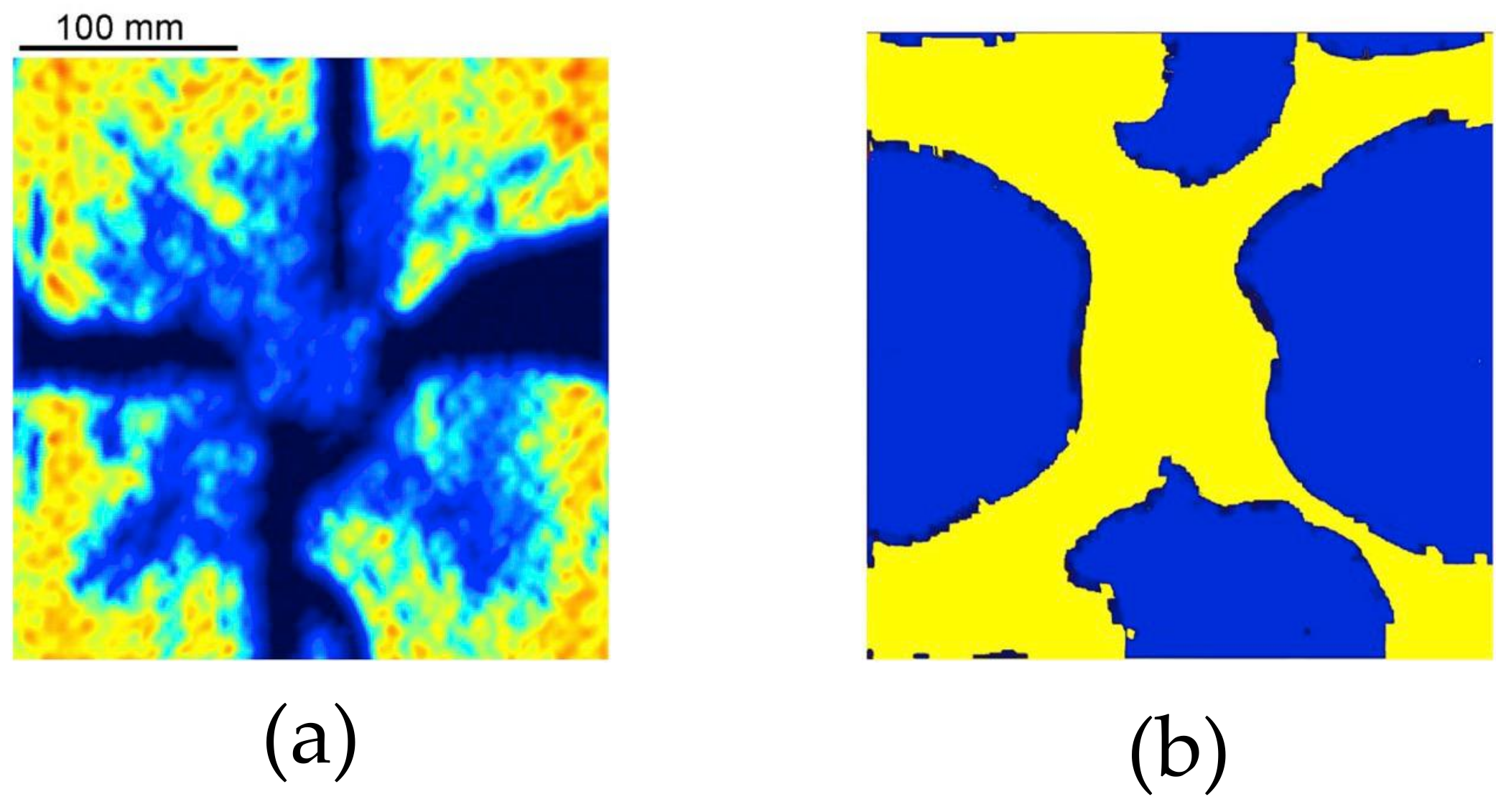
- The damage patterns identified in the simulations were comparable with the damage observed in the experiments.
- The analyses conducted with MAT_54 were found to be satisfactorily accurate, even though MAT_162 allowed for better matching with the experimental observations. However, MAT_54 is believed to provide the best tradeoff between ease of implementation and accuracy of the results. In fact, MAT_162 offers considerable freedom in calibrating the composite mechanical behavior, although a large number of parameters is required to calibrate damage initiation and propagation.
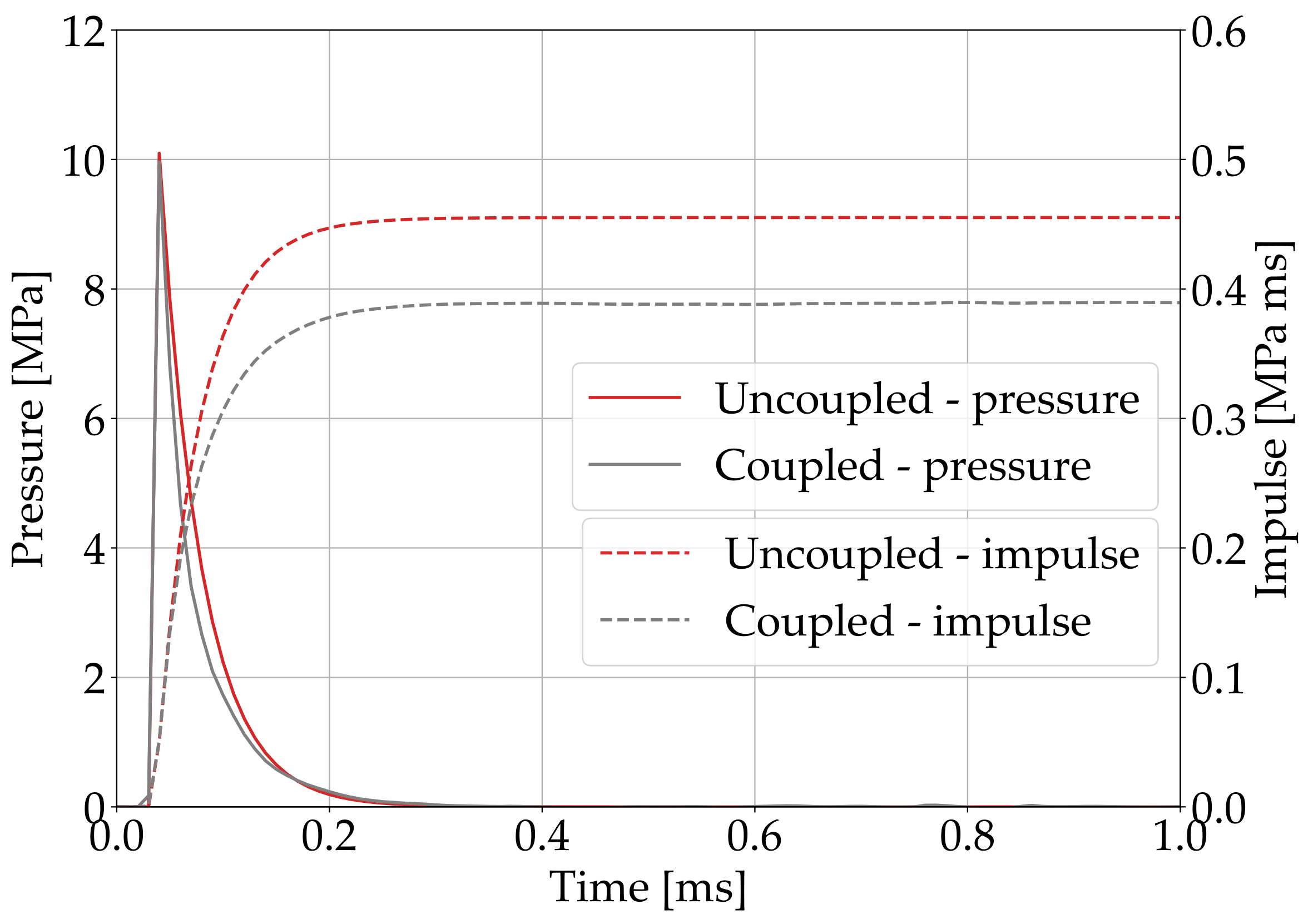
- Only the coupled method allows for comprehensive modeling of the blast event, also considering FSI, thermal effects and secondary blast effects, and can more accurately estimate the pressure load than uncoupled approaches. However, in most cases, the load predictions from uncoupled simulations are already sufficiently accurate, while the uncertainty associated with structural material parameters obscures the advantages that could be gained from utilizing more precise pressure loads.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FSI | Fluid–structure interaction |
| HE | High explosive |
| JWL | Jones–Wilkins–Lee |
| KB | Kingery–Bulmash |
| CEL | Coupled Eulerian–Lagrangian |
| TNT | Trinitrotoluene |
| VRI | Vacuum bag resin infusion |
References
- Muflikhun, M.A.; Yokozeki, T.; Aoki, T. The strain performance of thin CFRP-SPCC hybrid laminates for automobile structures. Compos. Struct. 2019, 220, 11–18. [Google Scholar] [CrossRef]
- Muflikhun, M.A.; Yokozeki, T. Systematic analysis of fractured specimens of composite laminates: Different perspectives between tensile, flexural, Mode I, and Mode II test. Int. J. Lightweight Mater. Manuf. 2023, 6, 329–343. [Google Scholar] [CrossRef]
- Nugraha, A.D.; Nuryanta, M.I.; Sean, L.; Budiman, K.; Kusni, M.; Muflikhun, M.A. Recent Progress on Natural Fibers Mixed with CFRP and GFRP: Properties, Characteristics, and Failure Behaviour. Polymers 2022, 14, 5138. [Google Scholar] [CrossRef] [PubMed]
- Langdon, G.S.; Cantwell, W.J.; Guan, Z.W.; Nurick, G.N. The response of polymeric composite structures to air-blast loading: A state-of-the-art. Int. Mater. Rev. 2014, 59, 159–177. [Google Scholar] [CrossRef]
- Mouritz, A. Advances in understanding the response of fibre-based polymer composites to shock waves and explosive blasts. Compos. Part Appl. Sci. Manuf. 2019, 125, 105502. [Google Scholar] [CrossRef]
- Comtois, J.; Edwards, M.; Oakes, M. The effect of explosives on polymer matrix composite laminates. Compos. Part A Appl. Sci. Manuf. 1999, 30, 181–190. [Google Scholar] [CrossRef]
- Gargano, A.; Das, R.; Mouritz, A. Finite element modelling of the explosive blast response of carbon fibre-polymer laminates. Compos. Part B Eng. 2019, 177, 107412. [Google Scholar] [CrossRef]
- Yahya, M.Y.; Cantwell, W.; Langdon, G.; Nurick, G. The blast resistance of a woven carbon fiber-reinforced epoxy composite. J. Compos. Mater. 2011, 45, 789–801. [Google Scholar] [CrossRef]
- LeBlanc, J.; Shukla, A. Dynamic response and damage evolution in composite materials subjected to underwater explosive loading: An experimental and computational study. Compos. Struct. 2010, 92, 2421–2430. [Google Scholar] [CrossRef]
- Gunaryo, K.; Heriana, H.; Sitompul, M.R.; Kuswoyo, A.; Hadi, B.K. Experimentation and numerical modeling on the response of woven glass/epoxy composite plate under blast impact loading. Int. J. Mech. Mater. Eng. 2020, 15, 4. [Google Scholar] [CrossRef]
- Aune, V.; Valsamos, G.; Casadei, F.; Langseth, M.; Børvik, T. Fluid-structure interaction effects during the dynamic response of clamped thin steel plates exposed to blast loading. Int. J. Mech. Sci. 2021, 195, 106263. [Google Scholar] [CrossRef]
- Lomazzi, L.; Morin, D.; Cadini, F.; Manes, A.; Aune, V. Deep learning-based analysis to identify fluid-structure interaction effects during the response of blast-loaded plates. Int. J. Prot. Struct. 2023. [Google Scholar] [CrossRef]
- Giuliano, D.; Lomazzi, L.; Giglio, M.; Manes, A. On Eulerian-Lagrangian methods to investigate the blast response of composite plates. Int. J. Impact Eng. 2023, 173, 104469. [Google Scholar] [CrossRef]
- Lomazzi, L.; Giglio, M.; Manes, A. Analysis of the blast wave—Structure interface phenomenon in case of explosive events. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1038, 012083. [Google Scholar] [CrossRef]
- Kingery, C.; Bulmash, G. Air Blast Parameters from TNT Spherical Air Burst and Hemispherical Surface Burst; Technical Report ARBRL; US Army Armament and Development Center, Ballistic Research Laboratory: Adelphi, MD, USA, 1984.
- Cranz, K.J.; von Eberhard, O.; Becker, K.E. Lehrbuch der Ballistik. Ergänzungen zum Band II; Springer: Berlin/Heidelberg, Germany, 1926. [Google Scholar]
- Hopkinson, B. British Ordnance Board Minutes, Report 13565; Technical Report; British Ordnance Office: London, UK, 1915. [Google Scholar]
- Shin, J.; Whittaker, A.S.; Cormie, D. Incident and Normally Reflected Overpressure and Impulse for Detonations of Spherical High Explosives in Free Air. J. Struct. Eng. 2015, 141, 04015057. [Google Scholar] [CrossRef]
- Randers-Pehrson, G.; Bannister, K.A. Airblast Loading Model for DYNA2D and DYNA3D; Technical Report; Army Research Laboratory: Adelphi, MD, USA, 1997. [Google Scholar]
- Bogosian, D.; Yokota, M.; Rigby, S. TNT equivalence of C-4 and PE4: A review of traditional sources and recent data. In Proceedings of the 24th Military Aspects of Blast and Shock, Halifax, NS, Canada, 19–23 September 2016. [Google Scholar]
- LSTC. LS-DYNA Keyword User’s Manual II; LSTC: Livermore, CA, USA, 2018. [Google Scholar]
- Maio, L.; Monaco, E.; Ricci, F.; Lecce, L. Simulation of low velocity impact on composite laminates with progressive failure analysis. Compos. Struct. 2013, 103, 75–85. [Google Scholar] [CrossRef]
- LSTC. LS-DYNA Keyword User’s Manual I; LSTC: Livermore, CA, USA, 2018. [Google Scholar]
- Hashin, Z. Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Dugdale, D. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Barenblatt, G. The Mathematical Theory of Equilibrium Cracks in Brittle Fracture. Adv. Appl. Mech. 1962, 7, 55–129. [Google Scholar] [CrossRef]
- Gama, B.A.; Gillespie, J.W. Finite element modeling of impact, damage evolution and penetration of thick-section composites. Int. J. Impact Eng. 2011, 38, 181–197. [Google Scholar] [CrossRef]
- Sridharan, S.; Pankow, M. Performance evaluation of two progressive damage models for composite laminates under various speed impact loading. Int. J. Impact Eng. 2020, 143, 103615. [Google Scholar] [CrossRef]
- Vescovini, A.; Balen, L.; Scazzosi, R.; da Silva, A.; Amico, S.; Giglio, M.; Manes, A. Numerical investigation on the hybridization effect in inter-ply S2-glass and aramid woven composites subjected to ballistic impacts. Compos. Struct. 2021, 276, 114506. [Google Scholar] [CrossRef]
- Tehrani, M.; Boroujeni, A.Y.; Al-Haik, M. Modeling and simulation of impact and perforation in fiber reinforced composites. In Proceedings of the 29th Annual American Society for Composites Technical Conference, San Diego, CA, USA, 8–10 September 2014. [Google Scholar]
- Haque, B.Z.G. A Progressive Composite Damage Model for Unidirectional and Woven Fabric Composites; Technical Report; Materials Sciences Corporation & University of Delaware Center for Composite Materials: Newark, DE, USA, 2014. [Google Scholar]
- Lee, S.; Byun, J.; Cho, H. Progressive damage structural analysis of carbon/epoxy composite laminates. In Proceedings of the 18th International Conference of Composite Materials, Jeju Island, Republic of Korea, 21–26 August 2011. [Google Scholar]
- Matzenmiller, A.; Lubliner, J.; Taylor, R. A constitutive model for anisotropic damage in fiber-composites. Mech. Mater. 1995, 20, 125–152. [Google Scholar] [CrossRef]
- Lomazzi, L.; Vescovini, A. Numerical study on the influence of boundary conditions on the blast response of composite plates. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1214, 012005. [Google Scholar] [CrossRef]
- Zhang, T.G.; Satapathy, S.S.; Dagro, A.M.; McKee, P.J. Numerical Study of Head/Helmet Interaction due to Blast Loading. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, San Diego, CA, USA, 15–21 November 2013; Volume 3A: Biomedical and Biotechnology Engineering. [Google Scholar] [CrossRef]


| Material Property | LS-DYNA Symbol | Value |
|---|---|---|
| Density | RO | 1600 |
| In-plane longitudinal Young’s modulus | EA | 55 GPa |
| In-plane transversal Young’s modulus | EB | 55 GPa |
| Out-of-plane Young’s modulus | EC | 7 GPa |
| In-plane Poisson’s ratio | PRBA | 0.25 |
| In-plane shear modulus | GAB | 4.5 GPa |
| Out-of-plane shear modulus | GBC | 1.8 GPa |
| Out-of-plane shear modulus | GCA | 1.8 GPa |
| Woven composite failure criteria flag | 2WAY | 1 |
| Maximum strain value for fiber tension | DFAILT | 1 |
| Maximum strain value for fiber compression | DFAILC | −1 |
| Longitudinal compressive strength | XC | 240 MPa |
| Longitudinal tensile strength | XT | 680 MPa |
| Transversal compressive strength | YC | 240 MPa |
| Transversal tensile strength | YT | 680 MPa |
| Shear strength | SC | 1000 MPa |
| Material Property | LS-DYNA Symbol | Value |
|---|---|---|
| Maximum normal stress | NFLS | 60 MPa |
| Maximum shear stress | SFLS | 60 MPa |
| Material Property | LS-DYNA Symbol | Value | Ref. |
|---|---|---|---|
| Density | RO | 1600 | [7] |
| In-plane longitudinal Young’s modulus | EA | 55 GPa | [7] |
| In-plane transversal Young’s modulus | EB | 55 GPa | [7] |
| Out-of-plane Young modulus | EC | 7 GPa | [7] |
| In-plane Poisson’s ratio | PRBA | 0.25 | [7] |
| Out-of-plane Poisson’s ratios | PRCA, PRCB | 0.05 | [7] |
| In-plane shear modulus | GAB | 4.5 GPa | [7] |
| Out-of-plane shear moduli | GBC, GCA | 1.8 GPa | [7] |
| Longitudinal tensile strength | SAT | 680 MPa | [7] |
| Longitudinal compressive strength | SAC | 240 MPa | [7] |
| Transversal tensile strength | SBT | 680 MPa | [7] |
| Transversal compressive strength | SBC | 240 MPa | [7] |
| Through the thickness tensile strength | SCT | 50 MPa | [30] |
| Crush strength | SFC | 700 MPa | [30] |
| Fiber-mode shear strength | SFS | 120 MPa | [30] |
| Matrix-mode in-plane shear strength | SAB | 80 MPa | [30] |
| Matrix-mode out-of-plane shear strength | SBC, SCA | 60 MPa | [30] |
| Scale factor for residual compressive strength | SFFC | 0.3 | [30] |
| Coulomb’s friction angle | PHIC | 10 | [30] |
| Element-eroding axial strain | E_LIMT | 3 | [30] |
| Scale factor for the delamination criterion | S | 1.1 | [30] |
| Limit damage parameter for elastic modulus reduction | OMGMX | 0.999 | [30] |
| Element-eroding axial strain | E_LIMIT | 3 | [30] |
| Limit compressive relative volume for elemental erosion | ECRSH | 0.001 | [31] |
| Limit tensile relative volume for elemental erosion | EEXPN | 3 | [30] |
| Coefficient for the strain-softening property | AM1, AM2 | 1 | [32] |
| Coefficient for the strain-softening property | AM3 | 0.35 | [30] |
| Coefficient for the strain-softening property | AM4 | 0.3 | [30] |
| Material Property | LS-DYNA Symbol | Value |
|---|---|---|
| Density | RO | 63 |
| Young’s modulus | E | 8.4 MPa |
| Hysteretic unloading factor | HU | 0.25 |
| Decay constant for creep unloading | BETA | 5.0 |
| Viscous coefficient for damping effects | DAMP | 0.5 |
| Shape factor for unloading | SHAPE | 5.0 |
| Stiffness coefficient for contact interface stiffness | KCON | 1150 MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vescovini, A.; Lomazzi, L.; Giglio, M.; Manes, A. Numerical Study on the Damage of a Carbon Woven Composite Panel Subjected to Blast Loading. Polymers 2023, 15, 4269. https://doi.org/10.3390/polym15214269
Vescovini A, Lomazzi L, Giglio M, Manes A. Numerical Study on the Damage of a Carbon Woven Composite Panel Subjected to Blast Loading. Polymers. 2023; 15(21):4269. https://doi.org/10.3390/polym15214269
Chicago/Turabian StyleVescovini, Alessandro, Luca Lomazzi, Marco Giglio, and Andrea Manes. 2023. "Numerical Study on the Damage of a Carbon Woven Composite Panel Subjected to Blast Loading" Polymers 15, no. 21: 4269. https://doi.org/10.3390/polym15214269
APA StyleVescovini, A., Lomazzi, L., Giglio, M., & Manes, A. (2023). Numerical Study on the Damage of a Carbon Woven Composite Panel Subjected to Blast Loading. Polymers, 15(21), 4269. https://doi.org/10.3390/polym15214269








