Fluid Mechanics of Droplet Spreading of Chitosan/PVA-Based Spray Coating Solution on Banana Peels with Different Wettability
Abstract
:1. Introduction
2. Materials and Methods
2.1. Plant Substrates
2.2. Liquid Droplets
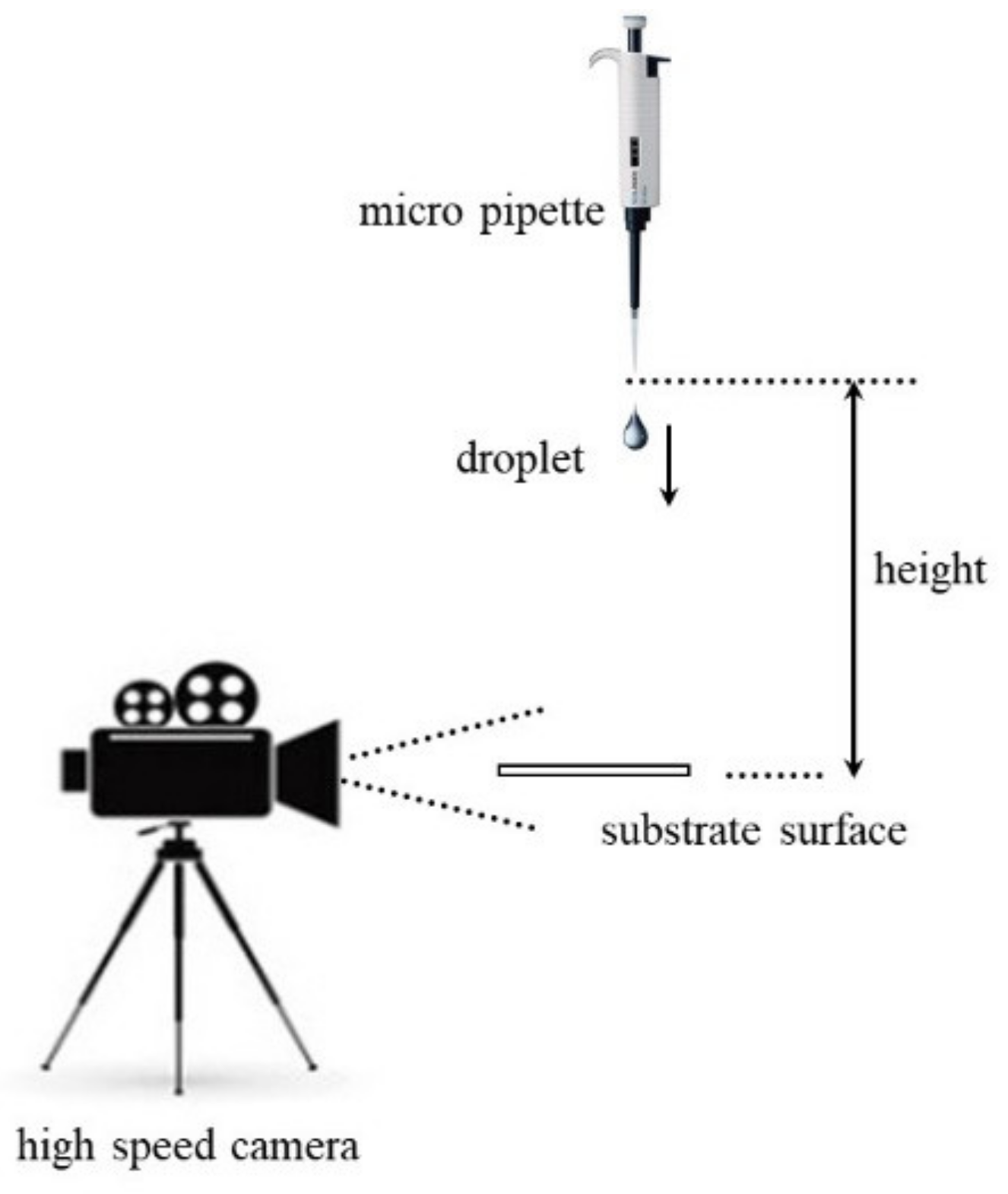
2.3. Impact Measurement
2.4. Impact Measurement
3. Results and Discussion
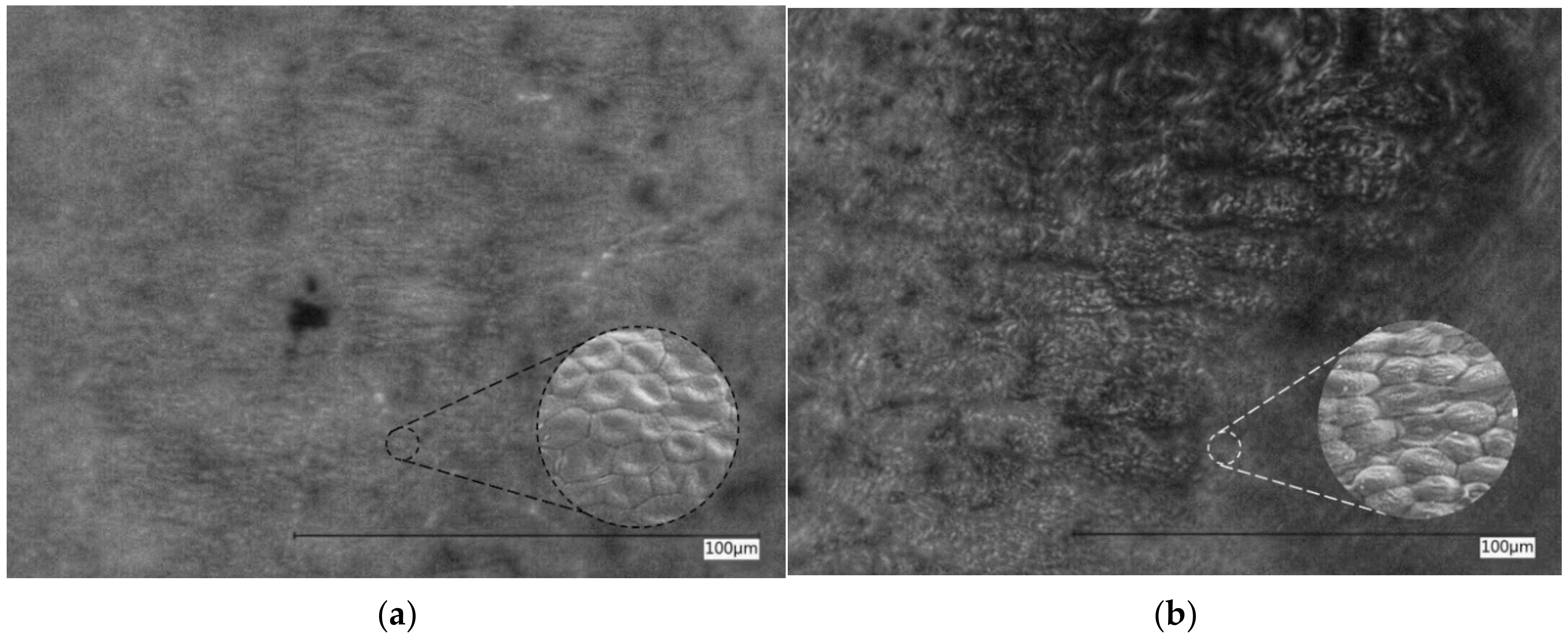
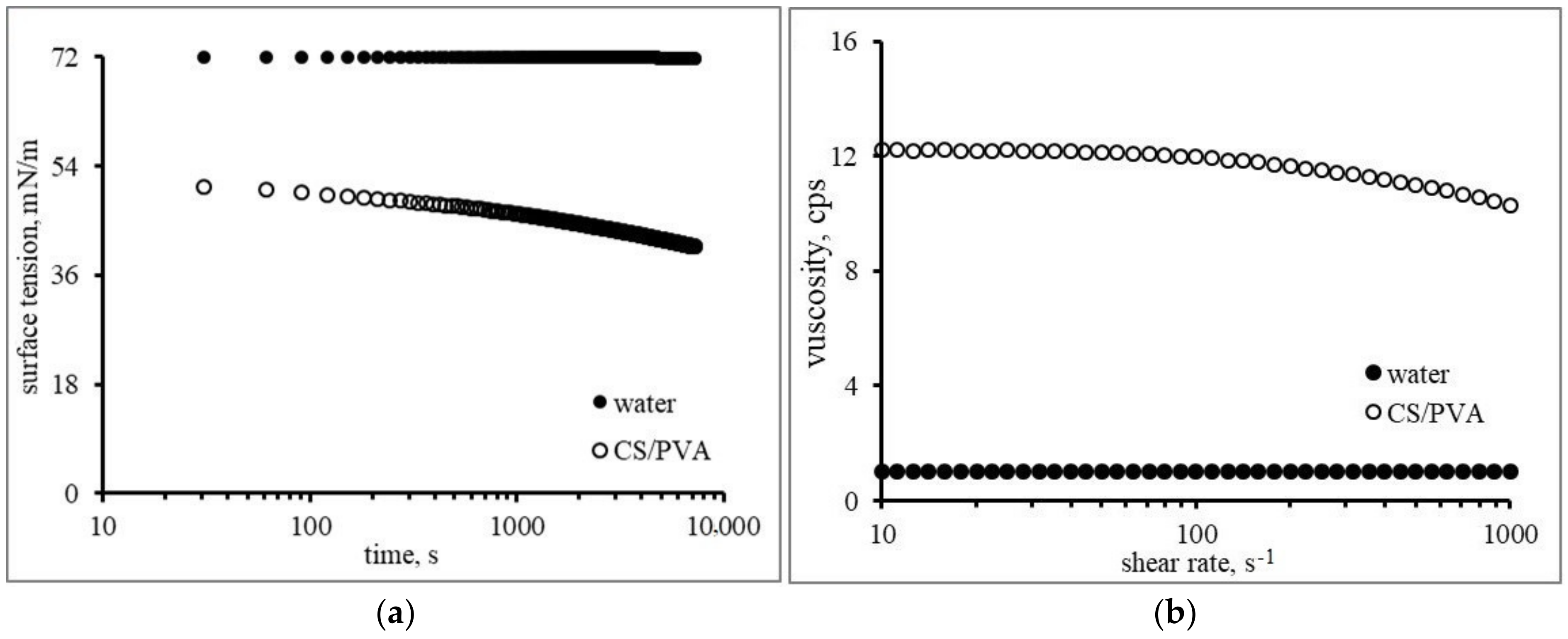
3.1. Substrate Properties
3.2. Droplet Properties and Impact Conditions
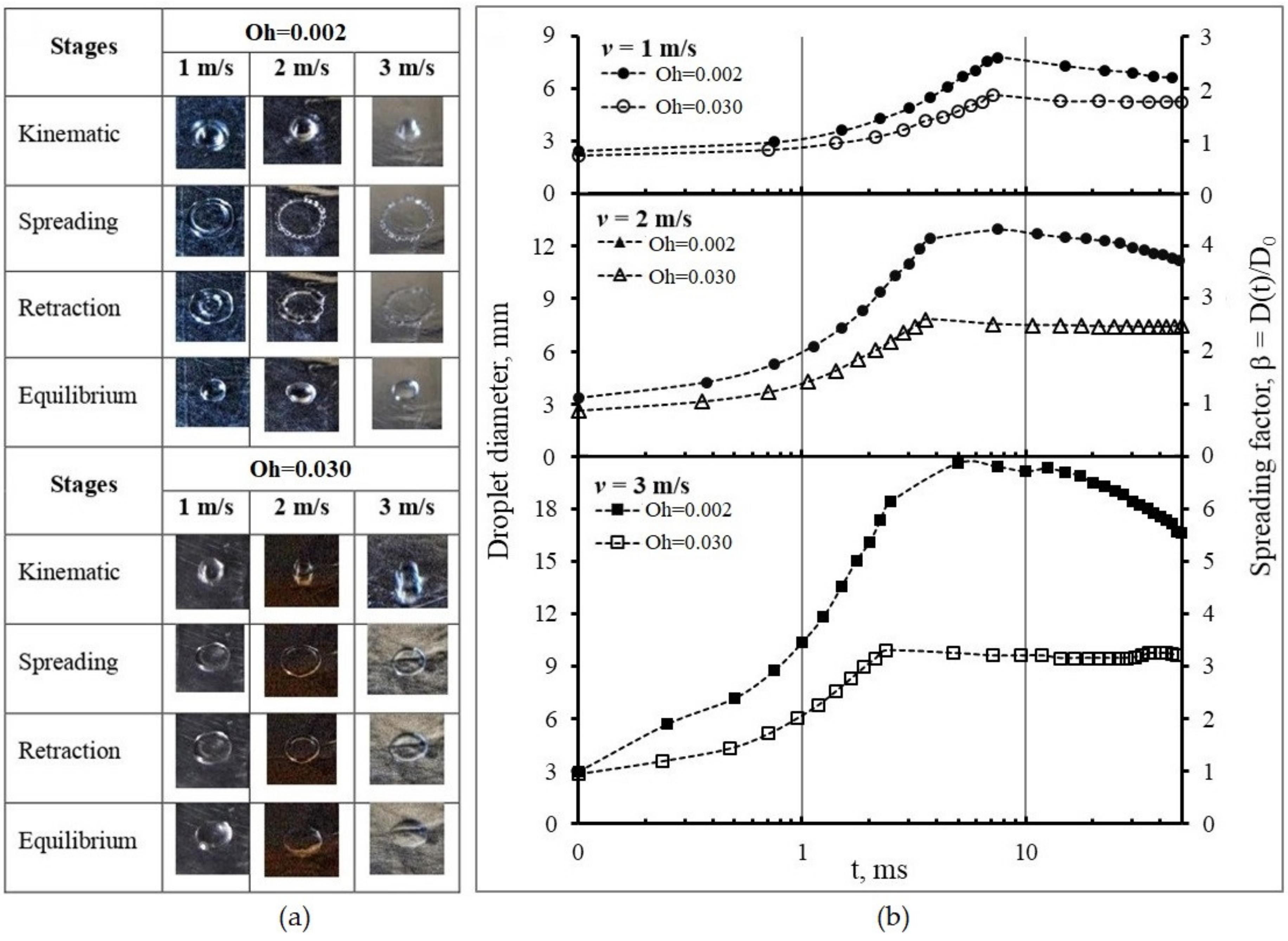
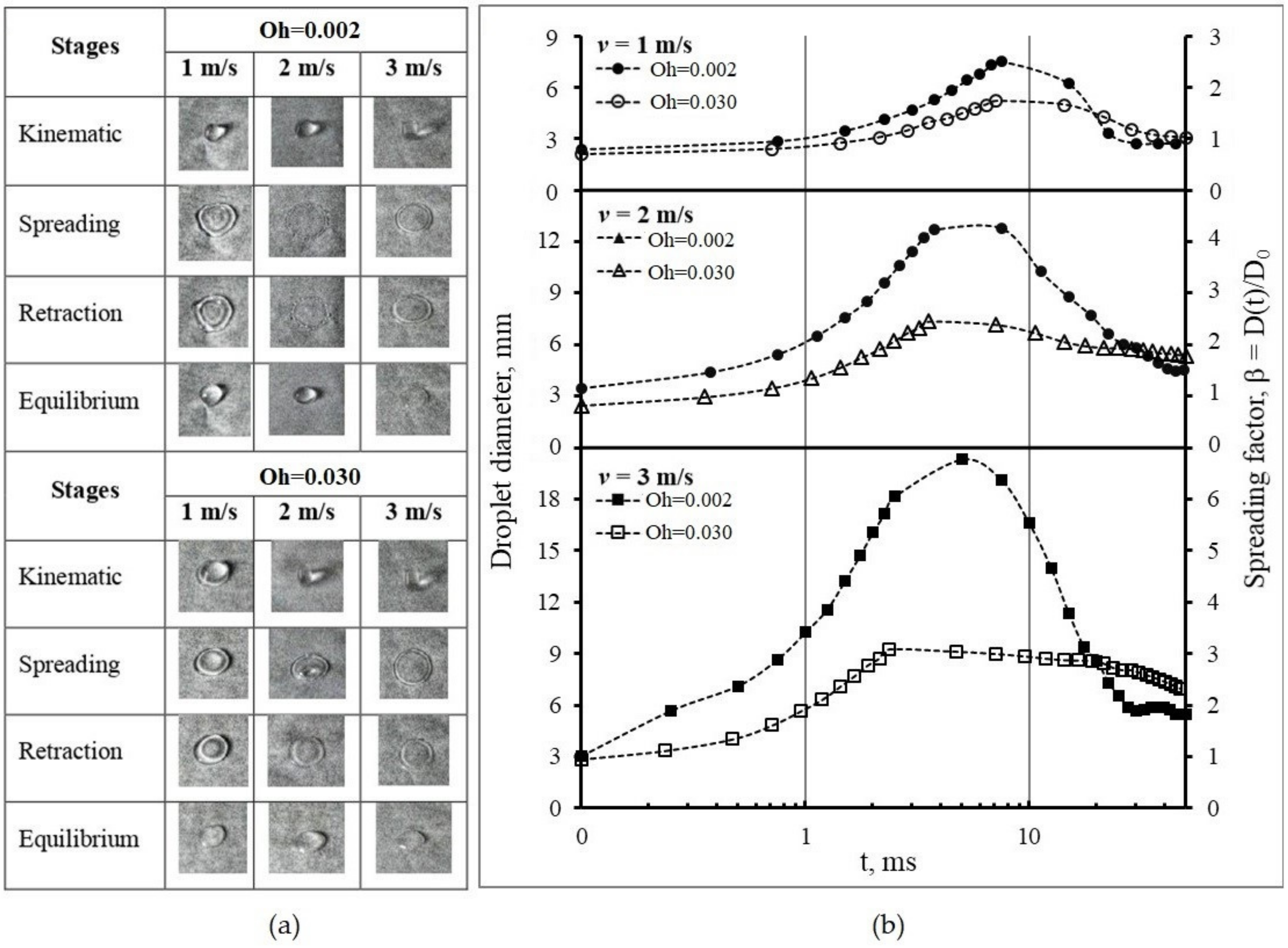
3.3. Spreading Behavior
3.3.1. Spreading on the Wetting Surface
3.3.2. Spreading on the Non-Wetting Surface
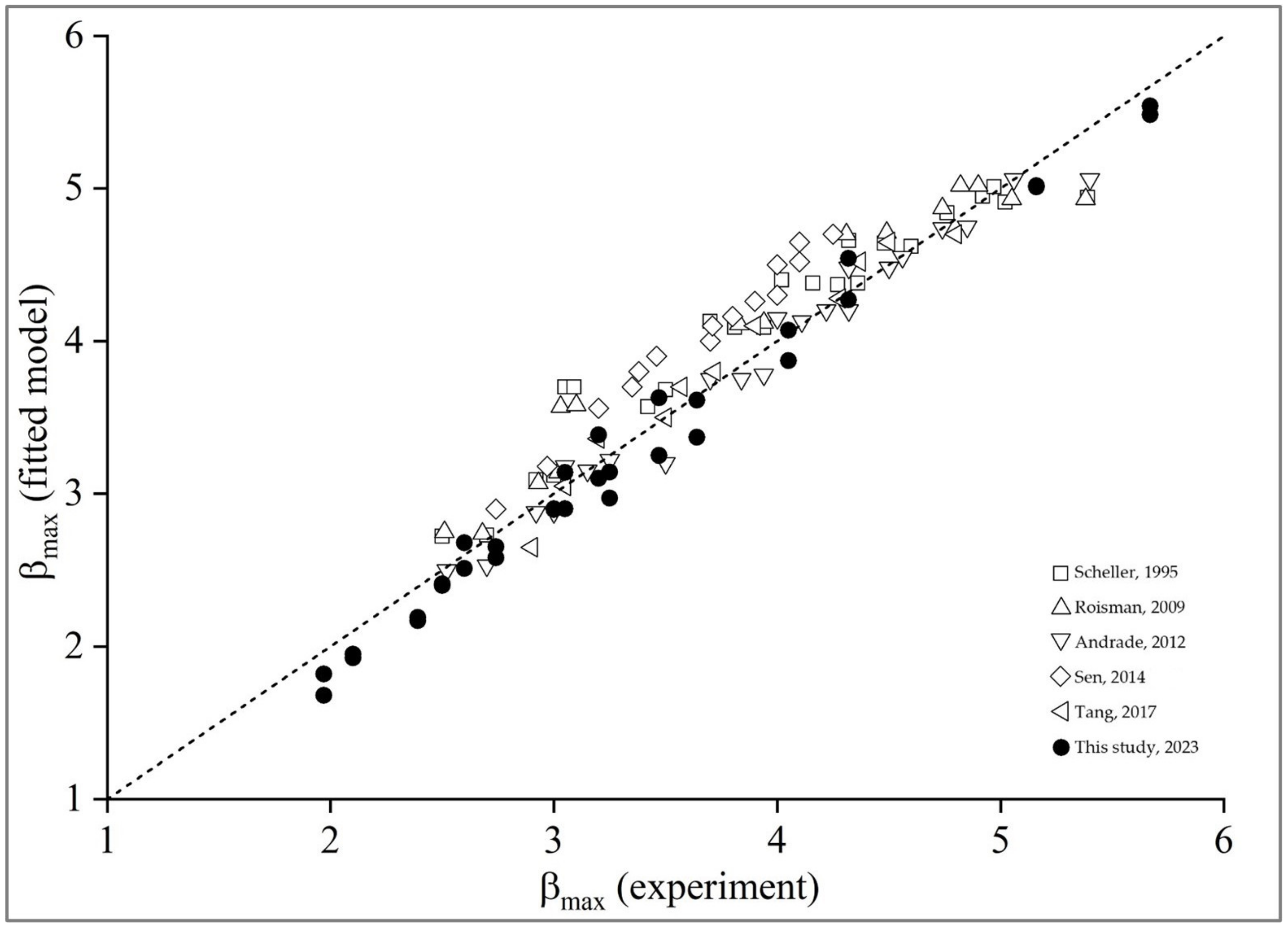
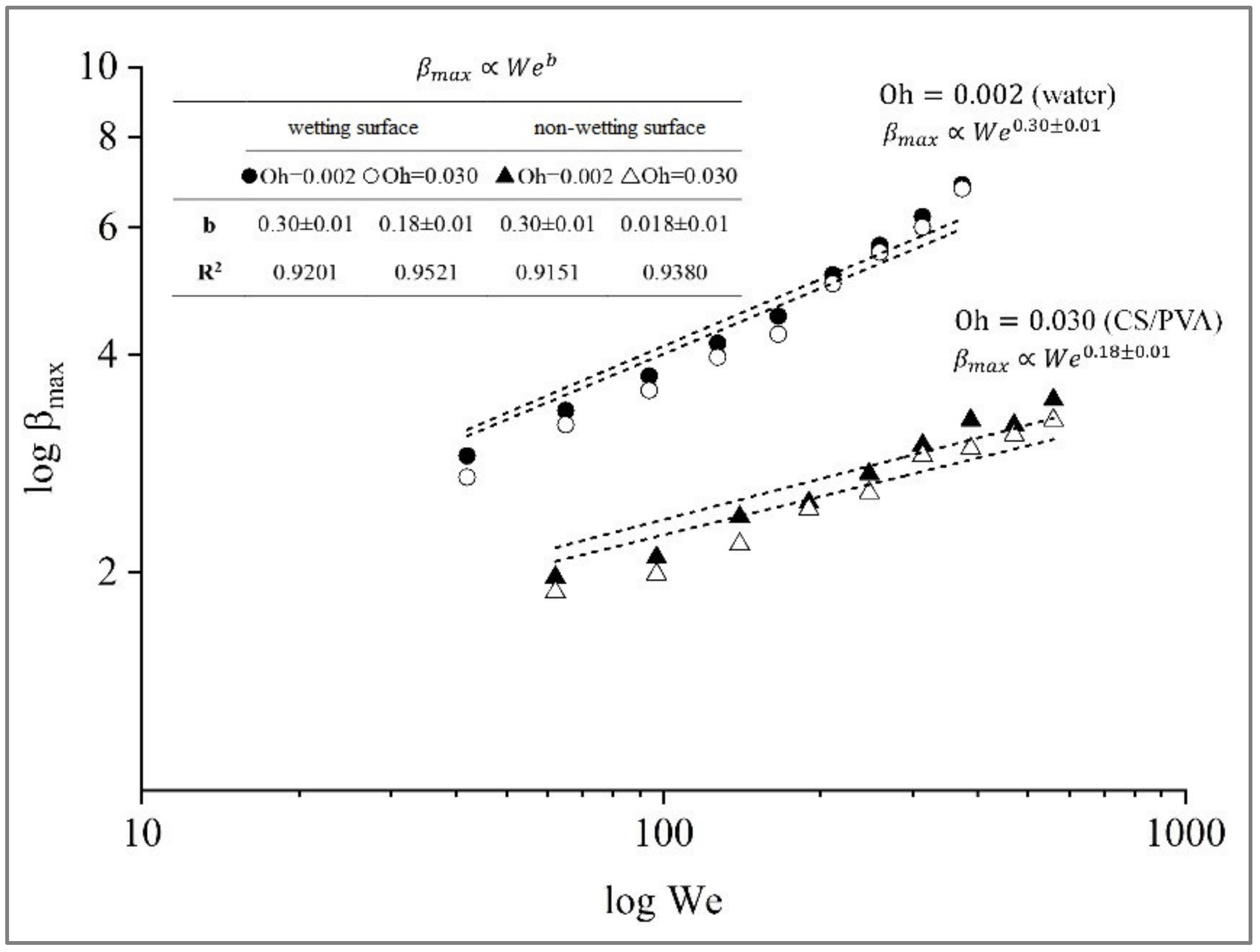
3.4. Maximum Spreading Factor
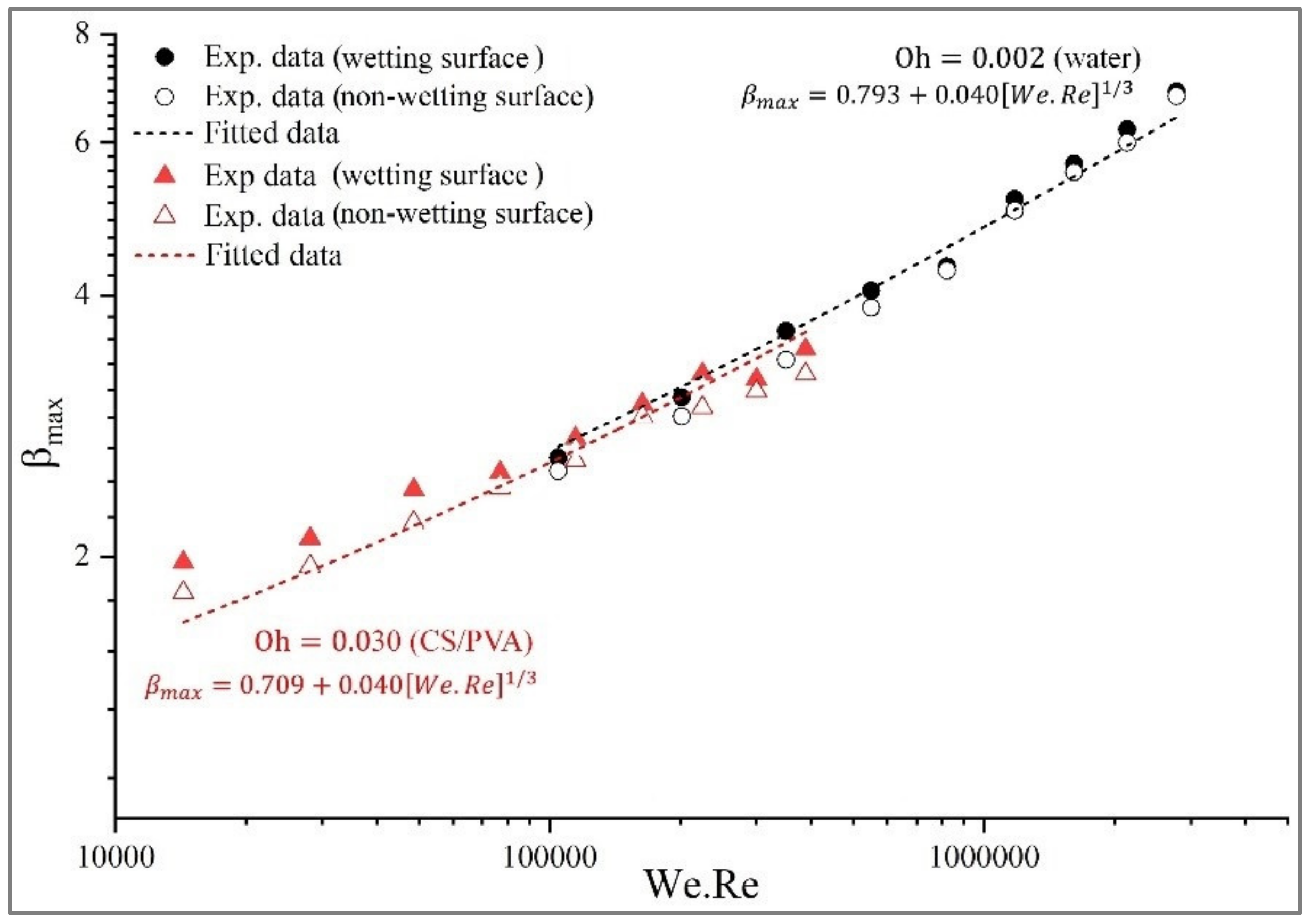
3.5. Mathematical Model of Spreading
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Petkoska, A.T.; Daniloski, D.; D’Cunha, N.M.; Naumovski, N.; Broach, A.T. Edible packaging: Sustainable solutions and novel trends in food packaging. Food Res. Int. 2021, 140, 109981. [Google Scholar] [CrossRef]
- Perera, K.Y.; Jaiswal, A.K.; Jaiswal, S. Biopolymer-Based Sustainable Food Packaging Materials: Challenges, Solutions, and Applications. Foods 2023, 12, 2422. [Google Scholar] [CrossRef] [PubMed]
- Atay, H.Y. Antibacterial Activity of Chitosan-Based Systems. In Functional Chitosan; Springer: Berlin/Heidelberg, Germany, 2019; pp. 457–489. [Google Scholar]
- Merzendorfer, H.; Cohen, E. Chitin/chitosan: Versatile ecological, industrial, and biomedical applications. In Extracellular Sugar-Based Biopolymers Matrices; Springer: Berlin/Heidelberg, Germany, 2019; pp. 541–624. [Google Scholar]
- Basumatary, K.; Daimary, P.; Das, S.K.; Thapa, M.; Singh, M.; Mukherjee, A.; Kumar, S. Lagerstroemia speciosa fruit-mediated synthesis of silver nanoparticles and its application as filler in agar based nanocomposite films for antimicrobial food packaging. Food Packag. Shelf Life 2018, 17, 99–106. [Google Scholar] [CrossRef]
- Werner, S.R.; Jones, J.R.; Paterson, A.H.; Archer, R.H.; Pearce, D.L. Droplet impact and spreading: Droplet formulation effects. Chem. Eng. Sci. 2007, 62, 2336–2345. [Google Scholar] [CrossRef]
- Kalantari, D.; Tropea, C. Phase Doppler measurements of spray impact onto rigid walls. Exp. Fluids 2007, 43, 285–296. [Google Scholar] [CrossRef]
- Igor, M.; Aidin, A.; Kyle, M.B. Magnetic Resonance Imaging measurements of a water spray upstream and downstream of a spray nozzle exit orifice. J. Magn. Reson. 2016, 266, 8–15. [Google Scholar]
- Fansler, T.D.; Parrish, S.E. Spray measurement technology: A review. Meas. Sci. Technol. 2014, 26, 012002. [Google Scholar] [CrossRef]
- Che, Z.; Matar, O.K. Impact of droplets on immiscible liquid films. Soft Matter 2018, 14, 1540–1551. [Google Scholar] [CrossRef]
- Aksoy, Y.T.; Eneren, P.; Koos, E.; Vetrano, M.R. Spreading of a droplet impacting on a smooth flat surface: How liquid viscosity influences the maximum spreading time and spreading ratio. Phys. Fluids 2022, 34, 042106. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, G.; Han, F. The spreading and superspeading behavior of new glucosamide-based trisiloxane surfactants on hydrophobic foliage. Colloids Surf. Physicochem. Eng. Asp. 2006, 276, 100–106. [Google Scholar] [CrossRef]
- Qin, M.; Tang, C.; Tong, S.; Zhang, P.; Huang, Z. On the role of liquid viscosity in affecting droplet spreading on a smooth solid surface. Int. J. Multiph. Flow 2019, 117, 53–63. [Google Scholar] [CrossRef]
- Bird, J.C.; Mandre, S.; Stone, H.A. Short-time dynamics of partial wetting. Phys. Rev. Lett. 2008, 100, 234501. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Chen, L.; Bonaccurso, E.; Venzmer, J. Dynamic wetting of hydrophobic polymers by aqueous surfactant and superspreader solutions. Langmuir 2013, 29, 14855–14864. [Google Scholar] [CrossRef] [PubMed]
- Mohapatra, D.; Mishra, S.; Sutar, N. Banana post harvest practices: Current status and future prospects-A review. Agric. Rev. 2010, 31, 56–62. [Google Scholar]
- Wardhono, E.Y.; Pinem, M.P.; Susilo, S.; Siom, B.J.; Sudrajad, A.; Pramono, A.; Meliana, Y.; Guénin, E. Modification of Physio-Mechanical Properties of Chitosan-Based Films via Physical Treatment Approach. Polymers 2022, 14, 5216. [Google Scholar] [CrossRef]
- Pinem, M.P.; Wardhono, E.Y.; Clausse, D.; Saleh, K.; Guénin, E. Droplet behavior of chitosan film-forming solution on the solid surface. South Afr. J. Chem. Eng. 2022, 41, 26–33. [Google Scholar] [CrossRef]
- ASTM D 854-14; Standard Test Method for Specific Gravity of Soil Solids. Annual Book of ASTM Standards. American Society for Testing and Materials: Philadelphia, PA, USA, 2014; Volume 04.08. Available online: www.astm.org (accessed on 1 October 2023).
- Palencia, M. Surface free energy of solids by contact angle measurements. J. Sci. Technol. Appl. 2017, 2, 84. [Google Scholar] [CrossRef]
- Koopal, L.K. Wetting of solid surfaces: Fundamentals and charge effects. Adv. Colloid Interface Sci. 2012, 179, 29–42. [Google Scholar] [CrossRef]
- Marcotte, F.; Zaleski, S. Density contrast matters for drop fragmentation thresholds at low Ohnesorge number. Phys. Rev. Fluids 2019, 4, 103604. [Google Scholar] [CrossRef]
- De Goede, T.; de Bruin, K.; Shahidzadeh, N.; Bonn, D. Droplet splashing on rough surfaces. Phys. Rev. Fluids 2021, 6, 043604. [Google Scholar] [CrossRef]
- Rioboo, R.; Marengo, M.; Tropea, C. Time evolution of liquid drop impact onto solid, dry surfaces. Exp. Fluids 2002, 33, 112–124. [Google Scholar] [CrossRef]
- Lee, J.B.; Laan, N.; de Bruin, K.G.; Skantzaris, G.; Shahidzadeh, N.; Derome, D.; Carmeliet, J.; Bonn, D. Universal rescaling of drop impact on smooth and rough surfaces. J. Fluid Mech. 2016, 786, R4. [Google Scholar] [CrossRef]
- Tang, C.; Qin, M.; Weng, X.; Zhang, X.; Zhang, P.; Li, J.; Huang, Z. Dynamics of droplet impact on solid surface with different roughness. Int. J. Multiph. Flow 2017, 96, 56–69. [Google Scholar] [CrossRef]
- Banks, D.; Ajawara, C.; Sanchez, R.; Surti, H.; Aguilar, G. Effects of liquid and surface characteristics on oscillation behavior of droplets upon impact. At. Sprays 2014, 24, 895–913. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Caner, F.C. Impact comminution of solids due to local kinetic energy of high shear strain rate: I. Continuum theory and turbulence analogy. J. Mech. Phys. Solids 2014, 64, 223–235. [Google Scholar] [CrossRef]
- Bolleddula, D.A.; Berchielli, A.; Aliseda, A. Impact of a heterogeneous liquid droplet on a dry surface: Application to the pharmaceutical industry. Adv. Colloid Interface Sci. 2010, 159, 144–159. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Qian, J.; Chen, X.; Li, E.; Chen, Y. Numerical investigation of Weber number and gravity effects on fluid flow and heat transfer of successive droplets impacting liquid film. Sci. China Technol. Sci. 2023, 66, 548–559. [Google Scholar] [CrossRef]
- Islamova, A.; Tkachenko, P.; Shlegel, N.; Kuznetsov, G. Effect of Liquid Properties on the Characteristics of Collisions between Droplets and Solid Particles. Appl. Sci. 2022, 12, 10747. [Google Scholar] [CrossRef]
- Clanet, C.; Béguin, C.; Richard, D.; Quéré, D. Maximal deformation of an impacting drop. J. Fluid Mech. 2004, 517, 199–208. [Google Scholar] [CrossRef]
- Tembely, M.; Vadillo, D.C.; Dolatabadi, A.; Soucemarianadin, A. A machine learning approach for predicting the maximum spreading factor of droplets upon impact on surfaces with various wettabilities. Processes 2022, 10, 1141. [Google Scholar] [CrossRef]
- Laan, N.; de Bruin, K.G.; Bartolo, D.; Josserand, C.; Bonn, D. Maximum diameter of impacting liquid droplets. Phys. Rev. Appl. 2014, 2, 044018. [Google Scholar] [CrossRef]
- Seo, J.; Lee, J.S.; Kim, H.Y.; Yoon, S.S. Empirical model for the maximum spreading diameter of low-viscosity droplets on a dry wall. Exp. Therm. Fluid Sci. 2015, 61, 121–129. [Google Scholar] [CrossRef]
- Lee, J.B.; Derome, D.; Guyer, R.; Carmeliet, J. Modeling the maximum spreading of liquid droplets impacting wetting and nonwetting surfaces. Langmuir 2016, 32, 1299–1308. [Google Scholar] [CrossRef]
- Wildeman, S.; Visser, C.W.; Sun, C.; Lohse, D. On the spreading of impacting drops. J. Fluid Mech. 2016, 805, 636–655. [Google Scholar] [CrossRef]
- Scheller, B.L.; Bousfield, D.W. Newtonian drop impact with a solid surface. AIChE J. 1995, 41, 1357–1367. [Google Scholar] [CrossRef]
- Sen, S.; Vaikuntanathan, V.; Sivakumar, D. Experimental investigation of biofuel drop impact on stainless steel surface. Exp. Therm. Fluid Sci. 2014, 54, 38–46. [Google Scholar] [CrossRef]
- Roisman, I.V. Inertia dominated drop collisions. II. An analytical solution of the Navier–Stokes equations for a spreading viscous film. Phys. Fluids 2009, 21, 052104. [Google Scholar] [CrossRef]
- Andrade, R.; Skurtys, O.; Osorio, F. Experimental study of drop impacts and spreading on epicarps: Effect of fluid properties. J. Food Eng. 2012, 109, 430–437. [Google Scholar] [CrossRef]
| Liquid | Banana Peels | |||
|---|---|---|---|---|
| Washed Surface | Unwashed Surface | |||
| CA (°) | ΔG (kJ/mole) | CA (°) | ΔG (kJ/mole) | |
| Water | 81.4 ± 1.8 | −0.21 | 108.1 ± 2.1 | 0.44 |
| CS/PVA | 63.8 ± 2.5 | −0.64 | 98.4 ± 2.4 | 0.23 |
| Liquids | ρ | μ | σ | Do | h | ||
|---|---|---|---|---|---|---|---|
| g/cm3 | cps | mN/m | mm | cm | |||
| Water | 0.998 | 1.00 | 72.00 | 3.00 ± 0.05 | 5–45 | 0.002 | 40–400 |
| CS/PVA | 1.125 | 12.25 | 51.62 | 2.85 ± 0.05 | 5–45 | 0.030 | 60–600 |
| Oh | v = 1 m/s | v = 2 m/s | v = 3 m/s | ||||||
|---|---|---|---|---|---|---|---|---|---|
| t | Dmax | βmax | t | Dmax | βmax | t | Dmax | βmax | |
| ms | mm | - | ms | Mm | - | ms | mm | - | |
| 0.002 | 7.50 | 7.80 | 2.60 | 7.50 | 12.96 | 4.32 | 5.00 | 20.61 | 6.87 |
| 0.030 | 7.13 | 5.01 | 1.97 | 3.56 | 7.81 | 2.74 | 2.38 | 9.89 | 3.47 |
| Oh | v = 1 m/s | v = 2 m/s | v = 3 m/s | ||||||
|---|---|---|---|---|---|---|---|---|---|
| t | Dmax | βmax | t | Dmax | βmax | t | Dmax | βmax | |
| ms | mm | - | ms | mm | - | Ms | mm | - | |
| 0.002 | 7.50 | 7.53 | 2.51 | 7.50 | 12.81 | 4.27 | 5.00 | 20.34 | 6.78 |
| 0.030 | 7.13 | 5.19 | 1.82 | 3.56 | 7.35 | 2.58 | 2.38 | 9.26 | 3.25 |
| Oh | Fitting Parameters | |||
|---|---|---|---|---|
| a | b | c | R2 | |
| 0.002 | 0.793 | 0.040 | 1/3 | 0.9623 |
| 0.030 | 0.709 | 0.040 | 1/3 | 0.9539 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wardhono, E.Y.; Kanani, N.; Pinem, M.P.; Sukamto, D.; Meliana, Y.; Saleh, K.; Guénin, E. Fluid Mechanics of Droplet Spreading of Chitosan/PVA-Based Spray Coating Solution on Banana Peels with Different Wettability. Polymers 2023, 15, 4277. https://doi.org/10.3390/polym15214277
Wardhono EY, Kanani N, Pinem MP, Sukamto D, Meliana Y, Saleh K, Guénin E. Fluid Mechanics of Droplet Spreading of Chitosan/PVA-Based Spray Coating Solution on Banana Peels with Different Wettability. Polymers. 2023; 15(21):4277. https://doi.org/10.3390/polym15214277
Chicago/Turabian StyleWardhono, Endarto Yudo, Nufus Kanani, Mekro Permana Pinem, Dwinanto Sukamto, Yenny Meliana, Khashayar Saleh, and Erwann Guénin. 2023. "Fluid Mechanics of Droplet Spreading of Chitosan/PVA-Based Spray Coating Solution on Banana Peels with Different Wettability" Polymers 15, no. 21: 4277. https://doi.org/10.3390/polym15214277
APA StyleWardhono, E. Y., Kanani, N., Pinem, M. P., Sukamto, D., Meliana, Y., Saleh, K., & Guénin, E. (2023). Fluid Mechanics of Droplet Spreading of Chitosan/PVA-Based Spray Coating Solution on Banana Peels with Different Wettability. Polymers, 15(21), 4277. https://doi.org/10.3390/polym15214277