The Challenges Facing the Current Paradigm Describing Viscoelastic Interactions in Polymer Melts
Abstract
1. Introduction
2. Development
2.1. The Great Myth of the Rouse Model: Its Failure to Describe the Rheology of Unentangled Melts (M < Mc)
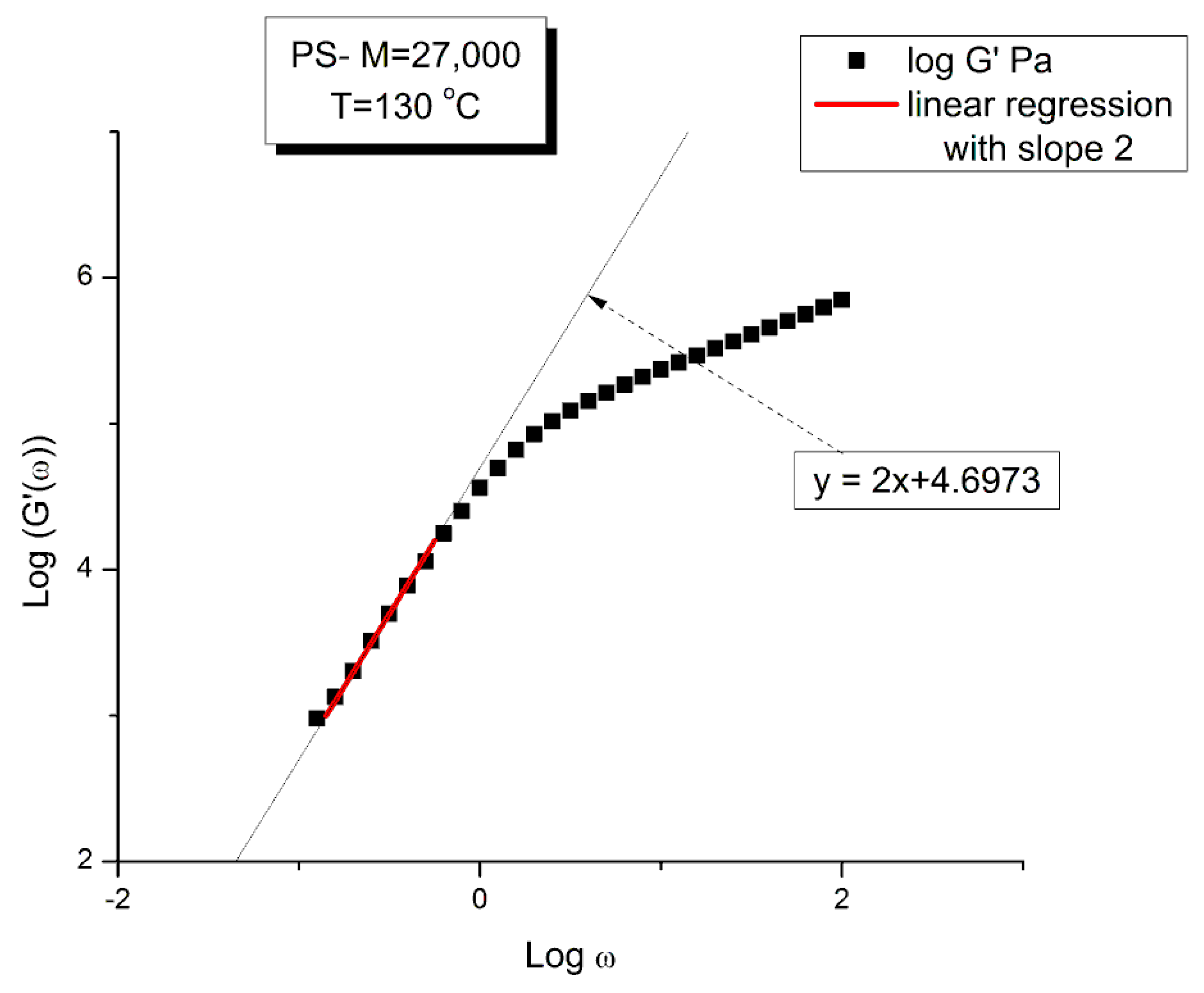
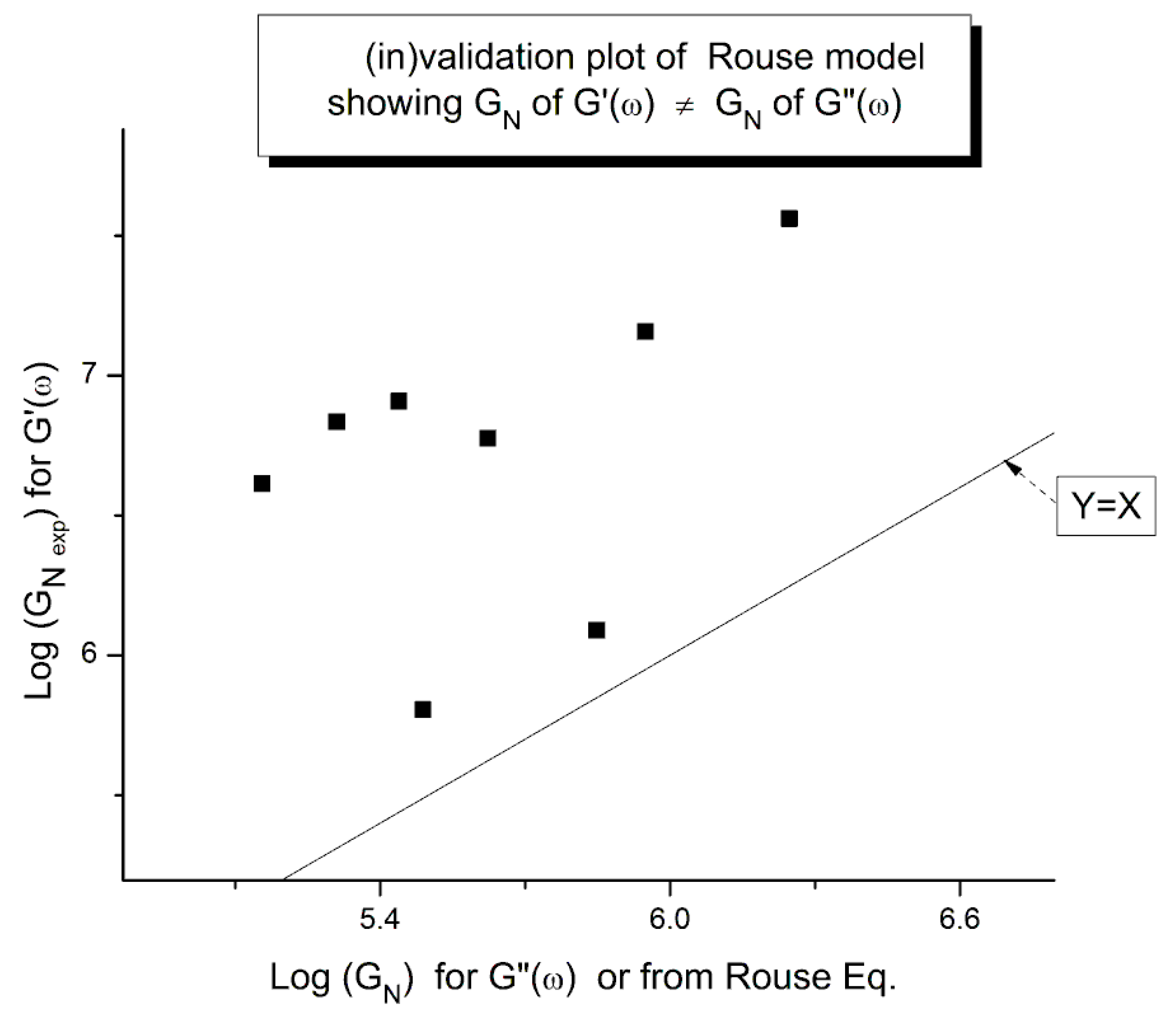
2.1.1. (In)validation of the Rouse Model Using Dynamic Data G′(ω), G″(ω)
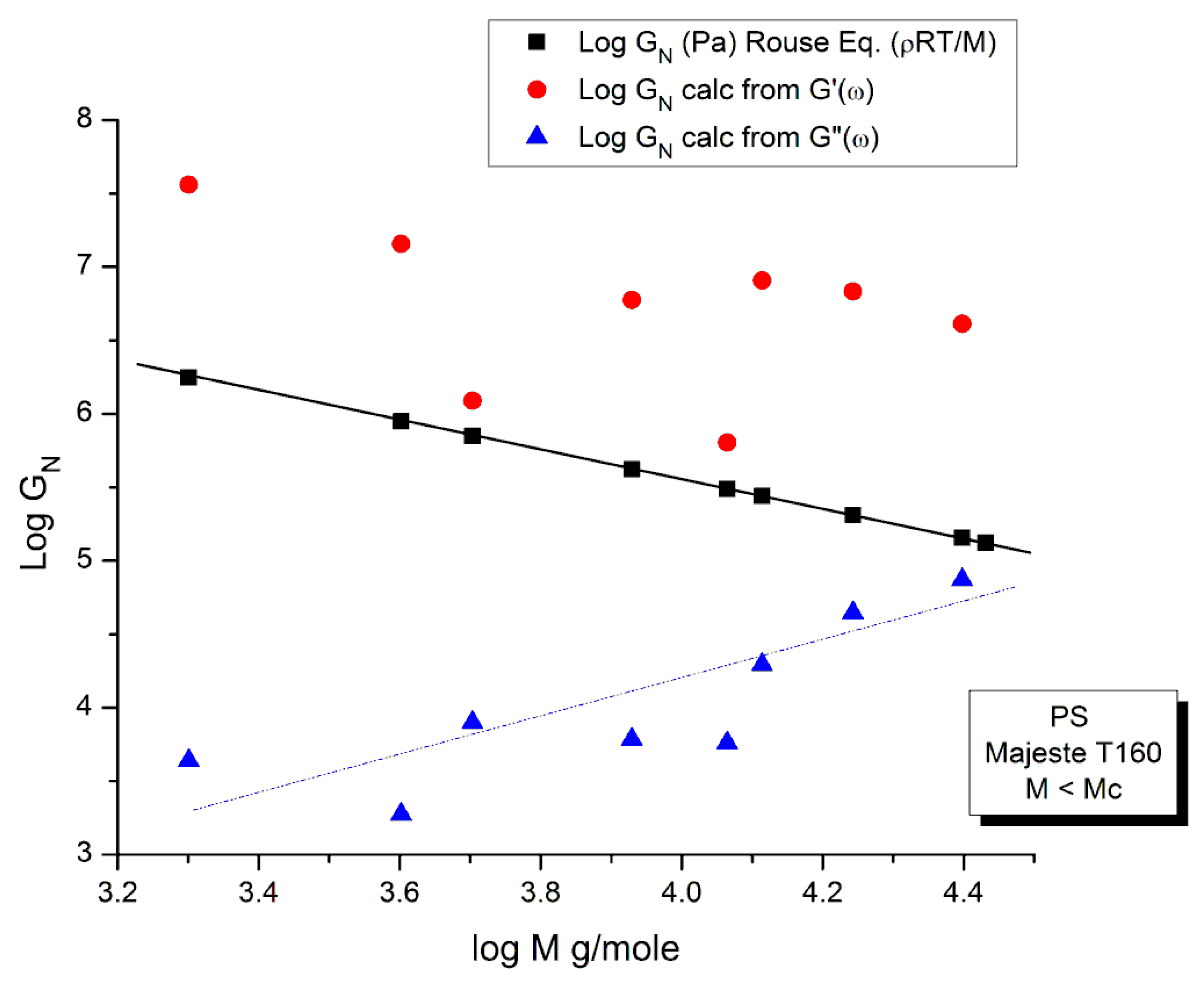
2.1.2. (In)validity of the Rouse Formula to Predict the Molecular Dependency of τR below Mc
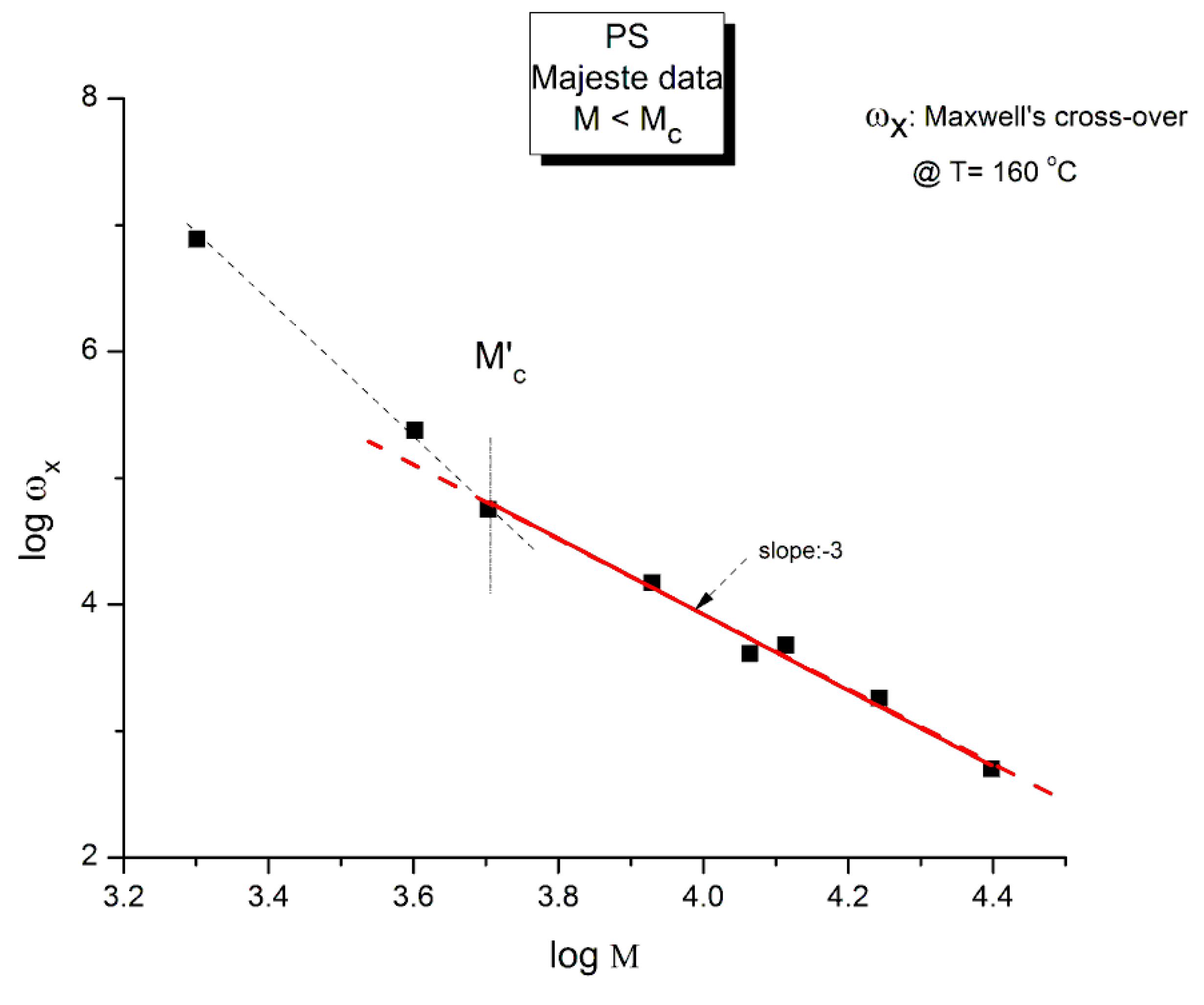
Molecular Weight Dependence of the Rouse Time, τR from the M < Mc Majeste Data
Temperature Dependence of τR at M Constant
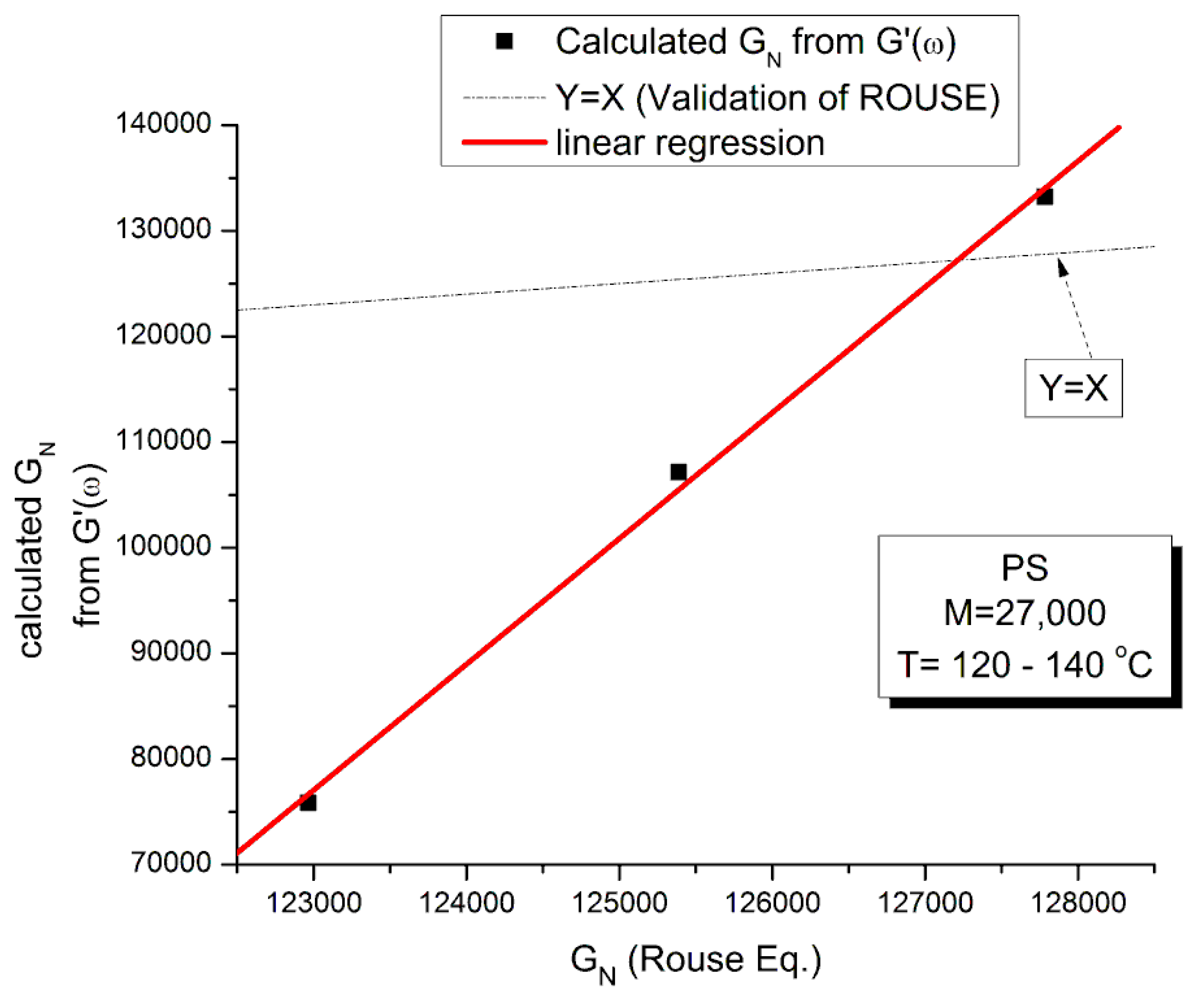
Comparing the Calculations of GN from the G′(ω) or G″(ω) Sides of the Rouse Equations and Invalidating the Rouse Approach
2.1.3. Conclusion Regarding the Myth of the Applicability of the Rouse Equation to the Rheology of Unentangled Polymer Melts
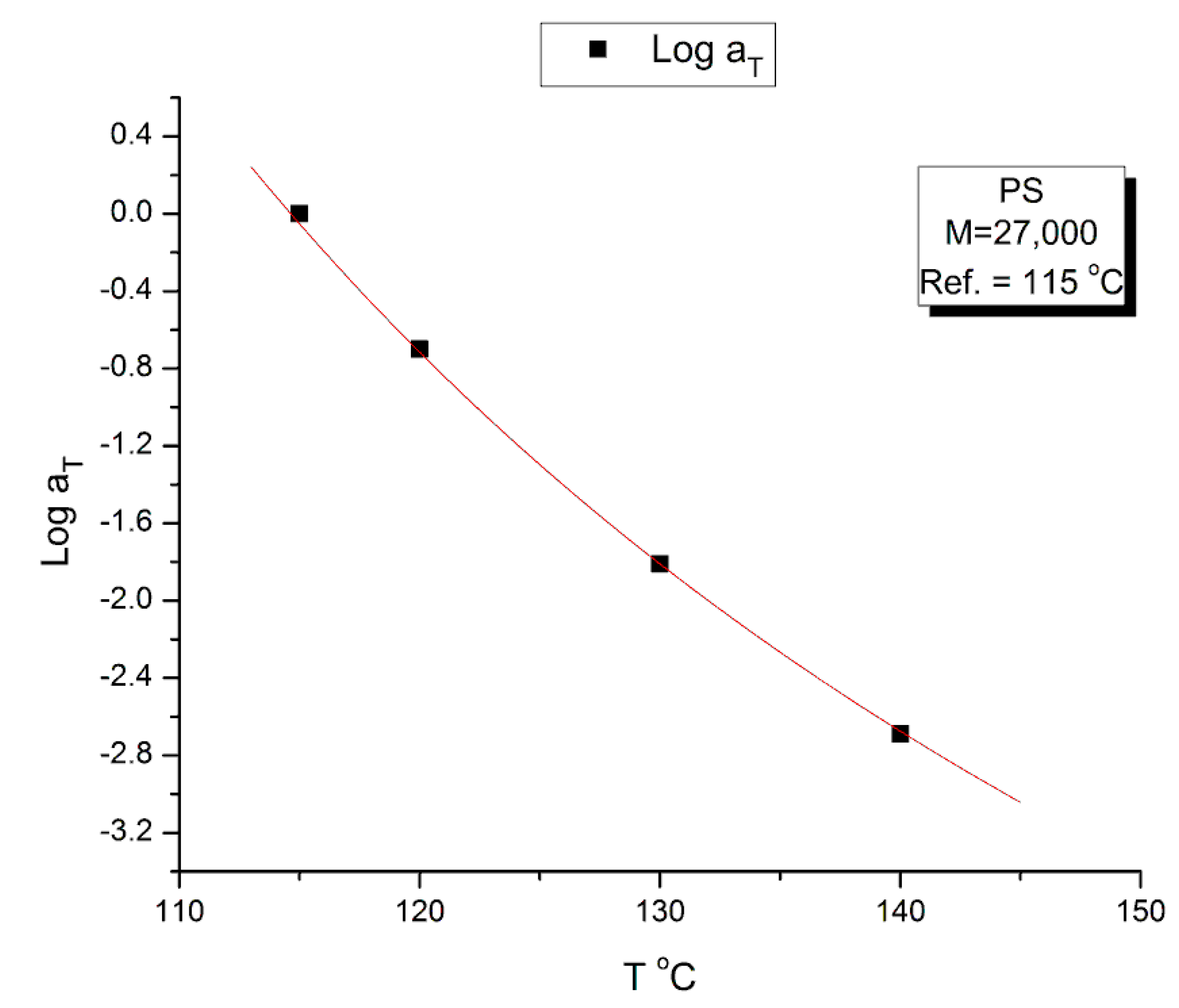
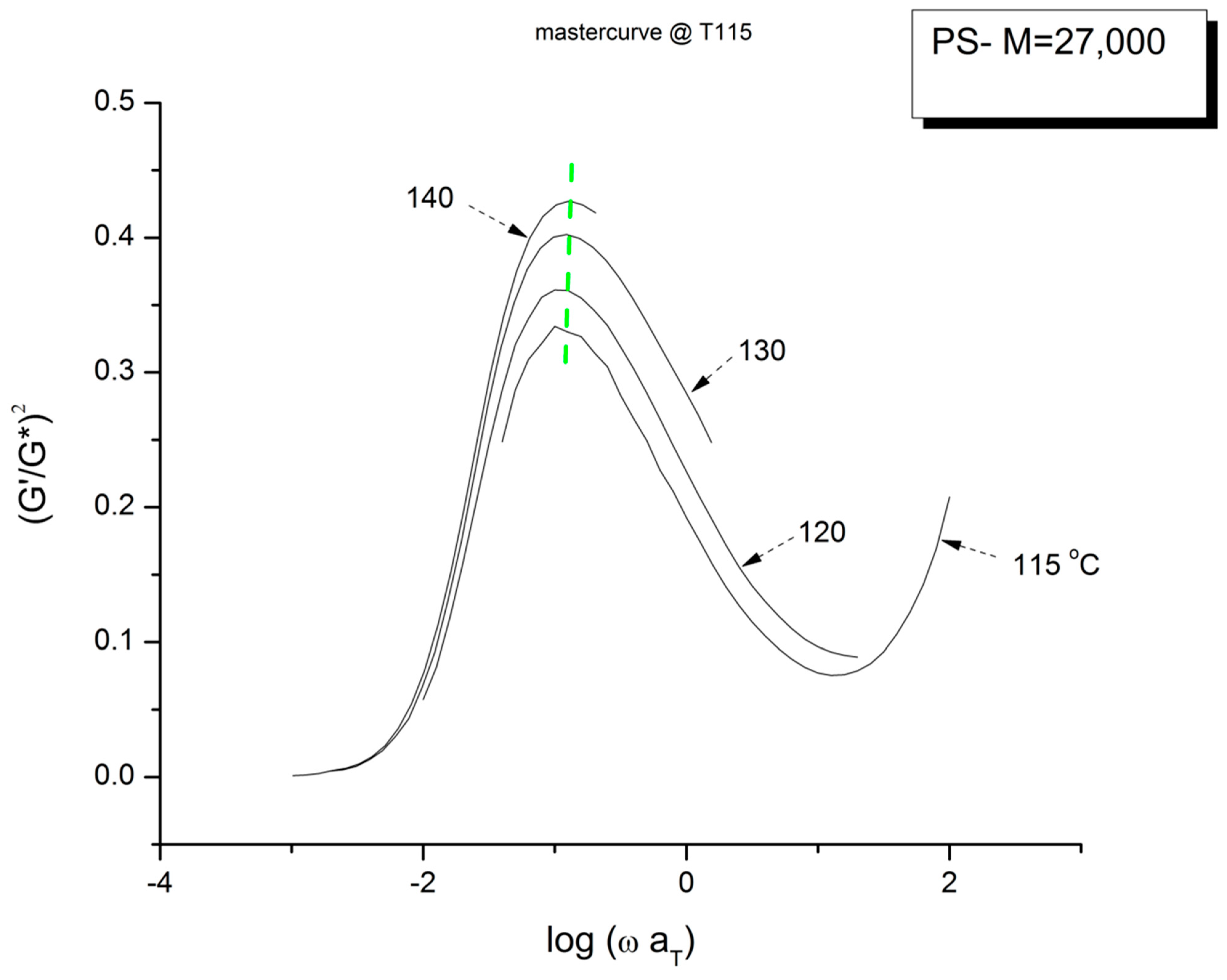
2.2. The Myth of the Extended Applicability of the Time–Temperature Superposition Principle
- The superposition of curves by horizontal shifting on the log time or log frequency is a good approximation over a rather short temperature interval. There are 3 ranges of temperature within which the tts works well for polymer melts: the (Tg to Tg + 23 ± 2) region, the (Tg + 23) to TLL region and the T > TLL region. For each temperature region a new set of WLF constants (or Vogel Fulcher constants) must be established. Superposition across regions is physically improper according to the Dual-Phase model [20].
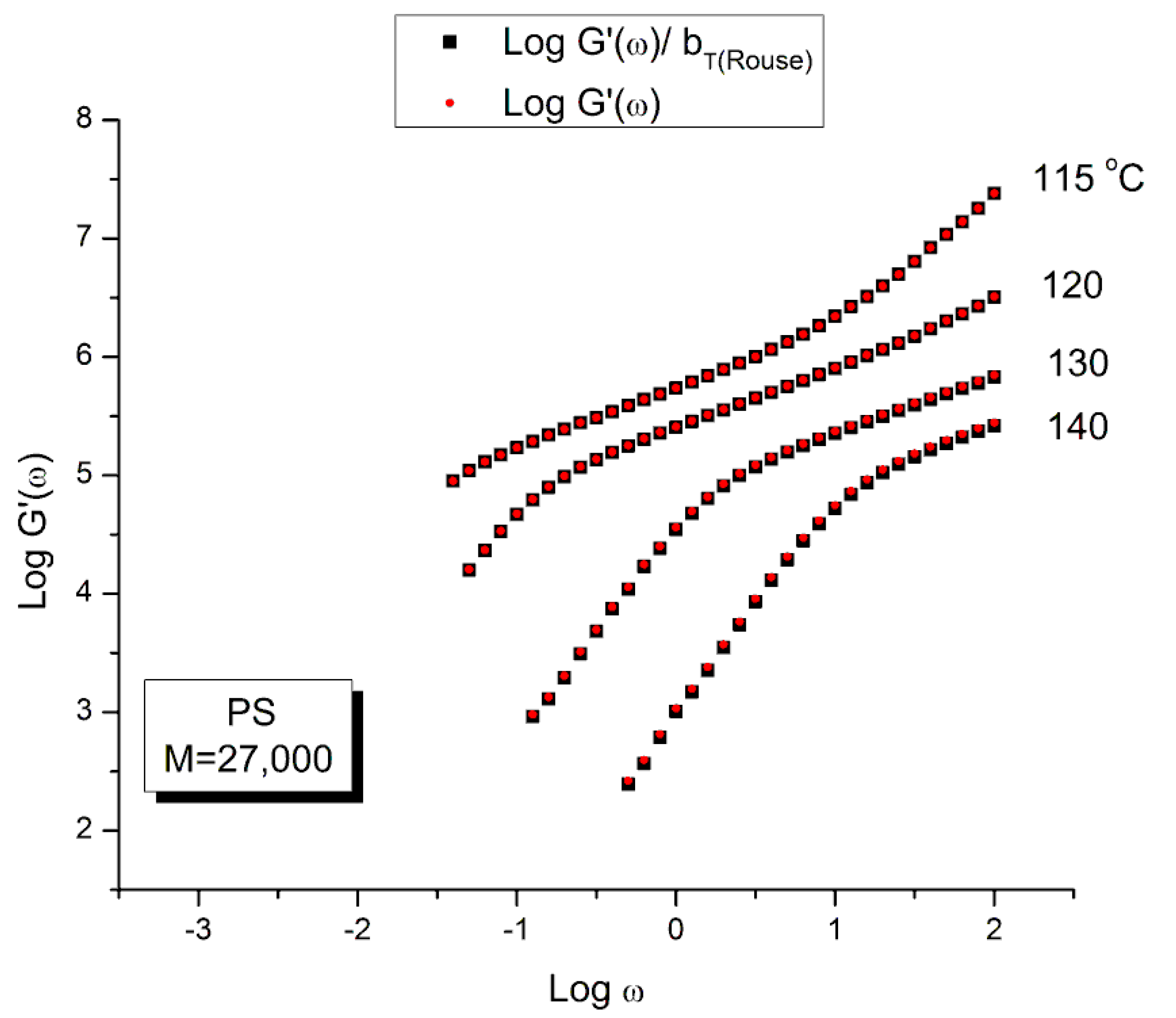
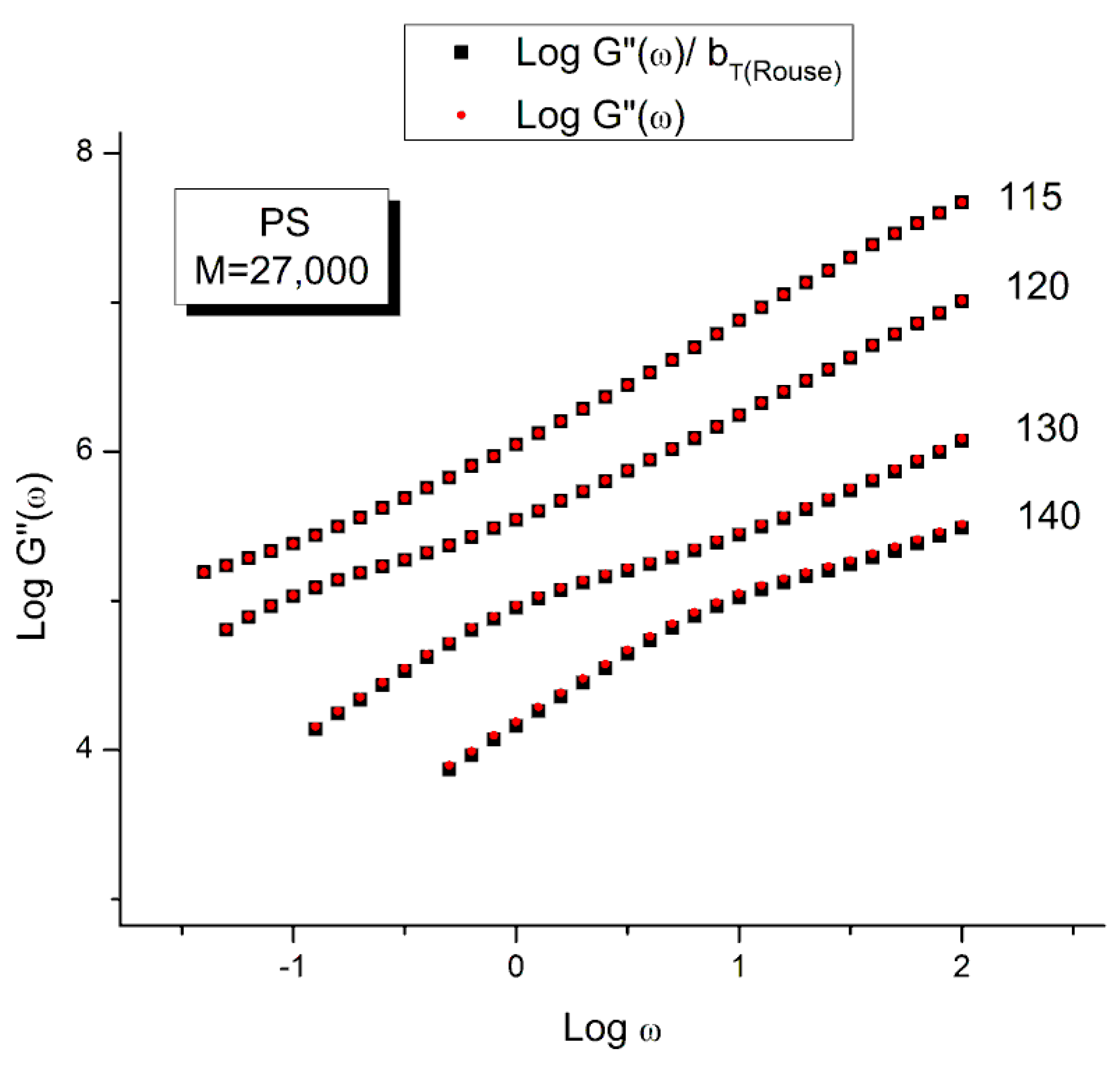
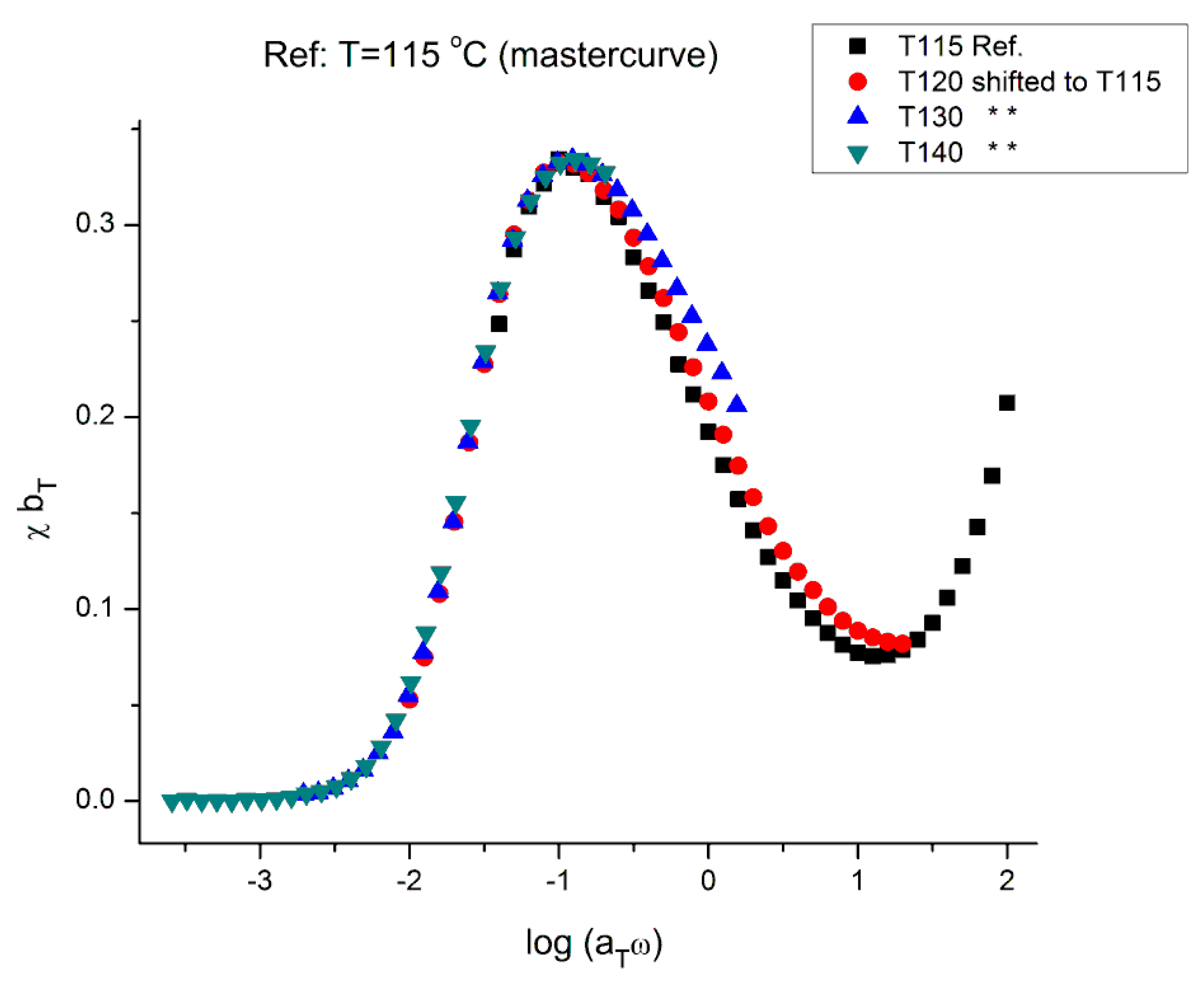
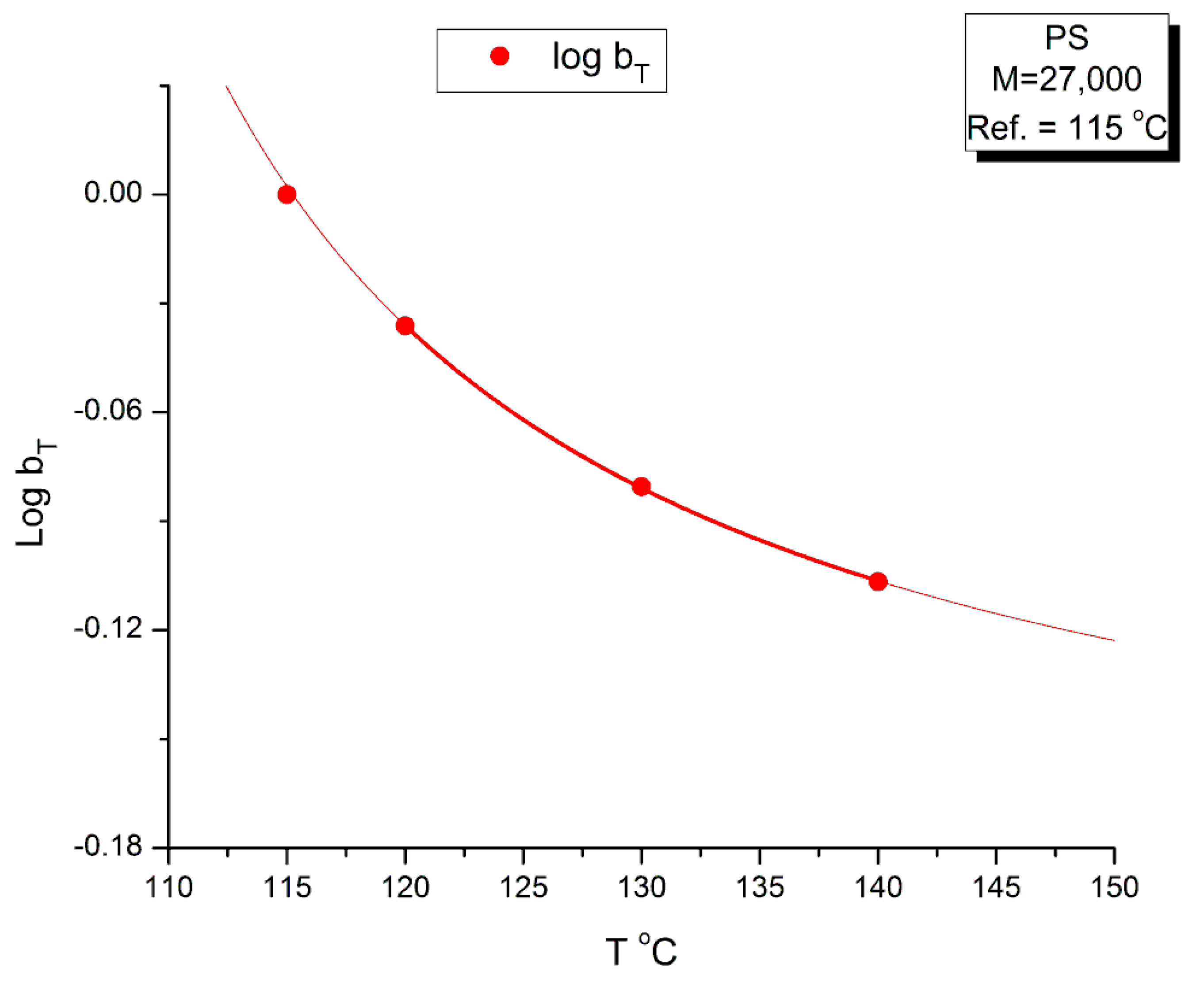
- The use of bT pursuant to the normalization of the moduli by the Rouse modulus GN is incorrect. The reason has been implicitly given in the previous section which showed the inadequacy of using GN except for G″(ω) and thus viscosity (Figure 10). To find the correct value of bT, a double-shifting regression is always required [33]. It has been shown, for instance, that the vertical shift factor, log bT, when it is obtained by regression-double-shifting, is not as predicted by the Rouse modulus GN/GN1, yet that its variation with T permits to detect the presence of transitions, such as the transition at Tg + 23 °C also visible from thermal stimulated depolarization data [19] or the TLL transition [24,34].
- The temperature range of applicability of the tts varies with the strain imposed during the frequency sweeps ([2] “Effect of Strain” (Section 5.8, p. 322) and with the thermal-mechanical history of the melt prior to the frequency sweep ([2] “Thermal-Mechanical History to create out-of-equilibrium melt properties”, Section 4.3.5.2 p. 206).
- The tts might be valid for a limited frequency range only or it might be valid on two or successive frequency ranges with different constants to express the 2 shift factors, log aT and log bT. It is the case for the 3 temperature ranges delimited by Tg + 23 and TLL.
Conclusion Regarding the Myth of the Time–Temperature Superposition Principle
- -
- The time–temperature superposition principle is not verified for the data we analyzed. Matsumiya and Watanabe recognized in their paper the shortcomings of the superposition applied to G′(ω) and G″(ω), yet they did not question why their data showed such a flagrant discrepancy. We believe that questioning why the tts does not work when performing super standard dynamic rheological experiments on a super standard polymer (PS) was worth the subsequent dedicated analysis time and effort it demands and triggers.
- -
- Why do the rheological curves for a simple PS studied in the linear range of visco-elasticity fail to superpose over a classical range of frequency (0.1 to 100 rad/s) using a span of temperature of only 25 °C? Why do the users of the current paradigm of polymer science avoid reporting the failures of a full superposition of their data? Why is there the need to restrict the frequency range or the temperature range for the sst to work? Is there no fundamental requirement for the prevailing theory of viscoelasticity to answer the following questions:
- -
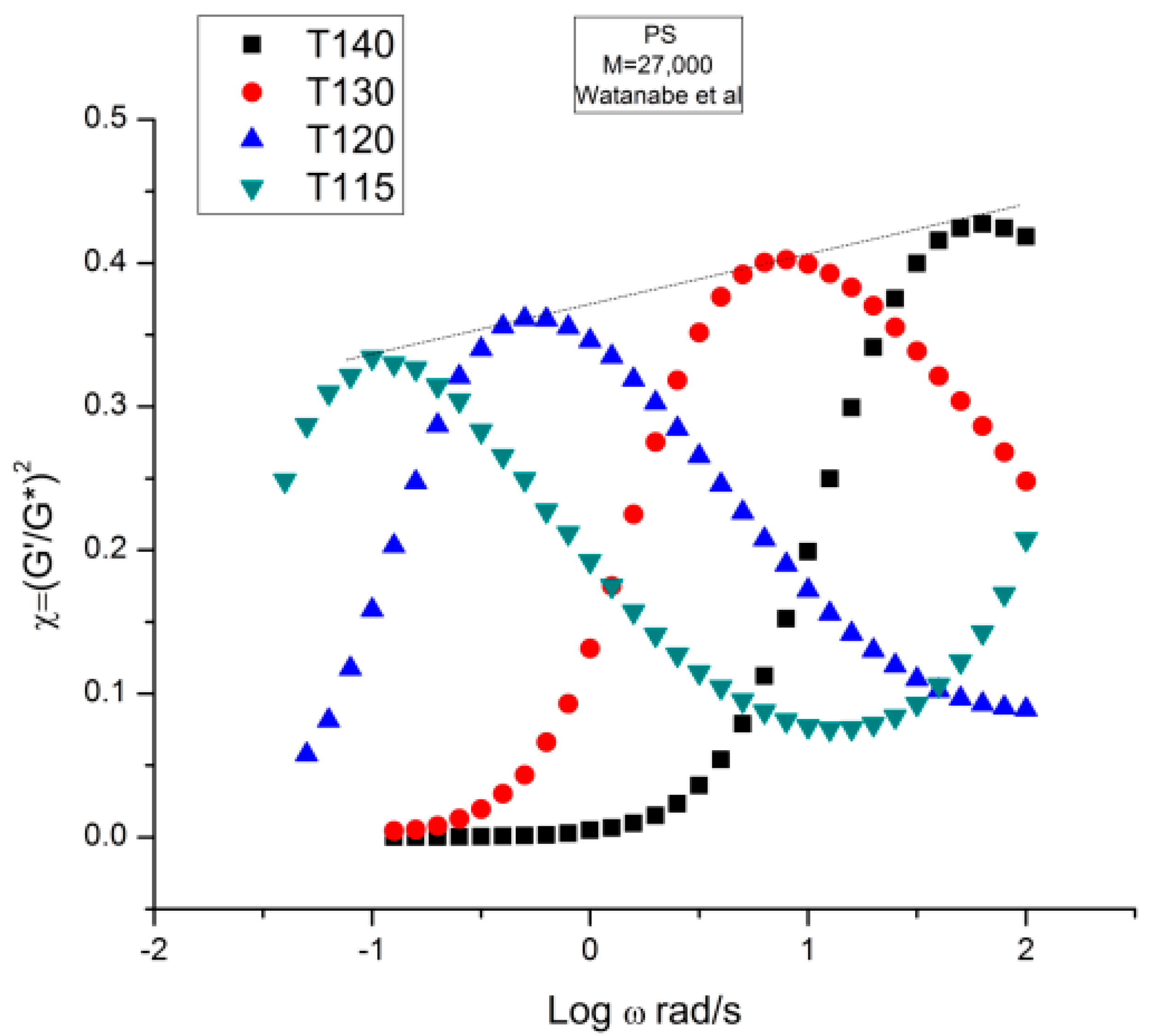
- Why is the tts valid only for the low (left) frequency side of the peak of χ vs. log ω?
- -
- Why does log η*(ω) only needs one horizontal shift of the curves, log aT, whereas the χ vs. log ω requires two shift factors, log aT and log bT when applying the tts,
- -
- Why are we systematically correcting vertically the rheological moduli by (ρT)−1 without checking if the Rouse modulus GN does normalize both G′(ω) and G″(ω)?
- -
- Why is the value of χ at the maximum increased and not decreased as T increases? This appears counter-intuitive with the explanation that glassy relaxation components are causing the maximum in the χ vs. log ω curve.
- -
- Why is the rheological behavior at T = 115 °C different than at T = 120 to 140 °C?
2.3. The Great Myth of Reptation. The Failure of the Reptation Model to Correctly Describe and Understand the Shear-Thinning Behavior of Entangled Polymeric Melts (M > Mc)
2.3.1. The Brilliance of the de Gennes’s Reptation Ideas
“…This result calls for a fundamental revision of the current theoretical picture for nonlinear rheological behavior of entangled polymeric liquids…the predictions by the tube model are not experimentally observed in a well-entangled polystyrene melt after a large uniaxial step deformation”.
2.3.2. Invalidation of Reptation by Rheo-SANS Results of Watanabe et al. (2007)
2.3.3. Invalidation of Reptation by Rheo-SANS Results of Noirez et al. (2009)
2.3.4. Invalidation of Reptation by Rheo-SANS Evidence That Chain Retraction Does Not Occur by Zhe Wang et al., 2017
“the two prominent spectral features associated with the chain retraction—peak shift of the leading anisotropic spherical harmonic expansion coefficient and anisotropy inversion in the intermediate wave number (Q) range around Rouse time—were not experimentally observed in a well-entangled polystyrene melt after a large uniaxial step deformation”.
“Unlike the previous investigations, there is no ambiguity associated with model fitting and no room for human bias. Therefore, our critical test clearly demonstrates that the chain retraction hypothesis of the tube model is not supported by small-angle neutron scattering experiments.”
“This result calls for a fundamental revision of the current theoretical picture for nonlinear rheological behavior of entangled polymeric liquids.”
“Therefore, without an alternative mechanism for molecular relaxation, the idea of nonaffine deformation alone does not seem to be able to explain the experimental observation.”
“Since the tube theory is of paramount importance for our current understanding of the flow and deformation behavior of entangled polymers, the invalidation of the chain retraction hypothesis has immense ramifications.”
2.3.5. Conclusion on the Great Myth of the Applicability of the Reptation Model to Entangled Polymer Melts (M > Mc)
2.4. Shear-Refinement and Sustained Orientation: The Lack of Understanding by the Current Paradigm
2.4.1. Shear-Refinement
“Intense working, producing high shear, will usually lead to a reduction in viscosity and also a decrease in the elastic response”.
Pre-Treatment on Branched Polymers
“The change is seen to be reversible by solution treatment. Molecular weight characterization indicated that all these samples were identical… [Shear-refinement effects] “might at first appear to be the result of degrading the polymer, are frequently reversed by cooking the melt, though the time for which the melt may need to be cooked to achieve reversion may be much longer than the natural time of the material (viscosity/modulus at zero shear)”.
The pre-treatment of the LCB-PP in the capillary rheometer at the highest shear stress applied causes a significant reduction of the tensile stress, which can be referred to the reduction of the mass-average molar mass. However, the significant decrease of the extrudate swell after the pre-treatment cannot be explained by the change of the molar mass, as the elastic behavior of polymer melts is known to be independent of the mass-average molar mass. Therefore, the reduction of the extrudate swell is an indication of a change of the entanglement network during the pre-treatment.
Pre-Treatment on Linear Polymers
2.4.2. Sustained Orientation
2.4.3. The Munstedt’s Exclusive Requisite That the Polymer Must Be an LCB (with Long Chain Branches) to Be Able to Obtain Shear-Refinement
Münstedt’s Critical Condition That Branching Must Be Present to Observe Shear-Refinement Is Wrong
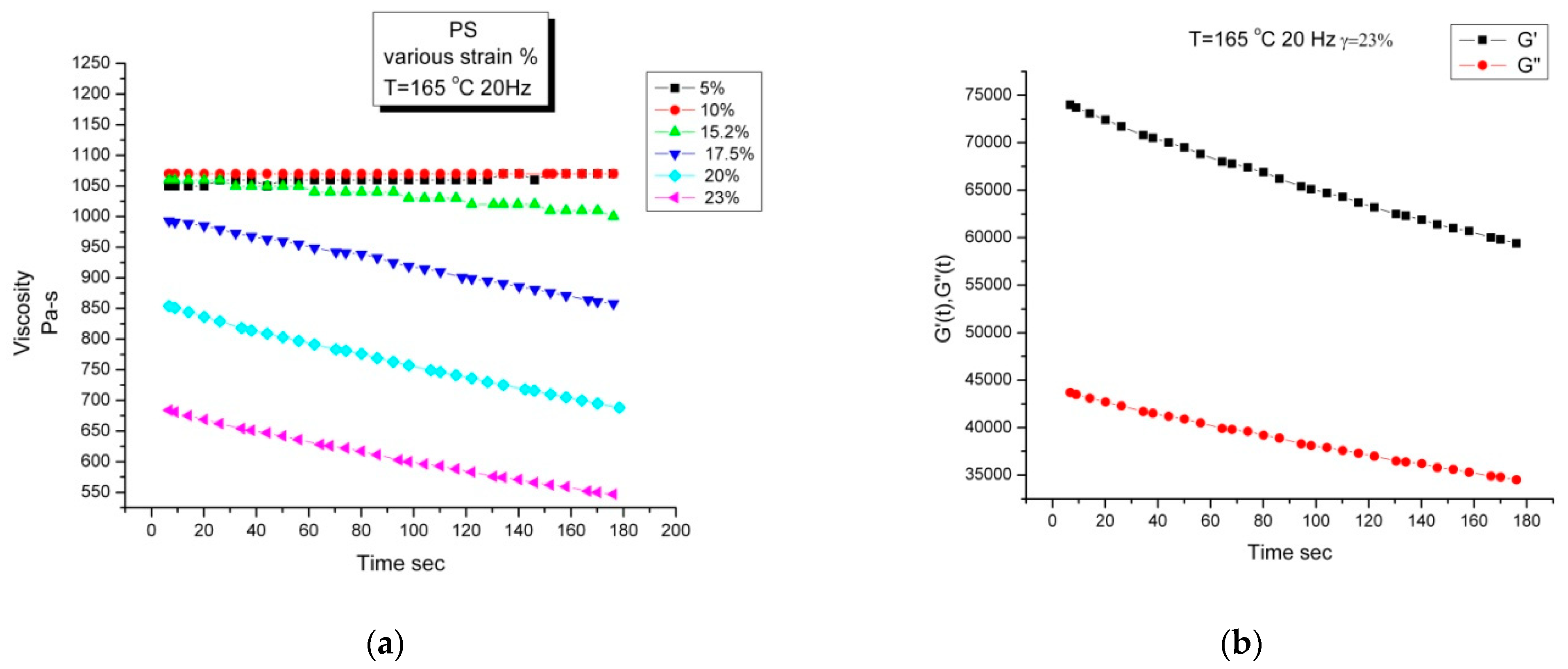
2.5. Strain-Induced Time Dependence of Rheological Functions
- Does a non-linear state obtained by increasing strain become immediately instable: time dependency starts as soon as its modulus differs from its linear value?
- Is the strain value for the end of linear viscoelasticity different from the strain value for the start of the time dependency of the non-linear modulus?
- Is the rate of the time dependency of modulus a function of the strain?
2.5.1. First Example of Strain Induced Transient of Viscosity (Inducement)
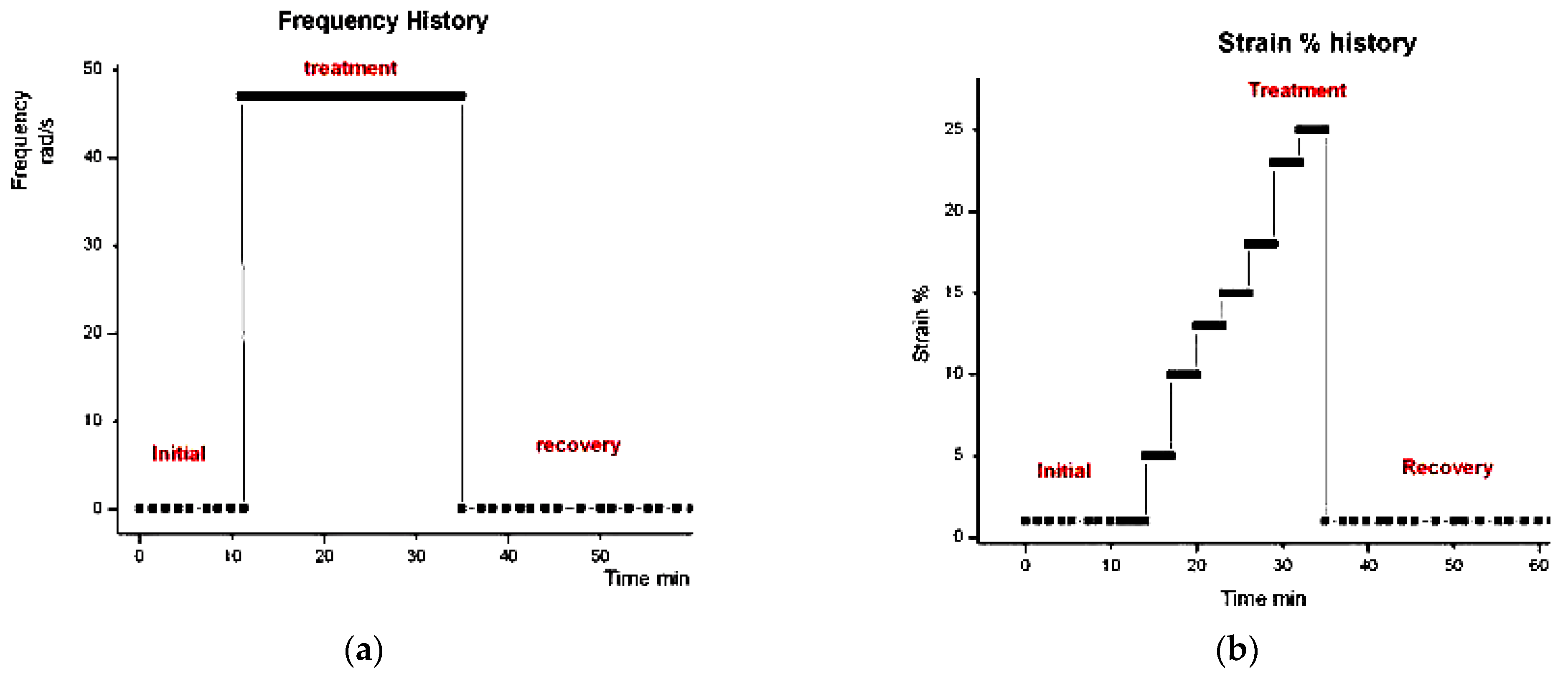
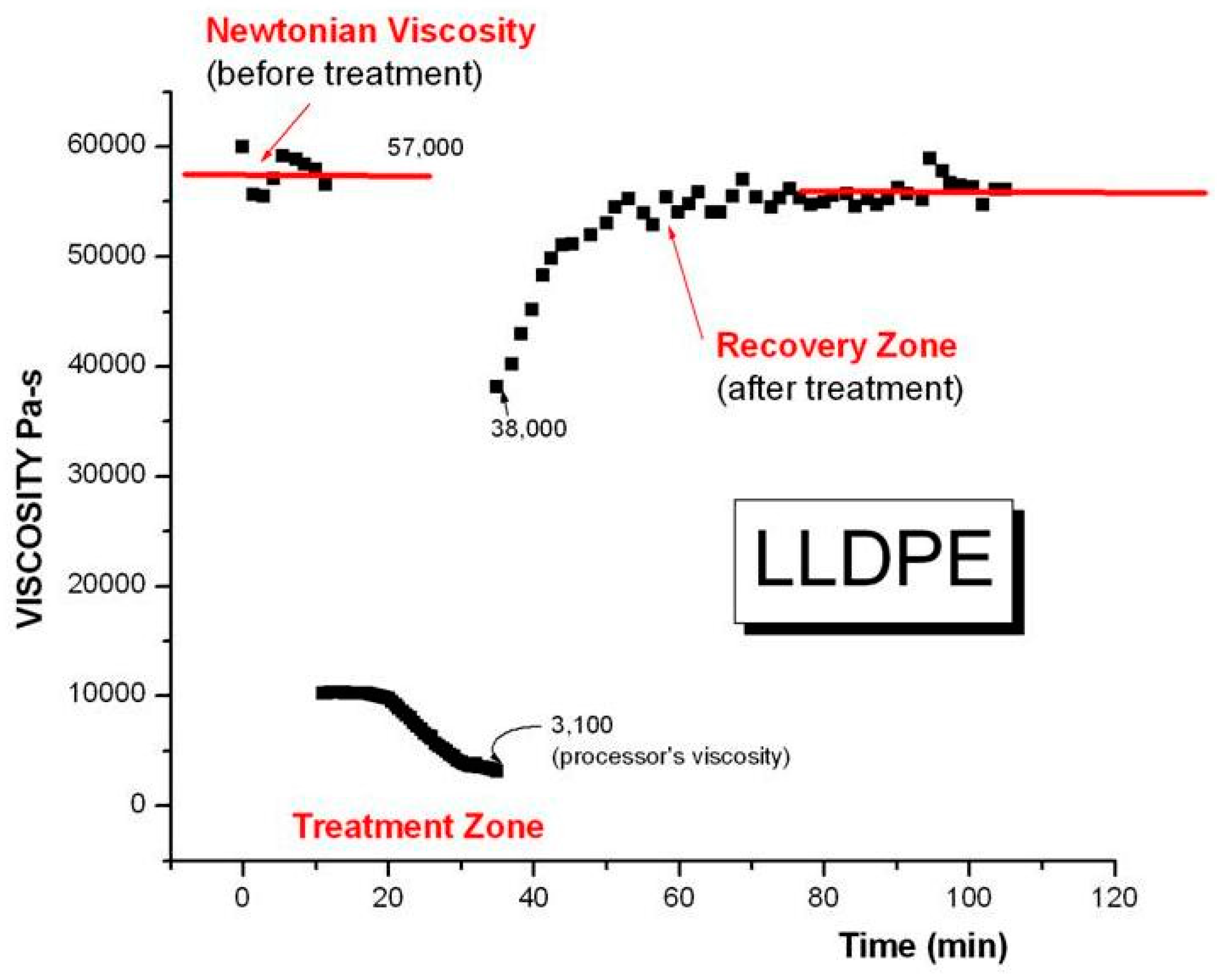
2.5.2. Second Example of Strain Induced Transient of Viscosity (Inducement and Recovery)
2.5.3. Conclusions on the Strain-Induced Time Dependence of Rheological Variables
The “Process Engineer” Interpretation of the Results
The Theoretical Physicist Interpretation of the Results
3. Conclusions
“In order to change an existing paradigm you do not struggle to try and change the problematic model. You create a new model and make the old one obsolete.”—Richard Buckminster Fuller
Funding
Conflicts of Interest
References
- Staudinger, H. Makromoleculare Chemie und Biologie; Wepf & Co.: Bale, Switzerland, 1947. [Google Scholar]
- Ibar, J.P. The Physics of Polymer Interactions—A Novel Approach to Rheology and Processing; Hanser Publishers: Munich, Germany, 2019. [Google Scholar]
- Flory, P.J. Spatial Configuration of Macromolecular Chains. Nobel Lecture. Available online: https://www.google.co.uk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwiHnuCy3uiBAxVWVN4KHaLXCqwQFnoECAEQAQ&url=https%3A%2F%2Fwww.nobelprize.org%2Fuploads%2F2018%2F06%2Fflory-lecture.pdf&usg=AOvVaw3357NM8tA3uiBA966iScGM&opi=89978449 (accessed on 11 December 1974).
- de Gennes, P.G. Soft Matter. Nobel Lecture. Available online: https://www.nobelprize.org/uploads/2018/06/gennes-lecture.pdf (accessed on 9 December 1991).
- Flory, P.J. Statistical Mechanics of Chain Molecules; Interscience Press: New York, NY, USA, 1969; 308p. [Google Scholar]
- de Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Rouse, P.E. A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
- de Gennes, P.G. Reptation of a Polymer Chain in the Presence of Fixed Obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
- Marrucci, G. Dynamics of Entanglements: A nonlinear model consistent with the Cox-Merz rule. J. Non-Newton. Fluid. Mech. 1996, 62, 279–289. [Google Scholar] [CrossRef]
- Marrucci, G.; Ianniruberto, G. Interchain pressure effect in extensional flows of entangled polymer melts. Macromolecules 2004, 37, 3934–3942. [Google Scholar] [CrossRef]
- Wagner, M.H.; Rubio, P.; Bastian, H. The molecular stress function model for polydisperse polymer melts with dissipative convective constraint release. J. Rheol. 2001, 45, 1387–1412. [Google Scholar] [CrossRef]
- McLeish, T.C.B.; Larson, R.G. Molecular constitutive equations for a class of branched polymers: The pom-pom polymer. J. Rheol. 1998, 42, 81–110. [Google Scholar] [CrossRef]
- Ibar, J.P. The Great Myths of Polymer Melt Rheology, Part I: Comparison of Experiment and Current Theory. J. Macromol. Sci. Part. B Phys. 2009, 48, 1143–1189. [Google Scholar] [CrossRef]
- Ibar, J.P. The Great Myths of Rheology, Part II: Transient and Steady-State Melt Deformation: The Question of Melt Entanglement Stability. J. Macromol. Sci. Part B Phys. 2010, 49, 1148–1258. [Google Scholar] [CrossRef]
- Ibar, J.P. Rebuttal to H. Munstedt’s article “ Mechanical Pretreatment of Polymer Melts. Critical Aspects and new rheological investigations on a linear and a long-chain branched Polypropylene”, J.O.R, 65.5(2021):871-885, DOI: 10.1122/8.0000237”. Glob. J. Sci. Front. Res. 2022, 22, 21–31. [Google Scholar]
- Ibar, J.P. Trouble with Polymer Physics: Development of “Sustained Orientation” Contradicts the Current Understanding of the Liquid State of Polymers. J. Macromol. Sci. Part. B 2015, 54, 722–748. [Google Scholar] [CrossRef]
- Ibar, J.P. Shear-Thinning of Polymeric Melts: The Failure of the Reptation Model. In The Physics of Polymer Interactions—A Novel Approach to Rheology and Processing; Hanser Publishers: Munich, Germany, 2019. [Google Scholar]
- Ibar, J.P. Do we need a new theory in polymer physics? J. Macromol. Sci. Part C Polym. Rev. 1997, 37, 389–458. [Google Scholar] [CrossRef]
- Ibar, J.P. A Dual and Cross-Dual interpretation of interactive coupling of conformers applied to thermally activated polarization and depolarization of polymers. In Dual-Phase Depolarization Analysis; Interactive Coupling in the Amorphous State of Polymers; De GRUYTER Publisher: Berlin, Germany, 2021. [Google Scholar]
- Ibar, J.P. The Dual-Phase Model of Polymer Interactions and the Cross-Dual-Phase Model of Entanglements. In Dual-Phase Rheology; De GRUYTER Publisher: Berlin, Germany, 2024. [Google Scholar]
- Ibar, J.P. Grain-Field Statistics of Open Dissipative Systems. Application to Polymer Conformers in Interactions; DE GRUYTER Publisher: Berlin, Germany, in preparation.
- Matsumiya, Y.; Watanabe, H. NonLinear Elongational Rheology of Unentangled Polystyrene and Poly(p-tert-butylstyrene) Melts. Macromolecules 2018, 51, 9710–9729. [Google Scholar] [CrossRef]
- Majeste, J.-C. Propriétés Viscoélastiques de Polymères Linéaires à Très Large Distribution de Masses Molaires. Ph.D. Thesis, Université de Pau et Pays de l’Adour, Pyrénées-Atlantiques, France, 1998. [Google Scholar]
- Ibar, J.P. A Dual-Phase Approach to reveal the presence and the impact of the TLL transition in Polymer Melts. Part I: Predicting the existence of Boyer’s TLL transition from the Vogel-Fulcher equation. J. Macromol. Sci. B. Phys. 2021, 60, 727–791. [Google Scholar] [CrossRef]
- Montfort, J.P. Dynamique Moleculaire et Comportement Rheologique des Polymers Enchevetres en Phase Fondue et en Solution Concentree. p. 75. Ph.D. Thesis, Université de Pau et Pays de l’Adour, Pyrénées-Atlantiques, France, 1984. [Google Scholar]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 1955, 77, 3701. [Google Scholar] [CrossRef]
- Ibar, J.P. The Great Myths of Rheology Part III: Elasticity of the Network of Entanglements. J. Macromol. Sci. Part B Phys. 2013, 52, 223–309. [Google Scholar] [CrossRef]
- Gray, R.W.; Harrison, G.; Lamb, J. Dynamic viscoelastic behaviour of low-molecular-mass polystyrene melts. Proc. Roy. Soc. 1977, A 356, 77. [Google Scholar]
- Davidson, D.W.; Cole, R.H. Dispersion and absorption in dielectrics I. Alternating current characteristics. J. Chem. Phys. 1941, 9, 341. [Google Scholar]
- Benallal, A.; Marin, G.; Montfort, J.P.; Derail, C. Linear viscoelasticity revisited: The relaxation function of monodisperse polymer melts. Macromolecules 1993, 26, 7229. [Google Scholar] [CrossRef]
- Leonardi, F. Determination de la Distribution des Masses Molaires D’Homopolymeres Lineaaires par Spectroscopie Mecanique. Table III-1 p. 146. Ph.D. Thesis, Universite de Pau et Pays de l’Adour, Pyrénées-Atlantiques, France, 1999. [Google Scholar]
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons: Hoboken, NJ, USA, 1970. [Google Scholar]
- Ibar, J.P. Non-Newtonian Flow Behavior of Amorphous Polymers in the T > Tg Temperature Range: A New Analysis of the Data According to the “Double-Shift” Procedure. J. Macromol. Sci. Phys. 1981, B19, 269–308. [Google Scholar] [CrossRef]
- Ibar, J.P. A Dual-Phase Approach to reveal the presence and the impact of the TLL transition in Polymer Melts. Part II: The theoretical and practical relevance of the TLL existence and characteristics on the understanding of the melt thermal analysis and rheological properties of polymers: Duality and Cross-Duality of the interactions. J. Macromol. Sci. B. Phys. 2021, 60, 792–838. [Google Scholar]
- Ibar, J.P. The Great Myths of Polymer Rheology: Elasticity of the Network of Entanglements. In The Physics of Polymer Interactions—A Novel Approach to Rheology and Processing; Hanser Publishers: Munich, Germany, 2019; pp. 307–311. [Google Scholar]
- Doi, M. Molecular Rheology of Concentrated Polymer Systems I. J. Polym. Sci. Polym. Phys. Ed. 1980, 18, 1005. [Google Scholar] [CrossRef]
- Milner, S.T.; McLeish, T.C.B. Reptation and Contour Length Fluctuations in Melts of Linear Polymers. Phys. Rev. Lett. 1998, 81, 725. [Google Scholar] [CrossRef]
- Likhtman, A.E.; McLeish, T.C.B. Quantitative Theory for Linear Dynamics of Linear Entangled Polymers. Macromolecules 2002, 35, 6332. [Google Scholar] [CrossRef]
- Daoud, M.; de Gennes, P.G. Some Remarks on the Dynamics of Polymer Melts. J. Polym. Sci., Polym. Phys. Ed. 1979, 17, 1971. [Google Scholar] [CrossRef]
- Klein, J. Dynamics of Entangled Linear, Branched, and Cyclic Polymers. Macromolecules 1986, 19, 105. [Google Scholar] [CrossRef]
- Mead, D.W.; Larson, R.G.; Doi, M. A Molecular Theory for Fast Flows of Entangled Polymers. Macromolecules 1998, 31, 7895. [Google Scholar] [CrossRef]
- Milner, S.T.; McLeish, T.C.B.; Likhtman, A.E. Reptation and Contour-Length Fluctuations in Melts of Linear Polymers. J. Rheol. 2001, 45, 539. [Google Scholar] [CrossRef]
- Marrucci, G.; Grizzuti, N. Fast Flows of Concentrated Polymers—Predictions of the Tube Model on Chain Stretching. Gazz. Chim. Ital. 1988, 118, 179. [Google Scholar]
- Pearson, D.; Herbolzheimer, E.; Grizzuti, N.; Marrucci, G. Transient Behavior of Entangled Polymers at High Shear Rates. J. Polym. Sci. B 1991, 29, 1589. [Google Scholar] [CrossRef]
- Graham, R.G.; Likhtman, A.E.; McLeish, T.C.B.; Milner, S.T. Microscopic Theory of Linear, Entangled Polymer Chains under Rapid Deformation Including Chain Stretch and Convective Constraint Release. J. Rheol. 2003, 47, 1171. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of Concentrated Polymer Systems Part 2.—Molecular Motion under Flow. J. Chem. Soc., Faraday Trans. 1978, 2, 1802. [Google Scholar] [CrossRef]
- Larson, R.G. Constitutive Equations for Polymer Melts and Solutions; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Watanabe, H.; Kanaya, T.; Takahashi, Y. Rheo-SANS behavior of Entangled Polymer Chains with Local Label Under Fast Shear Flow. In Activity Report on Neutron Scattering Research: Experimental Reports 14 (2007); Report Number: 146; Neutron Science Laboratory: Neutron Science Laboratory, Institute for Solid State Physics, University of Tokyo: Tokyo, Japan, 2007. [Google Scholar]
- Noirez, L.; Mendil-Jakani, H.; Baroni, P. New light on old wisdoms on molten polymers: Conformation, slippage and shear banding in sheared entangled and unentangled melts. Macromol. Rapid Commun. 2009, 30, 1709–1714. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Lam, C.N.; Chen, W.-R.; Wang, W.; Liu, J.; Liu, Y.; Porcar, L.; Stanley, C.B.; Zhao, Z.; Hong, K.; et al. Fingerprinting Molecular Relaxation in Deformed Polymers. Phys. Rev. X 2017, 7, 031003. [Google Scholar] [CrossRef]
- Cogswell, F.N. Polymer Melt Rheology, a Guide for Industrial Practice. Woodhead Publishing Ltd.: Sawston, UK, 1997; p. 57. [Google Scholar]
- Hanson, D.E. Shear Modification of Polyethylene. Polym. Eng. Sci. 1969, 9, 405–414. [Google Scholar] [CrossRef]
- Rokudai, M. Influence of shearing history on the rheological properties and processability of branched polymers. I. J. Appl. Polym. Sci. 1979, 23, 463–471. [Google Scholar] [CrossRef]
- Maxwell, B. Controlled Shear Modification of Low Density Polyethylene. In Proceedings of the 50th Anniversary Conference of the Society of Rheology, Boston, MA, USA, 28 October–1 November 1979. [Google Scholar]
- Agassant, J.F.; Avenas, P.; Sergent, J.-P.; Vergnes, B.; Vincent, M. La Mise en Forme des Matières Plastiques. Lavoisier Tec et Doc, 1996. Available online: https://www.paprec.com/fr/comprendre-le-recyclage/tout-savoir-sur-les-matieres-recyclables/plastiques/la-mise-en-oeuvre-des-matieres-plastiques/ (accessed on 8 October 2023).
- Schreiber, H.P. Cause and effect in time dependent flow of thermoplastics melts—A review. Polym. Eng. Sci. 1966, 317–323. [Google Scholar] [CrossRef]
- Ritzau, G. Shear modification of polyolefins and its integration on polymer processing. Int. Polym. Process. 1987, 1, 188–197. [Google Scholar] [CrossRef]
- Ritzau, G.; Ram, A.; Izrailov, L. Effect of shear modification on the rheological behaviour of two LDPE grades. Polym. Eng. Sci. 1989, 29, 214. [Google Scholar] [CrossRef]
- Leblans, P.J.R.; Bastiaansen, C. Shear modification of low density polyethylene: Its origin and its effect on the basic rheological functions of the melt. Macromolecules 1989, 22, 3312–3317. [Google Scholar] [CrossRef]
- Van Prooyen, M.; Bremner, T.; Rudin, A. Mechanism of shear modification of low density polyethylene. Polym. Eng. Sci. 1994, 34, 570–579. [Google Scholar] [CrossRef]
- Münstedt, H. The influence of various deformation histories on elongational properties of LDPE. Colloid. Polim. Sci. 1981, 259, 966–972. [Google Scholar] [CrossRef]
- Ram, A.; Izailov, L. Shear modification of polyethylene. J. Appl. Polym. Sci. 1986, 31, 85–100. [Google Scholar] [CrossRef]
- Bourrigaud, S. Etude de la Modification des Propriétés Rhéologiques Induite par L’écoulement: Application à L’extrusion-couchage. Ph.D. Thesis, Universite de Pau et Pays del’Adour, Pyrénées-Atlantiques, France, 2004. [Google Scholar]
- Berger, S. Einfluss der Mechanischen Vorgeschichte aud das Rheologische Verhalten von Langkettenierzweigtem Polypropylen. Ph.D. Thesis, University of Erlanden, Erlangen, Germany, 2005. [Google Scholar]
- Bourrigaud, S.; Marin, G.; Poitou, A. Shear-Modification of Long-Chain branched Polymers: A Theoretical Approach using the Pom-Pom Model. Macromolecules 2003, 36, 1388–1394. [Google Scholar] [CrossRef][Green Version]
- Stange, J.; Berger, S.; Munsted, H. Influence of Flow History in the Rheological Properties of a Long-Chain Branched Polypropylene; ESR AERC Grenoble: Grenoble, France, 2005. [Google Scholar]
- Ibar, J.P. Extrusion of Polymer Melts under Intensive Shear-Thinning Inducing Lower Pressure and Temperature Requirements. In ANTEC Proceedings 2001; ANTEC: Danbury, CT, USA, 2001; p. 481. [Google Scholar]
- Ibar, J.P. Control of Pseudo-Plasticity of Polymer Melts by Disentanglement Methods. In Proceedings of the 2nd Annual European Rheology Conference (AERC), Grenoble, France, 21–23 April 2005. [Google Scholar]
- Ibar, J.P. Process for the Control of Flow Properties of Polymers. U.S. Patent US2005/0267289A1, 1 December 2005. [Google Scholar]
- Munstedt, H. Mechanical pretreatment of polymer melts: Critical aspects and new rheological investigations on a linear and a long-chain branched polypropylene. J. Rheol. 2021, 65, 871–885. [Google Scholar] [CrossRef]
- Ibar, J.P. The Great Myths of Polymer Rheology: Transient and Steady State. The Question of Melt Entanglement Stability. In The Physics of Polymer Interactions—A Novel Approach to Rheology and Processing; Hanser Publishers: Munich, Germany, 2019; pp. 211–232. [Google Scholar]
- Vinogradov, G.V.; Malkin, A.Y.; Plotnikova, E.P.; Kargin, V.A. Thixotropy of polymers in the visco-fluid state. Dokl. Akad. Nauk. 1964, 154, 1421. [Google Scholar]
- Wang, S.-Q. Molecular transitions and dynamics at polymer/wall interfaces: Origins of flow instabilities and wall slip. Adv. Polym. Sci. 1999, 138, 227–275. [Google Scholar]
- Edwards, S.F.; Doi, M. The Theory of Polymer Dynamics; Clarendon: Oxford, UK, 1986. [Google Scholar]
- Rokudai, M.; Mihara, S.; Fujiki, T. Influence of shearing history on the rheological properties and processability of branched polymers. II. Optical properties of low-density polyethylene blown films. J. Appl. Polym. Sci. 1979, 23, 3289–3294. [Google Scholar] [CrossRef]
- Ibar, J.P. Control of Thixotropicity of Polymer Melts by Disentanglement Processing. In ANTEC Proceedings 2005; ANTEC: Danbury, CT, USA, 2005; p. 10370. [Google Scholar]

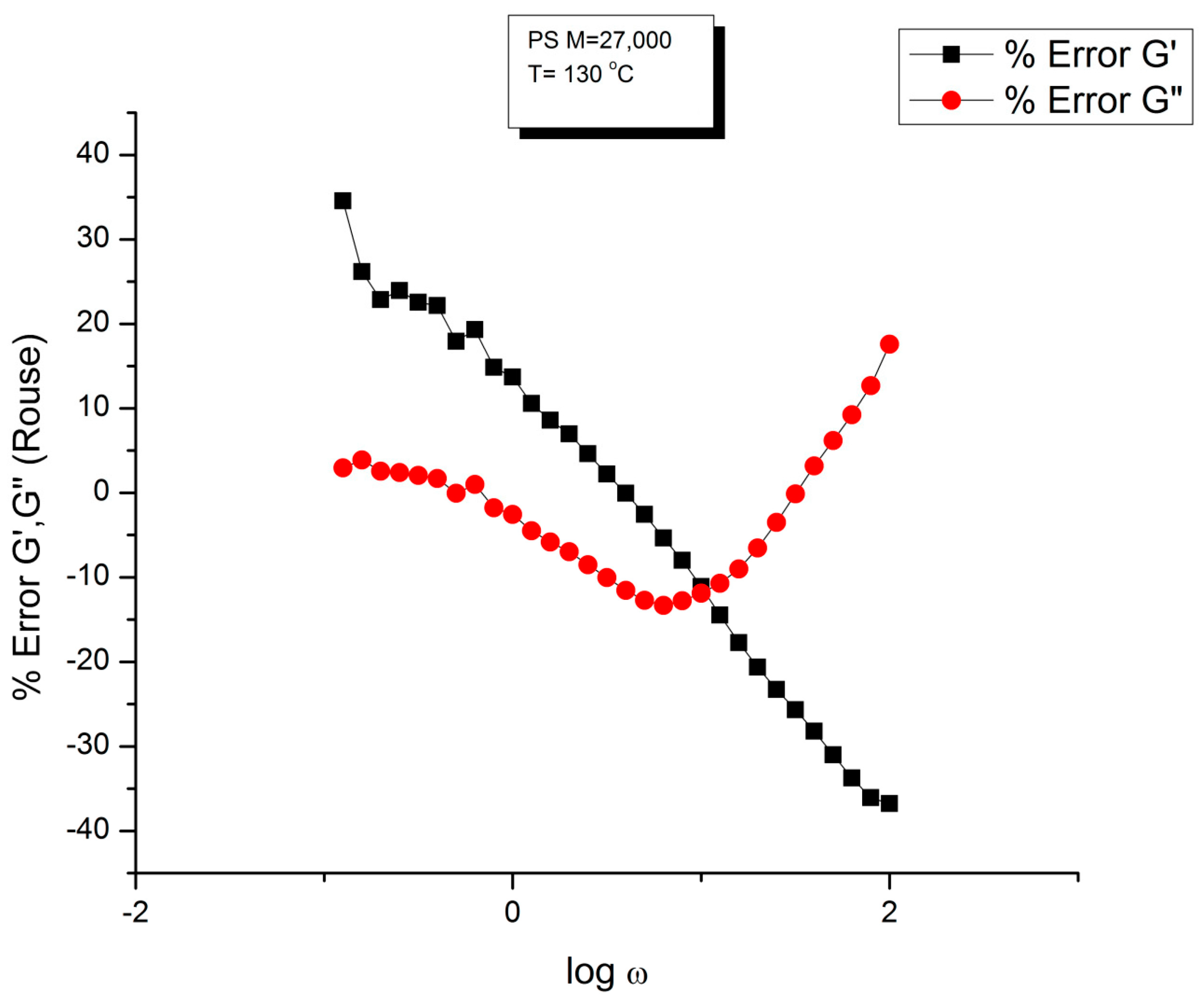
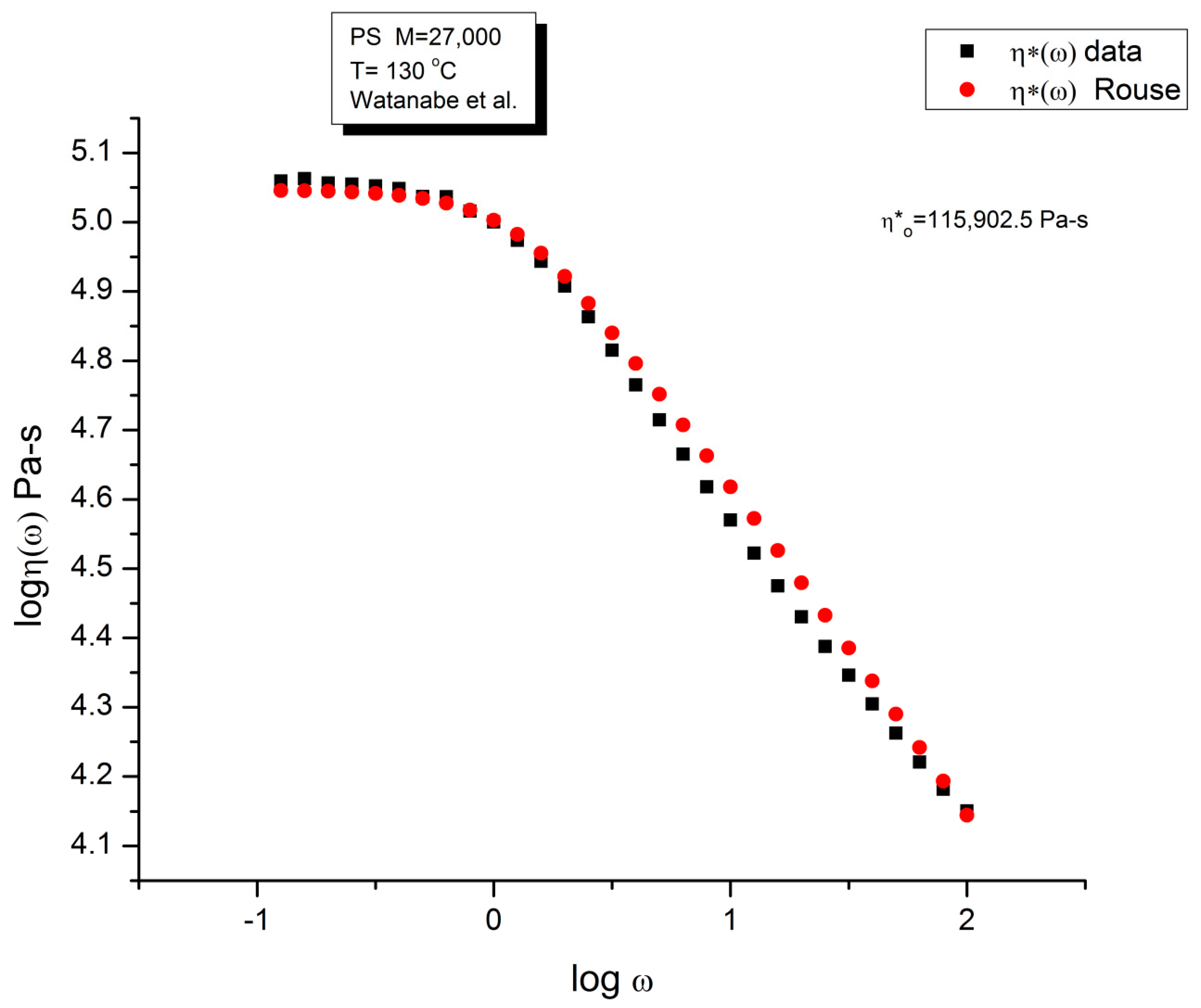
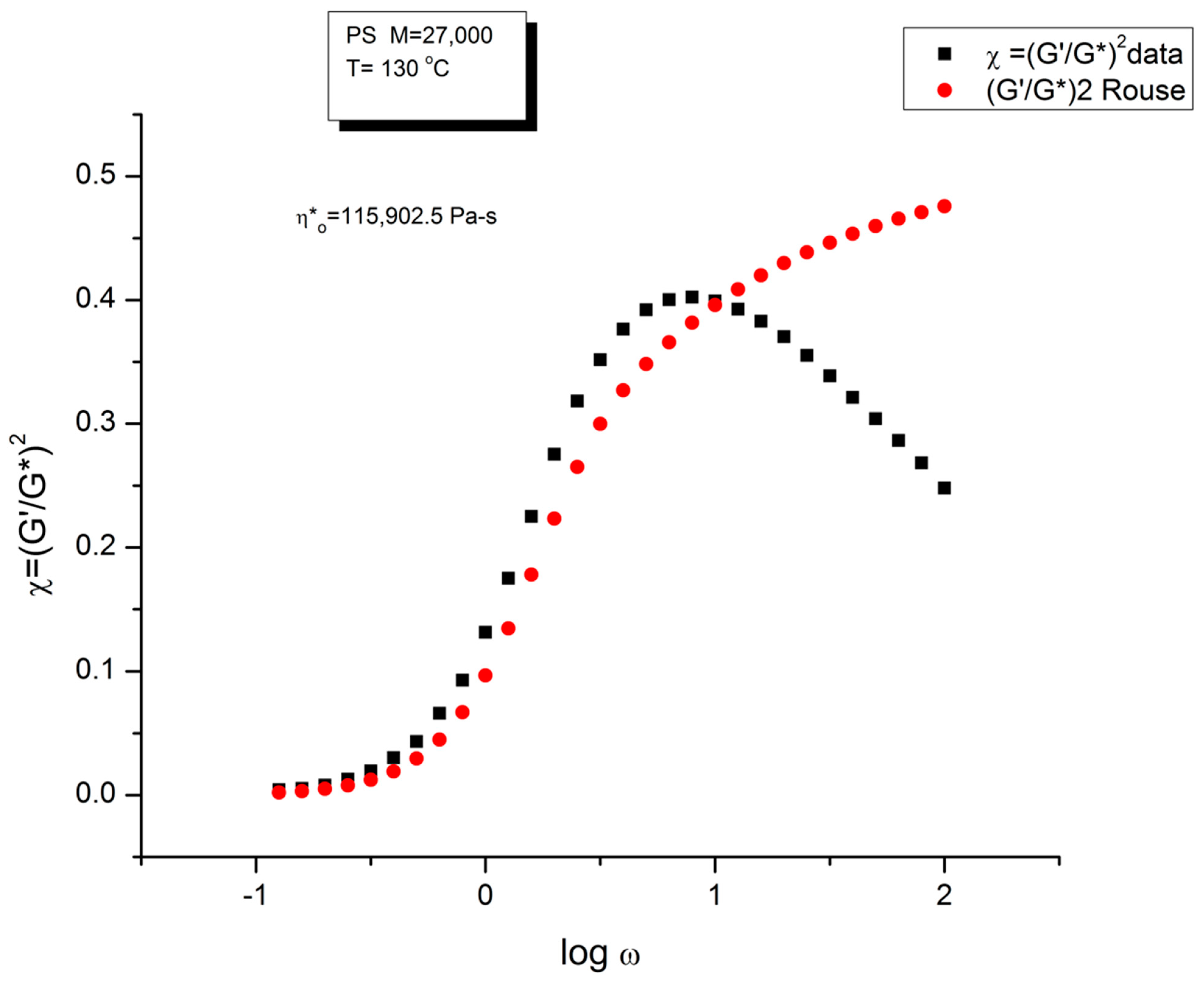

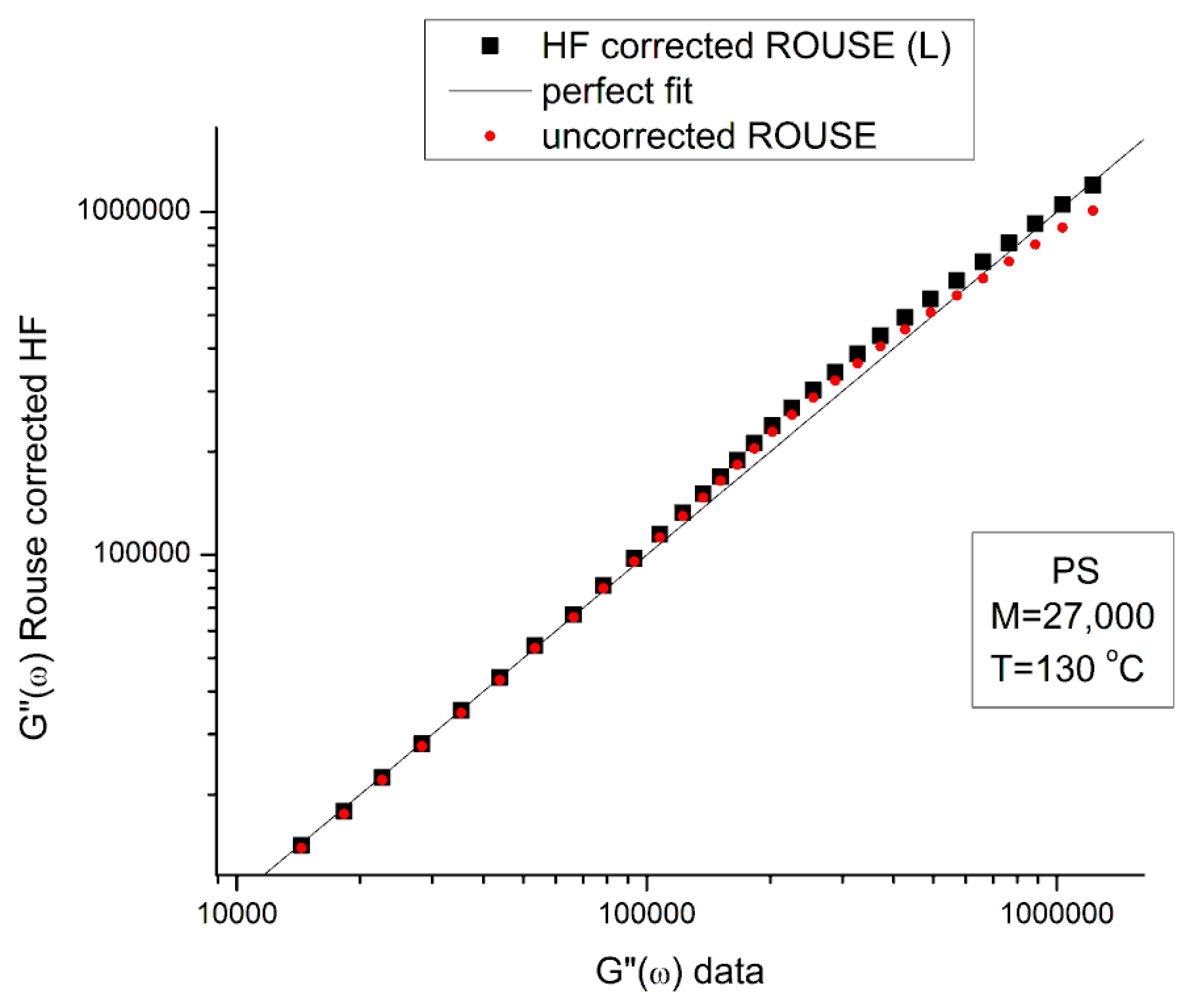


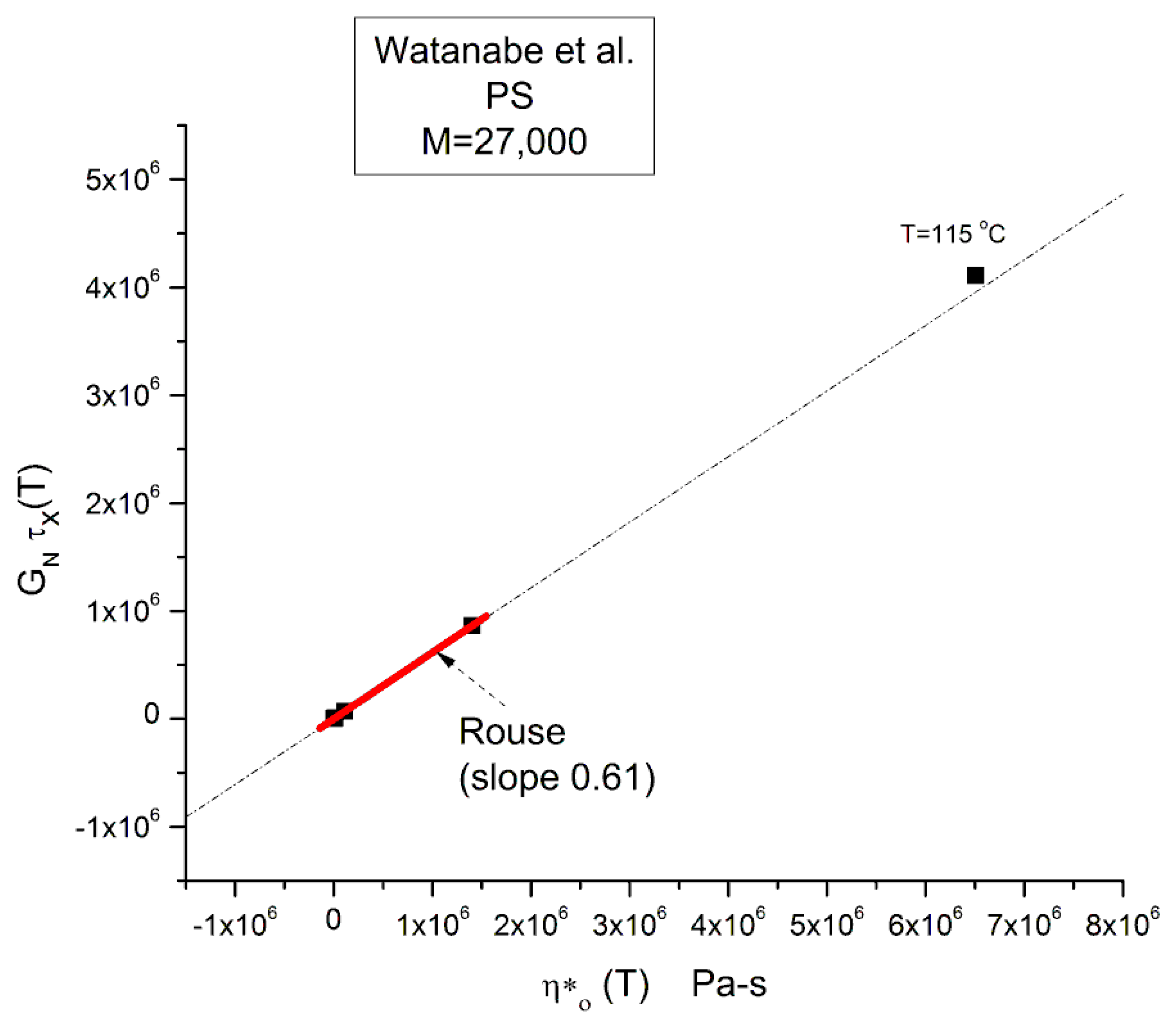

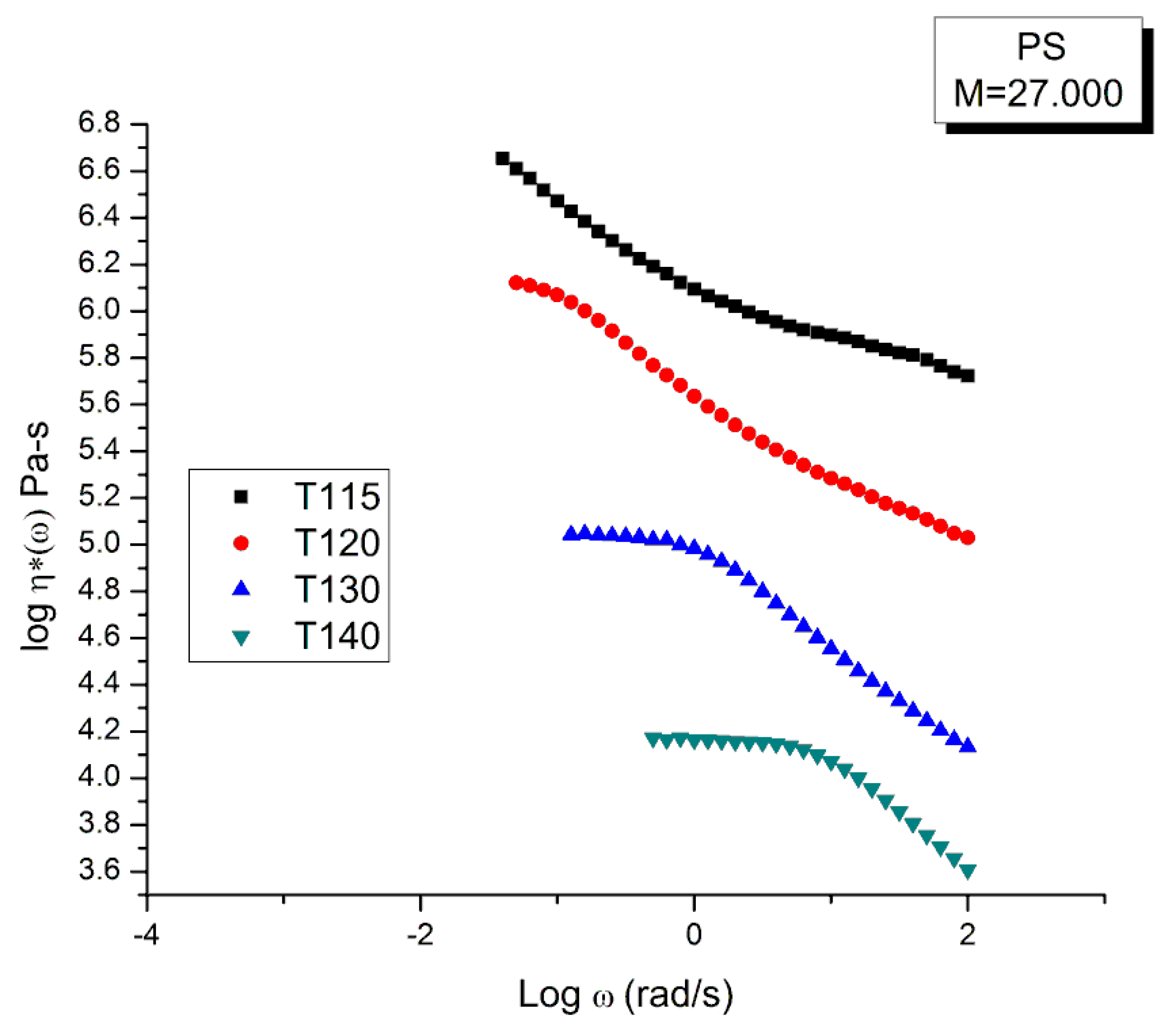

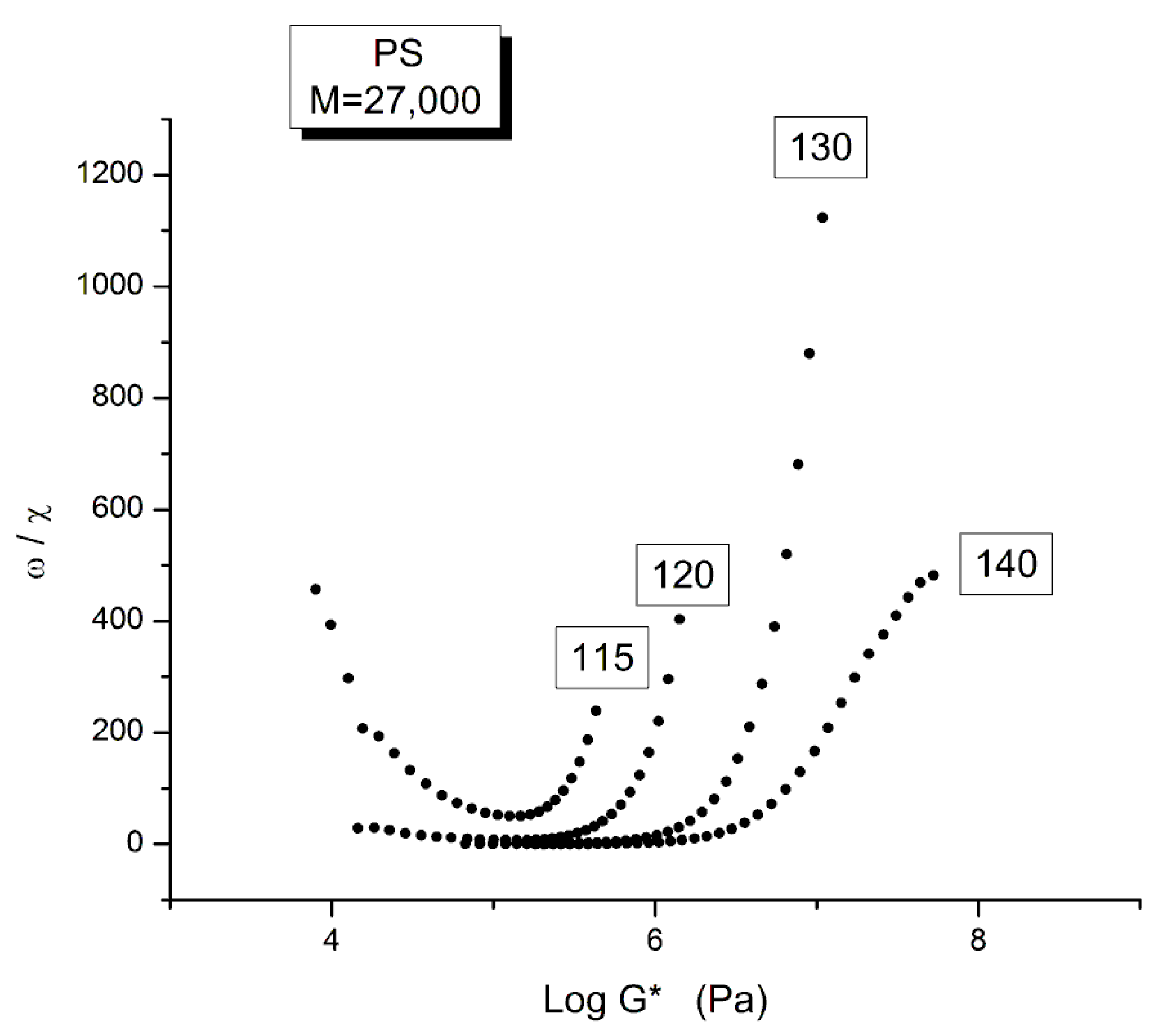
| T oC | Log τx τx =1/ωx | Log η*o Pa-s (Eq. (4)) | ρ (g/cc) melt density | GN (Pa) PS 27,000 ρRT/M | GN x τx | η*O Pa-s | I′M See text | GN calc. from G′(ω) | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 115 | 1.52824 | 6.8135 | 1.01854 | 121,744.4 | 4.11 × 106 | 6.51 × 106 | - | |
| 2 | 120 | 0.84678 | 6.14749 | 1.01568 | 122,966.2 | 864,105.4 | 1.40 × 106 | 6.78861 | 75,843.4 |
| 3 | 130 | −0.27389 | 5.04994 | 1.01 | 125,389.1 | 66,736.86 | 112,187.5 | 4.6973 | 107,141.6 |
| 4 | 140 | −1.15712 | 4.18292 | 1.00439 | 127,785.1 | 8899.472 | 15,237.84 | 3.02546 | 133,217.8 |
| M g/mole | ρ g/cm3 | Log GN calc from ρRT/M | I’M (see text) | ωx(M) Maxwell rad/s | Log GN calc from G′(ω) | Log η*o (Pa-s) [23] | Log GN calc from G″(ω) | |
|---|---|---|---|---|---|---|---|---|
| 1 | 2000 | 0.98129 | 6.24709 | −6 | 7.73 × 106 | 7.56106 | −3.03205 | 3.6399 |
| 2 | 4000 | 0.98803 | 5.94903 | −3.38286 | 238404.6 | 7.15664 | −1.88678 | 3.27439 |
| 3 | 5050 | 0.98945 | 5.84842 | −3.19938 | 56491.44 | 6.08946 | −0.6361 | 3.89974 |
| 4 | 8500 | 0.99164 | 5.62326 | −1.35373 | 14874.16 | 6.77601 | −0.17089 | 3.78539 |
| 5 | 11600 | 0.99251 | 5.4886 | −1.20429 | 4096.45 | 5.8054 | 0.36388 | 3.76014 |
| 6 | 13000 | 0.99276 | 5.43922 | −0.23375 | 4769.655 | 6.90809 | 0.83051 | 4.29285 |
| 7 | 17500 | 0.9933 | 5.31037 | 0.53143 | 1815.841 | 6.83446 | 1.6037 | 4.64663 |
| 8 | 25000 | 0.99378 | 5.15567 | 1.42833 | 501.593 | 6.6139 | 2.38771 | 4.87192 |
| Temperature °C | Log aT T Ref = 115 | Log bT (from χ) T Ref = 115 |
|---|---|---|
| 115 | 0 | 0 |
| 120 | −0.7 | −0.03617 |
| 130 | −1.81 | −0.08049 |
| 140 | −2.69 | −0.10672 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibar, J.P. The Challenges Facing the Current Paradigm Describing Viscoelastic Interactions in Polymer Melts. Polymers 2023, 15, 4309. https://doi.org/10.3390/polym15214309
Ibar JP. The Challenges Facing the Current Paradigm Describing Viscoelastic Interactions in Polymer Melts. Polymers. 2023; 15(21):4309. https://doi.org/10.3390/polym15214309
Chicago/Turabian StyleIbar, Jean Pierre. 2023. "The Challenges Facing the Current Paradigm Describing Viscoelastic Interactions in Polymer Melts" Polymers 15, no. 21: 4309. https://doi.org/10.3390/polym15214309
APA StyleIbar, J. P. (2023). The Challenges Facing the Current Paradigm Describing Viscoelastic Interactions in Polymer Melts. Polymers, 15(21), 4309. https://doi.org/10.3390/polym15214309








