Micromechanical Models for FDM 3D-Printed Polymers: A Review
Abstract
:1. Introduction
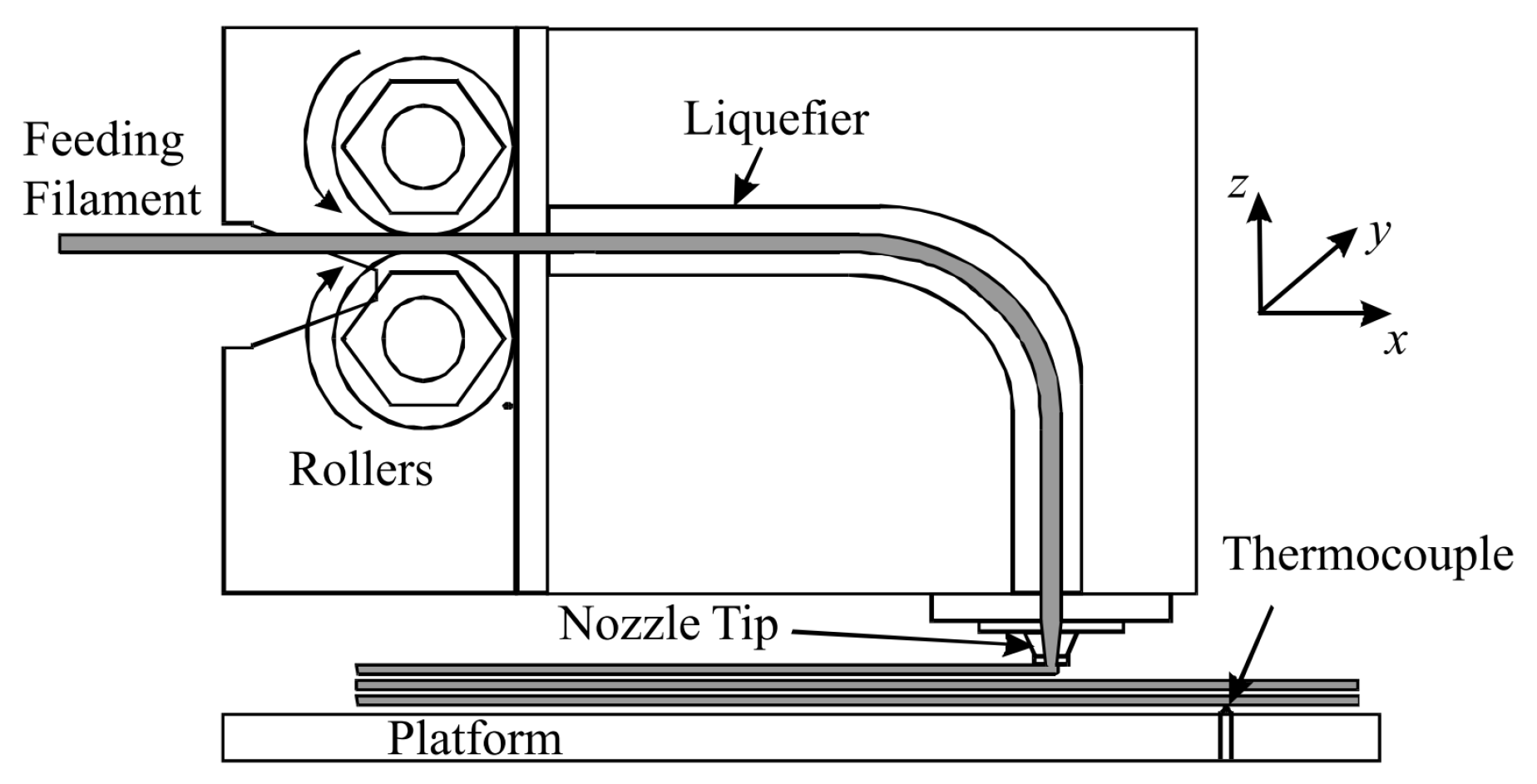
2. Identification of Printing Process Parameters
3. Characteristic Mechanical Properties
4. Available Characterization Techniques and Models
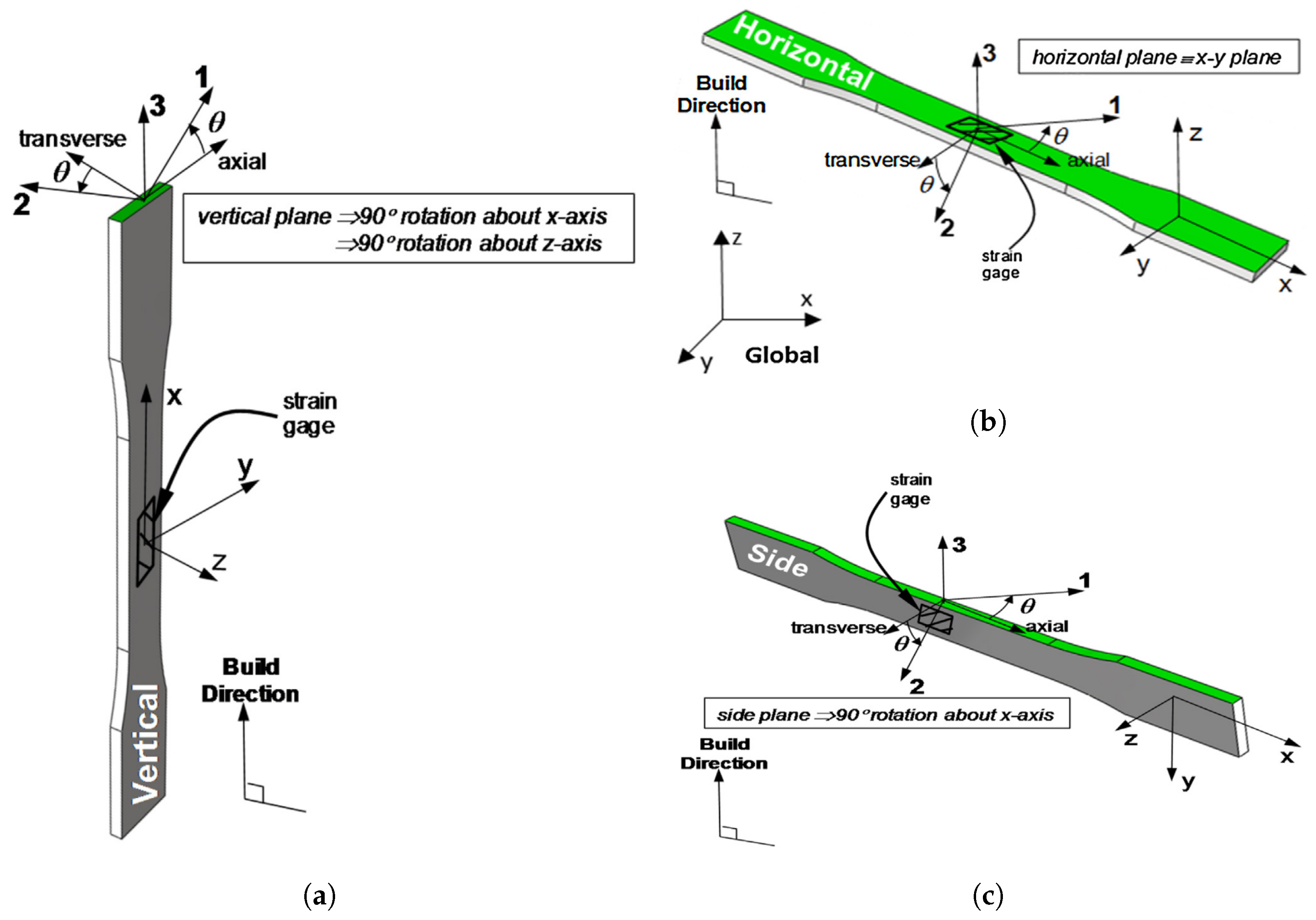
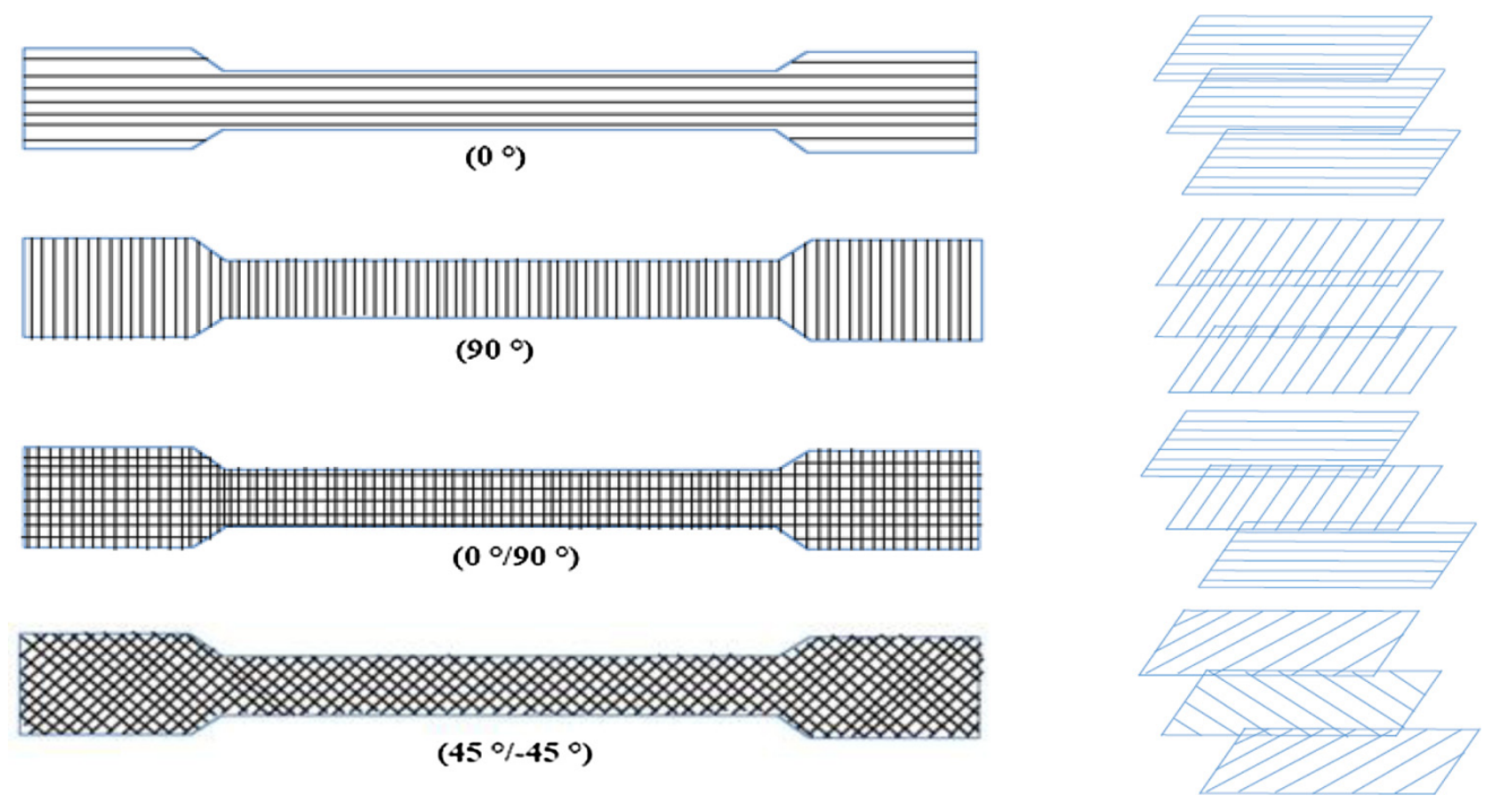
4.1. Experimental Analysis
4.2. Finite Element Analysis
4.2.1. Representative Volume Elements
Quantitative Characterization by X-ray Computed Tomography
Microstructural Images and Cross-Sectional Morphology
Homogenization Approaches
4.2.2. Specimen-Level Models
4.3. Analytical and Theoretical Models
4.3.1. Yield Criteria and Plasticity Models
4.3.2. Predictive and Generalized Strength Models
4.4. Microstructural and Fractographic Analyses
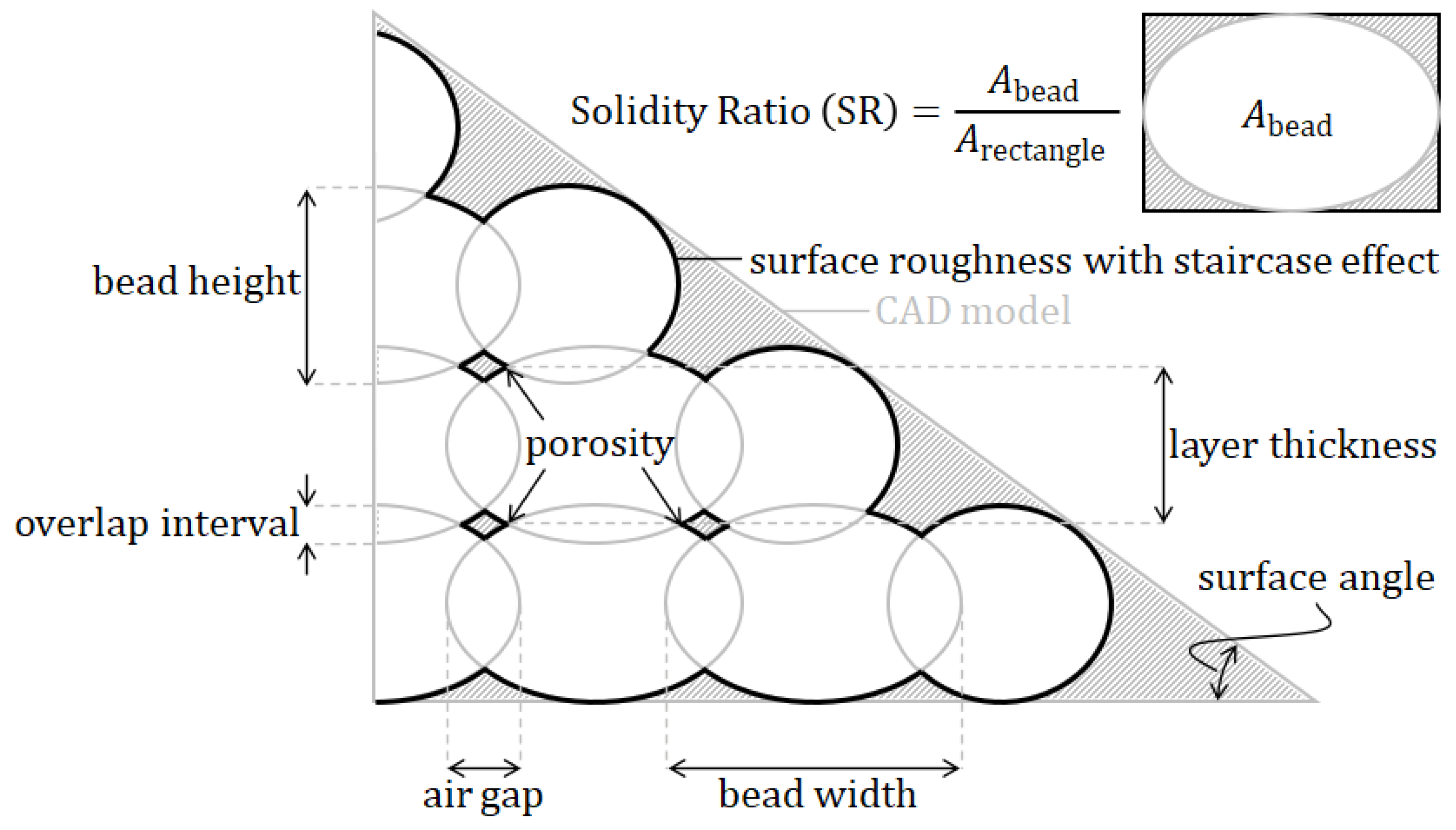
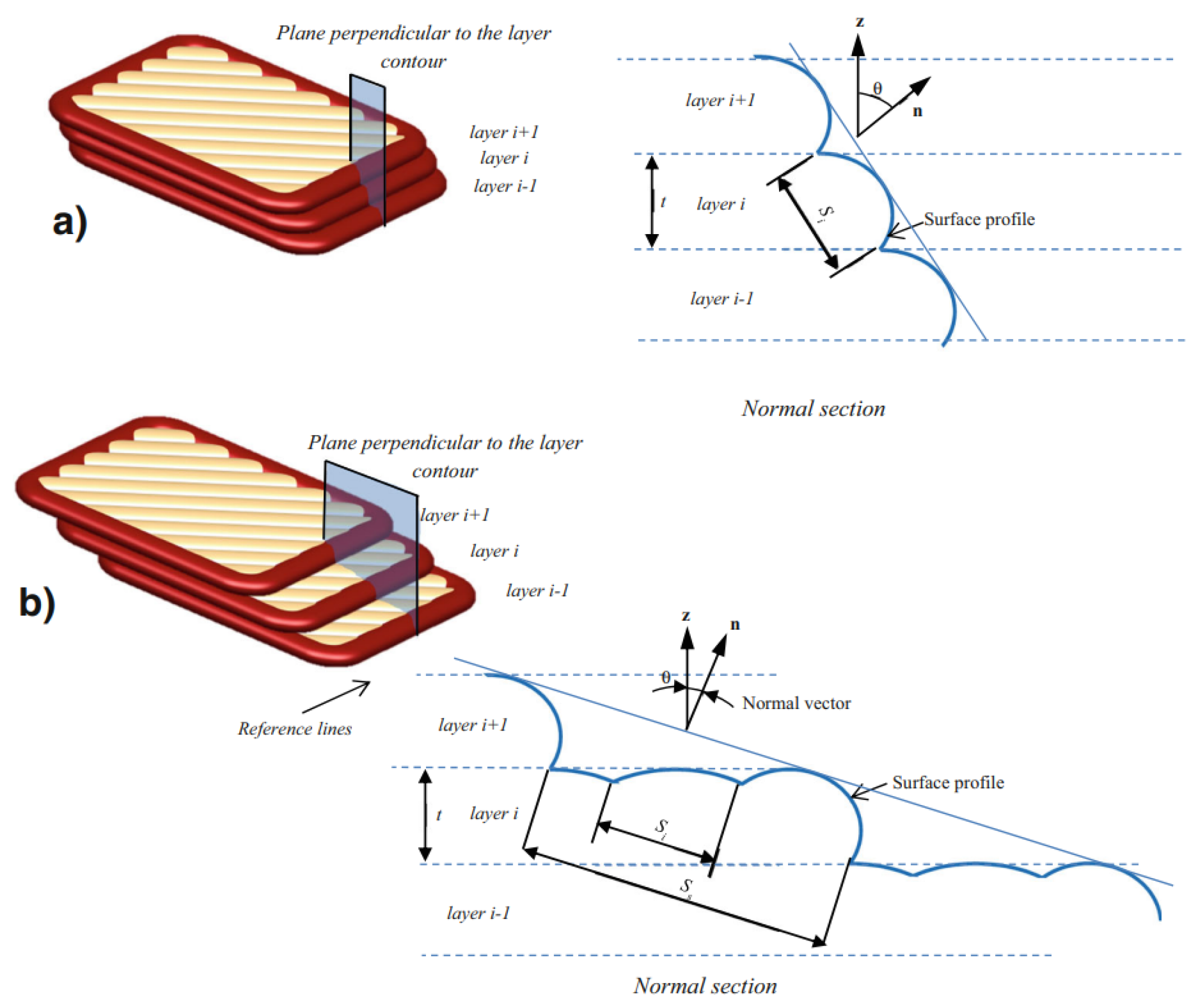
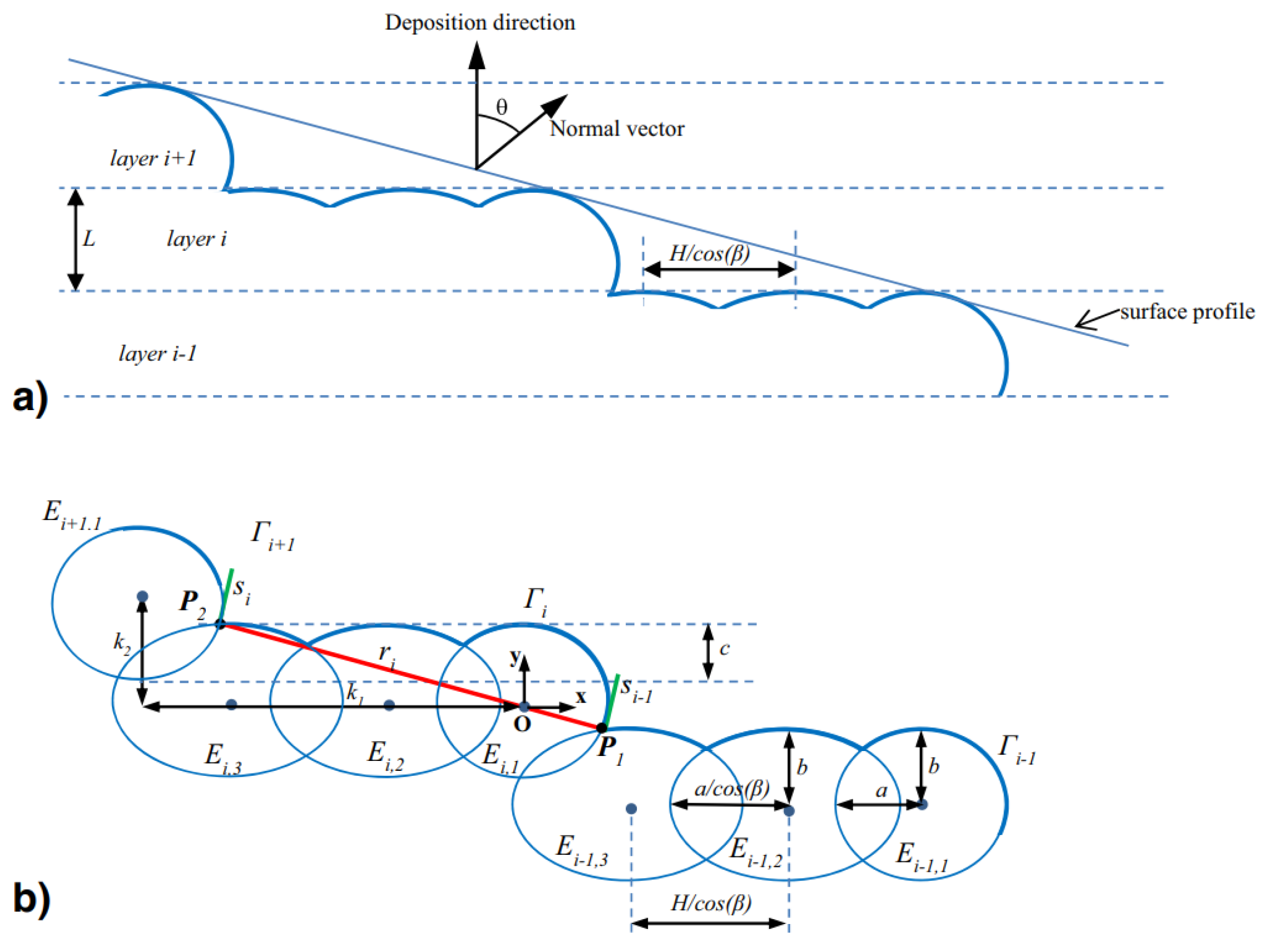
4.5. Geometrical Analysis
4.5.1. Edge Profile Simulations
4.5.2. Surface Roughness and Quality Models
| Characteristic Mechanical Property | Printing Process Parameter |
|---|---|
| Strength | Raster orientation [2,6,7,8,15,34,50,51,52,53] |
| Cross-sectional shape [6,8] | |
| Layer thickness [6,8] | |
| Overlap interval [6] | |
| Air gap [6,8] | |
| Porosity [5] | |
| Build direction [8] | |
| Bead width [8] | |
| Number of contours [8] | |
| Fracture toughness | Build direction [29] |
| Raster orientation [29,32,33] | |
| Inter-layer bond strength | Cross-sectional shape [2,6,24,25,27,28,31,32,33] |
| Printing temperature [31,32,33] | |
| Printing speed [31,32,33] | |
| Porosity [6] | |
| Raster orientation [15,50,51,52,53] | |
| Stiffness | Porosity [7,9,28] |
| Air gap [8,9,14,28] | |
| Raster orientation [2,7,8,14,28] | |
| Build direction [8,28] | |
| Cross-sectional shape [28] | |
| Layer thickness [8,28] | |
| Bead width [8,28] | |
| Overlap interval [28] | |
| Number of contours [8] |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| AM | Additive manufacturing |
| FDM | Fused deposition modeling |
| RP | Rapid prototyping |
| CAD | Computer-aided design |
| FFF | Fused filament fabrication |
| STL | Standard triangulation language |
| ABS | Acrylonitrile butadiene styrene |
| PLA | Poly-lactic acid |
| TPU | Thermoplastic polyUrethane |
| PC | Polycarbonate |
| PEI | Polyetherimide |
| PAEK | Polyaryletherketone |
| PEEK | Polyetheretherketone |
| SR | Solidity ratio |
| LWM | Low molecular weight |
| ML | Machine learning |
| TFS | Tensile failure strength |
| SFS | Shear failure strength |
| DCB | Double-cantilever beam |
| FEA | Finite element analysis |
| RVE | Representative volume element |
| XCT | X-ray computed tomography |
| UD | Unidirectional |
| ROM | Reduced-order model |
| FSDT | First-order shear deformation laminate theory |
| UC | Unit cell |
| TFA | Transformation field analysis |
| GT | Gurson–Tvergaard |
| SEM | Scanning electron microscope |
References
- Paul, S. Finite element analysis in fused deposition modeling research: A literature review. Meas. J. Int. Meas. Confed. 2021, 178. [Google Scholar] [CrossRef]
- Alaimo, G.; Marconi, S.; Costato, L.; Auricchio, F. Influence of meso-structure and chemical composition on FDM 3D-printed parts. Compos. Part B Eng. 2017, 113, 371–380. [Google Scholar] [CrossRef]
- Domingo-Espin, M.; Puigoriol-Forcada, J.M.; Garcia-Granada, A.A.; Llumà, J.; Borros, S.; Reyes, G. Mechanical property characterization and simulation of fused deposition modeling Polycarbonate parts. Mater. Des. 2015, 83, 670–677. [Google Scholar] [CrossRef]
- Song, Y.; Li, Y.; Song, W.; Yee, K.; Lee, K.Y.; Tagarielli, V.L. Measurements of the mechanical response of unidirectional 3D-printed PLA. Mater. Des. 2017, 123, 154–164. [Google Scholar] [CrossRef]
- Kerekes, T.W.; Lim, H.; Joe, W.Y.; Yun, G.J. Characterization of process–deformation/damage property relationship of fused deposition modeling (FDM) 3D-printed specimens. Addit. Manuf. 2019, 25, 532–544. [Google Scholar] [CrossRef]
- Garg, A.; Bhattacharya, A. An insight to the failure of FDM parts under tensile loading: Finite element analysis and experimental study. Int. J. Mech. Sci. 2017, 120, 225–236. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, L.; Fuh, J.Y.H.; Lee, H.P. Effect of porosity on mechanical properties of 3D printed polymers: Experiments and micromechanical modeling based on X-ray computed tomography analysis. Polymers 2019, 11, 1154. [Google Scholar] [CrossRef]
- Croccolo, D.; Agostinis, M.D.; Olmi, G. Experimental characterization and analytical modelling of the mechanical behaviour of fused deposition processed parts made of ABS-M30. Comput. Mater. Sci. 2013, 79, 506–518. [Google Scholar] [CrossRef]
- Anoop, M.S.; Senthil, P. Microscale representative volume element based numerical analysis on mechanical properties of fused deposition modelling components. Mater. Today Proc. 2020, 39, 563–571. [Google Scholar] [CrossRef]
- Guessasma, S.; Nouri, H.; Roger, F. Microstructural and mechanical implications of microscaled assembly in droplet-based multi-material additive manufacturing. Polymers 2017, 9, 372. [Google Scholar] [CrossRef]
- Dana, H.R.; Barbe, F.; Delbreilh, L.; Azzouna, M.B.; Guillet, A.; Breteau, T. Polymer additive manufacturing of ABS structure: Influence of printing direction on mechanical properties. J. Manuf. Process. 2019, 44, 288–298. [Google Scholar] [CrossRef]
- Sun, Q.; Rizvi, G.M.; Bellehumeur, C.T.; Gu, P. Effect of processing conditions on the bonding quality of FDM polymer filaments. Rapid Prototyp. J. 2008, 14, 72–80. [Google Scholar] [CrossRef]
- Riddick, J.C.; Haile, M.A.; Wahlde, R.V.; Cole, D.P.; Bamiduro, O.; Johnson, T.E. Fractographic analysis of tensile failure of acrylonitrile-butadiene-styrene fabricated by fused deposition modeling. Addit. Manuf. 2016, 11, 49–59. [Google Scholar] [CrossRef]
- Nasirov, A.; Fidan, I. Prediction of mechanical properties of fused filament fabricated structures via asymptotic homogenization. Mech. Mater. 2020, 145, 103372. [Google Scholar] [CrossRef]
- Yao, T.; Zhang, K.; Deng, Z.; Ye, J. A novel generalized stress invariant-based strength model for inter-layer failure of FFF 3D printing PLA material. Mater. Des. 2020, 193, 108799. [Google Scholar] [CrossRef]
- Qiao, D.; Wang, B.; Gu, H. Additive Manufacturing: Challenges and Solutions for Marine and Offshore Applications. Am. Soc. Mech. Eng. 2020, 8, V003T03A002. [Google Scholar] [CrossRef]
- Bacciaglia, A.; Ceruti, A.; Liverani, A. A design of experiment approach to 3D-printed mouthpieces sound analysis. Prog. Addit. Manuf. 2021, 6, 571–587. [Google Scholar] [CrossRef]
- Ahn, S.H.; Montero, M.; Odell, D.; Roundy, S.; Wright, P.K. Anisotropic material properties of fused deposition modeling ABS. Rapid Prototyp. J. 2002, 8, 248–257. [Google Scholar] [CrossRef]
- Koch, C.; Hulle, L.V.; Rudolph, N. Investigation of mechanical anisotropy of the fused filament fabrication process via customized tool path generation. Addit. Manuf. 2017, 16, 138–145. [Google Scholar] [CrossRef]
- Armillotta, A. Simulation of edge quality in fused deposition modeling. Rapid Prototyp. J. 2019, 25, 541–554. [Google Scholar] [CrossRef]
- Angelo, L.D.; Stefano, P.D.; Marzola, A. Surface quality prediction in FDM additive manufacturing. Int. J. Adv. Manuf. Technol. 2017, 93, 3655–3662. [Google Scholar] [CrossRef]
- Haque, M.E.; Banerjee, D.; Mishra, S.B.; Nanda, B.K. A Numerical Approach to Measure the Surface Roughness of FDM Build Part. Mater. Today Proc. 2019, 18, 5523–5529. [Google Scholar] [CrossRef]
- Ahn, D.; Kweon, J.H.; Kwon, S.; Song, J.; Lee, S. Representation of surface roughness in fused deposition modeling. J. Mater. Process. Technol. 2009, 209, 5593–5600. [Google Scholar] [CrossRef]
- Monaldo, E.; Marfia, S. Multiscale technique for the analysis of 3D-printed materials. Int. J. Solids Struct. 2021, 232, 111173. [Google Scholar] [CrossRef]
- Monaldo, E.; Marfia, S. Modelling of damage and plasticity phenomena in 3D printed materials via a multiscale approach. Eur. J. Mech. A/Solids 2023, 2023, 105140. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, H.; Gan, Y.; Šavija, B. Cementitious composites reinforced with 3D printed functionally graded polymeric lattice structures: Experiments and modelling. Addit. Manuf. 2021, 39. [Google Scholar] [CrossRef]
- Monaldo, E.; Ricci, M.; Marfia, S. Mechanical properties of 3D printed polylactic acid elements: Experimental and numerical insights. Mech. Mater. 2023, 177. [Google Scholar] [CrossRef]
- Sharafi, S.; Santare, M.H.; Gerdes, J.; Advani, S.G. A multiscale modeling approach of the Fused Filament Fabrication process to predict the mechanical response of 3D printed parts. Addit. Manuf. 2022, 51, 102597. [Google Scholar] [CrossRef]
- McLouth, T.D.; Severino, J.V.; Adams, P.M.; Patel, D.N.; Zaldivar, R.J. The impact of print orientation and raster pattern on fracture toughness in additively manufactured ABS. Addit. Manuf. 2017, 18, 103–109. [Google Scholar] [CrossRef]
- Gurrala, P.K.; Regalla, S.P. Part strength evolution with bonding between filaments in fused deposition modelling: This paper studies how coalescence of filaments contributes to the strength of final FDM part. Virtual Phys. Prototyp. 2014, 9, 141–149. [Google Scholar] [CrossRef]
- Davis, C.S.; Hillgartner, K.E.; Han, S.H.; Seppala, J.E. Mechanical strength of welding zones produced by polymer extrusion additive manufacturing. Addit. Manuf. 2017, 16, 162–166. [Google Scholar] [CrossRef]
- Aliheidari, N.; Tripuraneni, R.; Ameli, A.; Nadimpalli, S. Fracture resistance measurement of fused deposition modeling 3D printed polymers. Polym. Test. 2017, 60, 94–101. [Google Scholar] [CrossRef]
- Aliheidari, N.; Christ, J.; Tripuraneni, R.; Nadimpalli, S.; Ameli, A. Interlayer adhesion and fracture resistance of polymers printed through melt extrusion additive manufacturing process. Mater. Des. 2018, 156, 351–361. [Google Scholar] [CrossRef]
- Dawoud, M.; Taha, I.; Ebeid, S.J. Mechanical behaviour of ABS: An experimental study using FDM and injection moulding techniques. J. Manuf. Process. 2016, 21, 39–45. [Google Scholar] [CrossRef]
- Faes, M.; Ferraris, E.; Moens, D. Influence of Inter-layer Cooling time on the Quasi-static Properties of ABS Components Produced via Fused Deposition Modelling. Procedia CIRP 2016, 42, 748–753. [Google Scholar] [CrossRef]
- Khan, I.; Kumar, N. Fused deposition modelling process parameters influence on the mechanical properties of ABS: A review. Mater. Today Proc. 2020, 44, 4004–4008. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, H.; Šavija, B.; Figueiredo, S.C.; Schlangen, E. Deformation and fracture of 3D printed disordered lattice materials: Experiments and modeling. Mater. Des. 2019, 162, 143–153. [Google Scholar] [CrossRef]
- Naveed, N. Investigating the material properties and microstructural changes of fused filament fabricated PLA and tough-PLA parts. Polymers 2021, 13, 1487. [Google Scholar] [CrossRef] [PubMed]
- Shih, C.C.; Burnette, M.; Staack, D.; Wang, J.; Tai, B.L. Effects of cold plasma treatment on interlayer bonding strength in FFF process. Addit. Manuf. 2019, 25, 104–111. [Google Scholar] [CrossRef]
- Khudiakova, A.; Arbeiter, F.; Spoerk, M.; Wolfahrt, M.; Godec, D.; Pinter, G. Inter-layer bonding characterisation between materials with different degrees of stiffness processed by fused filament fabrication. Addit. Manuf. 2019, 28, 184–193. [Google Scholar] [CrossRef]
- Levenhagen, N.P.; Dadmun, M.D. Interlayer diffusion of surface segregating additives to improve the isotropy of fused deposition modeling products. Polymer 2018, 152, 35–41. [Google Scholar] [CrossRef]
- Zohdi, N.; Yang, R.C. Material anisotropy in additively manufactured polymers and polymer composites: A review. Polymers 2021, 13, 3368. [Google Scholar] [CrossRef] [PubMed]
- Prajapati, H.; Salvi, S.S.; Ravoori, D.; Qasaimeh, M.; Adnan, A.; Jain, A. Improved print quality in fused filament fabrication through localized dispensing of hot air around the deposited filament. Addit. Manuf. 2021, 40, 101917. [Google Scholar] [CrossRef]
- Ravoori, D.; Prajapati, H.; Talluru, V.; Adnan, A.; Jain, A. Nozzle-integrated pre-deposition and post-deposition heating of previously deposited layers in polymer extrusion based additive manufacturing. Addit. Manuf. 2019, 28, 719–726. [Google Scholar] [CrossRef]
- Ravi, A.K.; Deshpande, A.; Hsu, K.H. An in-process laser localized pre-deposition heating approach to inter-layer bond strengthening in extrusion based polymer additive manufacturing. J. Manuf. Process. 2016, 24, 179–185. [Google Scholar] [CrossRef]
- Ege, D.; Serttürk, S.; Acarkan, B.; Ademoğlu, A. Machine learning models to predict the relationship between printing parameters and tensile strength of 3D Poly (lactic acid) scaffolds for tissue engineering applications. Biomed. Phys. Eng. Express 2023. [Google Scholar] [CrossRef] [PubMed]
- ASTM D638-14; Standard Test Method for Tensile Properties of Plastic. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM D5045-14; Standard Test Methods for Plane-Strain Fracture Toughness and Strain Energy Release Rate of Plastic Materials. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM D1938-14; Standard Test Method for Tear-Propagation Resistance (Trouser Tear) of Plastic Film and Thin Sheeting by a Single-Tear Method. ASTM International: West Conshohocken, PA, USA, 2014.
- Lampron, O.; Therriault, D.; Lévesque, M. Phase-field modeling of fracture in fused filament fabricated thermoplastic parts and experimental validation. Eng. Fract. Mech. 2023, 2023, 109667. [Google Scholar] [CrossRef]
- Li, P.; Yvonnet, J.; Combescure, C.; Makich, H.; Nouari, M. Anisotropic elastoplastic phase field fracture modeling of 3D printed materials. Comput. Methods Appl. Mech. Eng. 2021, 386. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Rezaei, S.; Faroughi, S.; Reinicke, T. Experimental and numerical investigations of the fracture in 3D-printed open-hole plates. Theor. Appl. Fract. Mech. 2022, 121. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Rezaei, S.; Ruan, H.; Reinicke, T. Fracture behavior of anisotropic 3D-printed parts: Experiments and numerical simulations. J. Mater. Res. Technol. 2022, 19, 1260–1270. [Google Scholar] [CrossRef]

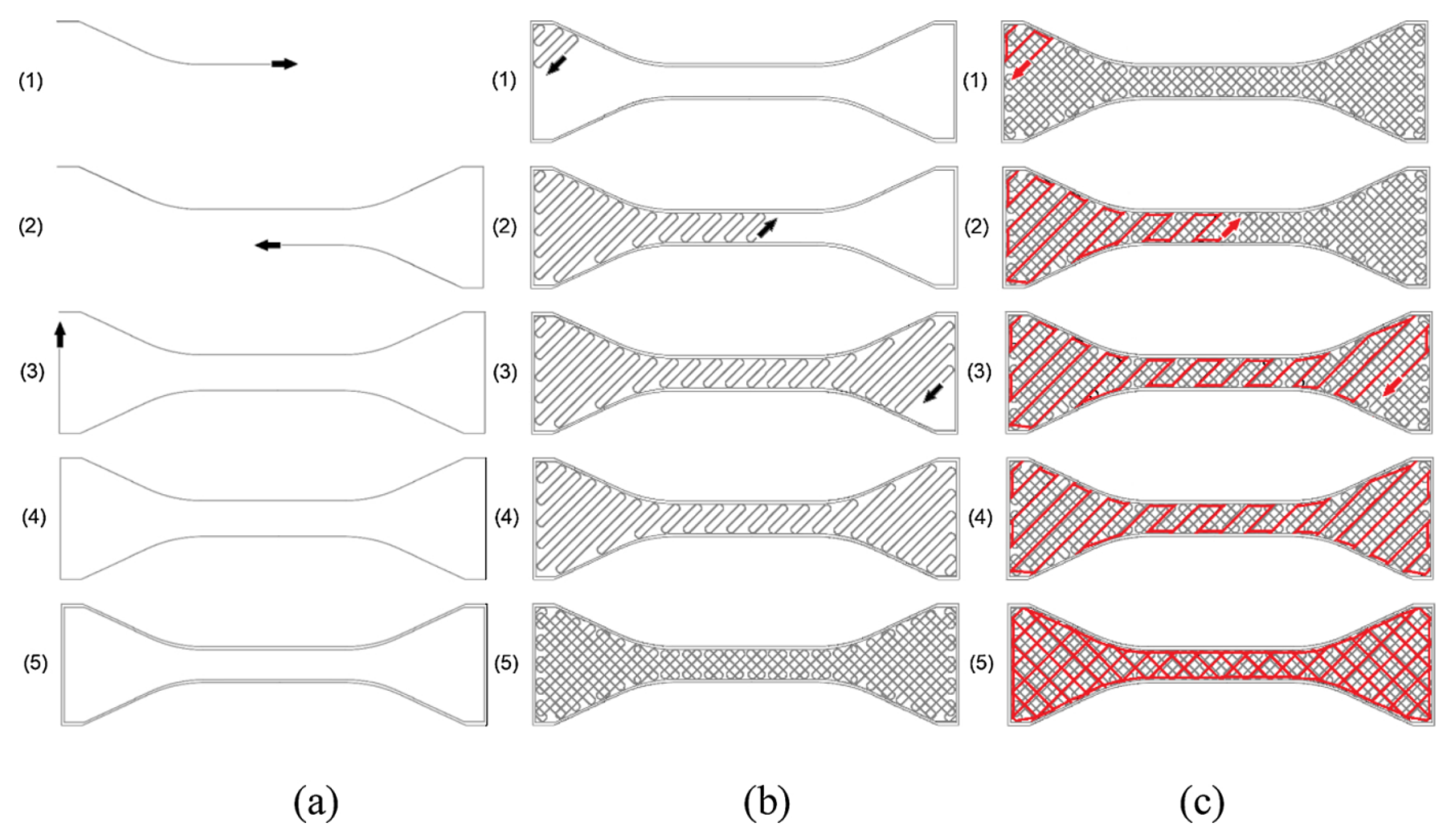

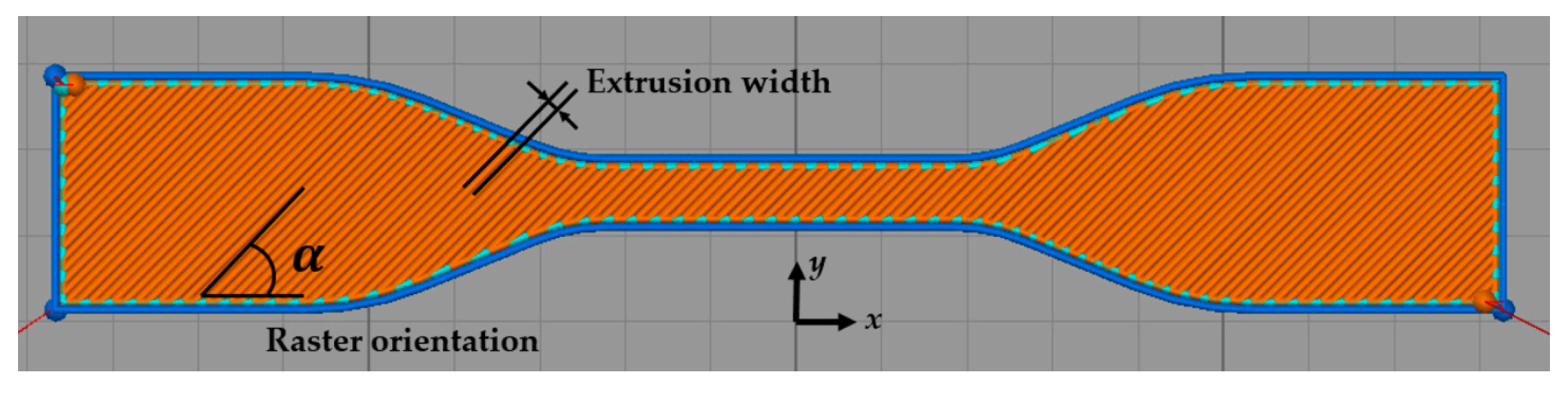


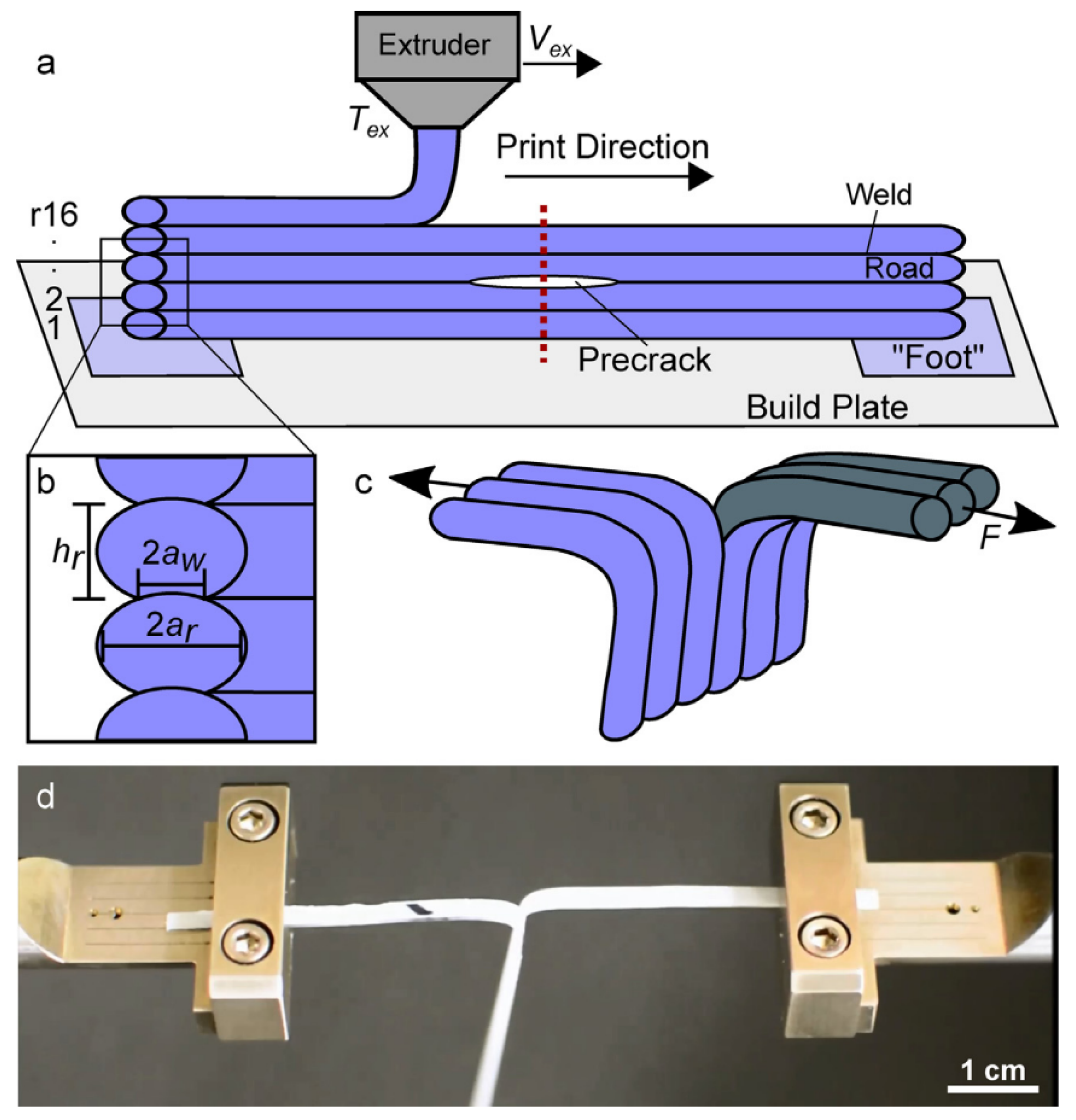
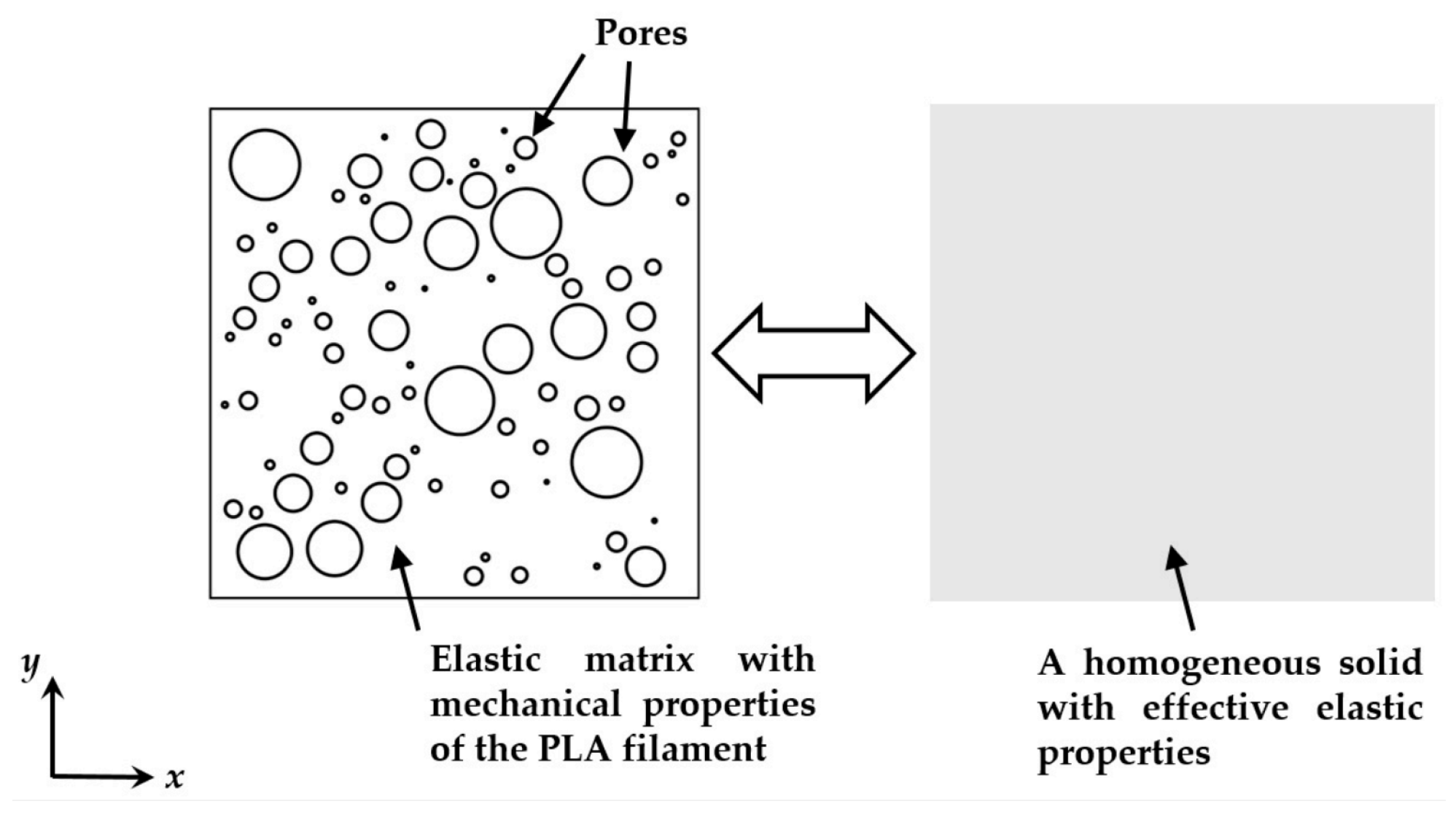

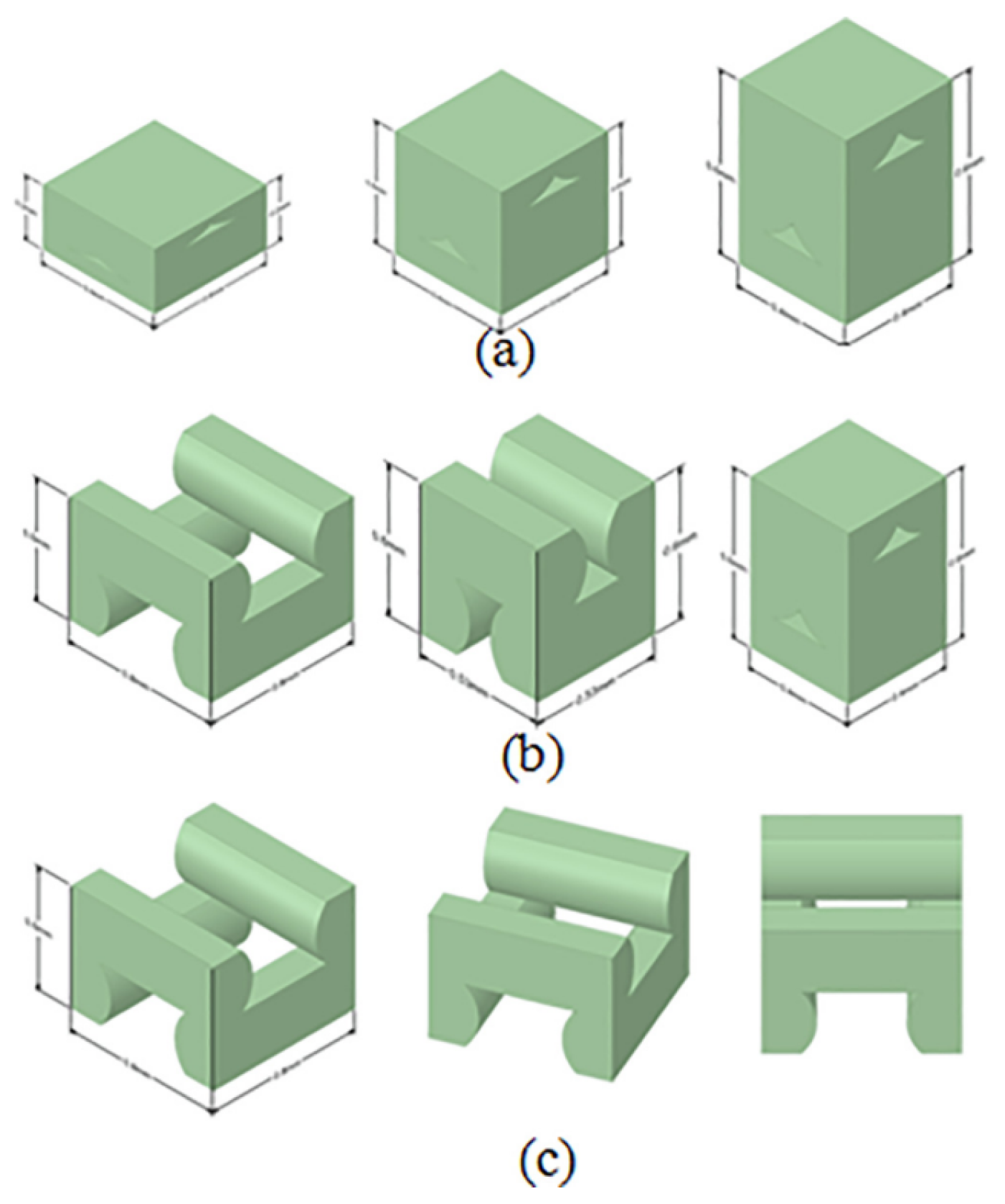
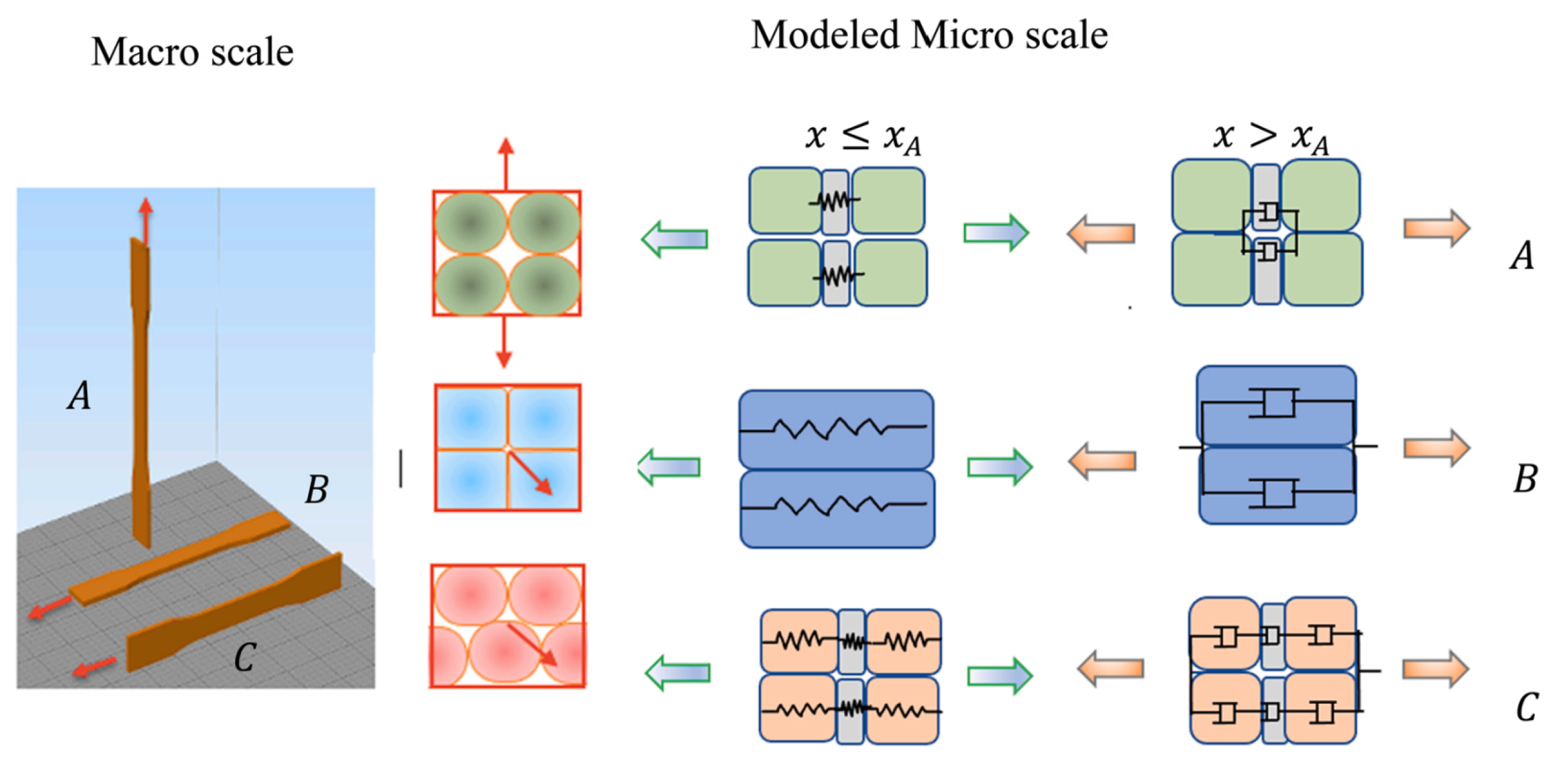
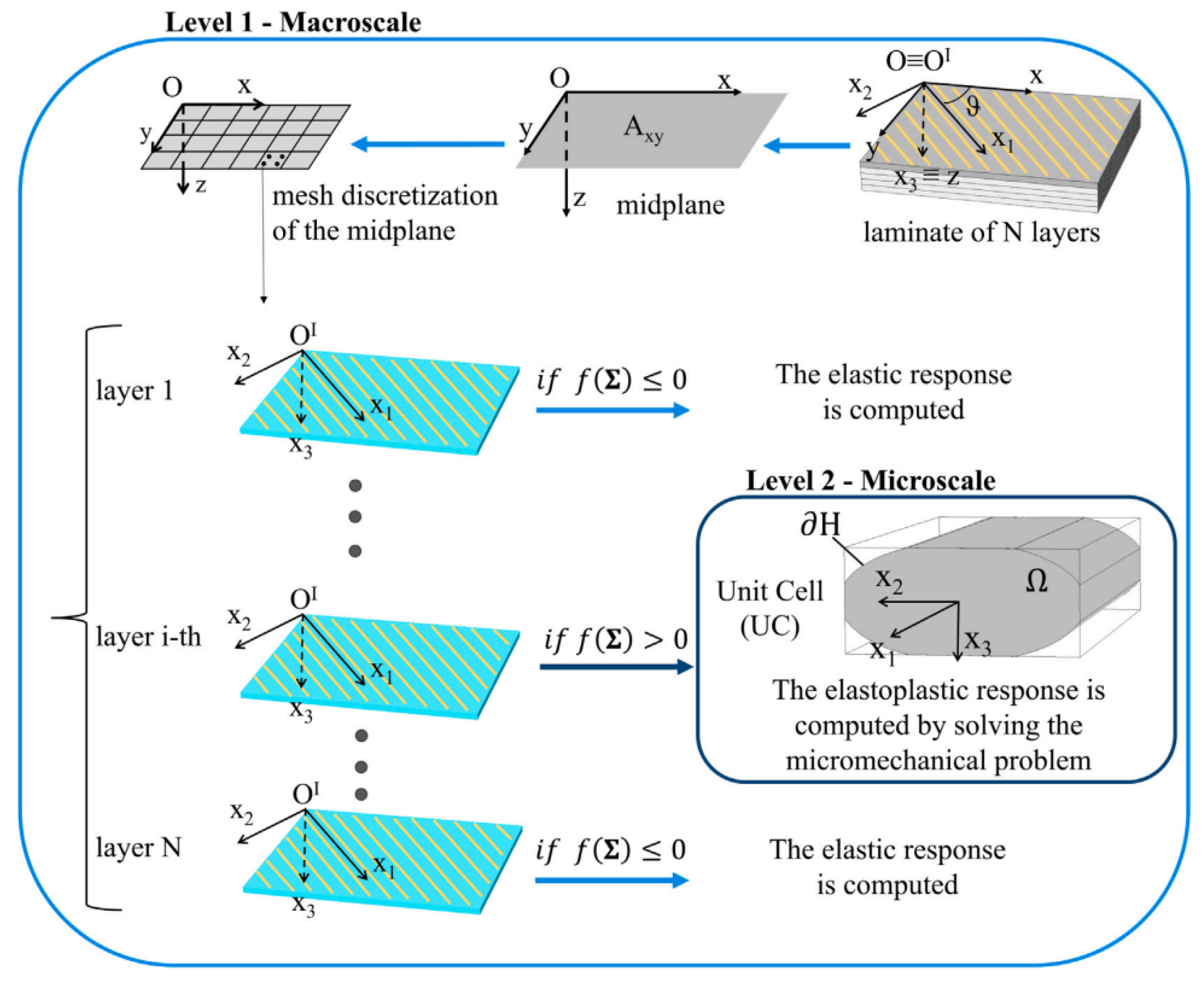

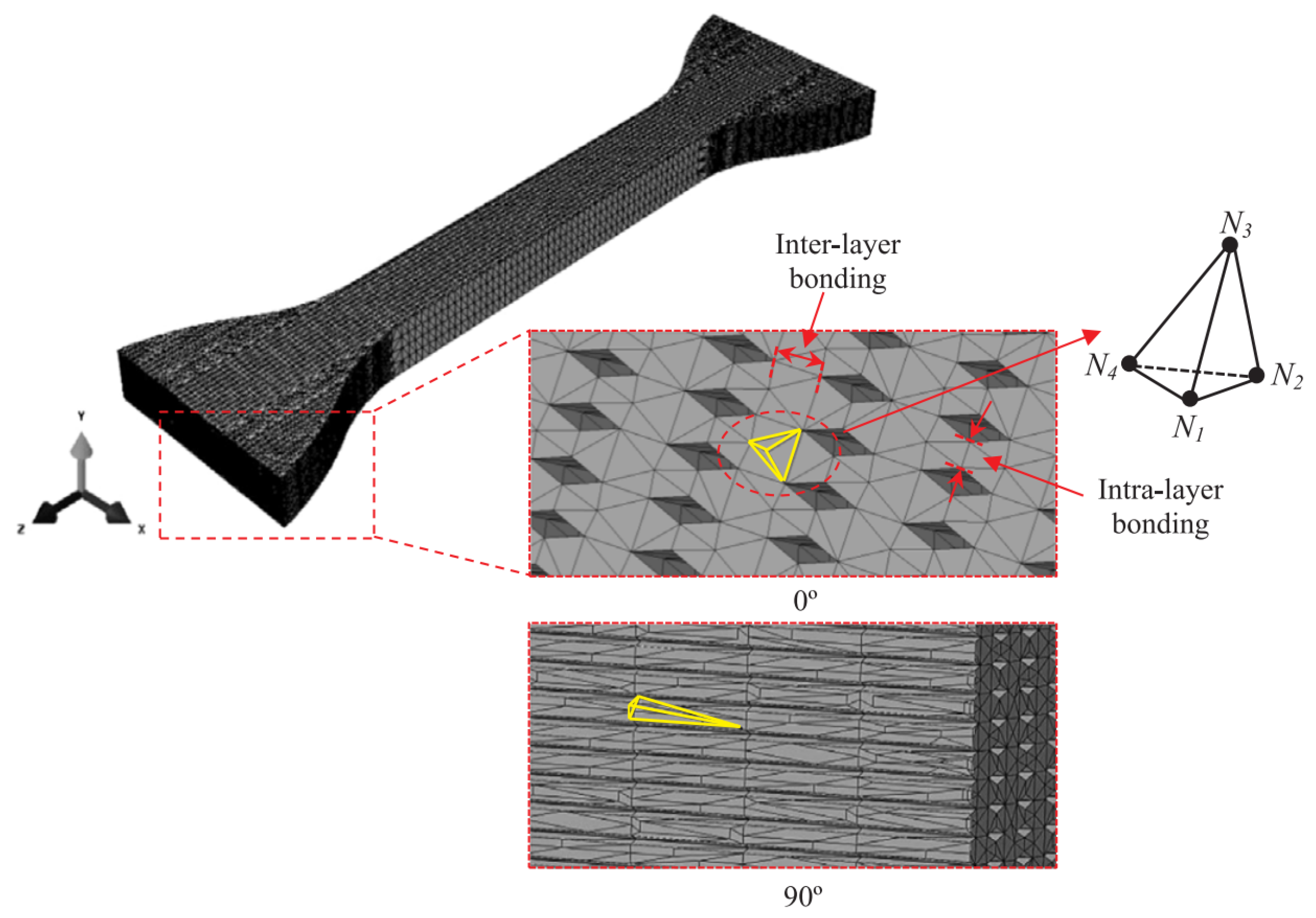





| Characteristic Mechanical Property | Printing Process Parameter |
|---|---|
| Tensile failure strength (TFS) | Raster orientation [18] |
| Infill density [18] | |
| Bead width [46] | |
| Printing speed [46] | |
| Inter-layer and intra-layer bonding | Raster orientation [6] |
| Temperature (thermal history) [35] | |
| Stiffness | Number of contours [8] |
| Porosity [11] | |
| Modulus of toughness | Infill density [5] |
| Build direction [29] | |
| Raster orientation [29] | |
| Deflection at failure | Infill density [28] |
| Build direction [28] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bol, R.J.M.; Šavija, B. Micromechanical Models for FDM 3D-Printed Polymers: A Review. Polymers 2023, 15, 4497. https://doi.org/10.3390/polym15234497
Bol RJM, Šavija B. Micromechanical Models for FDM 3D-Printed Polymers: A Review. Polymers. 2023; 15(23):4497. https://doi.org/10.3390/polym15234497
Chicago/Turabian StyleBol, Rowin J. M., and Branko Šavija. 2023. "Micromechanical Models for FDM 3D-Printed Polymers: A Review" Polymers 15, no. 23: 4497. https://doi.org/10.3390/polym15234497
APA StyleBol, R. J. M., & Šavija, B. (2023). Micromechanical Models for FDM 3D-Printed Polymers: A Review. Polymers, 15(23), 4497. https://doi.org/10.3390/polym15234497








