3D Printing of Flexible Mechanical Metamaterials: Synergistic Design of Process and Geometric Parameters
Abstract
:1. Introduction
2. Materials and Methods
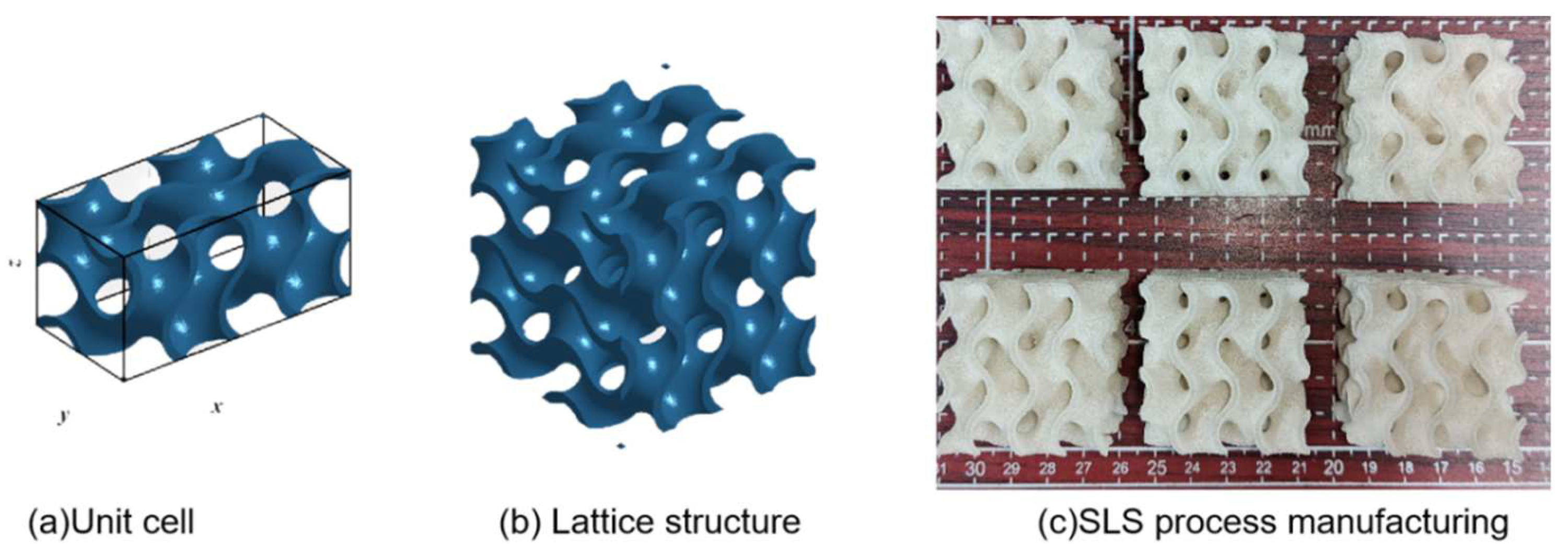
2.1. Parameterized Structural Design
2.2. Synergistic Design of the Process and Geometric Parameters
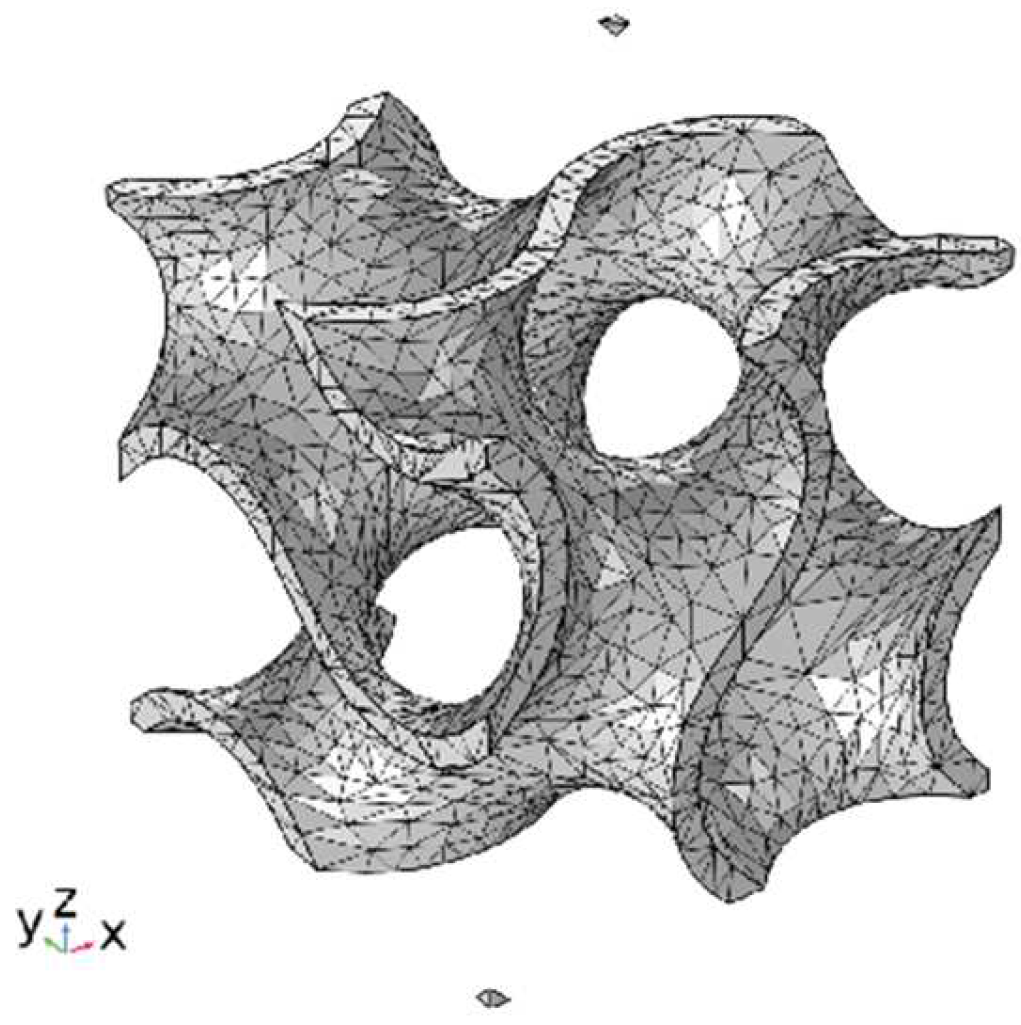
2.3. Experiment and Simulation
3. Results
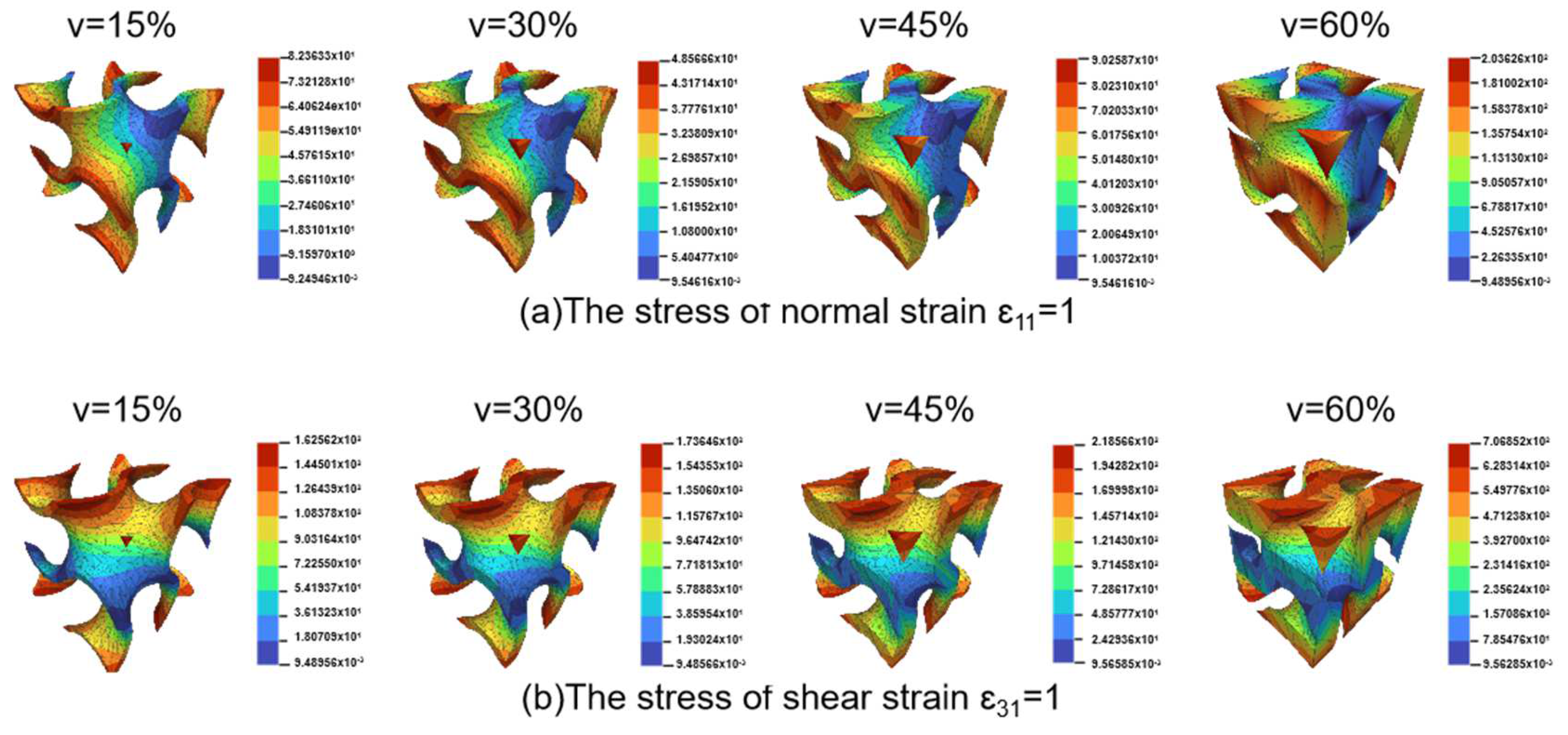
3.1. Influence of Interlayer Bonding on Mechanical Properties
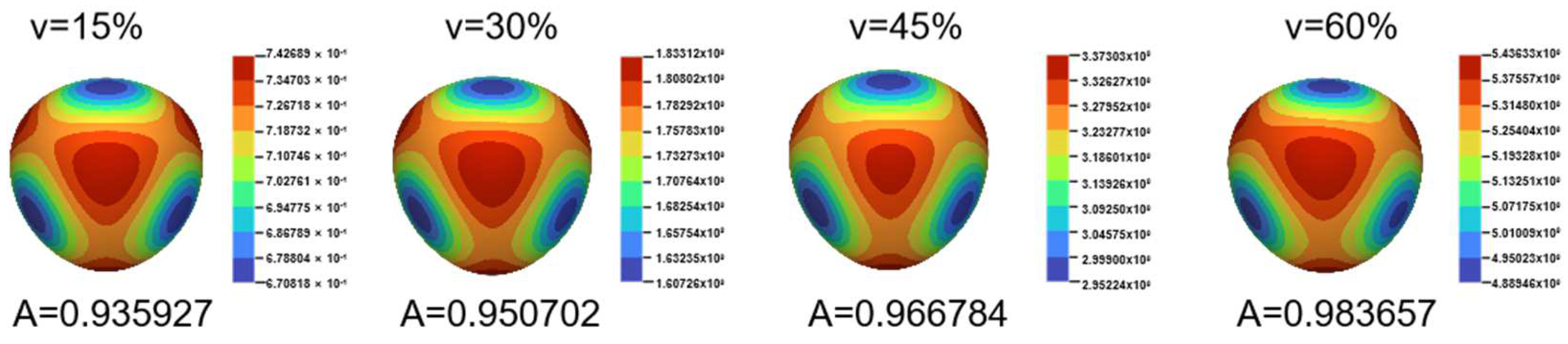
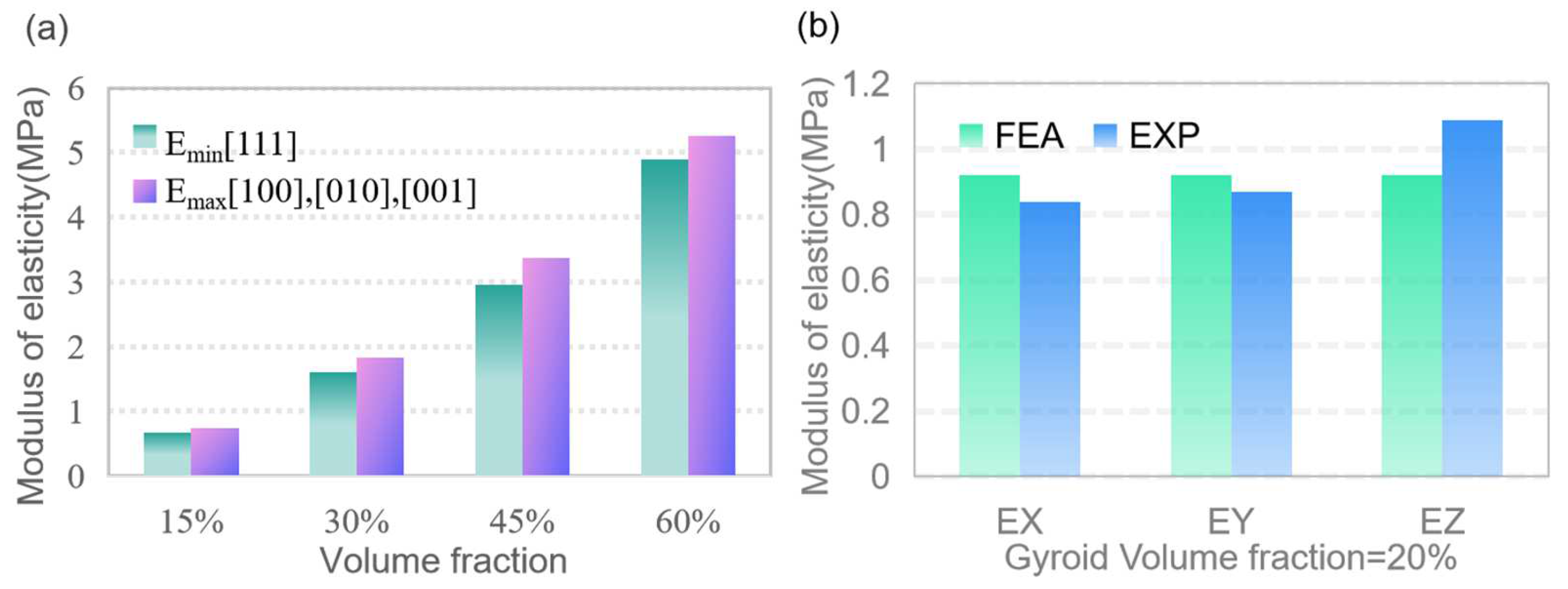
3.2. Collaborative Optimization Design of Process and Structural Parameters
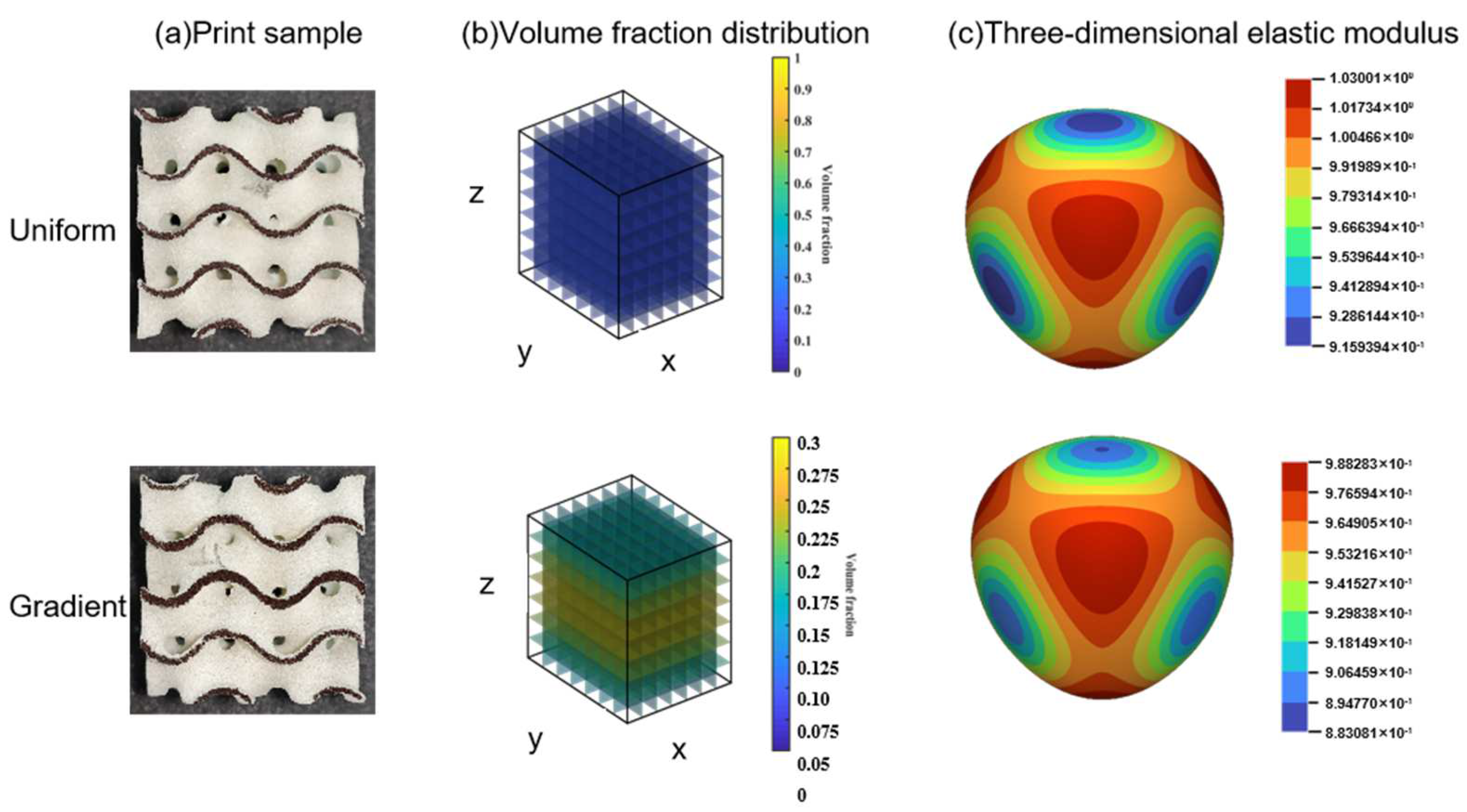
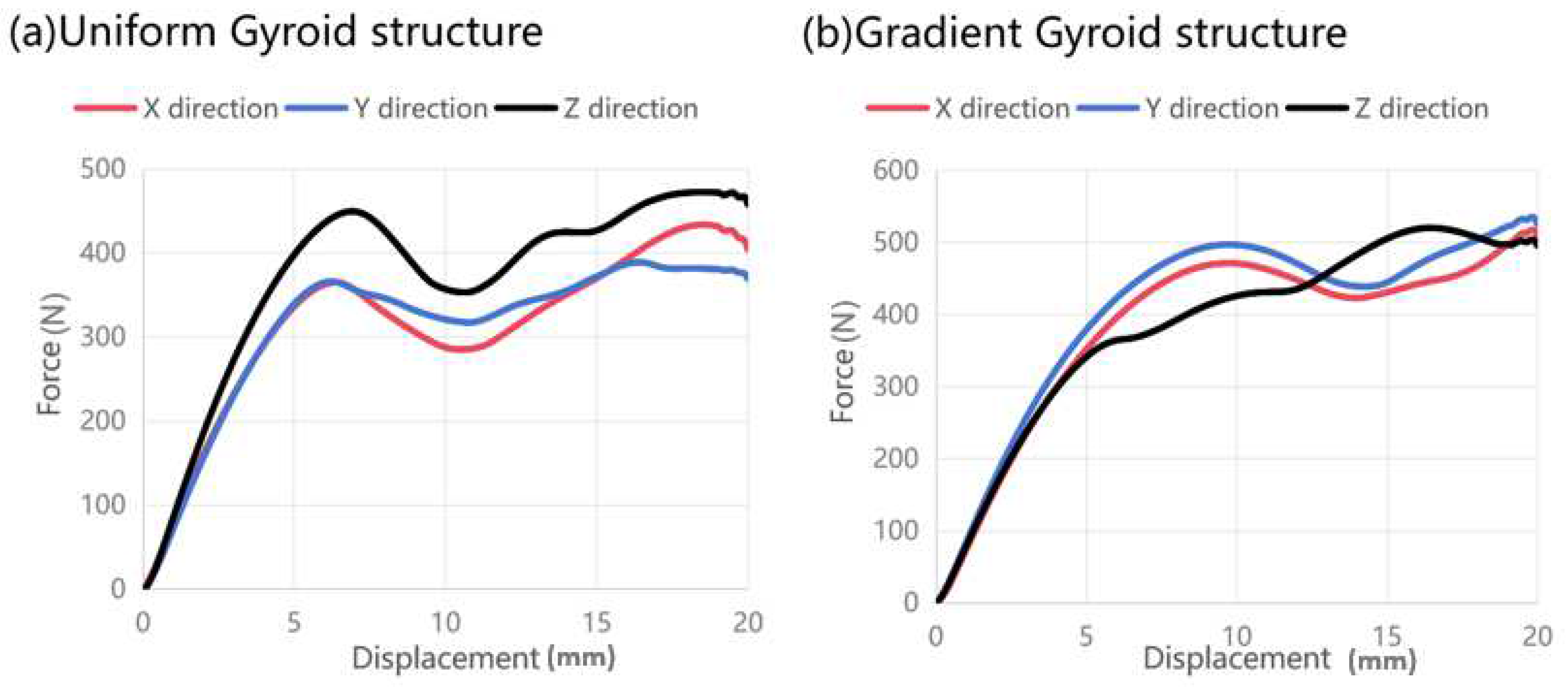
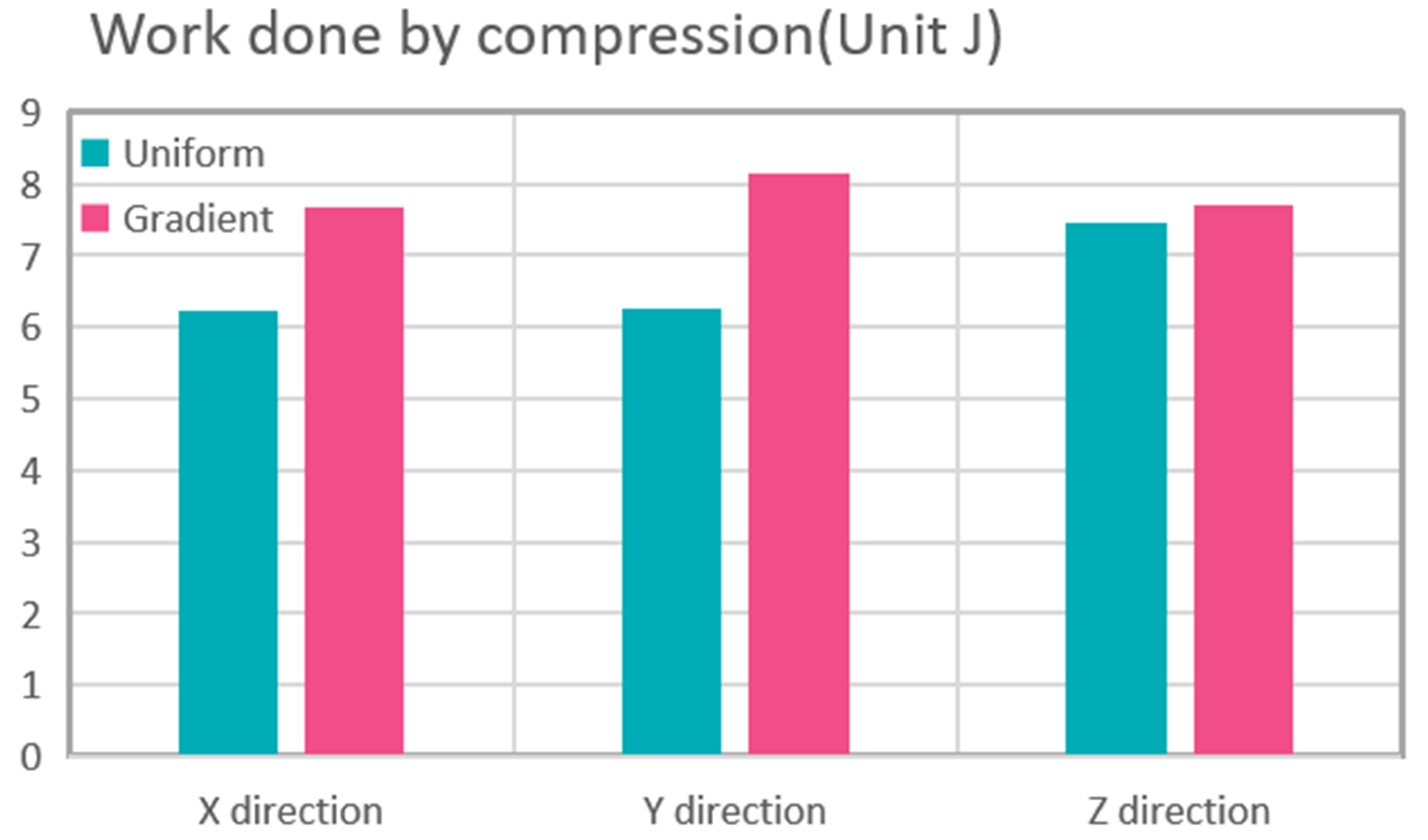
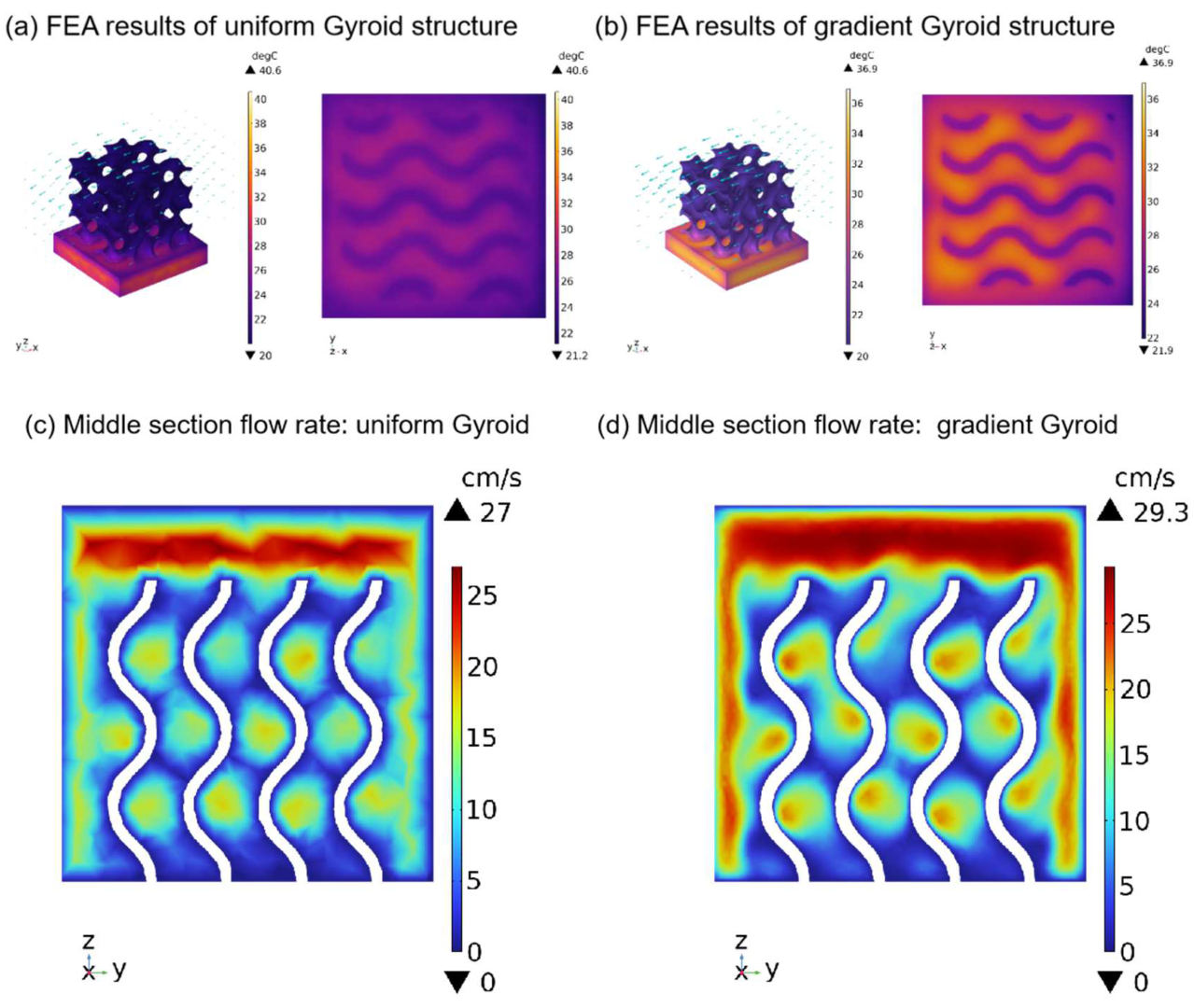
3.3. Functional Analysis of Gradient Lattice Structure
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Álvarez-Trejo, A.; Cuan-Urquizo, E.; Bhate, D.; Roman-Flores, A. Mechanical Metamaterials with Topologies Based on Curved Elements: An Overview of Design, Additive Manufacturing and Mechanical Properties. Mater. Des. 2023, 233, 112190. [Google Scholar] [CrossRef]
- Teawdeswan, L.; Dong, G. Inverse Design of Multi-Material Gyroid Structures Made by Additive Manufacturing. Int. J. Mech. Sci. 2023, 108734. [Google Scholar] [CrossRef]
- Tilton, M.; Borjali, A.; Griffis, J.C.; Varadarajan, K.M.; Manogharan, G.P. Fatigue Properties of Ti-6Al-4V TPMS Scaffolds Fabricated via Laser Powder Bed Fusion. Manuf. Lett. 2023, 37, 32–38. [Google Scholar] [CrossRef]
- Black, S.; Tzagiollari, A.; Mondal, S.; Dunne, N.; MacManus, D.B. Mechanical Behaviour of Gel-Filled Additively-Manufactured Lattice Structures under Quasi-Static Compressive Loading. Mater. Today Commun. 2023, 35, 106164. [Google Scholar] [CrossRef]
- Jiang, W.; Yin, G.; Xie, L.; Yin, M. Multifunctional 3D Lattice Metamaterials for Vibration Mitigation and Energy Absorption. Int. J. Mech. Sci. 2022, 233, 107678. [Google Scholar] [CrossRef]
- Berger, J.B.; Wadley, H.N.G.; McMeeking, R.M. Mechanical Metamaterials at the Theoretical Limit of Isotropic Elastic Stiffness. Nature 2017, 543, 533–537. [Google Scholar] [CrossRef]
- Novak, N.; Tanaka, S.; Hokamoto, K.; Mauko, A.; Yilmaz, Y.E.; Al-Ketan, O.; Vesenjak, M.; Ren, Z. High Strain Rate Mechanical Behaviour of Uniform and Hybrid Metallic TPMS Cellular Structures. Thin-Walled Struct. 2023, 191, 111109. [Google Scholar] [CrossRef]
- Liu, Z.; Gong, H.; Gao, J.; Liu, L. Bio-Inspired Design, Mechanical and Mass-Transport Characterizations of Orthotropic TPMS-Based Scaffold. Compos. Struct. 2023, 321, 117256. [Google Scholar] [CrossRef]
- Lal Lazar, P.J.; Subramanian, J.; Natarajan, E.; Markandan, K.; Ramesh, S. Anisotropic Structure-Property Relations of FDM Printed Short Glass Fiber Reinforced Polyamide TPMS Structures under Quasi-Static Compression. J. Mater. Res. Technol. 2023, 24, 9562–9579. [Google Scholar] [CrossRef]
- Viswanath, A.; Khan, K.A.; Barsoum, I. Design of Novel Isosurface Strut-Based Lattice Structures: Effective Stiffness, Strength, Anisotropy and Fatigue Properties. Mater. Des. 2022, 224, 111293. [Google Scholar] [CrossRef]
- Design for Additive Manufacturing of Functionally Graded Lattice Structures: A Design Method with Process Induced Anisotropy Consideration|SpringerLink. Available online: https://link.springer.com/article/10.1007/s40684-019-00173-7 (accessed on 12 September 2023).
- Clough, E.C.; Plaisted, T.A.; Eckel, Z.C.; Cante, K.; Hundley, J.M.; Schaedler, T.A. Elastomeric Microlattice Impact Attenuators. Matter 2019, 1, 1519–1531. [Google Scholar] [CrossRef]
- Feng, H.; Wang, W.; Wang, T.; Zhang, L.; Li, W.; Hou, J.; Chen, S. Preparation of Dynamic Polyurethane Networks with UV-Triggered Photothermal Self-Healing Properties Based on Hydrogen and Ion Bonds for Antibacterial Applications. J. Mater. Sci. Technol. 2023, 133, 89–101. [Google Scholar] [CrossRef]
- Yao, D.; Zhao, Z.; Wei, Y.; Li, J. Gradient Scaffolds Developed by Parametric Modeling with Selective Laser Sintering. Int. J. Mech. Sci. 2023, 248, 108221. [Google Scholar] [CrossRef]
- Sala, R. Insights into the Printing Parameters and Characterization of Thermoplastic Polyurethane Soft Triply Periodic Minimal Surface and Honeycomb Lattices for Broadening Material Extrusion Applicability. Addit. Manuf. 2022, 58, 102976. [Google Scholar] [CrossRef]
- Prajapati, M.J.; Kumar, A.; Lin, S.-C.; Jeng, J.-Y. Multi-Material Additive Manufacturing with Lightweight Closed-Cell Foam-Filled Lattice Structures for Enhanced Mechanical and Functional Properties. Addit. Manuf. 2022, 54, 102766. [Google Scholar] [CrossRef]
- Maskery, I.; Aremu, A.O.; Parry, L.; Wildman, R.D.; Tuck, C.J.; Ashcroft, I.A. Effective Design and Simulation of Surface-Based Lattice Structures Featuring Volume Fraction and Cell Type Grading. Mater. Des. 2018, 155, 220–232. [Google Scholar] [CrossRef]
- Ren, F.; Zhang, C.; Liao, W.; Liu, T.; Li, D.; Shi, X.; Jiang, W.; Wang, C.; Qi, J.; Chen, Y.; et al. Transition Boundaries and Stiffness Optimal Design for Multi-TPMS Lattices. Mater. Des. 2021, 210, 110062. [Google Scholar] [CrossRef]
- Feng, J.; Liu, B.; Lin, Z.; Fu, J. Isotropic Porous Structure Design Methods Based on Triply Periodic Minimal Surfaces. Mater. Des. 2021, 210, 110050. [Google Scholar] [CrossRef]
- Xu, Z.; Ha, C.S.; Kadam, R.; Lindahl, J.; Kim, S.; Wu, H.F.; Kunc, V.; Zheng, X. Additive Manufacturing of Two-Phase Lightweight, Stiff and High Damping Carbon Fiber Reinforced Polymer Microlattices. Addit. Manuf. 2020, 32, 101106. [Google Scholar] [CrossRef]
- Han, W.; Kong, L.; Xu, M. Advances in Selective Laser Sintering of Polymers. Int. J. Extrem. Manuf. 2022, 4, 042002. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, L.; Wei, S.; Zhang, Z.; Choi, S.-K.; Song, B.; Shi, Y. A Review of Additive Manufacturing of Metamaterials and Developing Trends. Mater. Today 2021, 50, 303–328. [Google Scholar] [CrossRef]
- Yuan, S.; Li, S.; Zhu, J.; Tang, Y. Additive Manufacturing of Polymeric Composites from Material Processing to Structural Design. Compos. Part B Eng. 2021, 219, 108903. [Google Scholar] [CrossRef]
- Martin, D.J.; Osman, A.F.; Andriani, Y.; Edwards, G.A. Thermoplastic Polyurethane (TPU)-Based Polymer Nanocomposites. In Advances in Polymer Nanocomposites; Elsevier: Amsterdam, The Netherlands, 2012; pp. 321–350. ISBN 978-1-84569-940-6. [Google Scholar]
- Rajitha, K.; Mohana, K.N.S.; Hegde, M.B.; Nayak, S.R.; Swamy, N.K. Fabrication of ZnO/rGO and ZnO/MWCNT Nanohybrids to Reinforce the Anticorrosion Performance of Polyurethane Coating. FlatChem 2020, 24, 100208. [Google Scholar] [CrossRef]
- Zhao, Z.; Wu, Z.; Yao, D.; Wei, Y.; Li, J. Mechanical Properties and Failure Mechanisms of Polyamide 12 Gradient Scaffolds Developed with Selective Laser Sintering. J. Mech. Behav. Biomed. Mater. 2023, 143, 105915. [Google Scholar] [CrossRef] [PubMed]
- Arefin, A.M.E.; Khatri, N.R.; Kulkarni, N.; Egan, P.F. Polymer 3D Printing Review: Materials, Process, and Design Strategies for Medical Applications. Polymers 2021, 13, 1499. [Google Scholar] [CrossRef]
- Lin, X.; Hao, M.; Ying, J.; Wang, R.; Lu, Y.; Gong, M.; Zhang, L.; Wang, D.; Zhang, L. An Insight into the Tensile Anisotropy of 3D-Printed Thermoplastic Polyurethane. Addit. Manuf. 2022, 60, 103260. [Google Scholar] [CrossRef]
- Dadbakhsh, S.; Verbelen, L.; Vandeputte, T.; Strobbe, D.; Van Puyvelde, P.; Kruth, J.-P. Effect of Powder Size and Shape on the SLS Processability and Mechanical Properties of a TPU Elastomer. Phys. Procedia 2016, 83, 971–980. [Google Scholar] [CrossRef]
- Xu, T.; Shen, W.; Lin, X.; Xie, Y.M. Mechanical Properties of Additively Manufactured Thermoplastic Polyurethane (TPU) Material Affected by Various Processing Parameters. Polymers 2020, 12, 3010. [Google Scholar] [CrossRef]
- Holmes, D.W. Mechanical behaviour of flexible 3D printed gyroid structures as a tuneable replacement for soft padding foa. Addit. Manuf. 2022, 50, 102555. [Google Scholar] [CrossRef]
- Maskery, I.; Ashcroft, I.A. The Deformation and Elastic Anisotropy of a New Gyroid-Based Honeycomb Made by Laser Sintering. Addit. Manuf. 2020, 36, 101548. [Google Scholar] [CrossRef]
- Maskery, I.; Parry, L.A.; Padrão, D.; Hague, R.J.M.; Ashcroft, I.A. FLatt Pack: A Research-Focussed Lattice Design Program. Addit. Manuf. 2022, 49, 102510. [Google Scholar] [CrossRef]



| Process Parameter | Value |
|---|---|
| Laser power | 20 w |
| Laser scan speed | 2500 mm/s |
| Laser hatch spacing | 0.1 mm |
| Powder deposition thickness | 0.15 mm |
| Type | Weight (g) | Dimension (X × Y × Z mm) | |
|---|---|---|---|
| Gradient Gyroid structure | Sample 1 | 14.31 | 39.38 × 39.44 × 40.51 |
| Sample 2 | 13.57 | 39.33 × 39.55 × 40.50 | |
| Sample 3 | 13.18 | 39.64 × 39.89 × 40.32 | |
| Uniform Gyroid structure | Sample 1 | 13.78 | 39.32 × 39.22 × 40.12 |
| Sample 2 | 14.26 | 39.53 × 39.23 × 40.48 | |
| Sample 3 | 13.54 | 39.25 × 39.64 × 40.33 | |
| Uniform Gyroid | Gradient Gyroid | ||||
|---|---|---|---|---|---|
| Modulus of Elasticity E (MPa) | Modulus of Elasticity E (MPa) | ||||
| X([100]) | Y([010]) | Z([001]) | X([100]) | Y([010]) | Z([001]) |
| 0.988 | 0.975 | 1.175 | 1.001 | 1.106 | 1.025 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Xue, C.; Chen, S.; Aiyiti, W.; Khan, S.B.; Liang, J.; Zhou, J.; Lu, B. 3D Printing of Flexible Mechanical Metamaterials: Synergistic Design of Process and Geometric Parameters. Polymers 2023, 15, 4523. https://doi.org/10.3390/polym15234523
Li N, Xue C, Chen S, Aiyiti W, Khan SB, Liang J, Zhou J, Lu B. 3D Printing of Flexible Mechanical Metamaterials: Synergistic Design of Process and Geometric Parameters. Polymers. 2023; 15(23):4523. https://doi.org/10.3390/polym15234523
Chicago/Turabian StyleLi, Nan, Chenhao Xue, Shenggui Chen, Wurikaixi Aiyiti, Sadaf Bashir Khan, Jiahua Liang, Jianping Zhou, and Bingheng Lu. 2023. "3D Printing of Flexible Mechanical Metamaterials: Synergistic Design of Process and Geometric Parameters" Polymers 15, no. 23: 4523. https://doi.org/10.3390/polym15234523
APA StyleLi, N., Xue, C., Chen, S., Aiyiti, W., Khan, S. B., Liang, J., Zhou, J., & Lu, B. (2023). 3D Printing of Flexible Mechanical Metamaterials: Synergistic Design of Process and Geometric Parameters. Polymers, 15(23), 4523. https://doi.org/10.3390/polym15234523







