An Investigation of the Inverted Structure of a PBDB:T/PZT:C1-Based Polymer Solar Cell
Abstract
:1. Introduction
2. Methods and Materials
| Symbols | Definitions | Units |
|---|---|---|
| U | Recombination’s rate. The impact of ionization, deep-traps, Auger’s and radiates recombination are considered. The calculation of the recombination’s rate by deep traps in the energy gaps is carried out by Shockley-Read-Hall (SRH) theorem [42,43]. | cm−3s−1 |
| Jp and Jn | Hole current density and electron current density. | A/cm2 |
| ε | Permittivity. | F/cm |
| ψ | Electrostatic potential. | V |
| q | Electron’s charge. | C |
| ND+ and NA− | The ionized concentrations of donors and acceptors, respectively. | cm−3 |
| nt and pt | The trapped densities of electrons and holes, respectively. | cm−3 |
| n and p | The concentration of electrons and holes, respectively. | cm−3 |
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shaheen, M.A.M.; Hasanien, H.M.; Turky, R.A.; Ćalasan, M.; Zobaa, A.F.; Aleem, S.H.E.A. OPF of Modern Power Systems Comprising Renewable Energy Sources Using Improved CHGS Optimization Algorithm. Energies 2021, 14, 6962. [Google Scholar] [CrossRef]
- Petrović-Ranđelović, M.; Kocić, N.; Stojanović-Ranđelović, B. The importance of renewable energy sources for sustainable development. Econ. Sustain. Dev. 2020, 4, 15–24. [Google Scholar] [CrossRef]
- Green, M.; Dunlop, E.; Hohl-Ebinger, J.; Yoshita, M.; Kopidakis, N.; Hao, X. Solar cell efficiency tables (version 57). Prog. Photovolt. Res. Appl. 2021, 29, 3–15. [Google Scholar] [CrossRef]
- Okil, M.; Salem, M.S.; Abdolkader, T.M.; Shaker, A. From Crystalline to Low-cost Silicon-based Solar Cells: A Review. Silicon 2021, 14, 1895–1911. [Google Scholar] [CrossRef]
- Putnam, M.C.; Boettcher, S.W.; Kelzenberg, M.D.; Turner-Evans, D.B.; Spurgeon, J.M.; Warren, E.L.; Briggs, R.M.; Lewis, N.S.; Atwater, H.A. Si microwire-array solar cells. Energy Environ. Sci. 2010, 3, 1037–1041. [Google Scholar] [CrossRef]
- Salem, M.S.; Zekry, A.; Shaker, A.; Abouelatta, M. Design and simulation of proposed low cost solar cell structures based on heavily doped silicon wafers. In Proceedings of the 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016; pp. 2393–2397. [Google Scholar]
- Salem, M.S.; Alzahrani, A.J.; Ramadan, R.A.; Alanazi, A.; Shaker, A.; Abouelatta, M.; Gontrand, C.; Elbanna, M.; Zekry, A. Physically Based Analytical Model of Heavily Doped Silicon Wafers Based Proposed Solar Cell Microstructure. IEEE Access 2020, 8, 138898–138906. [Google Scholar] [CrossRef]
- Salem, M.; Zekry, A.; Abouelatta, M.; Alshammari, M.T.; Alanazi, A.; Al-Dhlan, K.A.; Shaker, A. Influence of base doping level on the npn microstructure solar cell performance: A TCAD study. Opt. Mater. 2021, 121, 111501. [Google Scholar] [CrossRef]
- Kim, G.; Lim, J.W.; Kim, J.; Yun, S.J.; Park, M.A. Transparent Thin-Film Silicon Solar Cells for Indoor Light Harvesting with Conversion Efficiencies of 36% without Photodegradation. ACS Appl. Mater. Interfaces 2020, 12, 27122–27130. [Google Scholar] [CrossRef]
- Gnida, P.; Amin, M.F.; Pająk, A.K.; Jarząbek, B. Polymers in High-Efficiency Solar Cells: The Latest Reports. Polymers 2022, 14, 1946. [Google Scholar] [CrossRef]
- Khanam, J.J.; Foo, S.Y. Modeling of High-Efficiency Multi-Junction Polymer and Hybrid Solar Cells to Absorb Infrared Light. Polymers 2019, 11, 383. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, Y.; Wan, X.; Li, C.; Zhang, X.; Wang, Y.; Ke, X.; Xiao, Z.; Ding, L.; Xia, R.; et al. Organic and solution-processed tandem solar cells with 17.3% efficiency. Science 2018, 361, 1094–1098. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Zhang, Y.; Zhou, L.; Zhang, G.; Yip, H.-L.; Lau, T.-K.; Lu, X.; Zhu, C.; Peng, H.; Johnson, P.A.; et al. Single-Junction Organic Solar Cell with over 15% Efficiency Using Fused-Ring Acceptor with Electron-Deficient Core. Joule 2019, 3, 1140–1151. [Google Scholar] [CrossRef]
- Li, S.; Zhan, L.; Jin, Y.; Zhou, G.; Lau, T.; Qin, R.; Shi, M.; Li, C.; Zhu, H.; Lu, X.; et al. Asymmetric Electron Acceptors for High-Efficiency and Low-Energy-Loss Organic Photovoltaics. Adv. Mater. 2020, 32, e2001160. [Google Scholar] [CrossRef]
- Best Research-Cell Efficiency Chart|Photovoltaic Research|NREL. Available online: https://www.nrel.gov/pv/cell-efficiency.html (accessed on 1 January 2023).
- Lee, C.; Lee, S.; Kim, G.U.; Lee, W.; Kim, B.J. Recent Advances, Design Guidelines, and Prospects of All-Polymer Solar Cells. Chem. Rev. 2019, 119, 8028–8086. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Yuan, J.; Zhou, S.; Seifrid, M.; Ying, L.; Li, B.; Huang, F.; Bazan, G.C.; Ma, W. Ambient Processable and Stable All-Polymer Organic Solar Cells. Adv. Funct. Mater. 2019, 29, 1806747. [Google Scholar] [CrossRef]
- Luo, Z.; Liu, T.; Ma, R.; Xiao, Y.; Zhan, L.; Zhang, G.; Sun, H.; Ni, F.; Chai, G.; Wang, J.; et al. Precisely Controlling the Position of Bromine on the End Group Enables Well-Regular Polymer Acceptors for All-Polymer Solar Cells with Efficiencies over 15%. Adv. Mater. 2020, 32, e2005942. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, W.; Wang, T.; Sun, R.; Guo, J.; Wu, Y.; Jiao, X.; Brabec, C.J.; Li, Y.; Min, J. High-performance all-polymer solar cells with only 0.47 eV energy loss. Sci. China Chem. 2020, 63, 1449–1460. [Google Scholar] [CrossRef]
- Yu, H.; Qi, Z.; Yu, J.; Xiao, Y.; Sun, R.; Luo, Z.; Cheung, A.M.H.; Zhang, J.; Sun, H.; Zhou, W.; et al. Fluorinated End Group Enables High-Performance All-Polymer Solar Cells with Near-Infrared Absorption and Enhanced Device Efficiency over 14%. Adv. Energy Mater. 2020, 11, 2003171. [Google Scholar] [CrossRef]
- Peng, F.; An, K.; Zhong, W.; Li, Z.; Ying, L.; Li, N.; Huang, Z.; Zhu, C.; Fan, B.; Huang, F.; et al. A Universal Fluorinated Polymer Acceptor Enables All-Polymer Solar Cells with >15% Efficiency. ACS Energy Lett. 2020, 5, 3702–3707. [Google Scholar] [CrossRef]
- Wang, W.; Wu, Q.; Sun, R.; Guo, J.; Wu, Y.; Shi, M.; Yang, W.; Li, H.; Min, J. Controlling Molecular Mass of Low-Band-Gap Polymer Acceptors for High-Performance All-Polymer Solar Cells. Joule 2020, 4, 1070–1086. [Google Scholar] [CrossRef]
- Jia, T.; Zhang, J.; Zhong, W.; Liang, Y.; Zhang, K.; Dong, S.; Ying, L.; Liu, F.; Wang, X.; Huang, F.; et al. 14.4% efficiency all-polymer solar cell with broad absorption and low energy loss enabled by a novel polymer acceptor. Nano Energy 2020, 72, 104718. [Google Scholar] [CrossRef]
- Fu, H.; Li, Y.; Yu, J.; Wu, Z.; Fan, Q.; Lin, F.; Woo, H.Y.; Gao, F.; Zhu, Z.; Jen, A.K.-Y. High Efficiency (15.8%) All-Polymer Solar Cells Enabled by a Regioregular Narrow Bandgap Polymer Acceptor. J. Am. Chem. Soc. 2021, 143, 2665–2670. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.; Li, Y.; Wu, Z.; Lin, F.R.; Woo, H.Y.; Jen, A.K. Side-Chain Substituents on Benzotriazole-Based Polymer Acceptors Affecting the Performance of All-Polymer Solar Cells. Macromol. Rapid Commun. 2022, 43, e2200062. [Google Scholar] [CrossRef] [PubMed]
- Anrango-Camacho, C.; Pavón-Ipiales, K.; Frontana-Uribe, B.A.; Palma-Cando, A. Recent Advances in Hole-Transporting Layers for Organic Solar Cells. Nanomaterials 2022, 12, 443. [Google Scholar] [CrossRef]
- Xu, H.; Yuan, F.; Zhou, D.; Liao, X.; Chen, L.; Chen, Y. Hole transport layers for organic solar cells: Recent progress and prospects. J. Mater. Chem. A 2020, 8, 11478–11492. [Google Scholar] [CrossRef]
- Ogundele, A.K.; Mola, G.T. Ternary atoms alloy quantum dot assisted hole transport in thin film polymer solar cells. J. Phys. Chem. Solids 2022, 171, 110999. [Google Scholar] [CrossRef]
- Zhong, Y.; Li, Y.; Lan, X.; Wang, J.; Wang, J.; Zhang, Y. Enhancing Efficiency and Stability of Polymer Solar Cells Based on CuI Nanoparticles as the Hole Transport Layer. IEEE J. Photovoltaics 2021, 11, 668–673. [Google Scholar] [CrossRef]
- Wang, Z.; Zou, X.; Zhao, M.; Wang, J.; Wang, X.; Hao, Y.; Wang, H. A simple doping strategy to improve PEDOT:PSS charge extraction capability in polymer solar cells. Sol. Energy 2022, 247, 109–114. [Google Scholar] [CrossRef]
- Islam, S. Analytical modeling of organic solar cells including monomolecular recombination and carrier generation calculated by optical transfer matrix method. Org. Electron. 2017, 41, 143–156. [Google Scholar] [CrossRef]
- Zang, Y.; Xin, Q.; Zhao, J.; Lin, J. Effect of Active Layer Thickness on the Performance of Polymer Solar Cells Based on a Highly Efficient Donor Material of PTB7-Th. J. Phys. Chem. C 2018, 122, 16532–16539. [Google Scholar] [CrossRef]
- Abdelaziz, W.; Shaker, A.; Abouelatta, M.; Zekry, A. Possible efficiency boosting of non-fullerene acceptor solar cell using device simulation. Opt. Mater. 2019, 91, 239–245. [Google Scholar] [CrossRef]
- Alahmadi, A.N.M. Design of an Efficient PTB7:PC70BM-Based Polymer Solar Cell for 8% Efficiency. Polymers 2022, 14, 889. [Google Scholar] [CrossRef] [PubMed]
- Moiz, S.A.; Alzahrani, M.S.; Alahmadi, A.N.M. Electron Transport Layer Optimization for Efficient PTB7:PC70BM Bulk-Heterojunction Solar Cells. Polymers 2022, 14, 3610. [Google Scholar] [CrossRef] [PubMed]
- Widianto, E.; Firdaus, Y.; Shobih; Pranoto, L.M.; Triyana, K.; Santoso, I.; Nursam, N.M. Device modeling of two-dimensional hole transport materials for boosting the performance of non-fullerene acceptor bulk heterojunction organic solar cells. Opt. Mater. 2022, 132, 112771. [Google Scholar] [CrossRef]
- Sharma, B.; Mathur, A.; Rajput, V.; Singh, I.; Singh, B. Device modeling of non-fullerene organic solar cell by incorporating CuSCN as a hole transport layer using SCAPS. Optik 2021, 251, 168457. [Google Scholar] [CrossRef]
- Nowsherwan, G.A.; Samad, A.; Iqbal, M.A.; Mushtaq, T.; Hussain, A.; Malik, M.; Haider, S.; Pham, P.V.; Choi, J.R. Performance Analysis and Optimization of a PBDB-T:ITIC Based Organic Solar Cell Using Graphene Oxide as the Hole Transport Layer. Nanomaterials 2022, 12, 1767. [Google Scholar] [CrossRef] [PubMed]
- Abdelaziz, W.; Zekry, A.; Shaker, A.; Abouelatta, M. Numerical study of organic graded bulk heterojunction solar cell using SCAPS simulation. Sol. Energy 2020, 211, 375–382. [Google Scholar] [CrossRef]
- Salah, M.M.; Abouelatta, M.; Shaker, A.; Hassan, K.M.; Saeed, A. A comprehensive simulation study of hybrid halide perovskite solar cell with copper oxide as HTM. Semicond. Sci. Technol. 2019, 34, 115009. [Google Scholar] [CrossRef]
- Burgelman, M.; Decock, K.; Niemegeers, A.; Verschraegen, J.; Degrave, S. SCAPS Manual; University of Ghent: Ghent, Belgium, 2016. [Google Scholar]
- Shockley, W.; Read, W.T. Statistics of the Recombinations of Holes and Electrons. Phys. Rev. B 1952, 87, 835–842. [Google Scholar] [CrossRef]
- Hall, R.N. Electron-Hole Recombination in Germanium. Phys. Rev. B 1952, 87, 387. [Google Scholar] [CrossRef]
- Scharfetter, D.; Gummel, H. Large-signal analysis of a silicon Read diode oscillator. IEEE Trans. Electron Devices 1969, 16, 64–77. [Google Scholar] [CrossRef]
- Gummel, H. A self-consistent iterative scheme for one-dimensional steady state transistor calculations. IEEE Trans. Electron Devices 1964, 11, 455–465. [Google Scholar] [CrossRef]
- Boumaour, M.; Sali, S.; Kermadi, S.; Zougar, L.; Bahfir, A.; Chaieb, Z. High efficiency silicon solar cells with back ZnTe layer hosting IPV effect: A numerical case study. J. Taibah Univ. Sci. 2019, 13, 696–703. [Google Scholar] [CrossRef]
- Basyoni, M.S.S.; Salah, M.M.; Mousa, M.; Shaker, A.; Zekry, A.; Abouelatta, M.; Alshammari, M.T.; Al-Dhlan, K.A.; Gontrand, C. On the Investigation of Interface Defects of Solar Cells: Lead-Based vs Lead-Free Perovskite. IEEE Access 2021, 9, 130221–130232. [Google Scholar] [CrossRef]
- Hussain, S.S.; Riaz, S.; Nowsherwan, G.A.; Jahangir, K.; Raza, A.; Iqbal, M.J.; Sadiq, I.; Naseem, S. Numerical Modeling and Optimization of Lead-Free Hybrid Double Perovskite Solar Cell by Using SCAPS-1D. J. Renew. Energy 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Aeberhard, U.; Schiller, A.; Masson, Y.; Zeder, S.J.; Blülle, B.; Ruhstaller, B. Analysis and Optimization of Organic Tandem Solar Cells by Full Opto-Electronic Simulation. Front. Photon 2022, 3, 891565. [Google Scholar] [CrossRef]
- Salem, M.S.; Shaker, A.; Abouelatta, M.; Alanazi, A.; Al-Dhlan, K.A.; Almurayziq, T.S. Numerical analysis of hole transport layer-free antimony selenide solar cells: Possible routes for efficiency promotion. Opt. Mater. 2022, 129, 112473. [Google Scholar] [CrossRef]
- Leong, W.L.; Ooi, Z.-E.; Sabba, D.; Yi, C.; Zakeeruddin, S.M.; Graetzel, M.; Gordon, J.M.; Katz, E.A.; Mathews, N. Identifying Fundamental Limitations in Halide Perovskite Solar Cells. Adv. Mater. 2016, 28, 2439–2445. [Google Scholar] [CrossRef]
- Das, A.; Peu, S.D.; Akanda, A.M.; Salah, M.M.; Hossain, S.; Das, B.K. Numerical Simulation and Optimization of Inorganic Lead-Free Cs3Bi2I9-Based Perovskite Photovoltaic Cell: Impact of Various Design Parameters. Energies 2023, 16, 2328. [Google Scholar] [CrossRef]
- Wang, D.; Wu, J.; Guo, H.; Wu, M.; Wu, L.; Zhang, S.; Ao, J.; Wang, H.; Zhang, Y. Tuning the Work Function of the Metal Back Contact toward Efficient Cu 2 ZnSnSe 4 Solar Cells. Sol. RRL 2020, 5, 202000391. [Google Scholar] [CrossRef]
- Du, J.; Hu, K.; Zhang, J.; Meng, L.; Yue, J.; Angunawela, I.; Yan, H.; Qin, S.; Kong, X.; Zhang, Z.; et al. Polymerized small molecular acceptor based all-polymer solar cells with an efficiency of 16.16% via tuning polymer blend morphology by molecular design. Nat. Commun. 2021, 12, 5264. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Wang, L.; Zhao, C.; Wang, Y.; Hu, R.; Che, J.; He, S.; Chen, W.; Cao, L.; Luo, Z.; et al. Efficient All-Polymer Solar Cells Enabled by Interface Engineering. Polymers 2022, 14, 3835. [Google Scholar] [CrossRef] [PubMed]
- Ji, X.; Xiao, Z.; Sun, H.; Guo, X.; Ding, L. Polymer acceptors for all-polymer solar cells. J. Semicond. 2021, 42, 080202. [Google Scholar] [CrossRef]
- Wu, B.; Yin, B.; Duan, C.; Ding, L. All-polymer solar cells. J. Semicond. 2021, 42, 080301. [Google Scholar] [CrossRef]
- Jin, K.; Xiao, Z.; Ding, L. D18, an eximious solar polymer! J. Semicond. 2021, 42, 010502. [Google Scholar] [CrossRef]
- Salem, M.S.; Shaker, A.; Salah, M.M. Device Modeling of Efficient PBDB-T:PZT-Based All-Polymer Solar Cell: Role of Band Alignment. Polymers 2023, 15, 869. [Google Scholar] [CrossRef]




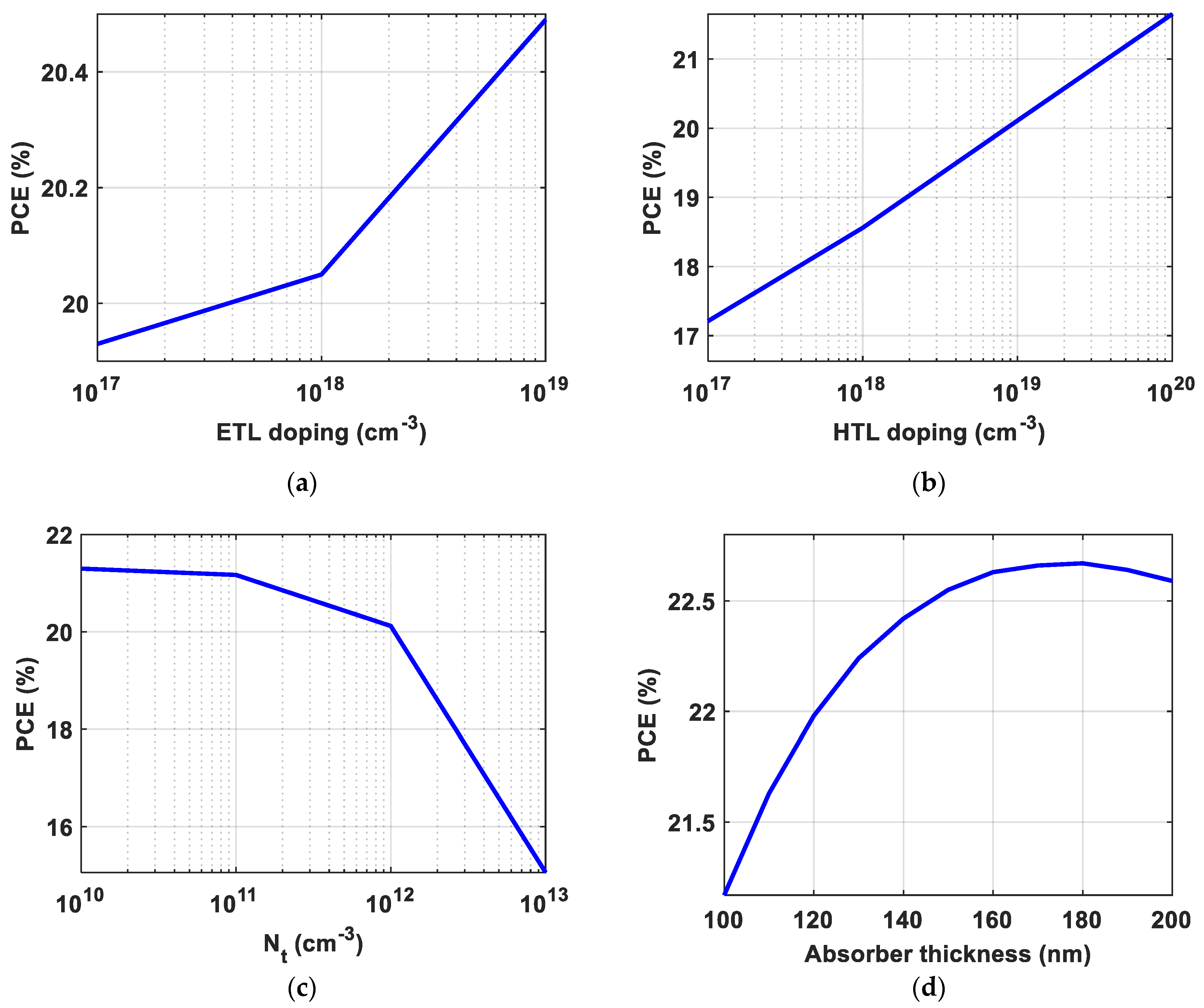
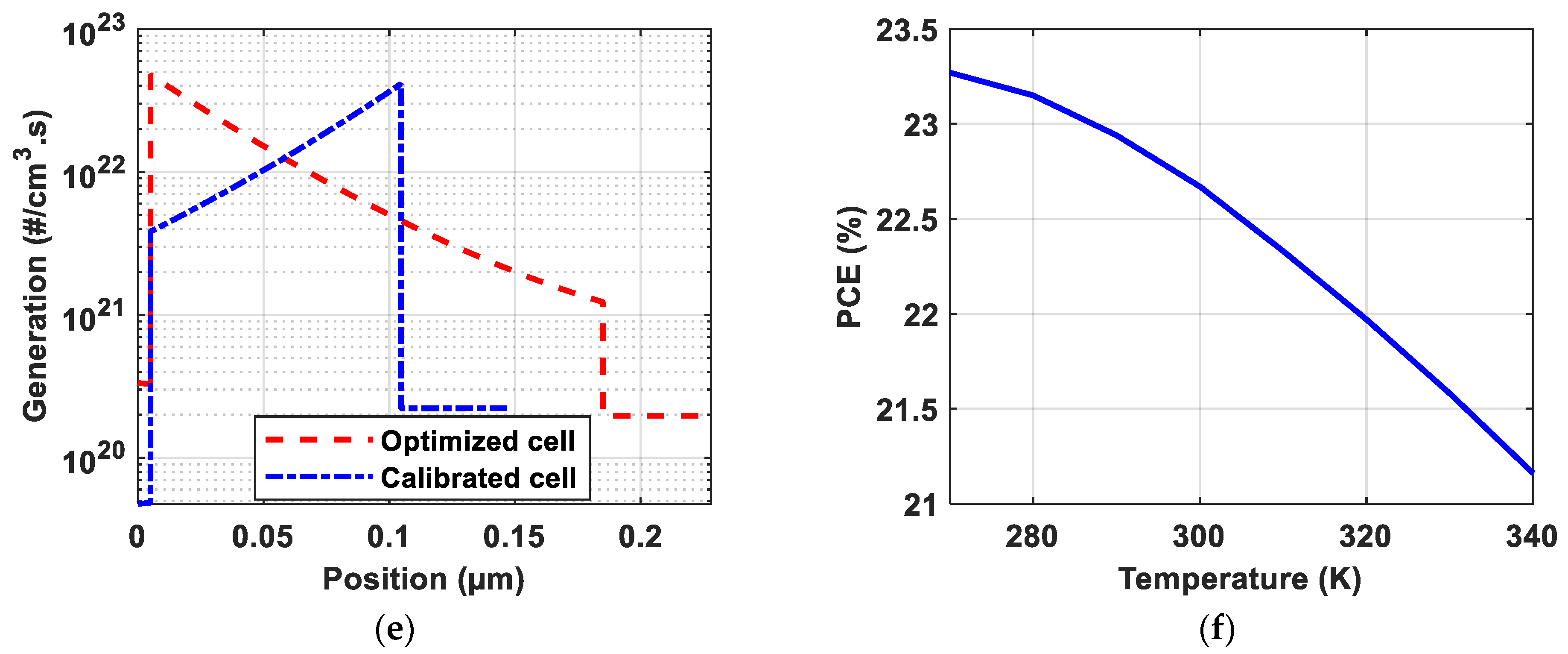

| Parameters | HTL (PEDOT:PSS) | Absorber (PBDB:T/PZT:C1) | ETL (PFN-Br) |
|---|---|---|---|
| Energy gap (eV) | 1.3 | 1.61 | 3 |
| Thickness (nm) | 43 | 100 | 5 |
| Affinity (eV) | 3.6 | 3.69 | 3.9 |
| Relative permittivity | 3.5 | ||
| (cm2V−1s−1) | 8.0 × 10−4 | 5.13 × 10−4 | 1.0 × 10−4 |
| (cm2V−1s−1) | 2.53 × 10−4 | 1.0 × 10−6 | |
| Conduction and valence bands’ density of states (cm−3) | 1 × 1021 | ||
| NA (cm−3) | 1 × 1019 | - | - |
| Contact | Work Functions (eV) | Holes’ Surface Recombination Velocity (cms−1) | Electrons’ Surface Recombination Velocity (cms−1) | |
|---|---|---|---|---|
| Back contact | Ag | 4.1 | 107 | 105 |
| Front contact | ITO | 4.7 | 105 | 107 |
| PCE [%] | VOC [V] | JSC [mA/cm2] | FF [%] | |
|---|---|---|---|---|
| Experimental [25] | 14.90 | 0.912 | 23.90 | 68.50 |
| Calibration | 14.91 | 0.912 | 23.90 | 68.45 |
| PCE [%] | VOC [V] | JSC [mA/cm2] | FF [%] | |
|---|---|---|---|---|
| Calibrated Cell | 14.91 | 0.912 | 23.90 | 68.45 |
| Optimized Cell | 22.67 | 0.938 | 30.94 | 78.08 |
| ETL | HTL | Absorber | PCE (%) | Type | Reference |
|---|---|---|---|---|---|
| PFN-Br | PEDOT:PSS | PM6/Y6 | 15.79 | Ex. | [14] |
| PFN-Br | PBDB-T/PZT-γ | 15.80 | [24] | ||
| PFN | PBDB:T/PZT:C1 | 14.90 | [25] | ||
| PDINN | PBDB-T/PN-Se | 16.16 | [54] | ||
| PDINN | PM6/PY-IT | 16.41 | [55] | ||
| ZrAcAc | PY-IT:BNT/PM6 | 16.09 | [56] | ||
| PDIN | PY2F-T/PYT/PM6 | 17.2 | [57] | ||
| PDIN | D18/N3 | 18.56 | [58] | ||
| PFN-Br | PTB7/PC70BM | 8.18 | Sim. | [34] | |
| Zn(O,S) | PTB7/PC70BM | 17.15 | [35] | ||
| PFN | CuI | PBDB:T/PZT:C1 | 20.87 | [59] | |
| PFN | PEDOT:PSS | PBDB:T/PZT:C1 | 22.67 | Sim. Inverted structure | This study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Muhimeed, T.I.; Alahmari, S.; Ahsan, M.; Salah, M.M. An Investigation of the Inverted Structure of a PBDB:T/PZT:C1-Based Polymer Solar Cell. Polymers 2023, 15, 4623. https://doi.org/10.3390/polym15244623
Al-Muhimeed TI, Alahmari S, Ahsan M, Salah MM. An Investigation of the Inverted Structure of a PBDB:T/PZT:C1-Based Polymer Solar Cell. Polymers. 2023; 15(24):4623. https://doi.org/10.3390/polym15244623
Chicago/Turabian StyleAl-Muhimeed, Tahani I., Shareefah Alahmari, Muhammad Ahsan, and Mostafa M. Salah. 2023. "An Investigation of the Inverted Structure of a PBDB:T/PZT:C1-Based Polymer Solar Cell" Polymers 15, no. 24: 4623. https://doi.org/10.3390/polym15244623
APA StyleAl-Muhimeed, T. I., Alahmari, S., Ahsan, M., & Salah, M. M. (2023). An Investigation of the Inverted Structure of a PBDB:T/PZT:C1-Based Polymer Solar Cell. Polymers, 15(24), 4623. https://doi.org/10.3390/polym15244623






