Connecting Structural Characteristics and Material Properties in Phase-Separating Polymer Solutions: Phase-Field Modeling and Physics-Informed Neural Networks
Abstract
:1. Introduction
2. Methods and Analysis
2.1. Numerical Pseudo-Spectral Method
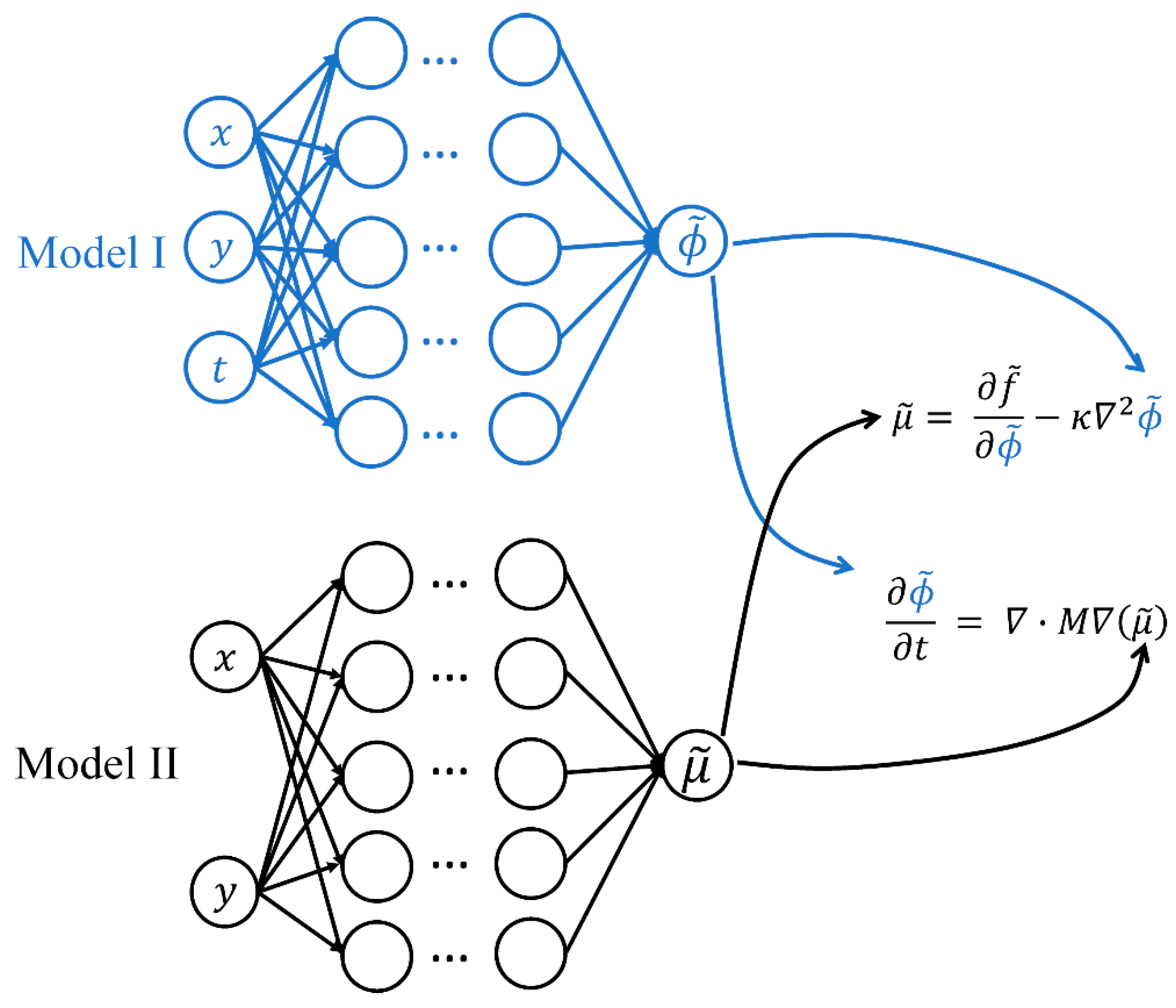
2.2. Physics-Informed Neural Networks
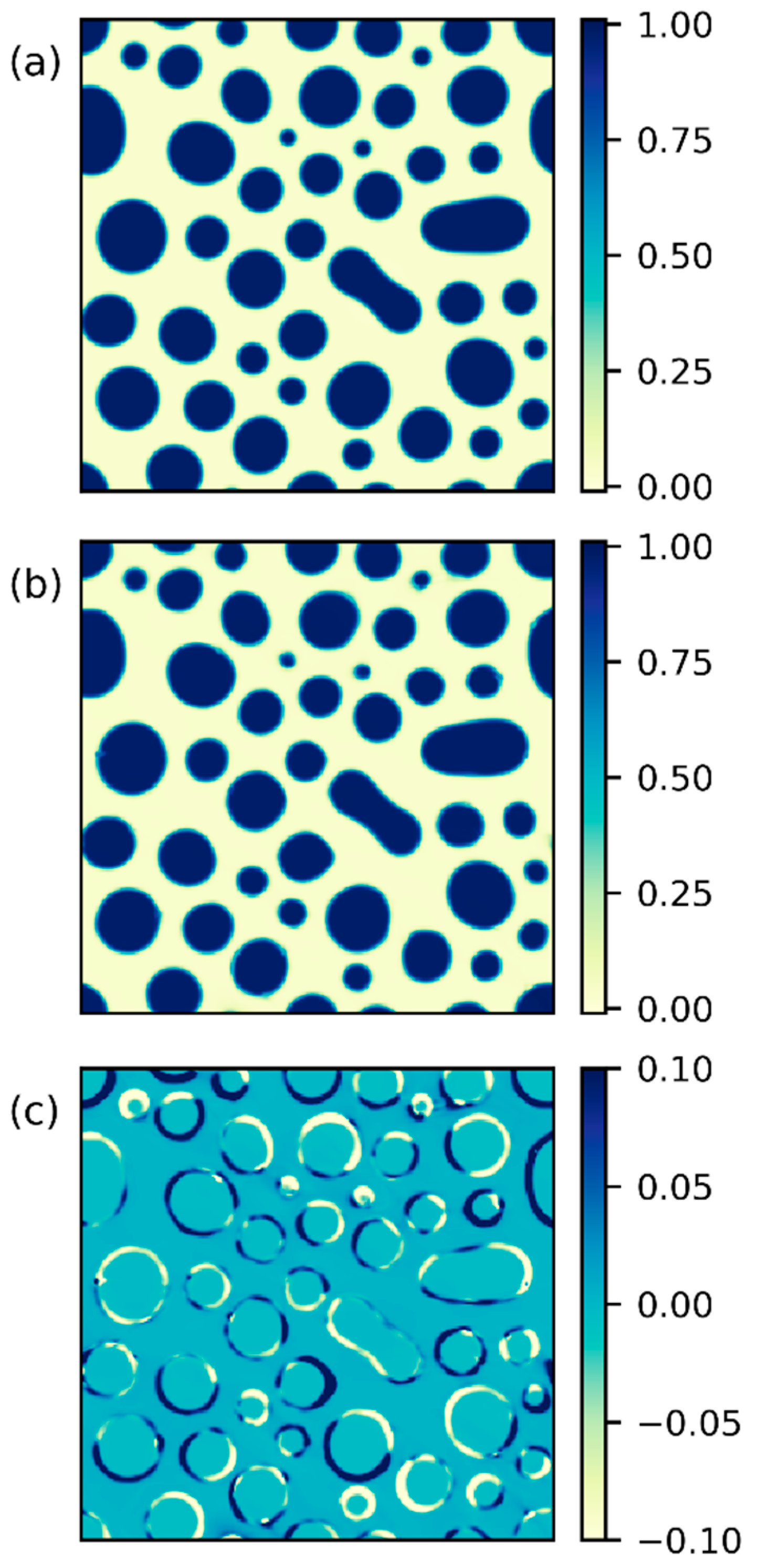
2.3. Morphology Analysis
3. Results and Discussion
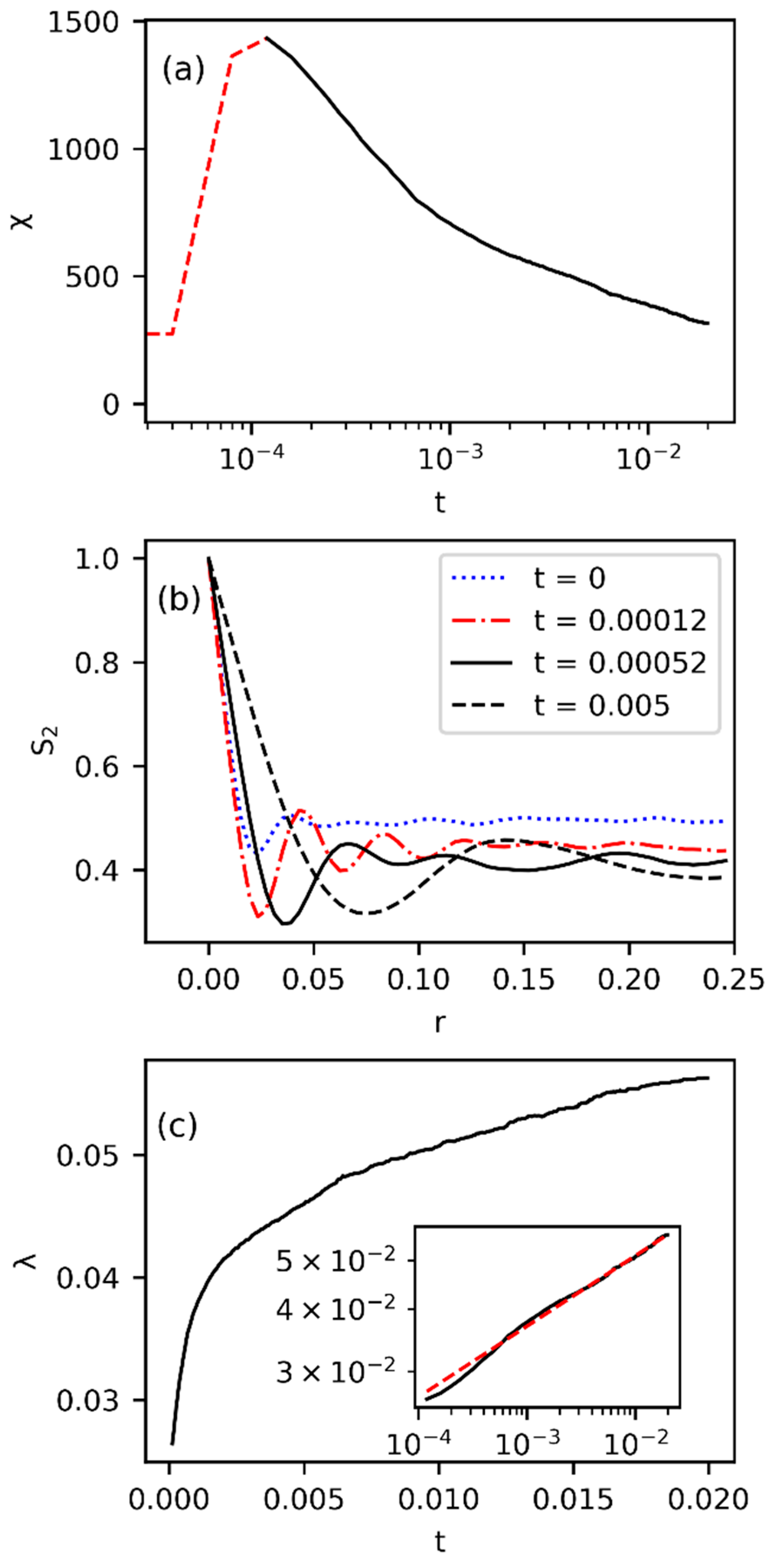
3.1. Phase Separation Characteristics
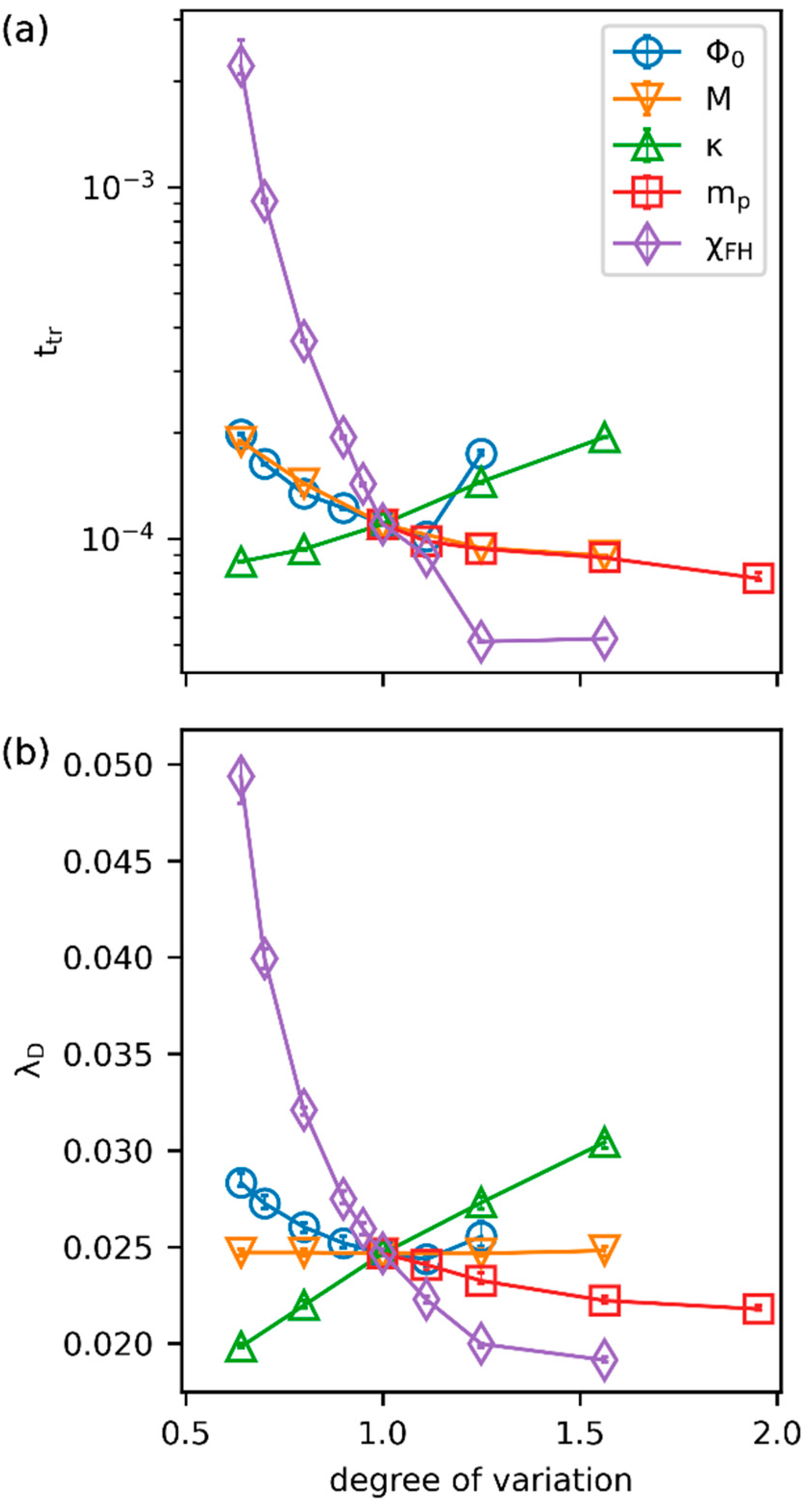
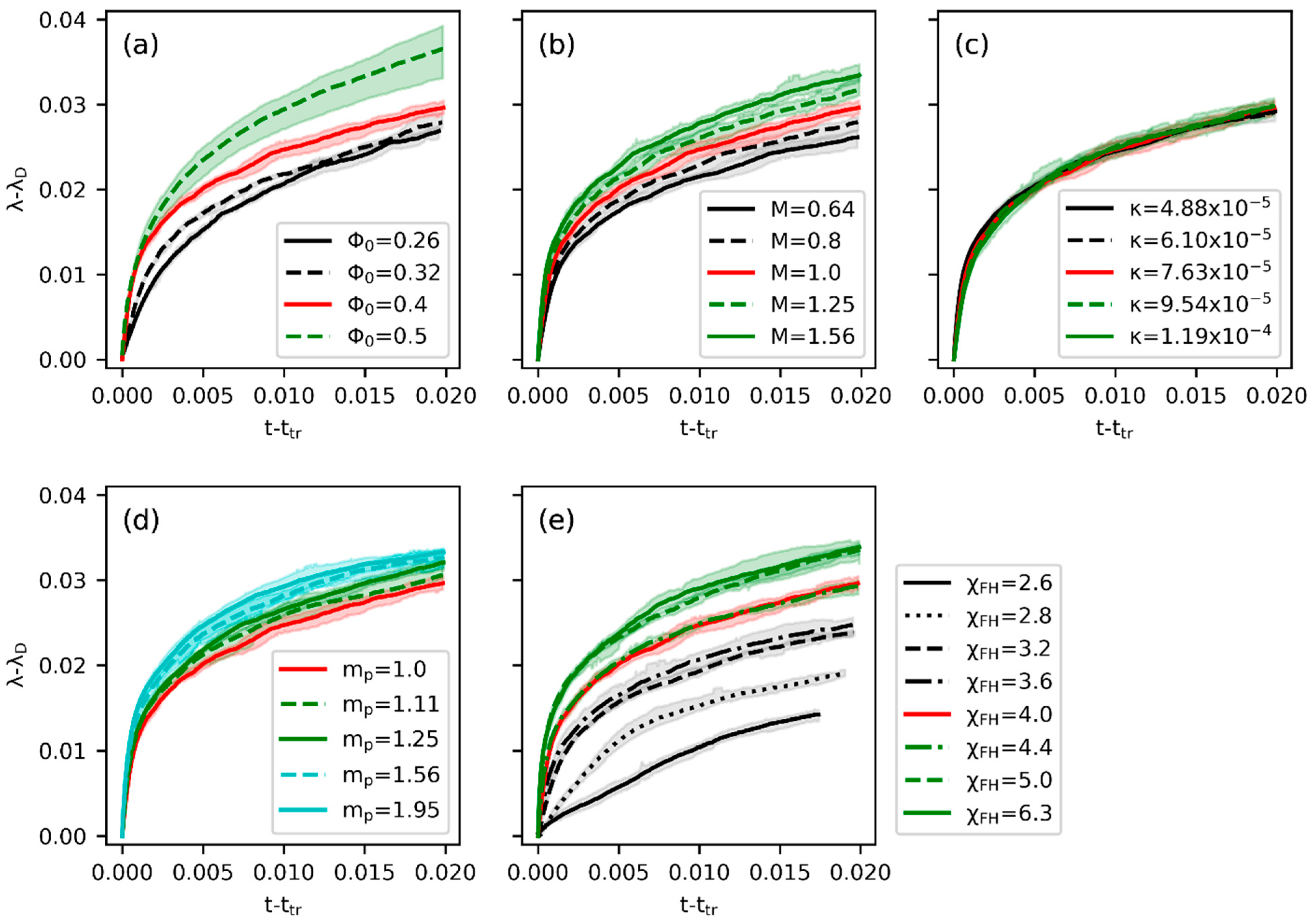
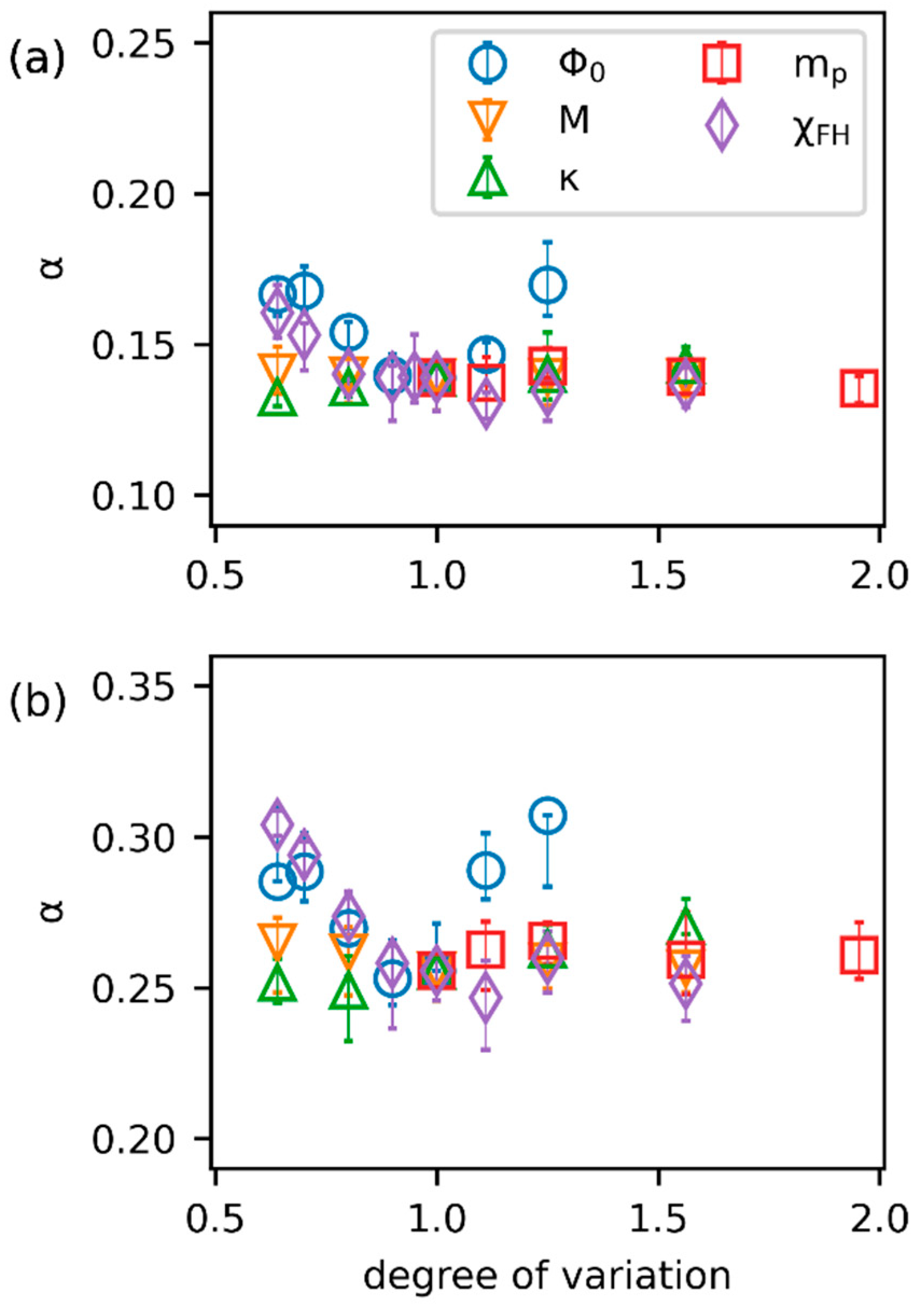
3.2. Effects of Parameters
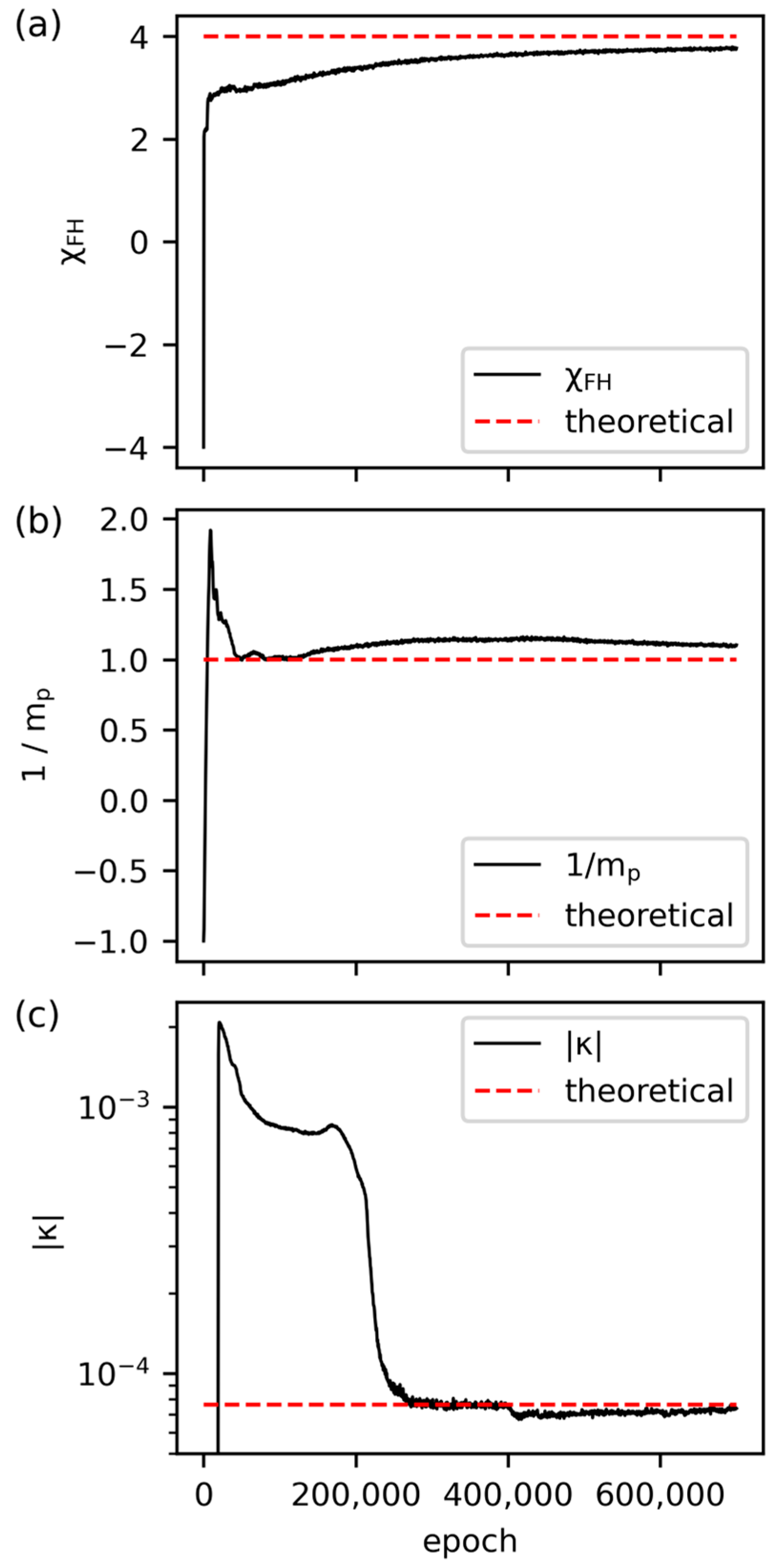
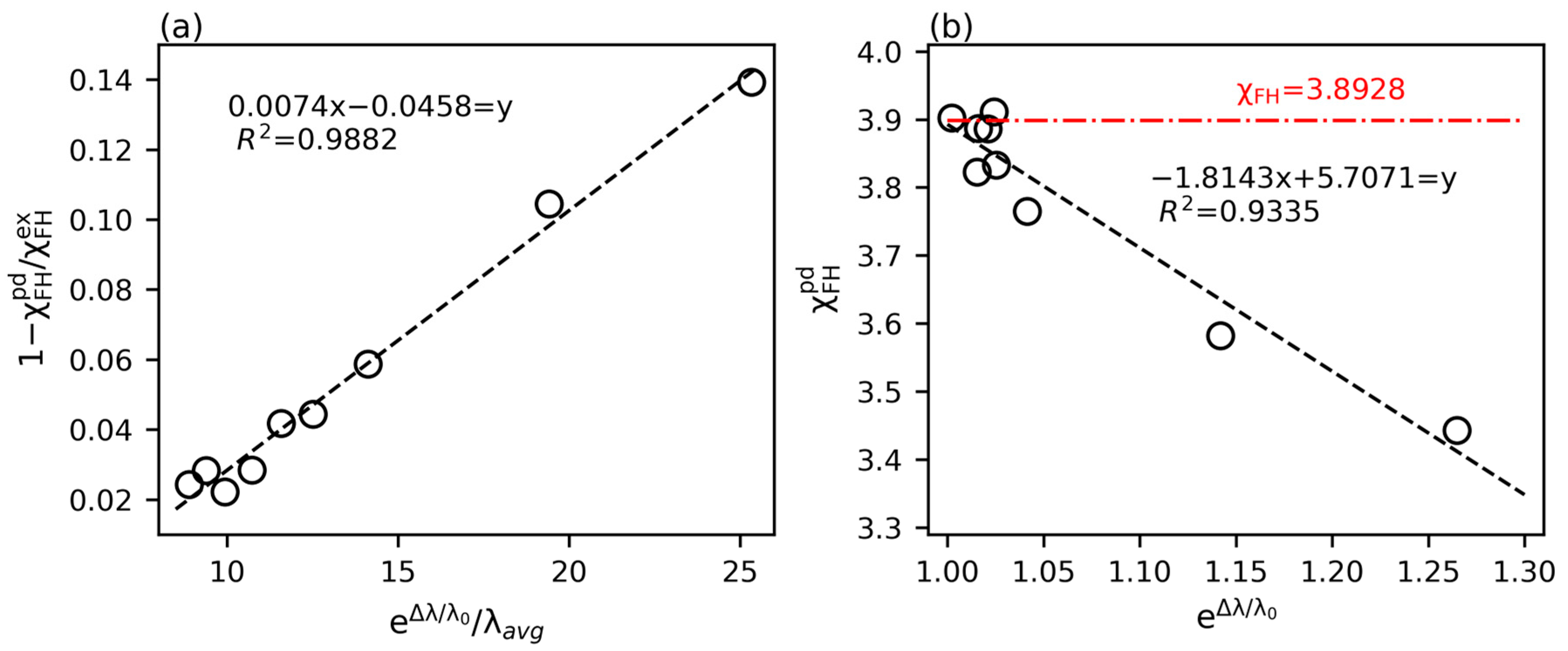
3.3. Inverse Prediction by PINN
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dagotto, E.; Hotta, T.; Moreo, A. Colossal magnetoresistant materials: The key role of phase separation. Phys. Rep. 2001, 344, 1–153. [Google Scholar] [CrossRef]
- Mezzenga, R.; Schurtenberger, P.; Burbidge, A.; Michel, M. Understanding foods as soft materials. Nat. Mater. 2005, 4, 729–740. [Google Scholar] [CrossRef] [PubMed]
- Ai, W.; Wu, B.; Martínez-Pañeda, E. A coupled phase field formulation for modelling fatigue cracking in lithium-ion battery electrode particles. J. Power Source 2022, 544, 231805. [Google Scholar] [CrossRef]
- Martínez, G.; Baibich, M.; Miranda, M.; Vargas, E. Nanostructural phases and giant magnetoresistance in Cu–Co alloys. J. Magn. Magn. Mater. 2004, 272, 1716–1717. [Google Scholar] [CrossRef]
- Bronnikov, S.; Dierking, I. Quench depth dependence of liquid crystal nucleus growth: A time resolved statistical analysis. Phys. B Condens. Matter 2005, 358, 339–347. [Google Scholar] [CrossRef]
- Martínez-Agustín, F.; Ruiz-Salgado, S.; Zenteno-Mateo, B.; Rubio, E.; Morales, M. 3D pattern formation from coupled Cahn-Hilliard and Swift-Hohenberg equations: Morphological phases transitions of polymers, bock and diblock copolymers. Comput. Mater. Sci. 2022, 210, 111431. [Google Scholar] [CrossRef]
- Radu, E.R.; Voicu, S.I.; Thakur, V.K. Polymeric membranes for biomedical applications. Polymers 2023, 15, 619. [Google Scholar] [CrossRef] [PubMed]
- Kang, G.-D.; Cao, Y.-M. Application and modification of poly(vinylidene fluoride)(PVDF) membranes—A review. J. Membr. Sci. 2014, 463, 145–165. [Google Scholar] [CrossRef]
- Ismail, N.; Venault, A.; Mikkola, J.-P.; Bouyer, D.; Drioli, E.; Kiadeh, N.T.H. Investigating the potential of membranes formed by the vapor induced phase separation process. J. Membr. Sci. 2020, 597, 117601. [Google Scholar] [CrossRef]
- Dong, X.; Lu, D.; Harris, T.A.; Escobar, I.C. Polymers and solvents used in membrane fabrication: A review focusing on sustainable membrane development. Membranes 2021, 11, 309. [Google Scholar] [CrossRef]
- Tan, X.; Rodrigue, D. A Review on Porous Polymeric Membrane Preparation. Part I: Production Techniques with Polysulfone and Poly(vinylidene fluoride). Polymers 2019, 11, 1160. [Google Scholar] [CrossRef] [PubMed]
- Feinle, A.; Elsaesser, M.S.; Huesing, N. Sol–gel synthesis of monolithic materials with hierarchical porosity. Chem. Soc. Rev. 2016, 45, 3377–3399. [Google Scholar] [CrossRef] [PubMed]
- Nakanishi, K.; Tanaka, N. Sol–gel with phase separation. Hierarchically porous materials optimized for high-performance liquid chromatography separations. Acc. Chem. Res. 2007, 40, 863–873. [Google Scholar] [CrossRef] [PubMed]
- Moelans, N.; Blanpain, B.; Wollants, P. An introduction to phase-field modeling of microstructure evolution. Calphad 2008, 32, 268–294. [Google Scholar] [CrossRef]
- Fang, P.; Cui, S.; Song, Z.; Zhu, L.; Du, M.; Yang, C. Phase-Field Simulation of the Effect of Coagulation Bath Temperature on the Structure and Properties of Polyvinylidene Fluoride Microporous Membranes Prepared by a Nonsolvent-Induced Phase Separation. ACS Omega 2023, 8, 180–189. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Powell, A.C. Phase field simulations of early stage structure formation during immersion precipitation of polymeric membranes in 2D and 3D. J. Membr. Sci. 2006, 268, 150–164. [Google Scholar] [CrossRef]
- Alikakos, N.D.; Fusco, G. Slow Dynamics for the Cahn-Hilliard Equation in Higher Space Dimensions: The Motion of Bubbles. Arch. Ration. Mech. Anal. 1998, 141, 1–61. [Google Scholar] [CrossRef]
- Blesgen, T.; Chenchiah, I.V. Cahn–Hilliard equations incorporating elasticity: Analysis and comparison to experiments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120342. [Google Scholar] [CrossRef]
- Bartels, A.; Kurzeja, P.; Mosler, J. Cahn–Hilliard phase field theory coupled to mechanics: Fundamentals, numerical implementation and application to topology optimization. Comput. Methods Appl. Mech. Eng. 2021, 383, 113918. [Google Scholar] [CrossRef]
- Matsuyama, A. Theory of binary mixtures of a rodlike polymer and a liquid crystal. J. Chem. Phys. 2010, 132, 214902. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Choi, Y.; Lee, S.-M.; Jeong, D. Basic principles and practical applications of the Cahn–Hilliard equation. Math. Probl. Eng. 2016, 2016, 9532608. [Google Scholar] [CrossRef]
- Mino, Y.; Ishigami, T.; Kagawa, Y.; Matsuyama, H. Three-dimensional phase-field simulations of membrane porous structure formation by thermally induced phase separation in polymer solutions. J. Membr. Sci. 2015, 483, 104–111. [Google Scholar] [CrossRef]
- Manzanarez, H.; Mericq, J.; Guenoun, P.; Chikina, J.; Bouyer, D. Modeling phase inversion using Cahn-Hilliard equations–Influence of the mobility on the pattern formation dynamics. Chem. Eng. Sci. 2017, 173, 411–427. [Google Scholar] [CrossRef]
- L’vov, P.; Sibatov, R. Effect of the Particle Size Distribution on the Cahn-Hilliard Dynamics in a Cathode of Lithium-Ion Batteries. Batteries 2020, 6, 29. [Google Scholar] [CrossRef]
- Singh, A.; Mukherjee, A.; Vermeulen, H.; Barkema, G.; Puri, S. Control of structure formation in phase-separating systems. J. Chem. Phys. 2011, 134, 044910. [Google Scholar] [CrossRef] [PubMed]
- Tateno, M.; Tanaka, H. Power-law coarsening in network-forming phase separation governed by mechanical relaxation. Nat. Commun. 2021, 12, 912. [Google Scholar] [CrossRef] [PubMed]
- Gameiro, M.; Mischaikow, K.; Wanner, T. Evolution of pattern complexity in the Cahn–Hilliard theory of phase separation. Acta Mater. 2005, 53, 693–704. [Google Scholar] [CrossRef]
- Zhou, S.; Xie, Y.M. Numerical simulation of three-dimensional multicomponent Cahn–Hilliard systems. Int. J. Mech. Sci. 2021, 198, 106349. [Google Scholar] [CrossRef]
- Wodo, O.; Ganapathysubramanian, B. Computationally efficient solution to the Cahn–Hilliard equation: Adaptive implicit time schemes, mesh sensitivity analysis and the 3D isoperimetric problem. J. Comput. Phys. 2011, 230, 6037–6060. [Google Scholar] [CrossRef]
- Forte, A.E.; Hanakata, P.Z.; Jin, L.; Zari, E.; Zareei, A.; Fernandes, M.C.; Sumner, L.; Alvarez, J.; Bertoldi, K. Inverse design of inflatable soft membranes through machine learning. Adv. Funct. Mater. 2022, 32, 2111610. [Google Scholar] [CrossRef]
- Liu, D.; Tan, Y.; Khoram, E.; Yu, Z. Training Deep Neural Networks for the Inverse Design of Nanophotonic Structures. ACS Photonics 2018, 5, 1365–1369. [Google Scholar] [CrossRef]
- Fang, Z.; Zhan, J. Deep physical informed neural networks for metamaterial design. IEEE Access 2019, 8, 24506–24513. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, L.; Karniadakis, G.E.; Dal Negro, L. Physics-informed neural networks for inverse problems in nano-optics and metamaterials. Opt. Express 2020, 28, 11618–11633. [Google Scholar] [CrossRef] [PubMed]
- Guan, J.; Huang, T.; Liu, W.; Feng, F.; Japip, S.; Li, J.; Wu, J.; Wang, X.; Zhang, S. Design and prediction of metal organic framework-based mixed matrix membranes for CO2 capture via machine learning. Cell Rep. Phys. Sci. 2022, 3, 100864. [Google Scholar] [CrossRef]
- Lin, D.; Yu, H.-Y. Deep learning and inverse discovery of polymer self-consistent field theory inspired by physics-informed neural networks. Phys. Rev. E 2022, 106, 014503. [Google Scholar] [CrossRef] [PubMed]
- Barnett, J.W.; Bilchak, C.R.; Wang, Y.; Benicewicz, B.C.; Murdock, L.A.; Bereau, T.; Kumar, S.K. Designing exceptional gas-separation polymer membranes using machine learning. Sci. Adv. 2020, 6, eaaz4301. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J. Discovering Phase Field Models from Image Data with the Pseudo-Spectral Physics Informed Neural Networks. Commun. Appl. Math. Comput. 2021, 3, 357–369. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific Machine Learning Through Physics–Informed Neural Networks: Where we are and What’s Next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M. Deep hidden physics models: Deep learning of nonlinear partial differential equations. J. Mach. Learn. Res. 2018, 19, 932–955. [Google Scholar]
- Cai, S.; Mao, Z.; Wang, Z.; Yin, M.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mech. Sin. 2021, 37, 1727–1738. [Google Scholar] [CrossRef]
- Moseley, B.; Markham, A.; Nissen-Meyer, T. Finite basis physics-informed neural networks (FBPINNs): A scalable domain decomposition approach for solving differential equations. Adv. Comput. Math. 2023, 49, 62. [Google Scholar] [CrossRef]
- Wang, S.; Wang, H.; Perdikaris, P. On the eigenvector bias of Fourier feature networks: From regression to solving multi-scale PDEs with physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2021, 384, 113938. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: A Navier-Stokes informed deep learning framework for assimilating flow visualization data. arXiv 2018, arXiv:1808.04327. [Google Scholar]
- Meng, X.; Karniadakis, G.E. A composite neural network that learns from multi-fidelity data: Application to function approximation and inverse PDE problems. J. Comput. Phys. 2020, 401, 109020. [Google Scholar] [CrossRef]
- Flory, P.J. Thermodynamics of high polymer solutions. J. Chem. Phys. 1942, 10, 51–61. [Google Scholar] [CrossRef]
- Sofonea, V.; Mecke, K. Morphological characterization of spinodal decomposition kinetics. Eur. Phys. J. B-Condens. Matter Complex Syst. 1999, 8, 99–112. [Google Scholar] [CrossRef]
- Hilou, E.; Joshi, K.; Biswal, S.L. Characterizing the spatiotemporal evolution of paramagnetic colloids in time-varying magnetic fields with Minkowski functionals. Soft Matter 2020, 16, 8799–8805. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, Y.; Zhang, L.; Lei, X.; Yao, W.; Wang, N. Temperature and initial composition dependence of pattern formation and dynamic behavior in phase separation under deep-quenched conditions. RSC Adv. 2019, 9, 10670–10678. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- König, B.; Ronsin, O.J.; Harting, J. Two-dimensional Cahn–Hilliard simulations for coarsening kinetics of spinodal decomposition in binary mixtures. Phys. Chem. Chem. Phys. 2021, 23, 24823–24833. [Google Scholar] [CrossRef] [PubMed]
- Inguva, P.K.; Walker, P.J.; Yew, H.W.; Zhu, K.; Haslam, A.J.; Matar, O.K. Continuum-scale modelling of polymer blends using the Cahn–Hilliard equation: Transport and thermodynamics. Soft Matter 2021, 17, 5645–5665. [Google Scholar] [CrossRef] [PubMed]
- Padilha Júnior, E.J.; Staudt, P.B.; Tessaro, I.C.; Medeiros Cardozo, N.S. A new approach to phase-field model for the phase separation dynamics in polymer membrane formation by immersion precipitation method. Polymer 2020, 186, 122054. [Google Scholar] [CrossRef]
- Wang, S.; Teng, Y.; Perdikaris, P. Understanding and mitigating gradient flow pathologies in physics-informed neural networks. SIAM J. Sci. Comput. 2021, 43, A3055–A3081. [Google Scholar] [CrossRef]
- Ji, W.; Qiu, W.; Shi, Z.; Pan, S.; Deng, S. Stiff-PINN: Physics-Informed Neural Network for Stiff Chemical Kinetics. J. Phys. Chem. A 2021, 125, 8098–8106. [Google Scholar] [CrossRef] [PubMed]
- Basir, S.; Senocak, I. Critical Investigation of Failure Modes in Physics-informed Neural Networks. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Wong, J.C.; Ooi, C.; Gupta, A.; Ong, Y.-S. Learning in sinusoidal spaces with physics-informed neural networks. IEEE Trans. Artif. Intell. 2022, 1–15. [Google Scholar] [CrossRef]
- Mattey, R.; Ghosh, S. A novel sequential method to train physics informed neural networks for Allen Cahn and Cahn Hilliard equations. Comput. Methods Appl. Mech. Eng. 2022, 390, 114474. [Google Scholar] [CrossRef]
- Wight, C. Numerical Approximations of Phase Field Equations with Physics Informed Neural Networks. Master’s Thesis, Utah State University, Logan, UT, USA, 2020. [Google Scholar]
- Zhu, Q.; Yang, J. A local deep learning method for solving high order partial differential equations. arXiv 2021, arXiv:2103.08915. [Google Scholar]
- Stein, M. Large Sample Properties of Simulations Using Latin Hypercube Sampling. Technometrics 1987, 29, 143–151. [Google Scholar] [CrossRef]
- Kinga, D.; Adam, J.B. A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Boelens, A.M.; Tchelepi, H.A. QuantImPy: Minkowski functionals and functions with Python. SoftwareX 2021, 16, 100823. [Google Scholar] [CrossRef]
- Sheng, G.; Wang, T.; Du, Q.; Wang, K.; Liu, Z.; Chen, L. Coarsening kinetics of a two phase mixture with highly disparate diffusion mobility. Commun. Comput. Phys. 2010, 8, 249. [Google Scholar] [CrossRef]
- Dai, S.; Du, Q. Computational studies of coarsening rates for the Cahn–Hilliard equation with phase-dependent diffusion mobility. J. Comput. Phys. 2016, 310, 85–108. [Google Scholar] [CrossRef]
- Andrews, W.B.; Voorhees, P.W.; Thornton, K. Simulation of coarsening in two-phase systems with dissimilar mobilities. Comput. Mater. Sci. 2020, 173, 109418. [Google Scholar] [CrossRef]
- Oommen, V.; Shukla, K.; Goswami, S.; Dingreville, R.; Karniadakis, G.E. Learning two-phase microstructure evolution using neural operators and autoencoder architectures. Npj Comput. Mater. 2022, 8, 190. [Google Scholar] [CrossRef]
- Kiyani, E.; Silber, S.; Kooshkbaghi, M.; Karttunen, M. Machine-learning-based data-driven discovery of nonlinear phase-field dynamics. Phys. Rev. E 2022, 106, 065303. [Google Scholar] [CrossRef] [PubMed]


| System Parameters | Value | |
|---|---|---|
| initial polymer volume fraction | 0.4 | |
| system temperature | T* | 300 K |
| unit volume of a lattice | ν0* | 10−3 m3 mol−1 |
| gas constant | R | 8.314 J K−1 mol−1 |
| degree of polymerization (polymer) | mp | 1 |
| degree of polymerization (solvent) | ms | fixed as 1 |
| Flory–Huggins parameter | χFH | 4 |
| surface tension parameter | * | 2 × 10−10 J m−1 |
| mobility constant | M* | 4 × 10−17 m5 s−1 J−1 |
| system domain | L* | 1024 nm |
| time | t* | 0.01 s |
| t0 | t1 | Relative Error (%) | ||
|---|---|---|---|---|
| 0.0008 | 0.0016 | 3.44 | 13.92 | 4.01 |
| 0.0016 | 0.0024 | 3.58 | 10.45 | 3.97 |
| 0.004 | 0.0048 | 3.76 | 5.87 | 4.00 |
| 0.0152 | 0.016 | 3.91 | 2.21 | 4.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, L.-C.; Chen, S.-J.; Yu, H.-Y. Connecting Structural Characteristics and Material Properties in Phase-Separating Polymer Solutions: Phase-Field Modeling and Physics-Informed Neural Networks. Polymers 2023, 15, 4711. https://doi.org/10.3390/polym15244711
Lin L-C, Chen S-J, Yu H-Y. Connecting Structural Characteristics and Material Properties in Phase-Separating Polymer Solutions: Phase-Field Modeling and Physics-Informed Neural Networks. Polymers. 2023; 15(24):4711. https://doi.org/10.3390/polym15244711
Chicago/Turabian StyleLin, Le-Chi, Sheng-Jer Chen, and Hsiu-Yu Yu. 2023. "Connecting Structural Characteristics and Material Properties in Phase-Separating Polymer Solutions: Phase-Field Modeling and Physics-Informed Neural Networks" Polymers 15, no. 24: 4711. https://doi.org/10.3390/polym15244711
APA StyleLin, L.-C., Chen, S.-J., & Yu, H.-Y. (2023). Connecting Structural Characteristics and Material Properties in Phase-Separating Polymer Solutions: Phase-Field Modeling and Physics-Informed Neural Networks. Polymers, 15(24), 4711. https://doi.org/10.3390/polym15244711







