The Energy Absorption Behavior of 3D-Printed Polymeric Octet-Truss Lattice Structures of Varying Strut Length and Radius
Abstract
:1. Introduction
2. Materials and Methods
2.1. 3D Printing Parameters
2.2. Resin Properties
2.3. Uniaxial Tensile Testing Method
2.4. Octet-Truss Geometry and Design
2.5. Octet-Truss Compression Testing Methods
3. Results
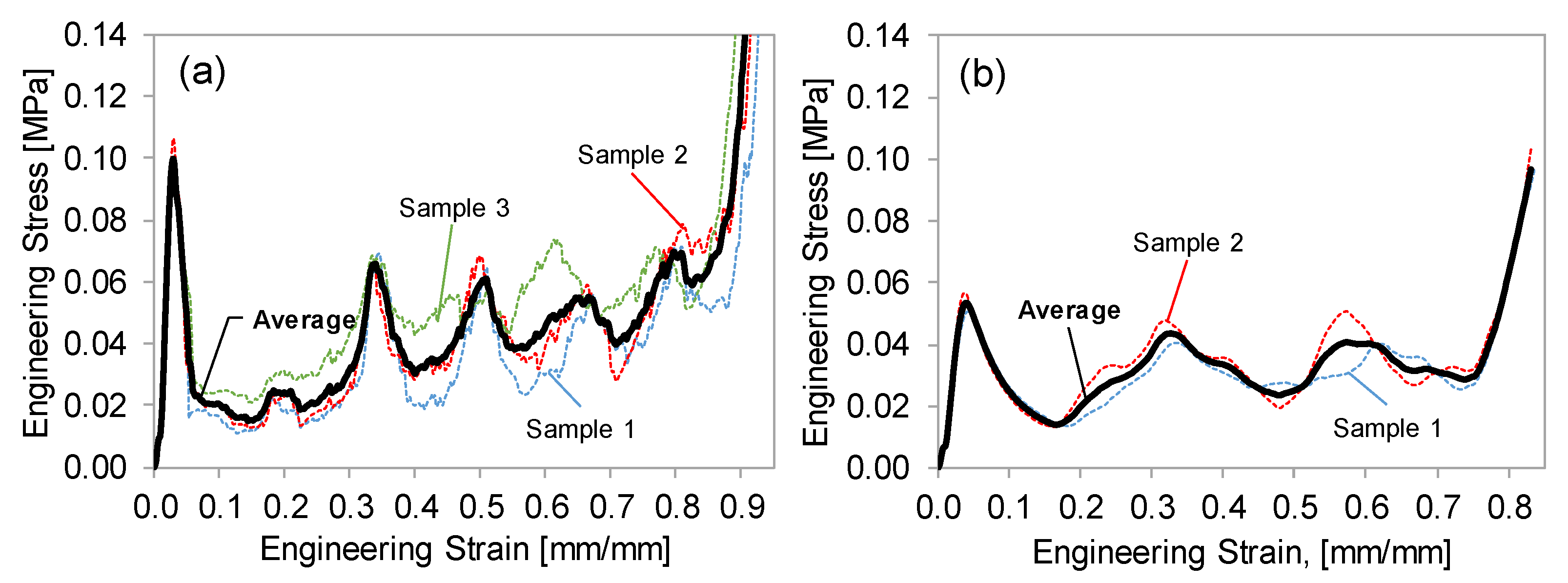
3.1. Uniaxial Tensile Test Results
3.2. Octet-Truss Compression Test Results
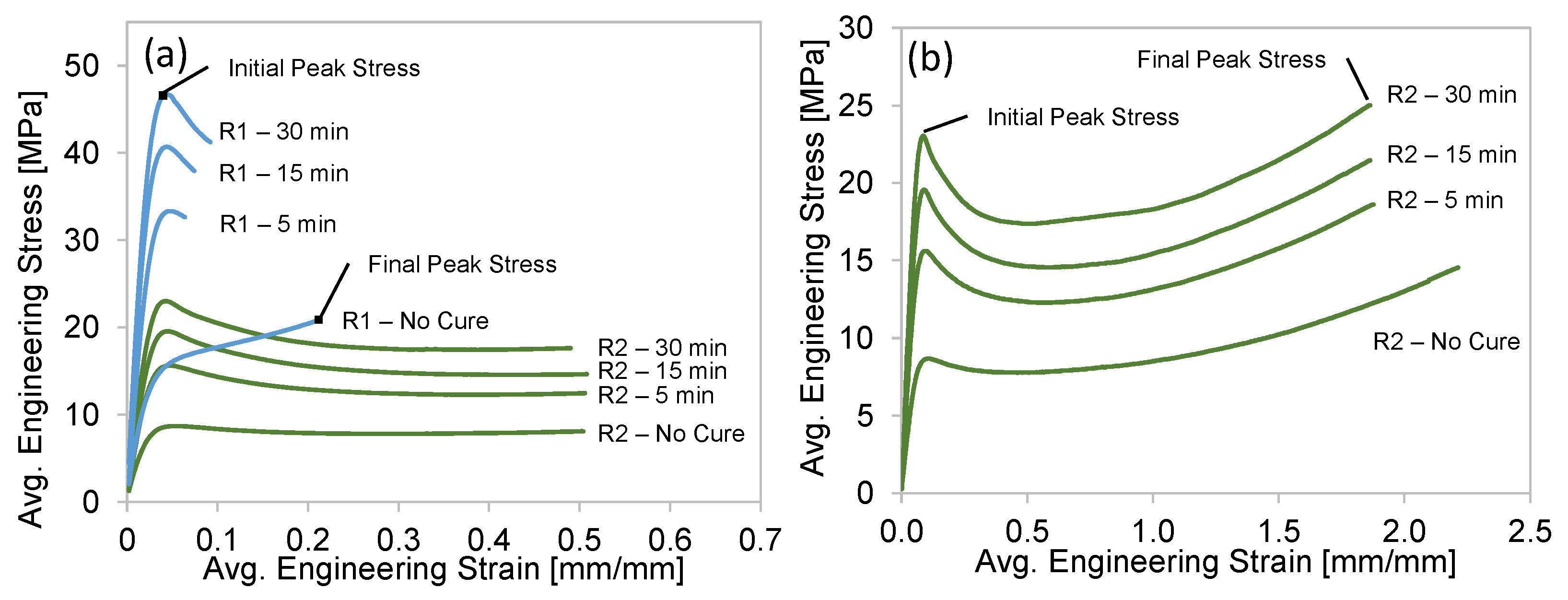
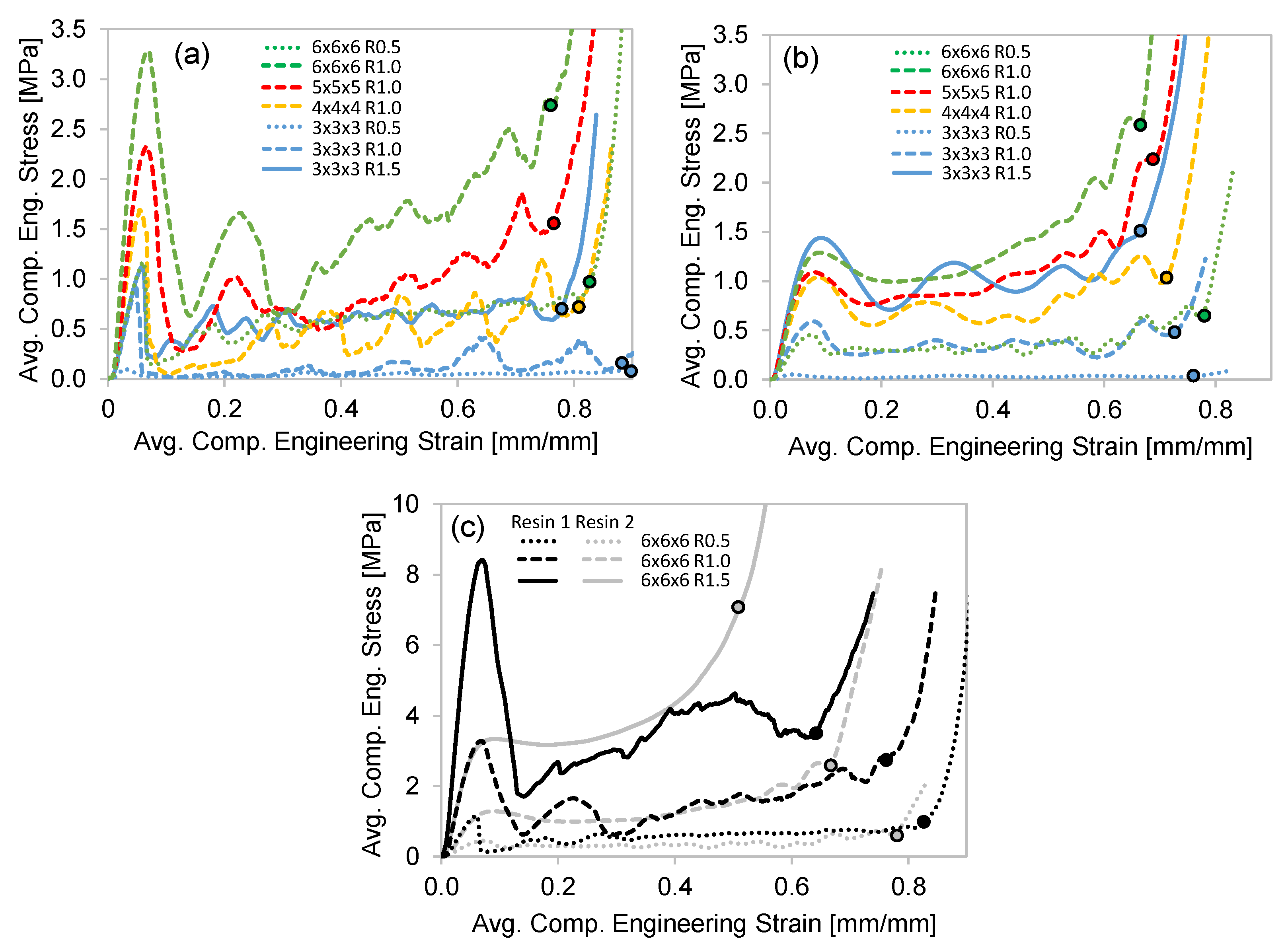
3.2.1. Compressive Stress–Strain
3.2.2. Compressive Energy Absorption
4. Discussion
4.1. Uniaxial Tensile Material Properties
4.2. Octet-Truss Compression Tests
4.2.1. Deformation Modes and Energy Absorption
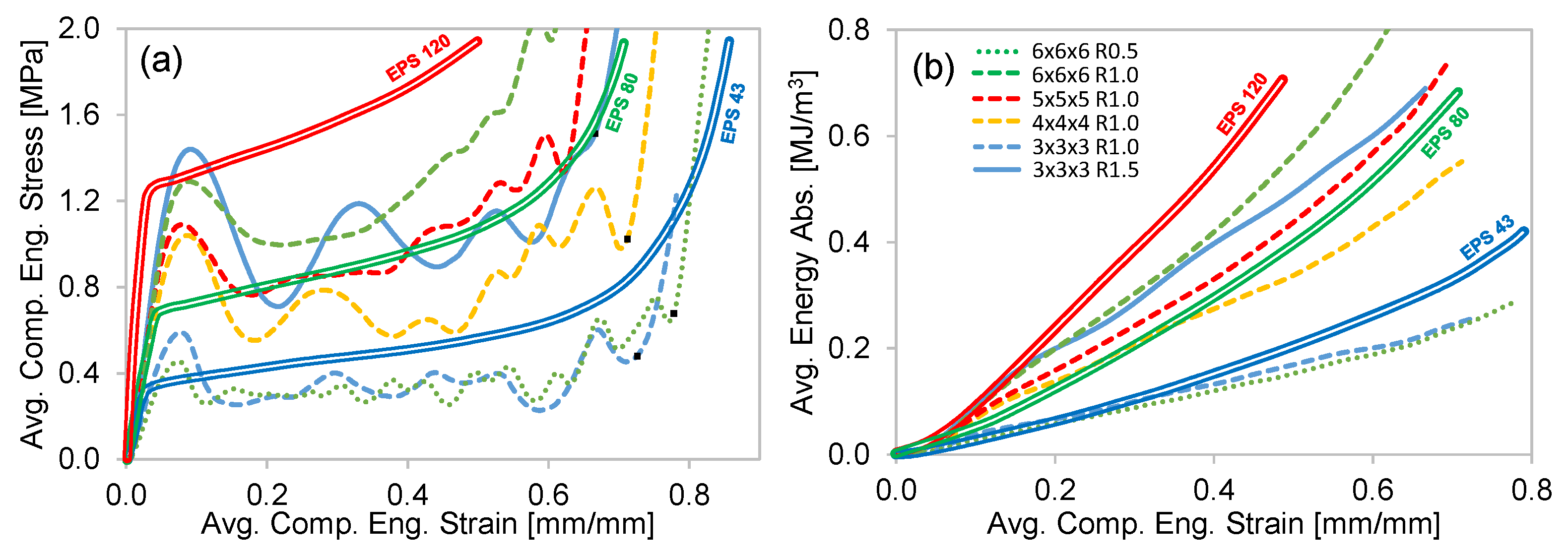
4.2.2. Stress–Strain and Energy Absorption Comparison to EPS Foams
4.3. Empirical Energy Absorption Model
5. Conclusions
- High-resolution SLA 3D printing was used to produce specimens with high geometric accuracy and no visible defects. This insured that the tensile/compression test results were not influenced by print defects.
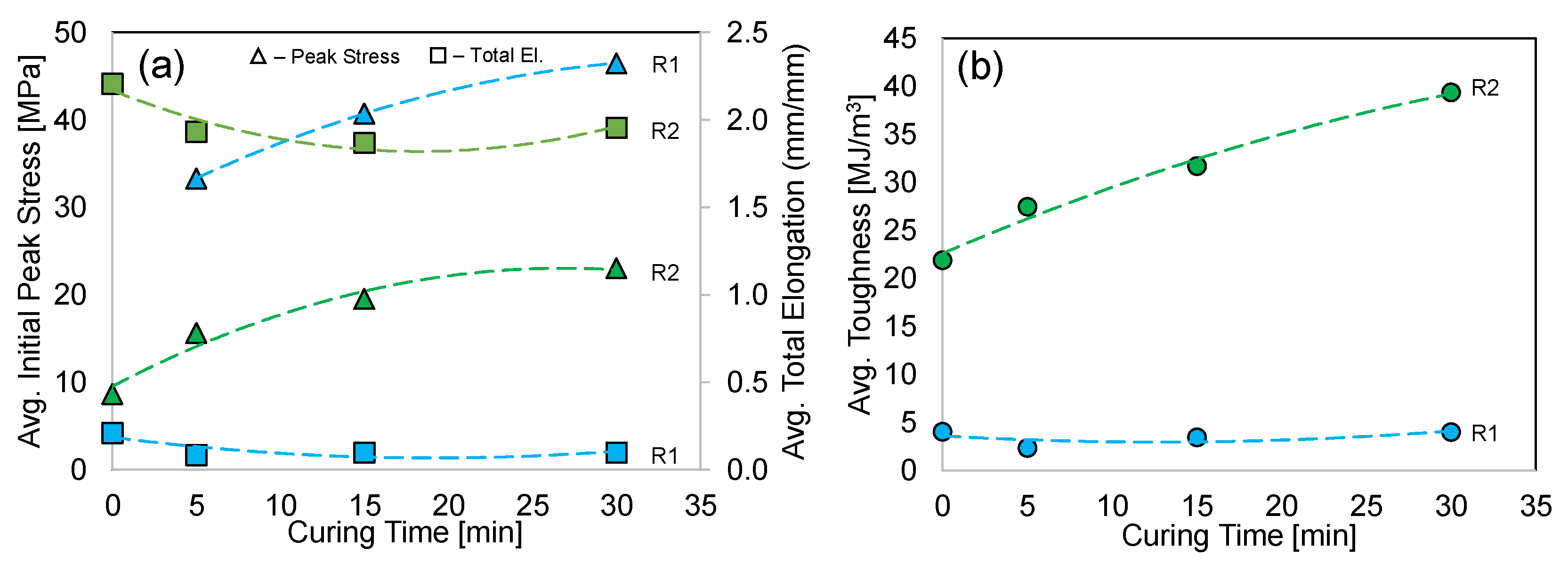
- Two different acrylate resin blends were used to print and test uniaxial tensile specimens. After a 30 min UV cure, Resin 1 exhibited a peak strength increase to 46 MPa (+124% compared to uncured) and a decreased total elongation strain to 0.09 (−57% compared to uncured). The post-cure peak strength of Resin 2 increased to 23 MPa (+67%), and the total elongation strain decreased slightly to 1.86 (−16%). There is the potential for further increases in strength with additional curing.
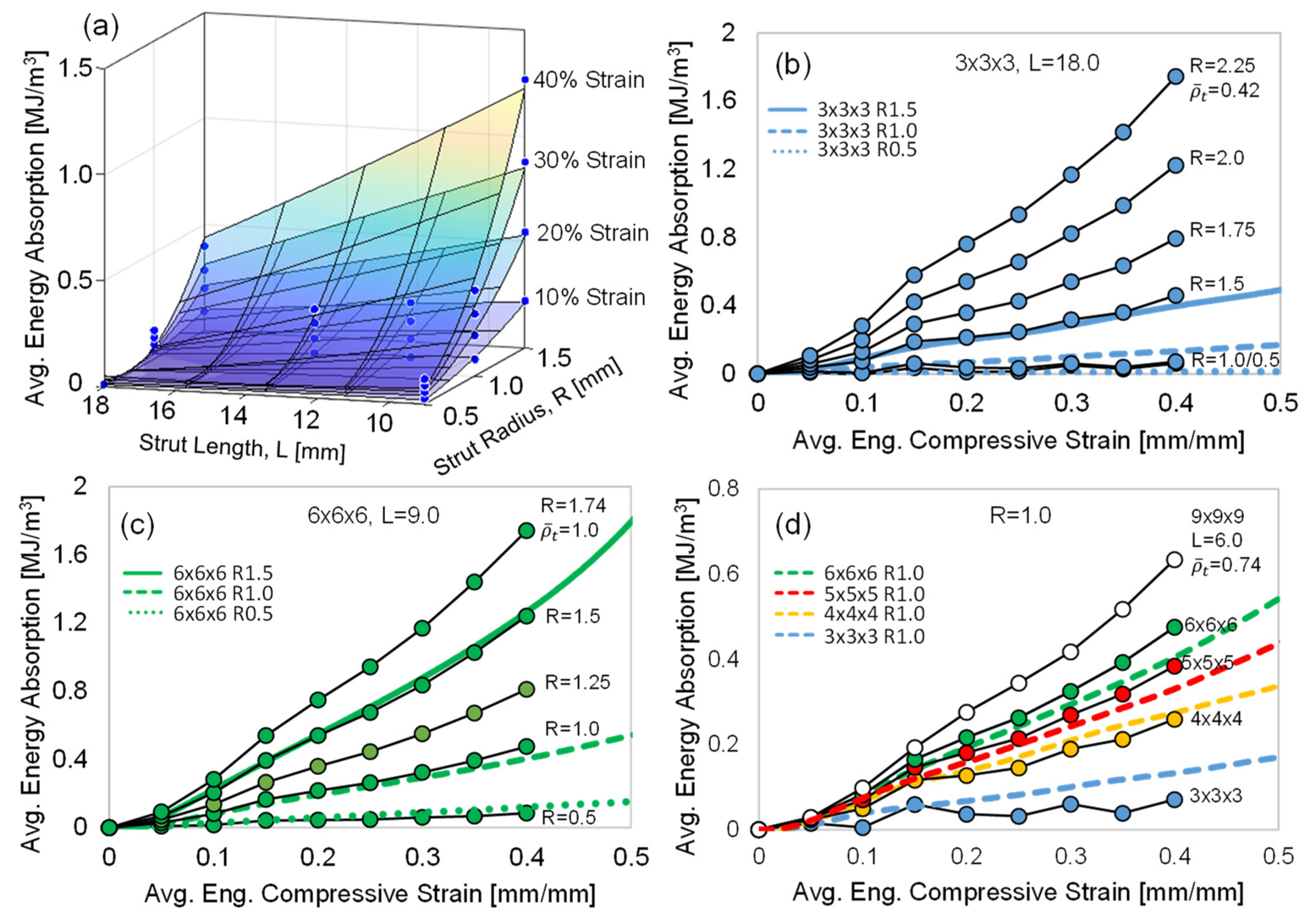
- Compression tests for the Resin 1 octet-truss structures exhibited a strong initial peak stress (maximum of 8.3 MPa for 6 × 6 × 6 R1.5) that was followed by a sudden strength reduction because of the catastrophic strut failure of the low-ductility material. Only the structure with the lowest relative density () failed layer-by-layer, while the other structures failed through multiple layers, resulting in sporadic stress–strain behavior. There is a clear increase in the compressive stress–strain behavior with decreasing strut length L and increasing strut radius R, which is also captured by an increase in .
- Similar increases (due to increased ) in compressive stress–strain behavior were shown for the Resin 2 structures, but the exceptional ductility of this resin resulted in no strut failure, and the severe initial peak stress (shown for Resin 1) was not observed, while a maximum initial stress of 3.3 MPa still resulted for the 6 × 6 × 6 R1.5 structure. The deformation mode transitioned from a twist mode (oscillating stress response), for structures with a low , to a stable collapse mode (plateaued stress response), at the highest values of .
- For both resins, the increase in EA was clearly related to reduced L and increased R. It was also shown that, despite the large difference in strength and ductility between the two resins, the total EA was similar with respect to L and R for both resins. For Resin 2, the EA at 0.5 compressive strain for the highest L and smallest R structure (3 × 3 × 3 R0.5) was 0.02 MJ/m3, while the structure with the highest L and smallest R (6 × 6 × 6 R1.5) was 1.86 MJ/m3. This difference was similar for the Resin 1 structure. When plotted against relative density, the EA data for both resins fit a polynomial trend very well, which is related to R and L.
- The Resin 2 EA versus compressive strain experimental data was used to develop an empirical model that can be used to predict the EA versus compressive strain curves for any R and L, within the bounds of the data that was used to develop the model. This can be used as a design tool for predicting octet-truss EA properties.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Meaning |
| AM | Additive manufacturing |
| EA | Energy absorption |
| FCC | Face-centered cubic |
| FDM | Fused deposition modeling |
| FE | Finite element |
| PPE | Personal protective equipment |
| SEA | Specific energy absorption |
| SLA | Stereolithography |
| SLM | Selective laser melting |
| UV | Ultraviolet |
References
- Bitzer, T. Honeycomb Technology: Materials, Design, Manufacturing, Applications and Testing, 1st ed.; Chapman and Hall: Glasgow, UK, 1997. [Google Scholar]
- Evans, A.G.; Hutchinson, J.W.; Ashby, M.F. Multifunctionality of cellular metal systems. Prog. Mater. Sci. 1998, 43, 171–221. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalazano, G.; Nguyen, K.T.Q.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Chiras, S.; Mumm, D.; Evans, A.; Wicks, N.; Hutchinson, J.W.; Dharmasena, K.; Wadley, H.N.G.; Fitcher, S. The structural performance of near-optimized truss core panels. Int. J. Solids Struct. 2002, 39, 4093–4115. [Google Scholar] [CrossRef] [Green Version]
- Rossiter, J.D.; Johnson, A.A.; Bingham, G.A. Assessing the Design and Compressive Performance of Material Extruded Lattice Structures. 3D Print. Addit. Manuf. 2020, 7, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, Y.; Li, Z.; Davies, C.M.; Maharaj, C.; Dear, J.P.; Hooper, P.A. Acoustic resonance testing of additive manufactured lattice structures. Addit. Manuf. 2018, 24, 566–576. [Google Scholar] [CrossRef]
- Park, K.; Min, K.; Roh, Y. Design Optimization of Lattice Structures under Compression: Study of Unit Cell Types and Cell Arrangements. Materials 2022, 15, 97. [Google Scholar] [CrossRef]
- Kantaros, A.; Laskaris, N.; Piromalis, D.; Ganetsos, T. Manufacturing Zero-Waste COVID-19 Personal Protection Equipment: A Case Study of Utilizing 3D Printing While Employing Waste Material Recycling. Circ. Econ. Sustain. 2021, 1, 851–869. [Google Scholar] [CrossRef]
- Kantaros, A.; Chatzidai, N.; Karalekas, D. 3D printing-assisted design of scaffold structures. Int. J. Adv. Manuf. Technol. 2016, 82, 559–571. [Google Scholar] [CrossRef]
- Eshraghi, S.; Das, S. Mechanical and microstructural properties of polycaprolactone scaffolds with one-dimensional, two-dimensional, and three-dimensional orthogonally oriented porous architectures produced by selective laser sintering. Acta Biomater. 2010, 6, 2467–2476. [Google Scholar] [CrossRef]
- Kantaros, A.; Piromalis, D. Fabricating Lattice Structures via 3D Printing: The Case of Porous Bio-Engineered Scaffolds. Appl. Mech. 2021, 2, 289–302. [Google Scholar] [CrossRef]
- Snelling, D.; Li, Q.; Meisel, N.; Williams, C.B.; Batra, R.C.; Druschitz, A.P. Lightweight Metal Cellular Structures Fabricated via 3D Printing of Sand Cast Molds. Adv. Eng. Mater. 2015, 17, 923–932. [Google Scholar] [CrossRef]
- Al-Saedi, D.S.J.; Masood, S.H.; Faizan-Ur-Rab, M.; Alomarah, A.; Ponnusamy, P. Mechanical properties and energy absorption capability of functionally graded F2BCC lattice fabricated by SLM. Mater. Des. 2018, 144, 32–44. [Google Scholar] [CrossRef]
- Santorinaios, M.; Brooks, W.; Sutcliffe, C.J.; Mines, R.A.W. Crush behaviour of open cellular lattice structures manufactured using selective laser melting, WIT Trans. Built Environ. 2006, 85, 481–490. [Google Scholar] [CrossRef] [Green Version]
- Gümrük, R.; Mines, R.A.W. Compressive behaviour of stainless steel micro-lattice structures. Int. J. Mech. Sci. 2013, 68, 125–139. [Google Scholar] [CrossRef]
- Brennan-Craddock, J.; Brackett, D.; Wildman, R.; Hague, R. The design of impact absorbing structures for additive manufacture. J. Phys. Conf. Ser. 2012, 382, 012042. [Google Scholar] [CrossRef]
- Silva, R.G.; Torres, M.J.; Vinuela, J.Z.; Zamora, A.G. Manufacturing and Characterization of 3D Miniature Polymer Lattice Structures Using Fused Filament Fabrication. Polymers 2021, 13, 635. [Google Scholar] [CrossRef]
- Silva, R.G.; Estay, C.S.; Pavez, G.M.; Vinuela, J.Z.; Torres, M.J. Influence of Geometric and Manufacturing Parameters on the Compressive Behavior of 3D Printed Polymer Lattice Structures. Materials 2021, 14, 1462. [Google Scholar] [CrossRef]
- Mohsenizadeh, M.; Gasbarri, F.; Munther, M.; Beheshti, A.; Davami, K. Additively-manufactured lightweight metamaterials for energy absorption, Mater. Des. 2018, 139, 521–530. [Google Scholar] [CrossRef]
- Muflikhun, M.A.; Sentanu, D.A. Characteristics of carabiner remodeling using 3D printing with graded filler and different orientation methods. Eng. Fail. Anal. 2021, 130, 105795. [Google Scholar] [CrossRef]
- Alfarisi, N.A.; Santos, G.N.C.; Norcahyo, R.; Sentanuhady, J.; Azizah, N.; Muflikhun, M.A. Model optimization and performance evaluation of hand cranked music box base structure manufactured via 3D printing. Heliyon 2021, 7, e08432. [Google Scholar] [CrossRef]
- Shin, C.S.; Chang, Y.C. Fabrication and Compressive Behavior of a Micro-Lattice Composite by High Resolution DLP Stereolithography. Polymers 2021, 13, 785. [Google Scholar] [CrossRef]
- Validating Isotropy in SLA 3D Printing. Available online: https://formlabs.com/blog/isotropy-in-SLA-3D-printing/ (accessed on 30 November 2022).
- Caserta, G.D.; Iannucci, L.; Galvanetto, U. Shock absorption performance of a motorbike helmet with honeycomb reinforced liner. Compos. Struct. 2011, 93, 2748–2759. [Google Scholar] [CrossRef]
- Schaedler, T.A.; Ro, C.J.; Sorensen, A.E.; Eckel, Z.; Yang, S.S.; Carter, W.B.; Jacobsen, A.J. Designing Metallic Microlattices for Energy Absorber Applications. Adv. Eng. Mater. 2014, 16, 276–283. [Google Scholar] [CrossRef]
- Ling, C.; Ivens, J.; Cardiff, P.; Gilchrist, M.D. Deformation response of EPS foam under combined compression-shear loading. Part I: Experimental design and quasi-static tests. Int. J. Mech. Sci. 2018, 144, 480–489. [Google Scholar] [CrossRef]
- Ling, C.; Cernicchi, A.; Gilchrist, M.D.; Cardiff, P. Mechanical behaviour of additively-manufactured polymeric octet-truss lattice structures under quasi-static and dynamic compressive loading. Mater. Des. 2019, 162, 106–118. [Google Scholar] [CrossRef]
- Di Landro, L.; Sala, G.; Olivieri, D. Deformation mechanisms and energy absorption of polystyrene foams for protective helmets. Polym. Test. 2002, 21, 217–228. [Google Scholar] [CrossRef]
- Rueda, M.A.F.; Cui, L.; Gilchrist, M.D. Optimisation of energy absorbing liner for equestrian helmets. Part I: Layered foam liner. Mater. Des. 2009, 30, 3405–3413. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Wang, J.; Xu, Y.; Zhang, W.; Zhu, J. Compressive behavior and energy absorption of polymeric lattice structures made by additive manufacturing. Front. Mech. Eng. 2020, 15, 319–327. [Google Scholar] [CrossRef]
- Mueller, J.; Matlock, K.H.; Shea, K.; Daraio, C. Energy Absorption Properties of Periodic and Stochastic 3D Lattice Materials. Adv. Theory Simul. 2019, 2, 1900081. [Google Scholar] [CrossRef]
- Fuller, R.B. Octet Truss. U.S. Patent 2,986,241,1961, 7 February 1956. [Google Scholar]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 2000, 49, 1747–1769. [Google Scholar] [CrossRef] [Green Version]
- Tancogne-Dejean, T.; Spierings, A.B.; Mohr, D. Additively-manufactured metallic micro-lattice materials for high specific energy absorption under static and dynamic loading. Acta Mater. 2016, 116, 14–28. [Google Scholar] [CrossRef]
- Bardelcik, A.; Yang, S.; Alderson, F.; Gadsden, A. The effect of wash treatment on the mechanical properties and energy absorption potential of a 3D printed polymethyl methacrylate (PMMA). Mater. Today Commun. 2021, 26, 101728. [Google Scholar] [CrossRef]
- BS ISO 13314:2011; Mechanical Testing of Metals-Ductility Testing-Compression Test for Porous and Cellular Materials. British Standards Institution: London, UK, 2011; Volume 2011. Available online: https://www.iso.org/standard/53669.html (accessed on 30 November 2022).
- Bolan, M.; Bardelcik, A. Specific Energy Absorption of 3D Printed Octet-Truss Lattice Structures with Hollow Struts. In Proceedings of the Materials Science and Technology Conference, Pittsburgh, PA, USA, 9–12 October 2022. [Google Scholar]
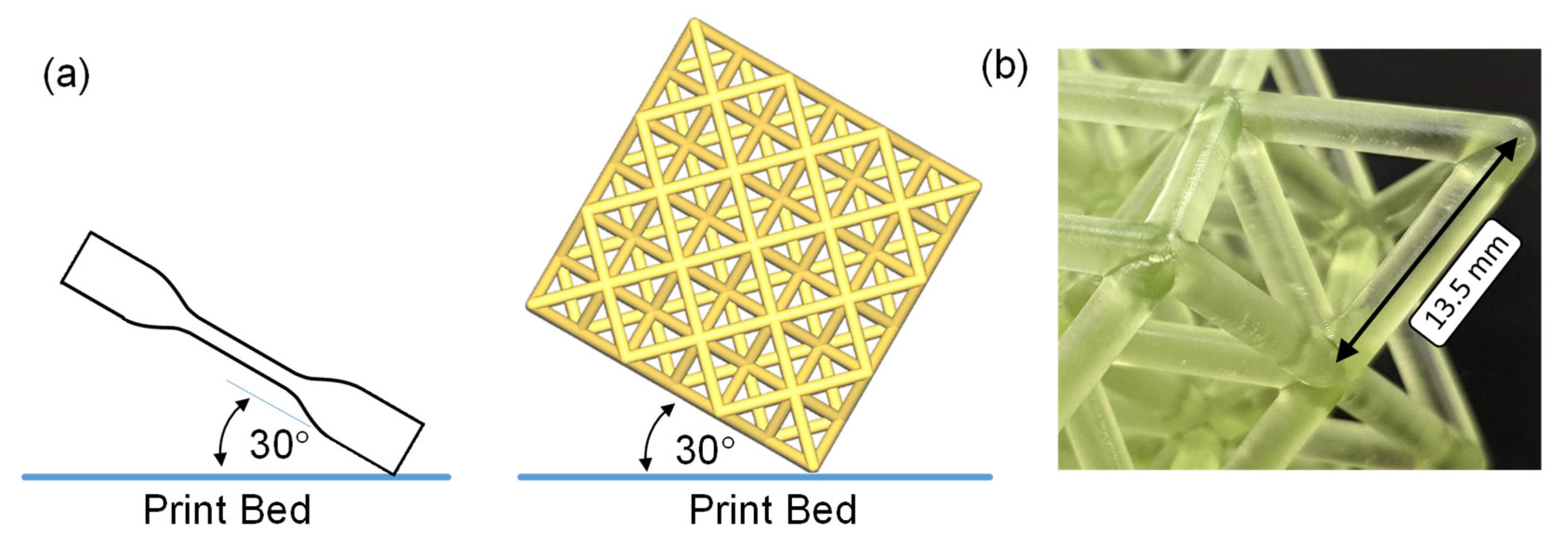

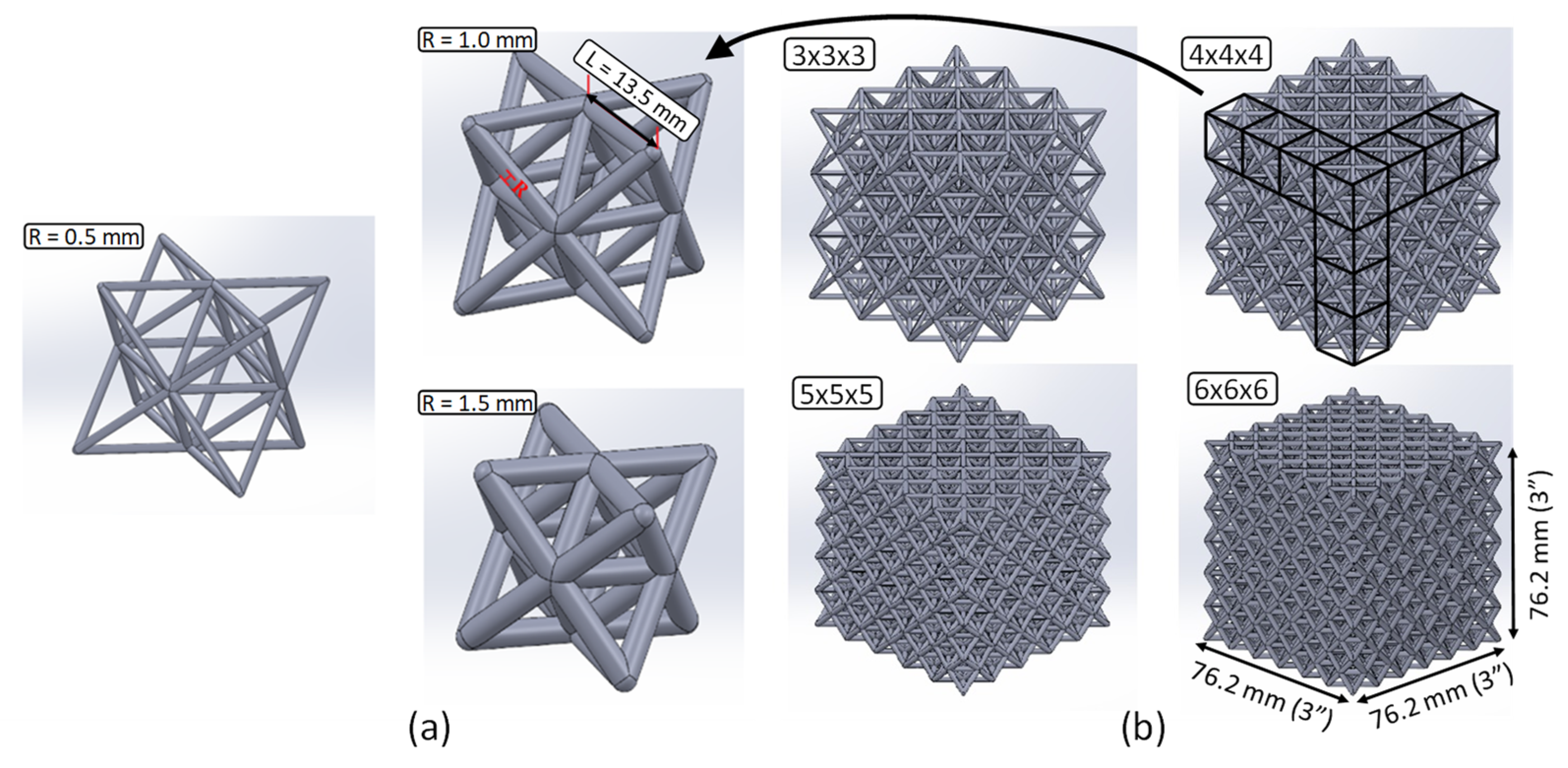



| Lattice Structure Density | Strut Length, L [mm] | Strut Radius, R [mm] | Number of Specimens, Resin 1, Resin 2 | Theoretical Relative Density, | Resin 1 (Blue), Avg. Meas. Rel. Density, | Resin 2 (Green), Avg. Meas. Rel. Density, |
|---|---|---|---|---|---|---|
| 3 × 3 × 3 | 18.0 | 0.5 | 3, 2 | 0.02 | 0.03 | 0.03 |
| 18.0 | 1.0 | 2, 2 | 0.08 | 0.10 | 0.11 | |
| 18.0 | 1.5 | 1, 2 | 0.19 | 0.19 | 0.20 | |
| 4 × 4 × 4 | 13.5 | 1.0 | 3, 2 | 0.15 | 0.16 | 0.17 |
| 5 × 5 × 5 | 10.8 | 1.0 | 3, 2 | 0.23 | 0.22 | 0.23 |
| 6 × 6 × 6 | 9.0 | 0.5 | 1, 2 | 0.08 | 0.09 | 0.11 |
| 9.0 | 1.0 | 2, 1 | 0.33 | 0.29 | 0.31 | |
| 9.0 | 1.5 | 2, 2 | 0.74 | 0.54 | 0.55 |
| R-Squared Value | ||||||||
|---|---|---|---|---|---|---|---|---|
| −412.5 | 18,739.2 | 327,039.6 | 2,569,483.8 | −10,103,339.0 | 19,292,288.6 | −14,228,271.0 | 0.99 | |
| −38.4 | 1121.7 | − | − | − | − | − | 0.99 | |
| 73.5 | −3274.8 | 55,856.4 | −430,961.3 | 1,664,155.3 | −3,124,910.8 | 2,269,996.2 | 1 | |
| 44. 7 | −1760.4 | 40,872.2 | −209,484.0 | 489,014.6 | −414,169.6 | − | 1 | |
| 4.7 | −150.8 | −178.3 | − | − | − | − | 1 | |
| 0.3 | −8.3 | −4.1 | 557.7 | −2409.5 | 2970.7 | − | 0.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bolan, M.; Dean, M.; Bardelcik, A. The Energy Absorption Behavior of 3D-Printed Polymeric Octet-Truss Lattice Structures of Varying Strut Length and Radius. Polymers 2023, 15, 713. https://doi.org/10.3390/polym15030713
Bolan M, Dean M, Bardelcik A. The Energy Absorption Behavior of 3D-Printed Polymeric Octet-Truss Lattice Structures of Varying Strut Length and Radius. Polymers. 2023; 15(3):713. https://doi.org/10.3390/polym15030713
Chicago/Turabian StyleBolan, Matthew, Mackenzie Dean, and Alexander Bardelcik. 2023. "The Energy Absorption Behavior of 3D-Printed Polymeric Octet-Truss Lattice Structures of Varying Strut Length and Radius" Polymers 15, no. 3: 713. https://doi.org/10.3390/polym15030713
APA StyleBolan, M., Dean, M., & Bardelcik, A. (2023). The Energy Absorption Behavior of 3D-Printed Polymeric Octet-Truss Lattice Structures of Varying Strut Length and Radius. Polymers, 15(3), 713. https://doi.org/10.3390/polym15030713







