Numerical Analysis of Curing Residual Stress and Strain in NEPE Propellant Grain
Abstract
:1. Introduction
- Thermal expansion and contraction during the curing process;
- Different thermal expansion coefficients between propellant and case;
- Difference between curing temperature and operating temperature of SRMs;
- Chemical shrinkage of the propellant during the curing process.
2. Theoretical Models
2.1. Thermo-Chemical Model
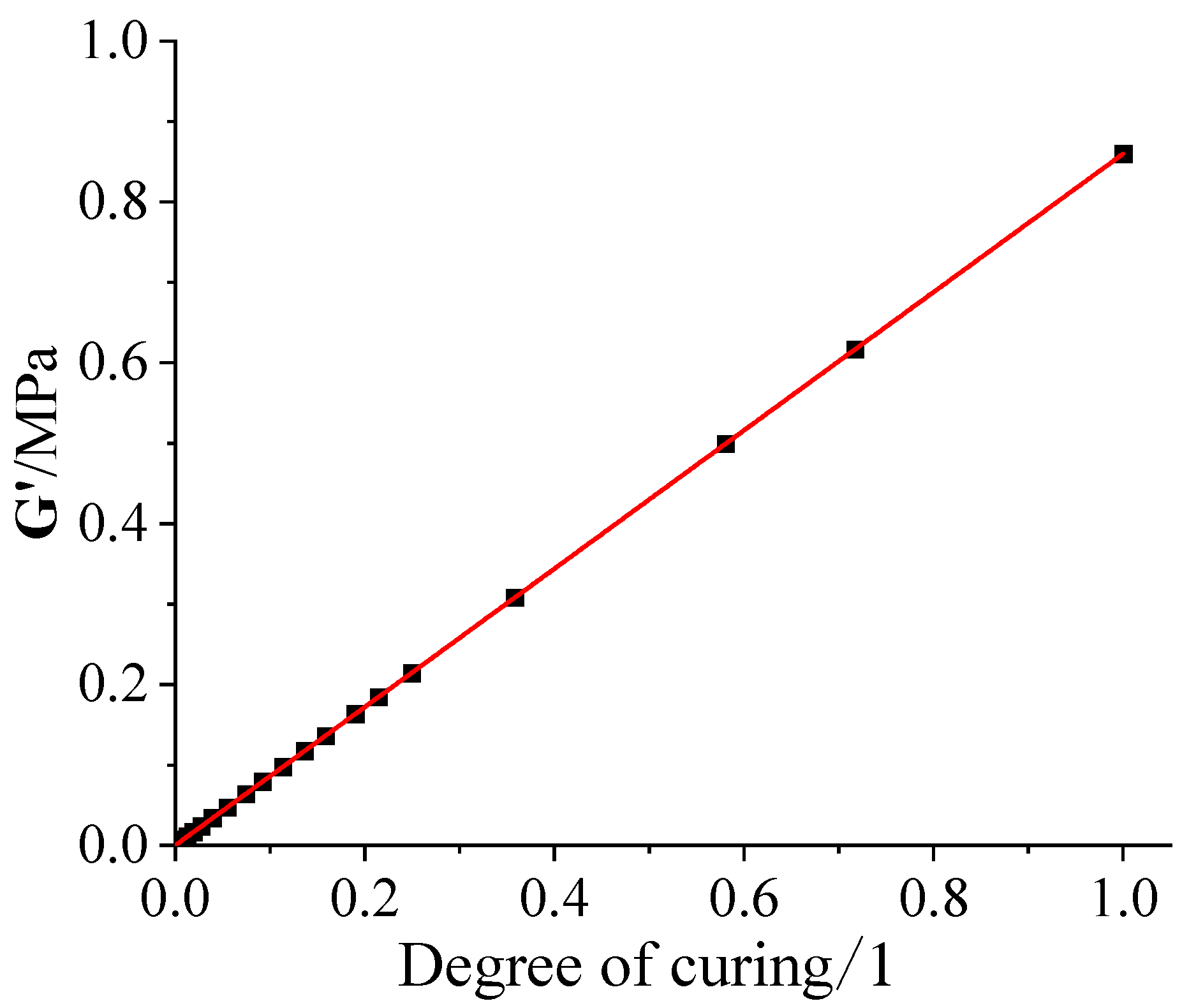
2.2. The Macro Residual Stresses and Strains Model
3. Finite Element Modeling
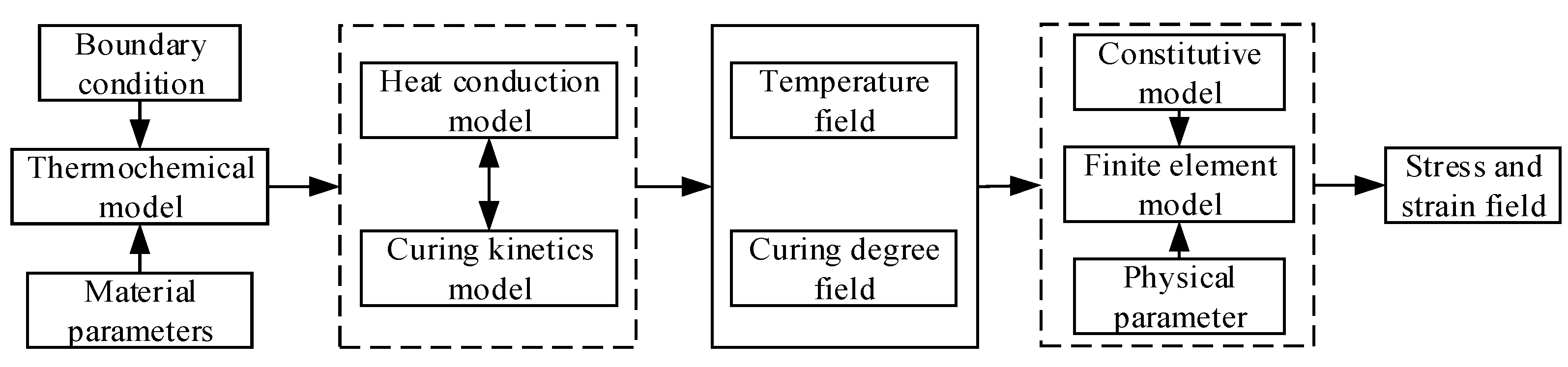
3.1. Simulation Flow
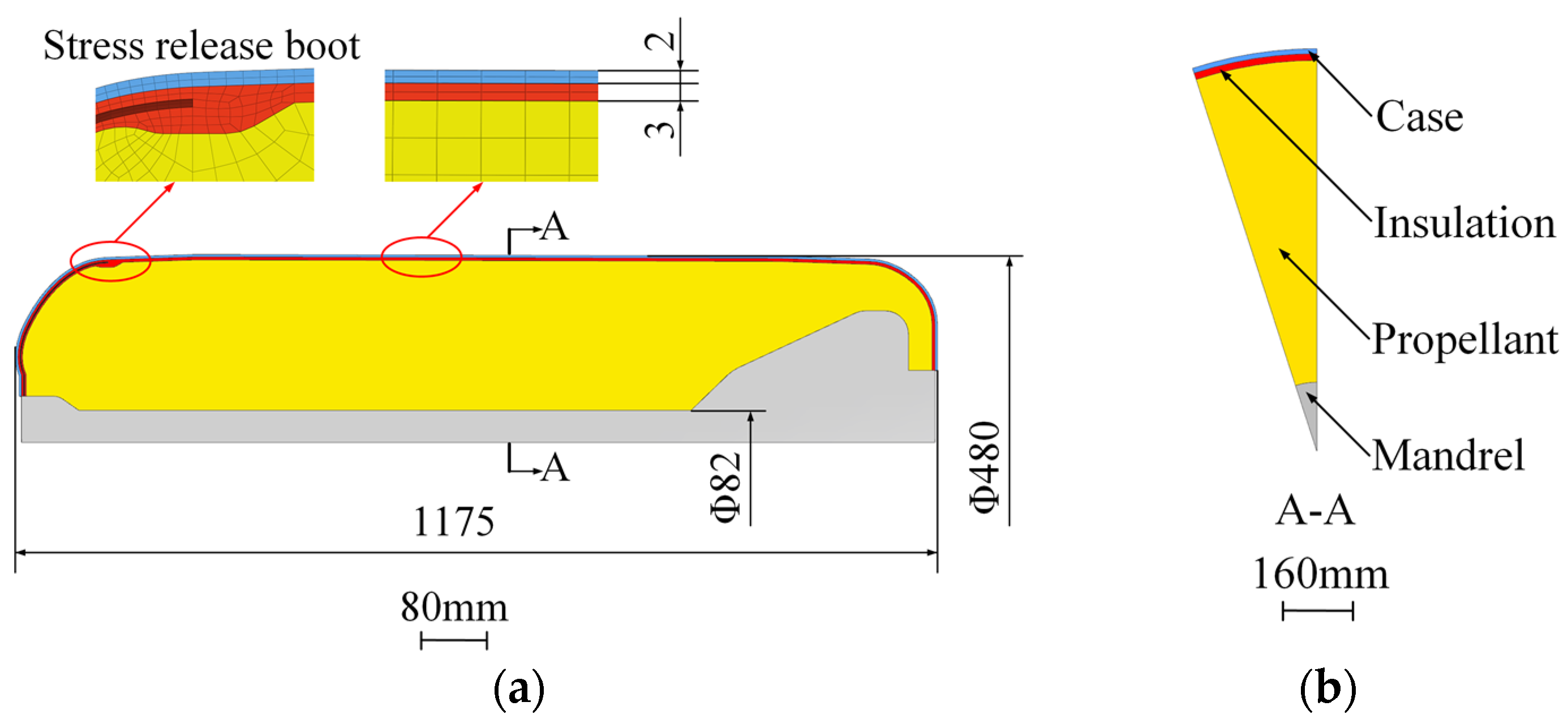
3.2. Finite Element Modeling
3.3. Model Parameters
- (i)
- Cooling down process
- (ii)
- Curing process
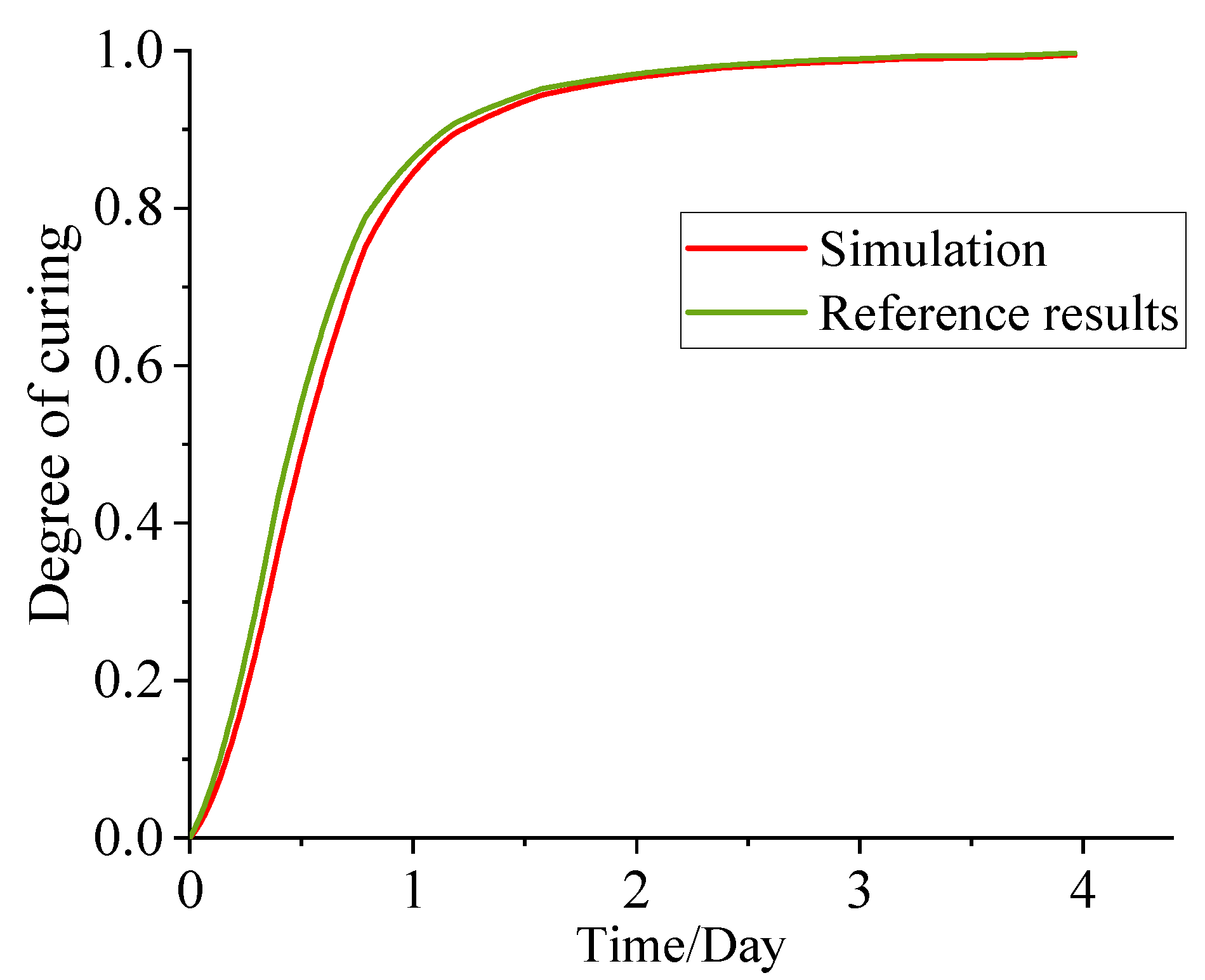
3.4. Modal Verification
4. Results and Discussion
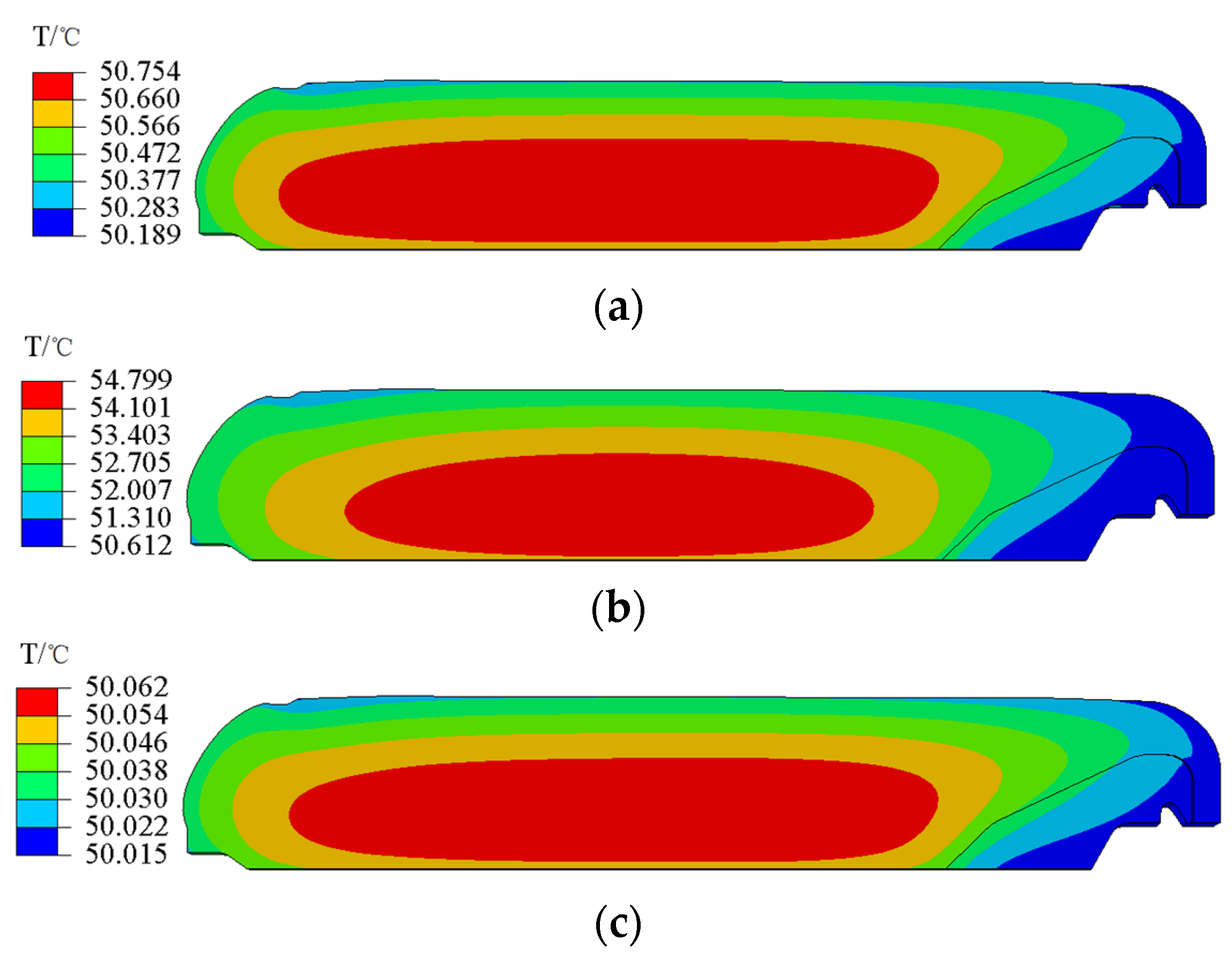
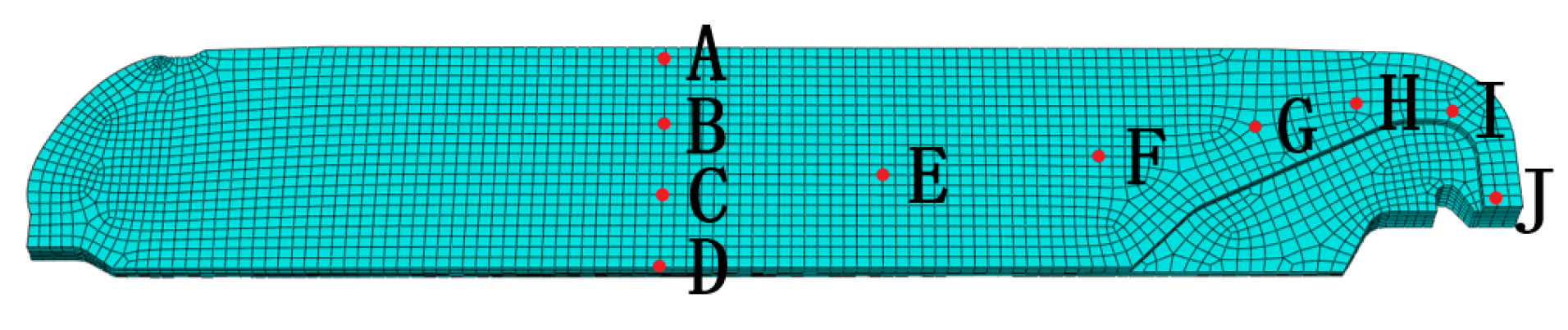
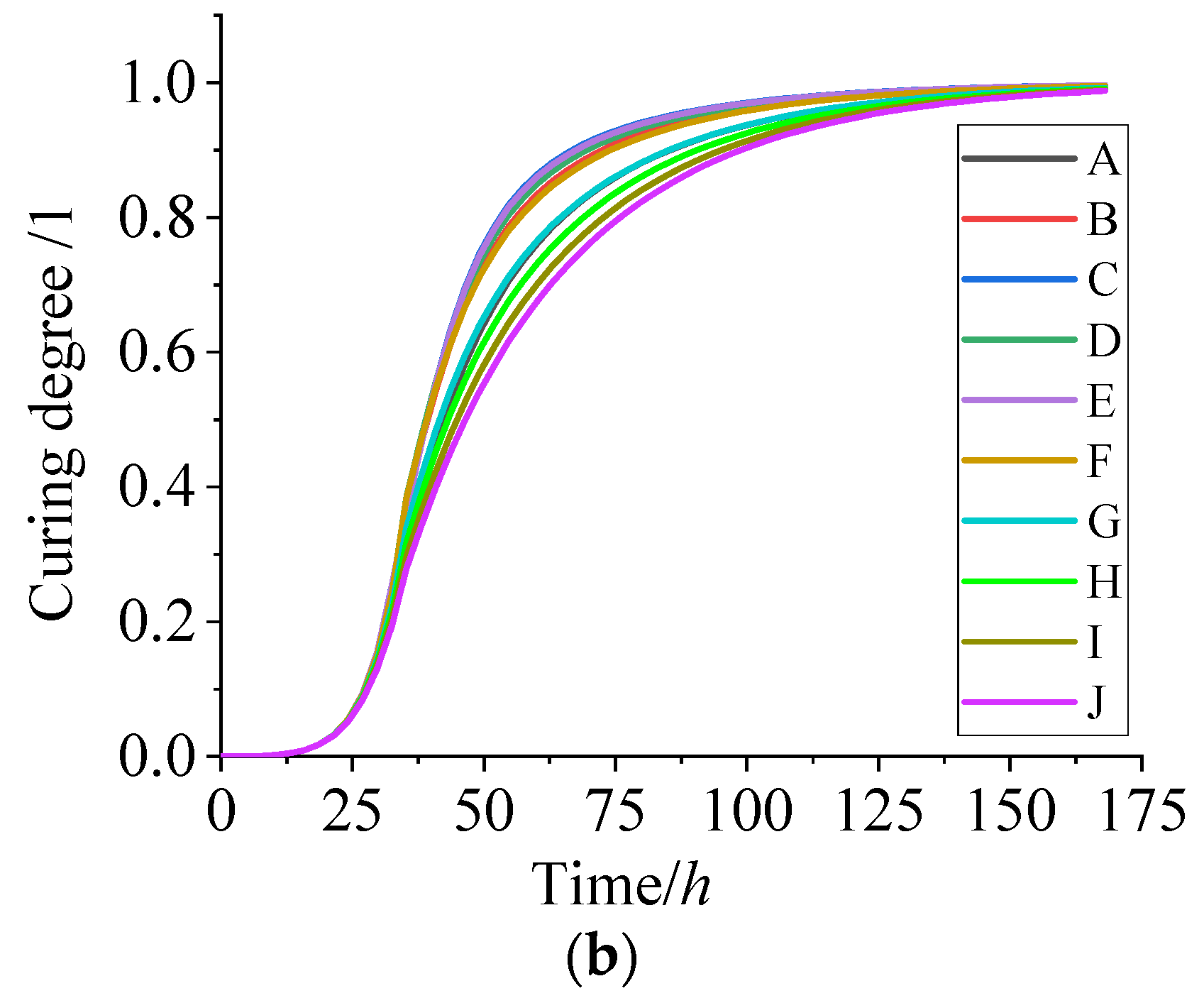
4.1. Temperature and Curing Degree during Curing Process
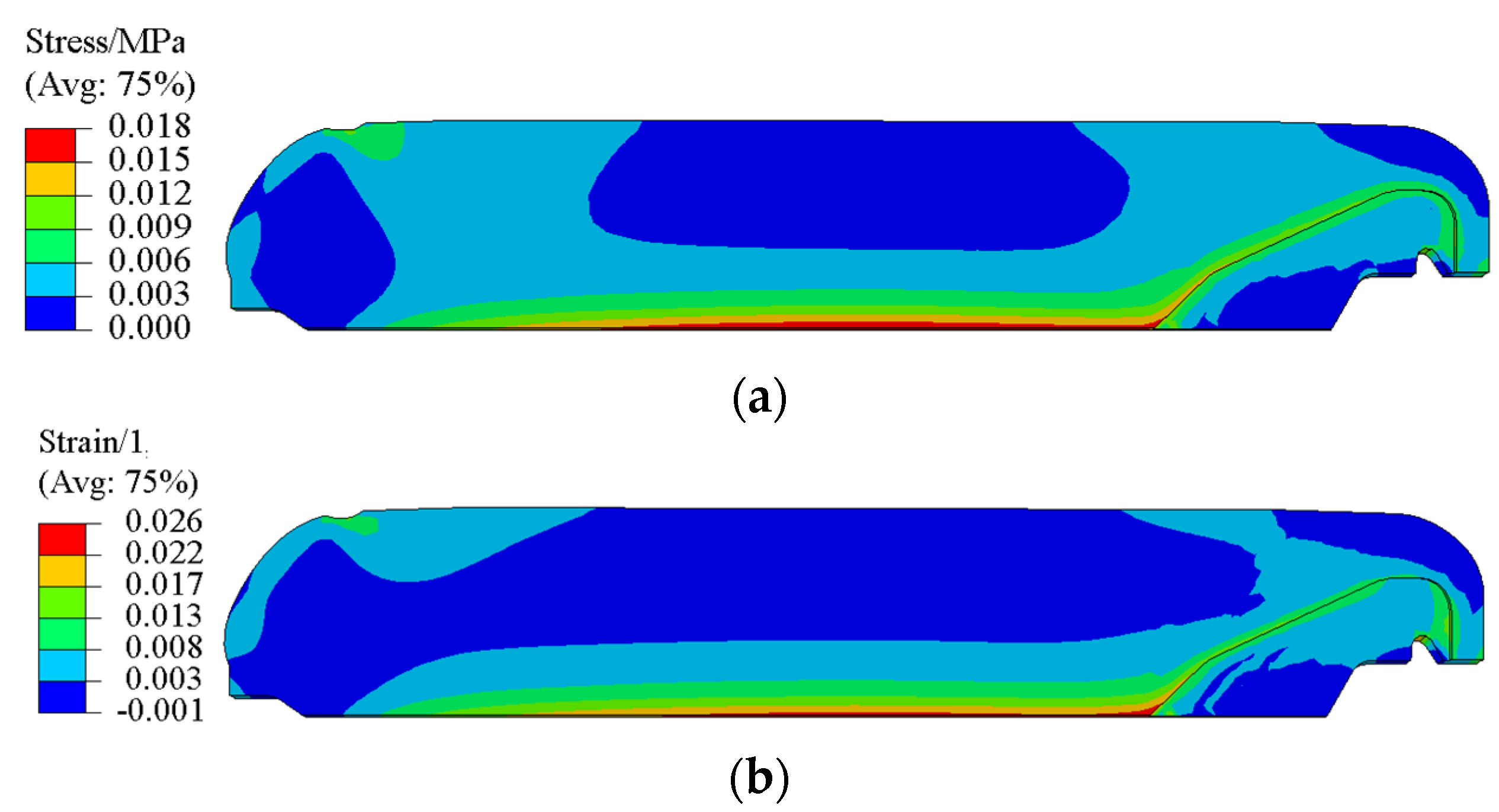
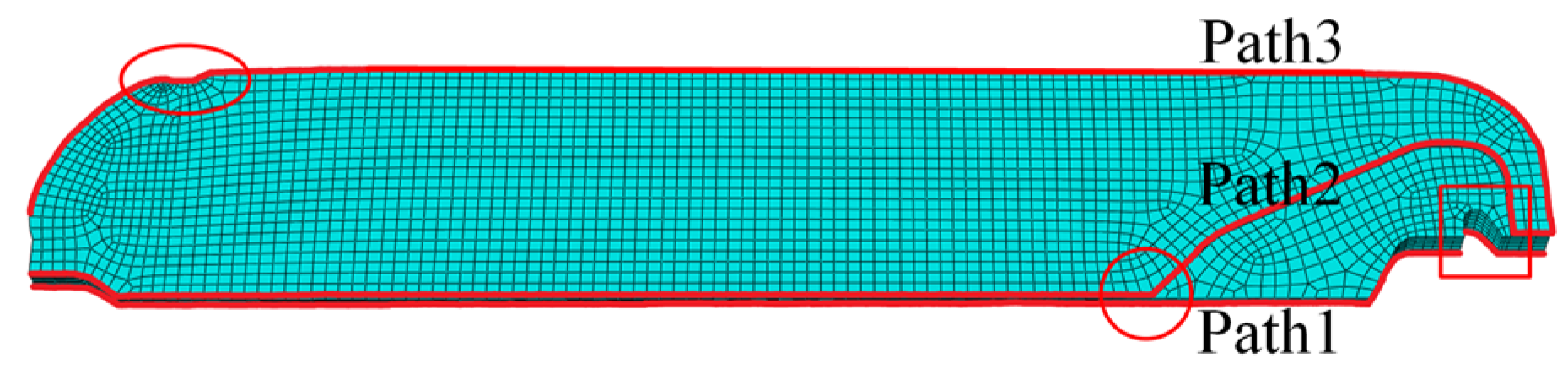
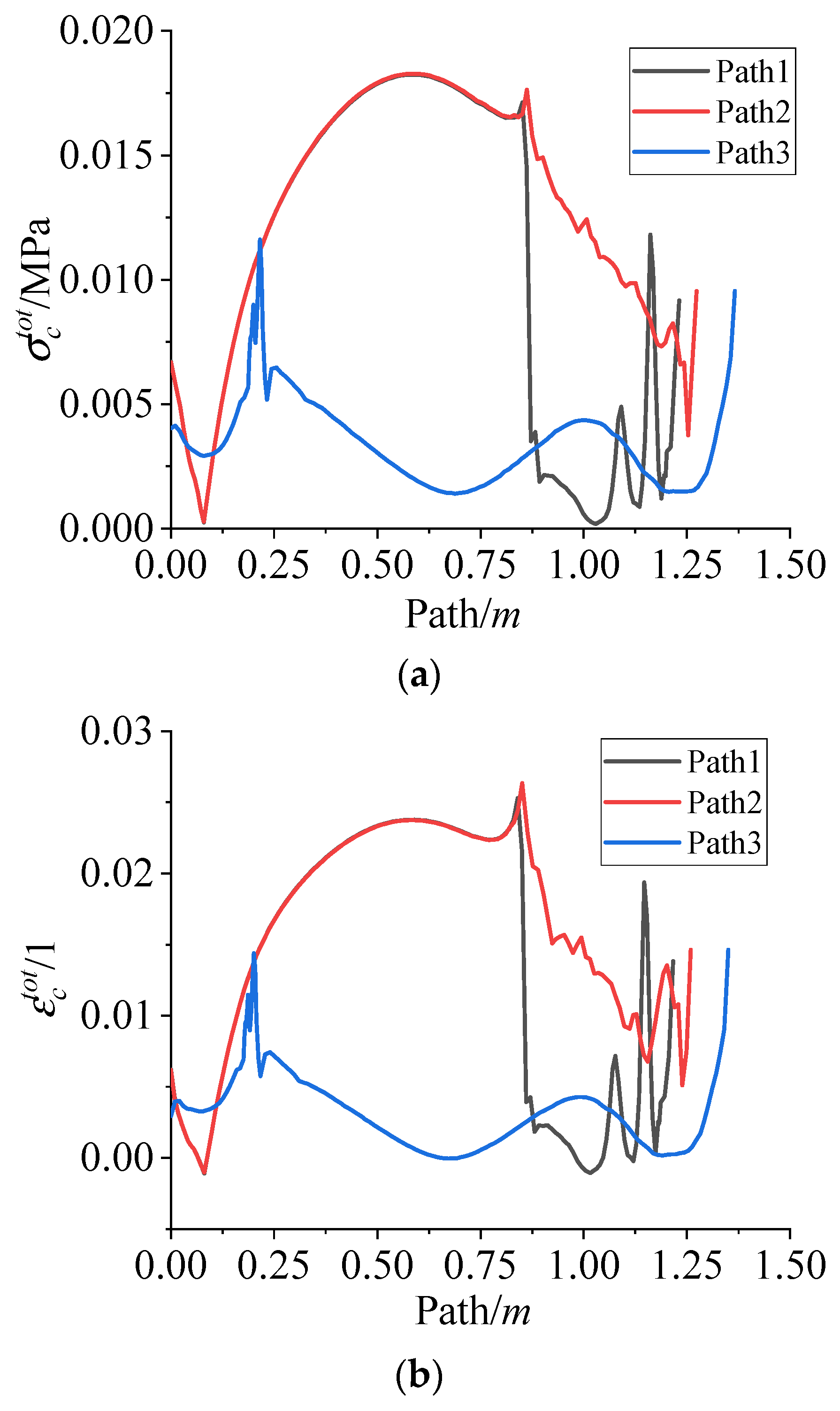
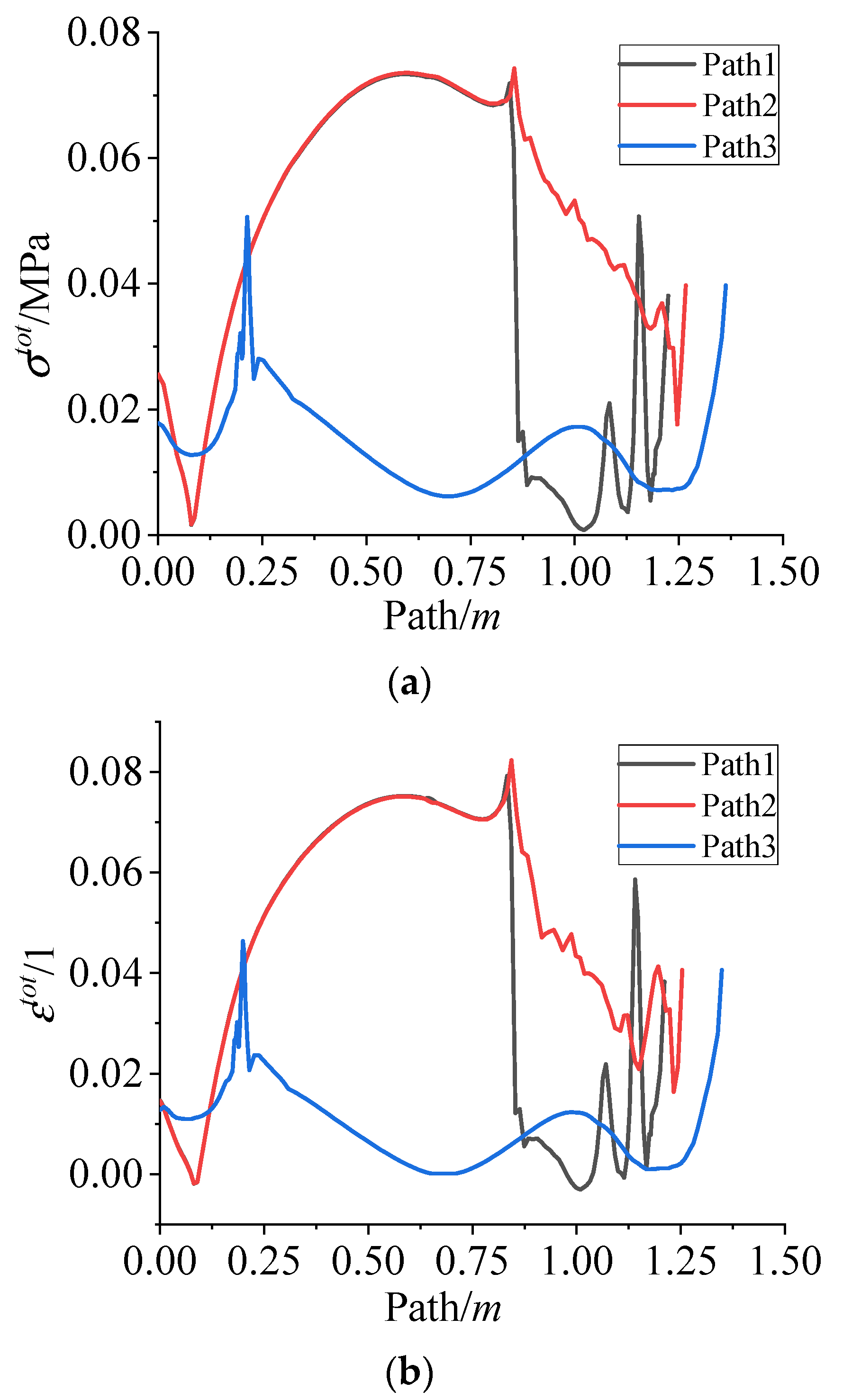
4.2. Residual Stress and Strain of Grain during Curing Process
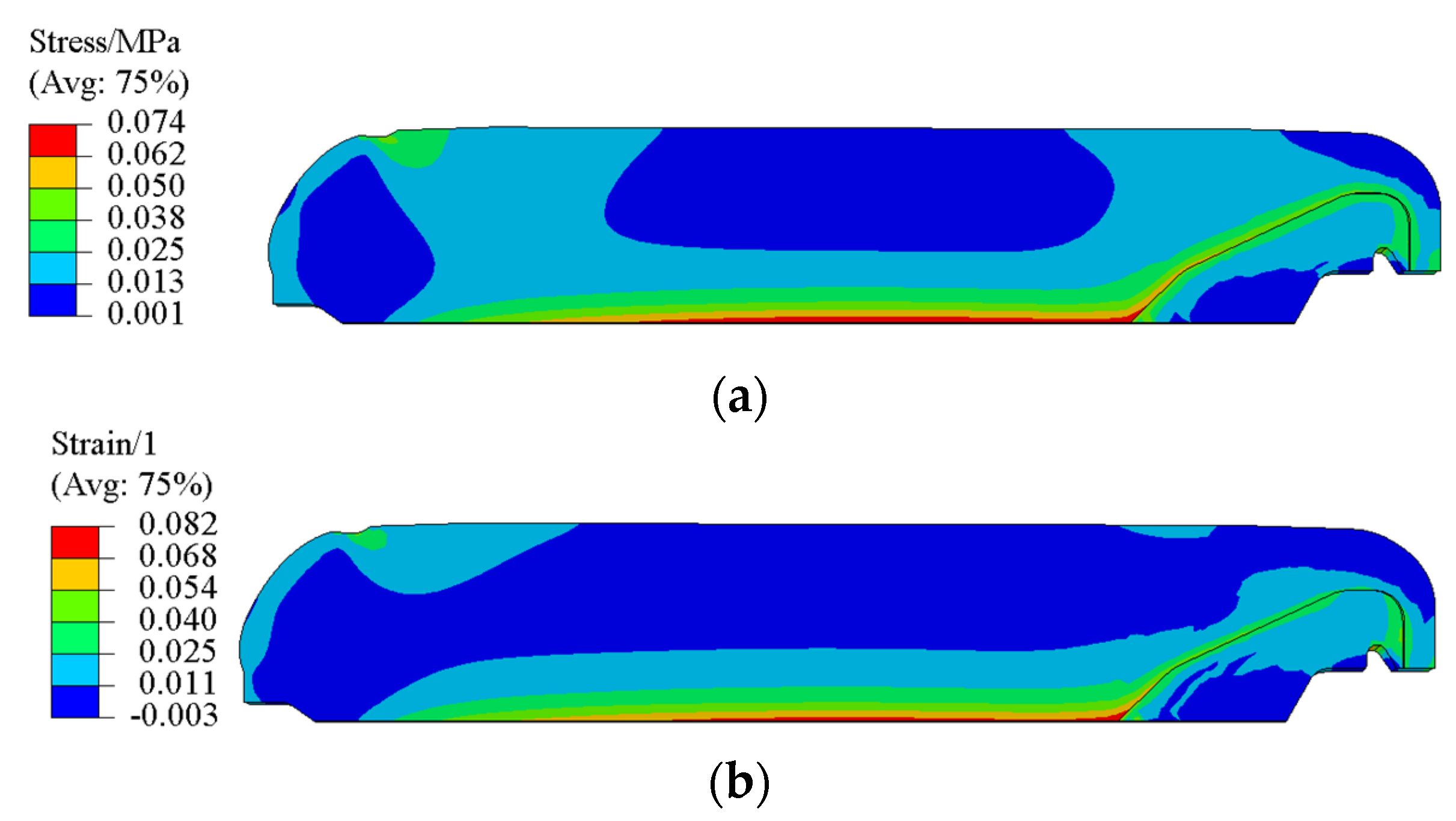
4.3. Residual Stress and Strain of Grain during Cooling down Process
5. Conclusions
- (1)
- There is a temperature gradient in the NEPE propellant grain during the curing at 50 °C. The maximum temperature difference is about 5 °C and the maximum temperature is located on the center of propellant grain. At the end of curing, the temperature in the interior of the grain tends to be uniform. The curing degree in the NEPE propellant grain during the curing process has the same trend as temperature.
- (2)
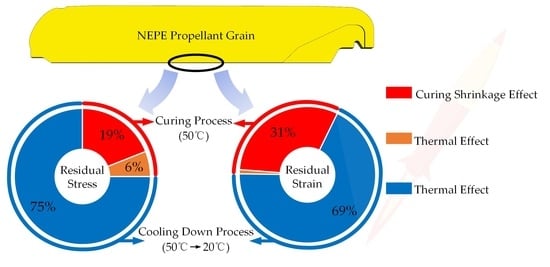
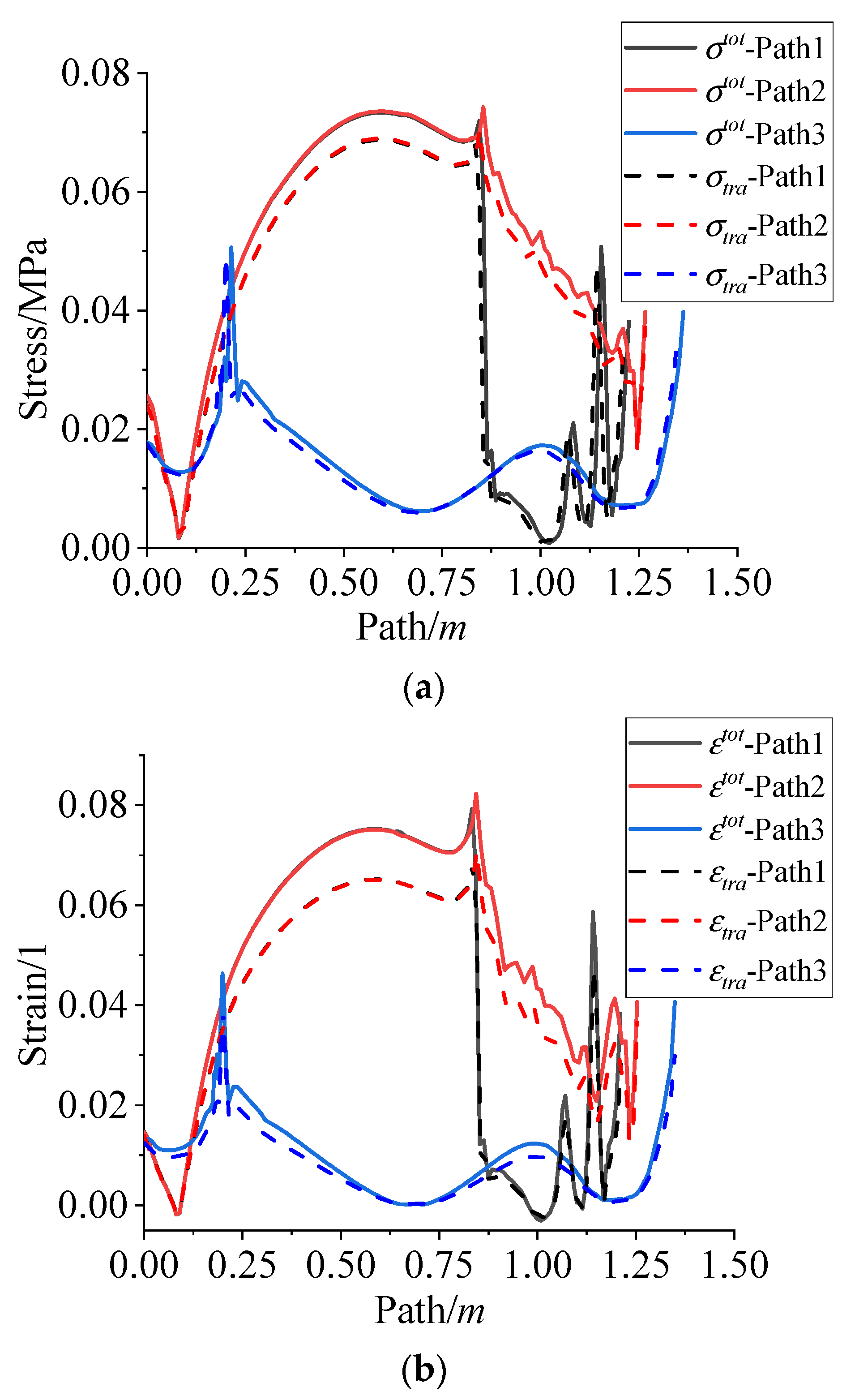
- The residual stress/strain of the NEPE propellant grain during the curing and cooling down process are mainly composed of curing shrinkage stress/strain in the curing process and thermal stress/strain in the cooling process. The curing shrinkage stress and strain in the curing process account for 19% and 31% of the whole process, respectively. The thermal stress and thermal strain in the cooling down process account for 75% and 69% of the whole process, respectively. The thermal stress and thermal strain in the curing process can nearly be ignored.
- (3)
- The residual stress and residual strain calculated by the traditional method are smaller than those obtained in this paper. The maximum deviation of the residual stress and residual strain are about 8% and 17%, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, X.T.; Xia, Z.X.; Huang, L.Y.; Na, X.D. Combustion of nitrate ester plasticized polyether propellants. J. Zhejiang Univ.-SC A 2020, 21, 834–847. [Google Scholar] [CrossRef]
- Marimuthu, R.; Nageswara Rao, B. Development of efficient finite elements for structural integrity analysis of solid rocket motor propellant grains. Int. J. Press. Vessel. Pip. 2013, 111–112, 131–145. [Google Scholar] [CrossRef]
- Li, D.; Li, X.; Dai, J.; Xi, S. A Comparison of Curing Process-Induced Residual Stresses and Cure Shrinkage in Micro-Scale Composite Structures with Different Constitutive Laws. Appl. Compos. Mater. 2017, 25, 67–84. [Google Scholar] [CrossRef]
- Arai, K.; Shi, X.F. Study on pressure solidification of solid rocket motor. Foreign Solid Rocket. Technol. 1984, 4, 54–62. (In Chinese) [Google Scholar]
- Zhao, L.G.; Warrior, N.A.; Long, A.C. A micromechanical study of residual stress and its effect on transverse failure in polymer–matrix composites. Int. J. Solids Struct. 2005, 43, 5449–5467. [Google Scholar] [CrossRef] [Green Version]
- Parlevliet, P.P.; Bersee, H.E.N.; Beukers, A. Residual stresses in thermoplastic composites—A study of the literature—Part I: Formation of residual stresses. Compos. Part. A Appl. Sci. Manuf. 2006, 37, 1847–1857. [Google Scholar] [CrossRef]
- Chu, H.T.; Chou, J.H. Effect of Cooling Load on the Safety Factor of Propellant Grains. J. Propuls. Power 2013, 29, 27–33. [Google Scholar] [CrossRef]
- Cui, H.; Tang, G.; Shen, Z. A three-dimensional viscoelastic constitutive model of solid propellant considering viscoelastic Poisson’s ratio and its implementation. Eur. J. Mech. A Solids 2017, 61, 235–244. [Google Scholar]
- Guo, X.; Zhang, J.T.; Zhang, M.; Liu, L.S.; Zhai, P.C.; Zhang, Q.J. Effects of liner properties on the stress and strain along liner/propellant interface in solid rocket motor. Aerosp. Sci. Technol. 2016, 58, 594–600. [Google Scholar] [CrossRef]
- Prasatya, P.; Mckenna, G.B.; Simon, S.L. A Viscoelastic Model for Predicting Isotropic Residual Stresses in Thermosetting Material: Effects of Processing Parameters. J. Compos. Mater. 2001, 35, 826–849. [Google Scholar] [CrossRef]
- Renganathan, K.; Nageswara Rao, B.; Jana, B.K. A multilayered thick cylindrical shell under internal pressure and thermal loads applicable to solid propellant rocket motors. Forsch. Im Ing. 2000, 66, 57–66. [Google Scholar] [CrossRef]
- Deng, B.; Tang, G.; Shen, Z. Structural Analysis of Solid Rocket Motor Grain with Aging and Damage Effects. J. Spacecr. Rockets 2015, 52, 331–339. [Google Scholar] [CrossRef]
- Le, A.Q.; Sun, L.Z.; Miller, T.C. Health Monitoring and Diagnosis of Solid Rocket Motors with Bore Cracks. J. Aerosp. Eng. 2016, 29, 04015058. [Google Scholar] [CrossRef]
- Hossain, M.; Possart, G.; Steinmann, P. A small-strain model to simulate the curing of thermosets. Comput. Mech. 2009, 43, 769–779. [Google Scholar] [CrossRef]
- Ji, Y.; Cao, L.; Li, Z.; Chen, G.; Cao, P.; Liu, T. Numerical Conversion Method for the Dynamic Storage Modulus and Relaxation Modulus of Hydroxy-Terminated Polybutadiene (HTPB) Propellants. Polymers 2022, 15, 3. [Google Scholar] [CrossRef]
- Babayevsky, P.G.; Gillham, J.K. Epoxy thermosetting systems: Dynamic mechanical analysis of the reactions of aromatic diamines with the diglycidyl ether of bisphenol A. J. Appl. Polym. Sci. 1973, 17, 2067–2088. [Google Scholar] [CrossRef]
- Kravchenko, O.G.; Kravchenko, S.G.; Casares, A.; Pipes, R.B. Digital image correlation measurement of resin chemical and thermal shrinkage after gelation. J. Mater. Sci. 2015, 50, 5244–5252. [Google Scholar] [CrossRef]
- Grassia, L.; D’Amore, A. Modeling the Residual Stresses in Reactive Resins-Based Materials: A Case Study of Photo-Sensitive Composites for Dental Applications. AIP Conf. Proc. 2010, 1255, 408–410. [Google Scholar]
- Muliana, A.H. Spatial and temporal changes in physical properties of epoxy during curing and their effects on the residual stresses and properties of cured epoxy and composites. Appl. Eng. Sci. 2021, 7, 100061. [Google Scholar] [CrossRef]
- Kamal, M.R. Thermoset characterization for moldability analysis. Polym. Eng. Sci. 1974, 14, 231–239. [Google Scholar] [CrossRef]
- Rad, H.M.; Roosta, S.T.; Shariati, S.H.M.; Hosseini, S.G. Numerical Simulation of HTPB Resin Curing Process Using OpenFOAM and Study the Effect of Different Conditions on its Curing Time. Propellants Explos. Pyrotech. 2021, 46, 1447–1457. [Google Scholar]
- Ding, A.; Li, S.; Sun, J.; Wang, J.; Zu, L. A thermo-viscoelastic model of process-induced residual stresses in composite structures with considering thermal dependence. Compos. Struct. 2016, 136, 34–43. [Google Scholar] [CrossRef]
- Huang, X.; Gillespie, J.W.; Bogetti, T. Process induced stress for woven fabric thick section composite structures. Compos. Struct. 2000, 49, 303–312. [Google Scholar] [CrossRef]
- Tu, C.Y.; Chen, X.; Li, Y.K.; Zhang, B.C. Experimental study of Al agglomeration on solid propellant burning surface and condensed combustion products. Def. Technol. 2022. [Google Scholar] [CrossRef]
- Cui, Z.; Li, H.; Shen, Z.; Cui, H. A viscoelastic constitutive model of propellant with pressure cure. Propellants Explos. Pyrotech. 2021, 46, 1036–1048. [Google Scholar] [CrossRef]
- Fu, Y.; Gao, X.; Yao, X. Mesoscopic simulation on curing deformation and residual stresses of 3D braided composites. Compos. Struct. 2020, 246, 112387. [Google Scholar] [CrossRef]
- Zhang, W.; Fan, X.Z.; Chen, Y.D.; Xie, W.X.; Liu, Z.R.; Wei, H.J. Rheological study on curing crosslinking of NEPE propellant. Chem J. Chin. U 2009, 30, 1230–1234. (In Chinese) [Google Scholar]
- Ueberschlag, P. PVDF piezoelectric polymer. Sens. Rev. 2001, 21, 118–126. [Google Scholar] [CrossRef]





| A0/s−1 | E/(kJ∙mol−1) | m | n | ∆H* (kJ∙mol−1) |
|---|---|---|---|---|
| 1.241×1015 | 120.6 | 0.83 | 1.53 | 212.34 |
| Material Parameters | Grain | Insulation | Case |
|---|---|---|---|
| Density/(kg∙m−3) | 1803 | 1226 | 7800 |
| Poisson’s ratio | 0.496 | 0.496 | 0.3 |
| Expansion coefficient/K−1 | 0.86 × 10−4 | 1.78 × 10−4 | 1.1 × 10−5 |
| Heat conductivity/(W∙(m∙K)−1) | 0.55 | 0.274 | 38.95 |
| Specific heat/(J∙(kg∙K)−1) | 1180 | 2116 | 512.91 |
| Elasticity modulus/MPa | - | 6.973 | 210 × 103 |
| Value | Component | Value | Proportion | ||
|---|---|---|---|---|---|
| Residual stress | 0.074 MPa | Curing stage | 0.014 MPa | 19% | |
| 0.004 MPa | 6% | ||||
| Cooling stage | 0.054 MPa | 75% | |||
| Residual strain | 0.082 | Curing stage | 0.025 | 31% | |
| −0.00043 | 0 | ||||
| Cooling stage | 0.056 | 69% | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Xie, X.; Zhou, D.; Wang, R. Numerical Analysis of Curing Residual Stress and Strain in NEPE Propellant Grain. Polymers 2023, 15, 1019. https://doi.org/10.3390/polym15041019
Liu X, Xie X, Zhou D, Wang R. Numerical Analysis of Curing Residual Stress and Strain in NEPE Propellant Grain. Polymers. 2023; 15(4):1019. https://doi.org/10.3390/polym15041019
Chicago/Turabian StyleLiu, Xiangyang, Xuyuan Xie, Dongmo Zhou, and Ruimin Wang. 2023. "Numerical Analysis of Curing Residual Stress and Strain in NEPE Propellant Grain" Polymers 15, no. 4: 1019. https://doi.org/10.3390/polym15041019
APA StyleLiu, X., Xie, X., Zhou, D., & Wang, R. (2023). Numerical Analysis of Curing Residual Stress and Strain in NEPE Propellant Grain. Polymers, 15(4), 1019. https://doi.org/10.3390/polym15041019