The Elasticity of Polymer Melts and Solutions in Shear and Extension Flows
Abstract
:1. Introduction
- -
- -
- -
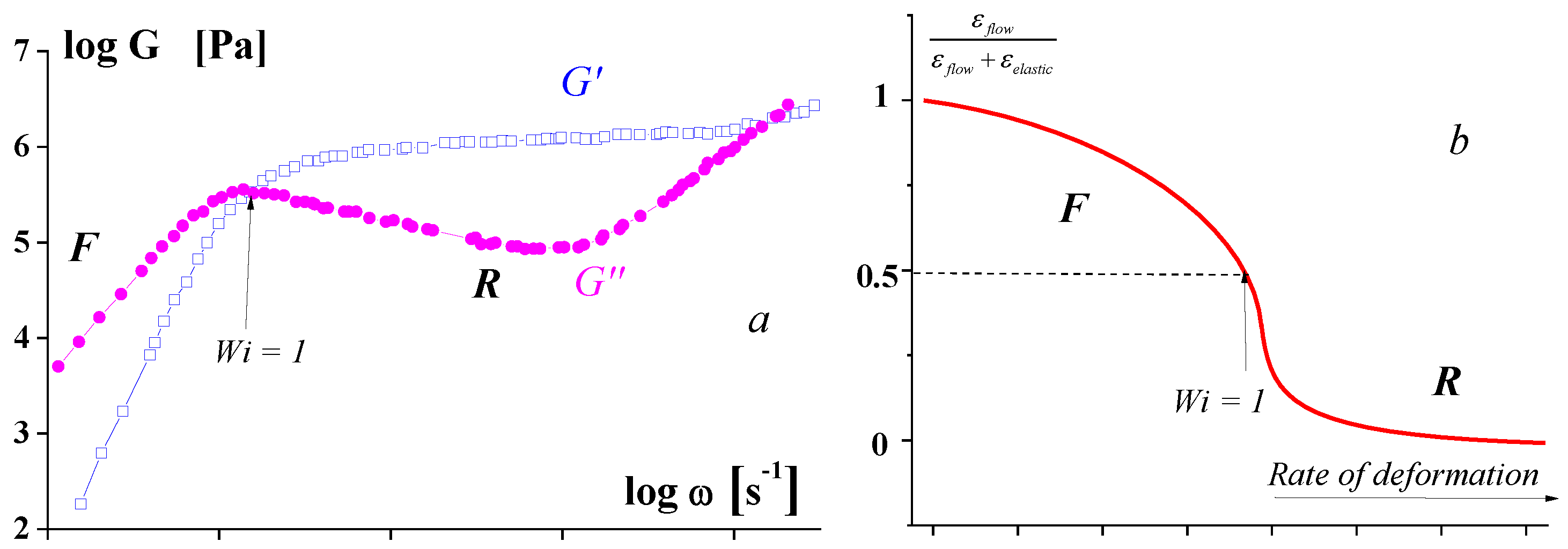
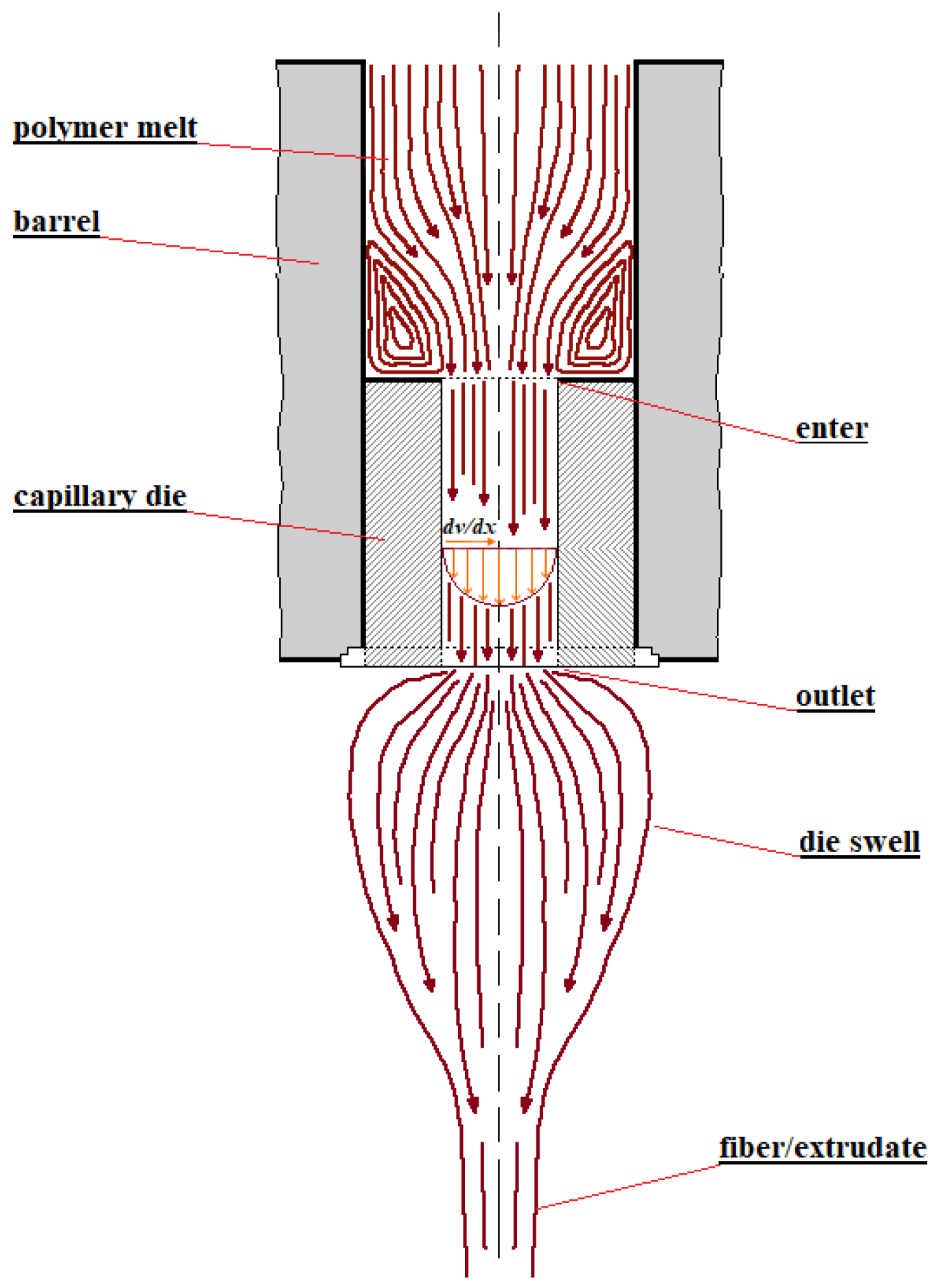
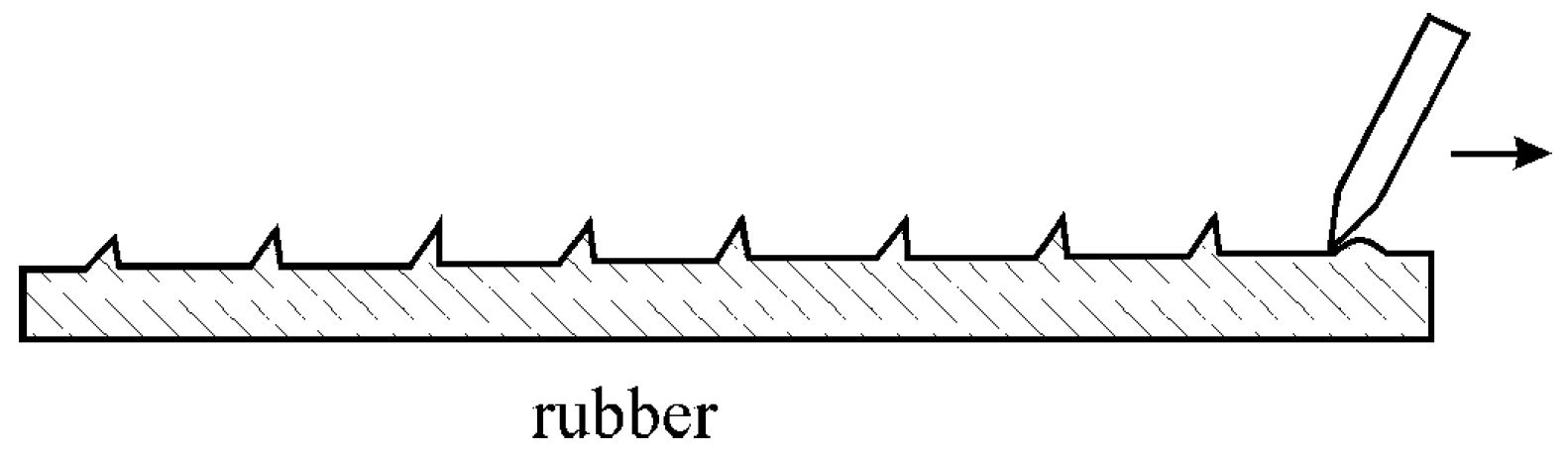
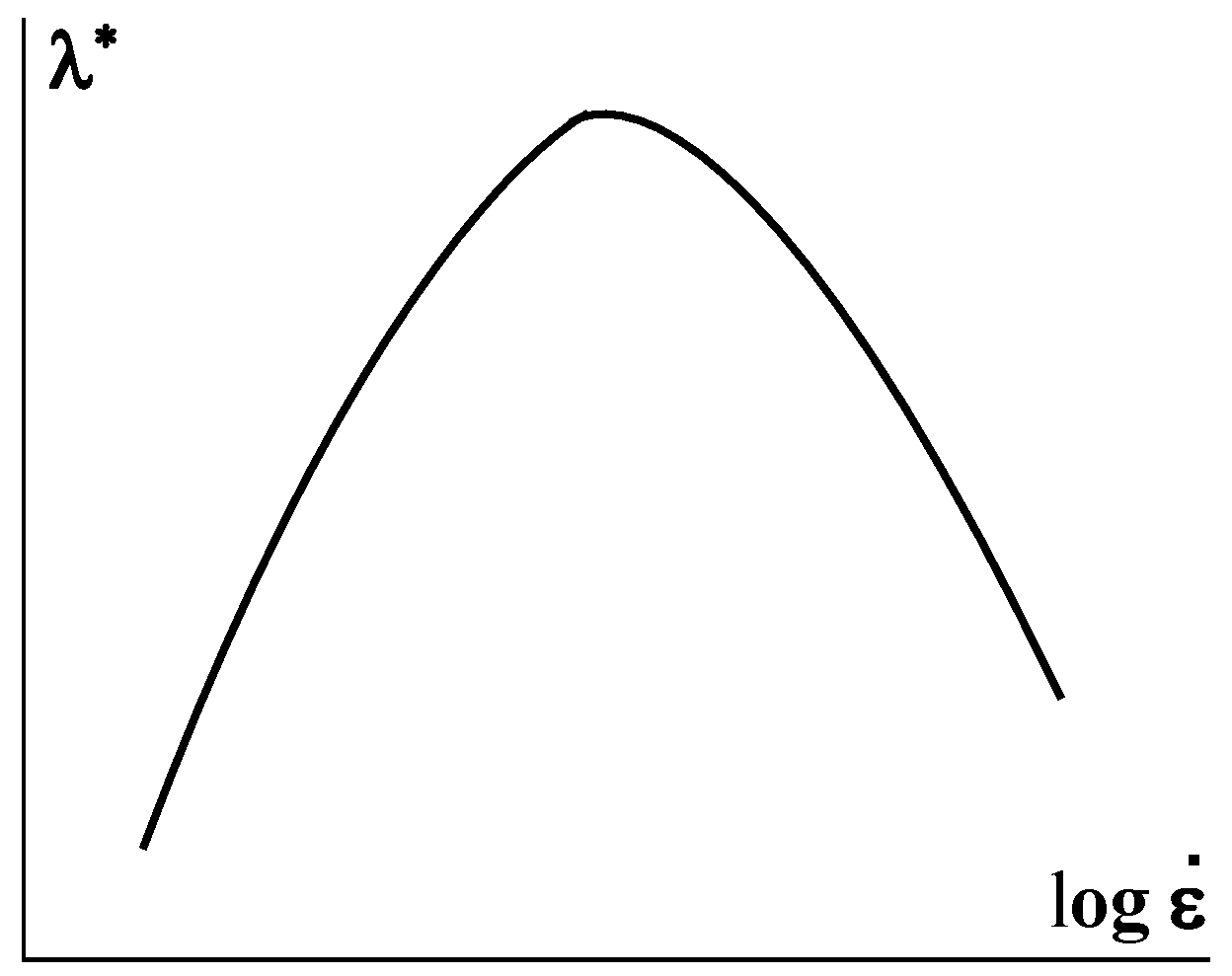
2. The Role of Elasticity in Polymer Processing
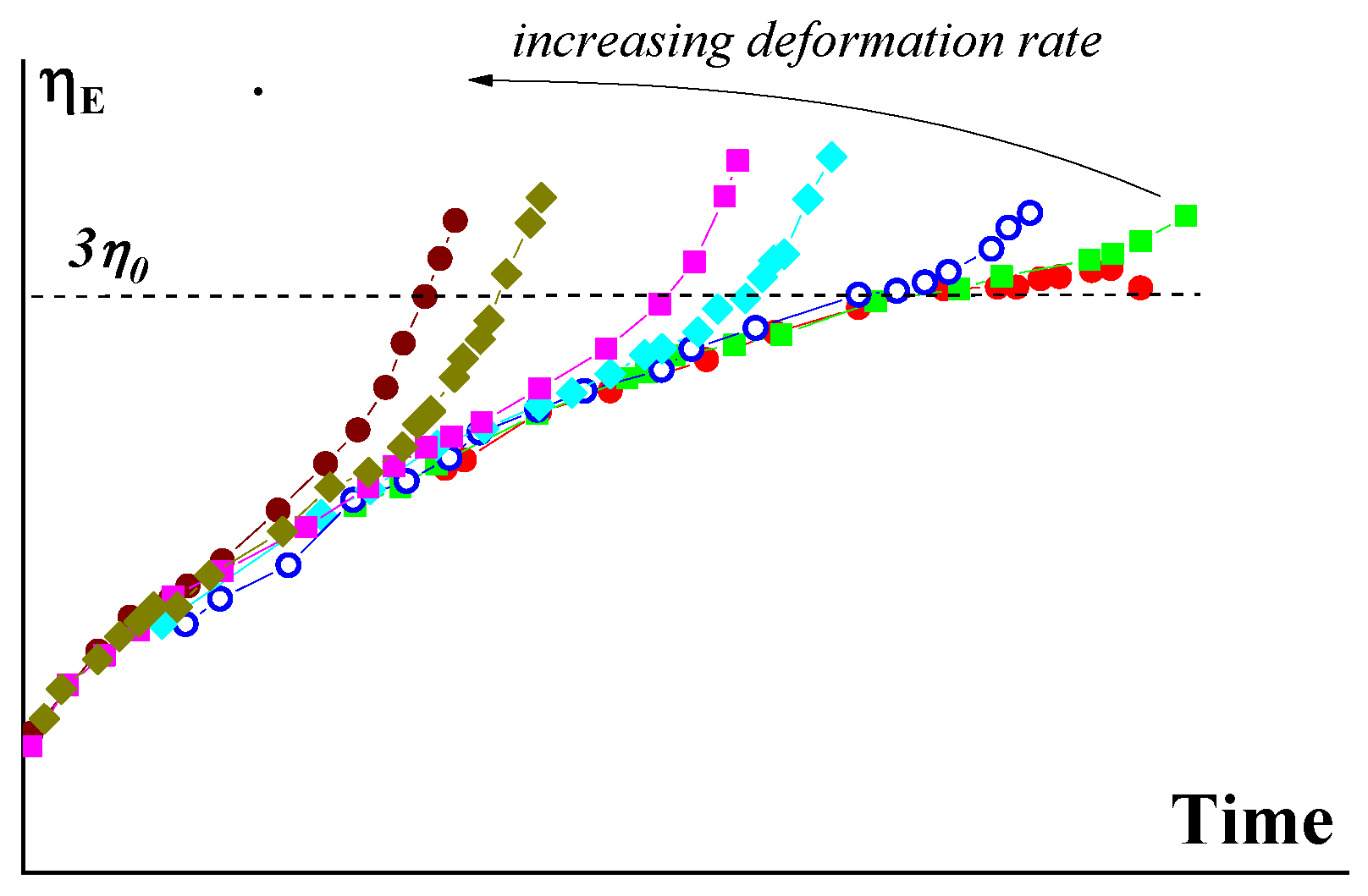
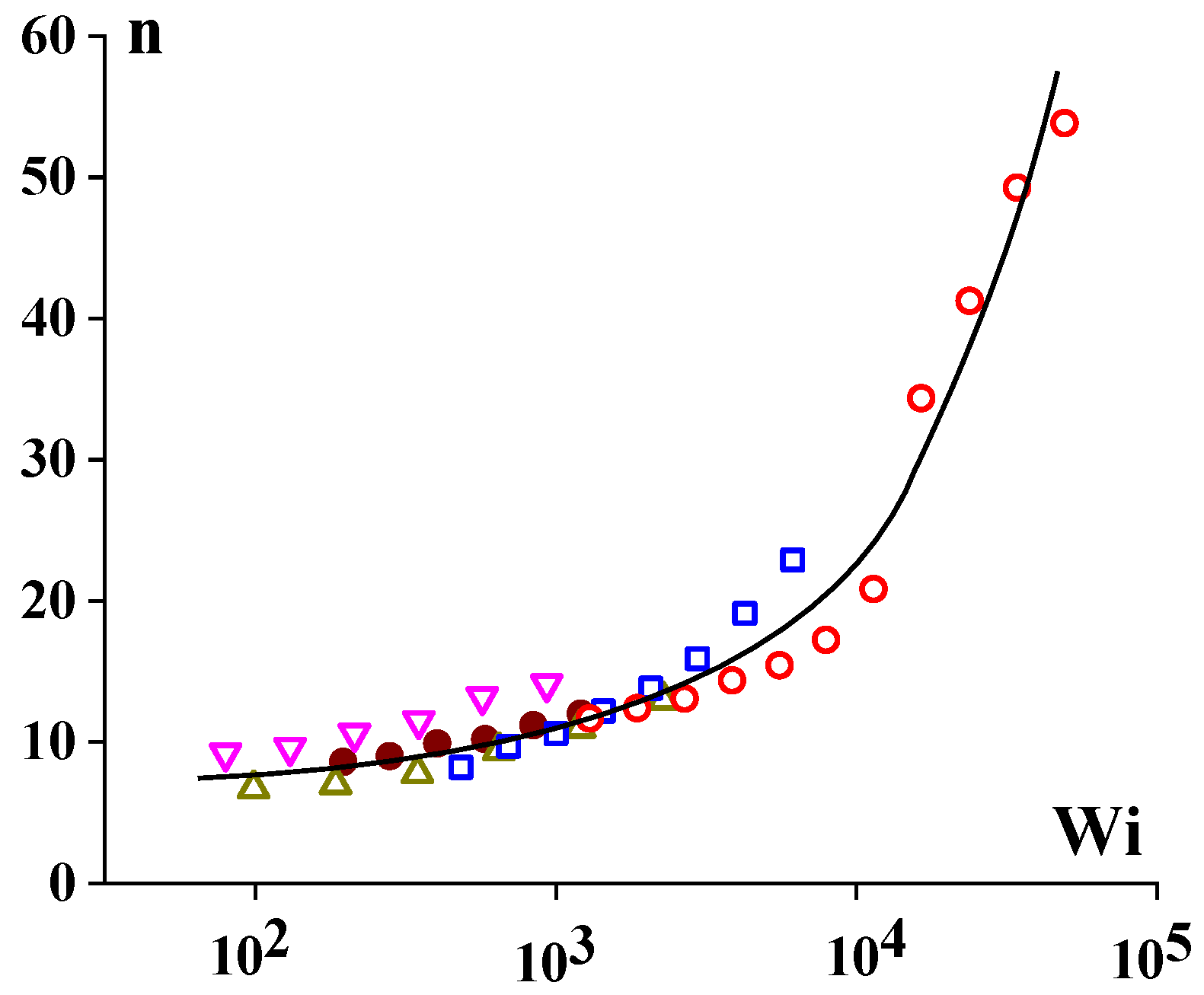
3. Elasticity in the Dynamics of Extension of Polymer Solutions
3.1. General Equations
3.2. Capillary Thinning of a Polymer Solution Thread
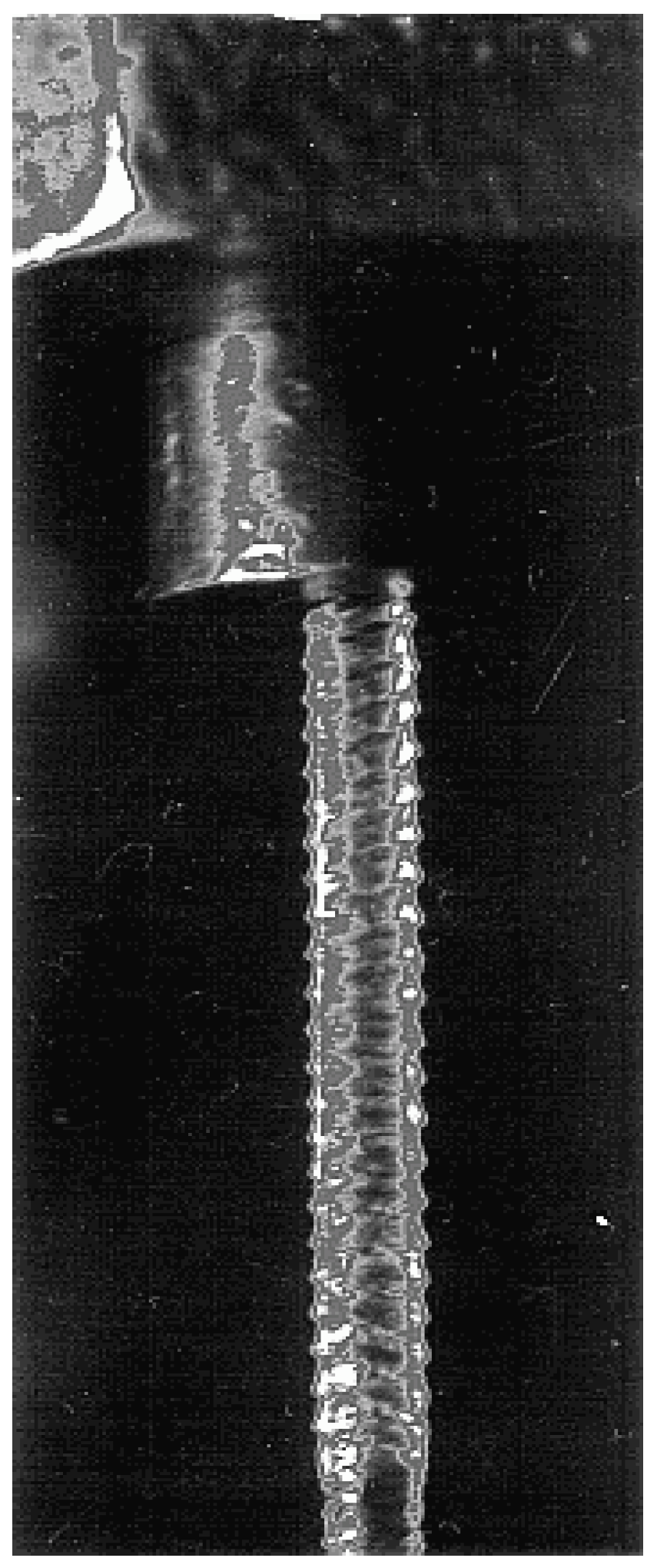
3.3. Blistering Instability
3.4. Stretching a Polymer Solution Jet by an External Load
3.5. Effect of Gravity
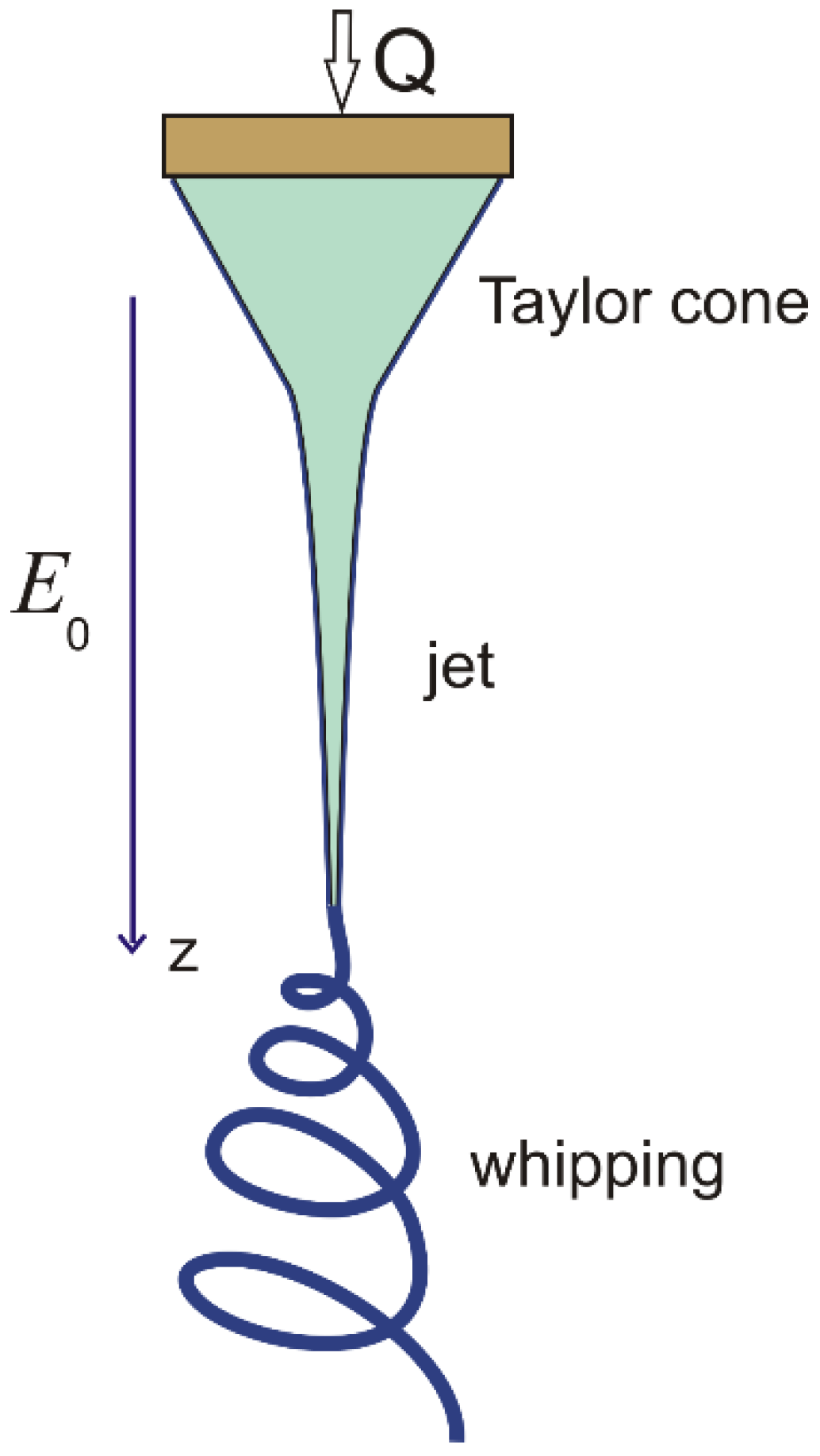
3.6. Electrospinning
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Reiner, M. The Deborah Number. Phys. Today 1964, 17, 62. [Google Scholar] [CrossRef]
- Weissenberg, K. Proceedings of the First International Congress on Rheology, Scheveningen, The Netherlands, 21–24 September 1948; Publ. North-Holland Publishing Co.: Amsterdam, The Netherlands, 1949; p. 29.
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: Chichester, UK; Brisbane, QLD, Australia; Toronto, ON, Canada; Singapore, 1980; ISBN 0-471-04894-1. [Google Scholar]
- Tobolsky, A.V. Properties and Structure of Polymers; John Wiley & Sons, Inc.: New York, NY, USA; London, UK, 1962; ASIN: B000NOCV46. [Google Scholar]
- Vinogradov, G.V.; Malkin, A.Y. Rheology of Polymers; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Malkin, A.Y.; Petrie, C.J.S. Some conditions for rupture of polymer liquids in extension. J. Rheol. 1997, 41, 1–25. [Google Scholar] [CrossRef]
- Baumgaertel, M.; Schausberger, A.; Winter, H.H. The relaxation of polymers with linear flexible chains of uniform length. Rheol. Acta 1990, 29, 400–408. [Google Scholar] [CrossRef]
- Münstedt, H. Extensional Rheology and Processing of Polymeric Materials. Int. Polym. Process. 2018, 33, 594–618. [Google Scholar] [CrossRef]
- Malkin, A.; Arinstein, A.; Kulichikhin, V. Polymer extension flows and instabilities. Prog. Polym. Sci. 2014, 39, 959–978. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Subbotin, A.V.; Kulichikhin, V.G. Stability of polymer jets in extension: Physicochemical and rheological mechanisms. Russ. Chem. Rev. 2020, 89, 811–823. [Google Scholar] [CrossRef]
- Huang, Q. When Polymer Chains Are Highly Aligned: A Perspective on Extensional Rheology. Macromolecules 2022, 55, 715–727. [Google Scholar] [CrossRef]
- Kékesi, T.; Amberg, G.; Wittberg, L.P. Drop deformation and breakup in flows with shear. Chem. Eng. Sci. 2016, 140, 319–329. [Google Scholar] [CrossRef]
- Ha, J.-W.; Leal, L.G. An experimental study of drop deformation and breakup in extensional flow at high capillary number. Phys. Fluids 2001, 13, 1568–1576. [Google Scholar] [CrossRef]
- Prieto, J.L. Viscoelastic Effects on Drop Deformation Using a Machine Learning-Enhanced, Finite Element Method. Polymers 2020, 12, 1652. [Google Scholar] [CrossRef]
- Saengow, C.; Giacomin, A.J. Fluid Elasticity in Plastic Pipe Extrusion: Loads on Die Barrel. Int. Polym. Process. 2017, 32, 648–658. [Google Scholar] [CrossRef] [Green Version]
- Papanastasiou, T.S.; Alaie, S.M.; Chen, Z. High-Speed, Non-Isothermal Fiber Spinning. Int. Polym. Process. 1994, 9, 148–158. [Google Scholar] [CrossRef]
- Zatloukal, M.; Vlček, J. Modeling of the film blowing process by using variational principles. J. Non-Newton. Fluid Mech. 2004, 123, 201–213. [Google Scholar] [CrossRef]
- Boger, D.V.; Walters, K. Rheological Phenomena in Focus; Elsevier: Amsterdam, The Netherlands, 1993; pp. 53–68. ISBN 9780444600684. [Google Scholar]
- Mitsoulis, E.; Hatzikiriakos, S.G. Annular Extrudate Swell of a Fluoropolymer Melt. Int. Polym. Process. 2012, 27, 535–546. [Google Scholar] [CrossRef]
- Mitsoulis, E. Effect of Viscoelasticity in Fountain Flow of Polyethylene Melts. Int. Polym. Process. 2009, 24, 439–451. [Google Scholar] [CrossRef] [Green Version]
- Malkin, A.; Ilyin, S.; Vasilyev, G.; Arinina, M.; Kulichikhin, V. Pressure losses in flow of viscoelastic polymeric fluids through short channels. J. Rheol. 2014, 58, 433–448. [Google Scholar] [CrossRef]
- Vinuesa, R.; Schlatter, P.; Nagib, H.M. Secondary flow in turbulent ducts with increasing aspect ratio. Phys. Rev. Fluids 2018, 3, 054606. [Google Scholar] [CrossRef]
- Nikitin, N.V.; Popelenskaya, N.V.; Stroh, A. Prandtl’s Secondary Flows of the Second Kind. Problems of Description, Prediction, and Simulation. Fluid Dyn. 2021, 56, 513–538. [Google Scholar] [CrossRef]
- Letelier, M.F.; Siginer, D.A. Secondary flows of viscoelastic liquids in straight tubes. Int. J. Solids Struct. 2003, 40, 5081–5095. [Google Scholar] [CrossRef]
- Alves, M.; Oliveira, P.; Pinho, F. Numerical Methods for Viscoelastic Fluid Flows. Annu. Rev. Fluid Mech. 2021, 53, 509–541. [Google Scholar] [CrossRef]
- Sun, X.; Wang, S.; Zhao, M. Viscoelastic flow in a curved duct with rectangular cross section over a wide range of Dean number. Phys. Fluids 2021, 33, 033101. [Google Scholar] [CrossRef]
- Browne, C.A.; Datta, S.S. Elastic turbulence generates anomalous flow resistance in porous media. Sci. Adv. 2021, 7, eabj2619. [Google Scholar] [CrossRef] [PubMed]
- Malkin, A.Y.; Kulichikhin, V.G.; Gumennyi, I.V. Comparing flow characteristics of viscoelastic liquids in long and short capillaries (entrance effects). Phys. Fluids 2021, 33, 013105. [Google Scholar] [CrossRef]
- Triliskii, K.K.; Ischuk, Y.L.; Malkin, A. On the nature of the flow of various plastic dispersions and polymers. Kolloid Zh. 1988, 50, 535–541. (In Russian) [Google Scholar]
- Siegbert, R.; Behr, M.; Elgeti, S. Die swell as an objective in the design of polymer extrusion dies. AIP Conf. Proc. 2016, 1769, 140003. [Google Scholar] [CrossRef]
- Ganvir, V.; Gautham, B.; Pol, H.; Bhamla, M.S.; Sclesi, L.; Thaokar, R.; Lele, A.; Mackley, M. Extrudate swell of linear and branched polyethylenes: ALE simulations and comparison with experiments. J. Non-Newton. Fluid Mech. 2011, 166, 12–24. [Google Scholar] [CrossRef]
- Comminal, R.; Pimenta, F.; Hattel, J.H.; Alves, M.A.; Spangenberg, J. Numerical simulation of the planar extrudate swell of pseudoplastic and viscoelastic fluids with the streamfunction and the VOF methods. J. Non-Newton. Fluid Mech. 2018, 252, 1–18. [Google Scholar] [CrossRef]
- Alzarzouri, F.; Deri, F. Evaluation of Die Swell Behavior During Capillary Extrusion of Poly(lactic acid)/High density polyethylene Blend Melts). Technium 2020, 2, 34–42. [Google Scholar] [CrossRef]
- Tammaro, D.; Walker, C.; Lombardi, L.; Trommsdorff, U. Effect of extrudate swell on extrusion foam of polyethylene terephthalate. J. Cell. Plast. 2020, 57, 911–925. [Google Scholar] [CrossRef]
- Yousefi, A.-M.; Smucker, B.; Naber, A.; Wyrick, C.; Shaw, C.; Bennett, K.; Szekely, S.; Focke, C.; Wood, K.A. Controlling the extrudate swell in melt extrusion additive manufacturing of 3D scaffolds: A designed experiment. J. Biomater. Sci. Polym. Ed. 2017, 29, 195–216. [Google Scholar] [CrossRef]
- Wang, Z.; Smith, D.E. Rheology Effects on Predicted Fiber Orientation and Elastic Properties in Large Scale Polymer Composite Additive Manufacturing. J. Compos. Sci. 2018, 2, 10. [Google Scholar] [CrossRef] [Green Version]
- Patlazhan, S.A.; Kravchanko, I.; Poldushov, M.; Miroshnikov, Y.; Kulichikhin, V. Deformation behavior of drops in the flow through a channel with sharp confinement. Kolloid Zh. 2022, 84, 186–191. (In Russian) [Google Scholar] [CrossRef]
- Burghelea, T.I.; Griess, H.J.; Münstedt, H. Comparative investigations of surface instabilities (“sharkskin”) of a linear and a long-chain branched polyethylene. J. Non-Newton. Fluid Mech. 2010, 165, 1093–1104. [Google Scholar] [CrossRef] [Green Version]
- Cogswell, F.N. Stretching flow instabilities at the exits of extrusion dies. J. Non-Newton. Fluid Mech. 1977, 2, 37–47. [Google Scholar] [CrossRef]
- Malkin, A.Y. Flow instability in polymer solutions and melts. Polym. Sci. Ser. C 2006, 48, 21–37. [Google Scholar] [CrossRef]
- Skvortsov, I.Y.; Malkin, A.Y.; Kulichikhin, V.G. Self-Oscillations Accompanying Shear Flow of Colloidal and Polymeric Systems. Reality and Instrumental Effects. Colloid J. 2019, 81, 176–186. [Google Scholar] [CrossRef]
- Kulichikhin, V.G.; Malkin, A.Y. The Role of Structure in Polymer Rheology: Review. Polymers 2022, 14, 1262. [Google Scholar] [CrossRef]
- Swain, D.; Philip, J.; Pillai, S.; Ramesh, K. A Revisit to the Frozen Stress Phenomena in Photoelasticity. Exp. Mech. 2016, 56, 903–917. [Google Scholar] [CrossRef]
- Isaza, C.A.V.; Posada, J.C.; Sierra, M.J.D.; Castro-Caicedo, A.J.; Botero-Cadavid, J.F. Analysis of Residual Stress of Injected Plastic Parts: A Multivariable Approach. Res. J. Appl. Sci. Eng. Technol. 2021, 18, 43–58. [Google Scholar] [CrossRef]
- Tedde, G.M.; Santo, L.; Bellisarbo, D.; Quandini, F. Frozen Stresses in Shape Memory Polymer Composites. Matriale Plast. 2022, 55, 2018494. [Google Scholar] [CrossRef]
- Tan, N.; Lin, L.; Deng, T.; Dong, Y. Evaluating the Residual Stress and Its Effect on the Quasi-Static Stress in Polyethylene Pipes. Polymers 2022, 14, 1458. [Google Scholar] [CrossRef]
- Weng, C.; Ding, T.; Zhou, M.; Liu, J.; Wang, H. Formation Mechanism of Residual Stresses in Micro-Injection Molding of PMMA: A Molecular Dynamics Simulation. Polymers 2020, 12, 1368. [Google Scholar] [CrossRef] [PubMed]
- Zhenga, R.; Kennedy, P.; Phan-Thien, N.; Fan, X.-J. Thermoviscoelastic simulation of thermally and pressure-induced stresses in injection molding for the prediction of shrinkage and warpage for fibre-reinforced thermoplastics. J. Non-Newton. Fluid Mech. 1999, 84, 159–190. [Google Scholar] [CrossRef]
- Wang, Y.; Boukany, P.; Wang, S.-Q.; Wang, X. Elastic Breakup in Uniaxial Extension of Entangled Polymer Melts. Phys. Rev. Lett. 2007, 99, 237801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoyle, D.; Fielding, S. Necking after extensional filament stretching of complex fluids and soft solids. J. Non-Newton. Fluid Mech. 2017, 247, 132–145. [Google Scholar] [CrossRef] [Green Version]
- Huang, Q.; Rasmussen, H.K. Extensional flow dynamics of polystyrene melt. J. Rheol. 2019, 63, 829–835. [Google Scholar] [CrossRef] [Green Version]
- Huang, Q.; Ahn, J.; Parisi, D.; Chang, T.; Hassager, O.; Panyukov, S.; Rubinstein, M.; Vlassopoulos, D. Unexpected Stretching of Entangled Ring Macromolecules. Phys. Rev. Lett. 2019, 122, 208001. [Google Scholar] [CrossRef] [Green Version]
- Hassager, O.; Wang, Y.; Huang, Q. Extensional rheometry of model liquids: Simulations of filament stretching. Phys. Fluids 2021, 33, 123108. [Google Scholar] [CrossRef]
- Eggers, J. Nonlinear dynamics and breakup of free-surface flows. Rev. Mod. Phys. 1997, 69, 865–930. [Google Scholar] [CrossRef] [Green Version]
- Huang, Q.; Alvarez, N.J.; Shabbir, A.; Hassager, O. Multiple Cracks Propagate Simultaneously in Polymer Liquids in Tension. Phys. Rev. Lett. 2016, 117, 087801. [Google Scholar] [CrossRef] [Green Version]
- Huang, Q.; Hassager, O. Polymer liquids fracture like solids. Soft Matter 2017, 13, 3470–3474. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wagner, M.H.; Narimissa, E.; Huang, Q. On the origin of brittle fracture of entangled polymer solutions and melts. J. Rheol. 2018, 62, 221–233. [Google Scholar] [CrossRef] [Green Version]
- Wagner, M.H.; Narimissa, E.; Huang, Q. Response to “Letter to the Editor: ‘Melt rupture unleashed by few chain scission events in fully stretched strands’” [J. Rheol. 63, 105 (2018)]. J. Rheol. 2019, 63, 419–421. [Google Scholar] [CrossRef]
- Wang, S.-Q. Letter to the Editor: Melt rupture unleashed by few chain scission events in fully stretched strands. J. Rheol. 2019, 63, 105–107. [Google Scholar] [CrossRef]
- Melcher, J.R.; Taylor, G.I. Electrohydrodynamics: A Review of the Role of Interfacial Shear Stresses. Annu. Rev. Fluid Mech. 1969, 1, 111–146. [Google Scholar] [CrossRef]
- Saville, D.A. ELECTROHYDRODYNAMICS: The Taylor-Melcher Leaky Dielectric Model. Annu. Rev. Fluid Mech. 1997, 29, 27–64. [Google Scholar] [CrossRef]
- Subbotin, A.V.; Semenov, A.N. Electrohydrodynamics of stationary cone-jet streaming. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20150290. [Google Scholar] [CrossRef] [Green Version]
- Subbotin, A.; Stepanyan, R.; Chiche, A.; Slot, J.J.M.; Brinke, G.T. Dynamics of an electrically charged polymer jet. Phys. Fluids 2013, 25, 103101. [Google Scholar] [CrossRef] [Green Version]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Fluids; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Larson, R.G. Constitutive Equations for Polymer Melts and Solutions; Butterworths: London, UK, 1988; ISBN 0409901199. [Google Scholar]
- Day, R.F.; Hinch, E.J.; Lister, J.R. Self-Similar Capillary Pinchoff of an Inviscid Fluid. Phys. Rev. Lett. 1998, 80, 704–707. [Google Scholar] [CrossRef] [Green Version]
- Eggers, J.; Villermaux, E. Physics of liquid jets. Rep. Prog. Phys. 2008, 71, 036601. [Google Scholar] [CrossRef] [Green Version]
- Dinic, J.; Sharma, V. Macromolecular relaxation, strain, and extensibility determine elastocapillary thinning and ex-tensional viscosity of polymer solutions. Proc. Natl. Acad. Sci. USA 2019, 116, 8766–8774. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sur, S.; Rothstein, J. Drop breakup dynamics of dilute polymer solutions: Effect of molecular weight, concentration, and viscosity. J. Rheol. 2018, 62, 1245–1259. [Google Scholar] [CrossRef] [Green Version]
- Wee, H.; Anthony, C.R.; Basaran, O.A. Breakup of a low-viscosity liquid thread. Phys. Rev. Fluids 2022, 7, L112001. [Google Scholar] [CrossRef]
- Rayleigh, L. On the Instability of Jets. Proc. Lond. Math. Soc. 1878, 1, 4–13. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.-J.; Steen, P.H. Dynamics of inviscid capillary breakup: Collapse and pinchoff of a film bridge. J. Fluid Mech. 1997, 341, 245–267. [Google Scholar] [CrossRef]
- Li, Y.; Sprittles, J.E. Capillary breakup of a liquid bridge: Identifying regimes and transitions. J. Fluid Mech. 2016, 797, 29–59. [Google Scholar] [CrossRef] [Green Version]
- Papageorgiou, D.T. On the breakup of viscous liquid threads. Phys. Fluids 1995, 7, 1529–1544. [Google Scholar] [CrossRef] [Green Version]
- Papageorgiou, D.T. Analytical description of the breakup of liquid jets. J. Fluid Mech. 1995, 301, 109–132. [Google Scholar] [CrossRef]
- Bazilevskii, A.V.; Voronkov, S.I.; Entov, V.M.; Rozhkov, A.N. Orientation effects in the breakup of jets and threads of dilute polymer solutions. Sov. Phys. Dokl. 1981, 26, 333–336. [Google Scholar]
- Bazilevskii, A.V.; Entov, V.M.; Lerner, M.M.; Rozhkov, A.N. Failure of polymer solution filaments. Polym. Sci. Ser. A 1997, 39, 316–324. [Google Scholar]
- Christanti, Y.; Walker, L.M. Surface tension driven jet break up of strain-hardening polymer solutions. J. Non-Newton. Fluid Mech. 2001, 100, 9–26. [Google Scholar] [CrossRef]
- Yarin, A.L. Free Liquid Jets and Films: Hydrodynamics and Rheology; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Entov, V.M.; Hinch, E.J. Effect of a spectrum of relaxation times on the capillary thinning of a filament of elastic liquid. J. Non-Newton. Fluid Mech. 1997, 72, 31–53. [Google Scholar] [CrossRef]
- Amarouchene, Y.; Bonn, D.; Meunier, J.; Kellay, H. Inhibition of the Finite-Time Singularity during Droplet Fission of a Polymeric Fluid. Phys. Rev. Lett. 2001, 86, 3558–3561. [Google Scholar] [CrossRef] [PubMed]
- Deblais, A.; Herrada, M.A.; Eggers, J.; Bonn, D. Self-similarity in the breakup of very dilute viscoelastic solutions. J. Fluid Mech. 2020, 904, R2. [Google Scholar] [CrossRef]
- Stelter, M.; Brenn, G.; Yarin, A.L.; Singh, R.P.; Durst, F. Validation and application of a novel elongational device for polymer solutions. J. Rheol. 2000, 44, 595–616. [Google Scholar] [CrossRef]
- Stelter, M.; Brenn, G.; Yarin, A.L.; Singh, R.P.; Durst, F. Investigation of the elongational behavior of polymer solutions by means of an elongational rheometer. J. Rheol. 2002, 46, 507–527. [Google Scholar] [CrossRef]
- Bazilevskii, A.V.; Entov, V.M.; Rozhkov, A.N. Breakup of an Oldroyd liquid bridge as a method for testing the rhe-ological properties of polymer solutions. Polym. Sci. Ser. A Ser. B 2001, 43, 716–726. [Google Scholar]
- Chang, H.-C.; Demekhin, E.A.; Kalaidin, E. Iterated stretching of viscoelastic jets. Phys. Fluids 1999, 11, 1717–1737. [Google Scholar] [CrossRef]
- Li, J.; Fontelos, M.A. Drop dynamics on the beads-on-string structure for viscoelastic jets: A numerical study. Phys. Fluids 2003, 15, 922–937. [Google Scholar] [CrossRef]
- Clasen, C.; Eggers, J.; Fontelos, M.A.; Li, J.; McKINLEY, G.H. The beads-on-string structure of viscoelastic threads. J. Fluid Mech. 2006, 556, 283. [Google Scholar] [CrossRef] [Green Version]
- Bhat, P.P.; Appathurai, S.; Harris, M.T.; Pasquali, M.; McKinley, G.H.; Basaran, O.A. Formation of beads-on-a-string structures during break-up of viscoelastic filaments. Nat. Phys. 2010, 6, 625–631. [Google Scholar] [CrossRef] [Green Version]
- Turkoz, E.; Lopez-Herrera, J.M.; Eggers, J.; Arnold, C.B.; Deike, L. Axisymmetric simulation of viscoelastic filament thinning with the Oldroyd-B model. J. Fluid Mech. 2018, 851, R2. [Google Scholar] [CrossRef] [Green Version]
- Dinic, J.; Zhang, Y.; Jimenez, L.N.; Sharma, V. Extensional Relaxation Time of Dilute, Aqueous, Polymer Solutions. ACS Macro Lett. 2015, 4, 804–808. [Google Scholar] [CrossRef] [PubMed]
- Dinic, J.; Jimenez, L.N.; Sharma, V. Pinch-off dynamics and dripping-onto-substrate (DoS) rheometry of complex fluids. Lab A Chip 2017, 17, 460–473. [Google Scholar] [CrossRef] [PubMed]
- Jimenez, L.N.; Dinic, J.; Parsi, N.; Sharma, V. Extensional Relaxation Time, Pinch-Off Dynamics, and Printability of Semidilute Polyelectrolyte Solutions. Macromolecules 2018, 51, 5191–5208. [Google Scholar] [CrossRef]
- Keshavarz, B.; Sharma, V.; Houze, E.C.; Koerner, M.R.; Moore, J.R.; Cotts, P.M.; Threlfall-Holmes, P.; McKinley, G.H. Studying the effects of elongational properties on atomization of weakly viscoelastic solutions using Rayleigh Ohnesorge Jetting Extensional Rheometry (ROJER). J. Non-Newton. Fluid Mech. 2015, 222, 171–189. [Google Scholar] [CrossRef]
- Mathues, W.; Formenti, S.; McIlroy, C.; Harlen, O.G.; Clasen, C. CaBER vs ROJER—Different time scales for the thinning of a weakly elastic jet. J. Rheol. 2018, 62, 1135–1153. [Google Scholar] [CrossRef]
- McKinley, G.H.; Tripathi, A. How to extract the Newtonian viscosity from capillary breakup measurements in a filament rheometer. J. Rheol. 2000, 44, 653–670. [Google Scholar] [CrossRef] [Green Version]
- Semenov, A.; Nyrkova, I. Capillary Thinning of Viscoelastic Threads of Unentangled Polymer Solutions. Polymers 2022, 14, 4420. [Google Scholar] [CrossRef]
- Zhou, J.; Doi, M. Dynamics of viscoelastic filaments based on Onsager principle. Phys. Rev. Fluids 2018, 3, 084004. [Google Scholar] [CrossRef] [Green Version]
- Bazilevskii, A.V. Dynamics of horizontal viscoelastic fluid filaments. Fluid Dyn. 2013, 48, 97–108. [Google Scholar] [CrossRef]
- Bazilevskii, A.V.; Rozhkov, A.N. Dynamics of Capillary Breakup of Elastic Jets. Fluid Dyn. 2014, 49, 827–843. [Google Scholar] [CrossRef]
- Bazilevskii, A.V.; Rozhkov, A.N. Dynamics of the Capillary Breakup of a Bridge in an Elastic Fluid. Fluid Dyn. 2015, 50, 800–811. [Google Scholar] [CrossRef]
- Tirtaatmadja, V.; McKinley, G.H.; Cooper-White, J.J. Drop formation and breakup of low viscosity elastic fluids: Effects of molecular weight and concentration. Phys. Fluids 2006, 18, 043101. [Google Scholar] [CrossRef] [Green Version]
- Muthukumar, M.; Freed, K.F. Theory of Concentration Dependence of Polymer Relaxation Times in Dilute Solutions. Macromolecules 1978, 11, 843–852. [Google Scholar] [CrossRef]
- Clasen, C.; Plog, J.P.; Kulicke, W.-M.; Owens, M.; Macosko, C.; Scriven, L.E.; Verani, M.; McKinley, G.H. How dilute are dilute solutions in extensional flows? J. Rheol. 2006, 50, 849–881. [Google Scholar] [CrossRef] [Green Version]
- Prabhakar, R.; Gadkari, S.; Gopesh, T.; Shaw, M.J. Influence of stretching induced self-concentration and self-dilution on coil-stretch hysteresis and capillary thinning of unentangled polymer solutions. J. Rheol. 2016, 60, 345–366. [Google Scholar] [CrossRef]
- Prabhakar, R.; Sasmal, C.; Nguyen, D.A.; Sridhar, T.; Prakash, J.R. Effect of stretching-induced changes in hydro-dynamic screening on coil-stretch hysteresis of unentangled polymer solutions. Phys. Rev. Fluids 2017, 2, 011301. [Google Scholar] [CrossRef] [Green Version]
- Subbotin, A.V.; Semenov, A.N. Dynamics of Dilute Polymer Solutions at the Final Stages of Capillary Thinning. Macromolecules 2022, 55, 2096–2108. [Google Scholar] [CrossRef]
- Ho, D.L.; Hammouda, B.; Kline, S.R. Clustering of poly(ethylene oxide) in water revisited. J. Polym. Sci. Part B Polym. Phys. 2003, 41, 135–138. [Google Scholar] [CrossRef]
- Hammouda, B.; Ho, D.L.; Kline, S.R. SANS from Poly(ethylene oxide)/Water Systems. Macromolecules 2002, 35, 8578–8585. [Google Scholar] [CrossRef]
- James, D.F.; Saringer, J.H. Extensional flow of dilute polymer solutions. J. Fluid Mech. 1980, 97, 666–671. [Google Scholar] [CrossRef]
- Rubinstein, M.; Semenov, A.N. Thermoreversible gelation in solutions of associating polymers: 2. Linear dynamics. Macromolecules 1998, 31, 1386–1397. [Google Scholar] [CrossRef]
- Oliveira, M.; McKinley, G. Iterated stretching and multiple beads-on-a-string phenomena in dilute solutions of highly extensible flexible polymers. Phys. Fluids 2005, 17, 071704. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, M.S.; Yeh, R.; McKinley, G.H. Iterated stretching, extensional rheology and formation of beads-on-a-string structures in polymer solutions. J. Non-Newton. Fluid Mech. 2006, 137, 137–148. [Google Scholar] [CrossRef] [Green Version]
- Sattler, R.; Wagner, C.; Eggers, J. Blistering Pattern and Formation of Nanofibers in Capillary Thinning of Polymer Solutions. Phys. Rev. Lett. 2008, 100, 164502. [Google Scholar] [CrossRef]
- Sattler, R.; Gier, S.; Eggers, J.; Wagner, C. The final stages of capillary break-up of polymer solutions. Phys. Fluids 2012, 24, 023101. [Google Scholar] [CrossRef]
- Deblais, A.; Velikov, K.P.; Bonn, D. Pearling Instabilities of a Viscoelastic Thread. Phys. Rev. Lett. 2018, 120, 194501. [Google Scholar] [CrossRef] [Green Version]
- Kibbelaar, H.V.M.; Deblais, A.; Burla, F.; Koenderink, G.H.; Velikov, K.P.; Bonn, D. Capillary thinning of elastic and viscoelastic threads: From elastocapillarity to phase separation. Phys. Rev. Fluids 2020, 5, 092001. [Google Scholar] [CrossRef]
- Semakov, A.V.; Kulichikhin, V.G.; Tereshin, A.K.; Antonov, S.V.; Malkin, A.Y. On the nature of phase separation of polymer solutions at high extension rates. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 559–565. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Semakov, A.V.; Skvortsov, I.Y.; Zatonskikh, P.; Kulichikhin, V.G.; Subbotin, A.V.; Semenov, A.N. Spinnability of Dilute Polymer Solutions. Macromolecules 2017, 50, 8231–8244. [Google Scholar] [CrossRef]
- Kulichikhin, V.G.; Skvortsov, I.Y.; Subbotin, A.V.; Kotomin, S.V.; Malkin, A.Y. A Novel Technique for Fiber Formation: Mechanotropic Spinning—Principle and Realization. Polymers 2018, 10, 856. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Subbotin, A.V.; Semenov, A.N. Phase separation in dilute polymer solutions at high-rate extension. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 1066–1073. [Google Scholar] [CrossRef]
- Semenov, A.N.; Subbotin, A.V. Phase Separation Kinetics in Unentangled Polymer Solutions Under High-Rate Ex-tension. J. Polym. Sci. Part B Polym. 2017, 55, 623–637. [Google Scholar] [CrossRef]
- Subbotin, A.V.; Semenov, A.N. Phase Separation in Polymer Solutions under Extension. Polym. Sci. Ser. C 2018, 60, 106–117. [Google Scholar] [CrossRef]
- Goren, S.L. The instability of an annular thread of fluid. J. Fluid Mech. 1962, 12, 309–319. [Google Scholar] [CrossRef]
- Donets, S.; Sommer, J.-U. Molecular Dynamics Simulations of Strain-Induced Phase Transition of Poly(ethylene oxide) in Water. J. Phys. Chem. B 2018, 122, 392–397. [Google Scholar] [CrossRef] [Green Version]
- Donets, S.; Guskova, O.; Sommer, J.-U. Flow-Induced Formation of Thin PEO Fibers in Water and Their Stability after the Strain Release. J. Phys. Chem. B 2020, 124, 9224–9229. [Google Scholar] [CrossRef]
- Eggers, J. Instability of a polymeric thread. Phys. Fluids 2014, 26, 033106. [Google Scholar] [CrossRef] [Green Version]
- Helfand, E.; Fredrickson, G.H. Large fluctuations in polymer solutions under shear. Phys. Rev. Lett. 1989, 62, 2468–2471. [Google Scholar] [CrossRef]
- Doi, M.; Onuki, A. Dynamic coupling between stress and composition in polymer solutions and blends. J. De Phys. II 1992, 2, 1631–1656. [Google Scholar] [CrossRef]
- Milner, S.T. Dynamical theory of concentration fluctuations in polymer solutions under shear. Phys. Rev. E 1993, 48, 3674–3691. [Google Scholar] [CrossRef]
- Subbotin, A.V.; Semenov, A.N. Capillary-Induced Phase Separation in Ultrathin Jets of Rigid-Chain Polymer Solutions. JETP Lett. 2020, 111, 55–61. [Google Scholar] [CrossRef]
- Subbotin, A.V.; Semenov, A.N. Multiple droplets formation in ultrathin bridges of rigid rod dispersions. J. Rheol. 2020, 64, 13–27. [Google Scholar] [CrossRef]
- Subbotin, A.V.; Semenov, A.N. Dynamics of annular solvent droplets under capillary thinning of non-entangled polymer solution. J. Rheol. 2023, 67, 53–65. [Google Scholar] [CrossRef]
- Senchenko, S.; Bohr, T. Shape and stability of a viscous thread. Phys. Rev. E 2005, 71, 056301. [Google Scholar] [CrossRef] [Green Version]
- Javadi, A.; Eggers, J.; Bonn, D.; Habibi, M.; Ribe, N.M. Delayed Capillary Breakup of Falling Viscous Jets. Phys. Rev. Lett. 2013, 110, 144501. [Google Scholar] [CrossRef]
- Clarke, N.S. A differential equation in fluid mechanics. Mathematika 1966, 13, 51–53. [Google Scholar] [CrossRef]
- Clarke, N.S. Two-dimensional flow under gravity in a jet of viscous liquid. J. Fluid Mech. 1968, 31, 481–500. [Google Scholar] [CrossRef]
- Montanero, J.M.; Herrada, M.A.; Ferrera, C.; Vega, E.J.; Ganan-Calvo, A. On the validity of a universal solution for viscous capillary jets. Phys. Fluids 2011, 23, 122103. [Google Scholar] [CrossRef]
- Clanet, C.; Lasheras, J.C. Transition from dripping to jetting. J. Fluid Mech. 1999, 383, 307–326. [Google Scholar] [CrossRef] [Green Version]
- Sauter, U.S.; Buggisch, H.W. Stability of initially slow viscous jets driven by gravity. J. Fluid Mech. 2005, 533, 237–257. [Google Scholar] [CrossRef]
- Alhushaybari, A.; Uddin, J. Convective and absolute instability of viscoelastic liquid jets in the presence of gravity. Phys. Fluids 2019, 31, 044106. [Google Scholar] [CrossRef]
- Subbotin, A.V.; Skvortsov, I.Y.; Kuzin, M.S.; Gerasimenko, P.S.; Kulichikhin, V.G.; Malkin, A.Y. The shape of a falling jet formed by concentrated polymer solutions. Phys. Fluids 2021, 33, 083108. [Google Scholar] [CrossRef]
- Taylor, G.I. Disintegration of water drops in an electric field. Proc. R. Soc. London Ser. A Math. Phys. Sci. 1964, 280, 383–397. [Google Scholar] [CrossRef]
- Fernández de la Mora, J. The fluid dynamics of Taylor cones. Annu. Rev. Fluid Mech. 2007, 39, 217–243. [Google Scholar] [CrossRef]
- Lauricella, M.; Succi, S.; Zussman, E.; Pisignano, D.; Yarin, A.L. Models of polymer solutions in electrified jets and solution blowing. Rev. Mod. Phys. 2020, 92, 035004. [Google Scholar] [CrossRef]
- Ramos, A.; Castellanos, A. Conical points in liquid-liquid interfaces subjected to electric fields. Phys. Lett. A 1994, 184, 268–272. [Google Scholar] [CrossRef]
- Subbotin, A. Electrohydrodynamics of cones on the surface of a liquid. JETP Lett. 2015, 100, 657–661. [Google Scholar] [CrossRef]
- Subbotin, A.; Semenov, A.N. Electrohydrodynamics of a Cone–Jet Flow at a High Relative Permittivity. JETP Lett. 2015, 102, 815–820. [Google Scholar] [CrossRef]
- Subbotin, A.V.; Semenov, A.N. Volume-Charged Cones on a Liquid Interface in an Electric Field. JETP Lett. 2018, 107, 186–191. [Google Scholar] [CrossRef]
- Subbotin, A.V.; Semenov, A.N. Micro-cones on a liquid interface in high electric field: Ionization effects. Phys. Fluids 2018, 30, 022108. [Google Scholar] [CrossRef]
- Belyaev, M.; Zubarev, N.; Zubareva, O. Space-charge-limited current through conical formations on the surface of a liquid with ionic conductivity. J. Electrost. 2020, 107, 103478. [Google Scholar] [CrossRef]
- Yarin, A.L.; Koombhongse, S.; Reneker, D.H. Taylor cone and jetting from liquid droplets in electrospinning of nanofibers. J. Appl. Phys. 2001, 90, 4836–4846. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.H.; Fridrikh, S.V.; Rutledge, G.C. The role of elasticity in the formation of electrospun fibers. Polymer 2006, 47, 4789–4797. [Google Scholar] [CrossRef]
- Helgeson, M.E.; Grammatikos, K.N.; Deitzel, J.M.; Wagner, N.J. Theory and kinematic measurements of the mechanics of stable electrospun polymer jets. Polymer 2008, 49, 2924–2936. [Google Scholar] [CrossRef]
- Han, T.; Yarin, A.L.; Reneker, D.H. Viscoelastic electrospun jets: Initial stresses and elongational rheometry. Polymer 2008, 49, 1651–1658. [Google Scholar] [CrossRef]
- Greenfeld, I.; Fezzaa, K.; Rafailovich, M.H.; Zussman, E. Fast X-ray Phase-Contrast Imaging of Electrospinning Polymer Jets: Measurements of Radius, Velocity, and Concentration. Macromolecules 2012, 45, 3616–3626. [Google Scholar] [CrossRef]
- Feng, J.J. The stretching of an electrified non-Newtonian jet: A model for electrospinning. Phys. Fluids 2002, 14, 3912–3926. [Google Scholar] [CrossRef] [Green Version]
- Hohman, M.M.; Shin, M.; Rutledge, G.; Brenner, M.P. Electrospinning and electrically forced jets. II. Applications. Phys. Fluids 2001, 13, 2221–2236. [Google Scholar] [CrossRef] [Green Version]
- Higuera, F.J. Stationary viscosity-dominated electrified capillary jets. J. Fluid Mech. 2006, 558, 143–152. [Google Scholar] [CrossRef]
- Reznik, S.N.; Zussman, E. Capillary-dominated electrified jets of a viscous leaky dielectric liquid. Phys. Rev. E 2010, 81, 026313. [Google Scholar] [CrossRef] [PubMed]
- Kirichenko, N.; Petryanov-Sokolov, I.V.; Suprun, N.N.; Shutov, A.A. Asymptotic radius of a slightly conducting liquid jet in an electric field. Sov. Phys. Dokl. 1986, 31, 611–613. [Google Scholar]
- Carroll, C.P.; Joo, Y.L. Electrospinning of viscoelastic Boger fluids: Modeling and experiments. Phys. Fluids 2006, 18, 053102. [Google Scholar] [CrossRef]
- Wang, C.; Hashimoto, T.; Wang, Y.; Lai, H.-Y.; Kuo, C.-H. Formation of Dissipative Structures in the Straight Segment of Electrospinning Jets. Macromolecules 2020, 53, 7876–7886. [Google Scholar] [CrossRef]
- Chen, G.; Lai, H.; Lu, P.; Chang, Y.; Wang, C. Light Scattering of Electrospinning Jet with Internal Structures by Flow-Induced Phase Separation. Macromol. Rapid Commun. 2022, 44, 2200273. [Google Scholar] [CrossRef]
- De La Mora, J.F.; Loscertales, I.G. The current emitted by highly conducting Taylor cones. J. Fluid Mech. 1994, 260, 155–184. [Google Scholar] [CrossRef]
- Subbotin, A.; Kulichikhin, V. Orientation and Aggregation of Polymer Chains in the Straight Electrospinning Jet. Materials 2020, 13, 4295. [Google Scholar] [CrossRef]
- Subbotin, A.V. Features of the Behavior of a Polymer Solution Jet in Electrospinning. Polym. Sci. Ser. A 2021, 63, 172–179. [Google Scholar] [CrossRef]
- Shin, Y.M.; Hohman, M.M.; Brenner, M.P.; Rutledge, G.C. Experimental characterization of electrospinning: The electrically forced jet and instabilities. Polymer 2001, 42, 09955–09967. [Google Scholar] [CrossRef]
- Xin, Y.; Reneker, D.H. Hierarchical polystyrene patterns produced by electrospinning. Polymer 2012, 53, 4254–4261. [Google Scholar] [CrossRef]
- Wang, C.; Hashimoto, T. Self-Organization in Electrospun Polymer Solutions: From Dissipative Structures to Ordered Fiber Structures through Fluctuations. Macromolecules 2018, 51, 4502–4515. [Google Scholar] [CrossRef]
- Wang, C.; Hashimoto, T. A Scenario of a Fiber Formation Mechanism in Electrospinning: Jet Evolves Assemblies of Phase-Separated Strings That Eventually Split into As-spun Fibers Observed on the Grounded Collector. Macromolecules 2020, 53, 9584–9600. [Google Scholar] [CrossRef]
- Choi, S.; Shin, D.; Chang, J. Nanoscale Fiber Deposition via Surface Charge Migration at Air-to-Polymer Liquid Interface in Near-Field Electrospinning. ACS Appl. Polym. Mater. 2020, 2, 2761–2768. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Subbotin, A.V.; Malkin, A.Y.; Kulichikhin, V.G. The Elasticity of Polymer Melts and Solutions in Shear and Extension Flows. Polymers 2023, 15, 1051. https://doi.org/10.3390/polym15041051
Subbotin AV, Malkin AY, Kulichikhin VG. The Elasticity of Polymer Melts and Solutions in Shear and Extension Flows. Polymers. 2023; 15(4):1051. https://doi.org/10.3390/polym15041051
Chicago/Turabian StyleSubbotin, Andrey V., Alexander Ya. Malkin, and Valery G. Kulichikhin. 2023. "The Elasticity of Polymer Melts and Solutions in Shear and Extension Flows" Polymers 15, no. 4: 1051. https://doi.org/10.3390/polym15041051
APA StyleSubbotin, A. V., Malkin, A. Y., & Kulichikhin, V. G. (2023). The Elasticity of Polymer Melts and Solutions in Shear and Extension Flows. Polymers, 15(4), 1051. https://doi.org/10.3390/polym15041051









