Effect of Fiber Fraction on Ballistic Impact Behavior of 3D Woven Composites
Abstract
1. Introduction
2. Materials and Testing Methods
2.1. Materials
2.1.1. 3D Woven Architecture
2.1.2. Specimen Preparation
2.2. Ballistic Impact Tests
2.3. Characterization of Damage Morphology
3. Results and Discussion
3.1. Ballistic Test Results
3.2. Energy Absorption Capability of 3DWCs
3.3. Damage Morphology and Damage Area of 3DWCs
4. Conclusions
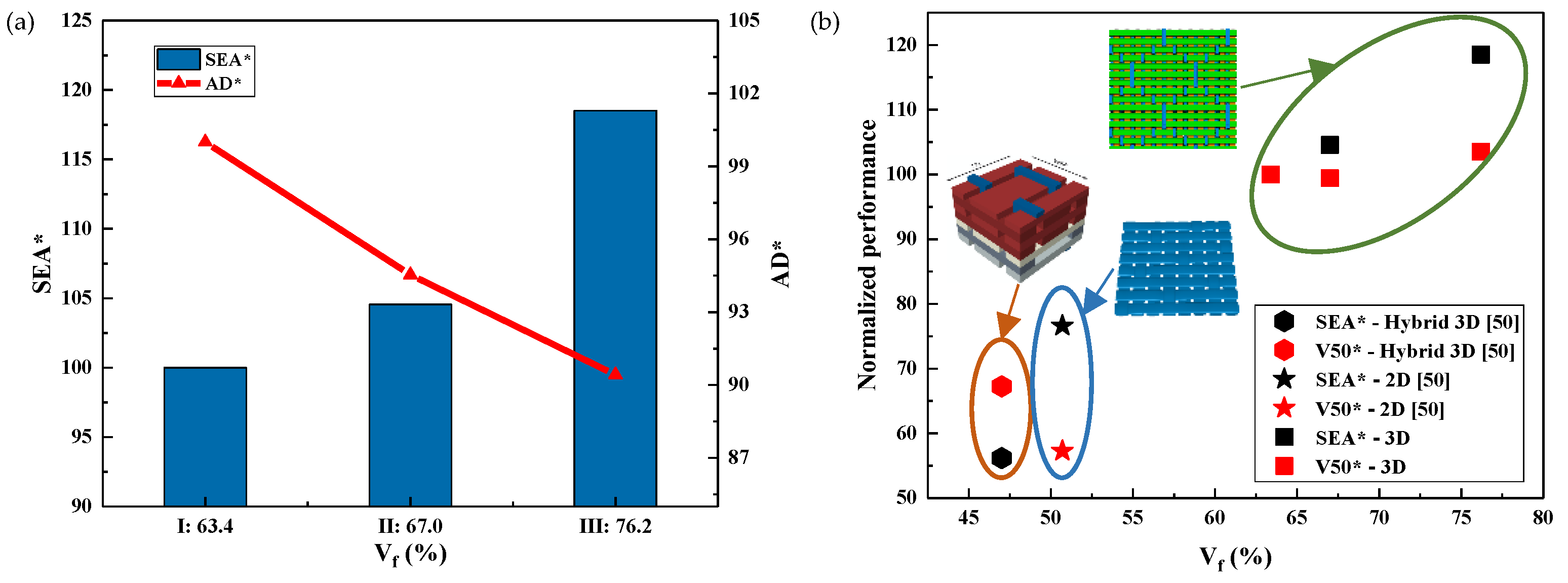
- Vf was the key factor affecting the V50 value of the 3DWCs. The ballistic results showed that when Vf increased from 63.4% to 76.2%, V50 still increased by 3.5% even when the thickness and AD decreased by 17.2% and 19.6%, respectively.
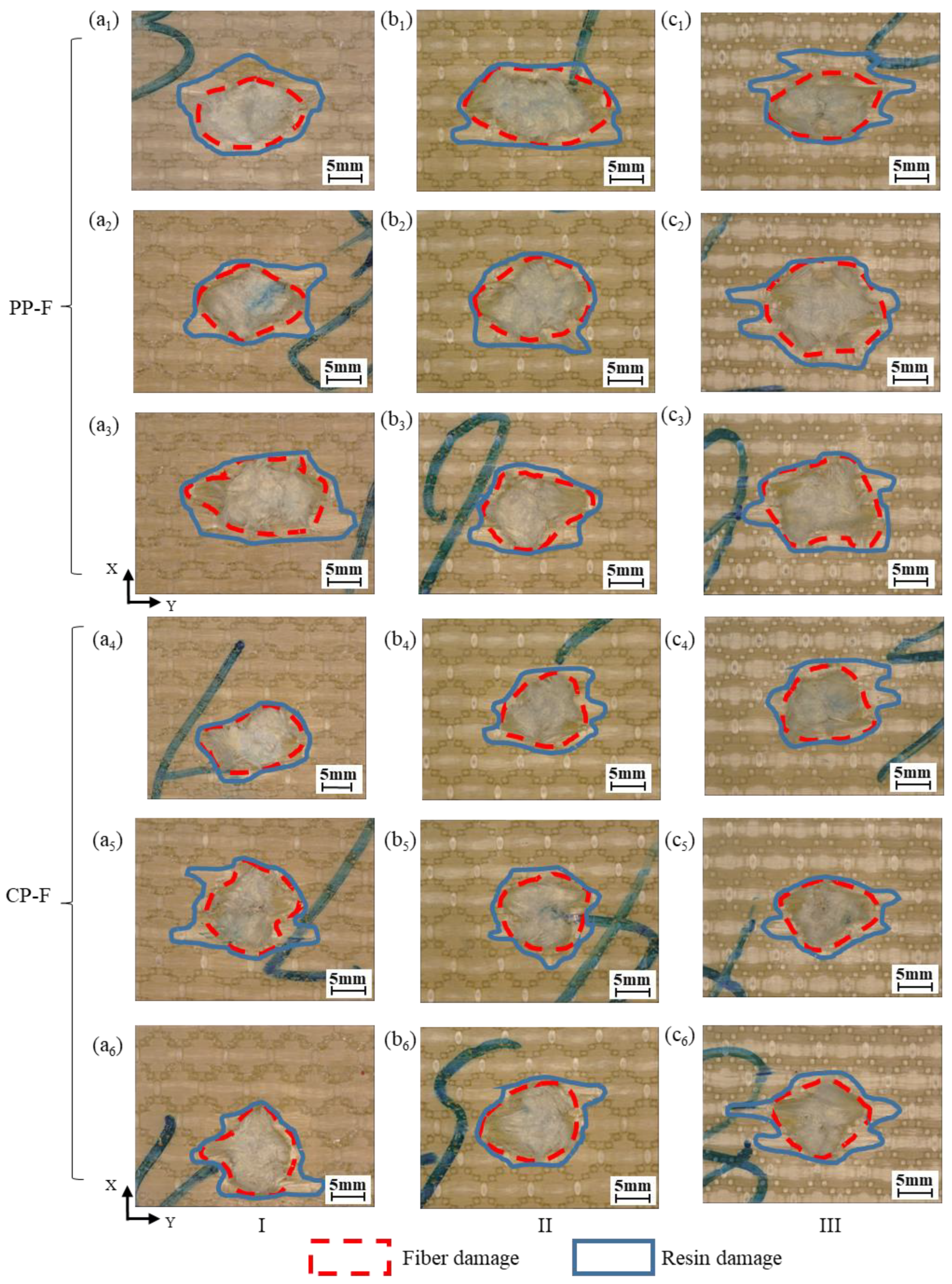
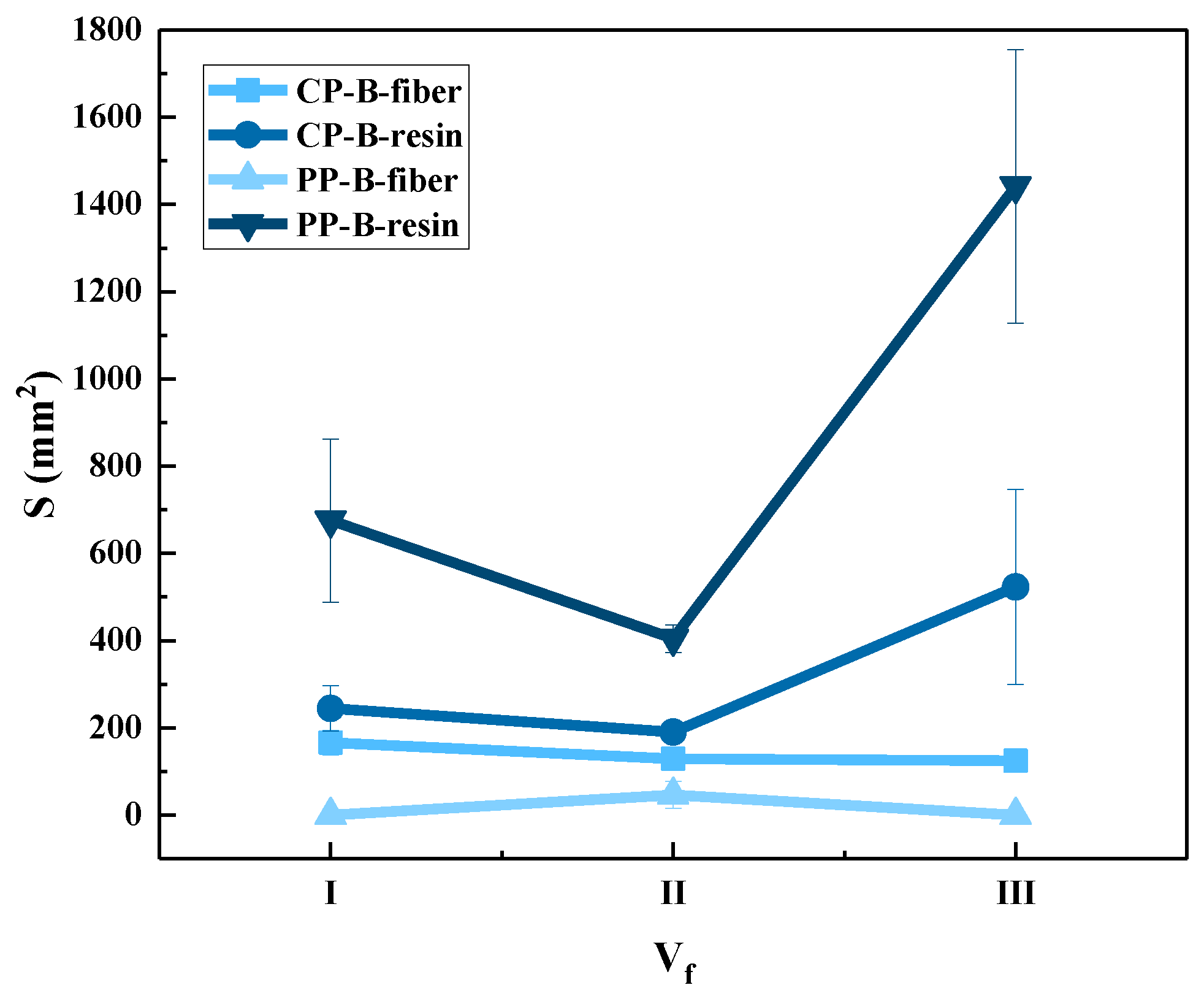
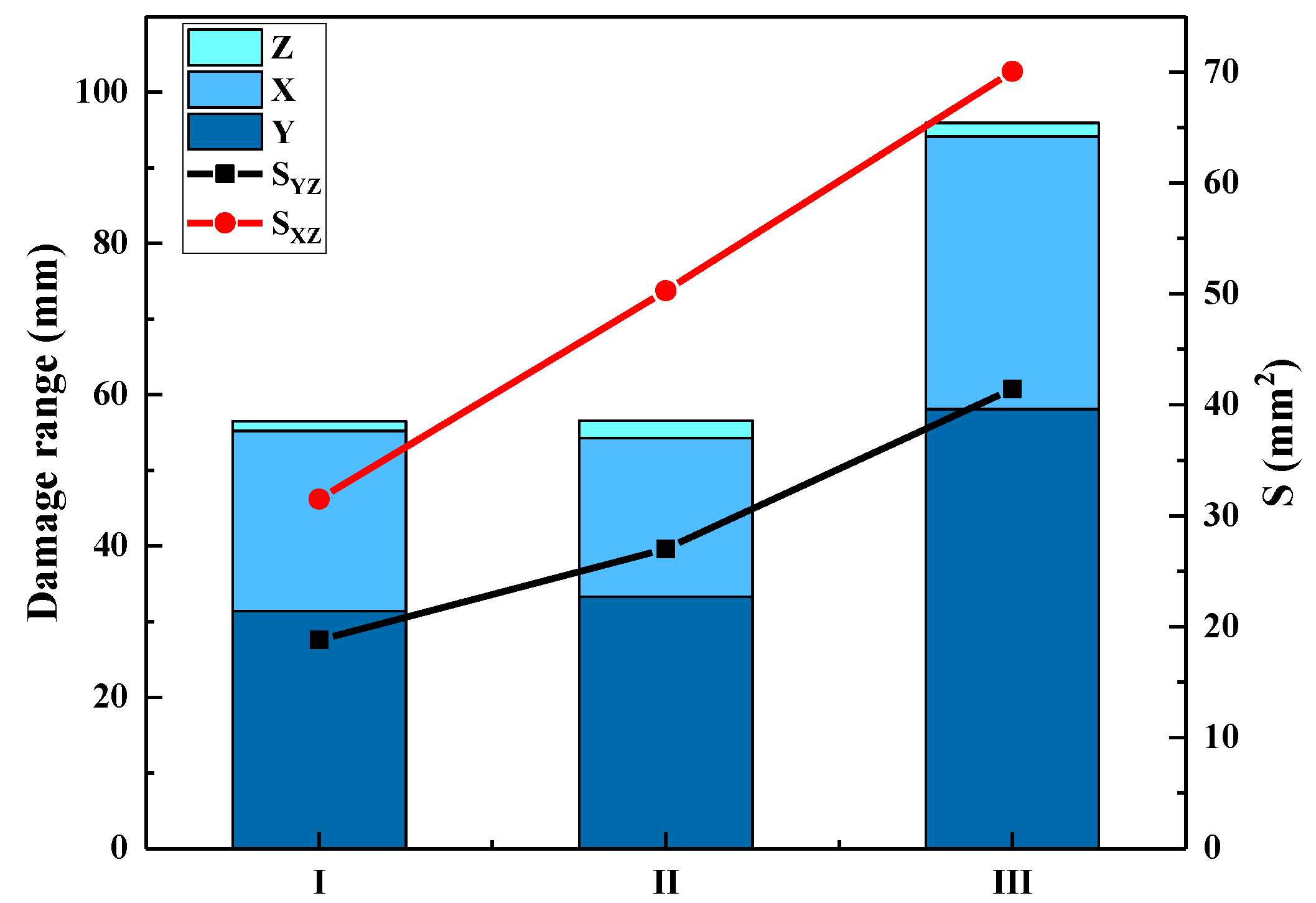
- The fiber and resin damage of the impact surface of the 3DWCs occurred in a small area centered on the shooting point, and the damage area was about 1.5~3 times the area of the projectile. With an increase in Vf, the damage area on the impact surface was slightly increased due to the lower resin content, which weakened the restraint of the resin on the fibers.
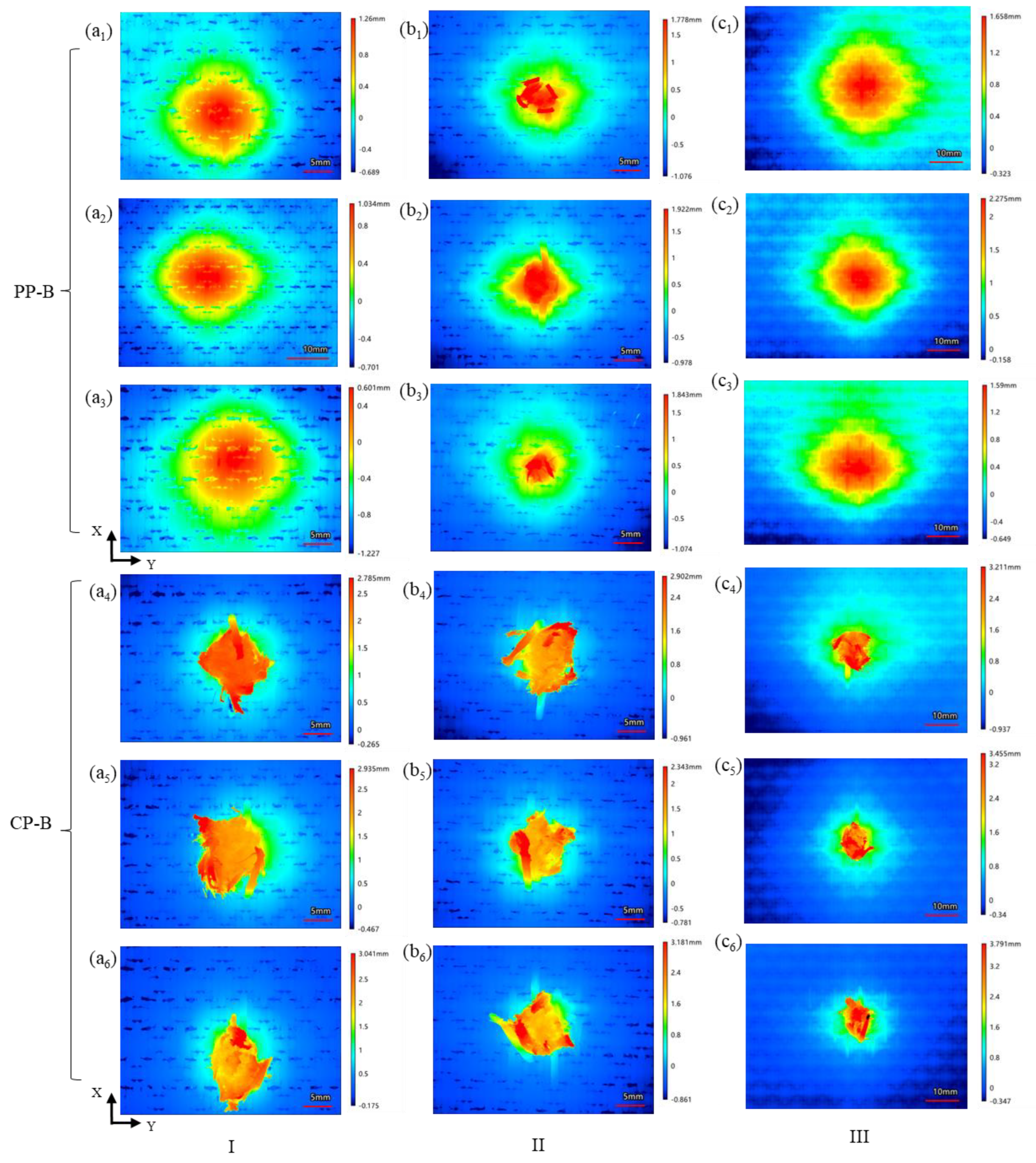
- When Vf was 63.4%, stiffness of the 3DWCs was high and deformation occurred only in a small area. When Vf was increased to 76.2%, the deformation area significantly increased (by 213.4%), more fiber participated in energy dissipation, and SEA and Eh increased by 18.5% and 28.8%, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abtew, M.A.; Boussu, F.; Bruniaux, P.; Liu, H. Fabrication and Mechanical Characterization of Dry Three-Dimensional Warp Interlock Para-Aramid Woven Fabrics: Experimental Methods toward Applications in Composite Reinforcement and Soft Body Armor. Materials 2020, 13, 4233. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.G.; Satapathy, S.S.; Vargas-Gonzalez, L.R.; Walsh, S.M. Ballistic impact response of Ultra-High-Molecular-Weight Polyethylene (UHMWPE). Compos. Struct. 2015, 133, 191–201. [Google Scholar] [CrossRef]
- Karthikeyan, K.; Russell, B.P.; Fleck, N.A.; Wadley, H.N.G.; Deshpande, V.S. The effect of shear strength on the ballistic response of laminated composite plates. Eur. J. Mech.—A/Solids 2013, 42, 35–53. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, X.; Yang, R.; Ye, Z.; Teng, Q. A modified model to predict the ballistic limit of a cubic fragment penetrating Kevlar/titanium fiber metal laminate. Int. J. Impact Eng. 2022, 168, 104292. [Google Scholar] [CrossRef]
- Wang, H.; Hazell, P.J.; Shankar, K.; Morozov, E.V.; Escobedo, J.P. Impact behaviour of Dyneema ® fabric-reinforced composites with different resin matrices. Polym. Test. 2017, 61, 17–26. [Google Scholar] [CrossRef]
- O’Masta, M.R.; Russell, B.P.; Ronan, W. Inter-ply angle influence on the out-of-plane compressive response of polyethylene fibre laminates. Compos. Part A Appl. Sci. Manuf. 2018, 110, 11–20. [Google Scholar] [CrossRef]
- Hu, P.; Yang, H.; Zhang, P.; Wang, W.; Liu, J.; Cheng, Y. Experimental and numerical investigations into the ballistic performance of ultra-high molecular weight polyethylene fiber-reinforced laminates. Compos. Struct. 2022, 290, 115499. [Google Scholar] [CrossRef]
- Zhang, R.; Han, B.; Zhong, J.-Y.; Qiang, L.-S.; Ni, C.-Y.; Zhang, Q.; Zhang, Q.-C.; Li, B.-C.; Lu, T.J. Enhanced ballistic resistance of multilayered cross-ply UHMWPE laminated plates. Int. J. Impact Eng. 2022, 159, 104035. [Google Scholar] [CrossRef]
- Kumar, A.M.; Parameshwaran, R.; Kumar, P.S.; Pal, S.K.; Prasath, M.M.; Krishnaraj, V.; Rajasekar, R. Effects of abaca fiber reinforcement on the dynamic mechanical behavior of vinyl ester composites. Mech. Test. 2017, 59, 555–562. [Google Scholar] [CrossRef]
- Abtew, M.A.; Boussu, F.; Bruniaux, P.; Loghin, C.; Cristian, I. Ballistic impact mechanisms—A review on textiles and fibre-reinforced composites impact responses. Compos. Struct. 2019, 223, 110966. [Google Scholar] [CrossRef]
- Li, Y.; Fan, H.; Gao, X.-L. Ballistic helmets: Recent advances in materials, protection mechanisms, performance, and head injury mitigation. Compos. Part B Eng. 2022, 238, 109890. [Google Scholar] [CrossRef]
- He, Y.; Jiao, Y.; Zhou, J.Q.; Lei, H.; Jia, N.; Chen, L.; Zhang, D. Ballistic response of ultra-high molecular weight polyethylene laminate impacted by mild steel core projectiles. Int. J. Impact Eng. 2022, 169, 104338. [Google Scholar] [CrossRef]
- Hamouda, A.M.S.; Sohaimi, R.M.; Zaidi, A.M.A.; Abdullah, S. Materials and design issues for military helmets. In Advances in Military Textiles and Personal Equipment; Sparks, E., Ed.; Woodhead Publishing: Sawston, UK, 2012; pp. 103–138. [Google Scholar]
- Min, S.; Chen, X.; Chai, Y.; Lowe, T. Effect of reinforcement continuity on the ballistic performance of composites reinforced with multiply plain weave fabric. Compos. Part B Eng. 2016, 90, 30–36. [Google Scholar] [CrossRef]
- Ha-Minh, C.; Boussu, F.; Kanit, T.; Crépin, D.; Imad, A. Analysis on failure mechanisms of an interlock woven fabric under ballistic impact. Eng. Fail. Anal. 2011, 18, 2179–2187. [Google Scholar] [CrossRef]
- Ha-Minh, C.; Boussu, F.; Kanit, T.; Crépin, D.; Imad, A. Effect of Frictions on the Ballistic Performance of a 3D Warp Interlock Fabric: Numerical Analysis. Appl. Compos. Mater. 2011, 19, 333–347. [Google Scholar] [CrossRef]
- Min, S.; Chai, Y.; Chu, Y.; Chen, X. Effect of Panel Construction on the Ballistic Performance of Multiply 3D through-the-Thickness Angle-Interlock fabrIc Reinforced Composites. Polymers 2019, 11, 198. [Google Scholar] [CrossRef]
- Min, S.; Chen, X. Study on the Ballistic Performance of Multiply Wadded Through-the-thickness Angle-interlock Fabric Reinforced Composites. Appl. Compos. Mater. 2021, 29, 263–272. [Google Scholar] [CrossRef]
- Ahmed, S.; Zheng, X.; Yan, L.; Zhang, C.; Wang, X. Influence of asymmetric hybridization on impact response of 3D orthogonal woven composites. Compos. Sci. Technol. 2020, 199, 108326. [Google Scholar] [CrossRef]
- Ha-Minh, C.; Imad, A.; Boussu, F.; Kanit, T. Experimental and numerical investigation of a 3D woven fabric subjected to a ballistic impact. Int. J. Impact Eng. 2016, 88, 91–101. [Google Scholar] [CrossRef]
- Abtew, M.A.; Boussu, F.; Bruniaux, P.; Loghin, C.; Cristian, I. Engineering of 3D warp interlock p-aramid fabric structure and its energy absorption capabilities against ballistic impact for body armour applications. Compos. Struct. 2019, 225, 111179. [Google Scholar] [CrossRef]
- Abtew, M.A.; Bruniaux, P.; Boussu, F.; Loghin, C.; Cristian, I.; Chen, Y.; Wang, L. A systematic pattern generation system for manufacturing customized seamless multi-layer female soft body armour through dome-formation (moulding) techniques using 3D warp interlock fabrics. J. Manuf. Syst. 2018, 49, 61–74. [Google Scholar] [CrossRef]
- Zhang, D.; Sun., Y.; Chen., L.; Zhang., S.; Pan., N. Influence of fabric structure and thickness on the ballistic impact behavior of Ultrahigh molecular weight polyethylene composite laminate. Mater. Des. 2014, 54, 315–322. [Google Scholar] [CrossRef]
- Abtew, M.A.; Boussu, F.; Bruniaux, P.; Hong, Y. Dynamic Impact Surface Damage Analysis of 3D Woven Para-Aramid Armour Panels Using NDI Technique. Polymers 2021, 13, 877. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Wei, Q.; Xin, B.; Chen, X. Research on the creation of TA/LOI compound structure fabric and its ballistic performance for 3D curved-surface ballistic application. Compos. Part B Eng. 2020, 201, 108275. [Google Scholar] [CrossRef]
- Bandaru, A.K.; Ahmad, S.; Bhatnagar, N. Ballistic impact performance of hybrid thermoplastic composite armors reinforced with2D/3D Kevlar and basalt fabrics. Compos. Part A Appl. Sci. Manuf. 2017, 97, 151–165. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Young, R.; Kinloch, I.; Wells, G. A numerical study of ply orientation on ballistic impact resistance of multi-ply fabric panels. Compos. Part B Eng. 2015, 68, 259–265. [Google Scholar] [CrossRef]
- Goda, I.; Girardot, J. A computational framework for energy absorption and damage assessment of laminated composites under ballistic impact and new insights into target parameters. Aerosp. Sci. Technol. 2021, 115, 106835. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, Y.; Wells, G. Numerical and experimental investigations into ballistic performance of hybrid fabric panels. Compos. Part B Eng. 2014, 58, 35–42. [Google Scholar] [CrossRef]
- Bandaru, A.K.; Vetiyatil, L.; Ahmad, S. The effect of hybridization on the ballistic impact behavior of hybrid composite armors. Compos. Part B Eng. 2015, 76, 300–319. [Google Scholar] [CrossRef]
- Mousavi, M.V.; Khoramishad, H. Investigation of energy absorption in hybridized fiber-reinforced polymer composites under high-velocity impact loading. Int. J. Impact Eng. 2020, 146, 103692. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, X. Study of energy absorption and failure modes of constituent layers in body armour panels. Compos. Part B Eng. 2016, 98, 250–259. [Google Scholar] [CrossRef]
- Nilakantan, G.; Gillespie, J.W. Ballistic impact modeling of woven fabrics considering yarn strength, friction, projectile impact location, and fabric boundary condition effects. Compos. Struct. 2012, 94, 3624–3634. [Google Scholar] [CrossRef]
- Liu, B.G.; Wadley, H.N.G.; Deshpande, V.S. Failure mechanism maps for ultra-high molecular weight polyethylene fibre composite beams impacted by blunt projectiles. Int. J. Solids Struct. 2019, 178, 180–198. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, F.; Wells, G. An analytical model for ballistic impact on textile based body armour. Compos. Part B Eng. 2013, 45, 1508–1514. [Google Scholar] [CrossRef]
- Mamivand, M.; Liaghat, G.H. A model for ballistic impact on multi-layer fabric targets. Int. J. Impact Eng. 2010, 37, 806–812. [Google Scholar] [CrossRef]
- Chocron, S.; Figueroa, E.; King, N.; Kirchdoerfer, T.; Nicholls, A.E.; Sagebiel, E.; Weiss, C.; Freitas, C.J. Modeling and validation of full fabric targets under ballistic impact. Compos. Sci. Technol. 2010, 70, 2012–2022. [Google Scholar] [CrossRef]
- Rodriguez-Millan, M.; Ito, T.; Loya, J.A.; Olmedo, A.; Miguelez, M.H. Development of numerical model for ballistic resistance evaluation of combat helmet and experimental validation. Mater. Des. 2016, 110, 391–403. [Google Scholar] [CrossRef]
- Ramakrishnan, S.; Krishnamurthy, K.; Prasath, M.M.; Kumar, R.S.; Dharmaraj, M.; Gowthaman, K.; Kumar, P.S.; Rajasekar, R. Theoretical Prediction on the Mechanical Behavior of Natural Fiber Reinforced Vinyl Ester Composites. Appl. Sci. Adv. Mater. Int. 2015, 1, 85–92. [Google Scholar]
- Tripathi, L.; Chowdhury, S.; Behera, B.K. Modeling and simulation of impact behavior of 3D woven solid structure for ballistic application. J. Ind. Text. 2020, 51, 6065S–6086S. [Google Scholar] [CrossRef]
- Wei, Q.; Gu, B.; Sun, B. Ballistic penetration damages and energy absorptions of stacked cross-plied composite fabrics and laminated panels. Int. J. Damage Mech. 2020, 29, 1465–1484. [Google Scholar] [CrossRef]
- Luan, K.; Sun, B.; Gu, B. Ballistic impact damages of 3-D angle-interlock woven composites based on high strain rate constitutive equation of fiber tows. Int. J. Impact Eng. 2013, 57, 145–158. [Google Scholar] [CrossRef]
- Tong, L.; Mouritz, A.P.; Bannister, M.K. 3D Fibre Reinforced Polymer Composites; Elsevier: Amsterdam, The Netherlands, 2002; pp. 13–46. [Google Scholar]
- Ma, P.; Jin, L.; Wu, L. Experimental and numerical comparisons of ballistic impact behaviors between 3D angle-interlock woven fabric and its reinforced composite. J. Ind. Text. 2018, 48, 1044–1058. [Google Scholar] [CrossRef]
- Dong, F.; Yuan, Q.; Liu, J.; Qian, K.; Sun, J.; Zhang, D. Impact behaviors and damage mechanisms of 2.5D woven composites: Experiment and simulation. J. Ind. Text. 2022, 52, 15280837221114631. [Google Scholar] [CrossRef]
- Zahid, B.; Chen, X. Properties of 5-layer angle-interlock Kevlar-based composite structure manufactured from vacuum bagging. J. Compos. Mater. 2012, 47, 3227–3234. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, Q.; Chen, X.; Xie, J.; Chen, L. Effect of apertures on tensile property of warp-reinforced 2.5D woven composites notched plates. Compos. Struct. 2020, 252, 112693. [Google Scholar] [CrossRef]
- Huang, L. Determining Micro- and Macro- Geometry of Fabric and Fabric Reinforced Composites; Kansas State University: Manhattan, KS, USA, 2013. [Google Scholar]
- GJB 4300A-2012; Requirements of Safety Technical Performance for Military Body Armor. GJB Professional Standard-Military: Beijing, China, 2012.
- Muñoz, R.; Martínez-Hergueta, F.; Gálvez, F.; González, C.; Llorca, J. Ballistic performance of hybrid 3D woven composites: Experiments and simulations. Compos. Struct. 2015, 127, 141–151. [Google Scholar] [CrossRef]
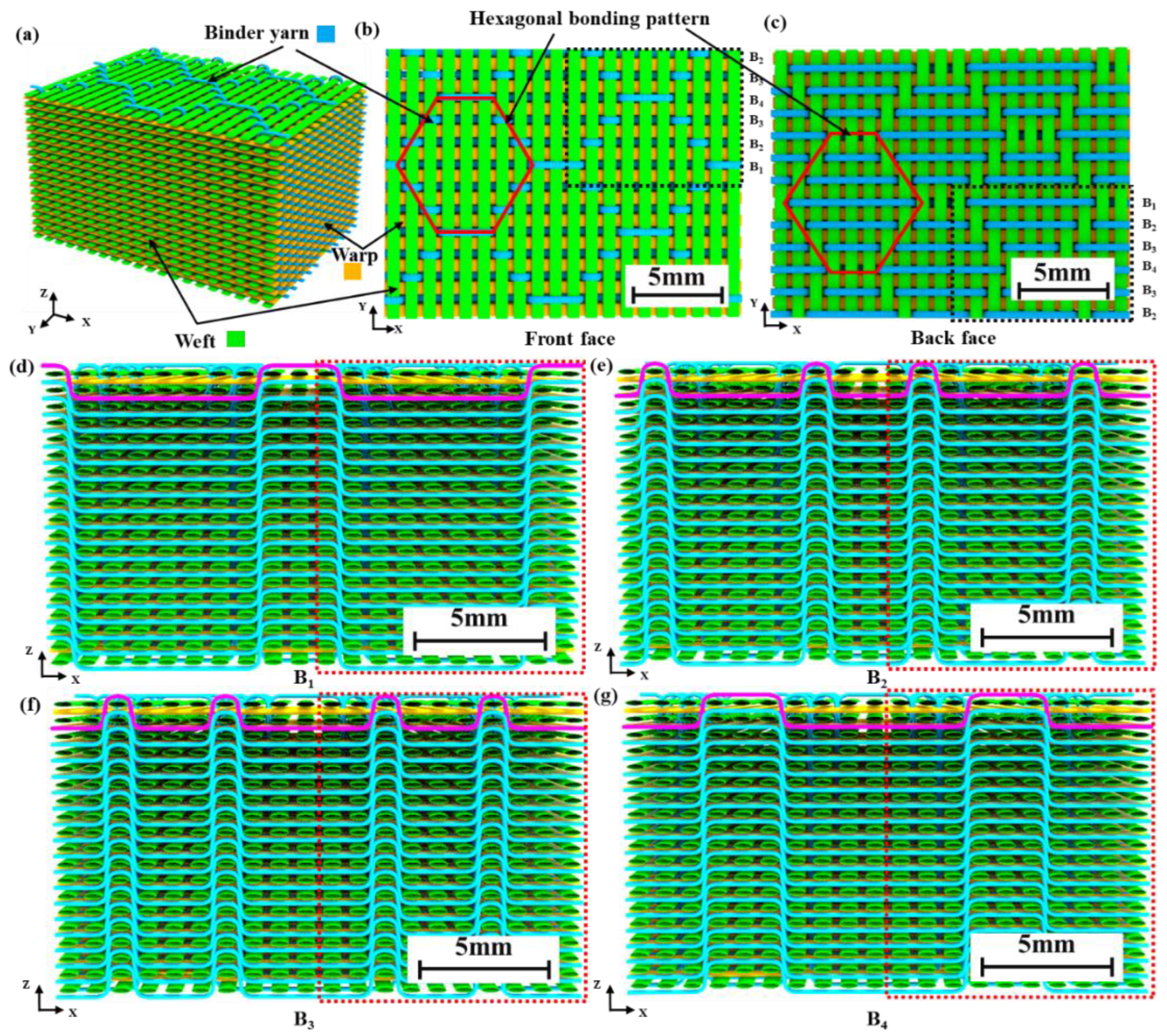
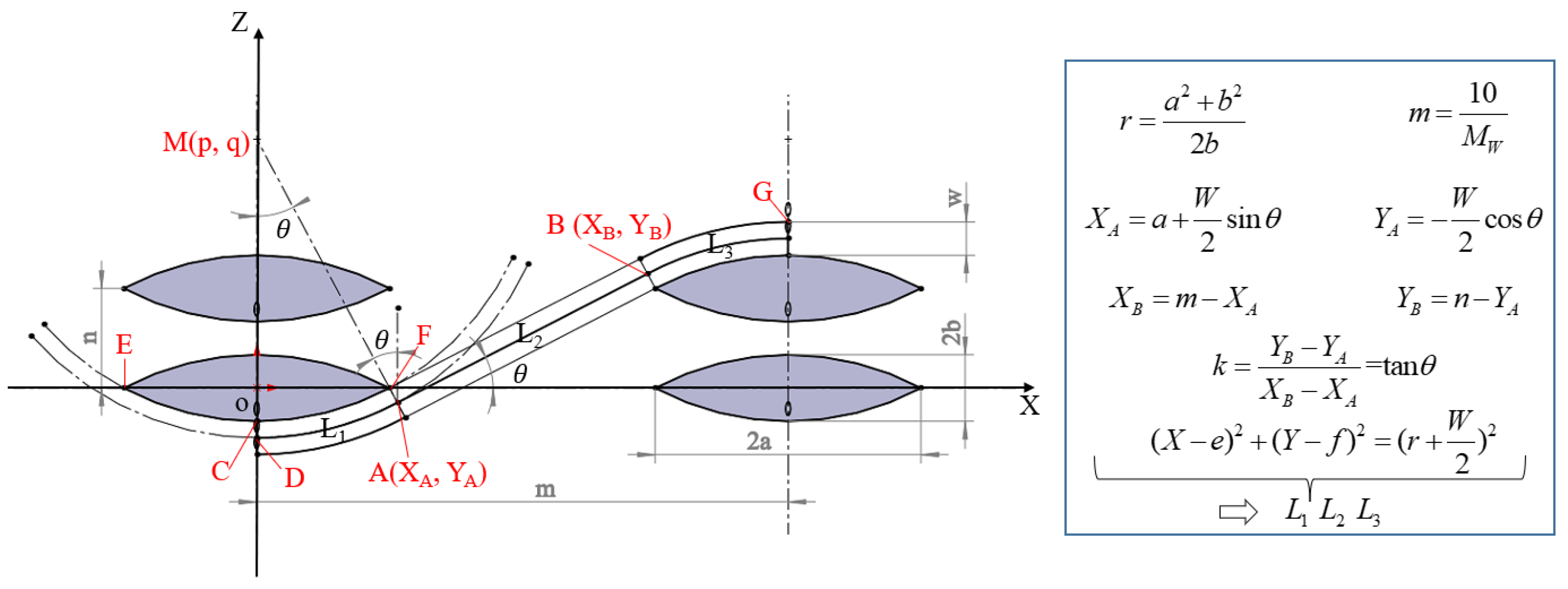
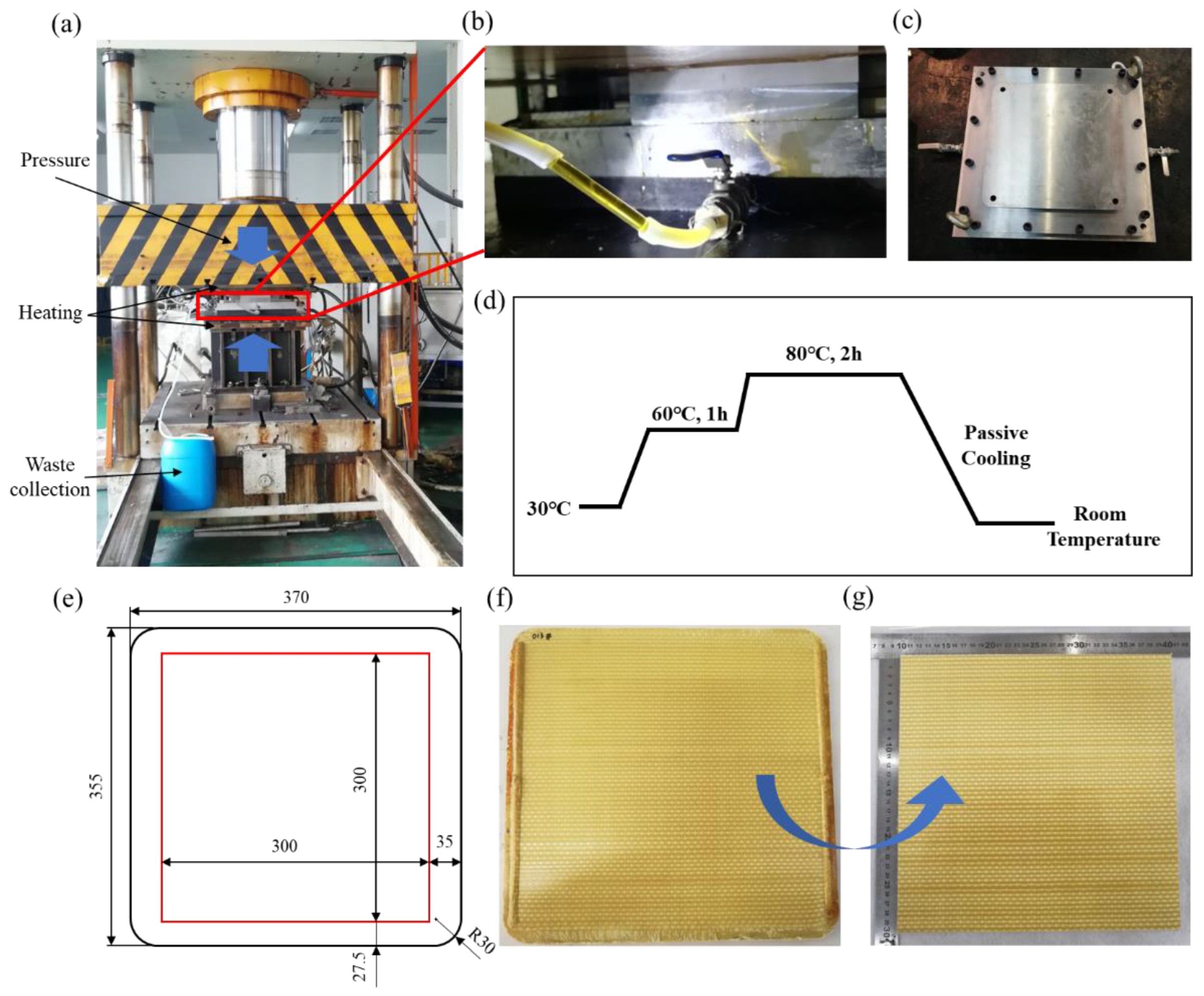
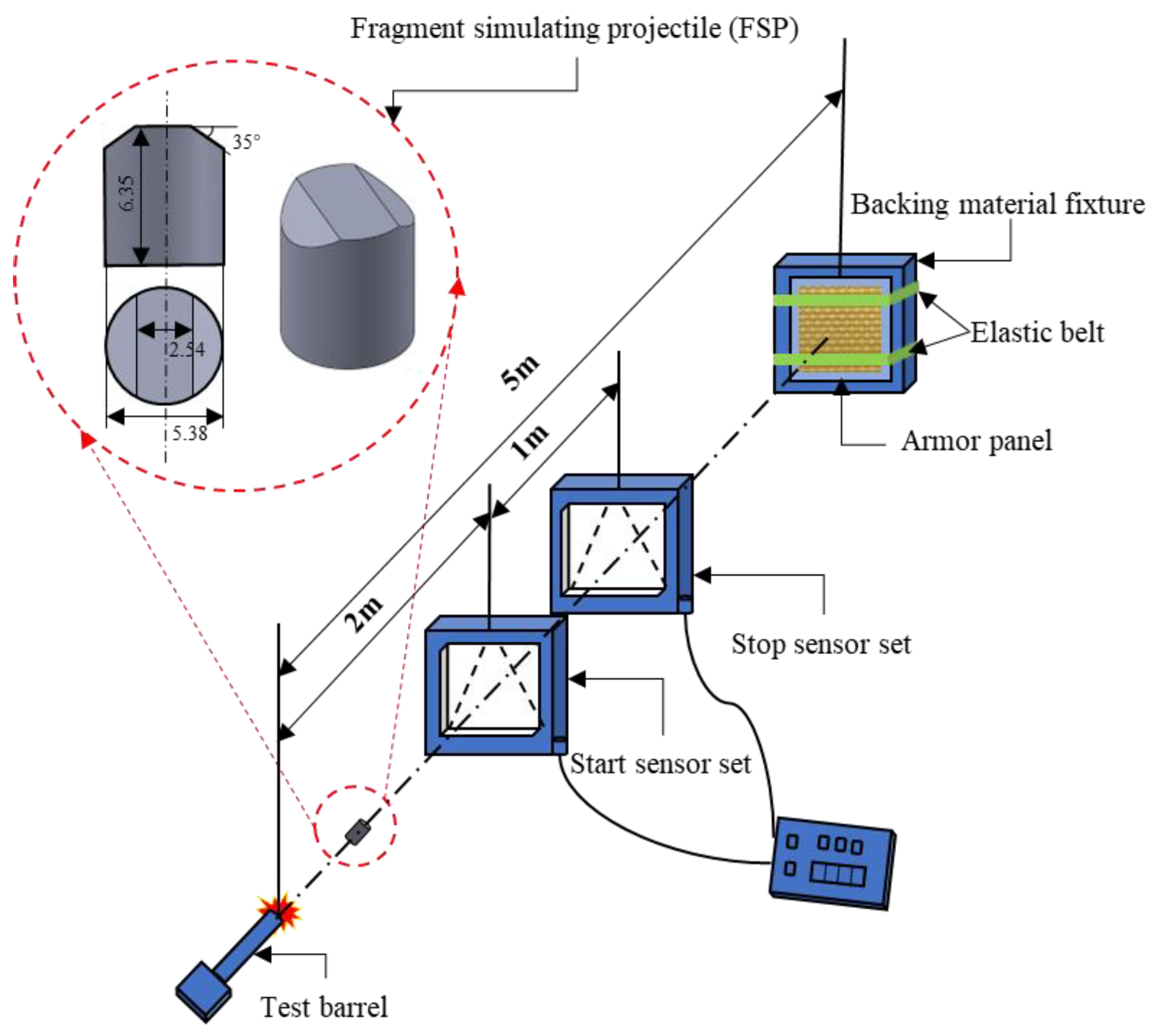




| Parameter | Value |
|---|---|
| Number of warp yarn layers | 18 |
| Number of weft yarn layers | 19 |
| Number of binder yarn layers | 18 |
| Warp yarn density per layer (ends/cm) | 8 |
| Weft yarn density per layer (picks/cm) | 10 |
| Binder yarn density per layer (ends/cm) | 8 |
| Warp yarn linear density (dtex) | 1100 × 2 |
| Weft yarn linear density (dtex) | 1100 × 2 |
| Binder yarn linear density (dtex) | 1100 |
| h (mm) | 12.4 |
| Materials | Density(g/cm3) | Young’s Modulus (GPa) | Tensile Strength (GPa) | Elongation at Break (%) |
|---|---|---|---|---|
| Tcparan® yarns | 1.44 | 97 | 3.425 | 3.75 |
| PU | 1.20 | 3.4 | 0.085 | >5 |
| Sample | AD (kg/m2) | Vf (%) | Mf (%) | H (mm) |
|---|---|---|---|---|
| I | 12.5 | 63.4 | 72.7 | 9.9 |
| II | 11.8 | 67.0 | 76.9 | 9.3 |
| III | 11.3 | 76.2 | 80.4 | 8.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, X.; Sun, Y.; Xu, J.; Chen, L.; Zhang, C.; Zhang, G. Effect of Fiber Fraction on Ballistic Impact Behavior of 3D Woven Composites. Polymers 2023, 15, 1170. https://doi.org/10.3390/polym15051170
Shi X, Sun Y, Xu J, Chen L, Zhang C, Zhang G. Effect of Fiber Fraction on Ballistic Impact Behavior of 3D Woven Composites. Polymers. 2023; 15(5):1170. https://doi.org/10.3390/polym15051170
Chicago/Turabian StyleShi, Xiaoping, Ying Sun, Jing Xu, Li Chen, Ce Zhang, and Guoli Zhang. 2023. "Effect of Fiber Fraction on Ballistic Impact Behavior of 3D Woven Composites" Polymers 15, no. 5: 1170. https://doi.org/10.3390/polym15051170
APA StyleShi, X., Sun, Y., Xu, J., Chen, L., Zhang, C., & Zhang, G. (2023). Effect of Fiber Fraction on Ballistic Impact Behavior of 3D Woven Composites. Polymers, 15(5), 1170. https://doi.org/10.3390/polym15051170





