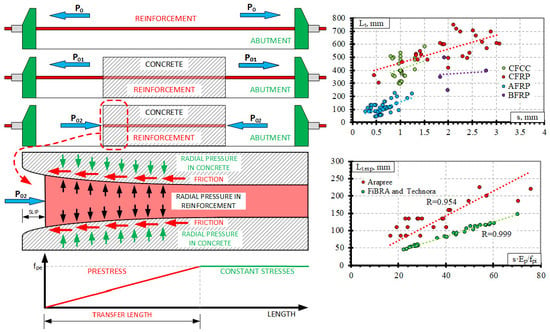
Transfer Length vs. Slip of Prestressed Fiber-Reinforced Polymer Reinforcement
Abstract
:1. Introduction
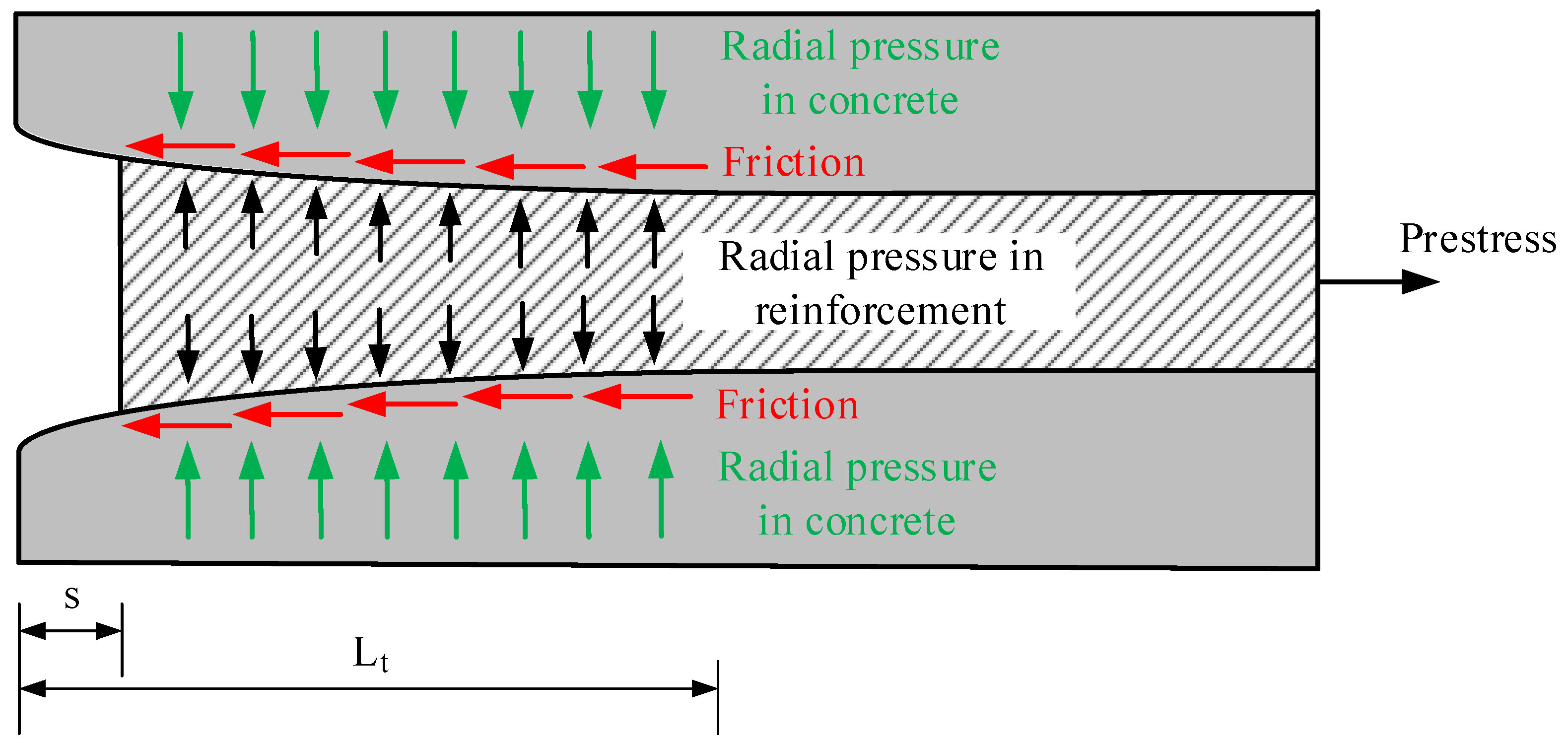
2. Methods of Measuring Transfer Length
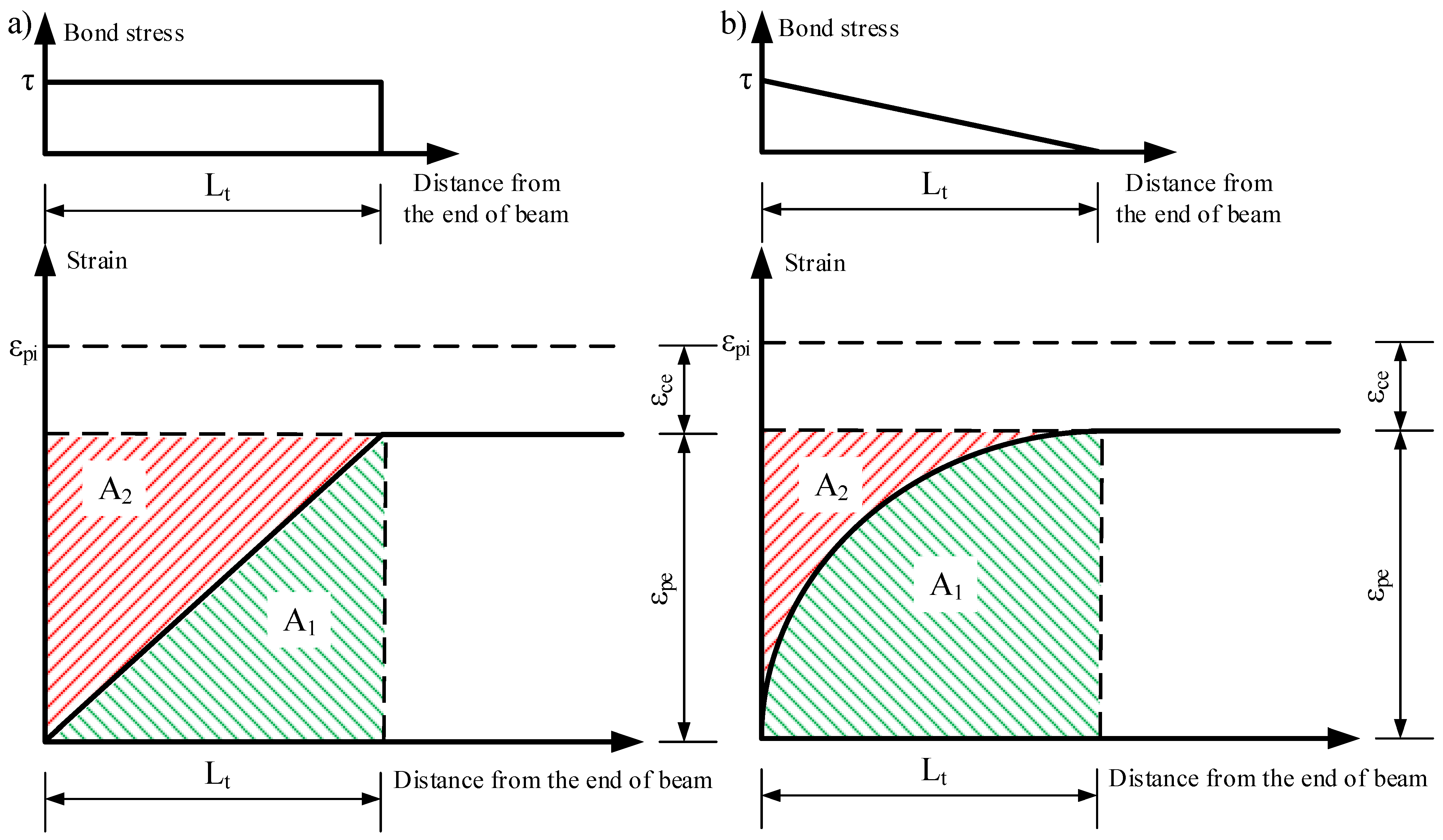
3. Theoretical Models
| Reference | Equation | Equation No. | Notes |
|---|---|---|---|
| [36] | (1) | α—bond shape factor s—end slip Ep—modulus of elasticity of the prestressing reinforcement fpi—reinforcement stress immediately before release | |
| [37] | (2) | s—end slip fpi—reinforcement stress immediately before release Ep—modulus of elasticity of the prestressing reinforcement | |
| [38] | (3) | s—end slip fpi—reinforcement stress immediately before release Ep—modulus of elasticity of the prestressing reinforcement | |
| [40] | (4) | s—end slip Ø—reinforcement diameter fci—concrete compressive strength at transfer | |
| [39] | (5) | s—end slip fci—concrete compressive strength at transfer fpi—reinforcement stress immediately before release Ep—modulus of elasticity of the prestressing reinforcement | |
| [41] | (6) | s—end slip K = 0.0000035 mm−1 for 12.7 mm 7-wire strand |
4. Results
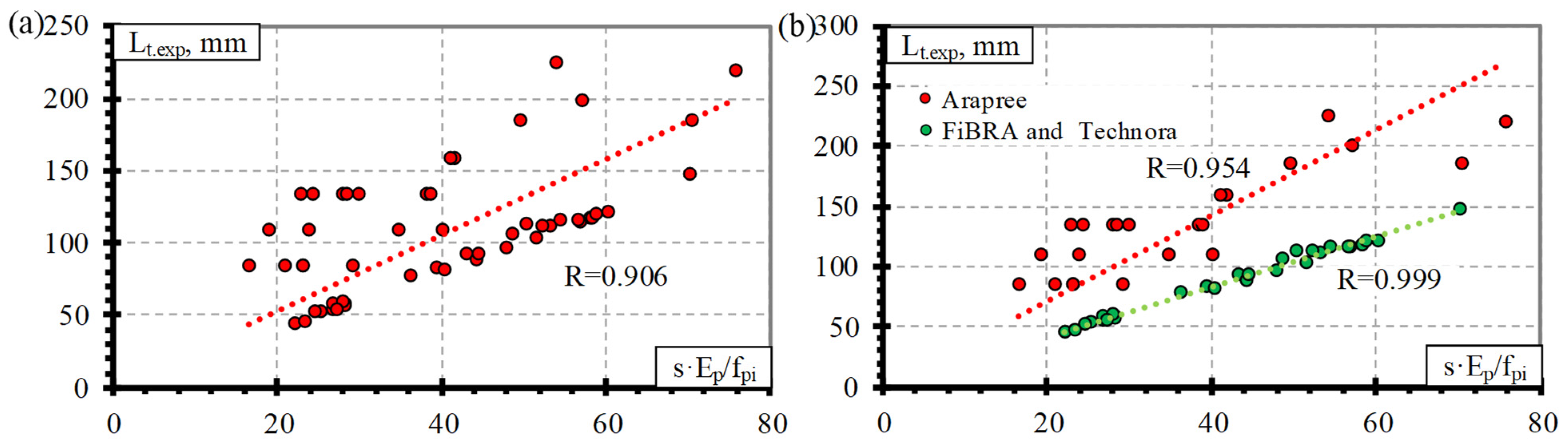
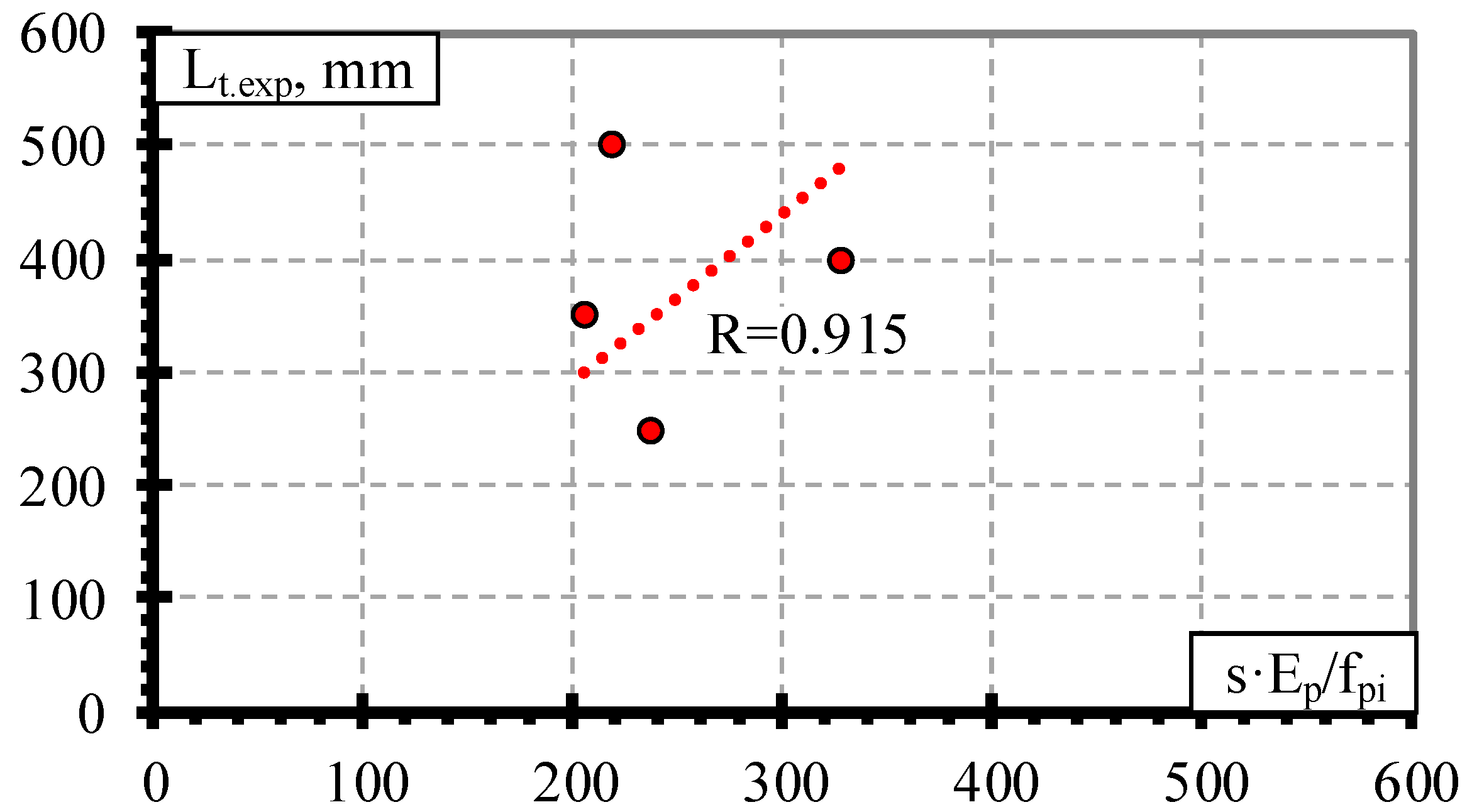
4.1. Results of Database of Transfer Length versus Slip
4.2. Analysis of Experimental Results
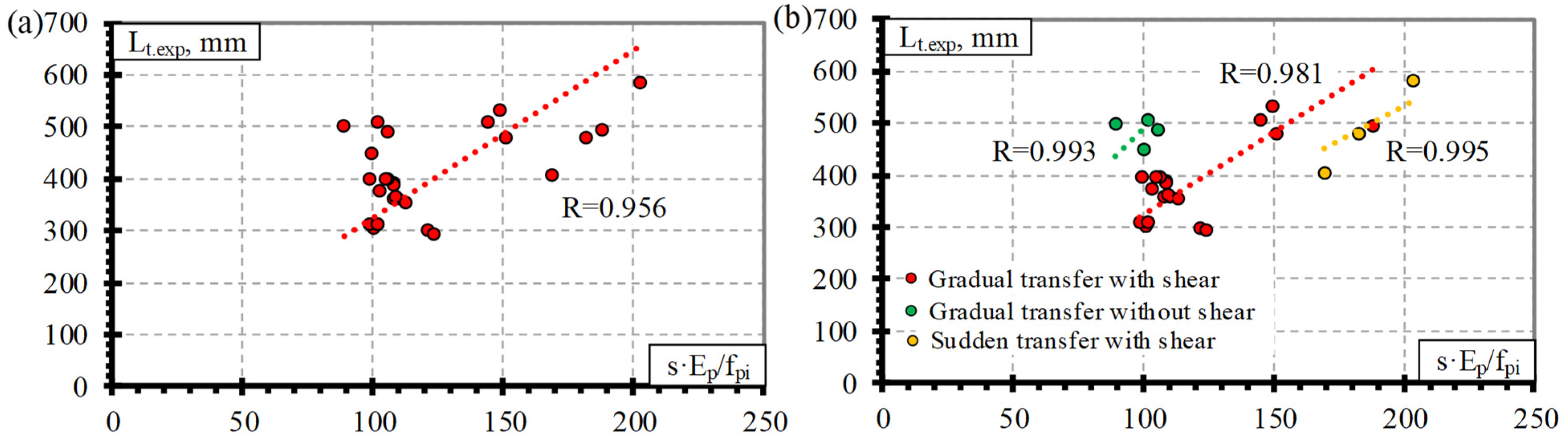
4.3. Derivation of Theoretical Coefficients
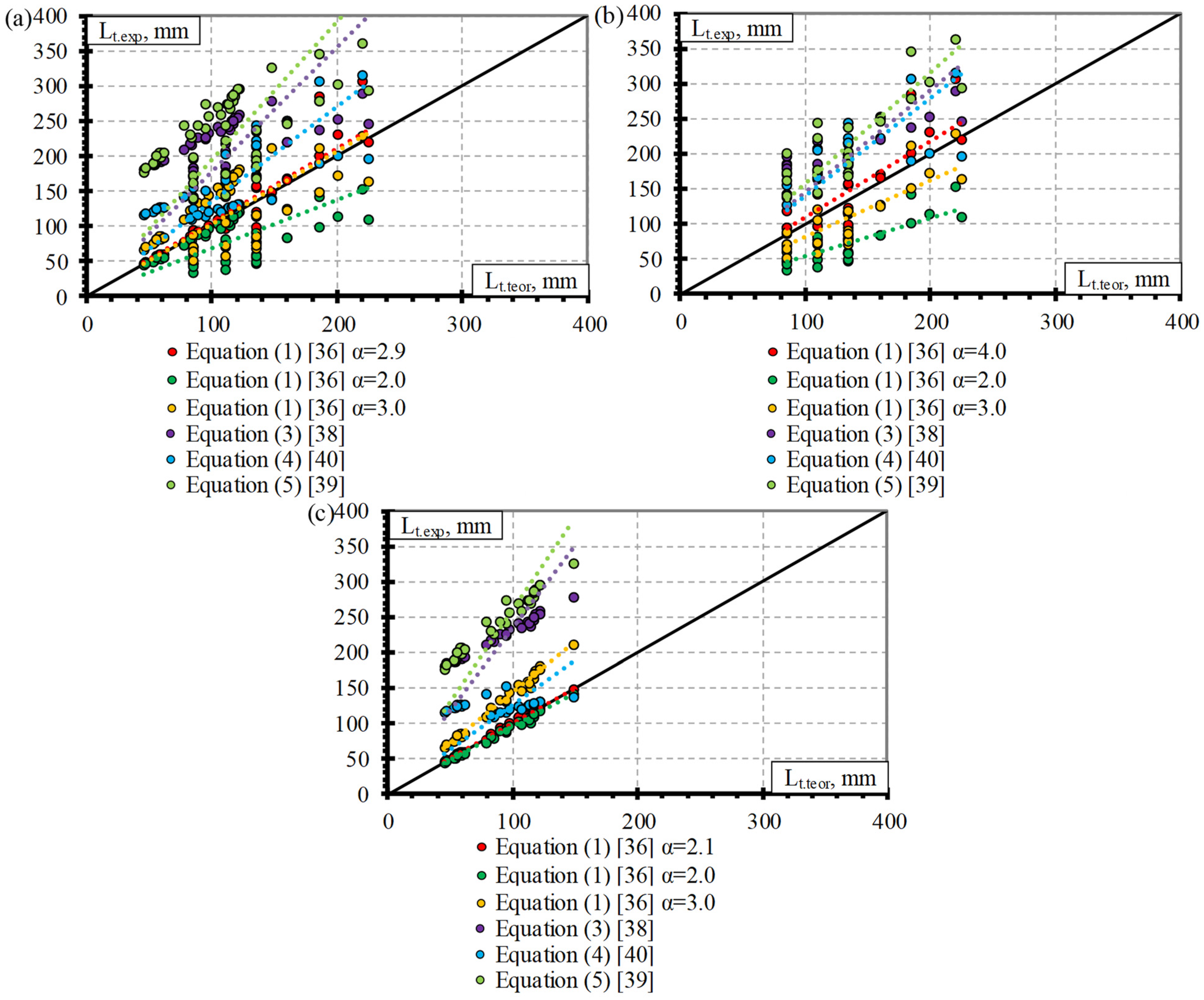
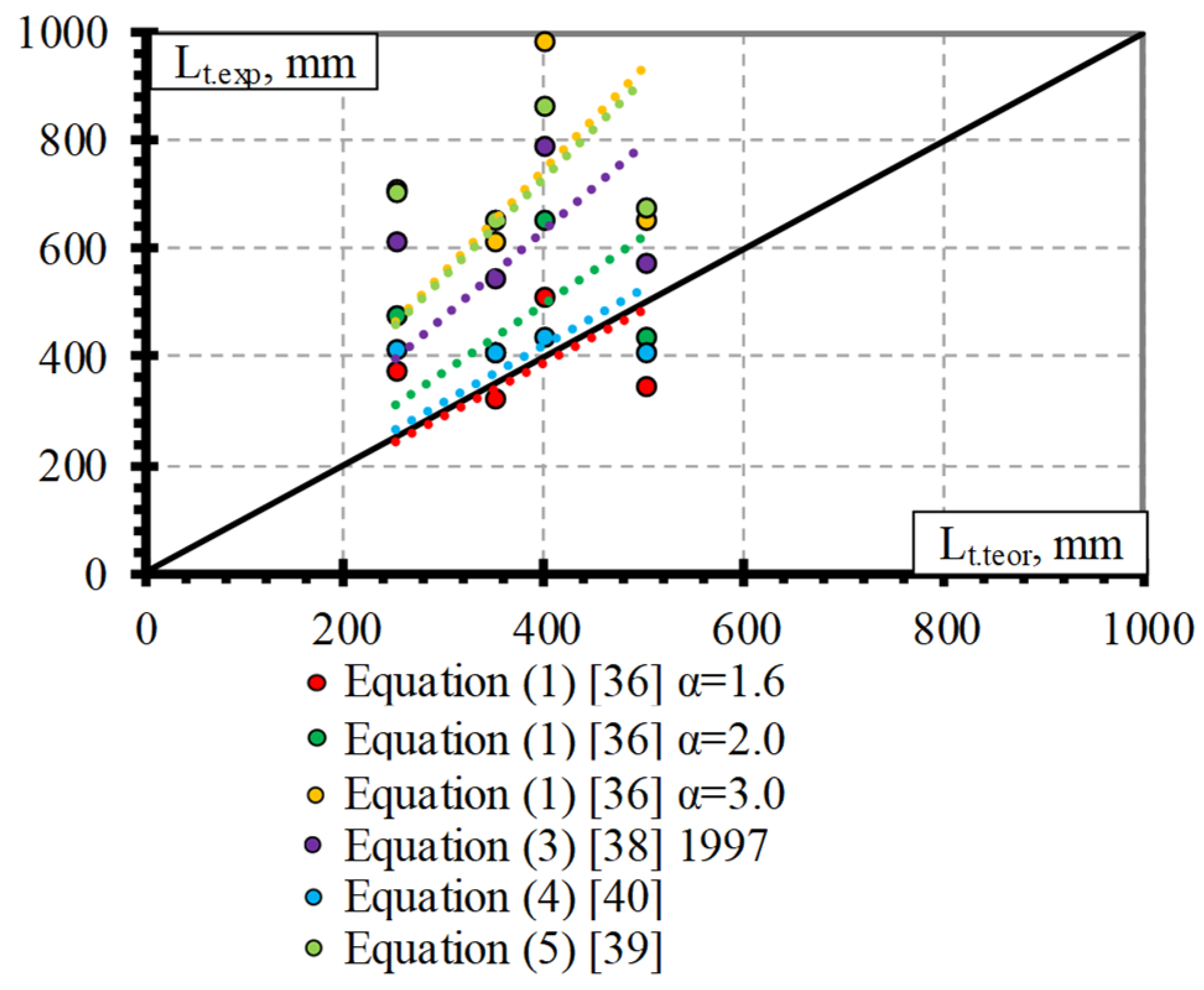
4.4. Comparison of Experimental and Theoretical Results
5. Conclusions
- From the review of methods for the determination of the transfer length of prestressed reinforcement, it is evident that each of the methods has advantages and disadvantages. The most accurate method to determine the transfer length of prestressed reinforcement is to measure the strains within the reinforcement. The most unreliable method is to measure the strains on the surface of reinforcement. However, the easiest and most straightforward method with sufficient accuracy is related to the slip of reinforcement;
- After the analysis of the results of a larger database, new bond shape factors α were proposed for the relationship between the transfer length and the slip of different FRP reinforcements. The proposed value for the CFCC strands is α = 3.5 (for concrete strength of 23–48 MPa, prestress level 0.49–0.81%, and reinforcement diameter 10.5–15.2 mm) and for CFRP bars is α = 2.5 (for concrete strength of 26–50.7 MPa, prestress level 0.33–0.86%, and reinforcement diameter 7.9–12.7 mm).
- It was determined that there is a correlation between the type of reinforcement (surface conditions) and the transfer length of the AFRP bars. Therefore, new values of α are proposed: α = 2.1 for AFRP FiBRA and Technora bars (for concrete strength of 56–58 MPa, prestress level 0.59–0.67%, and reinforcement diameter 3.7–4.0 mm) and α = 4.0 for AFRP Arapree bars (for concrete strength of 56.4–81.5 MPa, prestress level 0.50%, and reinforcement diameter 5.3–7.5 mm);
- The comparison of experimental and theoretical results showed that the theoretical models derived for steel strands in some cases can predict the transfer length of FRP reinforcement. However, different models showed a close prediction of the experimental results of different types of FRP reinforcement with no consistency. Therefore, Equations (3)–(5) are not sufficiently adequate to predict the transfer length of pretensioned FRP reinforcement;
- Equation (1) gives the most accurate prediction of the transfer length of different FRP reinforcements with the proposed bond shape factors α. Therefore, it can be applied not only to steel strands but also to prestressed FRP reinforcement with sufficient accuracy;
- Analysis of the relationship between transfer length and slip of FRP reinforcement during transfer together with the proposed new values of bond shape factor α provides possibilities to adopt the slippage monitoring method in the production and quality control of precast and prestressed concrete structures and perform additional research to increase the understanding of the transfer length of FRP reinforcement. In particular, more attention should be given to the release type of prestressed FRP reinforcement. Furthermore, the influence of the surface conditions of AFRP and CFRP reinforcement should be analyzed. The database should be increased with a wider range of initial variables (fci, fpi/fpu, Ø, c) for the transfer length of different types of AFRP reinforcement. Furthermore, additional research on the transfer length of BFRP reinforcement should be performed by analyzing the influence of the prestress transfer method, different surface conditions, and other important parameters (fci, fpi/fpu, c).
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Reference | Specimen No | FRP Type | FRP Surface | Specimen Type | Release Type | Shear Reinforcement | Specimen Dimensions (b × h × l, mm) | c, mm | Ø, mm | Ap, mm2 | Ep, GPa | fpu, MPa | fpi, MPa | fpi/fpu | fci, MPa | Lt, mm | Slip, mm |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [12,15] | BT11 | CFCC 7-wire Strand | Helical plain | Beam | Gradual | Yes | 80 × 250 × 1380 | 45.0 | 10.5 | 55.7 | 140 | 1725 | 1400 | 0.81 | 29.0 | 305.0 | 1.01 |
| BT12 | Beam | Gradual | Yes | 80 × 250 × 1381 | 45.0 | 10.5 | 55.7 | 140 | 1725 | 1400 | 0.81 | 29.0 | 312.5 | 0.99 | |||
| BT13 | Beam | Gradual | Yes | 80 × 250 × 1382 | 45.0 | 10.5 | 55.7 | 140 | 1725 | 1400 | 0.81 | 29.0 | 312.5 | 1.02 | |||
| BT14 | Beam | Gradual | Yes | 80×250×1383 | 45.0 | 10.5 | 55.7 | 140 | 1725 | 1400 | 0.81 | 29.0 | 312.5 | 1.02 | |||
| BT7 | Beam | Gradual | Yes | 100×250×1380 | 50.0 | 12.5 | 76.0 | 141 | 1868 | 1408 | 0.75 | 28.0 | 400.0 | 0.99 | |||
| BT8 | Beam | Gradual | Yes | 100 × 250 × 1381 | 50.0 | 12.5 | 76.0 | 141 | 1868 | 1408 | 0.75 | 28.0 | 375.0 | 1.03 | |||
| BT9 | Beam | Gradual | Yes | 100 × 250 × 1382 | 50.0 | 12.5 | 76.0 | 141 | 1868 | 1408 | 0.75 | 28.0 | 360.0 | 1.08 | |||
| BT10 | Beam | Gradual | Yes | 100 × 250 × 1383 | 50.0 | 12.5 | 76.0 | 141 | 1868 | 1408 | 0.75 | 28.0 | 360.0 | 1.1 | |||
| BT15 | Beam | Gradual | Yes | 100 × 250 × 2750 | 50.0 | 12.5 | 76.0 | 141 | 1868 | 1125 | 0.60 | 30.0 | 300.0 | 0.97 | |||
| BT16 | Beam | Gradual | Yes | 100 × 250 × 2751 | 50.0 | 12.5 | 76.0 | 141 | 1868 | 1125 | 0.60 | 30.0 | 295.0 | 0.99 | |||
| BT19 | Beam | Gradual | No | 175 × 250 × 2750 | 50.0 | 12.5 | 76.0 | 141 | 1868 | 1355 | 0.73 | 23.0 | 500.0 | 0.86 | |||
| BT20 | Beam | Gradual | No | 175×250×2750 | 50.0 | 12.5 | 76.0 | 141 | 1868 | 1355 | 0.73 | 23.0 | 450.0 | 0.96 | |||
| BT1 | Beam | Gradual | Yes | 120 × 300 × 1720 | 60.0 | 15.2 | 113.6 | 138 | 1750 | 1074 | 0.61 | 35.0 | 365.0 | 0.85 | |||
| BT2 | Beam | Gradual | Yes | 120 × 300 × 1720 | 60.0 | 15.2 | 113.6 | 138 | 1750 | 1074 | 0.61 | 35.0 | 355.0 | 0.88 | |||
| BT3 | Beam | Gradual | Yes | 120 × 300 × 1720 | 60.0 | 15.2 | 113.6 | 138 | 1750 | 1312 | 0.75 | 31.0 | 392.5 | 1.03 | |||
| BT4 | Beam | Gradual | Yes | 120 × 300 × 1721 | 60.0 | 15.2 | 113.6 | 138 | 1750 | 1312 | 0.75 | 31.0 | 387.5 | 1.03 | |||
| BT5 | Beam | Gradual | Yes | 120 × 300 × 1722 | 60.0 | 15.2 | 113.6 | 138 | 1750 | 1312 | 0.75 | 31.0 | 400.0 | 1.01 | |||
| BT6 | Beam | Gradual | Yes | 120 × 300 × 1723 | 60.0 | 15.2 | 113.6 | 138 | 1750 | 1312 | 0.75 | 31.0 | 400.0 | 1 | |||
| BT17 | Beam | Gradual | No | 200 × 300 × 3500 | 60.0 | 15.2 | 113.6 | 138 | 1750 | 1294 | 0.74 | 22.0 | 650.0 | 0.82 | |||
| BT18 | Beam | Gradual | No | 200 × 300 × 3500 | 60.0 | 15.2 | 113.6 | 138 | 1750 | 1294 | 0.74 | 22.0 | 600.0 | 0.89 | |||
| BT21 | Beam | Gradual | No | 175 × 300 × 3500 | 60.0 | 15.2 | 113.6 | 138 | 1750 | 1083 | 0.62 | 24.0 | 510.0 | 0.8 | |||
| BT22 | Beam | Gradual | No | 175 × 300 × 3500 | 60.0 | 15.2 | 113.6 | 138 | 1750 | 1083 | 0.62 | 24.0 | 490.0 | 0.83 | |||
| [17] | CDT2-1-WA-A1 | CFCC 7-wire Strand | Helical plain | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1868 | 925 | 0.50 | 48.0 | 501.5 | 1 |
| CDT2-1-WA-A2 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1869 | 901 | 0.48 | 48.0 | - | 2 | |||
| CDT2-1-WA-A3 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1870 | 878 | 0.47 | 48.0 | - | 2.3 | |||
| CDT2-1-WA-B1 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1871 | 954 | 0.51 | 48.0 | 419.0 | 1 | |||
| CDT2-1-WA-B2 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1872 | 954 | 0.51 | 48.0 | - | 0.3 | |||
| CDT2-1-WA-B3 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1873 | 913 | 0.49 | 48.0 | - | 0.8 | |||
| CDT2-2-WA-A1 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1874 | 954 | 0.51 | 48.0 | 482.5 | 1.3 | |||
| CDT2-2-WA-A2 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1875 | 959 | 0.51 | 48.0 | - | 1 | |||
| CDT2-2-WA-A3 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1876 | 942 | 0.50 | 48.0 | - | 1.8 | |||
| CDT2-2-WA-B1 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1877 | 913 | 0.49 | 48.0 | 468.5 | 1 | |||
| CDT2-2-WA-B2 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1878 | 924 | 0.49 | 48.0 | - | 1.3 | |||
| CDT2-2-WA-B3 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1879 | 977 | 0.52 | 48.0 | - | 0.5 | |||
| CDT2-3-WA-A1 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1880 | 1018 | 0.54 | 48.0 | 520.5 | 1.5 | |||
| CDT2-3-WA-A2 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1881 | 966 | 0.51 | 48.0 | - | 1 | |||
| CDT2-3-WA-A3 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1882 | 983 | 0.52 | 48.0 | - | 0.5 | |||
| CDT2-3-WA-B1 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1883 | 972 | 0.52 | 48.0 | 412.5 | 1.5 | |||
| CDT2-3-WA-B2 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1884 | 1001 | 0.53 | 48.0 | - | 1.3 | |||
| CDT2-3-WA-B3 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1885 | 1036 | 0.55 | 48.0 | - | 0.8 | |||
| CDT2-4-WA-A1 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1886 | 983 | 0.52 | 48.0 | 443.0 | 1.3 | |||
| CDT2-4-WA-A2 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1887 | 1095 | 0.58 | 48.0 | - | 1 | |||
| CDT2-4-WA-A3 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1888 | 995 | 0.53 | 48.0 | - | 0.8 | |||
| CDT2-4-WA-B1 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1889 | 1059 | 0.56 | 48.0 | 400.0 | 1.3 | |||
| CDT2-4-WA-B2 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1890 | 1024 | 0.54 | 48.0 | - | 1.3 | |||
| CDT2-4-WA-B3 | Girder | Sudden | Yes | Double T | 38.2 | 12.5 | 76.0 | 138 | 1891 | 1240 | 0.66 | 48.0 | - | 1.3 |
| Reference | Specimen No | FRP Type | FRP Surface | Specimen Type | Release Type | Shear Reinforcement | Specimen Dimensions (b × h × l, mm) | c, mm | Ø, mm | Ap, mm2 | Ep, GPa | fpu, MPa | fpi, MPa | fpi/fpu | fci, MPa | Lt, mm | Slip, mm |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [18] | B1-4-65 | CFRP Leadline Bar | Spirally Indented Sanded | Beam | Gradual | Yes | 139.7 × 247.7 × 4000 | 31.8 | 12.7 | 126.5 | 124 | 2275 | 1345 | 0.59 | 45.4 | 607.1 | 3.07 |
| B2-4-55 | Beam | Gradual | Yes | 139.7 × 247.7 × 4001 | 31.8 | 12.7 | 126.5 | 124 | 2275 | 1138 | 0.50 | 47.9 | 533.4 | 2.44 | |||
| B3-4-60 | Beam | Gradual | Yes | 139.7 × 247.7 × 4002 | 31.8 | 12.7 | 126.5 | 124 | 2275 | 1241 | 0.55 | 46.8 | 495.3 | 2.39 | |||
| B4-4-60 | Beam | Gradual | Yes | 139.7 × 247.7 × 4003 | 31.8 | 12.7 | 126.5 | 124 | 2275 | 1282 | 0.56 | 50.7 | 342.9 | 3.07 | |||
| [12,15] | BL1 | CFRP Leadline Bar | Spirally Indented | Beam | Gradual | Yes | 80 × 200 × 1700 | 35.0 | 8.0 | 46.1 | 147 | 1970 | 1193 | 0.61 | 34.0 | 452.5 | 0.88 |
| BL2 | Beam | Gradual | Yes | 80 × 200 × 1701 | 35.0 | 8.0 | 46.1 | 147 | 1970 | 1193 | 0.61 | 34.0 | 462.5 | 1.04 | |||
| BL3 | Beam | Gradual | Yes | 80 × 200 × 1702 | 35.0 | 8.0 | 46.1 | 147 | 1970 | 1410 | 0.72 | 35.0 | 480.0 | 1.56 | |||
| BL4 | Beam | Gradual | Yes | 80 × 200 × 1703 | 35.0 | 8.0 | 46.1 | 147 | 1970 | 1410 | 0.72 | 35.0 | 480.0 | 1.12 | |||
| BL5 | Beam | Gradual | Yes | 80 × 250 × 2500 | 35.0 | 8.0 | 46.1 | 147 | 1970 | 1497 | 0.76 | 28.0 | 620.0 | 2.71 | |||
| BL6 | Beam | Gradual | Yes | 80 × 250 × 1700 | 35.0 | 8.0 | 46.1 | 147 | 1970 | 1497 | 0.76 | 28.0 | 625.0 | - | |||
| BL7 | Beam | Gradual | Yes | 80 × 250 × 2100 | 35.0 | 8.0 | 46.1 | 147 | 1970 | 1497 | 0.76 | 28.0 | 610.0 | 3 | |||
| BL8 | Beam | Gradual | Yes | 80 × 250 × 2100 | 35.0 | 8.0 | 46.1 | 147 | 1970 | 1497 | 0.76 | 28.0 | 625.0 | - | |||
| BL9 | Beam | Gradual | No | 150 × 250 × 4000 | 36.0 | 8.0 | 46.1 | 147 | 1970 | 1258 | 0.64 | 26.0 | 700.0 | 2.25 | |||
| BL10 | Beam | Gradual | No | 150 × 250 × 4000 | 36.0 | 8.0 | 46.1 | 147 | 1970 | 1258 | 0.64 | 26.0 | 700.0 | 2.88 | |||
| BL11 | Beam | Gradual | No | 150 × 250 × 3900 | 36.0 | 8.0 | 46.1 | 147 | 1970 | 1518 | 0.77 | 42.0 | 600.0 | 1.88 | |||
| BL12 | Beam | Gradual | No | 150 × 250 × 3900 | 36.0 | 8.0 | 46.1 | 147 | 1970 | 1518 | 0.77 | 42.0 | 500.0 | 1.18 | |||
| PL1 | Prism | Gradual | No | 70 × 95 × 1884 | 35.0 | 8.0 | 46.1 | 147 | 1970 | 1193 | 0.61 | 34.0 | 490.0 | 0.73 | |||
| PL2 | Prism | Gradual | No | 70 × 95 × 1884 | 35.0 | 8.0 | 46.1 | 147 | 1970 | 1193 | 0.61 | 34.0 | 480.0 | 1.36 | |||
| PL3 | Prism | Gradual | No | 80 × 80 × 1884 | 40.0 | 8.0 | 46.1 | 147 | 1970 | 1410 | 0.72 | 31.0 | 540.0 | 0.97 | |||
| PL4 | Prism | Gradual | No | 80 × 80 × 1884 | 40.0 | 8.0 | 46.1 | 147 | 1970 | 1410 | 0.72 | 31.0 | 525.0 | 1.33 | |||
| [17] | CDT1-1-WA-A1 | CFRP Leadline Bar | Spirally Indented | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1740 | 0.77 | 48.0 | 557.5 | 5.2 |
| CDT1-1-WA-A2 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1830 | 0.81 | 48.0 | - | - | |||
| CDT1-1-WA-A3 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1300 | 0.58 | 48.0 | - | 2.2 | |||
| CDT1-1-WA-B1 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1540 | 0.68 | 48.0 | 507.5 | 2.8 | |||
| CDT1-1-WA-B2 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1540 | 0.68 | 48.0 | - | - | |||
| CDT1-1-WA-B3 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1360 | 0.60 | 48.0 | - | - | |||
| CDT1-2-WA-A1 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1640 | 0.73 | 48.0 | 470.0 | - | |||
| CDT1-2-WA-A2 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1740 | 0.77 | 48.0 | - | - | |||
| CDT1-2-WA-A3 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1120 | 0.50 | 48.0 | - | - | |||
| CDT1-2-WA-B1 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1540 | 0.68 | 48.0 | - | - | |||
| CDT1-2-WA-B2 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1640 | 0.73 | 48.0 | - | - | |||
| CDT1-2-WA-B3 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1120 | 0.50 | 48.0 | - | - | |||
| CDT1-3-WA-A1 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1640 | 0.73 | 48.0 | 502.5 | 7.9 | |||
| CDT1-3-WA-A2 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1640 | 0.73 | 48.0 | - | 3.3 | |||
| CDT1-3-WA-A3 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1050 | 0.47 | 48.0 | - | 0.8 | |||
| CDT1-3-WA-B1 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1930 | 0.86 | 48.0 | 415.0 | 2 | |||
| CDT1-3-WA-B2 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1540 | 0.68 | 48.0 | - | 1 | |||
| CDT1-3-WA-B3 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 930 | 0.41 | 48.0 | - | 1.3 | |||
| CDT1-4-WA-A1 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1640 | 0.73 | 48.0 | 487.5 | 2 | |||
| CDT1-4-WA-A2 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1640 | 0.73 | 48.0 | - | 5.1 | |||
| CDT1-4-WA-A3 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1240 | 0.55 | 48.0 | - | 2.5 | |||
| CDT1-4-WA-B1 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1740 | 0.77 | 48.0 | 502.5 | 2.3 | |||
| CDT1-4-WA-B2 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1350 | 0.60 | 48.0 | - | 3.3 | |||
| CDT1-4-WA-B3 | Girder | Sudden | Yes | Double T | 40.5 | 7.9 | 46.1 | 147 | 2256 | 1240 | 0.55 | 48.0 | 557.5 | 1.8 | |||
| [19,20] | I-SCC30-1 | CFRP Bar | Sanded | Beam | Gradual | Yes | 150 × 250 × 3600 | 38.1 | 12.7 | 126.7 | 144 | 1765 | 613 | 0.32 | 30.4 | - | 1.478 |
| I-SCC30-2 | Beam | Gradual | Yes | 150 × 250 × 3601 | 38.1 | 12.7 | 126.7 | 144 | 1765 | 601 | 0.31 | 30.4 | 355.0 | 0.443 | |||
| I-SCC30-3 | Beam | Gradual | Yes | 150 × 250 × 3602 | 38.1 | 12.7 | 126.7 | 144 | 1765 | 726 | 0.37 | 41.0 | - | 0.784 | |||
| I-SCC30-4 | Beam | Gradual | Yes | 150 × 250 × 3603 | 38.1 | 12.7 | 126.7 | 144 | 1765 | 647 | 0.35 | 41.0 | - | 0.688 | |||
| II-SCC45-1 | Beam | Gradual | Yes | 150 × 250 × 3604 | 38.1 | 12.7 | 126.7 | 144 | 1765 | 807 | 0.43 | 35.0 | - | 1.393 | |||
| II-SCC45-2 | Beam | Gradual | Yes | 150 × 250 × 3605 | 38.1 | 12.7 | 126.7 | 144 | 1765 | 884 | 0.46 | 35.0 | 505.0 | 1.406 | |||
| II-SCC45-3 | Beam | Gradual | Yes | 150 × 250 × 3606 | 38.1 | 12.7 | 126.7 | 144 | 1765 | 841 | 0.45 | 35.0 | 530.0 | 1.432 | |||
| II-SCC45-4 | Beam | Gradual | Yes | 150 × 250 × 3607 | 38.1 | 12.7 | 126.7 | 144 | 1765 | 805 | 0.43 | 35.0 | - | 1.320 | |||
| III-SCC60-1 | Beam | Gradual | Yes | 150 × 250 × 3608 | 38.1 | 12.7 | 126.7 | 144 | 1765 | 980 | 0.54 | 30.4 | 665.0 | 2.164 | |||
| III-SCC60-2 | Beam | Gradual | Yes | 150 × 250 × 3609 | 38.1 | 12.7 | 126.7 | 144 | 1765 | 1097 | 0.58 | 30.4 | - | 2.572 | |||
| III-SCC60-3 | Beam | Gradual | Yes | 150 × 250 × 3610 | 38.1 | 12.7 | 126.7 | 144 | 1765 | 1008 | 0.54 | 41.0 | 695.0 | 2.105 | |||
| III-SCC60-4 | Beam | Gradual | Yes | 150 × 250 × 3611 | 38.1 | 12.7 | 126.7 | 144 | 1765 | 1052 | 0.57 | 41.0 | 680.0 | 2.508 | |||
| IV-N30-1 | Beam | Gradual | Yes | 150 × 250 × 3612 | 38.1 | 12.7 | 126.7 | 144 | 1765 | 635 | 0.33 | 37.0 | 300.0 | 0.539 | |||
| IV-N60-2 | Beam | Gradual | Yes | 150 × 250 × 3613 | 38.1 | 12.7 | 126.7 | 144 | 1765 | 1168 | 0.63 | 37.0 | - | 2.075 | |||
| IV-N60-3 | Beam | Gradual | Yes | 150 × 250 × 3614 | 38.1 | 12.7 | 126.7 | 144 | 1765 | 1121 | 0.60 | 37.0 | 580.0 | 1.826 | |||
| IV-N60-4 | Beam | Gradual | Yes | 150 × 250 × 3615 | 38.1 | 12.7 | 126.7 | 144 | 1765 | 1153 | 0.62 | 37.0 | 590.0 | 1.908 |
| Reference | Specimen No | FRP Type | FRP Surface | Specimen Type | Release Type | Shear Reinforcement | Specimen Dimensions (b × h × l, mm) | c, mm | Ø, mm | Ap, mm2 | Ep, GPa | fpu, MPa | fpi, MPa | fpi/fpu | fci, MPa | Lt, mm | Slip, mm |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [21] | 7.5S-N-50-1 | AFRP Arapee Tendon | Sanded | Prism | Gradual | No | 50 × 50 × 1000 | 21.3 | 7.5 | 22.2 | 91 | 3000 | 1487 | 0.50 | 54.6 | - | - |
| 7.5S-N-60-1 | Sanded | Prism | Gradual | No | 60 × 60 × 1000 | 26.3 | 7.5 | 22.2 | 91 | 3000 | 1487 | 0.50 | 54.6 | 135.0 | 0.625 | ||
| 7.5S-N-70-1 | Sanded | Prism | Gradual | No | 70 × 70 × 1000 | 31.3 | 7.5 | 22.2 | 91 | 3000 | 1487 | 0.50 | 54.6 | 135.0 | 0.488 | ||
| 7.5S-N-50-2 | Sanded | Prism | Gradual | No | 50 × 50 × 1000 | 21.3 | 7.5 | 22.2 | 91 | 3000 | 1487 | 0.50 | 54.6 | 220.0 | 1.239 | ||
| 7.5S-N-60-2 | Sanded | Prism | Gradual | No | 60 × 60 × 1000 | 26.3 | 7.5 | 22.2 | 91 | 3000 | 1487 | 0.50 | 54.6 | 110.0 | 0.388 | ||
| 7.5S-N-60-2 | Sanded | Prism | Gradual | No | 60 × 60 × 1000 | 26.3 | 7.5 | 22.2 | 91 | 3000 | 1487 | 0.50 | 54.6 | 185.0 | 1.15 | ||
| 7.5S-N-70-2 | Sanded | Prism | Gradual | No | 70 × 70 × 1000 | 31.3 | 7.5 | 22.2 | 91 | 3000 | 1487 | 0.50 | 54.6 | 135.0 | 0.456 | ||
| 7.5S-N-50-3 | Sanded | Prism | Gradual | Fibers | 50 × 50 × 1000 | 21.3 | 7.5 | 22.2 | 91 | 3000 | 1487 | 0.50 | 54.6 | 135.0 | 0.374 | ||
| 7.5-S-N-50-4 | Sanded | Prism | Gradual | Fibers | 50 × 50 × 1000 | 21.3 | 7.5 | 22.2 | 91 | 3000 | 1487 | 0.50 | 54.6 | 160.0 | 0.681 | ||
| 7.5S-N-50-5 | Sanded | Prism | Gradual | Fibers | 50×50×1000 | 21.3 | 7.5 | 22.2 | 91 | 3000 | 1487 | 0.50 | 54.6 | 160.0 | 0.67 | ||
| 7.5S-H-45-1 | Sanded | Prism | Gradual | No | 45 × 45 × 1000 | 18.8 | 7.5 | 22.2 | 91 | 3000 | 1487 | 0.50 | 81.5 | 110.0 | 0.312 | ||
| 7.5S-H-50-1 | Sanded | Prism | Gradual | No | 50 × 50 × 1000 | 21.3 | 7.5 | 22.2 | 91 | 3000 | 1487 | 0.50 | 81.5 | 135.0 | 0.398 | ||
| 7.5S-H-50-2 | Sanded | Prism | Gradual | No | 50 × 50 × 1000 | 21.3 | 7.5 | 22.2 | 91 | 3000 | 1487 | 0.50 | 81.5 | 135.0 | 0.466 | ||
| 5.3S-N-45-1 | Sanded | Prism | Gradual | No | 45 × 45 × 1000 | 19.9 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | 85.0 | 0.378 | ||
| 5.3E-N-45-1 | Expancel | Prism | Gradual | No | 45 × 45 × 1000 | 19.9 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | 225.0 | 0.883 | ||
| 5.3ES-N-45-1 | Expancel Sanded | Prism | Gradual | No | 45 × 45 × 1000 | 19.9 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | 85.0 | 0.477 | ||
| 5.3S-N-40-1 | Sanded | Prism | Gradual | No | 40 × 40 × 1000 | 17.4 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | 85.0 | 0.27 | ||
| 5.3E-N-40-1 | Expancel | Prism | Gradual | No | 40 × 40 × 1000 | 17.4 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | 200.0 | 0.931 | ||
| 5.3S-N-35-1 | Sanded | Prism | Gradual | No | 35 × 35 × 1000 | 14.9 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | 85.0 | 0.376 | ||
| 5.3S-N-30-1 | Sanded | Prism | Gradual | No | 30 × 30 × 1000 | 12.4 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | - | - | ||
| 5.3E-N-35-1 | Expancel | Prism | Gradual | No | 35 × 35 × 1000 | 14.9 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | 185.0 | 0.811 | ||
| 5.3E-N-30-1 | Expancel | Prism | Gradual | No | 30 × 30 × 1000 | 12.4 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | - | - | ||
| 5.3ES-N-35-1 | Expancel Sanded | Prism | Gradual | No | 35 × 35 × 1000 | 14.9 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | 110.0 | 0.655 | ||
| 5.3ES-N-30-1 | Expancel Sanded | Prism | Gradual | No | 30 × 30 × 1000 | 12.4 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | - | - | ||
| 5.3S-N-40-2 | Sanded | Prism | Gradual | No | 40 × 40 × 1000 | 17.4 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | - | - | ||
| 5.3S-N-35-2 | Sanded | Prism | Gradual | No | 35 × 35 × 1000 | 14.9 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | 85.0 | 0.342 | ||
| 5.3-ES-N-40-1 | Expancel Sanded | Prism | Gradual | No | 40 × 40 × 1000 | 17.4 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | 135.0 | 0.633 | ||
| 5.3ES-N-40-2 | Expancel Sanded | Prism | Gradual | No | 40 × 40 × 1000 | 17.4 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | - | - | ||
| 5.3ES-N-35-2 | Expancel Sanded | Prism | Gradual | No | 35 × 35 × 1000 | 14.9 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | 110.0 | 0.568 | ||
| 5.3ES-N-30-2 | Expancel Sanded | Prism | Gradual | No | 30 × 30 × 1000 | 12.4 | 5.3 | 11.1 | 91 | 3000 | 1487 | 0.50 | 54.6 | - | - | ||
| [22] | FIB1/1a | FiBRA | Braided | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 873 | 0.61 | 56.0 | 118 | 0.74 |
| FIB1/2a | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 900 | 0.63 | 56.0 | 122 | 0.79 | |||
| FIB1/3a | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 891 | 0.62 | 56.0 | 94 | 0.56 | |||
| FIB1/1b | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 836 | 0.59 | 56.0 | 118.0 | 0.71 | |||
| FIB1/2b | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 900 | 0.63 | 56.0 | 148.0 | 0.92 | |||
| FIB1/3b | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 891 | 0.62 | 56.0 | 112.0 | 0.69 | |||
| FIB2/1a | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 909 | 0.64 | 56.3 | 117 | 0.72 | |||
| FIB2/2a | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 945 | 0.66 | 56.3 | 121 | 0.81 | |||
| FIB2/3a | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 955 | 0.67 | 56.3 | 114 | 0.7 | |||
| FIB2/1b | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 873 | 0.61 | 56.3 | 84.0 | 0.5 | |||
| FIB2/2b | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 918 | 0.64 | 56.3 | 104.0 | 0.69 | |||
| FIB2/3b | Beam | Gradual | No | 100×200×2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 945 | 0.66 | 56.3 | 113.0 | 0.72 | |||
| FAB/1a | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 918 | 0.64 | 58.0 | 107 | 0.65 | |||
| FAB/2a | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 918 | 0.64 | 58.0 | 116 | 0.76 | |||
| FAB/3a | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 900 | 0.63 | 58.0 | 82 | 0.53 | |||
| FAB/1b | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 900 | 0.63 | 58.0 | 89.0 | 0.58 | |||
| FAB/2b | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 945 | 0.66 | 58.0 | 117.0 | 0.78 | |||
| FAB/3b | Beam | Gradual | No | 100 × 200 × 2800 | 58.2 | 3.7 | 11.0 | 69 | 1427 | 918 | 0.64 | 58.0 | 97.0 | 0.64 | |||
| [22] | TIB1/1a | Technora | Spirally wounded | Beam | Gradual | No | 100 × 200 × 2800 | 68.0 | 4.0 | 12.6 | 54 | 1802 | 1151 | 0.64 | 56.0 | 45 | 0.47 |
| TIB1/2a | Beam | Gradual | No | 100 × 200 × 2800 | 68.0 | 4.0 | 12.6 | 54 | 1802 | 1167 | 0.65 | 56.0 | 94 | 0.96 | |||
| TIB1/1b | Beam | Gradual | No | 100 × 200 × 2800 | 68.0 | 4.0 | 12.6 | 54 | 1802 | 1135 | 0.63 | 56.0 | 54.0 | 0.53 | |||
| TIB1/2b | Beam | Gradual | No | 100 × 200 × 2800 | 68.0 | 4.0 | 12.6 | 54 | 1802 | 1190 | 0.66 | 56.0 | 78.0 | 0.8 | |||
| TIB2/1a | Beam | Gradual | No | 100 × 200 × 2800 | 68.0 | 4.0 | 12.6 | 54 | 1802 | 1175 | 0.65 | 56.3 | 55 | 0.58 | |||
| TIB2/2a | Beam | Gradual | No | 100 × 200 × 2800 | 68.0 | 4.0 | 12.6 | 54 | 1802 | 1151 | 0.64 | 56.3 | 59 | 0.6 | |||
| TIB2/1b | Beam | Gradual | No | 100 × 200 × 2800 | 68.0 | 4.0 | 12.6 | 54 | 1802 | 1167 | 0.65 | 56.3 | 53.0 | 0.53 | |||
| TIB2/2b | Beam | Gradual | No | 100 × 200 × 2800 | 68.0 | 4.0 | 12.6 | 54 | 1802 | 1151 | 0.64 | 56.3 | 58.0 | 0.6 | |||
| TAB/1a | Beam | Gradual | No | 100 × 200 × 2800 | 68.0 | 4.0 | 12.6 | 54 | 1802 | 1151 | 0.64 | 58.0 | 59 | 0.57 | |||
| TAB/2a | Beam | Gradual | No | 100 × 200 × 2800 | 68.0 | 4.0 | 12.6 | 54 | 1802 | 1159 | 0.64 | 58.0 | 61 | 0.6 | |||
| TAB/1b | Beam | Gradual | No | 100 × 200 × 2800 | 68.0 | 4.0 | 12.6 | 54 | 1802 | 1151 | 0.64 | 58.0 | 55.0 | 0.58 | |||
| TAB/2b | Beam | Gradual | No | 100 × 200 × 2800 | 68.0 | 4.0 | 12.6 | 54 | 1802 | 1159 | 0.64 | 58.0 | 47.0 | 0.5 |
| Reference | Specimen No | FRP Type | FRP Surface | Specimen Type | Release Type | Shear Reinforcement | Specimen Dimensions (b × h × l, mm) | c, mm | Ø, mm | Ap, mm2 | Ep, GPa | fpu, MPa | fpi, MPa | fpi/fpu | fci, MPa | Lt, mm | Slip, mm |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [23] | B1S | BFRP Bar | Sanded | Beam | Sudden | No | 3000 × 100 × 200 | 46 | 8 | 50.24 | 44 | 1126 | 393 | 0.34 | 27 | 350 | 1.83 |
| B1N | Beam | Sudden | No | 3000 × 100 × 201 | 46 | 8 | 50.24 | 44 | 1126 | 384 | 0.32 | 27 | 500 | 1.91 | |||
| B2S | Beam | Sudden | No | 3000 × 100 × 202 | 46 | 8 | 50.24 | 44 | 1126 | 369 | 0.31 | 27 | 250 | 1.99 | |||
| B2N | Beam | Sudden | No | 3000 × 100 × 203 | 46 | 8 | 50.24 | 44 | 1126 | 375 | 0.31 | 27 | 400 | 2.79 |
Appendix B
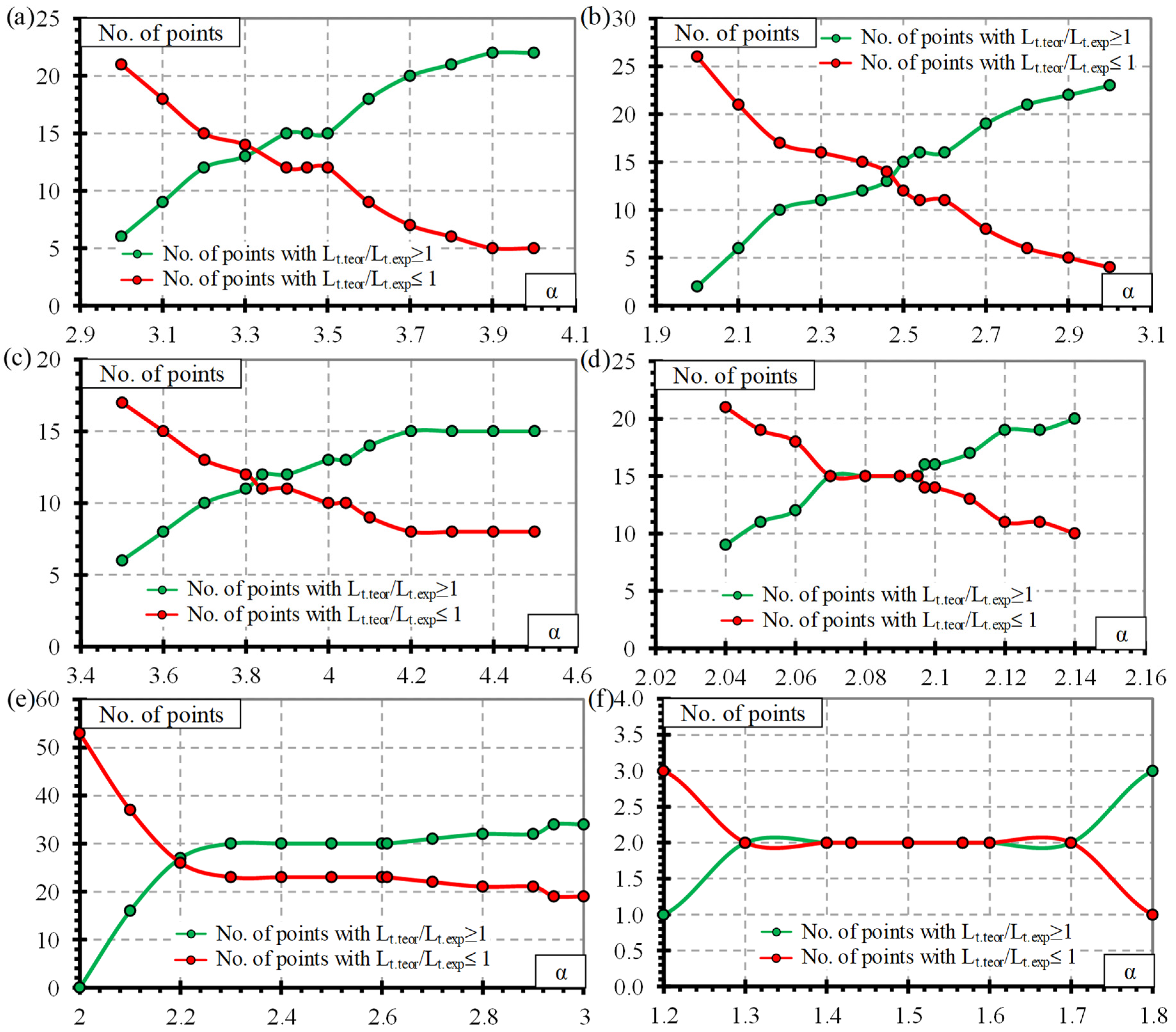
| α | 3 | 3.1 | 3.2 | 3.3 | 3.4 | 3.45 | 3.5 | 3.6 | 3.7 | 3.8 | 3.9 | 4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | 0.909 | 0.939 | 0.969 | 1.000 | 1.030 | 1.046 | 1.060 | 1.091 | 1.121 | 1.151 | 1.182 | 1.212 |
| STD | 0.189 | 0.195 | 0.201 | 0.208 | 0.214 | 0.217 | 0.220 | 0.226 | 0.233 | 0.239 | 0.245 | 0.252 |
| COV, % | 20.8 | 20.8 | 20.8 | 20.8 | 20.8 | 20.8 | 20.8 | 20.8 | 20.8 | 20.8 | 20.8 | 20.8 |
| Ntotal | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 |
| OV | 6 | 9 | 12 | 13 | 15 | 15 | 15 | 18 | 20 | 21 | 22 | 22 |
| UV | 21 | 18 | 15 | 14 | 12 | 12 | 12 | 9 | 7 | 6 | 5 | 5 |
| α | 2 | 2.1 | 2.2 | 2.3 | 2.4 | 2.46 | 2.5 | 2.54 | 2.6 | 2.7 | 2.8 | 2.9 | 3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | 0.813 | 0.854 | 0.894 | 0.935 | 0.976 | 1.000 | 1.016 | 1.034 | 1.057 | 1.098 | 1.138 | 1.179 | 1.220 |
| STD | 0.143 | 0.150 | 0.157 | 0.164 | 0.171 | 0.18 | 0.18 | 0.182 | 0.186 | 0.193 | 0.200 | 0.207 | 0.214 |
| COV, % | 17.6 | 17.6 | 17.6 | 17.6 | 17.6 | 17.6 | 17.6 | 17.6 | 17.6 | 17.6 | 17.6 | 17.6 | 17.6 |
| Ntotal | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 | 27 |
| OV | 2 | 6 | 10 | 11 | 12 | 13 | 15 | 16 | 16 | 19 | 21 | 22 | 23 |
| UV | 26 | 21 | 17 | 16 | 15 | 14 | 12 | 11 | 11 | 8 | 6 | 5 | 4 |
| α | 3.5 | 3.6 | 3.7 | 3.8 | 3.84 | 3.9 | 4 | 4.043 | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | 0.912 | 0.938 | 0.964 | 0.990 | 1.001 | 1.016 | 1.042 | 1.053 | 1.068 | 1.094 | 1.120 | 1.147 | 1.173 |
| STD | 0.212 | 0.218 | 0.224 | 0.230 | 0.232 | 0.236 | 0.242 | 0.245 | 0.248 | 0.254 | 0.260 | 0.266 | 0.272 |
| COV, % | 23.2 | 23.2 | 23.2 | 23.2 | 23.2 | 23.2 | 23.2 | 23.2 | 23.2 | 23.2 | 23.2 | 23.2 | 23.2 |
| Ntotal | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 |
| OV | 6 | 8 | 10 | 11 | 12 | 12 | 13 | 13 | 14 | 15 | 15 | 15 | 15 |
| UV | 17 | 15 | 13 | 12 | 11 | 11 | 10 | 10 | 9 | 8 | 8 | 8 | 8 |
| α | 2.040 | 2.050 | 2.060 | 2.070 | 2.080 | 2.090 | 2.095 | 2.097 | 2.1 | 2.110 | 2.120 | 2.130 | 2.140 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | 0.974 | 0.979 | 0.983 | 0.988 | 0.993 | 0.998 | 1.000 | 1.001 | 1.002 | 1.007 | 1.012 | 1.017 | 1.022 |
| STD | 0.032 | 0.032 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.034 | 0.034 | 0.034 |
| COV, % | 3.3 | 3.3 | 3.3 | 3.3 | 3.3 | 3.3 | 3.3 | 3.3 | 3.3 | 3.3 | 3.3 | 3.3 | 3.3 |
| Ntotal | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
| OV | 9 | 11 | 12 | 15 | 15 | 15 | 15 | 16 | 16 | 17 | 19 | 19 | 20 |
| UV | 21 | 19 | 18 | 15 | 15 | 15 | 15 | 14 | 14 | 13 | 11 | 11 | 10 |
| α | 2 | 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.61 | 2.7 | 2.8 | 2.9 | 2.941 | 3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | 0.767 | 0.805 | 0.843 | 0.882 | 0.920 | 0.958 | 0.997 | 1.000 | 1.035 | 1.073 | 1.112 | 1.127 | 1.150 |
| STD | 0.232 | 0.244 | 0.255 | 0.267 | 0.278 | 0.290 | 0.302 | 0.303 | 0.313 | 0.325 | 0.336 | 0.341 | 0.348 |
| COV, % | 30.3 | 30.3 | 30.3 | 30.3 | 30.3 | 30.3 | 30.3 | 30.3 | 30.3 | 30.3 | 30.3 | 30.3 | 30.3 |
| Ntotal | 53 | 53 | 53 | 53 | 53 | 53 | 53 | 53 | 53 | 53 | 53 | 53 | 53 |
| OV | 0 | 16 | 27 | 30 | 30 | 30 | 30 | 30 | 31 | 32 | 32 | 34 | 34 |
| UV | 53 | 37 | 26 | 23 | 23 | 23 | 23 | 23 | 22 | 21 | 21 | 19 | 19 |
| α | 1 | 1.1 | 1.2 | 1.3 | 1.4 | 1.43 | 1.5 | 1.57 | 1.6 | 1.7 | 1.8 | 1.9 | 2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | 0.698 | 0.767 | 0.837 | 0.907 | 0.977 | 0.998 | 1.046 | 1.093 | 1.116 | 1.186 | 1.256 | 1.326 | 1.395 |
| STD | 0.229 | 0.252 | 0.275 | 0.298 | 0.321 | 0.328 | 0.344 | 0.360 | 0.367 | 0.390 | 0.413 | 0.436 | 0.459 |
| COV, % | 32.9 | 32.9 | 32.9 | 32.9 | 32.9 | 32.9 | 32.9 | 32.9 | 32.9 | 32.9 | 32.9 | 32.9 | 32.9 |
| Ntotal | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| OV | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 |
| UV | 4 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 |
References
- Jokūbaitis, A.; Marčiukaitis, G.; Valivonis, J. Damage of Prestressed Concrete Railway Sleepers and Its Impact on Durability. In Proceedings of the 13th international conference “Modern Building Materials, Structures and Techniques” (MBMST 2019), Vilnius, Lithuania, 16–17 May 2019; Vilnius Gediminas Technical University: Vilnius, Lithuania, 2019; pp. 352–358. [Google Scholar]
- Jokūbaitis, A.; Marčiukaitis, G.; Valivonis, J. Experimental Research on the Behavior of the Rail Seat Section of Different Types of Prestressed Concrete Sleepers. Materials 2020, 13, 2432. [Google Scholar] [CrossRef] [PubMed]
- Jokūbaitis, A.; Marčiukaitis, G.; Valivonis, J. Analysis of Reinforcement Anchorage Zone Behavior of Prestressed Concrete Elements Under Static and Cyclic Loads. Procedia Eng 2017, 172, 457–464. [Google Scholar] [CrossRef]
- Jokūbaitis, A.; Marčiukaitis, G.; Valivonis, J.; Strauss, A. Influence of Cyclic Loading and Frost on the Behavior of Bond of Three-Wire Strand. Struct. Concr. 2018, 19, 1363–1375. [Google Scholar] [CrossRef]
- Solyom, S.; Balázs, G.L. Analytical and Statistical Study of the Bond of FRP Bars with Different Surface Characteristics. Compos Struct. 2021, 270, 113953. [Google Scholar] [CrossRef]
- Malvar, L.J.; Cox, J.V.; Cochran, K.B. Bond between Carbon Fiber Reinforced Polymer Bars and Concrete. I: Experimental Study. J. Compos. Constr. 2003, 7, 154–163. [Google Scholar] [CrossRef]
- Abed, M.A.; Alkurdi, Z.; Fořt, J.; Černý, R.; Solyom, S. Bond Behavior of FRP Bars in Lightweight SCC under Direct Pull-Out Conditions: Experimental and Numerical Investigation. Materials 2022, 15, 3555. [Google Scholar] [CrossRef]
- Nanni, A.; Utsunomiya, T.; Yonekura, H.; Tanigaki, M. Transmission of Prestressing Force to Concrete by Bonded Fiber Reinforced Plastic Tendons. ACI Struct. J. 1992, 89, 335–344. [Google Scholar]
- Nanni, A.; Bakis, C.E.; Boothby, T.E. Test Methods for FRP-Concrete Systems Subjected to Mechanical Loads: State of the Art Review. J. Reinf. Plast. Compos. 1995, 14, 524–558. [Google Scholar] [CrossRef]
- Jokūbaitis, A.; Valivonis, J. An Analysis of the Transfer Lengths of Different Types of Prestressed Fiber-Reinforced Polymer Reinforcement. Polymers 2022, 14, 3931. [Google Scholar] [CrossRef]
- Ehsani, M.R.; Saadatmanesh, H.; Nelson, C.T. Transfer and Flexural Bond Performance of Aramid and Carbon FRP Tendons. PCI J. 1997, 42, 76–86. [Google Scholar] [CrossRef]
- Mahmoud, Z.I. Bond Characteristics of Fibre Reinforced Polymers Prestressing Reinforcement. Ph.D. Thesis, Alexandria University, Alexandria, Egypt, 1997. [Google Scholar]
- Laskar, A.; Motwani, P.; Dhruw, S. Finite Element Analysis and Design of Test Setup for Determination of Transfer Length in BFRP Prestressed Concrete Beams. Adv. Mater. Lett. 2021, 12, 1–7. [Google Scholar] [CrossRef]
- Motwani, P.; Laskar, A. Finite Element Studies on Transfer Length of Fiber Reinforced Polymer Strands in Pretensioned Members. In Proceedings of the International Conference on Composite Materials and Structures-ICCMS 2017, Hyderabad, India, 27–29 December; 2017; pp. 1–10. [Google Scholar]
- Mahmoud, Z.I.; Rizkalla, S.H.; Zaghoul, E.E.R. Transfer and Development Lengths of Carbon Fiber Reinforced Polymers Prestressing Reinforcement. ACI Struct. J. 1999, 96, 594–602. [Google Scholar]
- Jokūbaitis, A.; Valivonis, J. An Analysis of Flexural Bond Length and Anchorage Length of Prestressed Fiber Reinforced Polymer Reinforcement. Eurasia Proc. Sci. Technol. Eng. Math. (EPSTEM) 2022, 21, 484–499. [Google Scholar] [CrossRef]
- Grace, N.F. Transfer Length of CFRP/CFCC Strands for Double-T Girders. PCI J. 2000, 45, 110–126. [Google Scholar] [CrossRef]
- Saeed, Y.M. Behavior of Prestressed Concrete Beams with CFRP Strands. Ph.D. Thesis, Portland State University, Portland, OR, USA, 2016. [Google Scholar]
- Krem, S. Bond and Flexural Behaviour of Self Consolidating Concrete Beams Reinforced and Prestressed with FRP Bars. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2013. [Google Scholar]
- Krem, S.S.; Soudki, K.A. Bond Behaviour of CFRP Bars Prestressed in Self-Consolidating Concrete Beams. ACI Symp. Pap. 2018, 327, 36.1–36.20. [Google Scholar]
- Taerwe, L.; Pallemans, I. Force Transfer of AFRP Bars in Concrete Prisms. In Non-Metallic (FRP) Reinforcement for Concrete Structures, Proceedings of the Second International RILEM Symposium, Quebec City, QC, Canada, 11 September 2006; CRC Press: Boca Raton, FL, USA, 1995; pp. 154–163. [Google Scholar]
- Lees, J.M.; Burgoyne, C.J. Transfer Bond Stresses Generated Between FRP Tendons and Concrete. Mag. Concr. Res. 1999, 51, 229–239. [Google Scholar] [CrossRef] [Green Version]
- Motwani, P.; Rather, A.I.; Laskar, A. Transfer Stage Parameters for Concrete Beams Prestressed with BFRP Bars: Experimental and Finite Element Studies. Constr Build Mater 2022, 315, 125639. [Google Scholar] [CrossRef]
- Zawam, M.H.M. Long-Term Behaviour of GFRP Prestressed Concrete Beams. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2015. [Google Scholar]
- Zawam, M.; Soudki, K.A. Factors Affecting the Transfer Length of Prestressed GFRP Bars in Concrete. ACI Symp. Pap. 2018, 322, 1–16. [Google Scholar]
- Zhao, W. Development of a Portable Optical Strain Sensor with Applications to Diagnostic Testing of Prestressed Concrete. Ph.D. Thesis, Kansas State University, Manhattan, Kansas, 1998. [Google Scholar]
- Murphy, R.; Zhao, W.; Peterman, R.; Beck, T. Determining the Transfer Length in Prestressed Concrete Railroad Ties Produced in the United States; Final Report 255-1121-0001-453; Mid-America Transportation Center: Lincoln, NE, USA, 2012. [Google Scholar]
- Zhao, W.; Larson, K.; Peterman, R.J.; Beck, B.T.; Wu, C.-H.J. Development of a Laser-Speckle Imaging Device to Determine the Transfer Length in Pretensioned Concrete Members. PCI J. 2012, 57, 135–143. [Google Scholar] [CrossRef] [Green Version]
- Lämmlein, T.D.; Justs, J.; Terrasi, G.; Lura, P. Prestressing Low Clinker Structural Concrete Elements by Ultra-High Modulus Carbon Fibre Reinforced Polymer Tendons. Mater Struct. 2021, 54, 51. [Google Scholar] [CrossRef]
- Jeon, S.-J.; Shin, H.; Kim, S.-H.; Park, S.Y.; Yang, J.-M. Transfer Lengths in Pretensioned Concrete Measured Using Various Sensing Technologies. Int. J. Concr. Struct. Mater. 2019, 13, 43. [Google Scholar] [CrossRef]
- Cousins, T.E.; Johnston, D.W.; Zia, P. Transfer and Development Length of Epoxy Coated and Uncoated Prestressing Strand. PCI J. 1990, 35, 92–103. [Google Scholar] [CrossRef]
- Russell, B.W.; Burns, N.H. Measured Transfer Lengths of 0.5 and 0.6 in. Strands in Pretensioned Concrete. PCI J. 1996, 41, 44–65. [Google Scholar] [CrossRef]
- Pozolo, A.M. Transfer and Development Lengths of Steel Strands in Full-Scale Prestressed Self-Consolidating Concrete Bridge Girders. Master’s Thesis, University of Illinois at Urbana-Champaign, Urbana, IL, USA, 2010. [Google Scholar]
- Bruggeling, A.S.G. Übertragen Der Vorspannung Mittels Verbund. Beton-Und Stahlbetonbau 2001, 96, 109–123. [Google Scholar] [CrossRef]
- Hoyer, E.; Friedrich, E. Beitrag Zur Frage Der Haftspannung in Eisenbetonbauteilen. Beton Und Eisen 1939, 38, 107–110. [Google Scholar]
- Guyon, Y. Prestressed Concrete: Volume 1; John Wiley and Sons Inc.: New York, NY, USA, 1960. [Google Scholar]
- EN 13369:2018; Common Rules for Precast Concrete Products. European Committee for Standardization: Brussels, Belgium, 2018.
- Rose, D.R.; Russell, B.W. Investigation of Standardized Tests to Measure the Bond Performance of Prestressing Strand. PCI J. 1997, 42, 56–80. [Google Scholar] [CrossRef]
- Balazs, G.L. Transfer Length of Prestressing Strand as a Function of Draw-In and Initial Prestress. PCI J. 1993, 38, 86–93. [Google Scholar] [CrossRef]
- Balazs, G.L. Transfer Control of Prestressing Strands. PCI J. 1992, 37, 60–71. [Google Scholar] [CrossRef]
- Marshall, W.T.; Krishnamurthy, D. Transfer Length of Prestressing Tendons from Concrete Cube Strength at Transfer. Indian Concr. J. 1969, 43, 244–275. [Google Scholar]
- Marti-Vargas, J.R.; Arbelaez, C.A.; Serna-Ros, P.; Castro-Bugallo, C. Reliability of Transfer Length Estimation from Strand End Slip. ACI Struct. J. 2007, 104, 487–494. [Google Scholar]
- Crossett, P.; Taylor, S.E.; Sonebi, M.; Robinson, D.; Taengua, E. Monitoring the Transfer Length of Pre-Stressed BFRP SCC Beams. In Proceedings of the Proceedings of SHMII-7 Conference, Torino, Italy, 1–3 July 2015; pp. 1–10. [Google Scholar]



| Reference | Reinforcement Type | α |
|---|---|---|
| [43] | BFRP sand coated bar | 2.82–3.32 |
| [12] | CFRP Leadline bar | 2.91 |
| CFCC strand | 2.48 | |
| [21] | AFRP Arapree sand coated bar | 3.03 |
| FRP Type | c, mm | Ø, mm | c/Ø | Ap, mm2 | Ep, GPa | fpu, MPa | fpi, MPa | fpi/fpu | fci, MPa |
|---|---|---|---|---|---|---|---|---|---|
| CFCC | 38.2–60 | 10.5–15.2 | 3.1–4.3 | 55.7–113.6 | 138–141 | 1725–1889 | 913–1408 | 0.49–0.81 | 23–48 |
| CFRP | 31.8–40.5 | 7.9–12.7 | 2.5–5.1 | 46.1–126.7 | 124.1–147 | 1765–2275 | 634–1930 | 0.33–0.86 | 26–50.7 |
| AFRP | 12.4–68 | 3.7–7.5 | 2.3–17 | 11–22.2 | 54–91 | 1427–3000 | 836–1486 | 0.50–0.67 | 54.6–81.5 |
| BFRP | 46.0 | 8.0 | 5.7 | 50.2 | 44 | 1126 | 369–381 | 0.31–0.34 | 27 |
| α | CFCC | CFRP | AFRP | BFRP | ||
|---|---|---|---|---|---|---|
| All | Arapree | FiBRA | ||||
| Mean | 3.45 | 2.54 | 2.94 | 4.04 | 2.1 | 1.57 |
| STD | 0.78 | 0.50 | 1.15 | 0.95 | 0.07 | 0.48 |
| COV, % | 22.6 | 19.6 | 39.2 | 23.5 | 3.37 | 30.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jokūbaitis, A.; Valivonis, J. Transfer Length vs. Slip of Prestressed Fiber-Reinforced Polymer Reinforcement. Polymers 2023, 15, 1190. https://doi.org/10.3390/polym15051190
Jokūbaitis A, Valivonis J. Transfer Length vs. Slip of Prestressed Fiber-Reinforced Polymer Reinforcement. Polymers. 2023; 15(5):1190. https://doi.org/10.3390/polym15051190
Chicago/Turabian StyleJokūbaitis, Aidas, and Juozas Valivonis. 2023. "Transfer Length vs. Slip of Prestressed Fiber-Reinforced Polymer Reinforcement" Polymers 15, no. 5: 1190. https://doi.org/10.3390/polym15051190
APA StyleJokūbaitis, A., & Valivonis, J. (2023). Transfer Length vs. Slip of Prestressed Fiber-Reinforced Polymer Reinforcement. Polymers, 15(5), 1190. https://doi.org/10.3390/polym15051190