Thermal and Electrical Properties of Additively Manufactured Polymer–Boron Nitride Composite
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Photopolymer Preparation
2.2.2. 3D Printing
2.2.3. Particle Morphology Analysis
2.2.4. Spectroscopic Characterization
2.2.5. Thermal Analysis
2.2.6. Mechanical Test
2.2.7. Thermal Conductivity Measurements
2.2.8. Electrical Properties
2.2.9. DFT Calculations
3. Results and Discussion
3.1. Sample Preparation
3.2. Particle Morphology Analysis
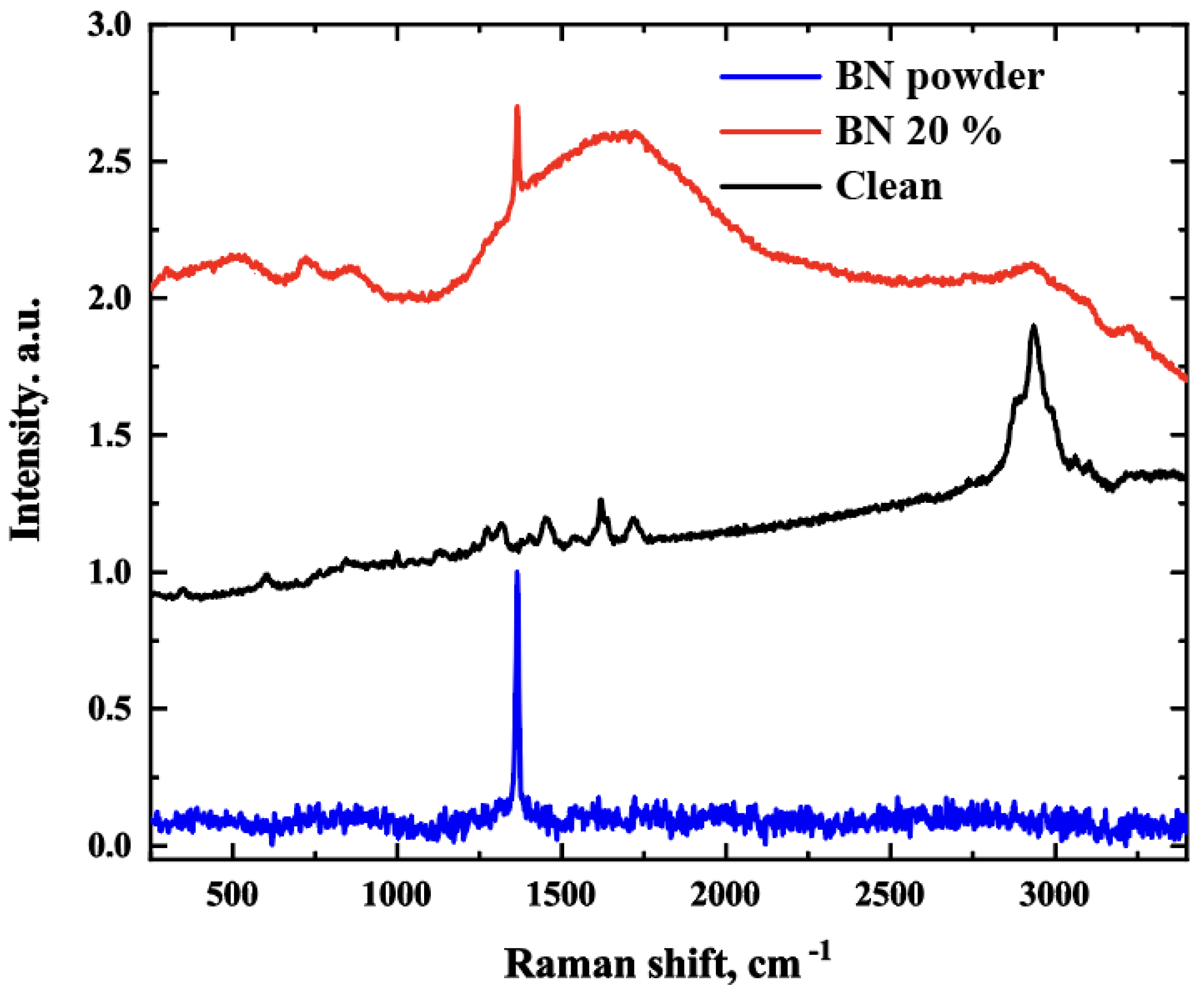
3.3. Spectroscopic Characterization
3.4. Thermal Analysis
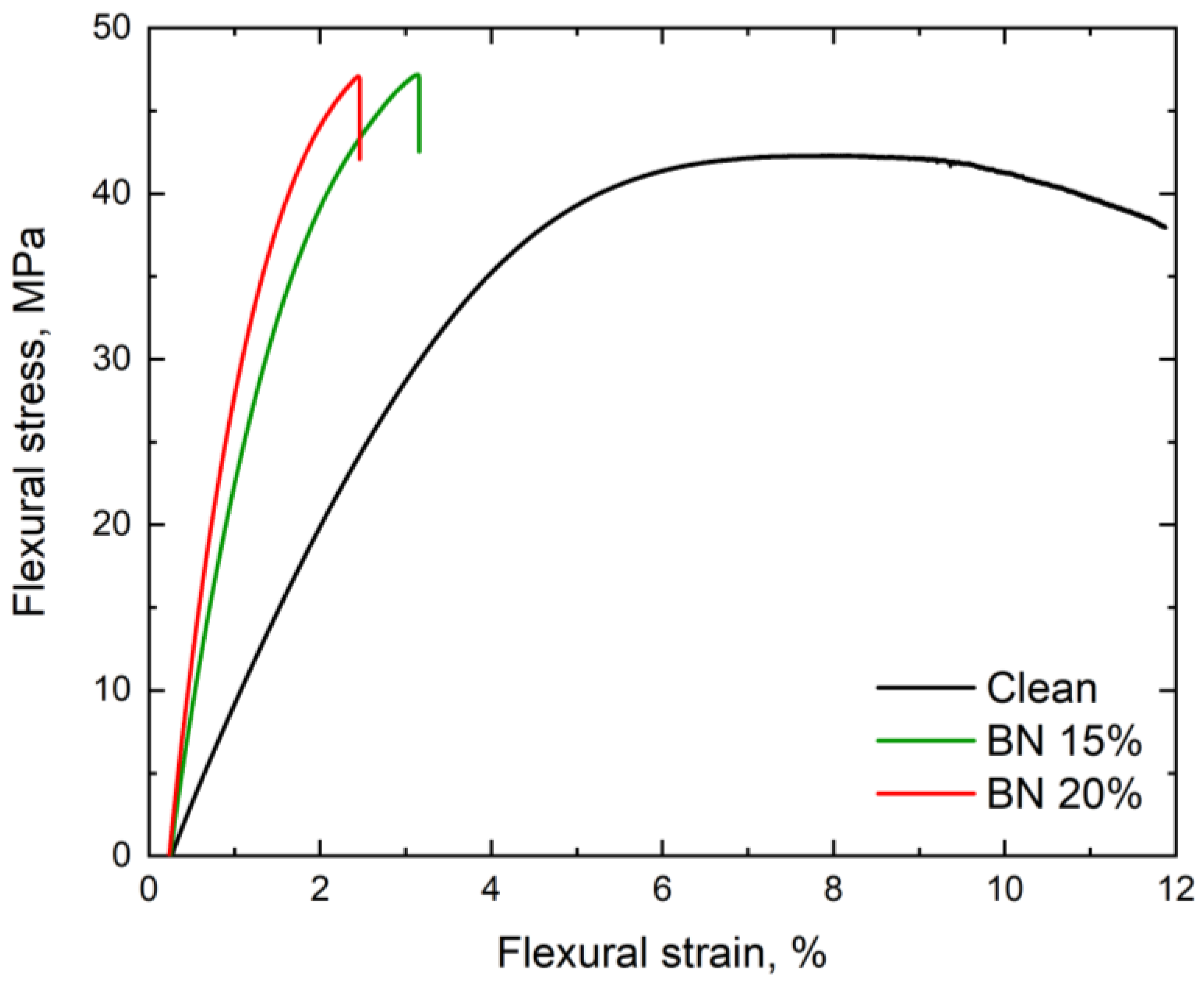
3.5. Mechanical Analysis
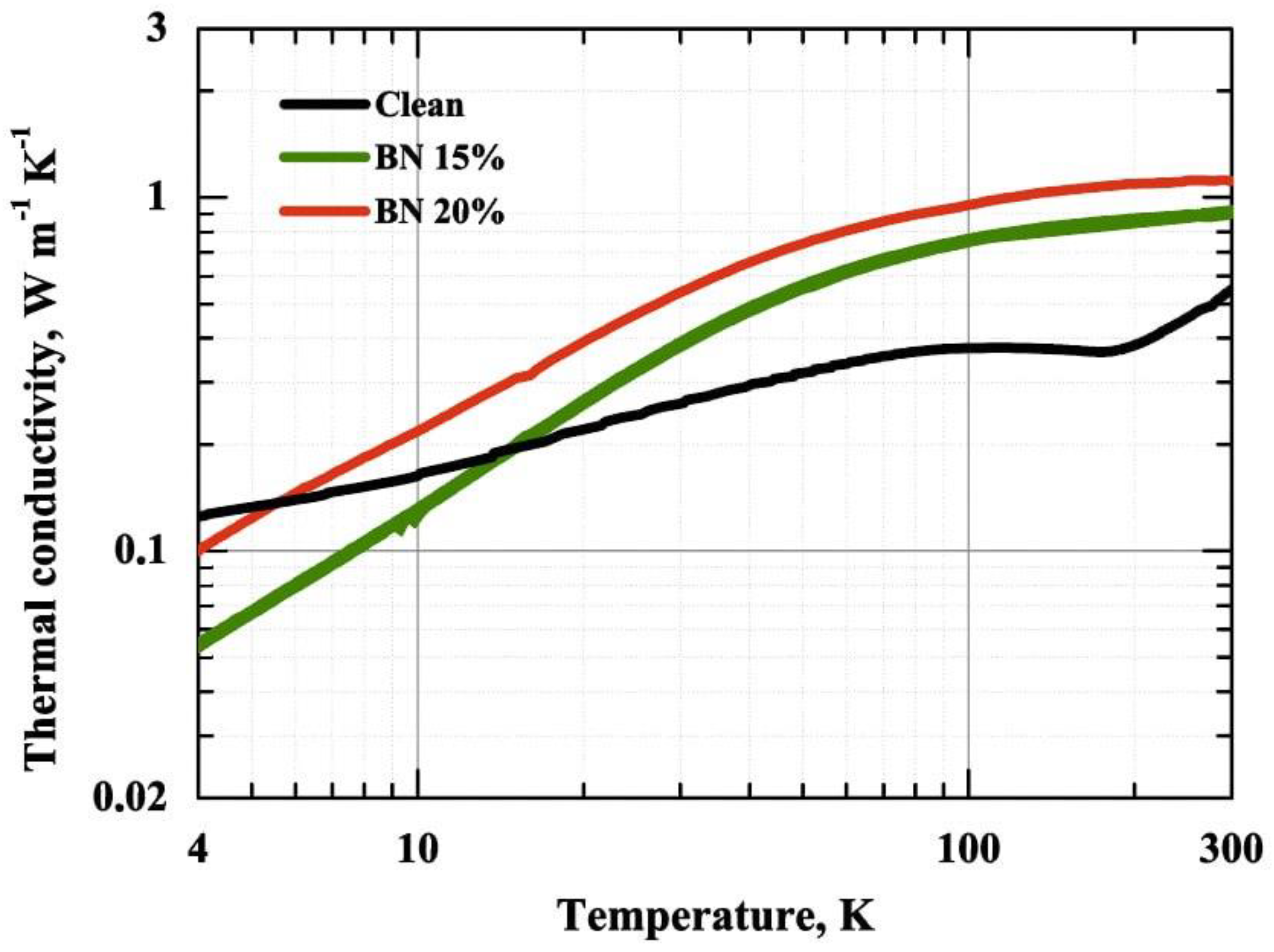
3.6. Thermal Conductivity Measurements
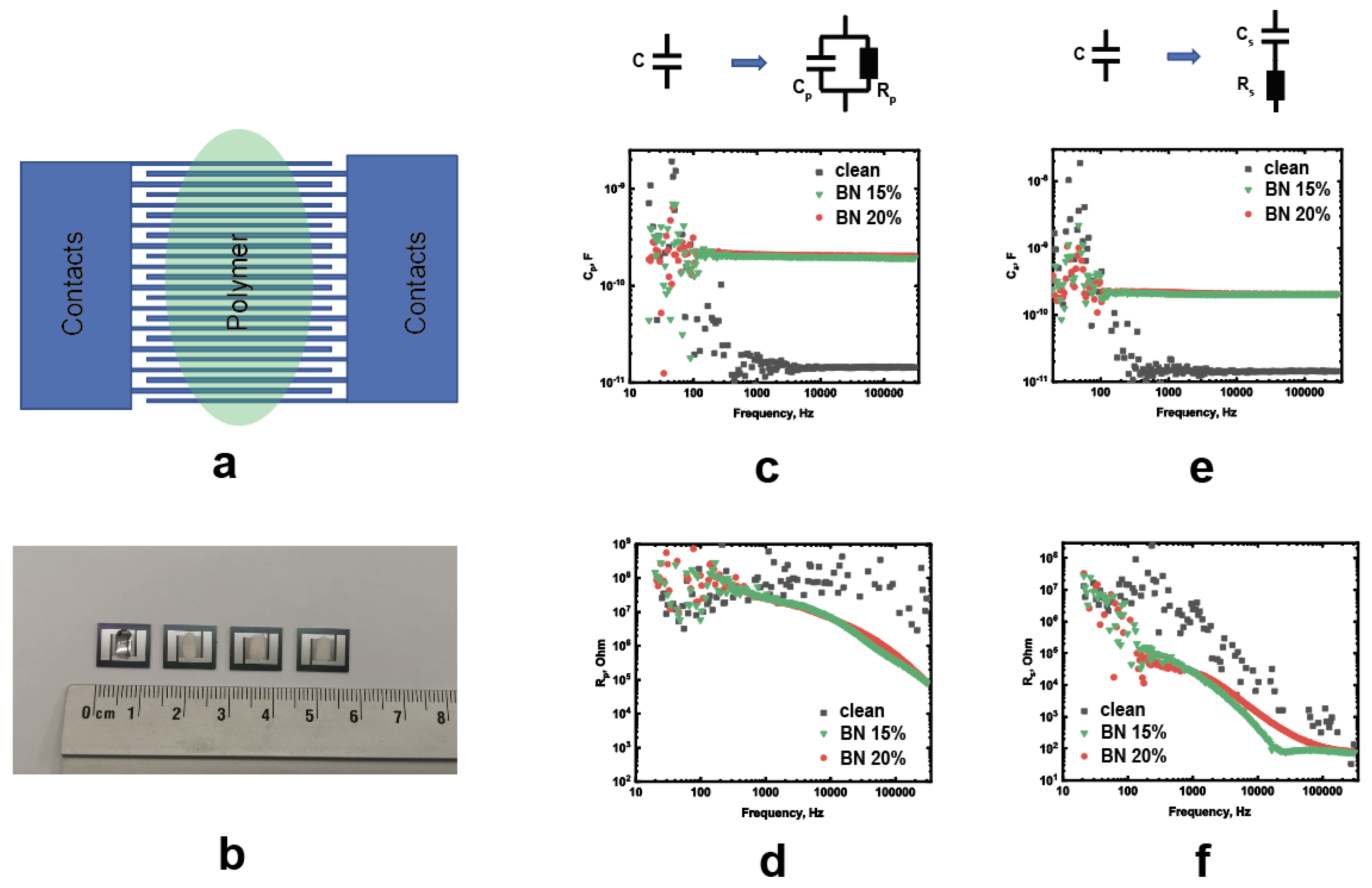
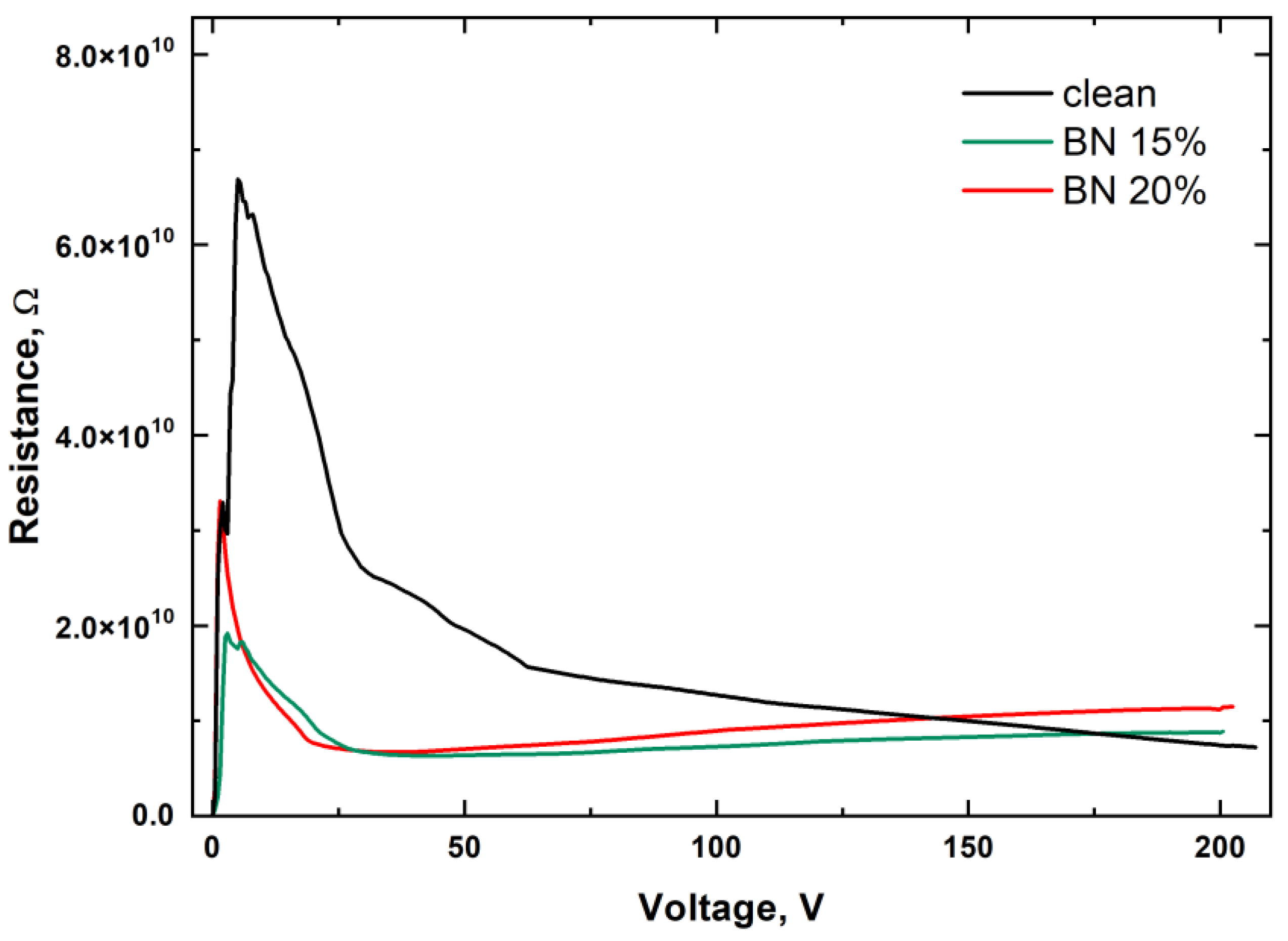
3.7. Electrical Properties
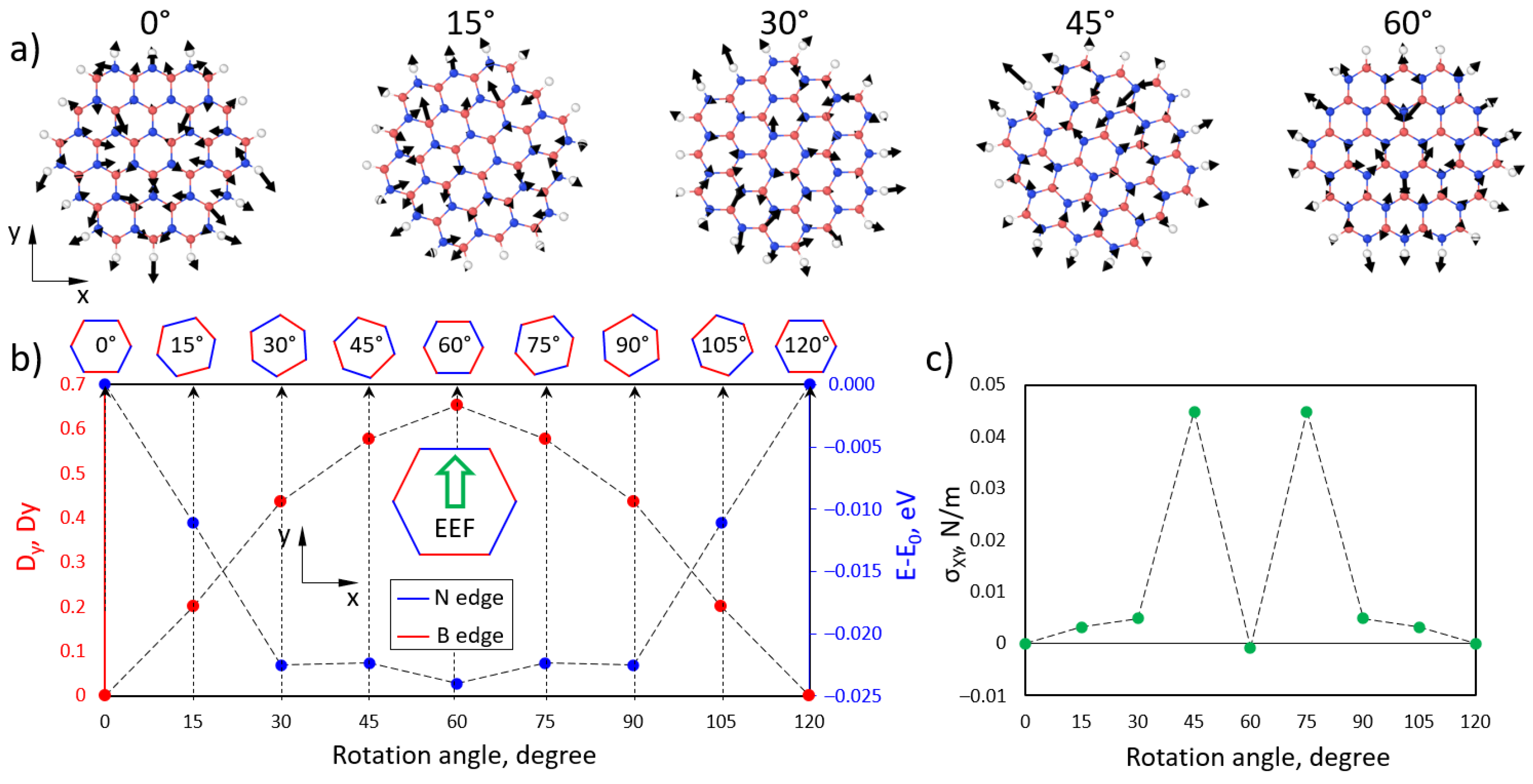
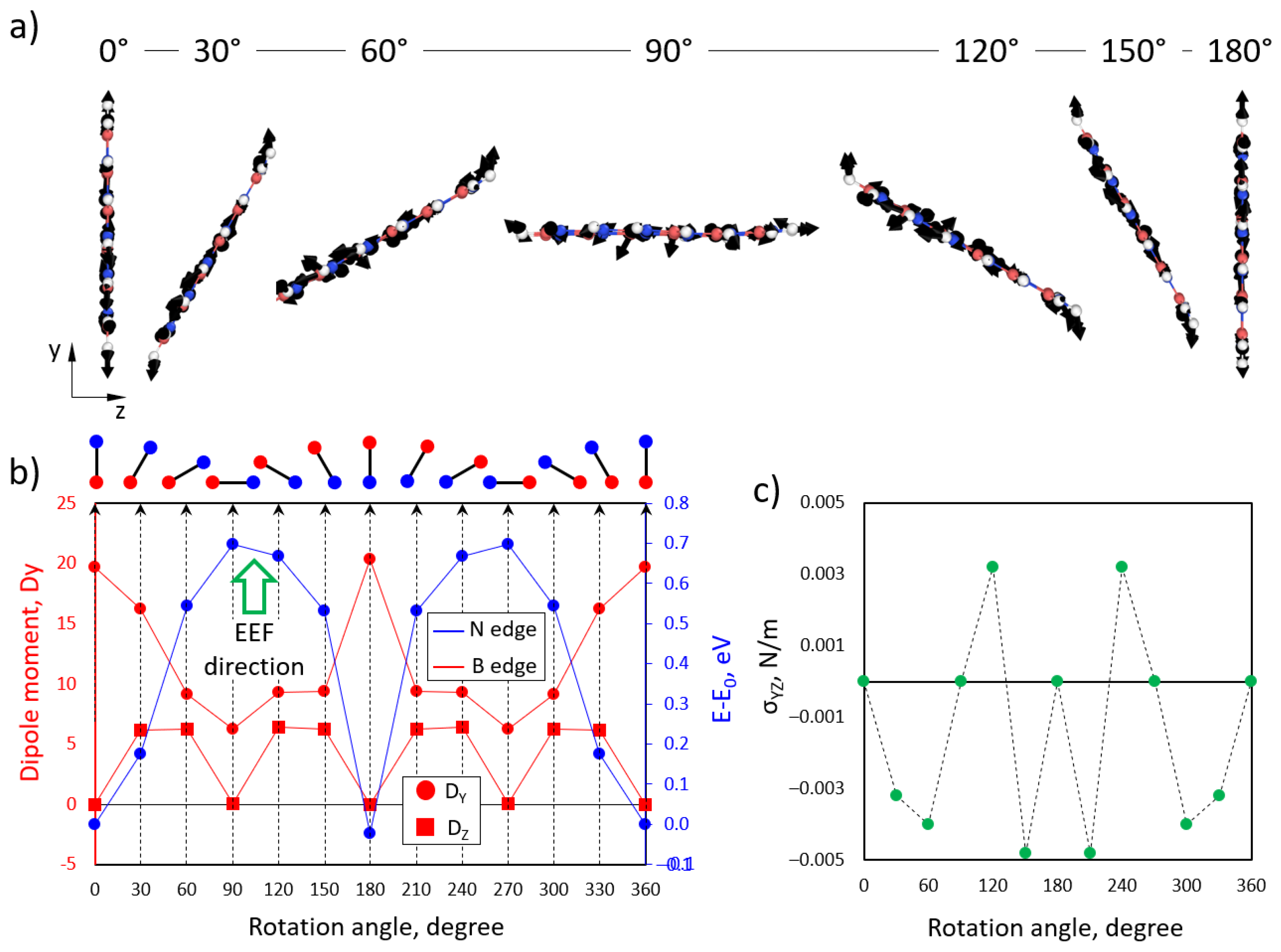
3.8. DFT Calculations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rho, H.; Jang, Y.S.; Bae, H.; Cha, A.-N.; Lee, S.H.; Ha, J.-S. Fanless, Porous Graphene-Copper Composite Heat Sink for Micro Devices. Sci. Rep. 2021, 11, 17607. [Google Scholar] [CrossRef] [PubMed]
- Cahill, D.G.; Braun, P.V.; Chen, G.; Clarke, D.R.; Fan, S.; Goodson, K.E.; Keblinski, P.; King, W.P.; Mahan, G.D.; Majumdar, A.; et al. Nanoscale Thermal Transport. II. 2003–2012. Appl. Phys. Rev. 2014, 1, 011305. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Ginzburg, V.V.; Yang, J.; Yang, Y.; Liu, W.; Huang, Y.; Du, L.; Chen, B. Thermal Conductivity of Polymer-Based Composites: Fundamentals and Applications. Prog. Polym. Sci. 2016, 59, 41–85. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Sun, M.; Liang, L.; Yang, H.; Li, Y.; Yang, K. Enhance the Thermal Conductivity and Maintain Insulation Property of Epoxy via Constructing a Three-Dimensional Network by Doping Hexagonal Boron Nitride and Carbon Nanofiber. J. Mater. Sci. Mater. Electron. 2021, 32, 28840–28855. [Google Scholar] [CrossRef]
- Al-Muallim, B.; Harun, W.S.W.; Al Rikabi, I.J.; Mohammed, H.A. Thermally Conductive Polymer Nanocomposites for Filament-Based Additive Manufacturing. J. Mater. Sci. 2022, 57, 3993–4019. [Google Scholar] [CrossRef]
- Wang, F.; Zeng, X.; Yao, Y.; Sun, R.; Xu, J.; Wong, C.-P. Silver Nanoparticle-Deposited Boron Nitride Nanosheets as Fillers for Polymeric Composites with High Thermal Conductivity. Sci. Rep. 2016, 6, 19394. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kargar, F.; Barani, Z.; Salgado, R.; Debnath, B.; Lewis, J.S.; Aytan, E.; Lake, R.K.; Balandin, A.A. Thermal Percolation Threshold and Thermal Properties of Composites with High Loading of Graphene and Boron Nitride Fillers. ACS Appl. Mater. Interfaces 2018, 10, 37555–37565. [Google Scholar] [CrossRef]
- Lewis, J.S.; Barani, Z.; Magana, A.S.; Kargar, F.; Balandin, A.A. Thermal and Electrical Conductivity Control in Hybrid Composites with Graphene and Boron Nitride Fillers. Mater. Res. Express 2019, 6, 085325. [Google Scholar] [CrossRef] [Green Version]
- Marske, F.; Lindenberg, T.; Martins de Souza e Silva, J.; Wehrspohn, R.B.; Maijenburg, A.W.; Hahn, T.; Enke, D. Size and Surface Effects of Hexagonal Boron Nitrides on the Physicochemical Properties of Monolithic Phase Change Materials Synthesized via Sol–Gel Route. Appl. Therm. Eng. 2021, 196, 117325. [Google Scholar] [CrossRef]
- Yang, J.; Cao, C.; Qiao, W.; Qiao, J.; Gao, H.; Bai, W.; Li, Z.; Wang, P.; Tang, C.; Xue, Y. Chemo-Mechanically Exfoliated Boron Nitride Nanosheet/Poly(Vinyl Alcohol) Composites as Efficient Heat Dissipation Components. ACS Appl. Nano Mater. 2022, 5, 15600–15610. [Google Scholar] [CrossRef]
- Gu, J.; Zhang, Q.; Dang, J.; Xie, C. Thermal Conductivity Epoxy Resin Composites Filled with Boron Nitride. Polym. Adv. Technol. 2012, 23, 1025–1028. [Google Scholar] [CrossRef]
- Sudhindra, S.; Ramesh, L.; Balandin, A.A. Graphene Thermal Interface Materials—State-of-the-Art and Application Prospects. IEEE Open J. Nanotechnol. 2022, 3, 169–181. [Google Scholar] [CrossRef]
- Naghibi, S.; Kargar, F.; Wright, D.; Huang, C.Y.T.; Mohammadzadeh, A.; Barani, Z.; Salgado, R.; Balandin, A.A. Noncuring Graphene Thermal Interface Materials for Advanced Electronics. Adv. Electron. Mater. 2020, 6, 1901303. [Google Scholar] [CrossRef]
- Coleman, J.N.; Lotya, M.; O’Neill, A.; Bergin, S.D.; King, P.J.; Khan, U.; Young, K.; Gaucher, A.; De, S.; Smith, R.J.; et al. Two-Dimensional Nanosheets Produced by Liquid Exfoliation of Layered Materials. Science 2011, 331, 568–571. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, P.; Qian, X.; Yang, R.; Lindsay, L. Anisotropic Thermal Transport in Bulk Hexagonal Boron Nitride. Phys. Rev. Mater. 2018, 2, 064005. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Z.; Li, J.; Liu, C.; Lao, C.; Fu, Y.; Liu, C.; Li, Y.; Wang, P.; He, Y. 3D Printing of Ceramics: A Review. J. Eur. Ceram. Soc. 2019, 39, 661–687. [Google Scholar] [CrossRef]
- Gao, J.; Hao, M.; Wang, Y.; Kong, X.; Yang, B.; Wang, R.; Lu, Y.; Zhang, L.; Gong, M.; Zhang, L.; et al. 3D Printing Boron Nitride Nanosheets Filled Thermoplastic Polyurethane Composites with Enhanced Mechanical and Thermal Conductive Properties. Addit. Manuf. 2022, 56, 102897. [Google Scholar] [CrossRef]
- Akintola, T.M.; Tran, P.; Downes Sweat, R.; Dickens, T. Thermomechanical Multifunctionality in 3D-Printed Polystyrene-Boron Nitride Nanotubes (BNNT) Composites. J. Compos. Sci. 2021, 5, 61. [Google Scholar] [CrossRef]
- Tao, X.; Du, J.; Li, Y.; Yang, Y.; Fan, Z.; Gan, Y.; Huang, H.; Zhang, W.; Dong, L.; Li, X. TaC Nanowire/Activated Carbon Microfiber Hybrid Structures from Bamboo Fibers. Adv. Energy Mater. 2011, 1, 534–539. [Google Scholar] [CrossRef]
- Tao, X.; Li, Y.; Du, J.; Xia, Y.; Yang, Y.; Huang, H.; Gan, Y.; Zhang, W.; Li, X. A Generic Bamboo-Based Carbothermal Method for Preparing Carbide (SiC, B4C, TiC, TaC, NbC, TixNb1−xC, and TaxNb1−xC) Nanowires. J. Mater. Chem. 2011, 21, 9095–9102. [Google Scholar] [CrossRef] [Green Version]
- Shahzadi, L.; Maya, F.; Breadmore, M.C.; Thickett, S.C. Functional Materials for DLP-SLA 3D Printing Using Thiol–Acrylate Chemistry: Resin Design and Postprint Applications. ACS Appl. Polym. Mater. 2022, 4, 3896–3907. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, M.; Ji, M.; Kuang, X.; Qi, H.J.; Wang, T. Recyclable Thermosetting Polymers for Digital Light Processing 3D Printing. Mater. Des. 2021, 197, 109189. [Google Scholar] [CrossRef]
- Rasaki, S.A.; Xiong, D.; Xiong, S.; Su, F.; Idrees, M.; Chen, Z. Photopolymerization-Based Additive Manufacturing of Ceramics: A Systematic Review. J. Adv. Ceram. 2021, 10, 442–471. [Google Scholar] [CrossRef]
- Halloran, J.W. Ceramic Stereolithography: Additive Manufacturing for Ceramics by Photopolymerization. Annu. Rev. Mater. Res. 2016, 46, 19–40. [Google Scholar] [CrossRef]
- Bice, J.E.; St. Germain, E.; Wohlever, S.J.; Goddard, G.; Erb, R.M. Thermoformable Boron Nitride Based All-Ceramics. Adv. Mater. 2022, 34, 2203939. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; Garcia, A.; Junquera, J.; Ordejon, P.; Sanchez-Portal, D. The SIESTA Method for Ab Initio Order-N Materials Simulation. J. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Yang, W. Comment on “Generalized Gradient Approximation Made Simple”. Phys. Rev. Lett. 1998, 80, 890. [Google Scholar] [CrossRef]
- Holzmond, O.; Li, X. In Situ Real Time Defect Detection of 3D Printed Parts. Addit. Manuf. 2017, 17, 135–142. [Google Scholar] [CrossRef]
- Tarabeux, J.; Pateloup, V.; Michaud, P.; Chartier, T. Development of a Numerical Simulation Model for Predicting the Curing of Ceramic Systems in the Stereolithography Process. J. Eur. Ceram. Soc. 2018, 38, 4089–4098. [Google Scholar] [CrossRef]
- Chaurasia, S.; Rao, U.; Mishra, A.K.; Sijoy, C.d.; Mishra, V. Raman Spectroscopy of Poly (Methyl Methacrylate) under Laser Shock and Static Compression. J. Raman Spectrosc. 2020, 51, 860–870. [Google Scholar] [CrossRef]
- Menezes, D.B.; Reyer, A.; Benisek, A.; Dachs, E.; Pruner, C.; Musso, M. Raman Spectroscopic Insights into the Glass Transition of Poly(Methyl Methacrylate). Phys. Chem. Chem. Phys. 2021, 23, 1649–1665. [Google Scholar] [CrossRef] [PubMed]
- Peterson, J.D.; Vyazovkin, S.; Wight, C.A. Kinetic Study of Stabilizing Effect of Oxygen on Thermal Degradation of Poly(Methyl Methacrylate). J. Phys. Chem. B 1999, 103, 8087–8092. [Google Scholar] [CrossRef]
- Holland, B.J.; Hay, J.N. The Kinetics and Mechanisms of the Thermal Degradation of Poly(Methyl Methacrylate) Studied by Thermal Analysis-Fourier Transform Infrared Spectroscopy. Polymer 2001, 42, 4825–4835. [Google Scholar] [CrossRef]
- Liaw, J.H.; Hsueh, T.Y.; Tan, T.-S.; Wang, Y.; Chiao, S.-M. Twin-Screw Compounding of Poly(Methyl Methacrylate)/Clay Nanocomposites: Effects of Compounding Temperature and Matrix Molecular Weight. Polym. Int. 2007, 56, 1045–1052. [Google Scholar] [CrossRef]
- Casimir, H.B.G. Note on the Conduction of Heat in Crystals. Physica 1938, 5, 495–500. [Google Scholar] [CrossRef]
- Berman, R. Thermal Conduction in Solids; Berman, R., Ed.; Oxford University Press: Oxford, UK, 1976. [Google Scholar]
- Mazumder, M.R.H.; Mathews, L.D.; Mateti, S.; Salim, N.V.; Parameswaranpillai, J.; Govindaraj, P.; Hameed, N. Boron Nitride Based Polymer Nanocomposites for Heat Dissipation and Thermal Management Applications. Appl. Mater. Today 2022, 29, 101672. [Google Scholar] [CrossRef]
- Mehra, N.; Mu, L.; Ji, T.; Yang, X.; Kong, J.; Gu, J.; Zhu, J. Thermal Transport in Polymeric Materials and across Composite Interfaces. Appl. Mater. Today 2018, 12, 92–130. [Google Scholar] [CrossRef]
- Swartz, E.T.; Pohl, R.O. Thermal Boundary Resistance. Rev. Mod. Phys. 1989, 61, 605–668. [Google Scholar] [CrossRef]
- Araujo, F.F.T.; Rosenberg, H.M. The Thermal Conductivity of Epoxy-Resin/Metal-Powder Composite Materials from 1.7 to 300K. J. Phys. Appl. Phys. 1976, 9, 665–675. [Google Scholar] [CrossRef]
- Putnam, S.A.; Cahill, D.G.; Ash, B.J.; Schadler, L.S. High-Precision Thermal Conductivity Measurements as a Probe of Polymer/Nanoparticle Interfaces. J. Appl. Phys. 2003, 94, 6785–6788. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bondareva, J.V.; Chernodoubov, D.A.; Dubinin, O.N.; Tikhonov, A.A.; Simonov, A.P.; Suetin, N.V.; Tarkhov, M.A.; Popov, Z.I.; Kvashnin, D.G.; Evlashin, S.A.; et al. Thermal and Electrical Properties of Additively Manufactured Polymer–Boron Nitride Composite. Polymers 2023, 15, 1214. https://doi.org/10.3390/polym15051214
Bondareva JV, Chernodoubov DA, Dubinin ON, Tikhonov AA, Simonov AP, Suetin NV, Tarkhov MA, Popov ZI, Kvashnin DG, Evlashin SA, et al. Thermal and Electrical Properties of Additively Manufactured Polymer–Boron Nitride Composite. Polymers. 2023; 15(5):1214. https://doi.org/10.3390/polym15051214
Chicago/Turabian StyleBondareva, Julia V., Daniil A. Chernodoubov, Oleg N. Dubinin, Andrey A. Tikhonov, Alexey P. Simonov, Nikolay V. Suetin, Mikhail A. Tarkhov, Zakhar I. Popov, Dmitry G. Kvashnin, Stanislav A. Evlashin, and et al. 2023. "Thermal and Electrical Properties of Additively Manufactured Polymer–Boron Nitride Composite" Polymers 15, no. 5: 1214. https://doi.org/10.3390/polym15051214
APA StyleBondareva, J. V., Chernodoubov, D. A., Dubinin, O. N., Tikhonov, A. A., Simonov, A. P., Suetin, N. V., Tarkhov, M. A., Popov, Z. I., Kvashnin, D. G., Evlashin, S. A., & Safonov, A. A. (2023). Thermal and Electrical Properties of Additively Manufactured Polymer–Boron Nitride Composite. Polymers, 15(5), 1214. https://doi.org/10.3390/polym15051214









