Influence on Elastic Wave Propagation Behavior in Polymers Composites: An Analysis of Inflection Phenomena
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Preparation
2.2. Characterization
2.2.1. Content Testing
2.2.2. Microstructure
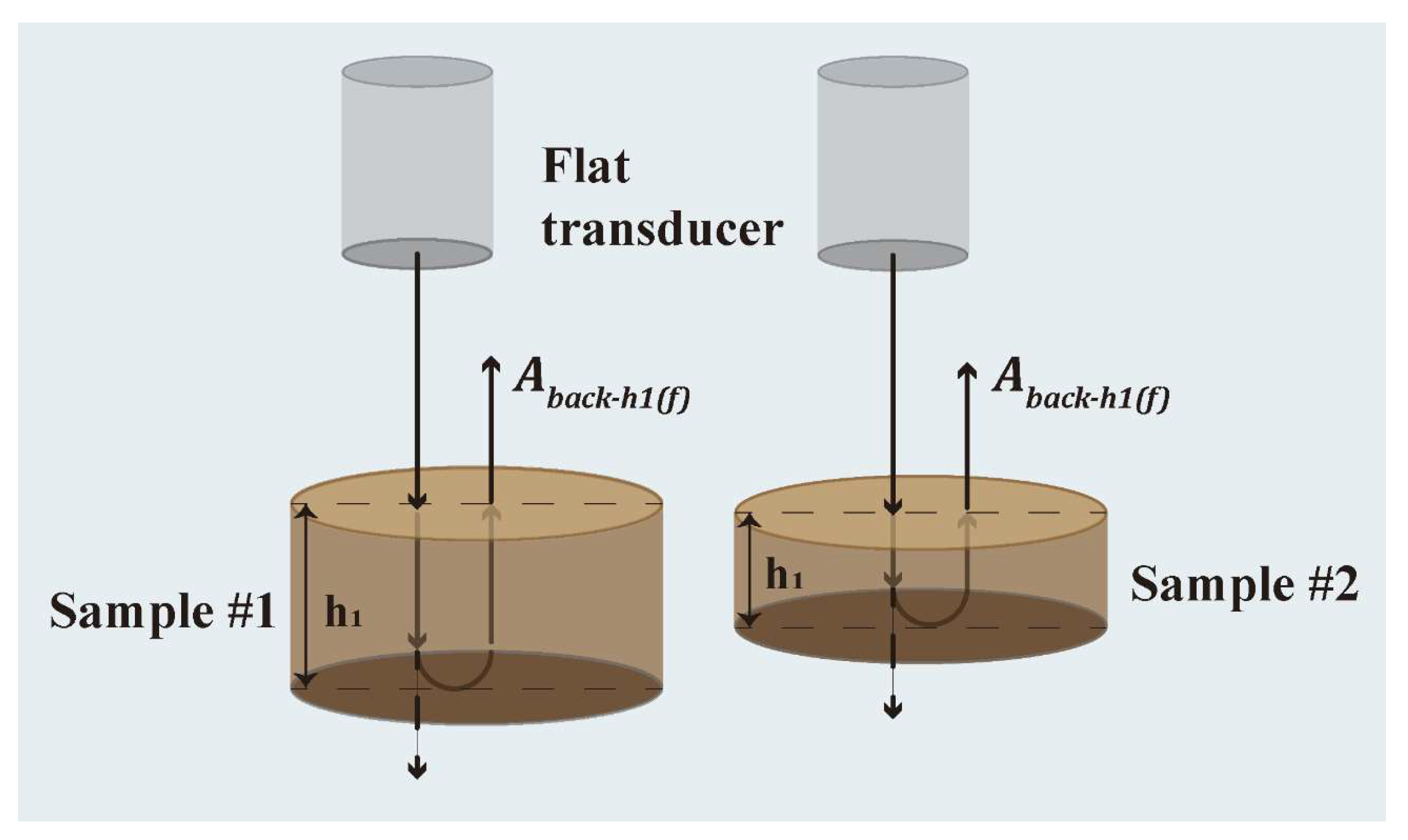
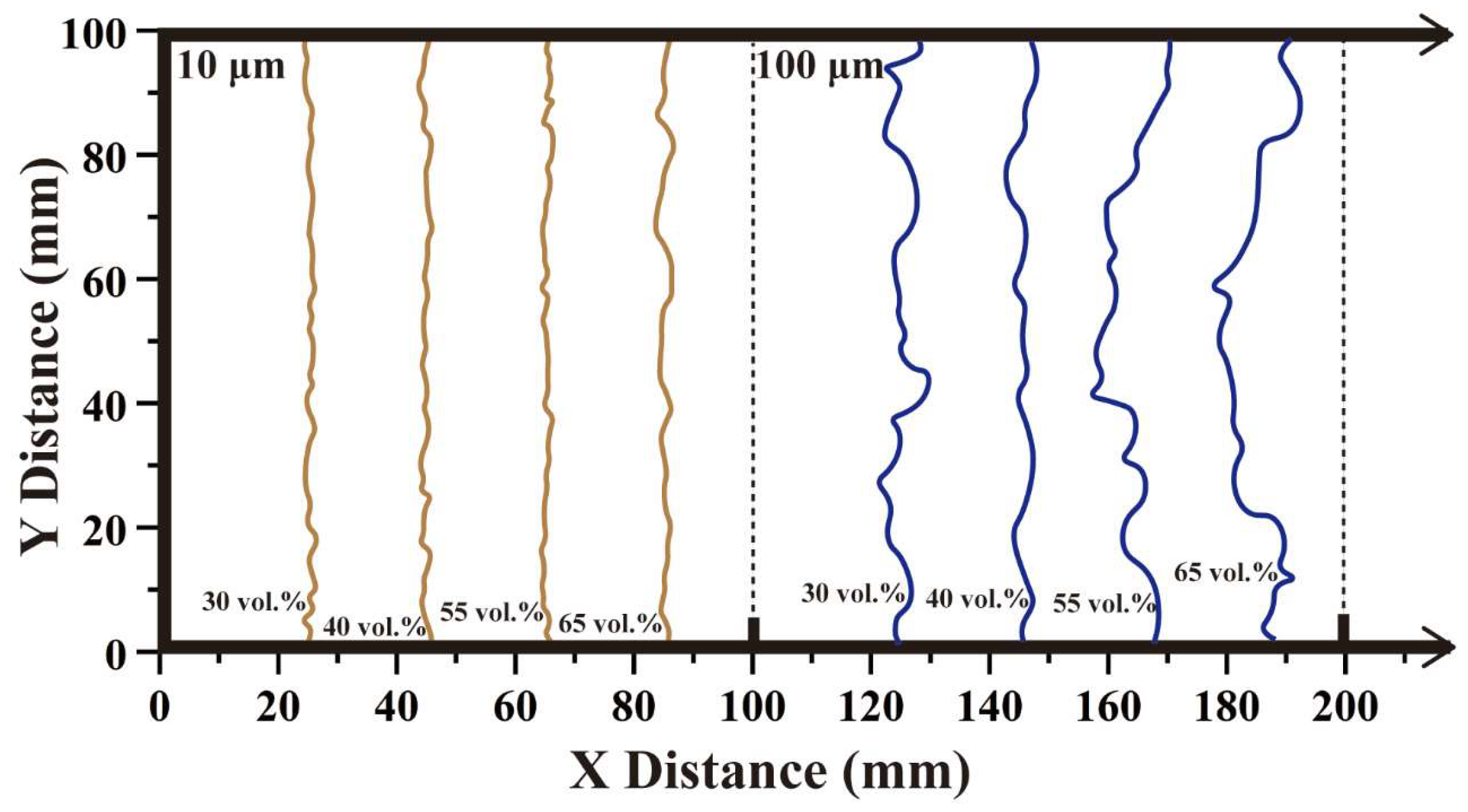
2.2.3. Elastic Wave Properties Measurements
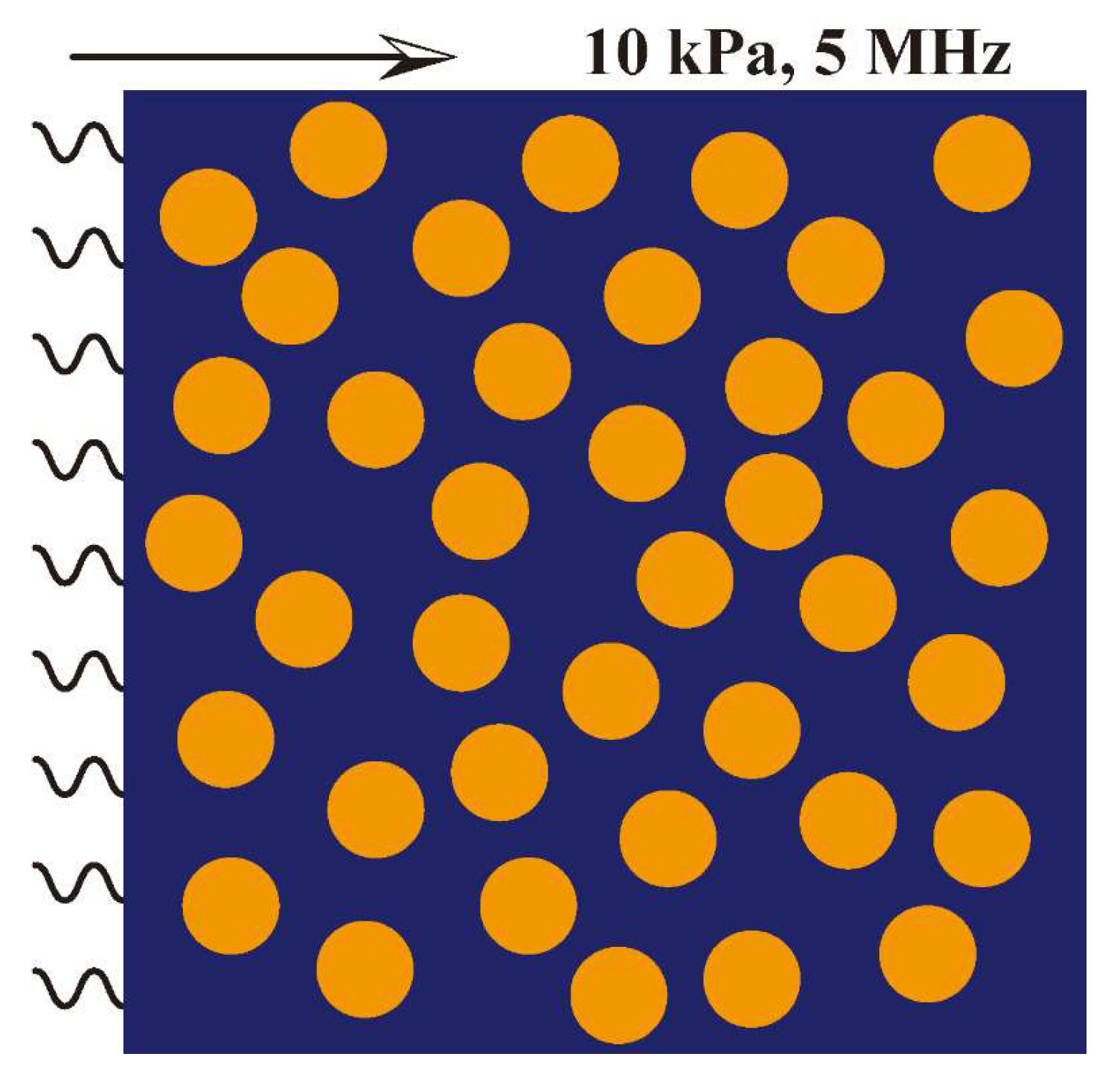
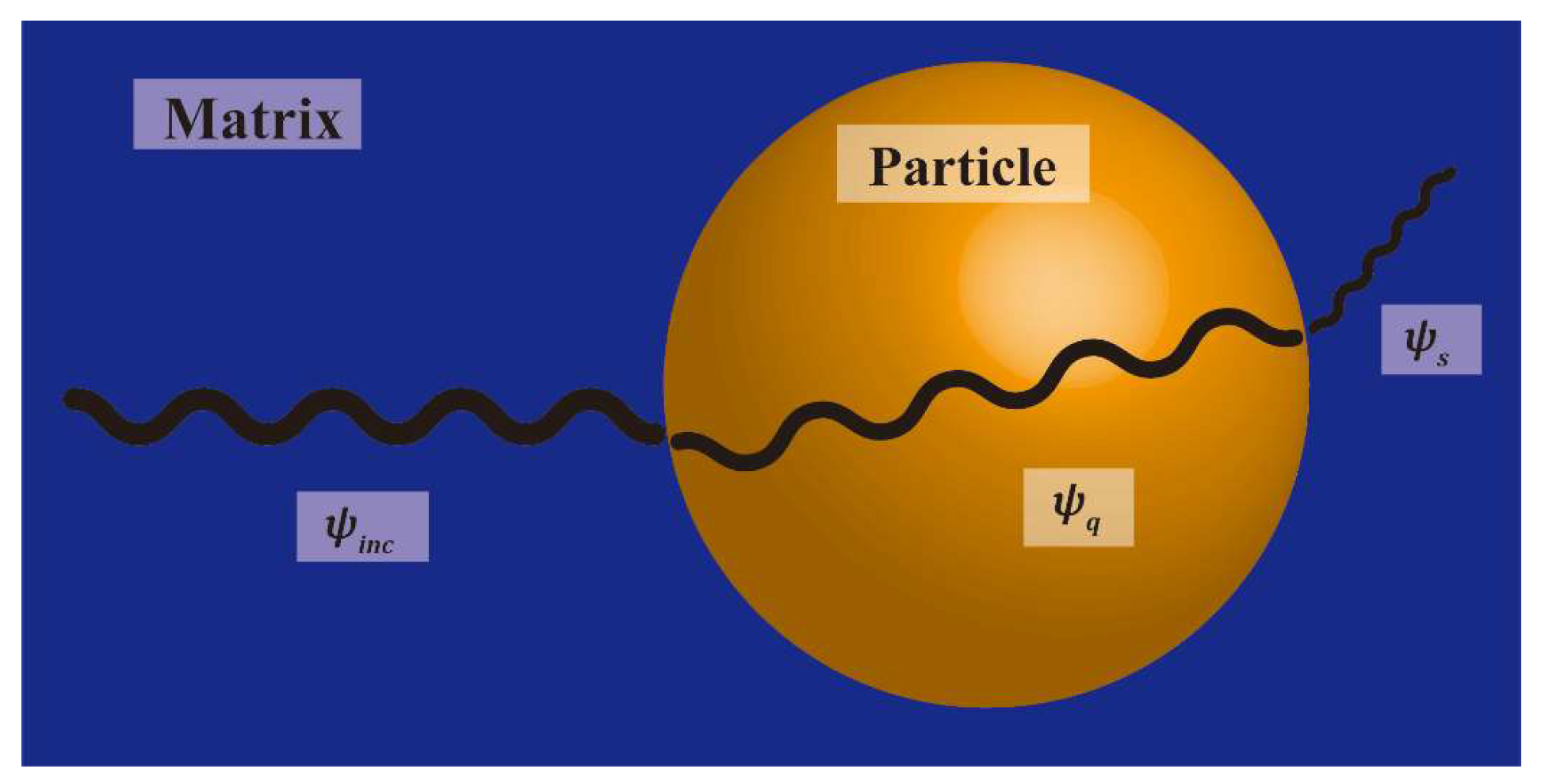
2.3. FEM Simulation
3. Results and Discussion
3.1. Composites Structures
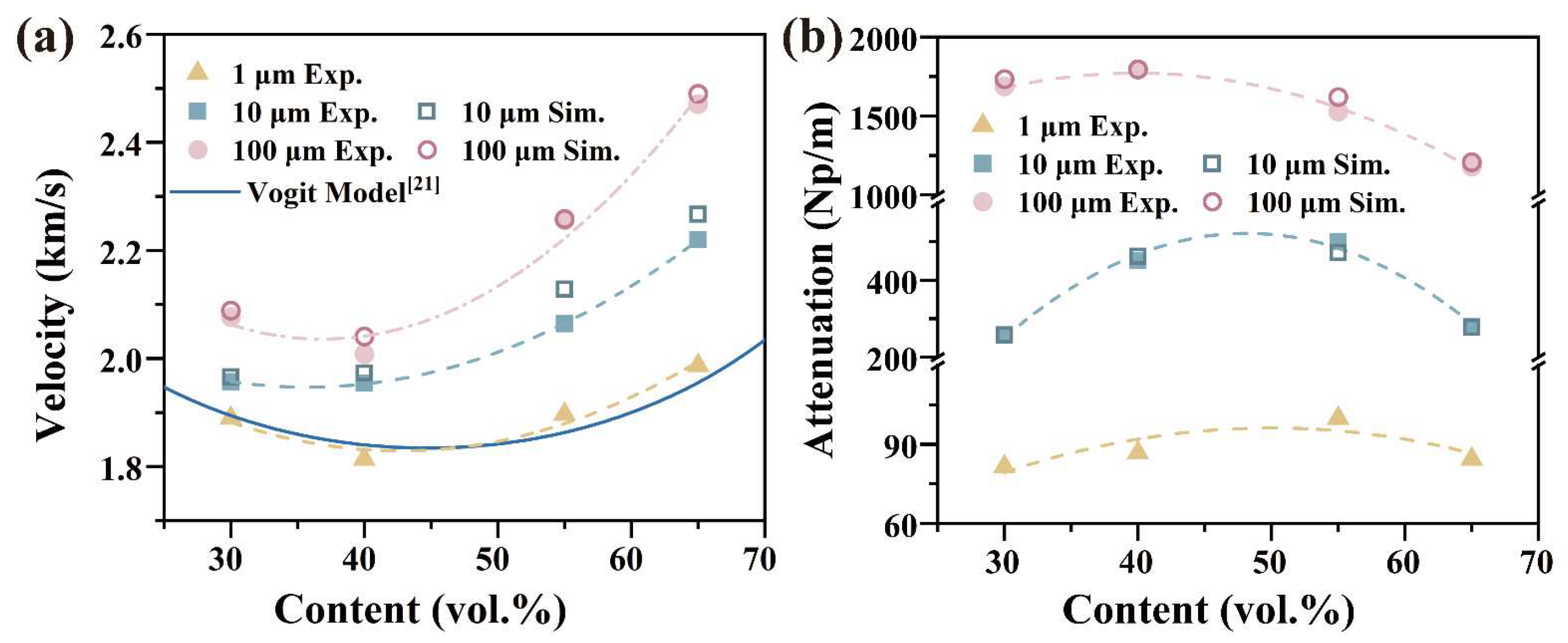
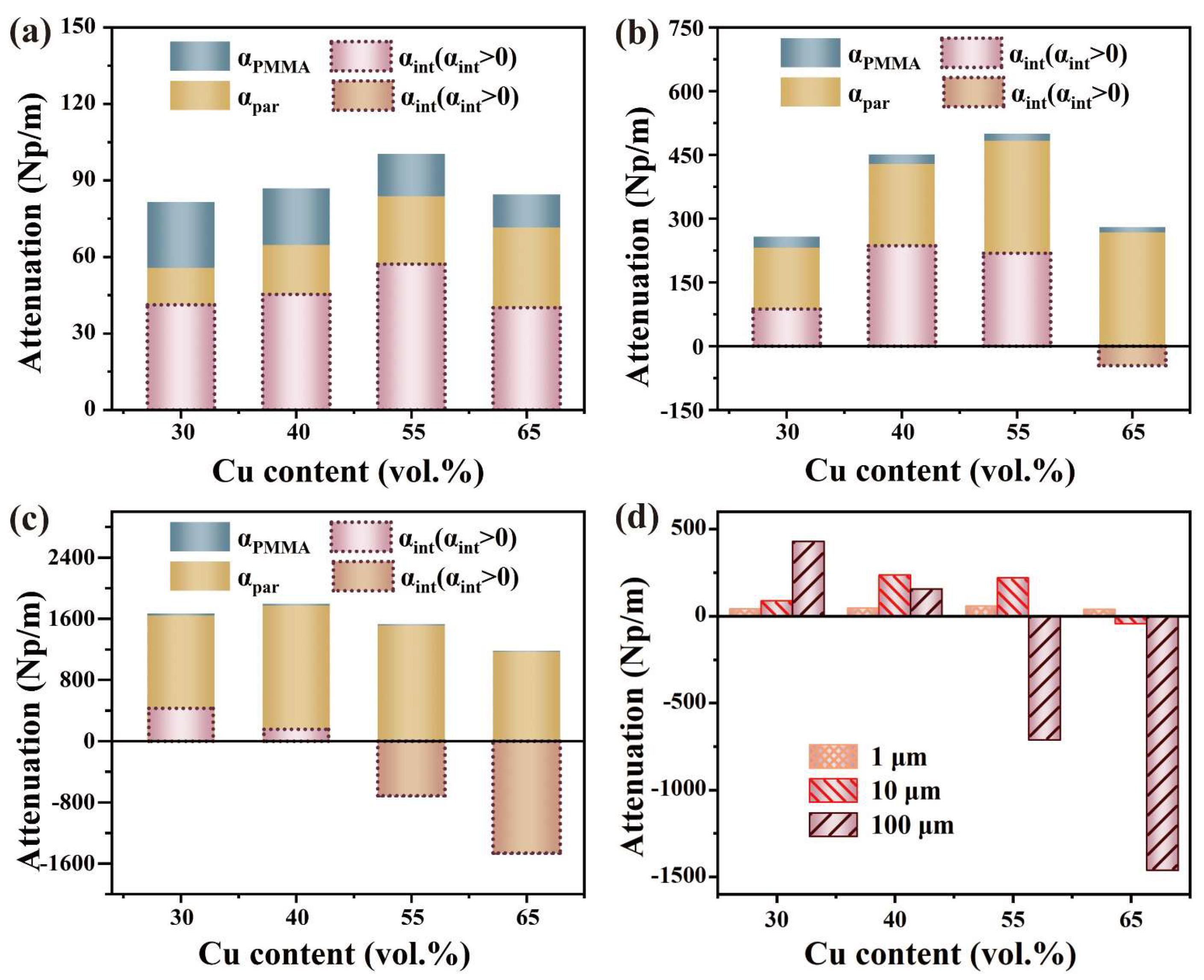
3.2. Elastic Wave Velocity and Attenuation
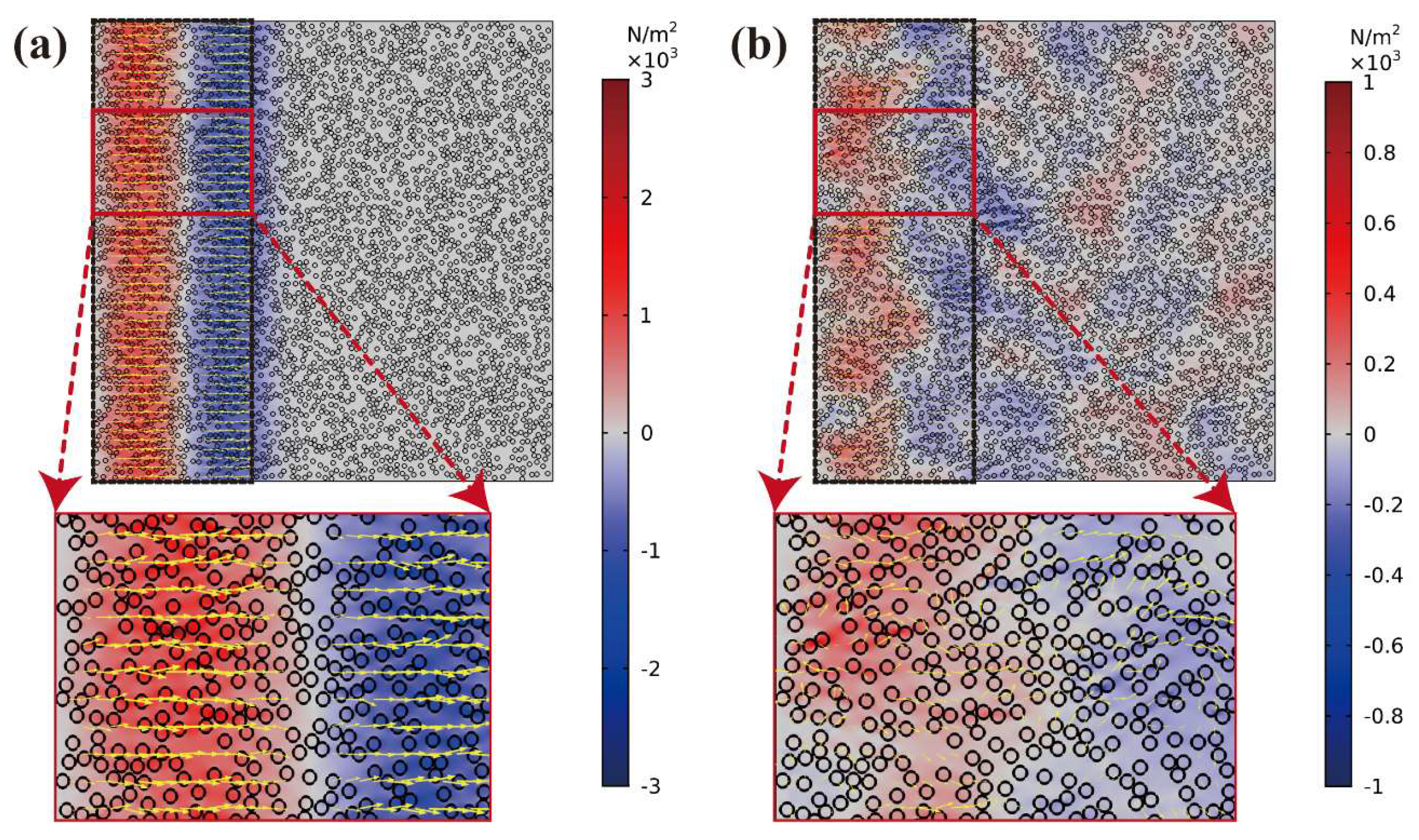
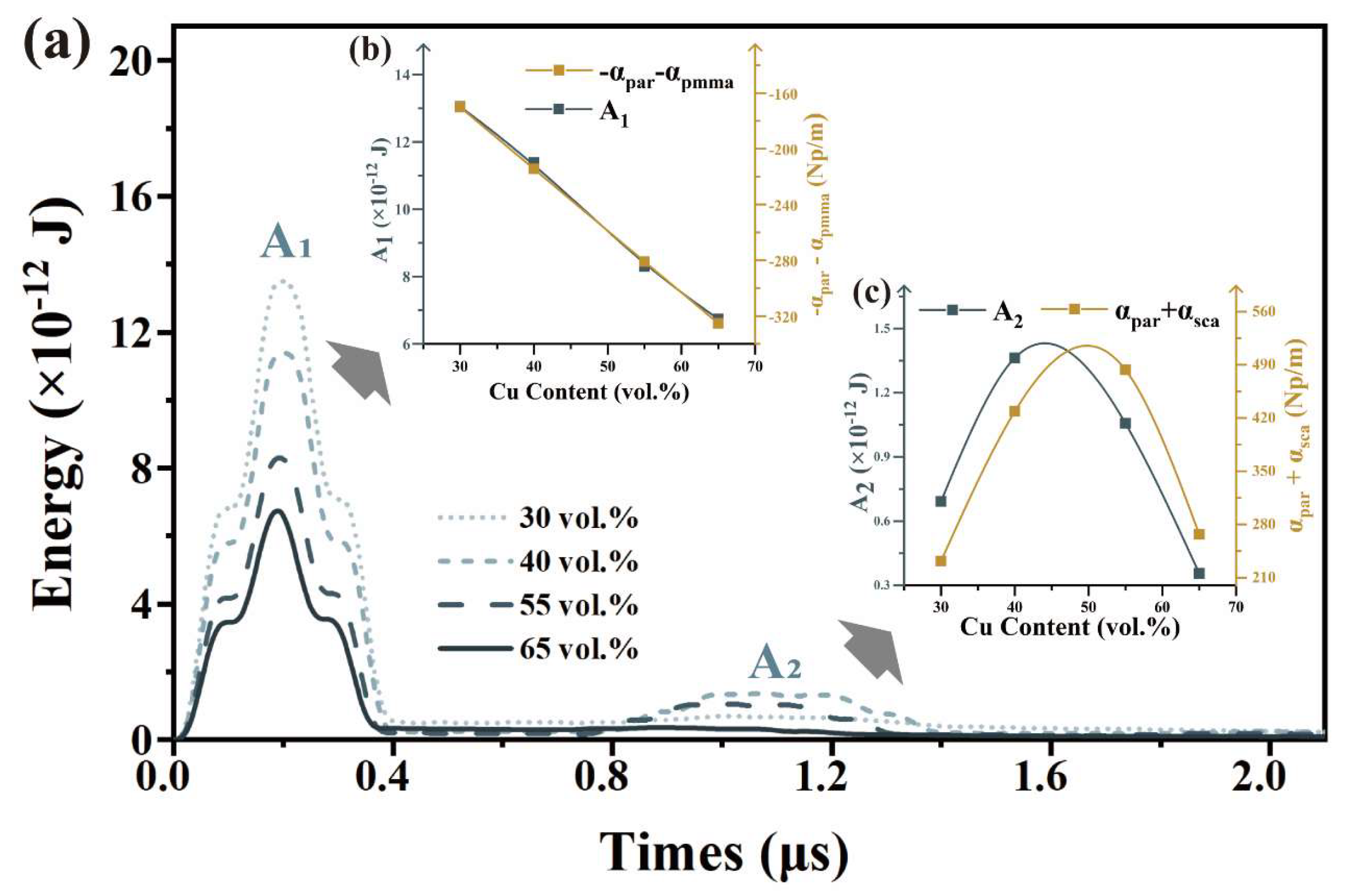
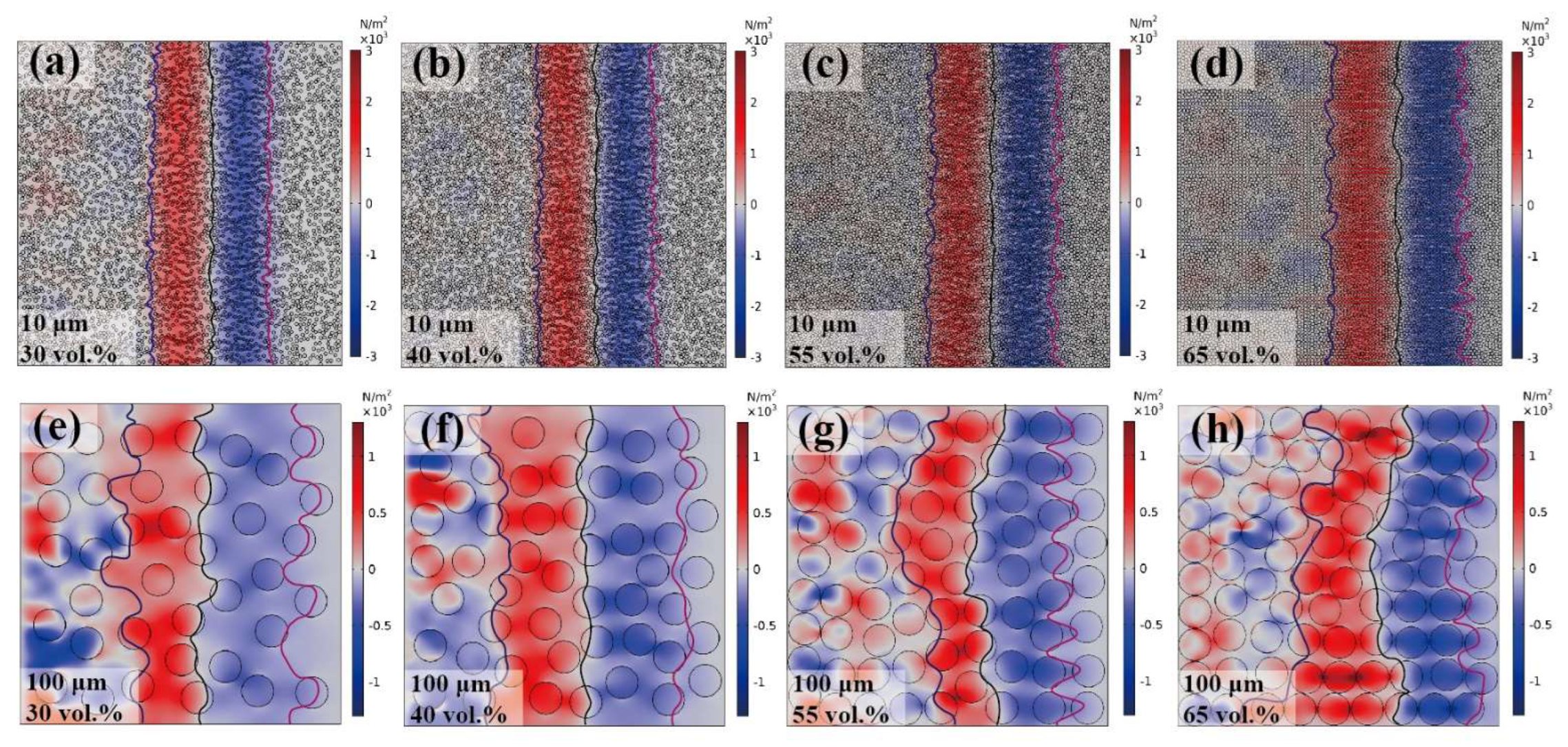
3.3. Analysis of Wave Velocity and Attenuation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bartczak, Z.; Argon, A.S.; Cohen, R.E.; Weinberg, M. Toughness mechanism in semi-crystalline polymer blends: II. High-density polyethylene toughened with calcium carbonate filler particles. Polymer 1999, 40, 2347–2365. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, Y.; Wan, Q.; Li, H.; Shi, X.; Tang, S.; Peng, X. A Hyperelastic Constitutive Model for Chain-Structured Particle Reinforced Neo-Hookean Composites. Mater. Des. 2016, 95, 580–590. [Google Scholar] [CrossRef]
- Xu, W.; Wu, F.; Jiao, Y.; Liu, M. A general micromechanical framework of effective moduli for the design of nonspherical nano- and micro-particle reinforced composites with interface properties. Mater. Des. 2017, 127, 162–172. [Google Scholar] [CrossRef]
- Bayan, M.F.; Jaradat, A.; Alyami, M.H.; Naser, A.Y. Smart Pellets for Controlled Delivery of 5-Fluorouracil. Molecules 2023, 28, 306. [Google Scholar] [CrossRef] [PubMed]
- Bayan, M.F.; Marji, S.M.; Salem, M.S.; Begum, M.Y.; Chidambaram, K.; Chandrasekaran, B. Development of Polymeric-Based Formulation as Potential Smart Colonic Drug Delivery System. Polymers 2022, 14, 3697. [Google Scholar] [CrossRef]
- Bhagyashekar, M.S.; Rao, K.; Rao, R. Studies on Rheological and Physical Properties of Metallic and Non-metallic Particulate Filled Epoxy Composites. J. Reinf. Plast. Compos. 2009, 28, 2869–2878. [Google Scholar] [CrossRef]
- Charalambopoulos, A.; Gergidis, L.N.; Kartalos, G. On the gradient elastic wave propagation in cylindrical waveguides with microstructure. Compos. Part B Eng. 2012, 43, 2613–2627. [Google Scholar] [CrossRef]
- Duernberger, E.; MacLeod, C.; Lines, D. Fibre volume fraction screening of pultruded carbon fibre reinforced polymer panels based on analysis of anisotropic ultrasonic sound velocity. Compos. Part B Eng. 2023, 254, 110577. [Google Scholar] [CrossRef]
- Wan, H.; Leung, N.; Jargalsaikhan, U.; Ho, E.; Wang, C.; Liu, Q.; Peng, H.-X.; Su, B.; Sui, T. Fabrication and characterisation of alumina/aluminium composite materials with a nacre-like micro-layered architecture. Mater. Des. 2022, 223, 111190. [Google Scholar] [CrossRef]
- Miracle, D.B.; Donaldson, S.L.; Henry, S.D.; Moosbrugger, C.; Anton, G.J.; Sanders, B.R.; Hrivnak, N.; Terman, C.; Kinson, J.; Muldoon, K. ASM Handbook; ASM International: Materials Park, OH, USA, 2001; Volume 21. [Google Scholar]
- Tekalur, S.A.; Shukla, A.; Shivakumar, K. Blast resistance of polyurea based layered composite materials. Compos. Struct. 2008, 84, 271–281. [Google Scholar] [CrossRef]
- Zigoneanu, L.; Popa, B.I.; Cummer, S.A. Three-dimensional broadband omnidirectional acoustic ground cloak. Nat. Mater. 2014, 13, 352–355. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Zhai, Z.; Zhao, X.; Tian, X.; Li, D.; Wang, Q.; Jiang, H. Modular Design for Acoustic Metamaterials: Low-Frequency Noise Attenuation. Adv. Funct. Mater. 2022, 32, 2105712. [Google Scholar] [CrossRef]
- Noguchi, Y.; Matsushima, K.; Yamada, T. Level set-based topology optimization for the design of labyrinthine acoustic metamaterials. Mater. Des. 2022, 219, 110832. [Google Scholar] [CrossRef]
- Man, X.; Luo, Z.; Liu, J.; Xia, B. Hilbert fractal acoustic metamaterials with negative mass density and bulk modulus on subwavelength scale. Mater. Des. 2019, 180, 107911. [Google Scholar] [CrossRef]
- Wei, Y.; Liu, X.; Hu, G. Quadramode materials: Their design method and wave property. Mater. Des. 2021, 210, 110031. [Google Scholar] [CrossRef]
- Cummer, S.A.; Christensen, J.; Alù, A. Controlling sound with acoustic metamaterials. Nat. Rev. Mater. 2016, 1, 16001. [Google Scholar] [CrossRef]
- Liu, J.; Guo, H.; Wang, T. A Review of Acoustic Metamaterials and Phononic Crystals. Crystals 2020, 10, 305. [Google Scholar] [CrossRef]
- Yang, M.; Ma, G.; Yang, Z.; Sheng, P. Coupled Membranes with Doubly Negative Mass Density and Bulk Modulus. Phys. Rev. Lett. 2013, 110, 134301. [Google Scholar] [CrossRef]
- Qiao, J.; Amirkhizi, A.V.; Schaaf, K.; Nemat-Nasser, S. Dynamic Mechanical Analysis of Fly Ash Filled Polyurea Elastomer. J. Eng. Mater. Technol. 2010, 133, 011016. [Google Scholar] [CrossRef]
- Hasheminejad, S.M.; Avazmohammadi, R. Size-dependent effective dynamic properties of unidirectional nanocomposites with interface energy effects. Compos. Sci. Technol. 2009, 69, 2538–2546. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, W.; Lü, C. Elastic waves in multiferroic cylinders of sectorial cross-section. Compos. Part B Eng. 2012, 43, 3001–3008. [Google Scholar] [CrossRef]
- Beltzer, A.I.; Bert, C.W.; Striz, A.G. On wave propagation in random particulate composites. Int. J. Solids Struct. 1983, 19, 785–791. [Google Scholar] [CrossRef]
- Toozandehjani, M.; Ostovan, F.; Jamaludin, K.R.; Amrin, A.; Matori, K.A.; Shafiei, E. Process−microstructure−properties relationship in Al−CNTs−Al2O3 nanocomposites manufactured by hybrid powder metallurgy and microwave sintering process. Trans. Nonferrous Met. Soc. China 2020, 30, 2339–2354. [Google Scholar] [CrossRef]
- Toozandehjani, M.; Ostovan, F.; Shamshirsaz, M.; Matori, K.A.; Shafiei, E. Velocity and attenuation of ultrasonic wave in Al–Al2O3 nanocomposite and their correlation to microstructural evolution during synthesizing procedure. J. Mater. Res. Technol. 2021, 15, 2529–2542. [Google Scholar] [CrossRef]
- Luo, G.Q.; Huang, Z.H.; Zhang, R.Z.; Sun, Y.; Zhang, J.; Shen, Q. Sound Velocity and Shock Response Behavior of Cu/PMMA Composites. Chin. J. High Press. Phys. 2021, 35, 011301. [Google Scholar] [CrossRef]
- Biwa, S. Independent scattering and wave attenuation in viscoelastic composites. Mech. Mater. 2001, 33, 635–647. [Google Scholar] [CrossRef]
- Biwa, S.; Idekoba, S.; Ohno, N. Wave attenuation in particulate polymer composites: Independent scattering/absorption analysis and comparison to measurements. Mech. Mater. 2002, 34, 671–682. [Google Scholar] [CrossRef]
- Biwa, S.; Watanabe, Y.; Ohno, N. Analysis of wave attenuation in unidirectional viscoelastic composites by a differential scheme. Compos. Sci. Technol. 2003, 63, 237–247. [Google Scholar] [CrossRef]
- Martin, L.P.; Patterson, J.R.; Orlikowski, D.; Nguyen, J.H. Application of tape-cast graded impedance impactors for light-gas gun experiments. J. Appl. Phys. 2007, 102. [Google Scholar] [CrossRef]
- He, B.B.; Yang, Y.; Zou, H.; Zhang, Q.; Fu, Q. Fast determination of phase inversion in polymer blends using ultrasonic technique. Polymer 2005, 46, 7624–7631. [Google Scholar] [CrossRef]
- Guillermic, R.M.; Lanoy, M.; Strybulevych, A.; Page, J.H. A PDMS-based broadband acoustic impedance matched material for underwater applications. Ultrasonics 2019, 94, 152–157. [Google Scholar] [CrossRef]
- Li, J.B.; Li, W.B.; Wang, X.M.; Li, W.B.; Hong, X.W. Mechanical properties and constitutive model of aluminum powder/rubber matrix composites compressed at various strain rates. Int. J. Impact Eng. 2018, 121, 55–62. [Google Scholar] [CrossRef]
- Li, R.; Ni, Q.Q.; Xia, H.; Natsuki, T. Analysis of individual attenuation components of ultrasonic waves in composite material considering frequency dependence. Compos. Part B Eng. 2018, 140, 232–240. [Google Scholar] [CrossRef]
- Ni, Q.Q.; Li, R.; Xia, H. A New Approach for Quantitative Evaluation of Ultrasonic Wave Attenuation in Composites. Applie Compos. Mater. 2017, 24, 23–37. [Google Scholar] [CrossRef]
- Li, R.; Natsuki, T.; Ni, Q.Q. A novel dynamic stress analysis in bimaterial composite with defect using ultrasonic wave propagation. Compos. Struct. 2015, 132, 255–264. [Google Scholar] [CrossRef]
- Yang, W.; Chang, W.; Zhang, J.; Yeoh, G.H.; Boyer, C.; Wang, C.H. Effects of waste coffee grounds on the mechanical properties, flame retardancy and toxic gas production of epoxy composites. Mater. Des. 2022, 224, 111347. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, Z.L.; Luo, C.C.; Li, T.; Li, Z.J.; Kang, Y.; Zhuang, Z. Revealing the high-frequency attenuation mechanism of polyurea-matrix composites. Acta Mech. Sin. 2020, 36, 130–142. [Google Scholar] [CrossRef]
- Mylavarapu, P.; Woldesenbet, E. A predictive model for ultrasonic attenuation coefficient in particulate composites. Compos. Part B Eng. 2010, 41, 42–47. [Google Scholar] [CrossRef]
- Ying, C.F.; Truell, R. Scattering of a Plane Longitudinal Wave by a Spherical Obstacle in an Isotropically Elastic Solid. J. Appl. Phys. 1956, 27, 1086–1097. [Google Scholar] [CrossRef]
- Liu, Z.; Oswald, J.; Belytschko, T. XFEM modeling of ultrasonic wave propagation in polymer matrix particulate/fibrous composites. Wave Motion 2013, 50, 389–401. [Google Scholar] [CrossRef]
- Li, R.; Xia, H.; Xu, Z.Z.; Ni, Q.Q.; Fu, Y.Q. U-DMA measurement and dynamic analysis of ultrasonic wave propagation in particulate composites. Compos. Sci. Technol. 2017, 151, 174–183. [Google Scholar] [CrossRef]
- Rauls, M.B.; Ravichandran, G. Structure of shock waves in particulate composites. J. Appl. Phys. 2020, 127, 065902. [Google Scholar] [CrossRef]


| cl | cs | |
|---|---|---|
| Cu | 4763 | 2318 |
| PMMA | 2740 | 1372 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, G.; Cheng, P.; Yu, Y.; Geng, X.; Zhao, Y.; Xia, Y.; Zhang, R.; Shen, Q. Influence on Elastic Wave Propagation Behavior in Polymers Composites: An Analysis of Inflection Phenomena. Polymers 2023, 15, 1680. https://doi.org/10.3390/polym15071680
Luo G, Cheng P, Yu Y, Geng X, Zhao Y, Xia Y, Zhang R, Shen Q. Influence on Elastic Wave Propagation Behavior in Polymers Composites: An Analysis of Inflection Phenomena. Polymers. 2023; 15(7):1680. https://doi.org/10.3390/polym15071680
Chicago/Turabian StyleLuo, Guoqiang, Pu Cheng, Yin Yu, Xiangwei Geng, Yue Zhao, Yulong Xia, Ruizhi Zhang, and Qiang Shen. 2023. "Influence on Elastic Wave Propagation Behavior in Polymers Composites: An Analysis of Inflection Phenomena" Polymers 15, no. 7: 1680. https://doi.org/10.3390/polym15071680
APA StyleLuo, G., Cheng, P., Yu, Y., Geng, X., Zhao, Y., Xia, Y., Zhang, R., & Shen, Q. (2023). Influence on Elastic Wave Propagation Behavior in Polymers Composites: An Analysis of Inflection Phenomena. Polymers, 15(7), 1680. https://doi.org/10.3390/polym15071680







