Evolution of the Viscoelastic Properties of Filler Reinforced Rubber under Physical Aging at Room Temperature
Abstract
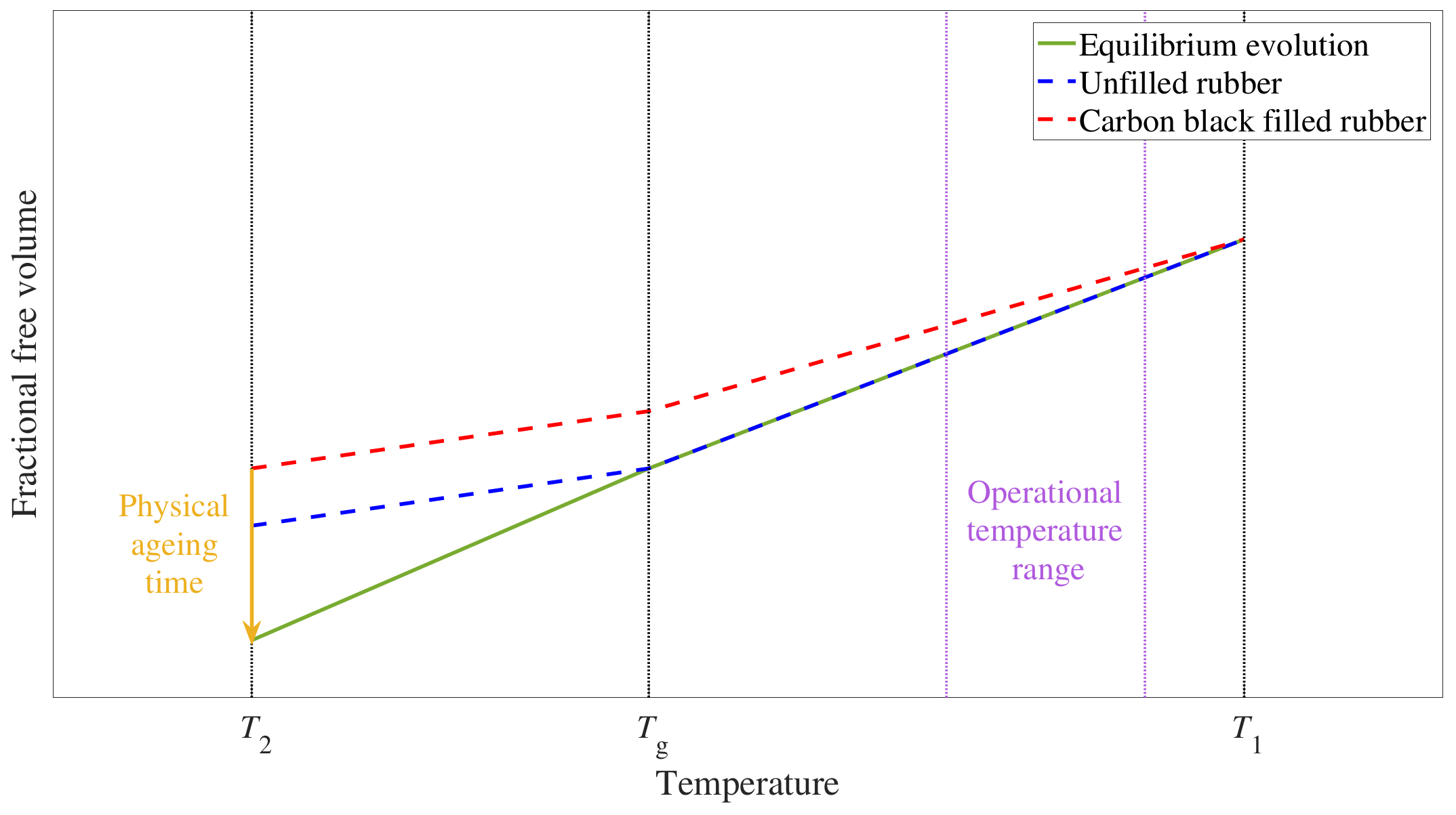
1. Introduction
2. Method
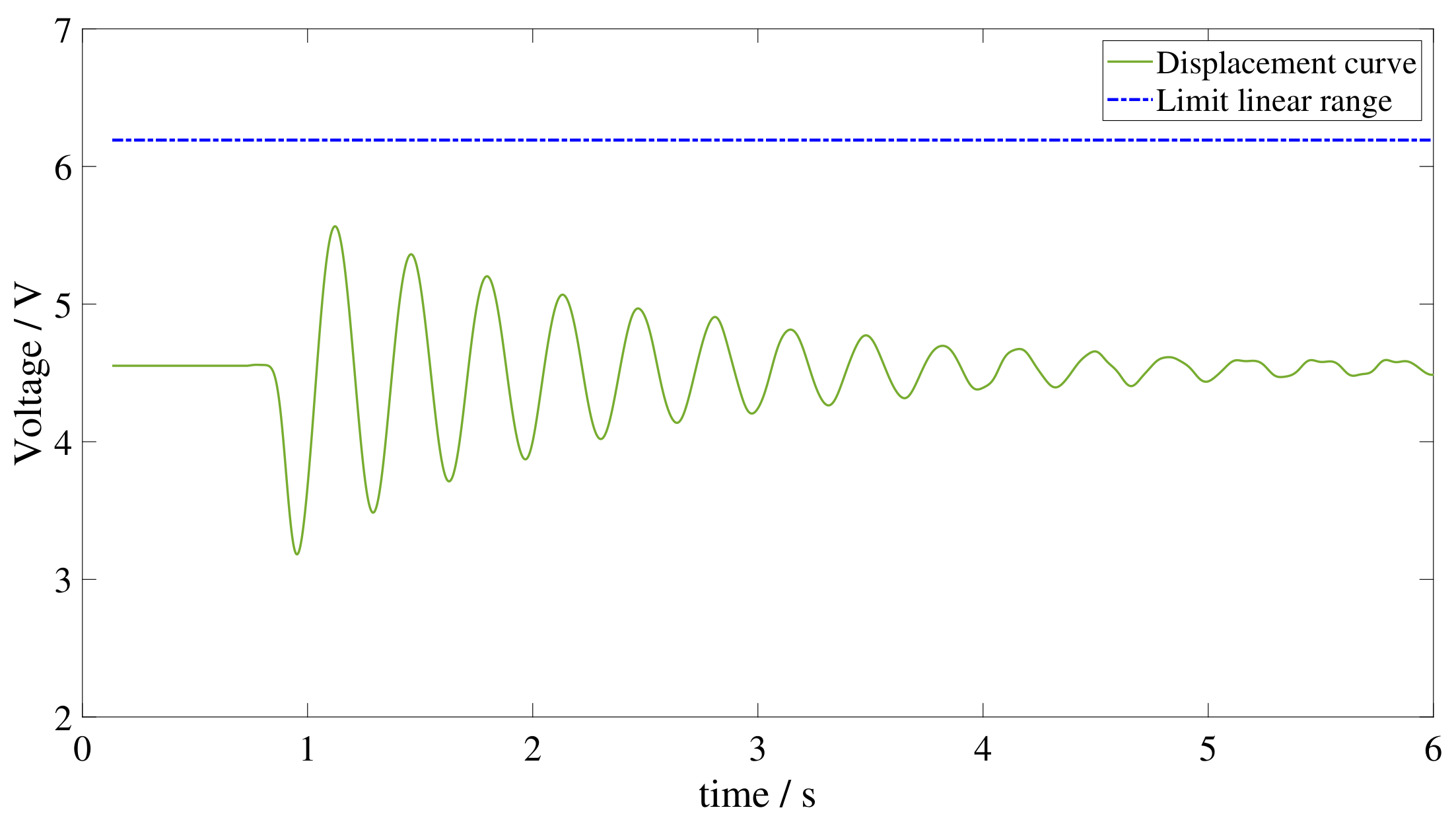
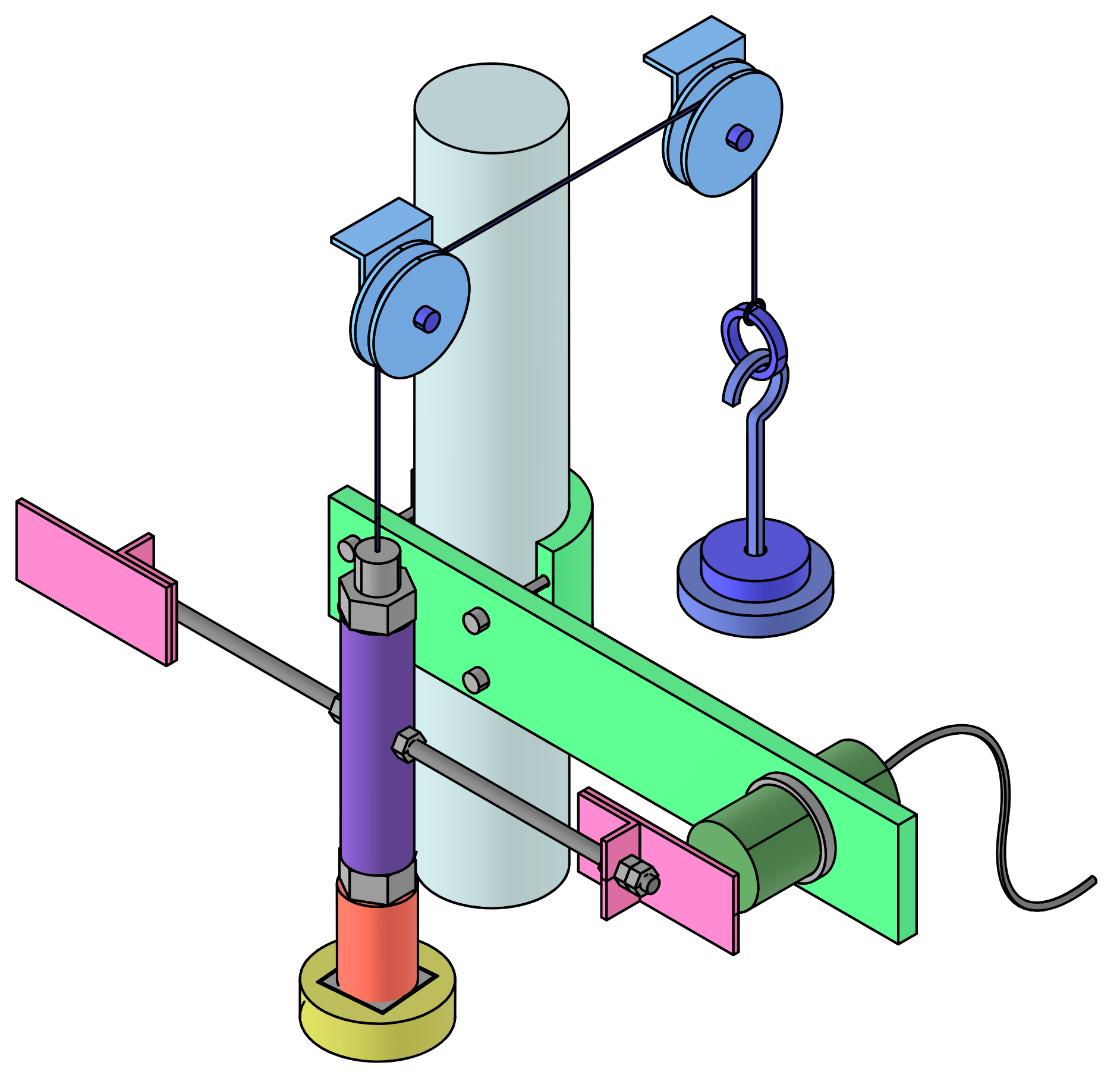
2.1. Equipment
2.2. Materials
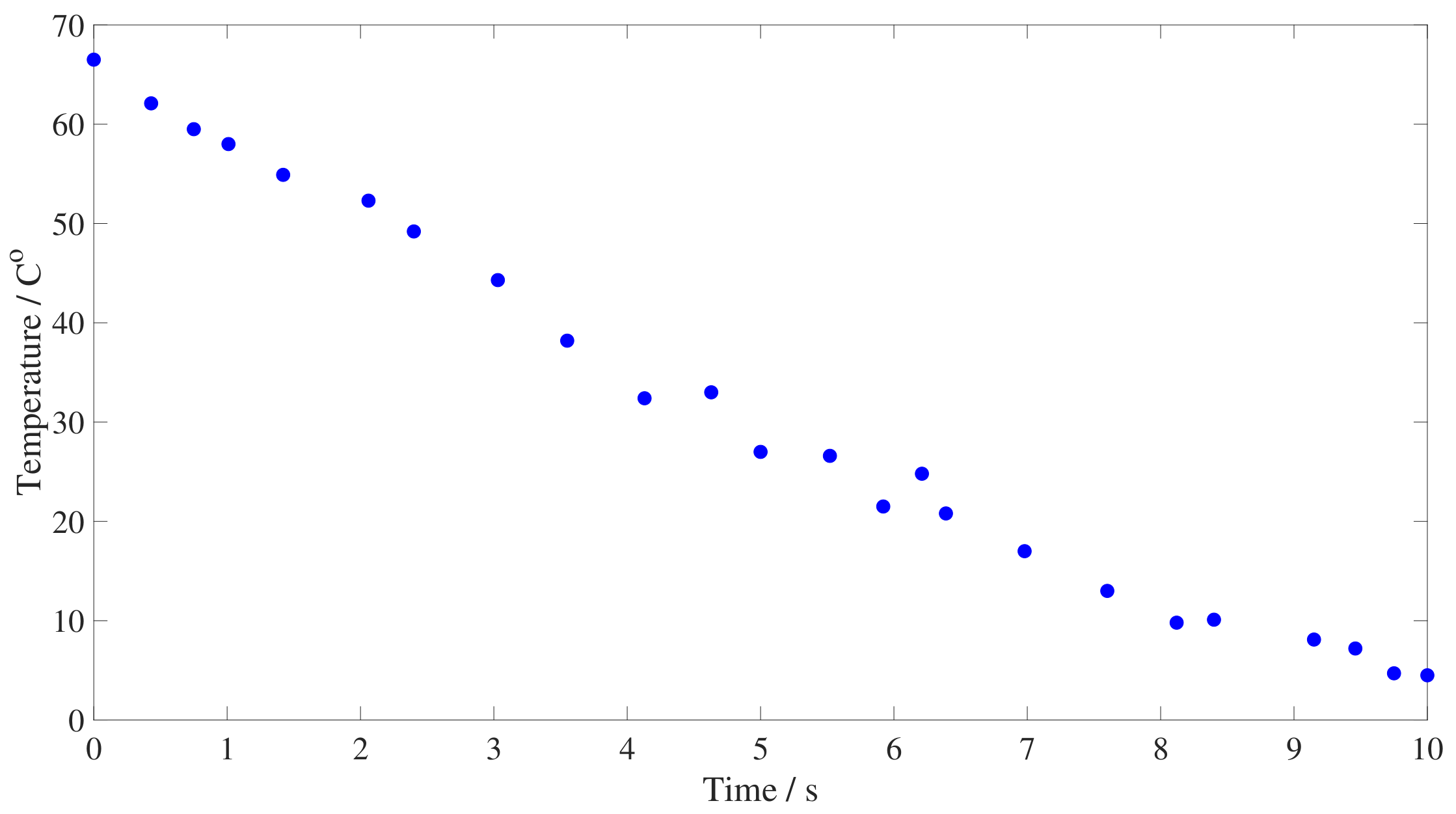
2.3. Experimental Procedure
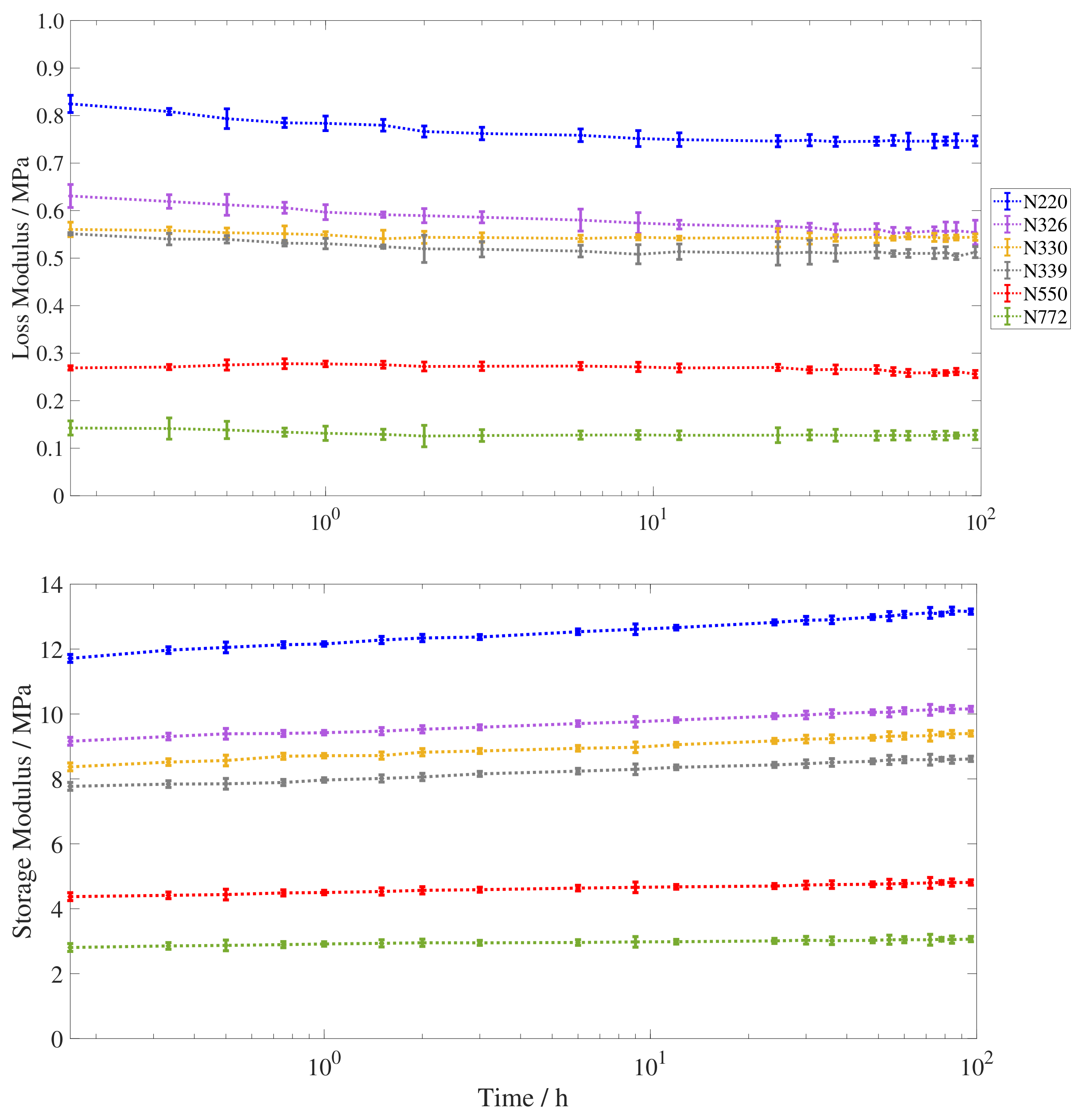
3. Results and Discussion
3.1. Torsion Pendulum Results
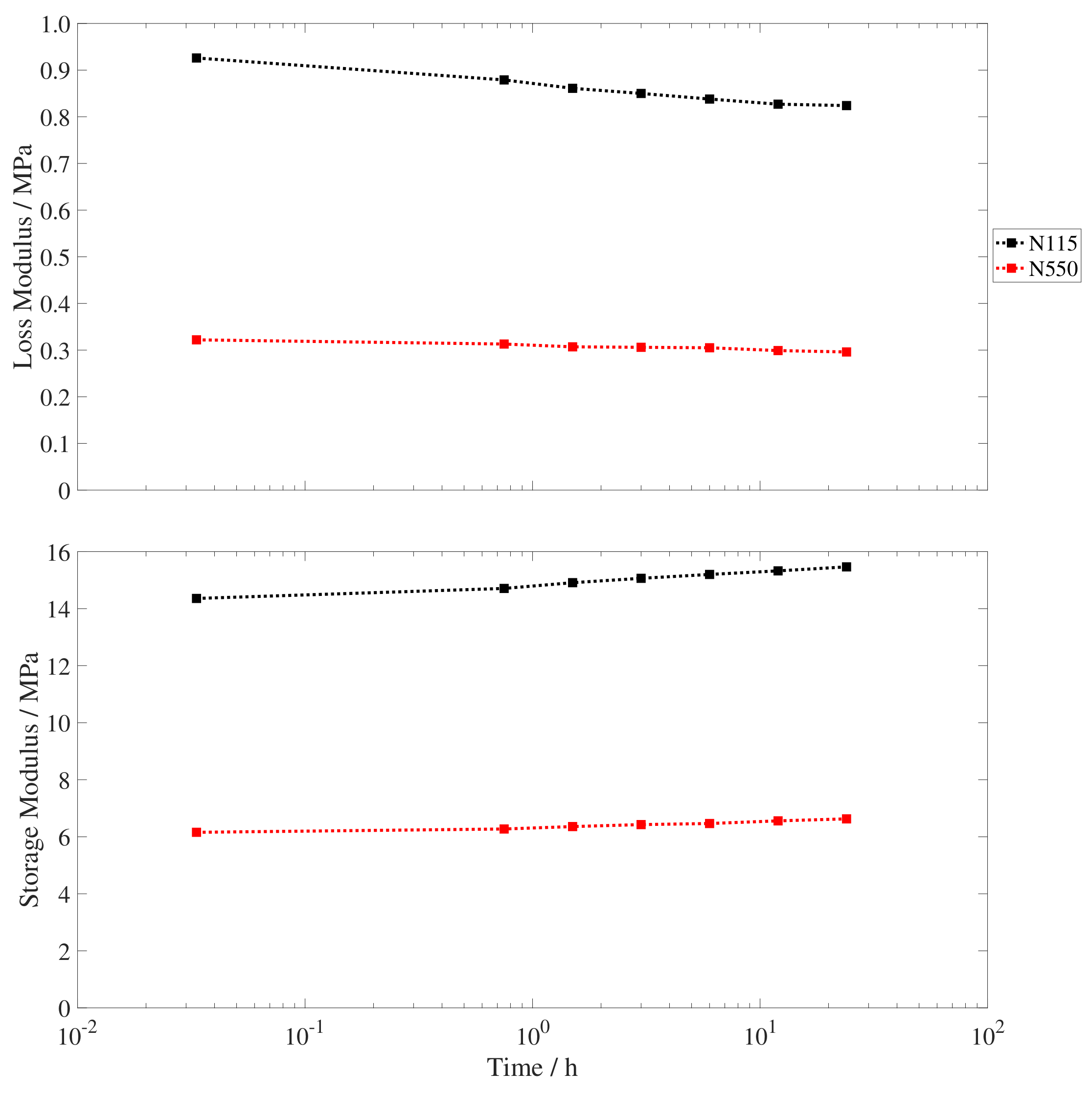
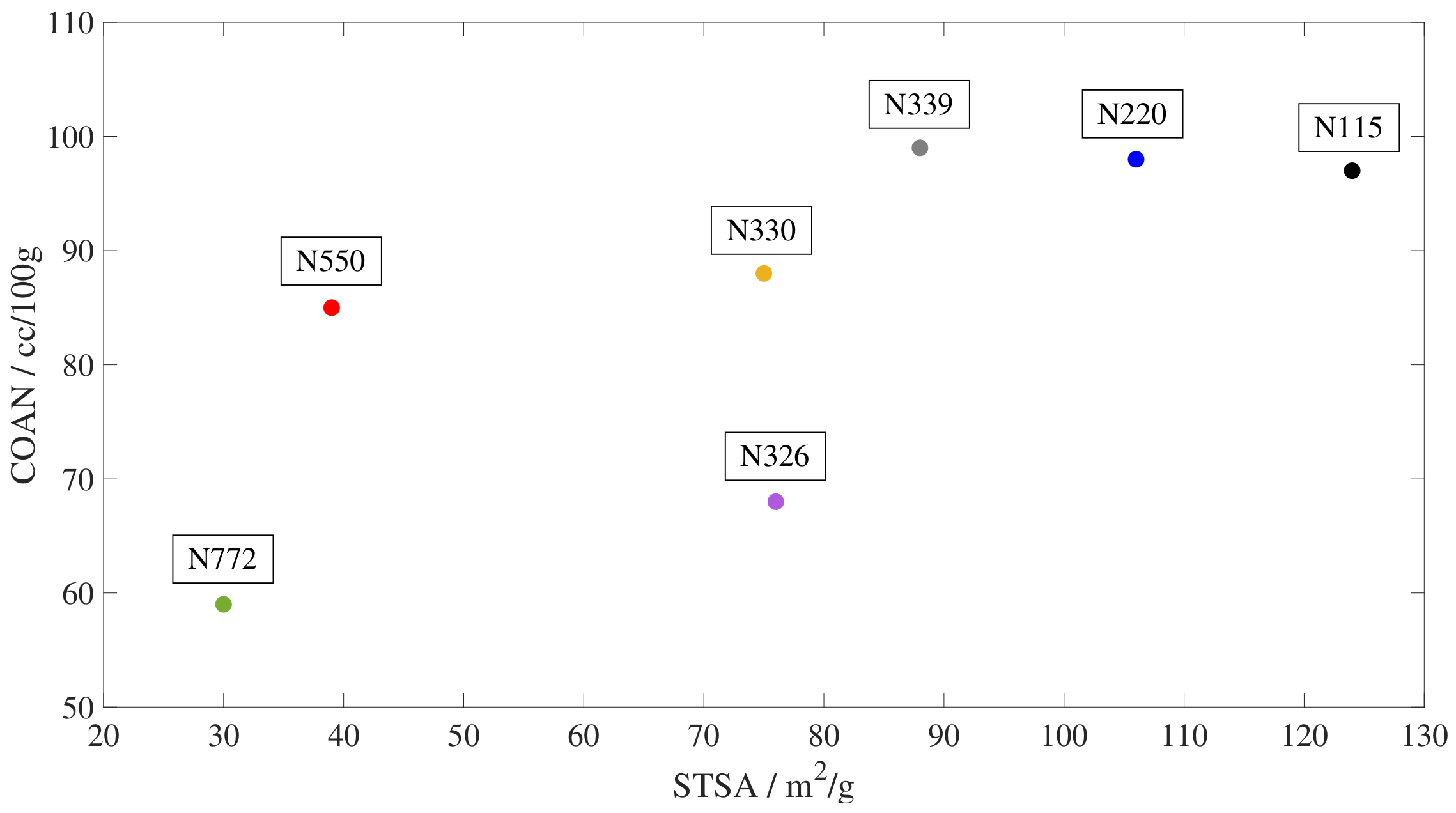
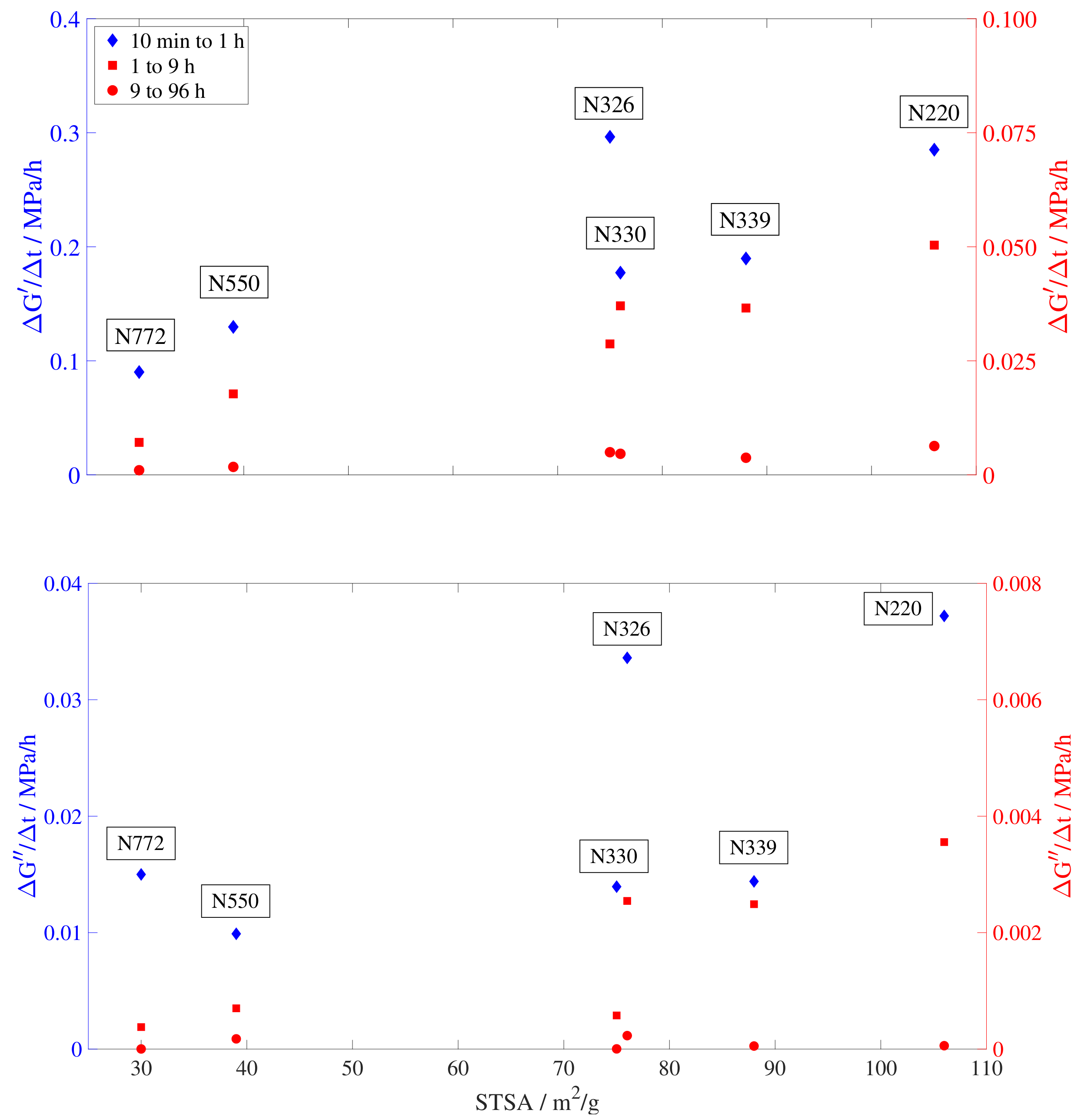
3.2. Carbon Black Properties Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Measurement times | 10 min, 20 min, 30 min, 45 min, 60 min, 90 min, |
| 2 h, 3 h, 6 h, 9 h, 12 h, 24 h, 30 h, 36 h, 48 h, 54 h, 72 h, 96 h |
Appendix B. Comparison with DMA Data
References
- Thomas, S.; Han Chan, C.; Pothen, L.; Joy, J.; Maria, H. (Eds.) Natural Rubber Materials; The Royal Society of Chemistry: London, UK, 2013. [Google Scholar]
- Mooney, M. A theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Crissman, J.M.; McKenna, G.B. Physical and chemical aging in PMMA and their effects on creep and creep rupture behavior. J. Polym. Sci. Pol. Phys. 1990, 28, 1463–1473. [Google Scholar] [CrossRef]
- Clough, R.L.; Gillen, K.T. Oxygen diffusion effects in thermally aged elastomers. Polym. Degrad. Stabil. 1992, 38, 47–56. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Ogden, R.W. Non-Linear Elastic Deformations; Dover Publications Inc.: Mineola, NY, USA, 1997. [Google Scholar]
- Kari, L. On the dynamic stiffness of preloaded vibration isolators in the audible frequency range: Modeling and experiments. J. Acoust. Soc. Am. 2003, 113, 1909–1921. [Google Scholar] [CrossRef]
- Marckmann, G.; Verron, E. Comparison of hyperelastic models for rubber-like materials. Rubber Chem. Technol. 2006, 79, 835–858. [Google Scholar] [CrossRef]
- Lion, A.; Johlitz, M. On the representation of chemical ageing of rubber in continuum mechanics. Int. J. Solids Struct. 2012, 49, 1227–1240. [Google Scholar] [CrossRef]
- Wang, B.; Kari, L. A nonlinear constitutive model by spring, fractional derivative and modified bounding surface model to represent the amplitude, frequency and the magnetic dependency for magneto-sensitive rubber. J. Sound Vib. 2019, 438, 344–352. [Google Scholar] [CrossRef]
- Hohenberger, T.W.; Windslow, R.J.; Pugno, N.M.; Busfield, J.J. A constitutive model for both low and high strain nonlinearities in highly filled elastomers and implementation with user-defined material subroutines in ABAQUS. Rubber Chem. Technol. 2019, 92, 653–686. [Google Scholar] [CrossRef]
- Chow, T.S. Stress-strain behaviour of physically ageing polymers. Polymer 1993, 34, 541–545. [Google Scholar] [CrossRef]
- Dean, G.D.; Tomlins, P.E.; Read, B.E. A model for nonlinear creep and physical aging in poly (vinyl chloride). Polym. Eng. Sci. 1995, 35, 1282–1289. [Google Scholar] [CrossRef]
- Kari, L. Dynamic stiffness of chemically and physically ageing rubber vibration isolators in the audible frequency range. Contin. Mech. Therm. 2017, 29, 1027–1046. [Google Scholar] [CrossRef]
- Cangialosi, D.; Boucher, V.M.; Alegría, A.; Colmenero, J. Physical aging in polymers and polymer nanocomposites: Recent results and open questions. Soft Matter 2013, 9, 8619–8630. [Google Scholar] [CrossRef]
- Struik, L. Free damped vibrations of linear viscoelastic materials. Rheol. Acta 1967, 6, 119–129. [Google Scholar] [CrossRef]
- Gedde, U.W.; Hedenqvist, M.S. Fundamental Polymer Science; Springer: Cham, Switzerland, 2019; Volume 2. [Google Scholar]
- Roland, C.M. Glass transition in rubbery materials. Rubber Chem. Technol. 2012, 85, 313–326. [Google Scholar] [CrossRef]
- Tunnicliffe, L.B.; Busfield, J.J. Reinforcement of rubber and filler network dynamics at small strains. In Designing of Elastomer Nanocomposites: From Theory to Applications; Springer: Cham, Switzerland, 2016; pp. 71–102. [Google Scholar] [CrossRef]
- Woo, C.S.; Park, H.S. Useful lifetime prediction of rubber component. Eng. Fail. Anal. 2011, 18, 1645–1651. [Google Scholar] [CrossRef]
- Bassan, M.; De Marchi, F.; Marconi, L.; Pucacco, G.; Stanga, R.; Visco, M. Torsion pendulum revisited. Phys. Lett. A 2013, 377, 1555–1562. [Google Scholar] [CrossRef]
- Gillies, G.; Ritter, R. Torsion balances, torsion pendulums, and related devices. Rev. Sci. Instrum. 1993, 64, 283–309. [Google Scholar] [CrossRef]
- Falconer, I. Henry Cavendish: The man and the measurement. Meas. Sci. Technol. 1999, 10, 470. [Google Scholar] [CrossRef]
- Meredith, R. 30-The torsional rigidity of textile fibres. J. Text. Inst. Trans. 1954, 45, T489–T503. [Google Scholar] [CrossRef]
- Adams, R.; Lloyd, D. Apparatus for measuring the torsional modulus and damping of single carbon fibres. J. Phys. E Sci. Instrum. 1975, 8, 475. [Google Scholar] [CrossRef]
- Liu, D.; He, Y.; Hu, P.; Gan, Z.; Ding, H. A modified torsion pendulum for measuring the shear modulus of a single micro-sized filament. Acta Mech. Solida Sin. 2014, 27, 221–233. [Google Scholar] [CrossRef]
- Yu, H.; Adams, R.; Da Silva, L. Development of a torsion pendulum and its application to measuring the dynamic modulus of adhesives from pre-gelation to the cured state. Meas. Sci. Technol. 2014, 25, 055603. [Google Scholar] [CrossRef]
- Suphadon, N.; Thomas, A.; Busfield, J. Viscoelastic behavior of rubber under a complex loading. J. Appl. Polym. Sci. 2009, 113, 693–699. [Google Scholar] [CrossRef]
- Suphadon, N.; Thomas, A.; Busfield, J. The viscoelastic behaviour of rubber under a small simple shear oscillation superimposed on a large pure shear. Polym. Test. 2010, 29, 440–444. [Google Scholar] [CrossRef]
- Tunnicliffe, L.B. Particulate Reinforcement of Elastomers at Small Strains. Ph.D. Thesis, Queen Mary University of London, London, UK, 2015. [Google Scholar]
- Vizcaíno-Vergara, M.; Tunnicliffe, L.B.; Busfield, J.J.C.; Kari, L. Viscoelastic characterisation of carbon black reinforced rubber using the torsion pendulum: Guidelines and temperature sweep results. Polym. Test. 2022, 114, 107692. [Google Scholar] [CrossRef]
- ISO 4664-2:2006; Rubber, Vulcanized or Thermoplastic—Determination of Dynamic Properties. International Organization for Standardization: Geneva, Switzerland, 2006; Volume 10, pp. 470–477.
- Brown, R. Physical Testing of Rubber; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Spahr, M.E.; Rothon, R. Carbon black as a polymer filler. In Polymers and Polymeric Composites: A Reference Series; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–31. [Google Scholar] [CrossRef]
- Semaan, M.E.; Quarles, C.A.; Nikiel, L. Positron annihilation spectroscopy of carbon black/silica filled rubber polymers. Materi. Sci. Forum 2001, 363, 278–280. [Google Scholar] [CrossRef]
- Geise, G.M.; Doherty, C.M.; Hill, A.J.; Freeman, B.D.; Paul, D.R. Free volume characterization of sulfonated styrenic pentablock copolymers using positron annihilation lifetime spectroscopy. J. Membr. Sci. 1940, 453, 425–434. [Google Scholar] [CrossRef]
- Payne, A.R. The dynamic properties of carbon black-loaded natural rubber vulcanizates. Part I. J. Appl. Polym. Sci. 1962, 6, 57–63. [Google Scholar] [CrossRef]
- Brostow, W.; Lobland, H.E.H. Materials: Introduction and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Kyei-Manu, W.A.; Tunnicliffe, L.B.; Plagge, J.; Herd, C.R.; Akutagawa, K.; Pugno, N.M.; Busfield, J.J.C. Thermomechanical Characterization of Carbon Black Reinforced Rubbers During Rapid Adiabatic Straining. Front. Mater. 2021, 8, 743146. [Google Scholar] [CrossRef]
- Dorfmann, A.; Ogden, R.W. A constitutive model for the Mullins effect with permanent set in particle-reinforced rubber. Int. J. Solids Struct. 2004, 41, 1855–1878. [Google Scholar] [CrossRef]
- Vizcaíno-Vergara, M.; Kari, L.; Busfield, J.J.C. Free volume evolution equation for physical ageing of filler reinforced rubber. In Constitutive Models for Rubber XI; CRC Press/Balkema: Leiden, The Netherlands, 2019; pp. 548–553. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Fritzsche, J.; Klüppel, M. Structural dynamics and interfacial properties of filler-reinforced elastomers. J. Phys. Condens. Mat. 2010, 23, 035104. [Google Scholar] [CrossRef]
- Odegard, G.M.; Bandyopadhyay, A. Physical aging of epoxy polymers and their composites. J. Polym. Sci. Part B Polym. Phys. 2011, 49, 1695–1716. [Google Scholar] [CrossRef]
- Roe, R.j.; Millman, G.M. Physical aging in polystyrene: Comparison of the changes in creep behavior with the enthalpy relaxation. Polym. Eng. Sci. 1983, 23, 318–322. [Google Scholar] [CrossRef]
- Pérez, J.; Cavaille, J.Y.; Calleja, R.D.; Ribelles, J.L.G.; Pradas, M.M.; Greus, A.R. Physical ageing of amorphous polymers. Theoretical analysis and experiments on poly (methyl methacrylate). Makromol. Chem. 1991, 192, 2141–2161. [Google Scholar] [CrossRef]
- McKenna, G.B.; Leterrier, Y.; Schultheisz, C.R. The evolution of material properties during physical aging. Polym. Eng. Sci. 1995, 35, 403–410. [Google Scholar] [CrossRef]
- Cowie, J.; Ferguson, R.; Harris, S.; McEwen, I. Physical ageing in poly(vinyl acetate)—3. Structural relaxation and its effect on the stress relaxation modulus. Polymer 1998, 39, 4393–4397. [Google Scholar] [CrossRef]
- D1765-16; Standard Classification System for Carbon Blacks Used in Rubber Products. ASTM International: Pennsylvania, PA, USA, 2016; pp. 1–4.
- Bera, M.; Gupta, P.; Maji, P.K. Structural/load-bearing characteristics of polymer–carbon composites. In Carbon-Containing Polymer Composites; Springer: Singapore, 2019; pp. 457–502. [Google Scholar] [CrossRef]
- Meier, J.G.; Klüppel, M. Carbon black networking in elastomers monitored by dynamic mechanical and dielectric spectroscopy. Macromol. Mater. Eng. 2008, 293, 12–38. [Google Scholar] [CrossRef]
- Kovacs, A.J.; Aklonis, J.J.; Hutchinson, J.M.; Ramos, A.R. Isobaric volume and enthalpy recovery of glasses. II. A transparent multiparameter theory. J. Polym. Sci. Polym. Phys. Ed. 1979, 17, 1097–1162. [Google Scholar] [CrossRef]
- Ramos, A.R.; Hutchinson, J.M.; Kovacs, A.J. Isobaric thermal behavior of glasses during uniform cooling and heating. III. Predictions from the multiparameter KAHR model. J. Polym. Sci. Pol. Phys. 1984, 22, 1655–1696. [Google Scholar] [CrossRef]
- Ramos, A.R.; Kovacs, A.J.; O’Reilly, J.M.; Tribone, J.J.; Greener, J. Effect of combined pressure and temperature changes on structural recovery of glass-forming materials. I. Extension of the KAHR model. J. Polym. Sci. Pol. Phys. 1988, 26, 501–513. [Google Scholar] [CrossRef]
- Robertson, C.G.; Vaikuntam, S.R.; Heinrich, G. A nonequilibrium model for particle networking/jamming and time-dependent dynamic rheology of filled polymers. Polymers 2020, 12, 190. [Google Scholar] [CrossRef] [PubMed]


| Component | Parts per Hundred (phr) |
|---|---|
| NR-SMR CV-60 | 100 |
| Carbon Black | 50 |
| Zinc Oxide | 5 |
| Stearic Acid | 3 |
| Sulfur | 2.5 |
| TBBS | 0.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vizcaíno-Vergara, M.; Kari, L.; Tunnicliffe, L.B.; Busfield, J.J.C. Evolution of the Viscoelastic Properties of Filler Reinforced Rubber under Physical Aging at Room Temperature. Polymers 2023, 15, 1806. https://doi.org/10.3390/polym15071806
Vizcaíno-Vergara M, Kari L, Tunnicliffe LB, Busfield JJC. Evolution of the Viscoelastic Properties of Filler Reinforced Rubber under Physical Aging at Room Temperature. Polymers. 2023; 15(7):1806. https://doi.org/10.3390/polym15071806
Chicago/Turabian StyleVizcaíno-Vergara, María, Leif Kari, Lewis B. Tunnicliffe, and James J. C. Busfield. 2023. "Evolution of the Viscoelastic Properties of Filler Reinforced Rubber under Physical Aging at Room Temperature" Polymers 15, no. 7: 1806. https://doi.org/10.3390/polym15071806
APA StyleVizcaíno-Vergara, M., Kari, L., Tunnicliffe, L. B., & Busfield, J. J. C. (2023). Evolution of the Viscoelastic Properties of Filler Reinforced Rubber under Physical Aging at Room Temperature. Polymers, 15(7), 1806. https://doi.org/10.3390/polym15071806







