Influence of FFF Process Conditions on the Thermal, Mechanical, and Rheological Properties of Poly(hydroxybutyrate-co-hydroxy Hexanoate)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Rheological Characterization
2.3. 3D Printing of the Samples
2.4. Printing Conditions
2.5. Thermal Characterization of the Polymer
2.5.1. Differential Scanning Calorimetry (DSC)
2.5.2. Pressure–Volume–Temperature (PVT) Measurements
2.6. Compression Molding
2.7. Tensile Tests
2.8. Cross-Sectional Morphology
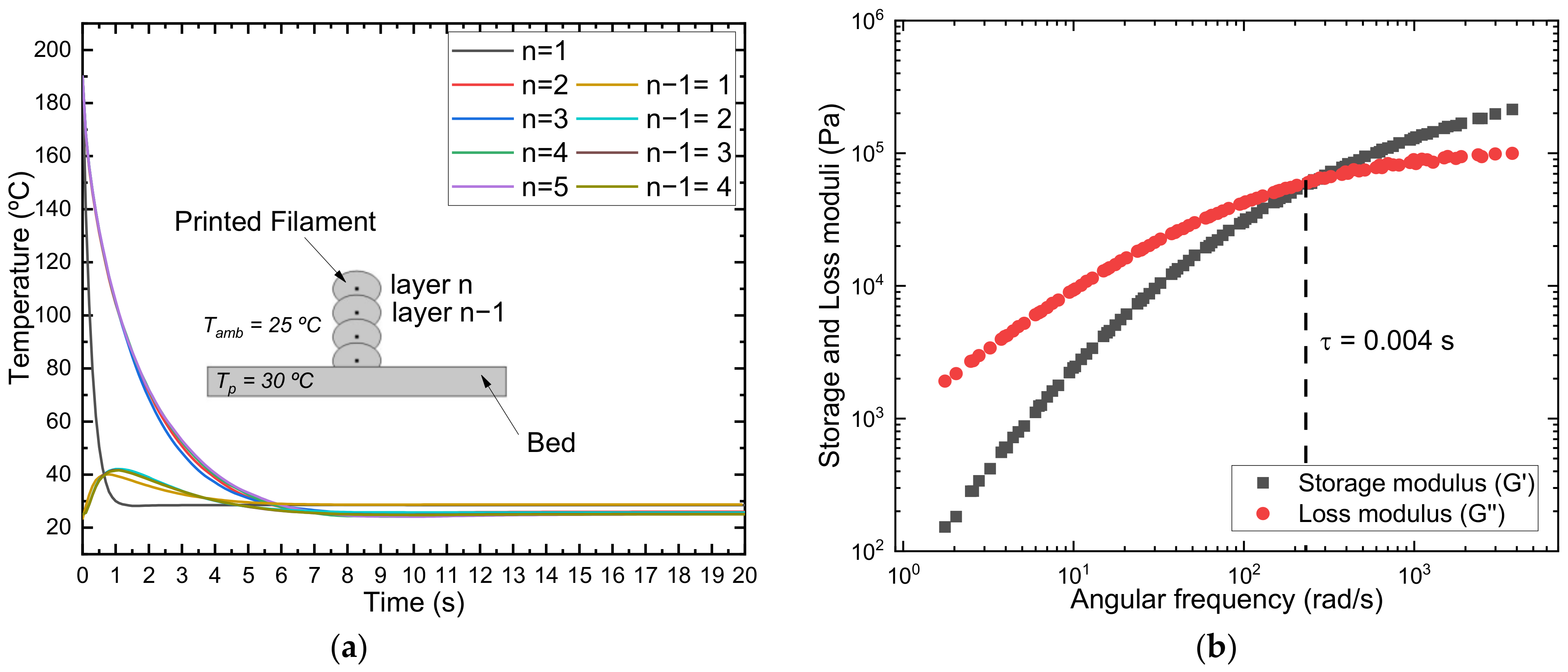
2.9. Simulation
3. Results
3.1. Thermal Analysis
3.1.1. Differential Scanning Calorimetry (DSC)
- Virgin material (filament)
- b.
- Printed part (Tower)
3.1.2. Rheological Characterization
3.1.3. Evaluation of the Effect of Pressure and Temperature on Specific Volume/Density
3.2. Mechanical Properties
3.2.1. Effect of the Bed and Nozzle Temperatures
3.2.2. Effect of the Printing Velocity
3.2.3. Effect of the Raster Angle
3.2.4. FFF vs. Compression Molding
3.3. SEM Analysis: Cross-Sectional Morphology
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- European Bioplastics e.V. Bioplastics Market Data. 2020b. Available online: https://www.european-bioplastics.org/market/ (accessed on 10 March 2020).
- Lee, S.Y. Bacterial polyhydroxyalkanoates. Biotechnol. Bioeng. 1996, 49, 1–14. [Google Scholar] [CrossRef]
- Lee, S.Y. Plastic bacteria? Progress and prospects for polyhydroxyalkanoate production in bacteria. Trends Biotechnol. 1996, 14, 431–438. [Google Scholar] [CrossRef]
- Sudesh, K.; Abe, H.; Doi, Y. Synthesis, structure and properties of polyhydroxyalkanoates: Biological polyesters. Prog. Polym. Sci. 2000, 25, 1503–1555. [Google Scholar] [CrossRef]
- Yan, S.; Tyagi, R.D.; Surampalli, R.Y. Polyhydroxyalkanoates (PHA) production using wastewater as carbon source and activated sludge as microorganisms. Water Sci. Technol. 2006, 53, 175–180. [Google Scholar] [CrossRef]
- Raza, Z.A.; Abid, S.; Banat, I.M. Polyhydroxyalkanoates: Characteristics, production, recent developments and applications. Int. Biodeterior. Biodegrad. 2018, 126, 45–56. [Google Scholar] [CrossRef]
- Madison, L.L.; Huisman, G.W. Metabolic engineering of poly (3-hydroxyalkanoates): From DNA to plastic. Microbiol. Mol. Biol. Rev. 1999, 63, 21–53. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reddy, C.S.K.; Ghai, R.; Kalia, V. Polyhydroxyalkanoates: An overview. Bioresour. Technol. 2003, 87, 137–146. [Google Scholar] [CrossRef] [PubMed]
- Serrano, J. Polyhydroxyalkanoates (PHAs) polymers produced by microorganisms. A solution to environmental pollution 2010. Teoría Y Prax. Investig. 2010, 5, 79–84. [Google Scholar]
- Gonzalez Garcia, Y.; Meza Contrera, J.C.; Gonzalez Reynoso, O.; Cordova Lopez, J.A. Synthesis and biodegradation of polyhydroxialkanoates: Bacterially produced plastics. Rev. Int. Contam. Ambient. 2013, 29, 77–115. [Google Scholar]
- Sharma, V.; Sehgal, R.; Gupta, R. Polyhydroxyalkanoate (PHA): Properties and Modifications. Polymer 2021, 212, 123161. [Google Scholar] [CrossRef]
- Li, S.; Cai, L.; Wu, L.; Zeng, G.; Chen, J.; Wu, Q.; Chen, G.-Q. Microbial synthesis of functional homo-, random, and block polyhydroxyalkanoates by β-oxidation deleted Pseudomonas entomophila. Biomacromolecules 2014, 15, 2310–2319. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Chen, J.-C.; Ma, Y.-M.; Chen, G.-Q. Engineering biosynthesis of polyhydroxyalkanoates (PHA) for diversity and cost reduction. Metab. Eng. 2020, 58, 82–93. [Google Scholar] [CrossRef] [PubMed]
- Sodian, R.; Sperling, J.S.; Martin, D.P.; Egozy, A.; Stock, U.; Mayer, J.E., Jr.; Vacanti, J.P. Technical report: Fabrication of a trileaflet heart valve scaffold from a polyhydroxyalkanoate biopolyester for use in tissue engineering. Tissue Eng. 2000, 6, 183–188. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.-P. Polyhydroxyalkanoates (PHA): Biosynthesis, Industrial Production and Applications in Medicine; Nova Science Publishers: New York, NY, USA, 2014. [Google Scholar]
- Porter, M.M.; Lee, S.; Tanadchangsaeng, N.; Jaremko, M.J.; Yu, J.; Meyers, M.; McKittrick, J. Porous hydroxyapatite-polyhydroxybutyrate composites fabricated by a novel method via centrifugation. In Mechanics of Biological Systems and Materials; Springer: Berlin/Heidelberg, Germany, 2013; Volume 5, pp. 63–71. [Google Scholar]
- Hong, S.K.; Shirai, Y.; Nor, A.; Hassan, M.A. Semi-continuous and continuous anaerobic treatment of palm oil mill effluent for the production of organic acids and polyhydroxyalkanoates. Res. J. Environ. Sci. 2009, 3, 552–559. [Google Scholar] [CrossRef] [Green Version]
- Hazari, A.; Wiberg, M.; Johansson-Ruden, G.; Green, C.; Terenghi, G. A resorbable nerve conduit as an alternative to nerve autograft in nerve gap repair. Br. J. Plast. Surg. 1999, 52, 653–657. [Google Scholar] [CrossRef]
- Bugnicourt, E.; Cinelli, P.; Lazzeri, A.; Alvarez, V.A. Polyhydroxyalkanoate (PHA): Review of synthesis, characteristics, processing and potential applications in packaging. eXPRESS Polym. Lett. 2014, 8, 791–808. [Google Scholar] [CrossRef]
- Lizarraga-Valderrama, L.R.; Nigmatullin, R.; Taylor, C.; Haycock, J.W.; Claeyssens, F.; Knowles, J.C.; Roy, I. Nerve tissue engineering using blends of poly (3-hydroxyalkanoates) for peripheral nerve regeneration. Eng. Life Sci. 2015, 15, 612–621. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.-Q.; Wu, Q. Microbial production and applications of chiral hydroxyalkanoates. Appl. Microbiol. Biotechnol. 2005, 67, 592–599. [Google Scholar] [CrossRef] [PubMed]
- Baptist, J.N.; Ziegler, J.B. Method of Making Absorbable Surgical Sutures from Poly Beta Hydroxy Acids. U.S. Patent 3,225,766, 28 December 1965. [Google Scholar]
- Shishatskaya, E.I.; Nikolaeva, E.D.; Vinogradova, O.N.; Volova, T.G. Experimental wound dressings of degradable PHA for skin defect repair. J. Mater. Sci. Mater. Med. 2016, 27, 165. [Google Scholar] [CrossRef] [Green Version]
- Dhania, S.; Rani, R.; Kumar, R.; Thakur, R. Fabricated polyhydroxyalkanoates blend scaffolds enhance cell viability and cell proliferation. J. Biotechnol. 2023, 361, 30–40. [Google Scholar] [CrossRef]
- Ni, J.; Wang, M. In vitro evaluation of hydroxyapatite reinforced polyhydroxybutyrate composite. Mater. Sci. Eng. C 2002, 20, 101–109. [Google Scholar] [CrossRef]
- Reis, E.C.C.; Borges, A.P.B.; Fonseca, C.C.; Martinez, M.M.M.; Eleotério, R.B.; Morato, G.O.; Oliveira, P.M. Biocompatibility, osteointegration, osteoconduction, and biodegradation of a hydroxyapatite-polyhydroxybutyrate composite. Braz. Arch. Biol. Technol. 2010, 53, 817–826. [Google Scholar] [CrossRef] [Green Version]
- Alves, M.I.; Macagnan, K.L.; Rodrigues, A.A.; de Assis, D.A.; Torres, M.M.; de Oliveira, P.D.; Furlan, L.; Vendruscolo, C.T.; Moreira, A. da S. Poly (3-hydroxybutyrate)-P (3HB): Review of production process technology. Ind. Biotechnol. 2017, 13, 192–208. [Google Scholar] [CrossRef]
- Karahaliloglu, Z.; Ercan, B.; Taylor, E.N.; Chung, S.; Denkbaş, E.B.; Webster, T.J. Antibacterial nanostructured polyhydroxybutyrate membranes for guided bone regeneration. J. Biomed. Nanotechnol. 2015, 11, 2253–2263. [Google Scholar] [CrossRef]
- Akaraonye, E.; Moreno, C.; Knowles, J.C.; Keshavarz, T.; Roy, I. Poly (3-hydroxybutyrate) production by Bacillus cereus SPV using sugarcane molasses as the main carbon source. Biotechnol. J. 2012, 7, 293–303. [Google Scholar] [CrossRef]
- Yano, T.; Nomoto, T.; Kozaki, S.; Imamura, T.; Honma, T.; Canon, K.K. U.S. Patent No. 2006263432, 2006.
- Pouton, C.W.; Akhtar, S. Biosynthetic polyhydroxyalkanoates and their potential in drug delivery. Adv. Drug Deliv. Rev. 1996, 18, 133–162. [Google Scholar] [CrossRef]
- Yagmurlu, M.F.; Korkusuz, F.; Gürsel, I.; Korkusuz, P.; Örs, Ü.; Hasirci, V. Sulbactam-cefoperazone polyhydroxybutyrate-co-hydroxyvalerate (PHBV) local antibiotic delivery system: In vivo effectiveness and biocompatibility in the treatment of implant-related experimental osteomyelitis. J. Biomed. Mater. Res. Off. J. Soc. Biomater. Jpn. Soc. Biomater. Aust. Soc. Biomater. Korean Soc. Biomater. 1999, 46, 494–503. [Google Scholar] [CrossRef]
- Gursel, I.; Yagmurlu, F.; Korkusuz, F.; Hasirci, V. In vitro antibiotic release from poly (3-hydroxybutyrate-co-3-hydroxyvalerate) rods. J. Microencapsul. 2002, 19, 153–164. [Google Scholar] [CrossRef] [PubMed]
- Valappil, S.P.; Peiris, D.; Langley, G.J.; Herniman, J.M.; Boccaccini, A.R.; Bucke, C.; Roy, I. Polyhydroxyalkanoate (PHA) biosynthesis from structurally unrelated carbon sources by a newly characterized Bacillus spp. J. Biotechnol. 2007, 127, 475–487. [Google Scholar] [CrossRef]
- Valappil, S.P.; Misra, S.K.; Boccaccini, A.R.; Roy, I. Biomedical applications of polyhydroxyalkanoates, an overview of animal testing and in vivo responses. Expert Rev. Med. Devices 2006, 3, 853–868. [Google Scholar] [CrossRef]
- Yao, Y.C.; Zhan, X.Y.; Zhang, J.; Zou, X.H.; Wang, Z.H.; Xiong, Y.C.; Chen, J.C.G. A specific drug targeting system based on polyhydroxyalkanoate granule binding protein PhaP fused with targeted cell ligands. Biomaterials 2008, 36, 4823–4830. [Google Scholar] [CrossRef]
- Avérous, L.; Pollet, E. Biorenewable nanocomposites. MRS Bull. 2011, 36, 703–710. [Google Scholar] [CrossRef]
- Abid, S.; Raza, Z.A.; Rehman, A. Synthesis of poly (3-hydroxybutyrate) nanospheres and deposition thereof into porous thin film. Mater. Res. Express 2016, 3, 105042. [Google Scholar] [CrossRef]
- Plackett, D.; Siró, I. Polyhydroxyalkanoates (PHAs) for food packaging. In Multifunctional and Nanoreinforced Polymers for Food Packaging; Elsevier: Amsterdam, The Netherlands, 2011; pp. 498–526. [Google Scholar]
- Samaniego, K.; Matos, A.; Sánchez-Safont, E.; Candal, M.V.; Lagaron, J.M.; Cabedo, L.; Gamez-Perez, J. Role of Plasticizers on PHB/bio-TPE Blends Compatibilized by Reactive Extrusion. Materials 2022, 15, 1226. [Google Scholar] [CrossRef] [PubMed]
- Anderson, A.J.; Dawes, E. Occurrence, metabolism, metabolic role, and industrial uses of bacterial polyhydroxyalkanoates. Microbiol. Rev. 1990, 54, 450–472. [Google Scholar] [CrossRef] [PubMed]
- Vinet, L.; Zhedanov, A. A “missing” family of classical orthogonal polynomials. J. Phys. A Math. Theor. 2010, 54, 450–472. [Google Scholar] [CrossRef]
- Zhao, W.; Chen, G.-Q. Production and characterization of terpolyester poly (3-hydroxybutyrate-co-3-hydroxyvalerate-co-3-hydroxyhexanoate) by recombinant Aeromonas hydrophila 4AK4 harboring genes phaAB. Process Biochem. 2007, 42, 1342–1347. [Google Scholar] [CrossRef]
- Tan, D.; Yin, J.; Chen, G.-Q. Production of polyhydroxyalkanoates. In Current Developments in Biotechnology and Bioengineering; Elsevier: Amsterdam, The Netherlands, 2017; pp. 655–692. [Google Scholar]
- Eraslan, K.; Aversa, C.; Nofar, M.; Barletta, M.; Gisario, A.; Salehiyan, R.; Goksu, Y.A. Poly (3-hydroxybutyrate-co-3-hydroxyhexanoate)(PHBH): Synthesis, properties, and applications-A Review. Eur. Polym. J. 2022, 167, 111044. [Google Scholar] [CrossRef]
- Sato, H.; Nakamura, M.; Padermshoke, A.; Yamaguchi, H.; Terauchi, H.; Ekgasit, S.; Noda, I.; Ozaki, Y. Thermal behavior and molecular interaction of poly (3-hydroxybutyrate-co-3-hydroxyhexanoate) studied by wide-angle X-ray diffraction. Macromolecules 2004, 37, 3763–3769. [Google Scholar] [CrossRef]
- Wu, C.-S.; Liao, H.-T.; Cai, Y.-X. Characterisation, biodegrad-ability and application of palm fibre-reinforced polyhy-droxyalkanoate composites. Polym. Degrad. Stab. 2017, 140, 55–63. [Google Scholar] [CrossRef]
- Wu, C.L.; Liao, H.T. Interface design of environmentally friendly carbon nanotube-filled polyester composites: Fabrication, characterisation, functionality and application. Express Polym. Lett. 2017, 11, 187–198. [Google Scholar] [CrossRef]
- Wu, C.-S. Characterization, functionality and application of siliceous sponge spicules additive-based manufacturing biopolymer composites. Addit. Manuf. 2018, 22, 13–20. [Google Scholar] [CrossRef]
- Tian, J.; Zheng, Y.; Ouyang, Q.; Xue, P.; Guo, B.; Xu, J. Structure and Properties of Biodegradable Polymer Materials for Fused Deposition Modeling 3D Printing. In Advances in 3D Printing; American Chemical Society: Washington, DC, USA, 2023. [Google Scholar] [CrossRef]
- Kovalcik, A.; Sangroniz, L.; Kalina, M.; Skopalova, K.; Humpolíček, P.; Omastova, M.; Mundigler, N.; Müller, A.J. Properties of scaffolds prepared by fused deposition modeling of poly(hydroxyalkanoates). Int. J. Biol. Macromol. 2020, 161, 364–376. [Google Scholar] [CrossRef] [PubMed]
- Kovalcik, A.; Smilek, J.; Machovsky, M.; Kalina, M.; Enev, V.; Dugova, H.; Cernekova, N.; Kovacova, M.; Spitalsky, Z. Properties and structure of poly (3-hydroxybutyrate-co-4-hydroxybutyrate) filaments for fused deposition modelling. Int. J. Biol. Macromol. 2021, 183, 880–889. [Google Scholar] [CrossRef] [PubMed]
- Stanzani, V.; Giubilini, A.; Checchi, M.; Messori, M.; Bondioli, F.; Palumbo, C. Eco-friendly biodegradable materials as new promising 3D-printed scaffold for eco-sustainable regenerative medicine. Ital. J. Anat. Embryol. 2021, 125, 159. [Google Scholar]
- Giubilini, A.; Siqueira, G.; Clemens, F.J.; Sciancalepore, C.; Messori, M.; Nyström, G.; Bondioli, F. 3D-Printing Nanocellulose-Poly(3-hydroxybutyrate- co-3-hydroxyhexanoate) Biodegradable Composites by Fused Deposition Modeling. ACS Sustain. Chem. Eng. 2020, 8, 10292–10302. [Google Scholar] [CrossRef]
- Valentini, F.; Dorigato, A.; Rigotti, D.; Pegoretti, A. Polyhydroxyalkanoates/fibrillated nanocellulose composites for additive manufacturing. J. Polym. Environ. 2019, 27, 1333–1341. [Google Scholar] [CrossRef]
- Cox, W.; Mertz, E. Correlation of Dynamic and Steady Flow Viscosities. J. Polym. Sci. 1958, 28, 619–622. [Google Scholar] [CrossRef]
- Candal, M.V.; Calafel, I.; Aranburu, N.; Fernández, M.; Gerrica-Echevarria, G.; Santamaría, A.; Müller, A.J. Thermo-rheological effects on successful 3D printing of biodegradable polyesters. Addit. Manuf. 2020, 36, 101408. [Google Scholar] [CrossRef]
- Van Krevelen, D.W.; Te Nijenhuis, K. Properties of Polymers: Their Correlation with Chemical Structure; Their Numerical Estimation and Prediction from Additive Group Contributions; Elsevier: Amsterdam, The Netherlands, 2009; ISBN 0080915108. [Google Scholar]
- Wang, J.; Hopmann, C.; Schmitz, M.; Hohlweck, T.; Wipperfürth, J. Modeling of pvT behavior of semi-crystalline polymer based on the two-domain Tait equation of state for injection molding. Mater. Des. 2019, 183, 108149. [Google Scholar] [CrossRef]
- ASTM. Standard Test Method for Tensile Properties of Plastics (ASTM D638-14); ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Caputo, M.R.; Tang, X.; Westlie, A.H.; Sardon, H.; Chen, E.Y.-X.; Müler, A.J. Effect of Chain Stereoconfiguration on Poly (3-hydroxybutyrate) Crystallization Kinetics. Biomacromolecules 2022, 23, 3847–3859. [Google Scholar] [CrossRef]
- Jiang, Z.; Liu, P.; Sue, H.-J.; Bremner, T. Effect of annealing on the viscoelastic behavior of poly (ether-ether-ketone). Polymer 2019, 160, 231–237. [Google Scholar] [CrossRef]
- Yasuniwa, M.; Tsubakihara, S.; Sugimoto, Y.; Nakafuku, C. Thermal analysis of the double-melting behavior of poly (L-lactic acid). J. Polym. Sci. Part B Polym. Phys. 2004, 42, 25–32. [Google Scholar] [CrossRef]
- Sangroniz, L.; Cavallo, D.; Müller, A.J. Self-nucleation effects on polymer crystallization. Macromolecules 2020, 53, 4581–4604. [Google Scholar] [CrossRef]
- Seppala, J.E.; Migler, K.D. Infrared thermography of welding zones produced by polymer extrusion additive manufacturing. Addit. Manuf. 2016, 12, 71–76. [Google Scholar] [CrossRef] [Green Version]
- Candal, M.V.; Calafel, I.; Fernández, M.; Aranburu, N.; Aguirresarobe, R.H.; Gerrica-Echevarria, G.; Santamaría, A.; Müller, A.J. Study of the interlayer adhesion and warping during material extrusion-based additive manufacturing of a carbon nanotube/biobased thermoplastic polyurethane nanocomposite. Polymer 2021, 224, 123734. [Google Scholar] [CrossRef]
- Vaes, D.; Van Puyvelde, P. Semi-crystalline feedstock for filament-based 3D printing of polymers. Prog. Polym. Sci. 2021, 118, 101411. [Google Scholar] [CrossRef]
- Mackay, M.E. The importance of rheological behavior in the additive manufacturing technique material extrusion. J. Rheol. 2018, 62, 1549–1561. [Google Scholar] [CrossRef]
- Thumsorn, S.; Prasong, W.; Kurose, T.; Ishigami, A.; Kobayashi, Y.; Ito, H. Rheological behavior and dynamic mechanical properties for interpretation of layer adhesion in FDM 3D printing. Polymers 2022, 14, 2721. [Google Scholar] [CrossRef] [PubMed]
- Phan, D.D.; Swain, Z.R.; Mackay, M.E. Rheological and heat transfer effects in fused filament fabrication. J. Rheol. 2018, 62, 1097–1107. [Google Scholar] [CrossRef]
- Cross, M.M. Rheology of non-Newtonian fluids: A new flow equation for pseudoplastic systems. J. Colloid Sci. 1965, 20, 417–437. [Google Scholar] [CrossRef]
- McIlroy, C.; Olmsted, P.D. Disentanglement effects on welding behaviour of polymer melts during the fused-filament-fabrication method for additive manufacturing. Polymer 2017, 123, 376–391. [Google Scholar] [CrossRef] [Green Version]
- Costanzo, A.; Spotorno, R.; Candal, M.V.; Fernández, M.M.; Müller, A.J.; Graham, R.S.; Cavallo, D.; McIlroy, C. Residual alignment and its effect on weld strength in material-extrusion 3D-printing of polylactic acid. Addit. Manuf. 2020, 36, 101415. [Google Scholar] [CrossRef]
- Likhtman, A.E.; McLeish, T.C.B. Quantitative theory for linear dynamics of linear entangled polymers. Macromolecules 2002, 35, 6332–6343. [Google Scholar] [CrossRef]
- Boudara, A.H.; Read, D.J. RepTate rheology software: Toolkit for the analysis of theories and experiments. J. Rheol. 2020, 64, 709. [Google Scholar] [CrossRef] [Green Version]
- Palade, L.-I.; Lehermeier, H.J.; Dorgan, J.R. Melt rheology of high L-content poly (lactic acid). Macromolecules 2001, 34, 1384–1390. [Google Scholar] [CrossRef]
- Shmueli, Y.; Jiang, J.; Zhou, Y.; Xue, Y.; Chang, C.-C.; Yuan, G.; Satija, S.K.; Lee, S.; Nam, C.-Y.; Kim, T. Simultaneous in situ X-ray scattering and infrared imaging of polymer extrusion in additive manufacturing. ACS Appl. Polym. Mater. 2019, 1, 1559–1567. [Google Scholar] [CrossRef]
- Yang, F.; Pitchumani, R. Healing of thermoplastic polymers at an interface under nonisothermal conditions. Macromolecules 2002, 35, 3213–3224. [Google Scholar] [CrossRef]
- Ausejo, J.G.; Rydz, J.; Musioł, M.; Sikorska, W.; Sobota, M.; Włodarczyk, J.; Adamus, G.; Janeczek, H.; Kwiecień, I.; Hercog, A. A comparative study of three-dimensional printing directions: The degradation and toxicological profile of a PLA/PHA blend. Polym. Degrad. Stab. 2018, 152, 191–207. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Vyas, C.; Poologasundarampillai, G.; Pape, I.; Hinduja, S.; Mirihanage, W.; Bartolo, P. Structural evolution of PCL during melt extrusion 3D printing. Macromol. Mater. Eng. 2018, 303, 1700494. [Google Scholar] [CrossRef] [Green Version]
- de Jager, B.; Moxham, T.; Besnard, C.; Salvati, E.; Chen, J.; Dolbnya, I.P.; Korsunsky, A.M. Synchrotron X-ray scattering analysis of nylon-12 crystallisation variation depending on 3D printing conditions. Polymers 2020, 12, 1169. [Google Scholar] [CrossRef]
- Ianniruberto, G.; Marrucci, G. Convective constraint release (CCR) revisited. J. Rheol. 2014, 58, 89–102. [Google Scholar] [CrossRef]
- Graham, R.S.; Likhtman, A.E.; McLeish, T.C.B.; Milner, S.T. Microscopic theory of linear, entangled polymer chains under rapid deformation including chain stretch and convective constraint release. J. Rheol. 2003, 47, 1171–1200. [Google Scholar] [CrossRef] [Green Version]
- Das, A.; Riet, J.A.; Bortner, M.J.; McIlroy, C. Rheology, crystallization, and process conditions: The effect on interlayer properties in three-dimensional printing. Phys. Fluids 2022, 34, 123108. [Google Scholar] [CrossRef]
- Cunha, M.A.G.; Robbins, M.O. Effect of Flow-Induced Molecular Alignment on Welding and Strength of Polymer Interfaces. Macromolecules 2020, 53, 8417–8427. [Google Scholar] [CrossRef]
- Seppala, J.E.; Han, S.H.; Hillgartner, K.E.; Davis, C.S.; Migler, K.B. Weld Formation during Material Extrusion Additive Manufacturing. Soft Matter 2017, 13, 6761–6769. [Google Scholar] [CrossRef]
- Costanzo, A.; Cavallo, D.; McIlroy, C. High-Performance Co-Polyesters for Material-Extrusion 3D Printing: A Molecular Perspective of Weld Properties. Addit. Manuf. 2022, 49, 102474. [Google Scholar] [CrossRef]
- McIlroy, C. A fundamental rule: Determining the importance of flow prior to polymer crystallization. Phys. Fluids 2019, 31, 113103. [Google Scholar] [CrossRef]
- Wang, J.; Hopmann, C.; Kahve, C.; Hohlweck, T.; Alms, J. Measurement of specific volume of polymers under simulated injection molding processes. Mater. Des. 2020, 196, 109136. [Google Scholar] [CrossRef]
- Mishra, A.A.; Momin, A.; Strano, M.; Rane, K. Implementation of viscosity and density models for improved numerical analysis of melt flow dynamics in the nozzle during extrusion-based additive manufacturing. Prog. Addit. Manuf. 2022, 7, 41–54. [Google Scholar] [CrossRef]
- Kazmer, D.O.; Colon, A.R.; Peterson, A.M.; Kim, S.K. Concurrent characterization of compressibility and viscosity in extrusion-based additive manufacturing of acrylonitrile butadiene styrene with fault diagnoses. Addit. Manuf. 2021, 46, 102106. [Google Scholar] [CrossRef]
- Garzon-Hernandez, S.; Garcia-Gonzalez, D.; Jérusalem, A.; Arias, A. Design of FDM 3D printed polymers: An experimental-modelling methodology for mechanical property prediction. Mater. Des. 2019, 188, 108414. [Google Scholar] [CrossRef]
- Yadav, D.; Chhabra, D.; Garg, R.K.; Ahlawat, A.; Phogat, A. Optimization of FDM 3D printing process parameters for multi-material using artificial neural network. Mater. Today Proc. 2020, 21, 1583–1591. [Google Scholar] [CrossRef]
- Ding, S.; Zou, B.; Wang, P.; Ding, H. Effects of nozzle temperature and building orientation on mechanical properties and microstructure of PEEK and PEI printed by 3D-FDM. Polym. Test. 2019, 78, 105948. [Google Scholar] [CrossRef]
- Pulipaka, A.; Gide, K.M.; Beheshti, A.; Bagheri, Z.S. Effect of 3D printing process parameters on surface and mechanical properties of FFF-printed PEEK. J. Manuf. Process. 2023, 85, 368–386. [Google Scholar] [CrossRef]
- Shuto, R.; Norimatsu, S.; Arola, D.D.; Matsuzaki, R. Effect of the nozzle temperature on the microstructure and interlaminar strength in 3D printing of carbon fiber/polyphenylene sulfide composites. Compos. Part C Open Access 2022, 9, 100328. [Google Scholar] [CrossRef]
- Gao, X.; Qi, S.; Kuang, X.; Su, Y.; Li, J.; Wang, D. Fused filament fabrication of polymer materials: A review of interlayer bond. Addit. Manuf. 2021, 37, 101658. [Google Scholar] [CrossRef]
- Spoerk, M.; Arbeiter, F.; Raguž, I.; Weingrill, G.; Fischinger, T.; Traxler, G.; Schuschnigg, S.; Cardon, L.; Holzer, C. Polypropylene filled with glass spheres in extrusion-based additive manufacturing: Effect of filler size and printing chamber temperature. Macromol. Mater. Eng. 2018, 303, 1800179. [Google Scholar] [CrossRef]
- Spoerk, M.; Holzer, C.; Gonzalez-Gutierrez, J. Material extrusion-based additive manufacturing of polypropylene: A review on how to improve dimensional inaccuracy and warpage. J. Appl. Polym. Sci. 2020, 137, 48545. [Google Scholar] [CrossRef] [Green Version]
- Hertle, S.; Drexler, M.; Drummer, D. Additive manufacturing of poly (propylene) by means of melt extrusion. Macromol. Mater. Eng. 2016, 301, 1482–1493. [Google Scholar] [CrossRef]
- Benwood, C.; Anstey, A.; Andrzejewski, J.; Misra, M.; Mohanty, A.K. Improving the impact strength and heat resistance of 3D printed models: Structure, property, and processing correlationships during fused deposition modeling (FDM) of poly (lactic acid). ACS Omega 2018, 3, 4400–4411. [Google Scholar] [CrossRef] [PubMed]
- Xiaoyong, S.; Liangcheng, C.; Honglin, M.; Peng, G.; Zhanwei, B.; Cheng, L. Experimental analysis of high temperature PEEK materials on 3D printing test. In Proceedings of the 2017 9th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Changsha, China, 14–15 January 2017; pp. 13–16. [Google Scholar]
- Hsueh, M.-H.; Lai, C.-J.; Wang, S.-H.; Zeng, Y.-S.; Hsieh, C.-H.; Pan, C.-Y.; Huang, W.-C. Effect of printing parameters on the thermal and mechanical properties of 3d-printed pla and petg, using fused deposition modeling. Polymers 2021, 13, 1758. [Google Scholar] [CrossRef]
- Abeykoon, C.; Sri-Amphorn, P.; Fernando, A. Optimization of fused deposition modeling parameters for improved PLA and ABS 3D printed structures. Int. J. Lightweight Mater. Manuf. 2020, 3, 284–297. [Google Scholar] [CrossRef]
- Yang, T.-C.; Yeh, C.-H. Morphology and mechanical properties of 3D printed wood fiber/polylactic acid composite parts using fused deposition modeling (FDM): The effects of printing speed. Polymers 2020, 12, 1334. [Google Scholar] [CrossRef] [PubMed]
- Ziemian, C.; Sharma, M.; Ziemian, S. Anisotropic mechanical properties of ABS parts fabricated by fused deposition modelling. Mech. Eng. 2012, 23, 2397. [Google Scholar]
- Spoerk, M.; Savandaiah, C.; Arbeiter, F.; Traxler, G.; Cardon, L.; Holzer, C.; Sapkota, J. Anisotropic properties of oriented short carbon fibre filled polypropylene parts fabricated by extrusion-based additive manufacturing. Compos. Part A Appl. Sci. Manuf. 2018, 113, 95–104. [Google Scholar] [CrossRef]
- Ang, K.C.; Leong, K.F.; Chua, C.K.; Chandrasekaran, M. Investigation of the mechanical properties and porosity relationships in fused deposition modelling-fabricated porous structures. Rapid Prototyp. J. 2006, 12, 100–105. [Google Scholar]
- Anitha, R.; Arunachalam, S.; Radhakrishnan, P. Critical parameters influencing the quality of prototypes in fused deposition modelling. J. Mater. Process. Technol. 2001, 118, 385–388. [Google Scholar] [CrossRef]
- Perez, C.J.L. Analysis of the surface roughness and dimensional accuracy capability of fused deposition modelling processes. Int. J. Prod. Res. 2002, 40, 2865–2881. [Google Scholar] [CrossRef]
- Pandey, P.M.; Reddy, N.V.; Dhande, S.G. Real time adaptive slicing for fused deposition modelling. Int. J. Mach. Tools Manuf. 2003, 43, 61–71. [Google Scholar] [CrossRef]
- Lay, M.; Thajudin, N.L.N.; Hamid, Z.A.A.; Rusli, A.; Abdullah, M.K.; Shuib, R.K. Comparison of physical and mechanical properties of PLA, ABS and nylon 6 fabricated using fused deposition modeling and injection molding. Compos. Part B Eng. 2019, 176, 107341. [Google Scholar] [CrossRef]








| Mn (kDa) | Mw (kDa) | Đ | MVR (cm3 10 min−1) | MFI (g 10 min−1) |
|---|---|---|---|---|
| 121 | 163 | 1.35 | 18.3 | 2 (at 165 °C, 5 kg) |
| Name | Nozzle Temperature (°C) | Bed Temperature (°C) | Printing Velocity (mm/s) |
|---|---|---|---|
| L12 | 180 | 30 | 30 |
| L22 | 180 | 50 | 30 |
| M12 | 190 | 30 | 30 |
| M22 | 190 | 50 | 30 |
| M21 | 190 | 50 | 20 |
| M23 | 190 | 50 | 40 |
| H12 | 200 | 30 | 30 |
| H22 | 200 | 50 | 30 |
| M12 [90°, 90°] | 190 | 30 | 30 |
| Parameter | Description |
|---|---|
| Density (ρ)in kg/m3 | 1216 |
| Heat capacity (cp) in J/(kg·°C) | cp(T) = −0.033T2 + 14.277T + 912.36 |
| Thermal conductivity (k) in W/(m·°C) | k(T) = 0.0002T + 0.1294 (30 °C < T < 95 °C) |
| k(T) = 0.0013T + 0.0262 (95 °C < T < 105 °C) | |
| k(T) = 0.000Tx + 0.132 (105 °C < T < 105 °C) |
| Sample | Cooling | Second Heating | |||||
|---|---|---|---|---|---|---|---|
| Tc (°C) | ΔHc (J/g) | Tcc (°C) | ΔHcc (J/g) | Tm (°C) | ΔHm (J/g) | xc (%) | |
| Filament | 50.2 | 43 | 51.2 | 17 | 124.1/143.5 | 60 | 49 |
| Solid State | Molten State | Liquid-Solid Transition | |||
|---|---|---|---|---|---|
| b1s (cm3/g) | 0.8540 | b1m (cm3/g) | 0.9100 | b5 (°C) | 98 |
| b2s (cm3/g °C) | 4.5 × 10−4 | b2m (cm3/g °C) | 6.628 × 10−4 | b6 (°C/Pa2) | 2.32 × 10−7 |
| b3s (Pa) | 1.119108 | b3m (Pa) | 6.5970 × 107 | ||
| b4s (°C−1) | 1.12310−3 | b4m (°C−1) | 1.75 × 103 | ||
| b7 (cm3/g) | 6.06 × 10−2 | ||||
| b8 (°C−1) | 5.4 × 10−2 | ||||
| b9 (Pa−1) | 1.9 × 10−8 | ||||
| Condition | Nozzle T (°C) | Bed T (°C) | Printing Velocity (mm/s) | Young Modulus, E (MPa) | Tensile Strength, σM (MPa) | Strain at Break, εB (%) |
|---|---|---|---|---|---|---|
| L12 | 180 | 30 | 30 | 1110 ± 27 | 14.9 ± 1.0 | 2.15 ± 0.02 |
| L22 | 180 | 50 | 30 | 1150 ± 78 | 17.0 ± 1.3 | 2.67 ± 0.22 |
| M12 | 190 | 30 | 30 | 1200 ± 66 | 16.5 ± 1.4 | 2.55 ± 0.25 |
| M22 | 190 | 50 | 30 | 1260 ± 30 | 18.5 ± 1.4 | 2.89 ± 0.03 |
| H12 | 200 | 30 | 30 | 1241 ± 85 | 16.3 ± 2.0 | 2.31 ± 0.05 |
| H22 | 200 | 50 | 30 | 1210 ± 98 | 17.6 ± 2.6 | 2.60 ± 0.16 |
| Condition | Nozzle T (°C) | Bed T (°C) | Printing Velocity (mm/s) | Young Modulus, E (MPa) | Tensile Strengh, σM (MPa) | Strain at Break, εB (%) |
|---|---|---|---|---|---|---|
| M21 | 190 | 50 | 20 | 970 ± 90 | 13.2 ± 3.0 | 2.53 ± 0.23 |
| M22 | 190 | 50 | 30 | 1260 ± 30 | 18.5 ± 1.4 | 2.89 ± 0.03 |
| M23 | 190 | 50 | 40 | 1090 ± 105 | 16.8 ± 1.5 | 2.91 ± 0.41 |
| Condition | Nozzle T (°C) | Bed T (°C) | Printing Velocity (mm/s) | Young Modulus, E (MPa) | Tensile Strength, σM (MPa) | Strain at Break, εB (%) |
|---|---|---|---|---|---|---|
| M12 [45°, 45°] | 190 | 30 | 30 | 1200 ± 66 | 16.5 ± 1.4 | 2.55 ± 0.25 |
| M12 [90°, 90°] | 190 | 30 | 30 | 1280 ± 51 | 20.1 ± 1.0 | 3.58 ± 0.12 |
| Compression Molding | - | - | - | 1320 ± 90 | 24.0 ± 1.9 | 6.78 ± 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caputo, M.R.; Fernández, M.; Aguirresarobe, R.; Kovalcik, A.; Sardon, H.; Candal, M.V.; Müller, A.J. Influence of FFF Process Conditions on the Thermal, Mechanical, and Rheological Properties of Poly(hydroxybutyrate-co-hydroxy Hexanoate). Polymers 2023, 15, 1817. https://doi.org/10.3390/polym15081817
Caputo MR, Fernández M, Aguirresarobe R, Kovalcik A, Sardon H, Candal MV, Müller AJ. Influence of FFF Process Conditions on the Thermal, Mechanical, and Rheological Properties of Poly(hydroxybutyrate-co-hydroxy Hexanoate). Polymers. 2023; 15(8):1817. https://doi.org/10.3390/polym15081817
Chicago/Turabian StyleCaputo, Maria Rosaria, Mercedes Fernández, Robert Aguirresarobe, Adriana Kovalcik, Haritz Sardon, María Virginia Candal, and Alejandro J. Müller. 2023. "Influence of FFF Process Conditions on the Thermal, Mechanical, and Rheological Properties of Poly(hydroxybutyrate-co-hydroxy Hexanoate)" Polymers 15, no. 8: 1817. https://doi.org/10.3390/polym15081817









