Study on Dynamic Modulus and Damping Characteristics of Modified Expanded Polystyrene Lightweight Soil under Cyclic Load
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Test Instrument and Test Scheme
2.3. Specimen Preparation
- (1)
- The soil was dried, crushed, and sieved in a 2 mm sieve before being mechanically combined with lime and fly ash until it was uniformly dispersed. Simultaneously, water and the sodium silicate solution were mixed and stirred evenly.
- (2)
- The mixture of sodium silicate solution and water was poured into the mixture of lime, fly ash, and soil and stirred for 3 min. Finally, it was poured into weighed EPS particles and stirred until the EPS particles were evenly distributed in the soil.
- (3)
- The mixture was loaded into a binding sample maker (D = 39.1 mm, H = 80 mm) 3 times and vibrated 50 times after each loading. The mixture was allowed to stand for 3 h after being vibrated 3 times. A scraper was then used to smooth the surface of the sample. The bottom plates at both ends and the sample maker were removed, and the sample was demolded, then obtained.
- (4)
- The sample was placed in a standard curing room for 28 d. During curing, the temperature in the standard curing room fluctuated at 20 ± 2 °C, and the humidity was always above 90%.
3. Test Results and Discussion
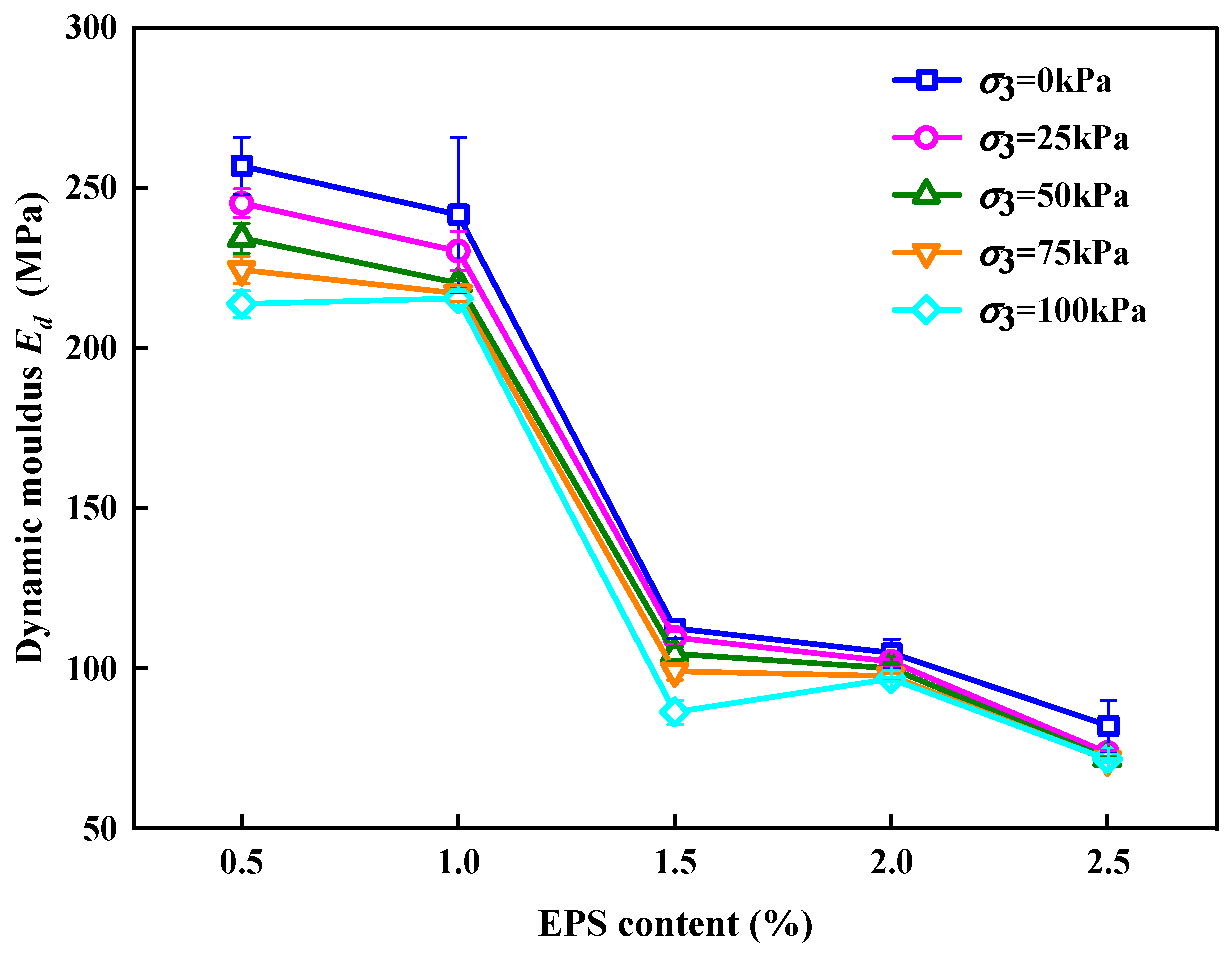
3.1. Influence of EPS Particle Content on Ed and λ
3.1.1. Effect of EPS Particle Content on Ed
- (1)
- Slow-descent stage
- (2)
- Rapid descent stage
- (3)
- Slow decline to stabilize stage
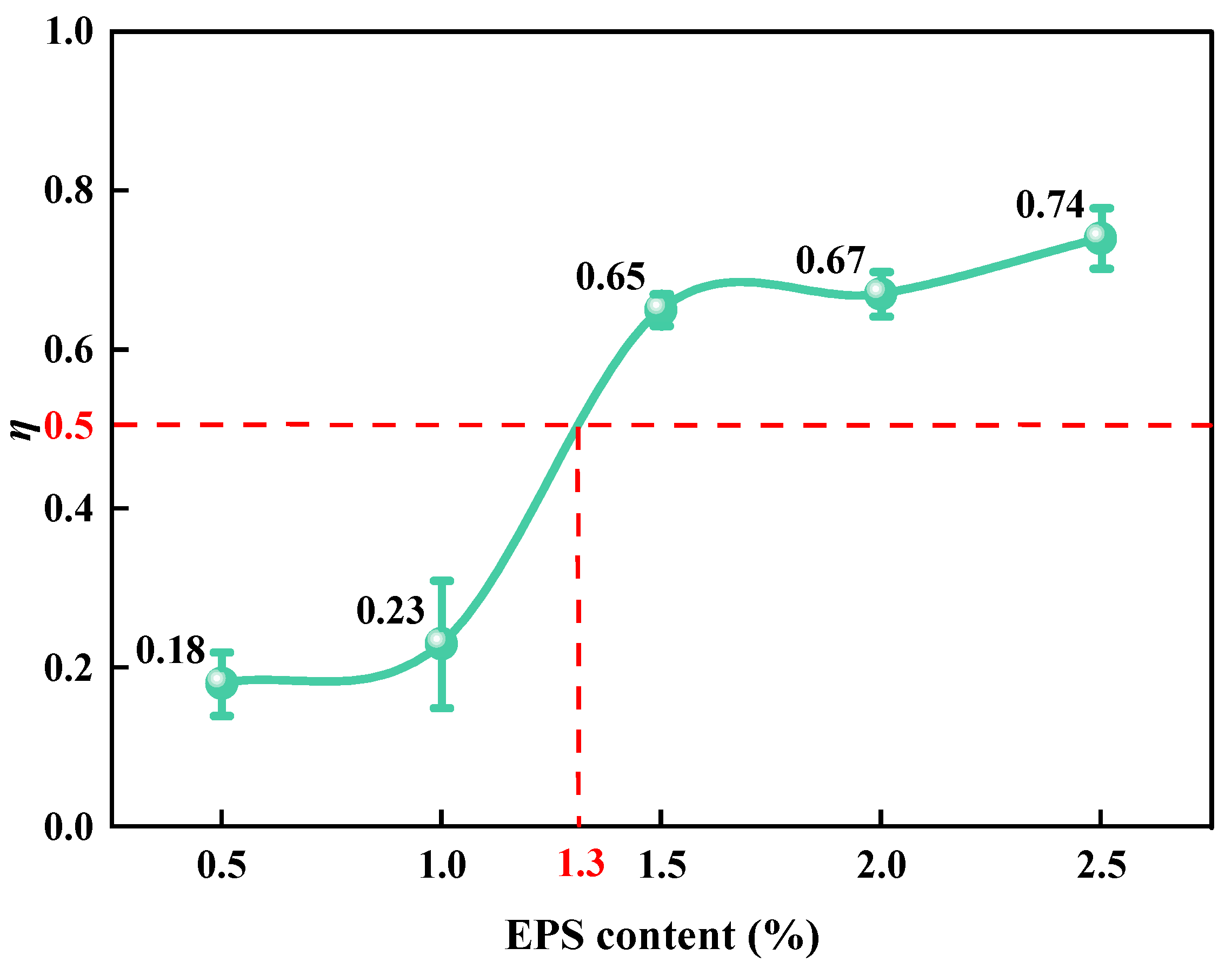
3.1.2. Series Parallel Model for Ed of SLS
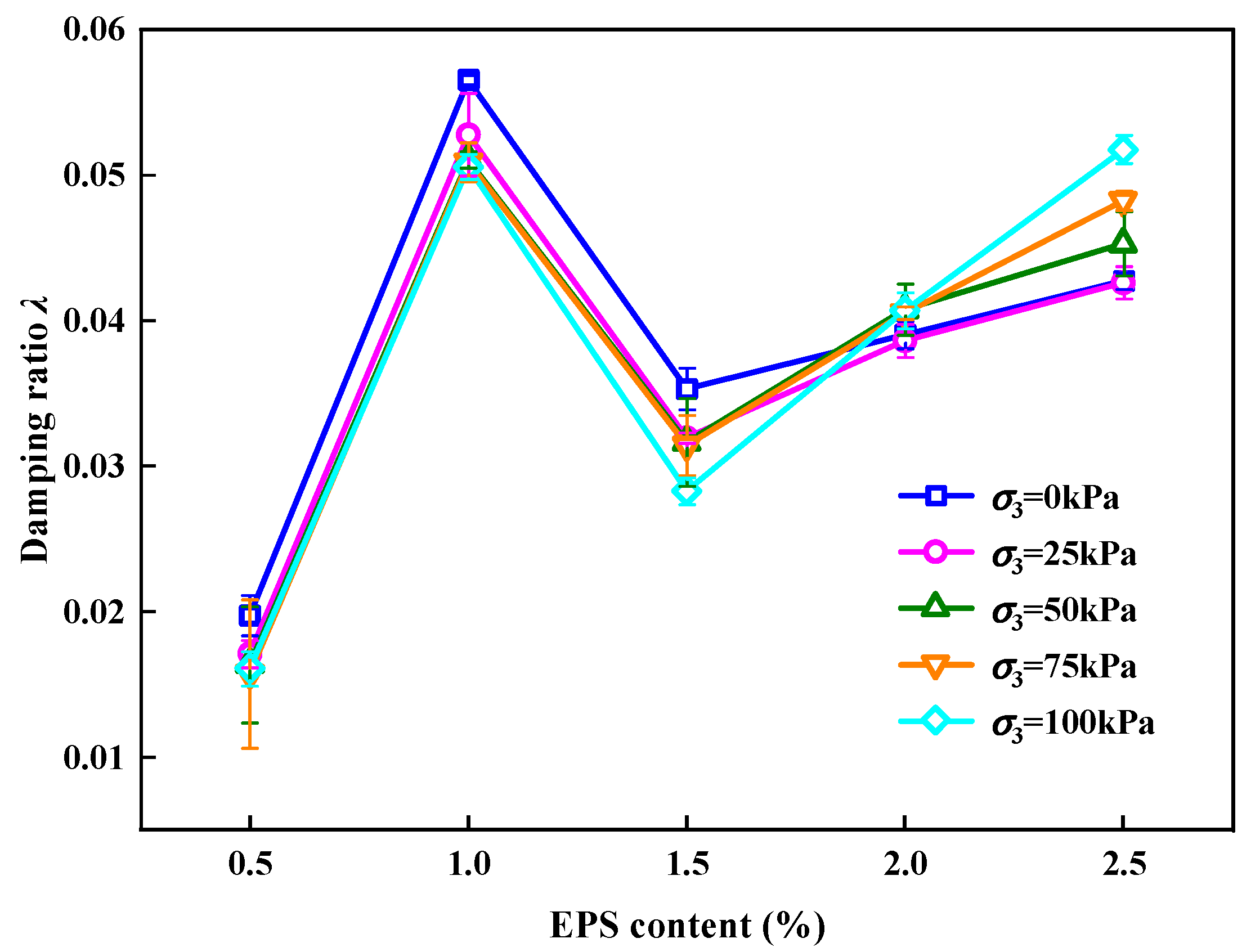
3.1.3. Effect of EPS Particle Content on λ
- (1)
- When EC < 1%, λ first increased with an increase in EC. This was because, as the cyclic load progressed, the overall skeleton loosened, and λ increased because the energy dissipated by friction increased.
- (2)
- When 1% < EC < 1.5%, λ decreased with an increase in EC. This was because, as the cyclic load progressed and when the EC was approximately 1.5%, the EPS particles in SLS were completely compacted. The slip and dislocation of particles in the SLS were reduced, and λ decreased owing to the reduction in energy dissipated by friction and elastic deformation of EPS particles.
- (3)
- When EC > 1.5%, λ increased with increasing EPS particle content. This was caused by the increase in the EPS particle content, which replaced the LFS. As the pore structure in the SLS increased, the LFS volume decreased, and more energy was lost in the propagation of stress waves in the SLS, which contained a large proportion of EPS particles. As the cyclic loading continued, there were still many EPS particles that were not compacted. This portion of the EPS particles produced elastic deformation and consumed energy; thus, λ increased again.
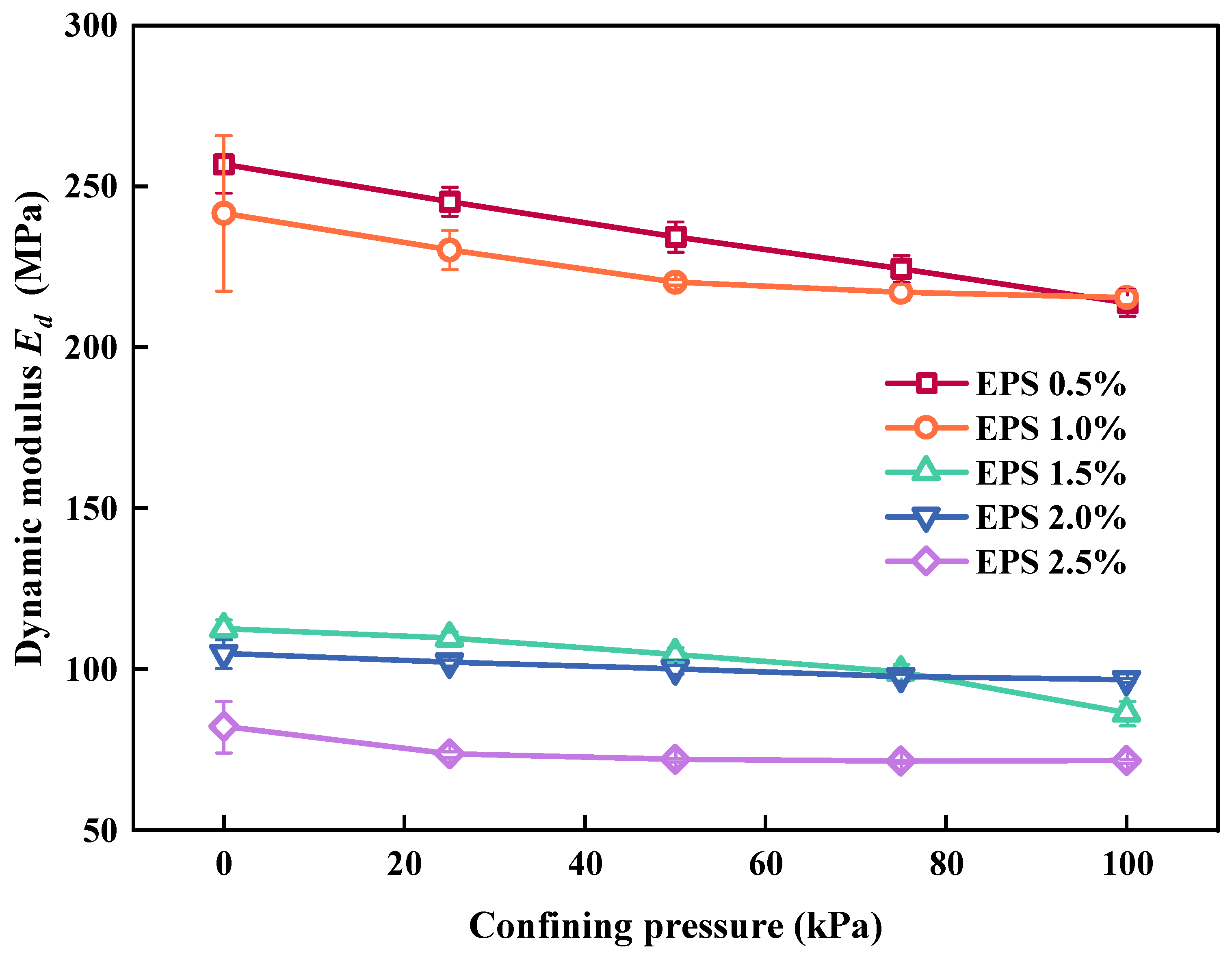
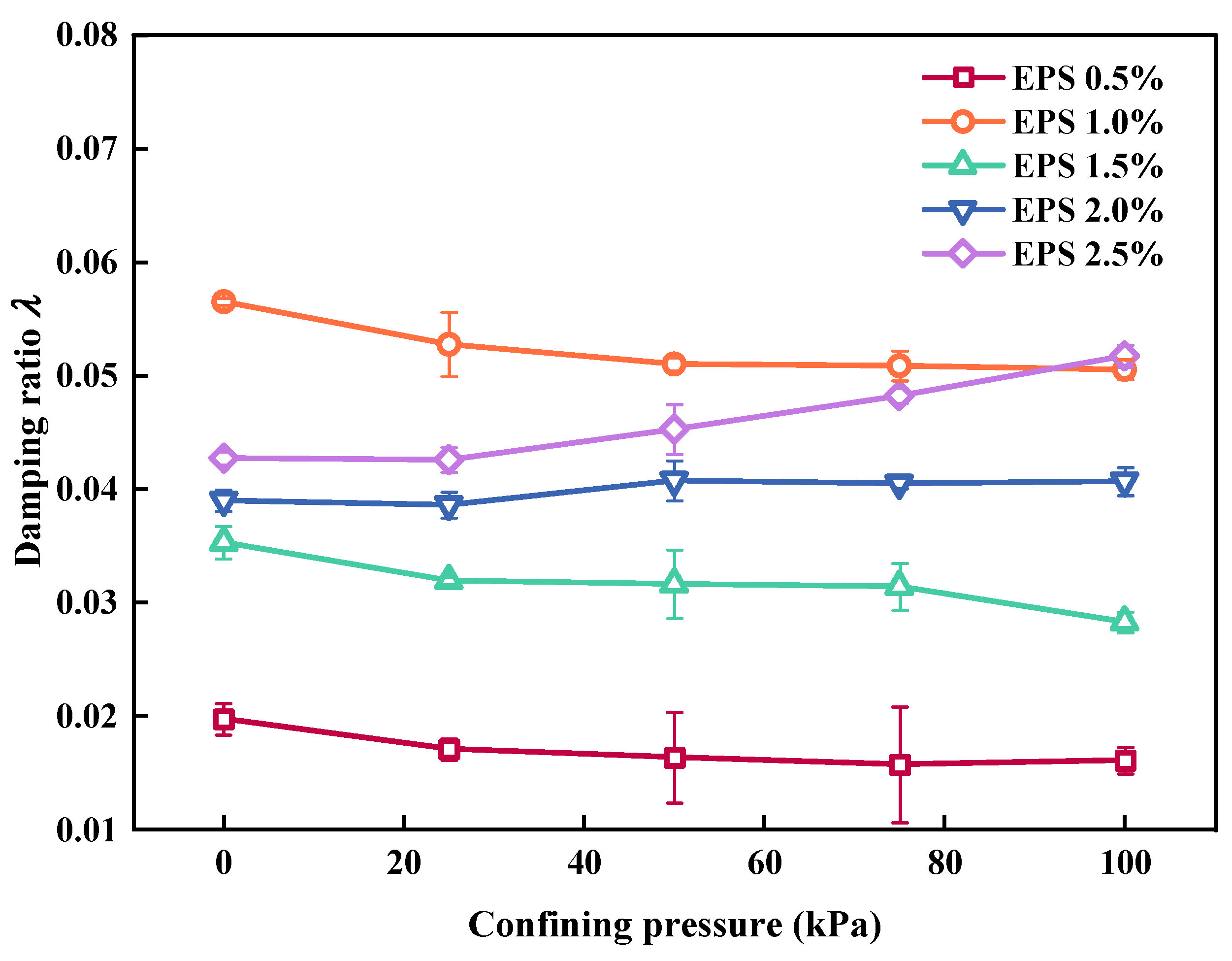
3.2. Influence of Confining Pressure on Ed and λ
3.2.1. Effect of Confining Pressure on Ed
3.2.2. Effect of Confining Pressure on λ
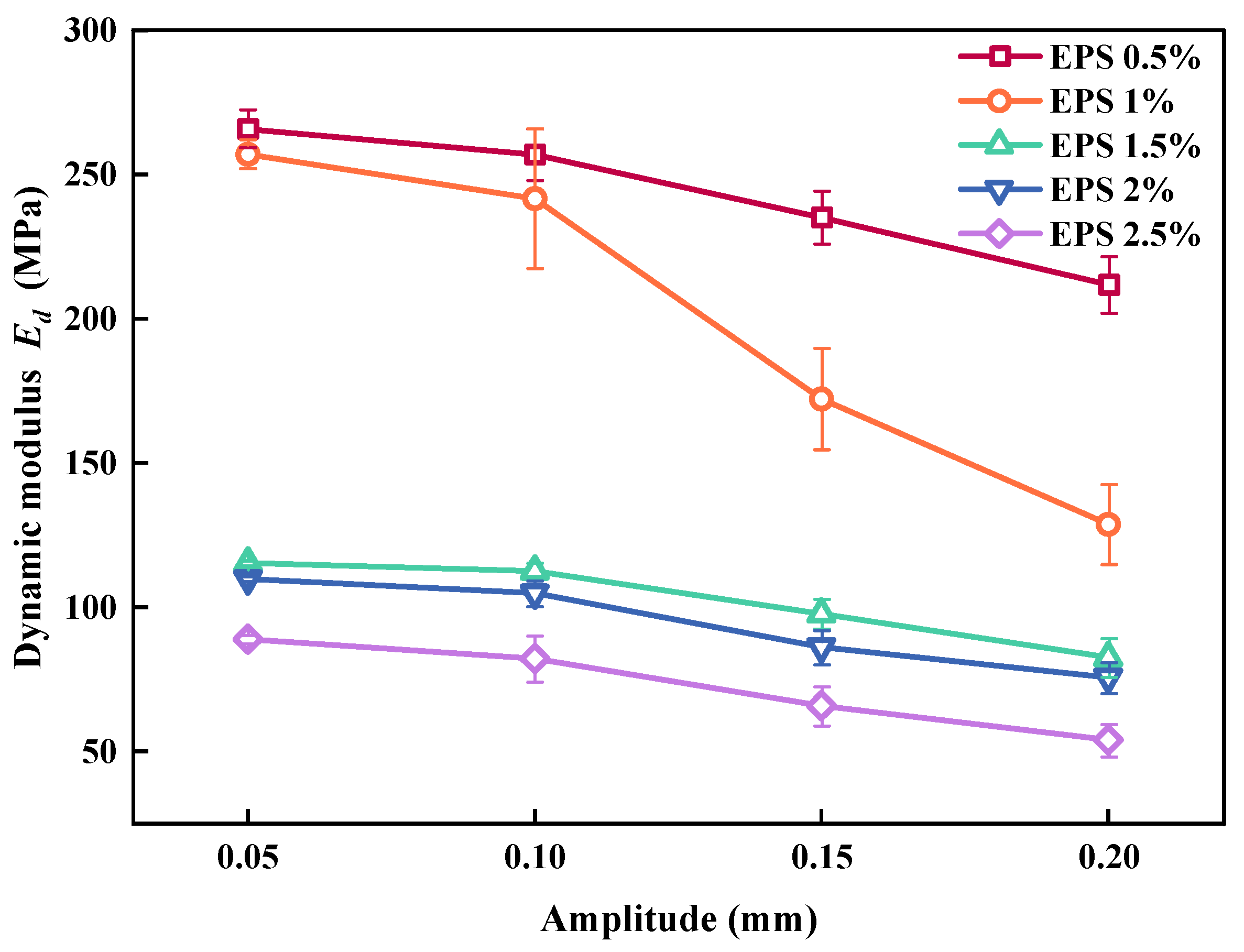
3.3. Influence of Amplitude on Ed and λ
3.3.1. Effect of Amplitude on Ed
3.3.2. Effect of Amplitude on λ
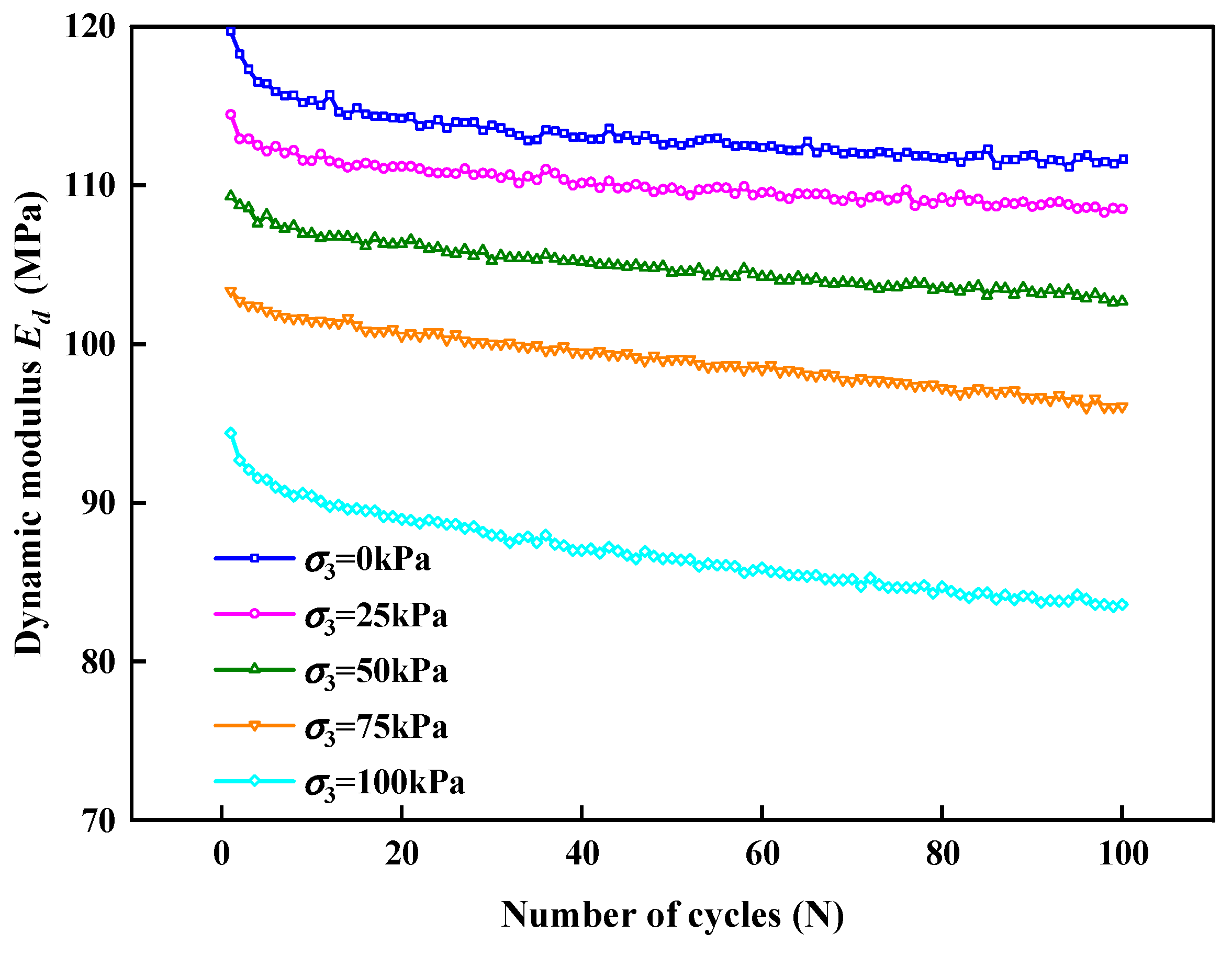
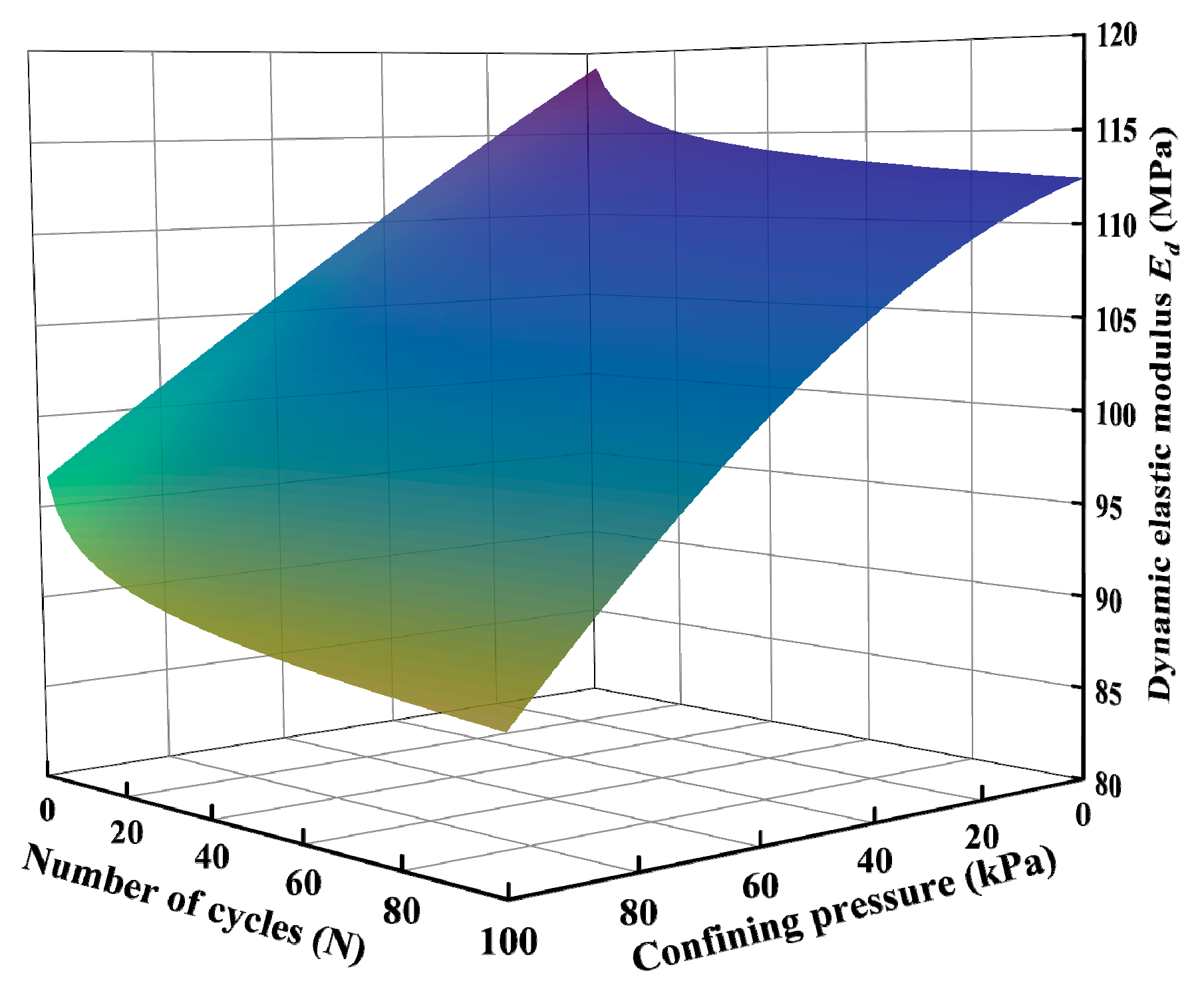
3.4. Influence of Cycle Times on Ed and λ
4. Conclusions
- (1)
- The EPS particle content played a decisive role in the Ed and λ of the SLS, and the optimal dosage of EPS particles is between 0.5% and 1%. When σ3 and amplitude are constant, η increases with the increase of EC, and the layout of EPS and LFS in SLS is transferred from parallel to series. When EC increased from 1% to1.5%, Ed decreases by 60%, resulting in a Z-shaped decline in Ed of SLS. The λ of SLS is N-shaped with the increase in EPS particle content.
- (2)
- When EC was constant, the Ed of the SLS decreased with an increase in σ3 and amplitude; however, the effect of change in confining pressure and amplitude on Ed was not obvious under high EC values. This was because the number of EPS particles was too high and some EPS particles in the SLS provided elastic properties; thus, the reduction in Ed was not obvious. The λ of the SLS generally decreased with an increase in the confining pressure and amplitude, and the variation range was small (within 0.5%).
- (3)
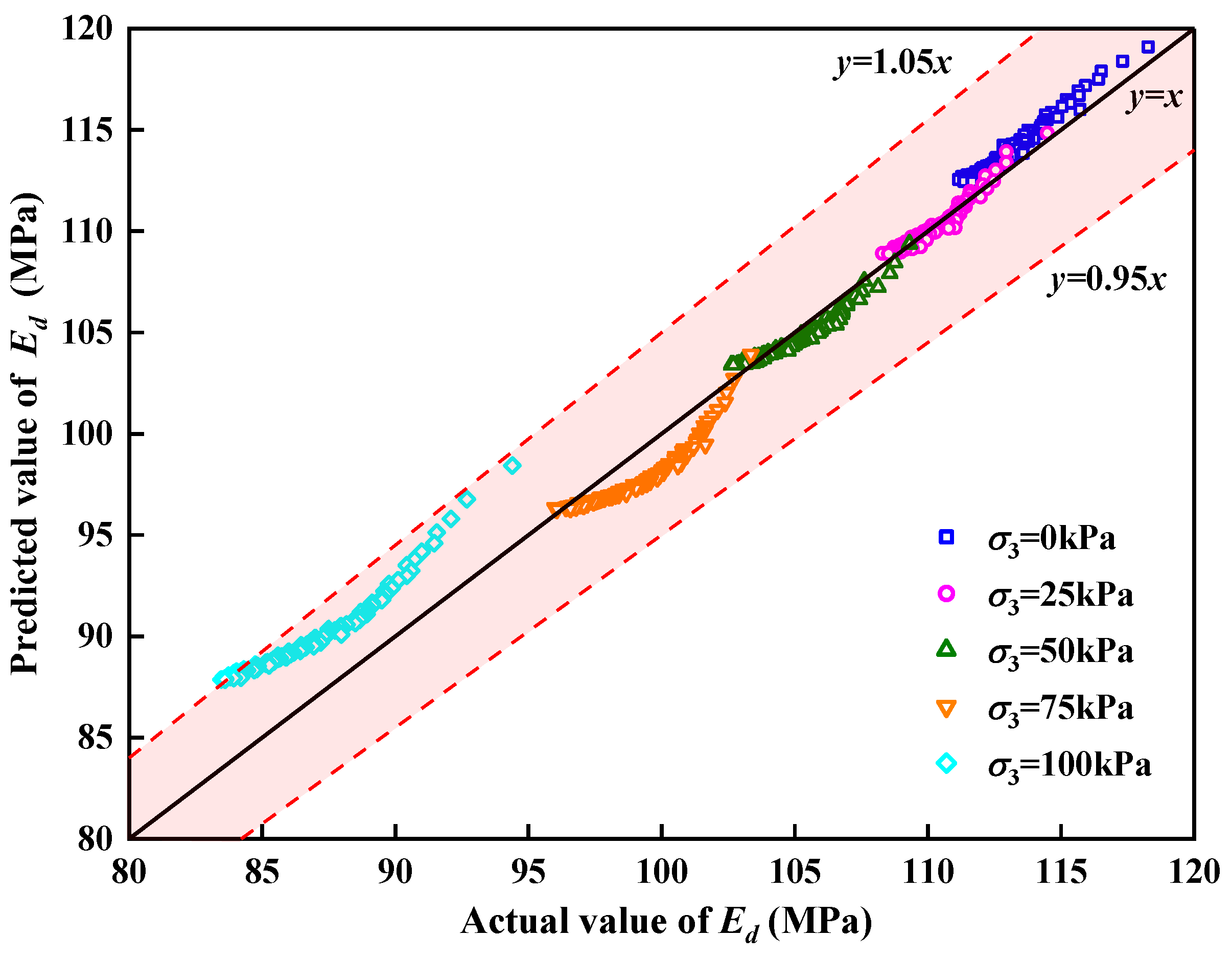
- The Ed of the SLS satisfied the power function relationship with the number of load actions. The Ed value predicted by the model established in this study was consistent with the actual value, and the error was within 5%. The model predicted well the varying trend of the Ed under various σ3 values and cycle times.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Miao, L.C.; Wang, F.; Han, J.; Lv, W.H.; Li, J. Properties and applications of cement-treated sand-expanded polystyrene bead lightweight fill. J. Mater. Civ. Eng. 2013, 25, 86–93. [Google Scholar] [CrossRef]
- Badrawi, E.F.; El-kady, M.S. Stabilizing soft clay using geo-foam beads and cement bypass dust. Undergr. Space 2019, 5, 292–297. [Google Scholar] [CrossRef]
- Lu, W.H.; Miao, L.C.; Zhang, J.H.; Zhang, Y.X.; Li, J. Characteristics of deformation and damping of cement treated and expanded polystyrene mixed lightweight subgrade fill under cyclic load. Appl. Sci. 2019, 9, 167. [Google Scholar] [CrossRef]
- Puppala, A.J.; Ruttanaporamakul, P.; Congress, S.S.C. Design and construction of lightweight EPS geofoam embedded geomaterial embankment system for control of settlements. Geotext. Geomembr. 2019, 47, 295–305. [Google Scholar] [CrossRef]
- Abdollahi, M.; Moghaddas Tafreshi, S.N.; Leshchinsky, B. Protection of buried utilities against repeated loading: Application of geogrid-EPS geofoam system. Int. J. Geomech. 2021, 21, 04021158. [Google Scholar] [CrossRef]
- Kong, D.; Deng, M.X.; Liu, Y.; Wang, X.M. The environmental study on consolidated undrained triaxial compression tests on lightweight soil mixed with rubber chips of scrap tires. Constr. Build. Mater. 2018, 27, 1503–1510. [Google Scholar]
- Mohajerani, A.; Ashdown, M.; Abdihashi, L.; Nazem, M. Expanded polystyrene geofoam in pavement construction. Constr. Build. Mater. 2017, 157, 438–448. [Google Scholar] [CrossRef]
- Liu, H.; Deng, A.; Chu, J. Effect of different mixing ratios of polystyrene pre-puff beads and cement on the mechanical behaviour of lightweight fill. Geotext. Geomembr. 2006, 24, 331–338. [Google Scholar] [CrossRef]
- Sun, Y.; You, J.J.; Zhou, J.; Liu, X.P.; Yu, L.W.; Bu, C.M.; Yan, Z.T.; Chen, X.R. Quantified research on the nonuniform distribution of expanded polystyrene beads in sandwich panels. Constr. Build. Mater. 2020, 263, 120672. [Google Scholar] [CrossRef]
- Cheng, C.M.; Hong, S.L.; Zhang, Y.F.; He, J. Effect of expanded polystyrene on the flexural behavior of lightweight glass fiber reinforced cement. Constr. Build. Mater. 2020, 265, 120328. [Google Scholar] [CrossRef]
- Dueramae, S.; Sanboonsiri, S.; Suntadyon, T.; Aoudta, B.; Tangchirapat, W.; Jongpradist, P.; Pulngern, T.; Jitsangiam, P.; Jaturapitakkul, C. Properties of lightweight alkali activated controlled Low-Strength material using calcium carbide residue—Fly ash mixture and containing EPS beads. Constr. Build. Mater. 2021, 297, 123769. [Google Scholar] [CrossRef]
- Chenari, R.J.; Fard, M.K.; Maghfarati, S.P.; Pishgar, F.; Machado, S.L. An investigation on the geotechnical properties of sand–EPS mixture using large oedometer apparatus. Constr. Build. Mater. 2016, 113, 773–782. [Google Scholar] [CrossRef]
- Kazempour, S.; Chenari, R.J.; Ahmadi, H.; Payan, M.; Senetakis, K. Assessment of the compression characteristics and coefficient of lateral earth pressure of aggregate-expanded polystyrene beads composite fill-backfill using large oedometer experiments. Constr. Build. Mater. 2021, 302, 124145. [Google Scholar] [CrossRef]
- Tiwari, N.; Satyam, N.; Shukla, S.K. An experimental study on micro-structural and geotechnical characteristics of expansive clay mixed with EPS granules. Soils Found. 2020, 60, 705–713. [Google Scholar] [CrossRef]
- Khajeh, A.; Ebrahimi, S.A.; MolaAbasi, H.; Chenari, R.J.; Payan, M. Effect of EPS beads in lightening a typical zeolite and cement-treated sand. Bull. Eng. Geol. Environ. 2021, 80, 8615–8632. [Google Scholar] [CrossRef]
- Siabil, S.M.A.G.; Tafreshi, S.N.M.; Dawson, A.R.; Omran, M.P. Behavior of expanded polystyrene (EPS) blocks under cyclic pavement foundation loading. Geosynth. Int. 2018, 26, 1–25. [Google Scholar] [CrossRef]
- Lu, W.; Wang, J.; Zhang, Y. Strength characteristics of cement treated and expanded polystyrene mixed lightweight of waste soil from the construction site of a Yangtze River bridge in China. Adv. Civ. Eng. 2020, 2020, 3640510. [Google Scholar] [CrossRef]
- Silveira, M.V.; Calheiros, A.V.; Casagrande, M.D. Applicability of the expanded polystyrene as a soil improvement tool. J. Mater. Civ. Eng. 2018, 30, 06018006. [Google Scholar] [CrossRef]
- Li, M.D.; Wen, K.J.; Li, L.; Tian, A.G. Mechanical properties of expanded polystyrene beads stabilized lightweight soil. Geomech. Eng. 2017, 13, 459–474. [Google Scholar] [CrossRef]
- Li, Z.X.; Chen, W.S.; Hao, H.; Khan, M.Z.N.; Pham, T.M. Dynamic compressive properties of novel lightweight ambient-cured EPS geopolymer composite. Constr. Build. Mater. 2021, 273, 122044. [Google Scholar] [CrossRef]
- Edinçliler, A.; Özer, A.T. Effects of EPS bead inclusions on stress–strain behaviour of sand. Geosynth. Int. 2014, 21, 89–102. [Google Scholar] [CrossRef]
- Nik, S.A.; Chenari, R.J.; Najafi, E.K.; Payan, M. Assessment of the hydraulic characteristics of aggregate-Expanded polystyrene beads composite using enhanced standard proctor compaction test configuration. Iran. J. Sci. Technol. Trans. Civ. Eng. 2023, 47, 627–637. [Google Scholar] [CrossRef]
- Chenari, R.J.; Fatahi, B.; Ghorbani, A.; Alamoti, M.N. Evaluation of strength properties of cement stabilized sand mixed with EPS beads and fly ash. Geomech. Eng. 2018, 14, 533–544. [Google Scholar] [CrossRef]
- Onishi, K.; Tsukamoto, Y.; Saito, R.; Chiyoda, T. Strength and small-strain modulus of lightweight geomaterials: Cement-stabilised sand mixed with compressible expanded polystyrene beads. Geosynth. Int. 2010, 17, 380–388. [Google Scholar] [CrossRef]
- Khajeh, A.; Jamshidi Chenari, R.; Payan, M. A review of the studies on soil-EPS composites: Beads and blocks. Geotech. Geol. Eng. 2020, 38, 3363–3383. [Google Scholar] [CrossRef]
- Wang, F.; Miao, L.C. A proposed lightweight fill for embankments using cement-treated Yangzi River sand and expanded polystyrene (EPS) beads. Bull. Eng. Geol. Environ. 2009, 68, 517–524. [Google Scholar] [CrossRef]
- Jiang, P.; Chen, Y.W.; Li, N.; Zhou, L.; Pu, S.Y.; Wang, W. Strength properties and microscopic mechanism of lime and fly ash modified expandable poly styrene lightweight soil reinforced by polypropylene fiber. Case Stud. Constr. Mater. 2022, 17, e01250. [Google Scholar] [CrossRef]
- Padade, A.H.; Mandal, J.N. Expanded polystyrene-based geomaterial with fly ash. Int. J. Geomech. 2014, 14, 06014013. [Google Scholar] [CrossRef]
- Lang, L.; Chen, B.; Li, J.S. High-efficiency stabilization of dredged sediment using nano-modified and chemical-activated binary cement. J. Rock Mech. Geotech. Eng. 2023; in press. [Google Scholar] [CrossRef]
- Gao, H.M.; Bu, C.Y.; Wang, Z.H.; Shen, Y.Q.; Chen, G.X. Dynamic characteristics of expanded polystyrene composite soil under traffic loadings considering initial consolidation state. Soil Dyn. Earthq. Eng. 2017, 102, 86–98. [Google Scholar] [CrossRef]
- El-Sherbiny, R.; Ramadan, S.; El-Khouly, M. Dynamic properties of Sand-EPS bead mixtures. Geosynth. Int. 2018, 25, 1–52. [Google Scholar] [CrossRef]
- Zhou, Y.D.; Li, M.D.; Wen, K.J.; Tong, R.M. Stress-strain behaviour of reinforced dredged sediment and expanded polystyrenes mixture under cyclic loading. Geomech. Eng. 2019, 17, 507–513. [Google Scholar] [CrossRef]
- Zhou, Y.D.; Li, M.D.; He, Q.B.; Wen, K.J. Deformation and damping characteristics of lightweight clay-eps soil under cyclic loading. Adv. Civ. Eng. 2018, 2018, 8093719. [Google Scholar] [CrossRef]
- Gao, H.M.; Li, X.; Wang, Z.H.; Stuedlein, A.W.; Wang, Y. Dynamic shear modulus and damping of expanded polystyrene composite soils at low strains. Geosynth. Int. 2019, 26, 436–450. [Google Scholar] [CrossRef]
- Gökhan, G. The evaluation with anova of the effect of lime admixture and thermal cure time on fly ash paste activated with sodium silicate solution. Constr. Build. Mater. 2015, 94, 228–234. [Google Scholar] [CrossRef]
- Puri, A.; Badanoiu, A.; Voicu, G. Eco-friendly binders based on fly ash. Rev. Roum. Chim. 2008, 53, 1069–1076. [Google Scholar] [CrossRef]
- JTG/T F20-2015; Technical Guidelines for Construction of Highway Roadbases. China Communications Press: Beijing, China, 2015.
- Yao, Z.; Ai, Y.Z.; Shang, Q.S.; Li, F.Z.; Yang, G. Mixture ratio of Yellow River silty soil stabilized with lime-fly ash. Rock Soil Mech. 2008, 29, 1943–1948. [Google Scholar] [CrossRef]
- Du, J.; Liu, B.Y.; Wang, Z.C.; Zheng, G.; Jiang, N.J.; Zhou, M.L.; Zhou, H.Z. Dynamic behavior of cement-stabilized organic-matter-disseminated sand under cyclic triaxial condition. Soil Dyn. Earthq. Eng. 2021, 147, 106777. [Google Scholar] [CrossRef]
- Zhang, J.; Cao, J.T.; Huang, S.J.; Shi, B.C. Experimental study on the dynamic shear modulus and damping ratio of saturated sand under cyclic loading. Mater. Tehnol. 2021, 55, 741–749. [Google Scholar] [CrossRef]
- Jiang, P.; Zhou, X.H.; Qian, J.; Li, N. Experimental study on the influence of dry-wet cycles on the static and dynamic characteristics of fiber-modified lime and fly ash-stabilized iron tailings at early curing age. Crystals 2022, 12, 568. [Google Scholar] [CrossRef]
- Jiang, P.; Chen, Y.; Song, X.J.; Li, N.; Wang, W.; Wu, E.L. Study on compressive properties and dynamic characteristics of polypropylene-fiber-and-cement-modified iron-ore tailing under traffic load. Polymers 2022, 14, 1995. [Google Scholar] [CrossRef]
- Alaie, R.; Chenari, R.J. Dynamic properties of EPS-sand mixtures using cyclic triaxial and bender element tests. Geosynth. Int. 2019, 26, 563–579. [Google Scholar] [CrossRef]
- Golpazir, I.; Ghalandarzadeh, A.; Jafari, M.K.; Mahdavi, M. Dynamic properties of polyurethane foam-sand mixtures using cyclic triaxial tests. Constr. Build. Mater. 2016, 118, 104–115. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, H.C.; Cheng, M.Y.; Lu, H.W.; Wang, Z.J.; Feng, P.Y. Dynamic triaxial test and microscopic study of solidified muddy soil with different mixing ratios and curing ages. Front. Mater. 2021, 8, 731449. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, W.; Jiang, P.; Li, C. The elastic modulus and damage stress-strain model of polypropylene fiber and nano clay modified lime treated soil under axial load. Polymers 2022, 14, 2606. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Hu, Z.P.; Ren, X.; Li, F.T.; Zhang, F. Dynamic modulus and damping ratio of compacted loess under long-term traffic loading. Road Mater. Pavement 2021, 23, 1731–1745. [Google Scholar] [CrossRef]
- Liu, F.R.; Zhou, Z.W.; Wei, M.; Zhang, S.J.; Sun, Z.Z. Dynamic parameters and hysteresis loop characteristics of frozen silt clay under different cyclic stress paths. Adv. Mater. Sci. Eng. 2021, 2021, 3763181. [Google Scholar] [CrossRef]
- Maaroufi, M.; Abahri, K.; El Hachem, C.; Belarbi, R. Characterization of EPS lightweight concrete microstructure by X-ray tomography with consideration of thermal variations. Constr. Build. Mater. 2018, 178, 339–348. [Google Scholar] [CrossRef]
- Alaie, R.; Chenari, R.J. Cyclic and post-cyclic shear behaviour of interface between geogrid and EPS beads-sand backfill. KSCE J. Civ. Eng. 2018, 22, 3340–3357. [Google Scholar] [CrossRef]
- Shekhawat, P.; Sharma, G.; Singh, R.M. Microstructural and morphological development of eggshell powder and flyash-based geopolymers. Constr. Build. Mater. 2020, 260, 119886. [Google Scholar] [CrossRef]
- Selvakumar, S.; Kulanthaivel, P.; Soundara, B. Influence of nano-silica and sodium silicate on the strength characteristics of clay soil. Nanotechnol. Environ. Eng. 2021, 6, 46. [Google Scholar] [CrossRef]
- Kazemian, S.; Prasad, A.; Huat, B.B.K.; Ghiasi, V.; Ghareh, S. Effects of cement–sodium silicate system grout on tropical organic soils. Arab. J. Sci. Eng. 2012, 37, 2137–2148. [Google Scholar] [CrossRef]
- Woodside, W.; Messmer, J.H. Thermal conductivity of porous media. I. unconsolidated sands. J. Appl. Phys. 1961, 32, 1688–1699. [Google Scholar] [CrossRef]
- Tokoro, T.; Ishikawa, T.; Shirai, S.; Nakamura, T. Estimation methods for thermal conductivity of sandy soil with electrical characteristics. Soils Found. 2016, 56, 927–936. [Google Scholar] [CrossRef]
- Tang, N.H.; Lei, D.; Huang, D.W.; Xiao, R. Mechanical performance of polystyrene foam (EPS): Experimental and numerical analysis. Polym. Test. 2019, 73, 359–365. [Google Scholar] [CrossRef]
- Zhuang, X.S.; Wang, J.X.; Li, K.; Wang, K.; Hu, Z. Comparative study on characteristic of hysteretic curves of expansive soil improved by weathered sand. Chin. J. Rock Mech. Eng. 2019, 38, 3709–3716. (In Chinese) [Google Scholar] [CrossRef]
- Monismith, C.L.; Ogawa, N.; Freeme, C.R. Permanent deformation characteristics of subgrade soils due to repeated loading. Transp. Res. Rec. 1975, 537, 1–17. [Google Scholar]








| Plastic Limit (%) | Liquid Limit (%) | Natural Density (g·cm−3) | Moisture Content (%) | Organic Content (%) |
|---|---|---|---|---|
| 24.60 | 40.90 | 1.84 | 50 | 6.50 |
| Al2O3 (%) | SiO2 (%) | SO3 (%) | CaO (%) | TiO2 (%) | Fe2O3 (%) | Other (%) |
|---|---|---|---|---|---|---|
| 23.45 | 22.94 | 6.35 | 33.7 | 3.56 | 7.26 | 2.74 |
| CaO (%) | MgO (%) | Fe2O3 (%) | Al2O3 (%) | TiO2 (%) | SiO2 (%) | Other (%) |
|---|---|---|---|---|---|---|
| 89.42 | 1.76 | 0.18 | 0.25 | 7.47 | 0.58 | 0.34 |
| Influence Factor | EPS Content (%) | Confining Pressure (kPa) | Amplitude (mm) |
|---|---|---|---|
| EPS particle content | 0.5 | 0, 25, 50, 75, 100 | 0.1 |
| 1 | |||
| 1.5 | |||
| 2 | |||
| 2.5 | |||
| Confining pressure | 0.5 | 0, 25, 50, 75, 100 | 0.1 |
| 1 | |||
| 1.5 | |||
| 2 | |||
| 2.5 | |||
| Amplitude | 0.5 | 0 | 0.05, 0.1, 0.15, 0.2 |
| 1 | |||
| 1.5 | |||
| 2 | |||
| 2.5 | |||
| Number of cycles | 1.5 | 0, 25, 50, 75, 100 | 0.1 |
| EPS Content (%) | 0.5 | 1 | 1.5 | 2 | 2.5 |
| Weight of the sample (g) | 131.1 | 114.3 | 104.7 | 92.2 | 83.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, H.; Zheng, W.; Zhou, X.; Zhou, L.; Li, C.; Yu, Y.; Jiang, P. Study on Dynamic Modulus and Damping Characteristics of Modified Expanded Polystyrene Lightweight Soil under Cyclic Load. Polymers 2023, 15, 1865. https://doi.org/10.3390/polym15081865
Tao H, Zheng W, Zhou X, Zhou L, Li C, Yu Y, Jiang P. Study on Dynamic Modulus and Damping Characteristics of Modified Expanded Polystyrene Lightweight Soil under Cyclic Load. Polymers. 2023; 15(8):1865. https://doi.org/10.3390/polym15081865
Chicago/Turabian StyleTao, Huaqiang, Wenqian Zheng, Xuhui Zhou, Lin Zhou, Cuihong Li, Yanfei Yu, and Ping Jiang. 2023. "Study on Dynamic Modulus and Damping Characteristics of Modified Expanded Polystyrene Lightweight Soil under Cyclic Load" Polymers 15, no. 8: 1865. https://doi.org/10.3390/polym15081865
APA StyleTao, H., Zheng, W., Zhou, X., Zhou, L., Li, C., Yu, Y., & Jiang, P. (2023). Study on Dynamic Modulus and Damping Characteristics of Modified Expanded Polystyrene Lightweight Soil under Cyclic Load. Polymers, 15(8), 1865. https://doi.org/10.3390/polym15081865







