Fatigue Performance of a Step-Lap Joint under Tensile Load: A Numerical Study
Abstract
1. Introduction
2. Numerical Modelling
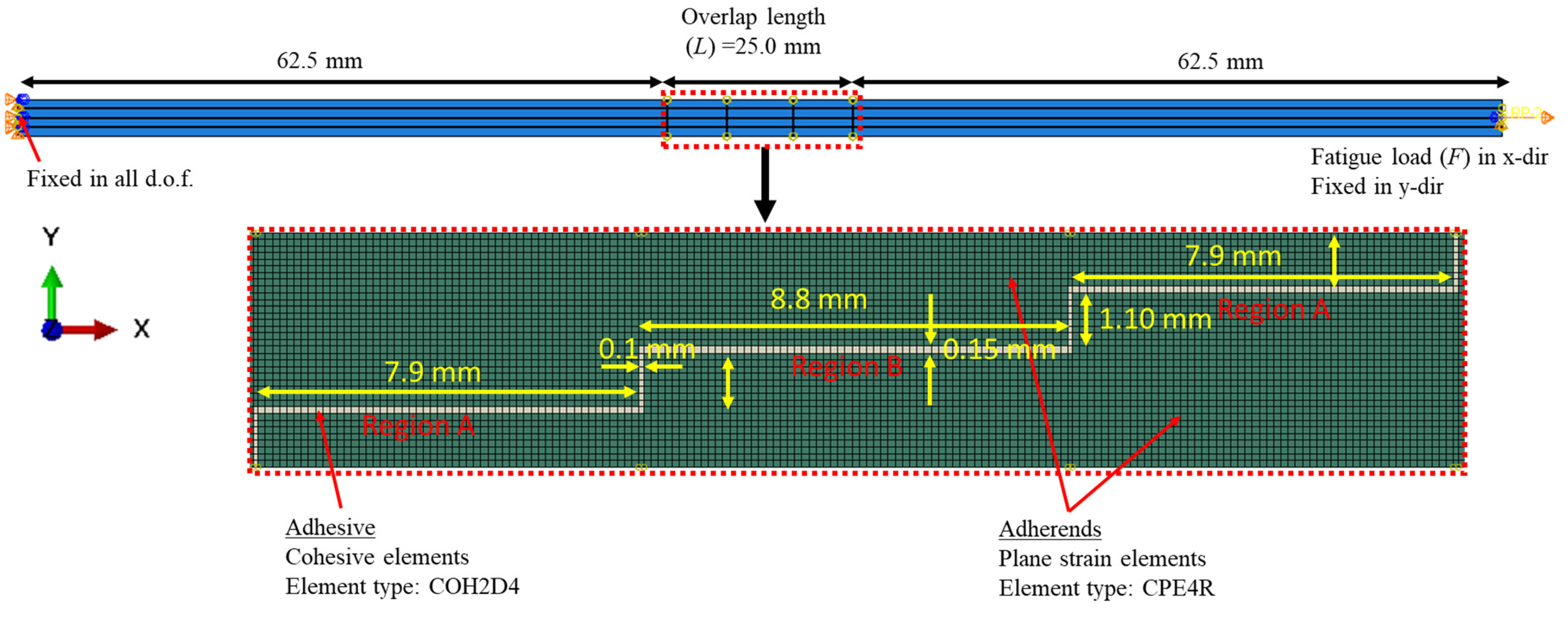
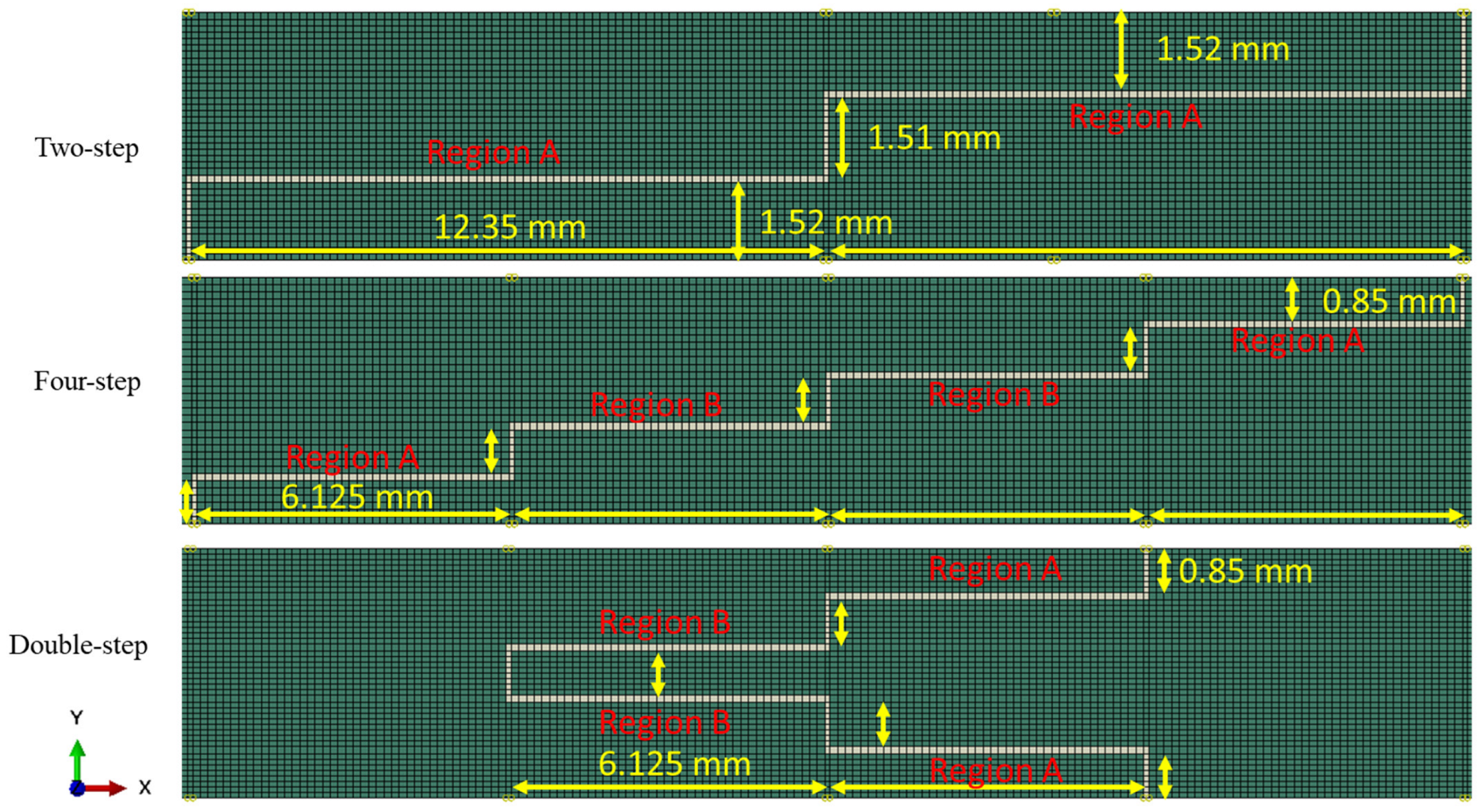
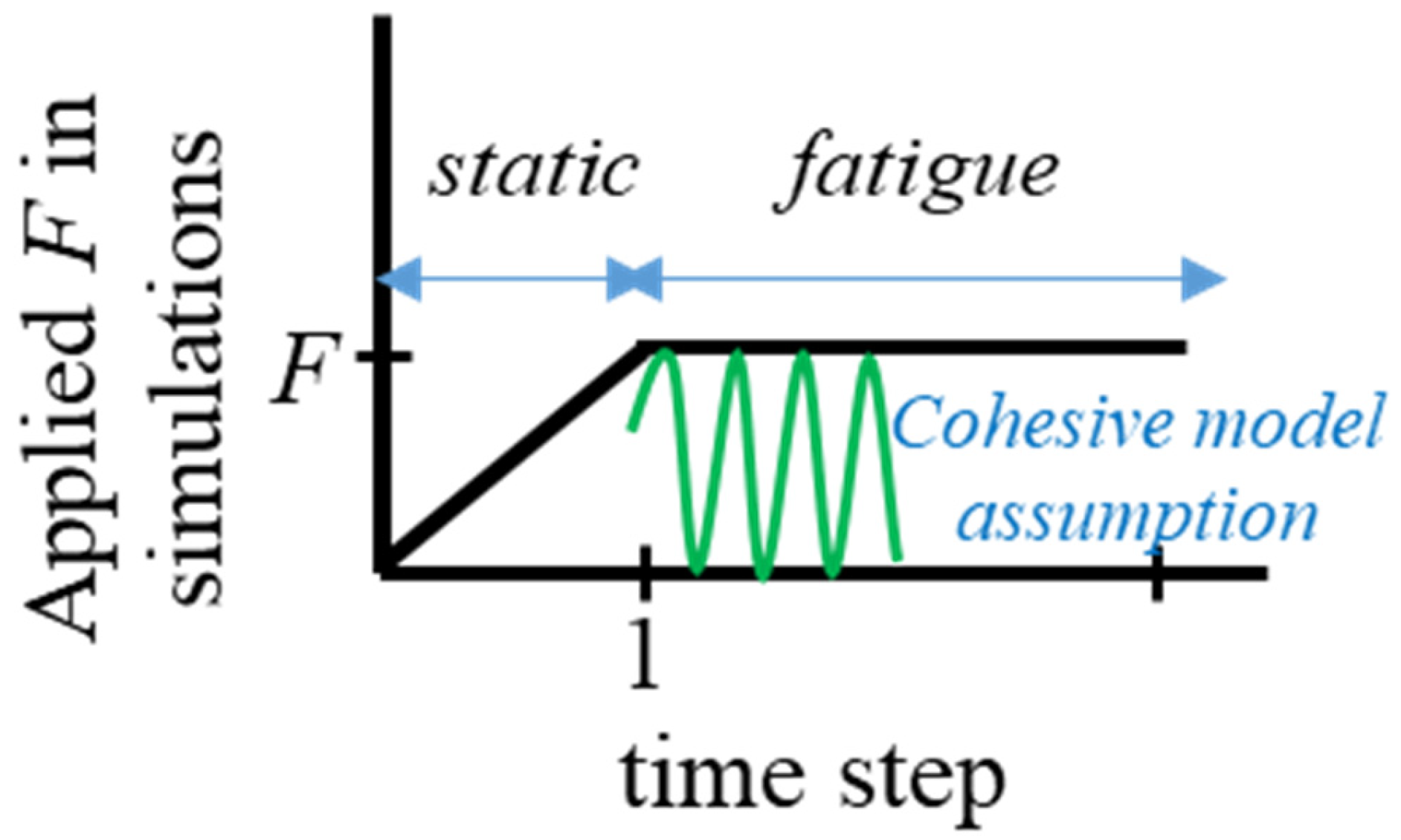
2.1. Finite Element Modelling
2.2. Constitutive Equations
3. Results and Discussion
3.1. Validation of the FE Model
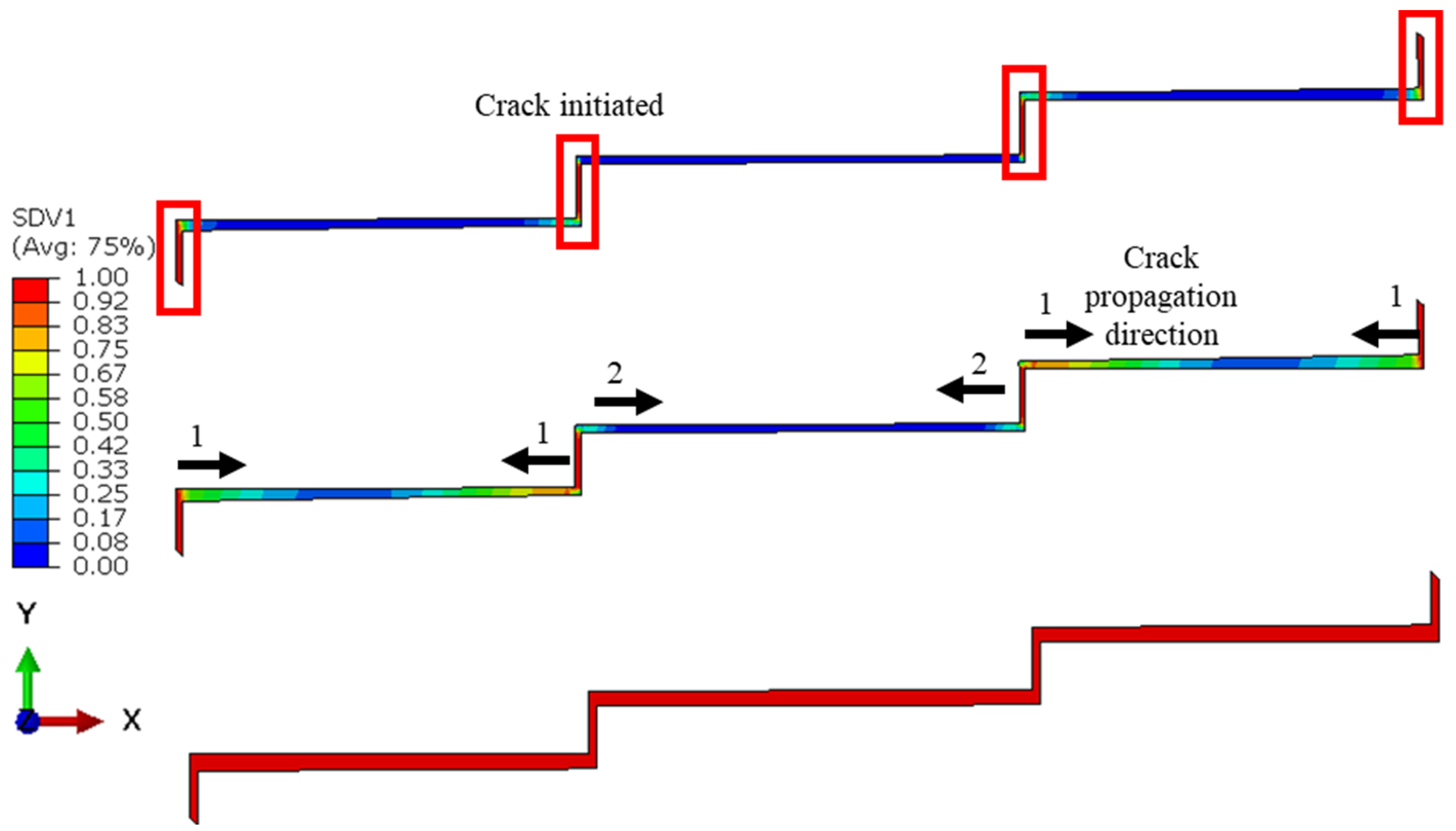
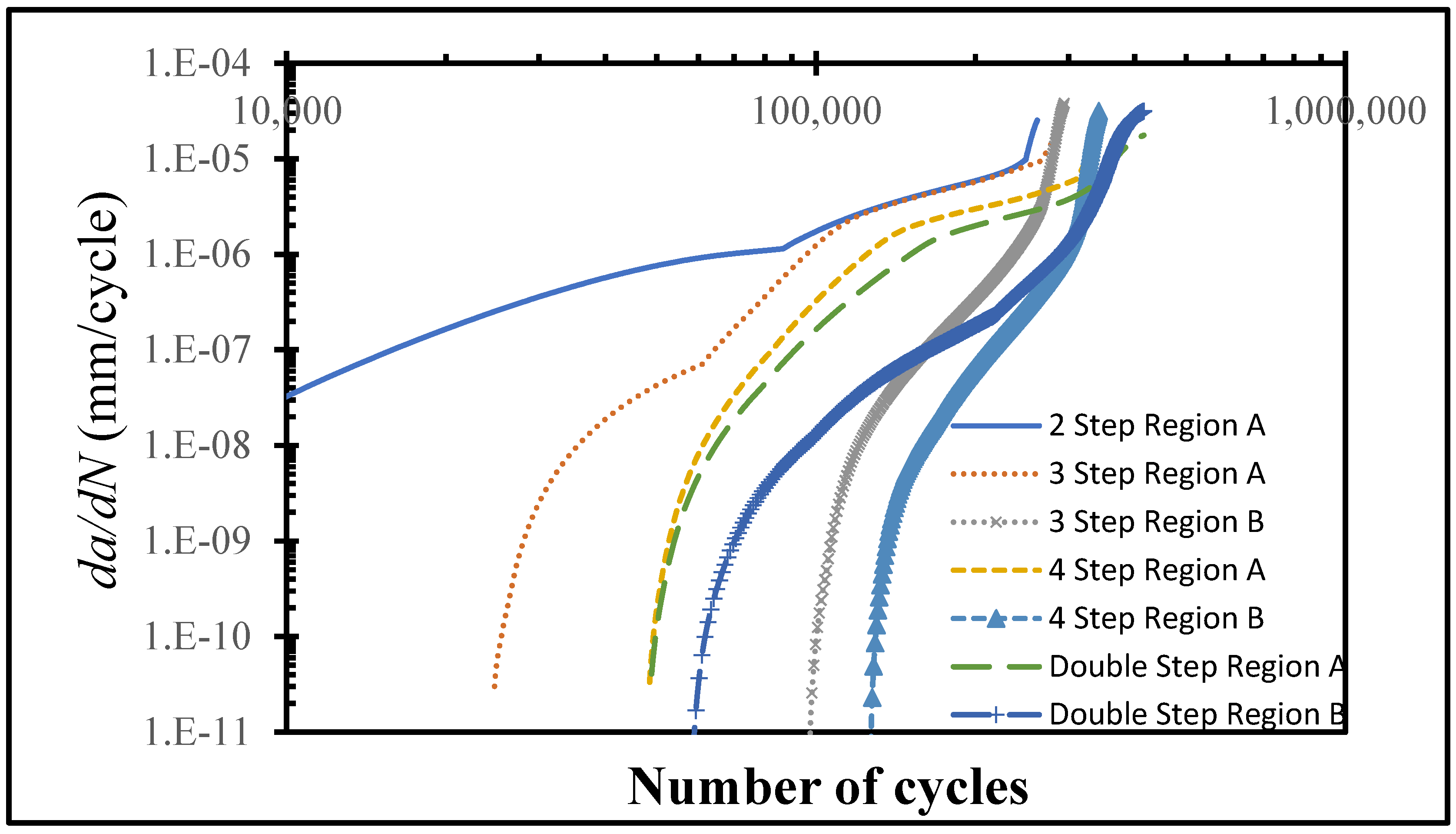
3.2. Effect of the Number of Steps
3.3. Influence of the Configuration: Double Stepping
4. Concluding Remarks
- The service life of step-lap joints increased with an increase in the number of steps;
- The onset of damage in the adhesive layer of the step-lap joint was delayed with an increase in the step number, where the crack growth rate also became smaller;
- The characteristics of da/dN curve for the outer steps of the adhesive layer were different from those of the inner steps;
- The lifetime of the double-step-lap joint was 21.8% longer than that of its counterpart, the four-step-lap joint.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Veisytabar, M.; Reza, A.; Shekari, Y. Stress analysis of adhesively bonded single stepped-lap joints with functionally graded adherents based on the four-parameter fractional viscoelastic model. Eur. J. Mech. 2023, 98, 1–32. [Google Scholar] [CrossRef]
- Kadioglu, F.; Demiral, M. Failure behaviour of the single lap joints of angle-plied composites under three point bending tests. J. Adhes. Sci. Technol. 2020, 34, 531–548. [Google Scholar] [CrossRef]
- Durmus, M.; Akpinar, S. The experimental and numerical analysis of the adhesively bonded three step-lap joints with different step lengths. Theor. Appl. Fract. Mech. 2020, 105, 102427. [Google Scholar] [CrossRef]
- Brito, R.; Campilho, R.; Moreira, R.; Sancez-Arce, I.; Silva, F. Composite stepped-lap adhesive joint analysis by cohesive zone modelling. Procedia Struct. Integr. 2021, 33, 665–672. [Google Scholar] [CrossRef]
- Adin, H. The effect of angle on the strain of scarf lap joints subjected to tensile loads. Appl. Math. Model. 2012, 36, 2858–2867. [Google Scholar] [CrossRef]
- Wu, C.H.; Chen, C.H.; He, L.; Yan, W. Comparison on damage tolerance of scarf and stepped-lap bonded composite joints under quasi-static loading. Compos. Part B Eng. 2018, 155, 19–30. [Google Scholar] [CrossRef]
- Doru, M.O.; Ozel, A.; Akpinar, S.; Aydın, M.D. Effect of the spew fillet on adhesively bonded single-lap joint subjected to tensile loading: Experimental and 3-D nonlinear stress analysis. J. Adhes. 2014, 90, 195–209. [Google Scholar] [CrossRef]
- Silva, L.F.M.; Adams, R.D. Techniques to reduce the peel stresses in adhesive joints with composites. Int. J. Adhes. Adhes. 2007, 27, 227–235. [Google Scholar] [CrossRef]
- Bendemra, H.; Compston, P.; Crothers, P.J. Optimisation study of tapered scarf and stepped-lap joints in composite repair patches. Compos. Struct. 2015, 130, 1–8. [Google Scholar] [CrossRef]
- Mistry, S.; Joshi, P.; Dhandhukiya, R.; Gandhi, S.H.; Bhanushali, N.; Desai, C.H. Finite element studies of bolted, riveted, bonded and hybrid step-lap joints of thick plate. Mater. Today Proc. 2022, 50, 1080–1087. [Google Scholar] [CrossRef]
- Silva, J.O.S.; Campilho, R.D.S.G.; Rocha, R.J.B.; Silva, F.J.G. Comparative evaluation of adhesively-bonded single-lap and stepped-lap joints. Procedia Manuf. 2019, 38, 1189–1196. [Google Scholar] [CrossRef]
- Wang, S.; Xie, Z.; Li, X. A modified analytical model for stress analysis of adhesively bonded stepped-lap joints under tensile load. Eur. J. Mech. A Solids 2019, 77, 1–13. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Xie, Z. Free vibration analysis of adhesively bonded lap joints through layer wise finite element. Compos. Struct. 2019, 223, 1–11. [Google Scholar] [CrossRef]
- Sawa, T.; Ichikawa, K.; Shin, Y.; Kobayashi, T. A three-dimensional finite element stress analysis and strength prediction of stepped-lap adhesive joints of dissimilar adherends subjected to bending moments. Int. J. Adhes. Adhes. 2010, 30, 298–305. [Google Scholar] [CrossRef]
- Gavgali, E.; Sahin, R.; Akpinar, S. An investigation of the fatigue performance of adhesively bonded step-lap joints: An experimental and numerical analysis. Int. J. Adhes. Adhes. 2021, 104, 102736. [Google Scholar] [CrossRef]
- Chowdhury, N.M.; Wang, J.; Chiu, W.K.; Chang, P. Static and fatigue testing bolted, bonded and hybrid step lap joints of thick carbon fibre/epoxy laminates used on aircraft structures. Compos. Struct. 2016, 142, 96–106. [Google Scholar] [CrossRef]
- Ravi Chandran, K.S. Fatigue of Fiber-Reinforced Composites, Damage and Failure. J. Indian Inst. Sci. 2022, 142, 439–460. [Google Scholar] [CrossRef]
- Prakash, R.V.; Patil, A.J. Fatigue Damage Estimation From Pseudo-Random Load Sequence Generated for Metals and Fiber Reinforced Composites. In Proceedings of the Pressure Vessels and Piping Conference, Las Vegas, NV, USA, 17–22 July 2022; American Society of Mechanical Engineers: New York, NY, USA, 2022. [Google Scholar]
- Godzimirski, J.; Rośkowicz, M.; Jasztal, M.; Barca, I. Static and Fatigue Strength and Failure Mechanisms of Riveted Lap Joints of CFRP Composites. Materials 2023, 16, 1768. [Google Scholar] [CrossRef]
- Kang, K.W.; Lim, D.M.; Kim, J.K. Probabilistic analysis for the fatigue life of carbon/epoxy laminates. Compos. Struct. 2008, 85, 258–264. [Google Scholar] [CrossRef]
- Demiral, M.; Abbasi, F.; Muhammad, R.; Akpinar, S. Service Life Modelling of Single Lap Joint Subjected to Cyclic Bending Load. Aerospace 2023, 10, 8. [Google Scholar] [CrossRef]
- Systemes, D. Abaqus 6.14 Documentation; Simulia Co.: Providence, RI, USA, 2014. [Google Scholar]
- Belnoue, J.; Giannis, S.; Dawson, M.; Hallett, S. Cohesive/adhesive failure interaction in ductile adhesive joints Part II: Quasi-static and fatigue analysis of double lap-joint specimens subjected to through-thickness compressive loading. Int. J. Adhes. Adhes. 2016, 68, 369–378. [Google Scholar] [CrossRef]
- Turon, A.; Costa, J.; Camanho, P.; Dávila, C. Simulation of delamination in composites under high-cycle fatigue. Compos. Part A Appl. Sci. Manuf. 2007, 38, 2270–2282. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A Critical Analysis of Crack Propagation Laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Chen, C.; Araby, S.; Demiral, M.; Cai, R.; Yang, X.; Wang, W.; Meng, Q. Fatigue behavior and tribological properties of laser additive manufactured aluminum alloy/boron nitride nanosheet nanocomposites. J. Mater. Res. Technol. 2022, 20, 3930–3948. [Google Scholar] [CrossRef]
- Van Paepegem, W.; Degrieck, J. Fatigue degradation modelling of plain woven glass/epoxy composites. Compos. Part A Appl. Sci. Manuf. 2001, 32, 1433–1441. [Google Scholar] [CrossRef]
- Smeets, E. Development of a Fatigue Analysis Tool Using Cohesive Zone Modelling for Composite Specimens. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2019. [Google Scholar]
- Kanar, B.; Akpinar, S.; Akpinar, I.A.; Akbulut, H.; Ozel, A. The fracture behaviour of nanostructure added adhesives under ambient temperature and thermal cyclic conditions. Theor. Appl. Fract. Mech. 2018, 97, 120–130. [Google Scholar] [CrossRef]
- Liu, Y.; Mahadevan, S. Multiaxial high-cycle fatigue criterion and life prediction for metals. Int. J. Fatigue 2005, 27, 790–800. [Google Scholar] [CrossRef]
- Duran, E.T. Comparative Multi-Axial High-Cycle Fatigue Analysis of Spot Weld Models Using Findley’s Damage Criteria. SAE International. J. Mater. Manuf. 2022, 16, 59–70. [Google Scholar]
- Machado, J.J.; Marques, E.A.; Barbosa, A.Q.; da Silva, L.F. Fatigue performance of single lap joints with CFRP and aluminium substrates prior and after hygrothermal aging. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 2325–2339. [Google Scholar] [CrossRef]



| AA2024-T3 | E (MPa) | (MPa) | |||||
| 72,400 | 0.33 | 324 | |||||
| DP460 | K (N/mm3) | , i = normal, shear (MPa) | , i = normal, shear (N/mm) | (N/mm3) | m | n | |
| 1014 | 0.38 | 32.6, 28.5 | 2.56, 11.71 | 10−12 | 2.0 | 2.1 |
| Load (N), t (mm) | Two Step | Three Step | Four Step | Double Step |
|---|---|---|---|---|
| Ni | 127,420 | 166,310 | 198,930 | 212,940 |
| Nf | 262,620 | 294,310 | 342,130 | 416,940 |
| Ni/Nf (%) | 48.50 | 56.51 | 58.14 | 51.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demiral, M.; Mamedov, A. Fatigue Performance of a Step-Lap Joint under Tensile Load: A Numerical Study. Polymers 2023, 15, 1949. https://doi.org/10.3390/polym15081949
Demiral M, Mamedov A. Fatigue Performance of a Step-Lap Joint under Tensile Load: A Numerical Study. Polymers. 2023; 15(8):1949. https://doi.org/10.3390/polym15081949
Chicago/Turabian StyleDemiral, Murat, and Ali Mamedov. 2023. "Fatigue Performance of a Step-Lap Joint under Tensile Load: A Numerical Study" Polymers 15, no. 8: 1949. https://doi.org/10.3390/polym15081949
APA StyleDemiral, M., & Mamedov, A. (2023). Fatigue Performance of a Step-Lap Joint under Tensile Load: A Numerical Study. Polymers, 15(8), 1949. https://doi.org/10.3390/polym15081949








