Elastic Electrically Conductive Composites Based on Vapor-Grown Carbon Fibers for Use in Sensors
Abstract
:1. Introduction
2. Experimental
2.1. Materials
2.2. Sample Preparation and Morphology
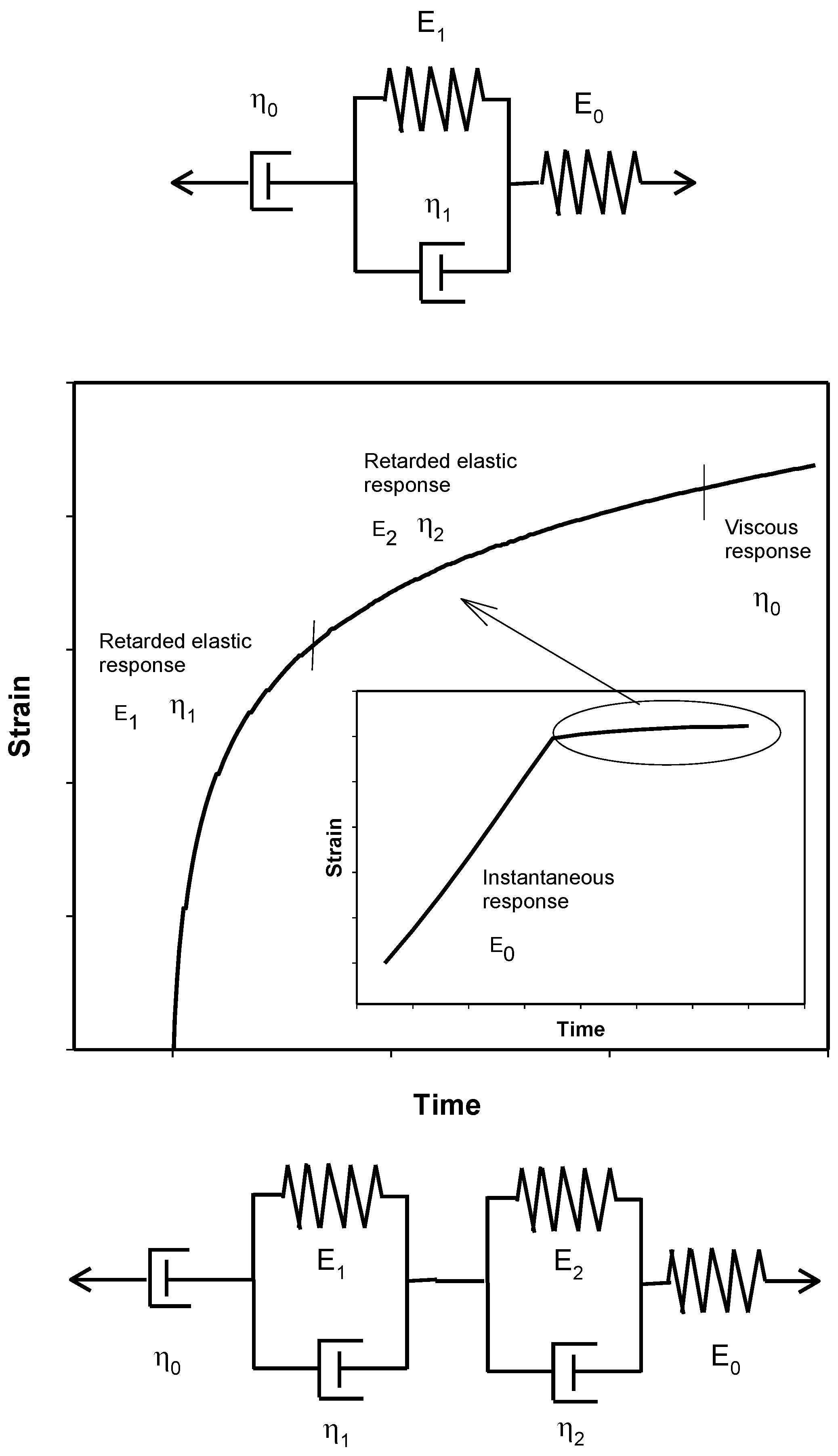
2.3. Mechanical Properties
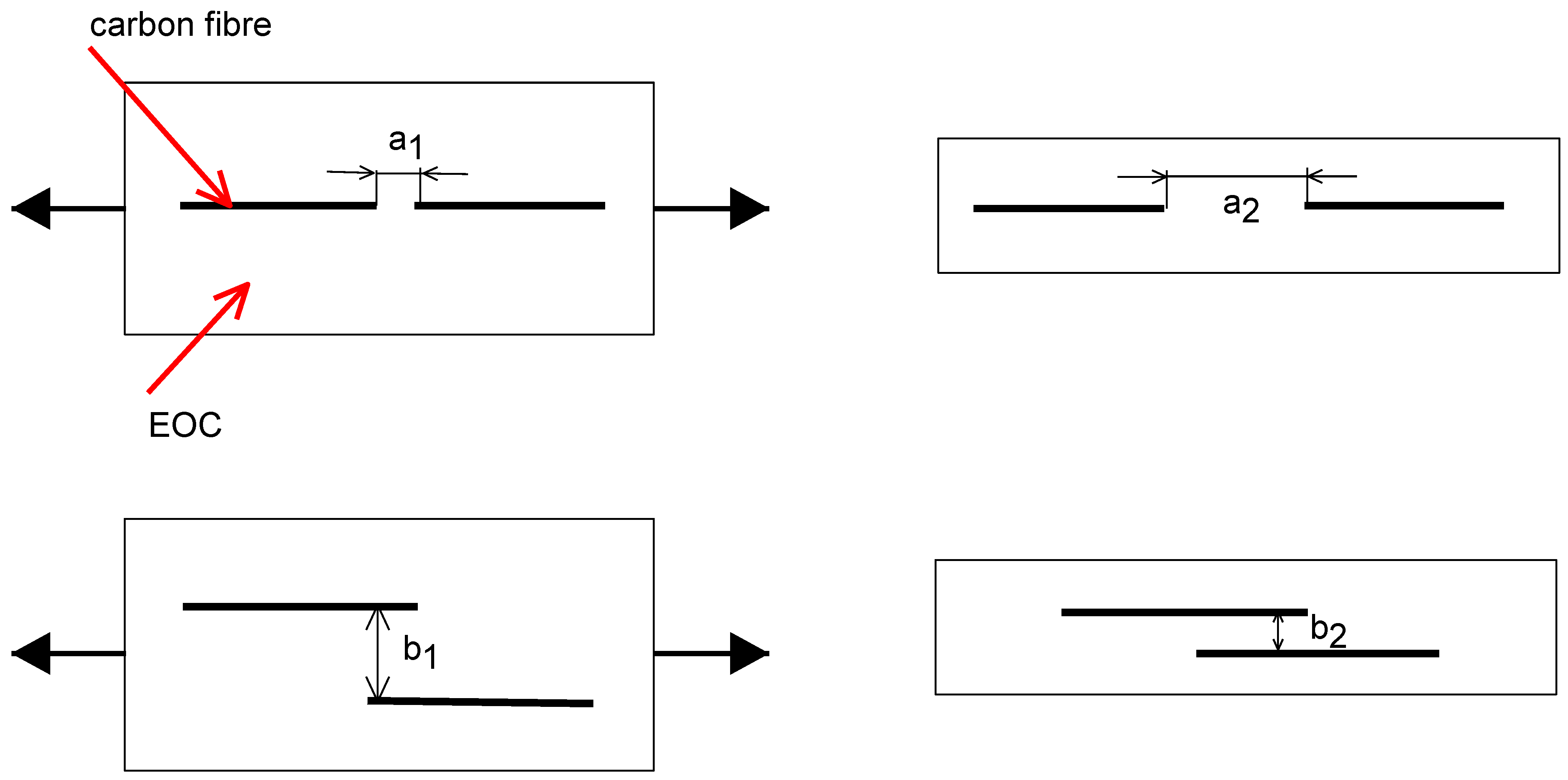
2.4. Electrical Properties
3. Results and Discussion
3.1. Sample Morphology
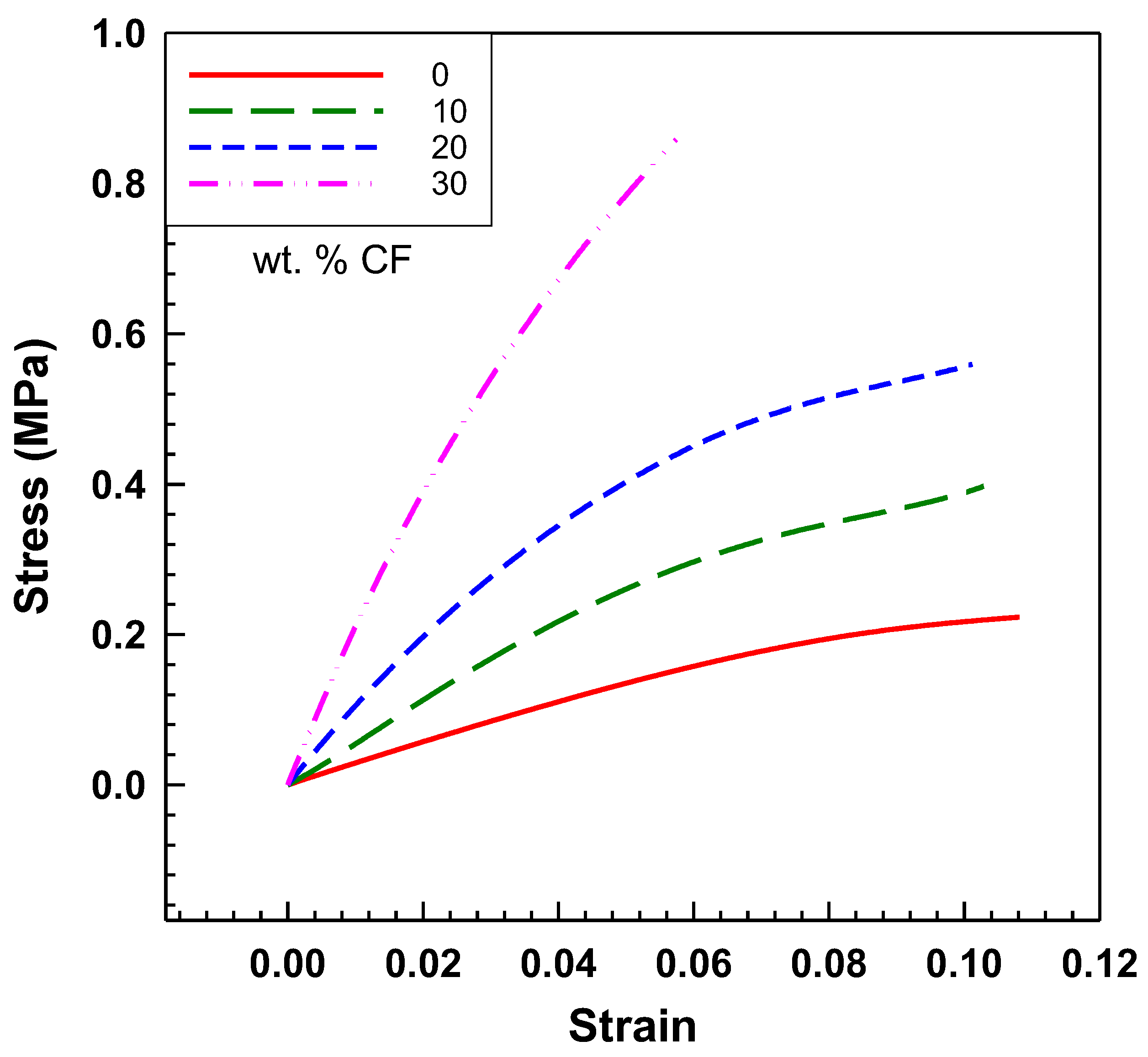
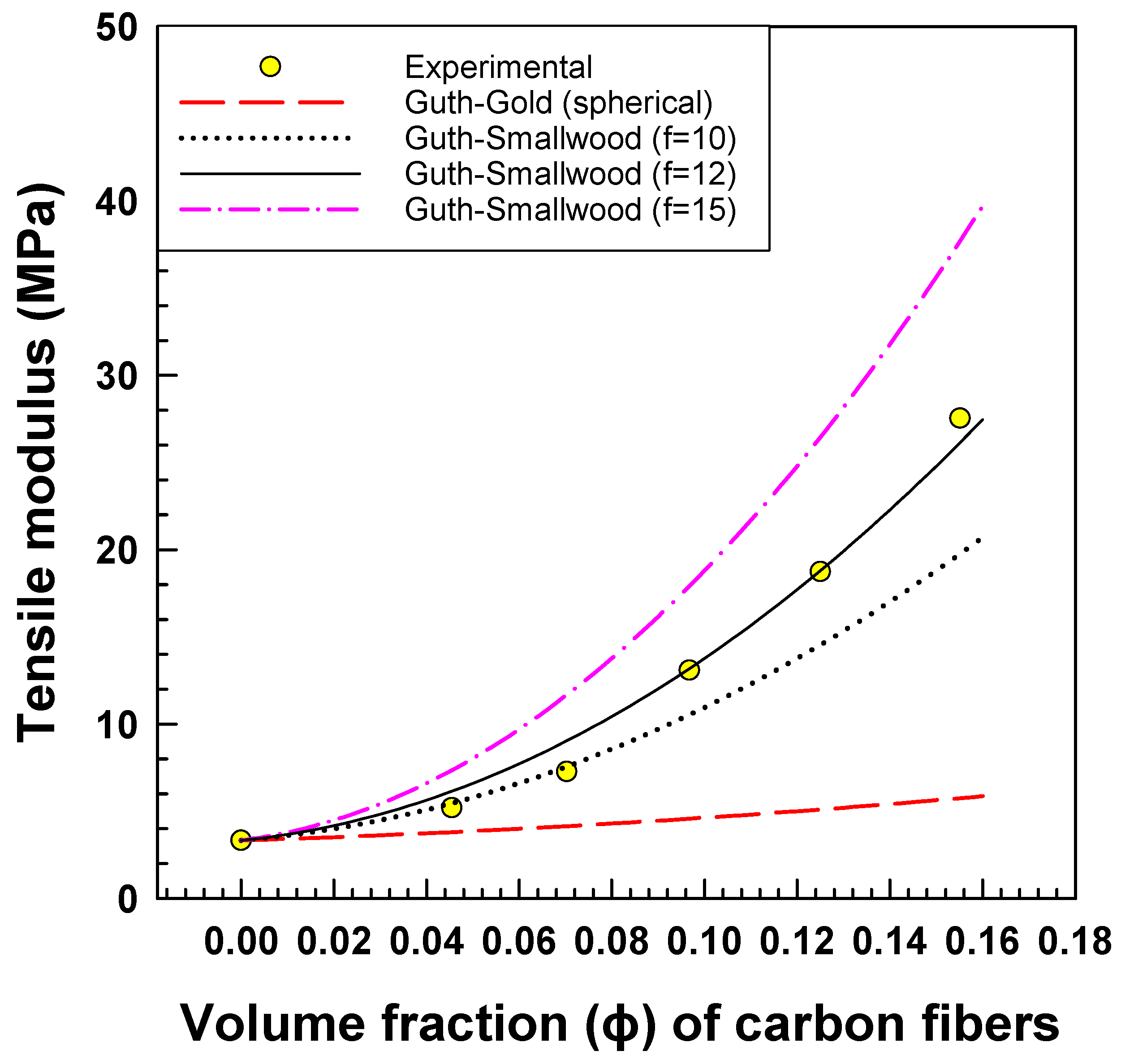
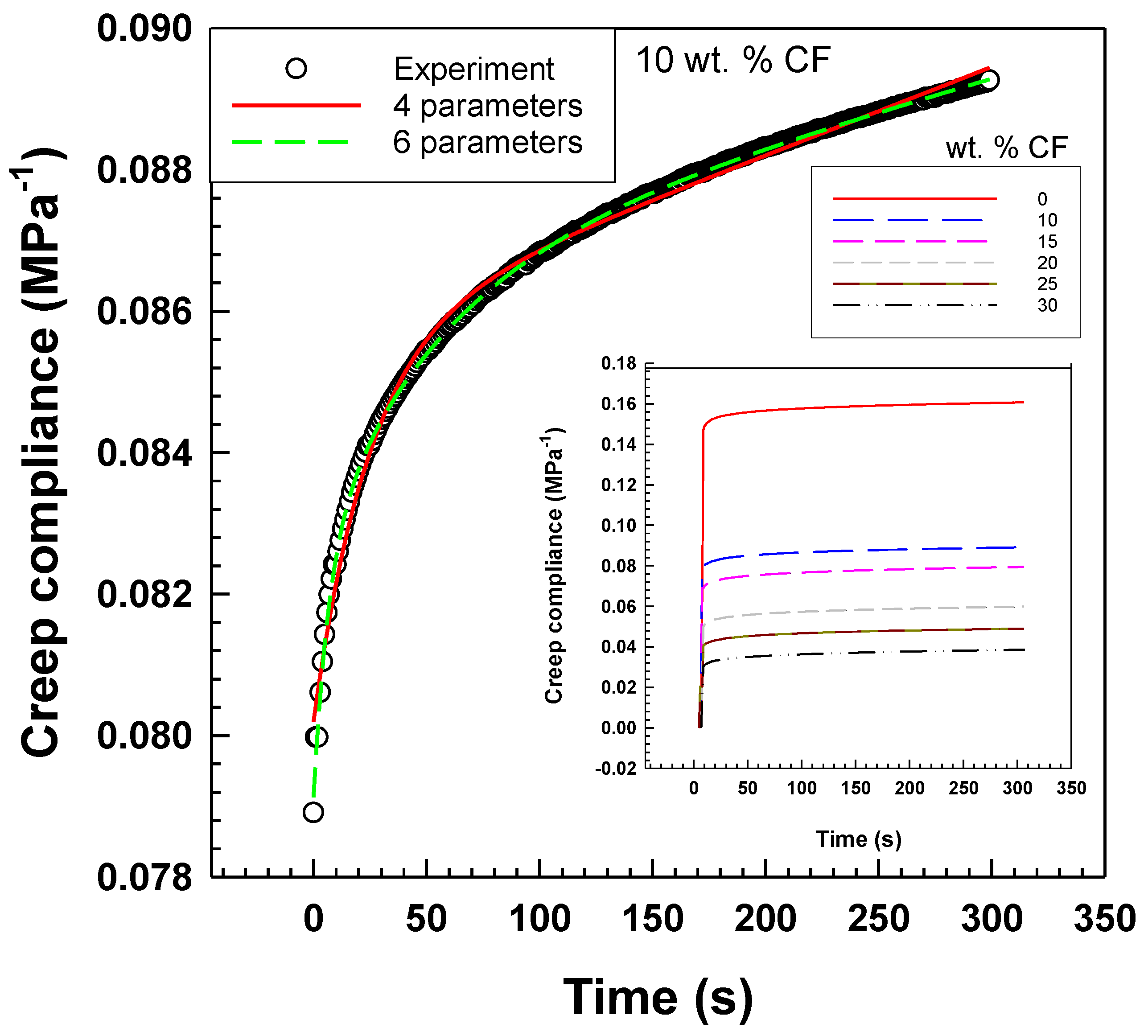
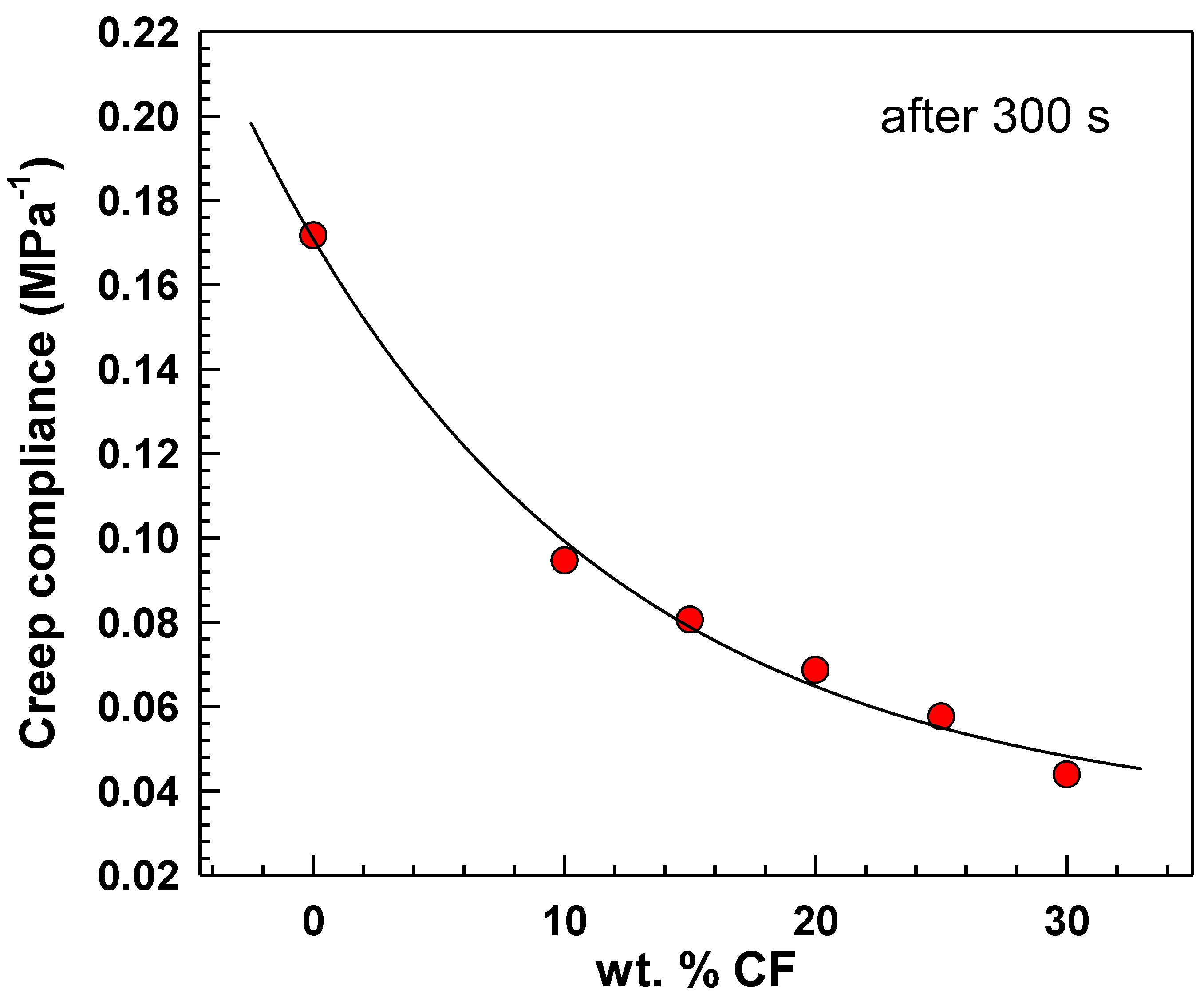
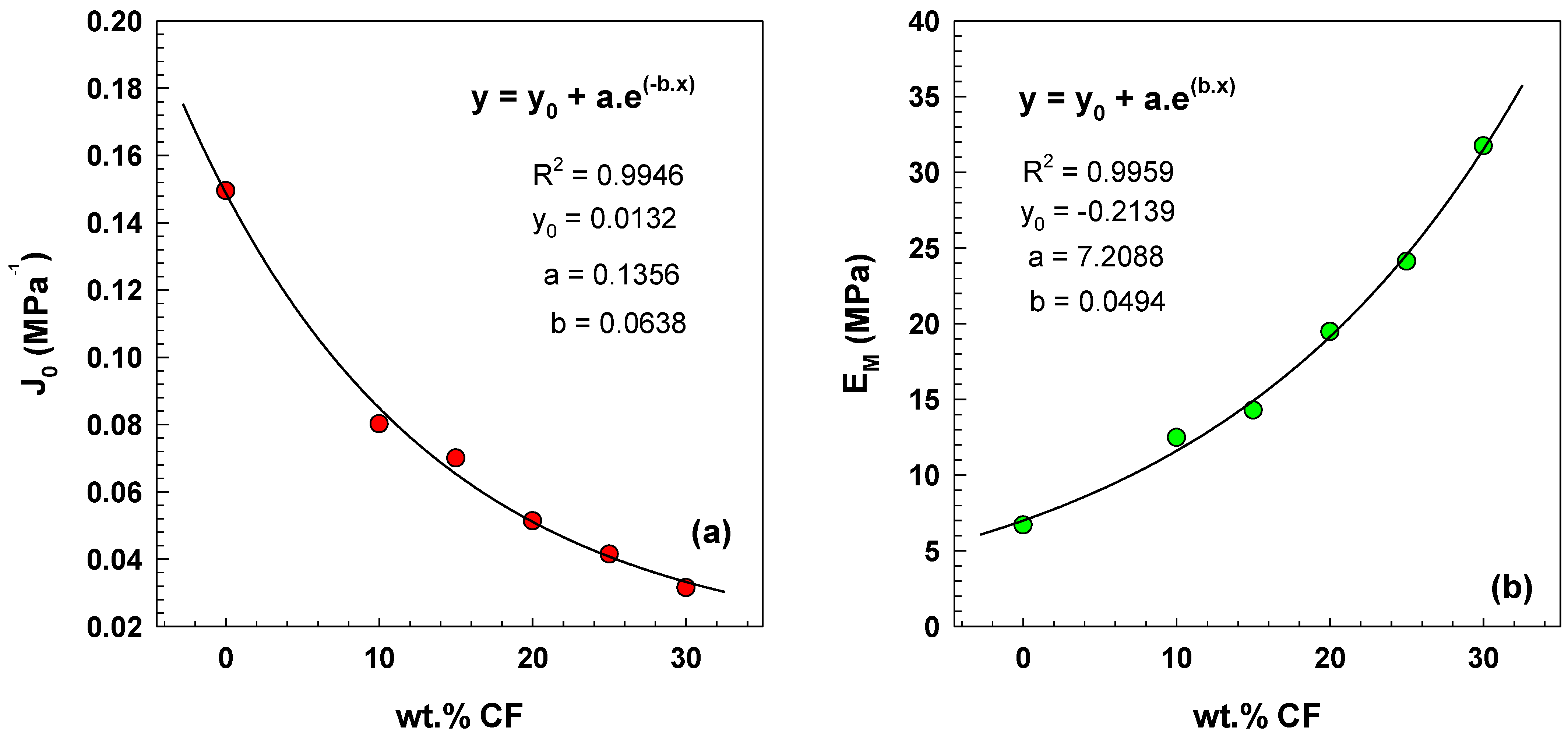
3.2. Mechanical Properties
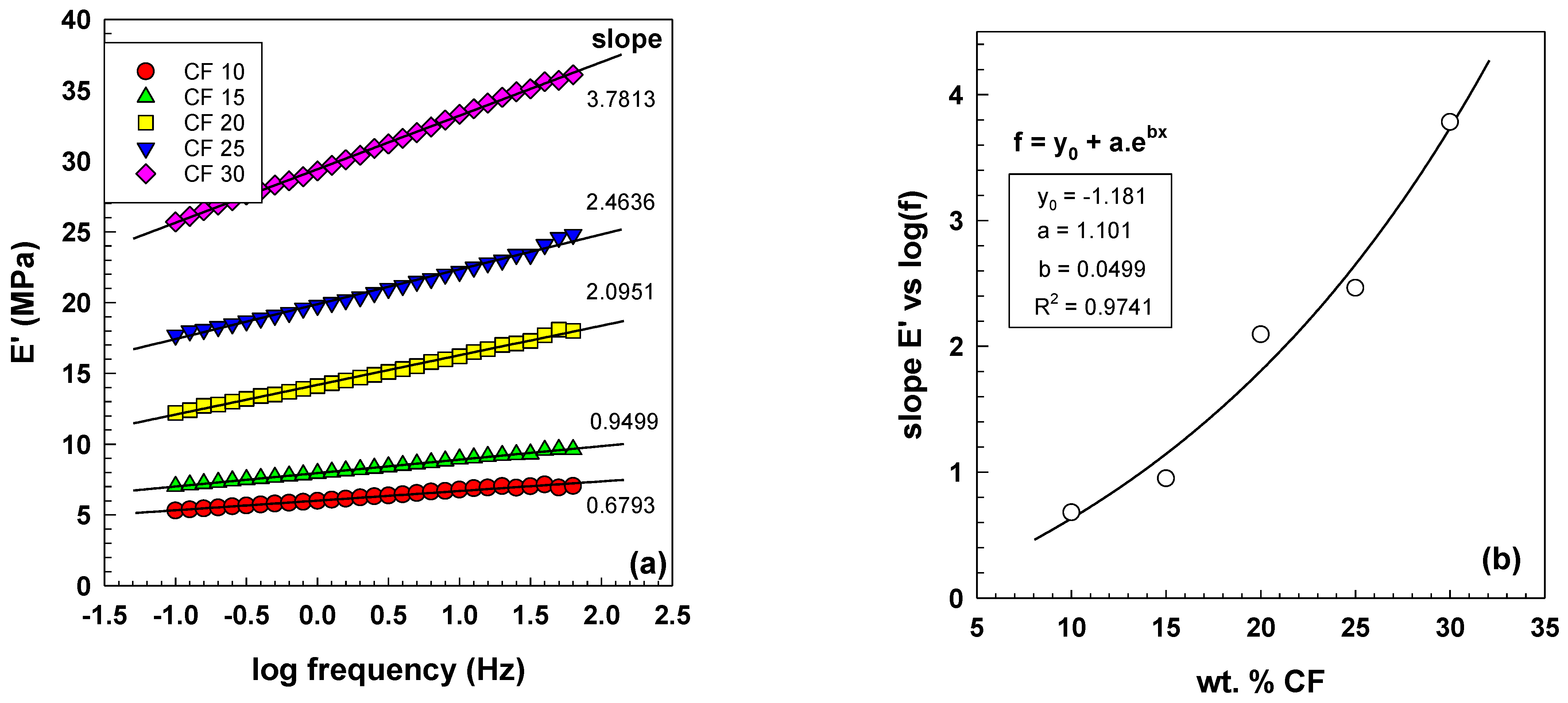
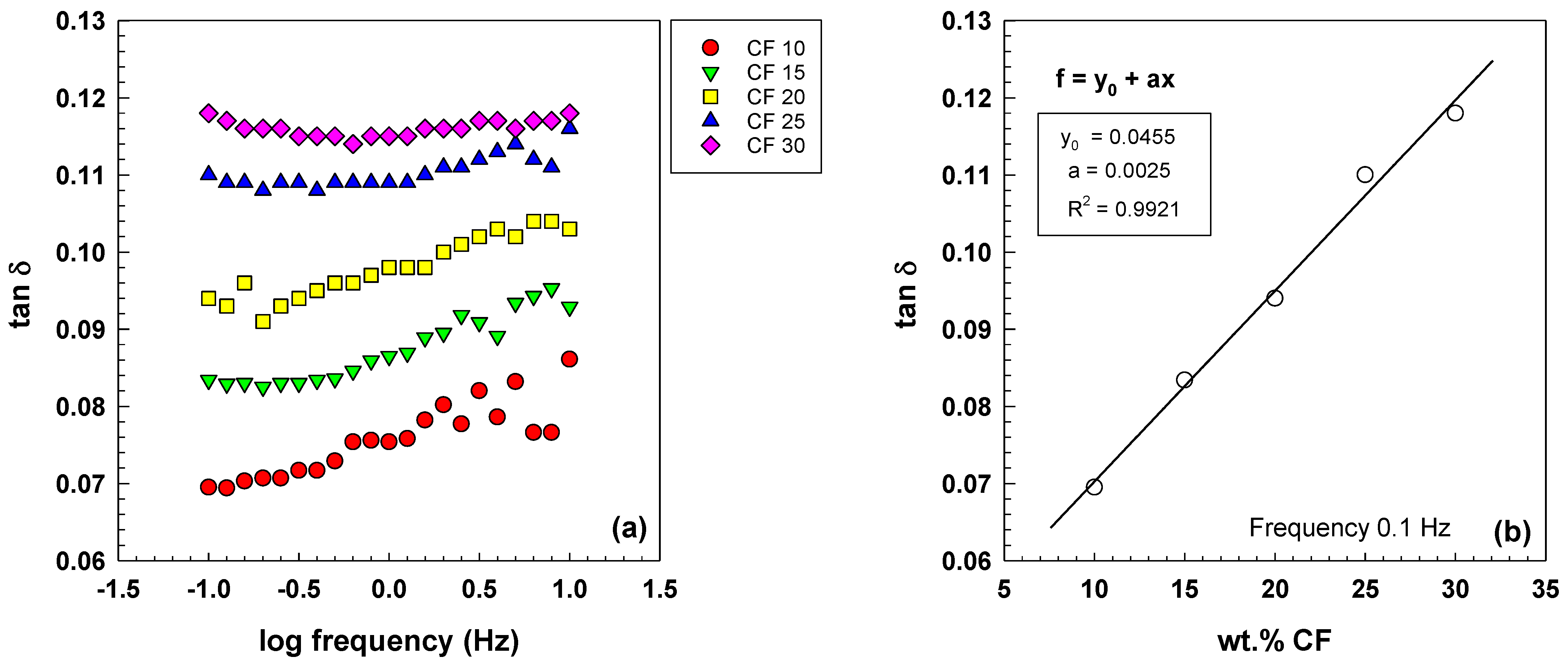
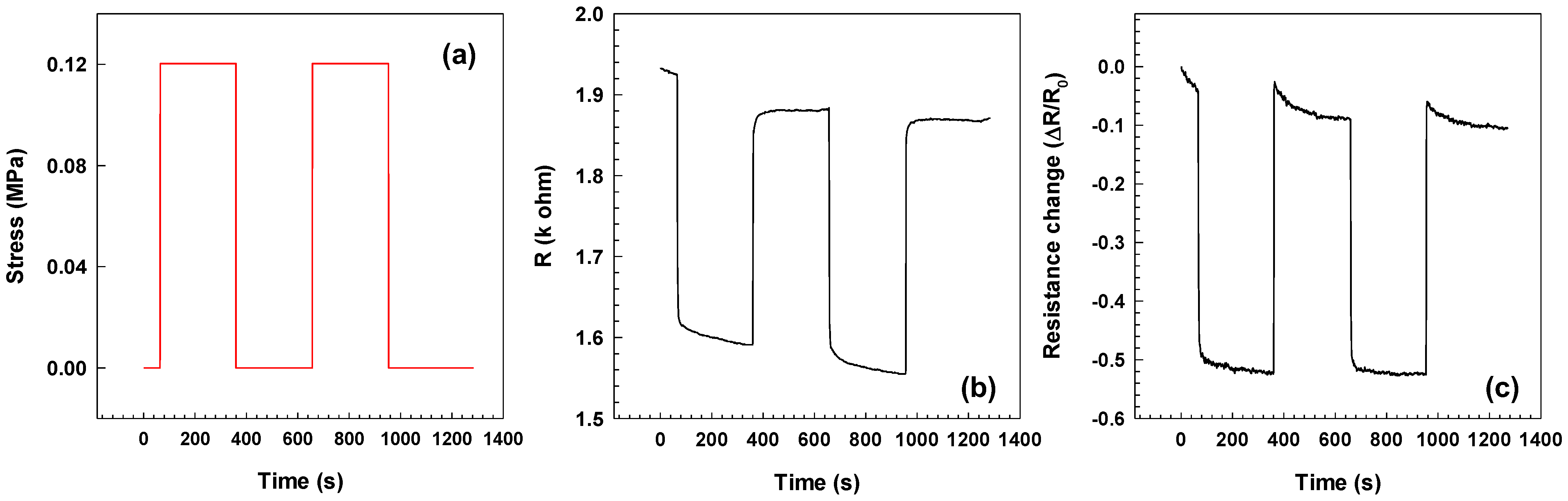
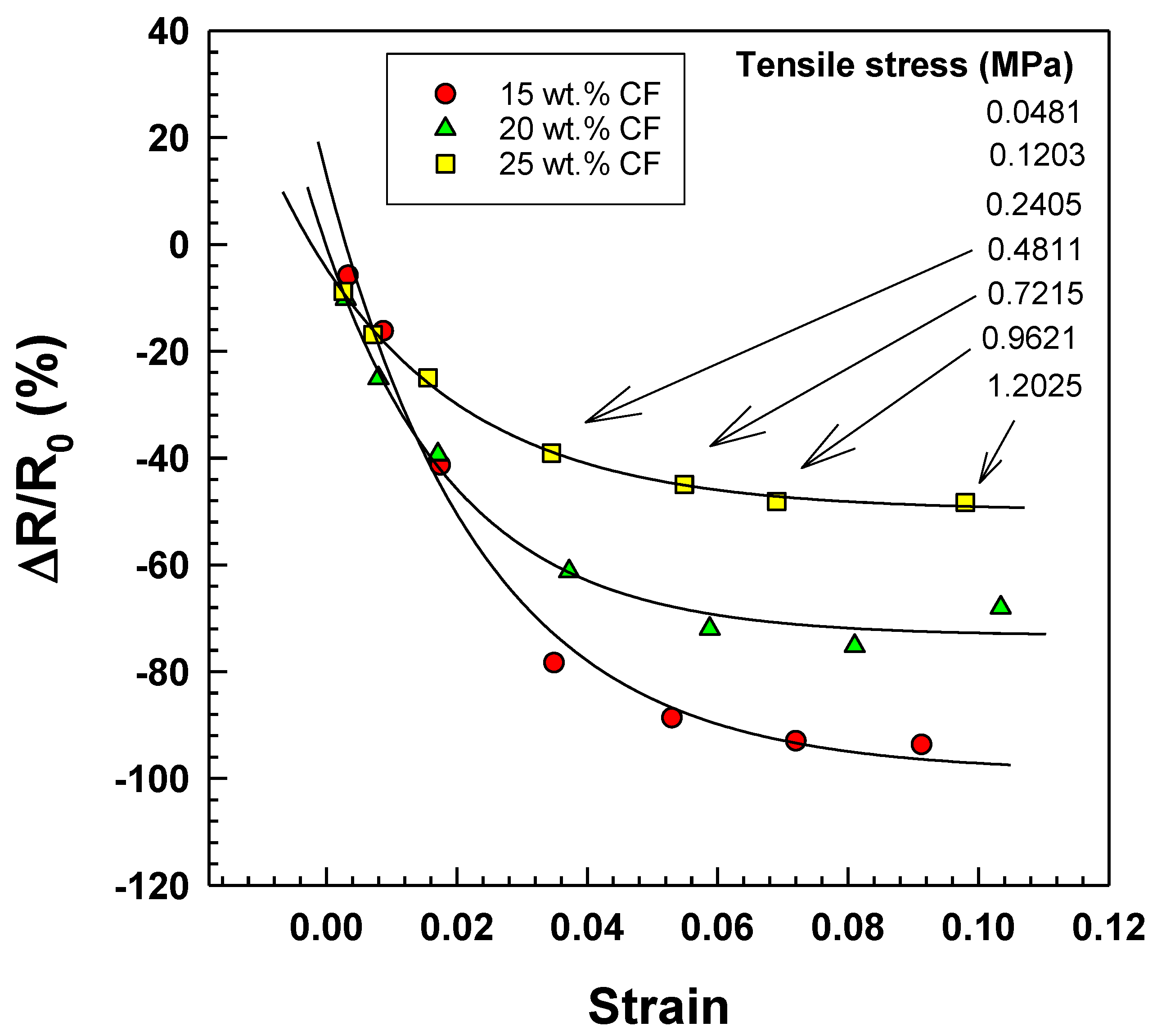
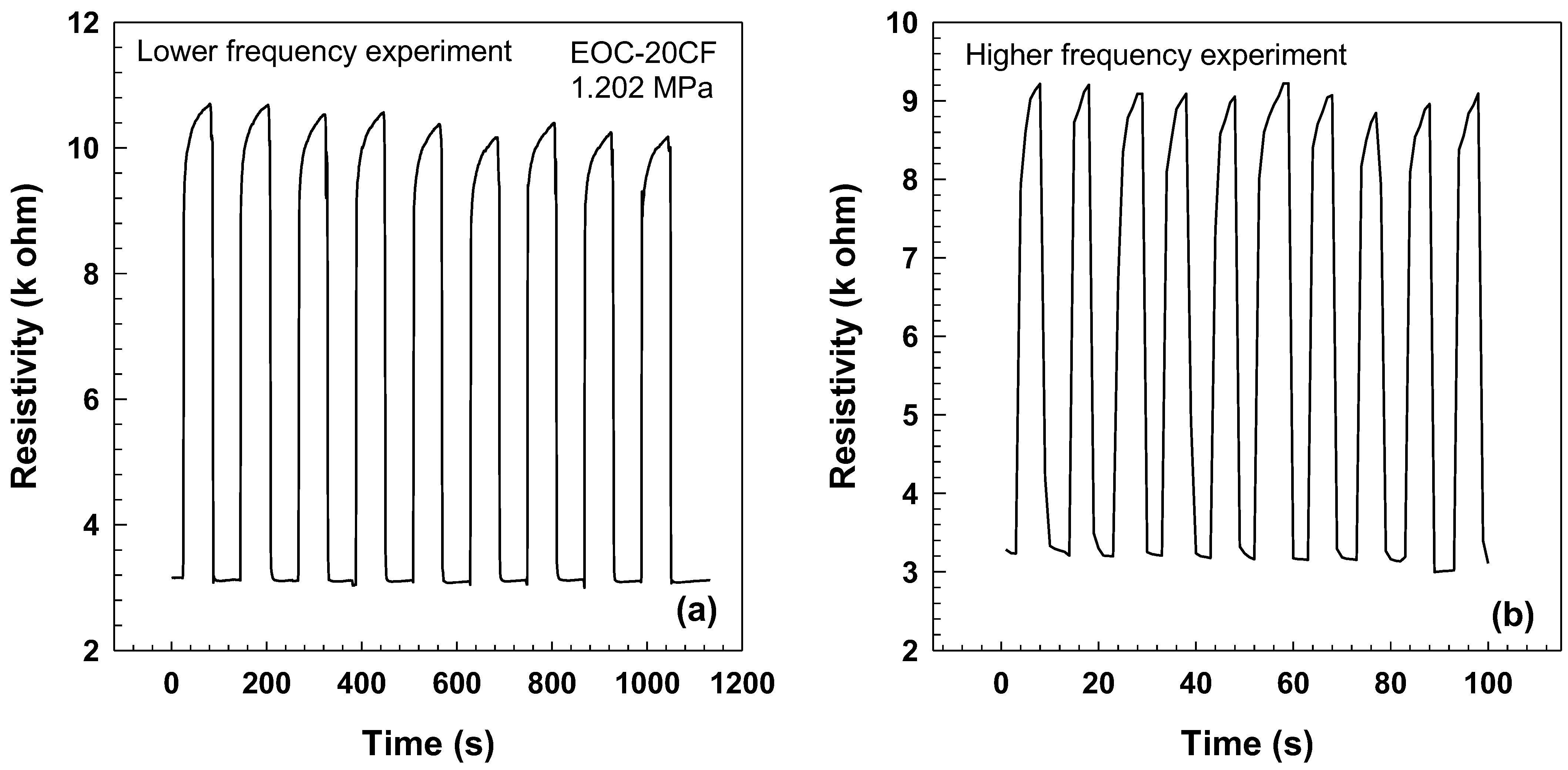
3.3. Electrical Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ding, S.Q.; Han, B.G.; Dong, X.F.; Yu, X.; Ni, Y.Q.; Zheng, Q.F.; Ou, J.P. Pressure-Sensitive Behaviors, Mechanisms and Model of Field Assisted Quantum Tunneling Composites. Polymer 2017, 113, 105–118. [Google Scholar] [CrossRef]
- Lv, W.; Jiang, N.; Ding, J.N.; Liu, Z.F.; Yuan, N.Y.; Ovalle-Robles, R.; Inoue, K.; Lepro, X.; Fang, S.L. Three-Dimensional Conducting Elastomeric Composites Based on Buckling Carbon Nanotube Sheets for Interconnects and Temperature Sensor. J. Nanosci. Nanotechnol. 2017, 17, 1934–1941. [Google Scholar] [CrossRef]
- Njuguna, M.K.; Yan, C.; Hu, N.; Bell, J.M.; Yarlagadda, P.k.D.V. Sandwiched Carbon Nanotube Film as Strain Sensor. Compos. Part B Eng. 2012, 43, 2711–2717. [Google Scholar] [CrossRef]
- Slobodian, P.; Riha, P.; Lengalova, A.; Svoboda, P.; Saha, P. Multi-Wall Carbon Nanotube Networks as Potential Resistive Gas Sensors for Organic Vapor Detection. Carbon 2011, 49, 2499–2507. [Google Scholar] [CrossRef]
- Chae, H.G.; Choi, Y.H.; Minus, M.L.; Kumar, S. Carbon Nanotube Reinforced Small Diameter Polyacrylonitrile Based Carbon Fiber. Compos. Sci. Technol. 2009, 69, 406–413. [Google Scholar] [CrossRef]
- Chae, H.G.; Sreekumar, T.V.; Uchida, T.; Kumar, S. A Comparison of Reinforcement Efficiency of Various Types of Carbon Nanotubes in Poly Acrylonitrile Fiber. Polymer 2005, 46, 10925–10935. [Google Scholar] [CrossRef]
- Gong, S.; Zhu, Z.H.; Meguid, S.A. Carbon Nanotube Agglomeration Effect on Piezoresistivity of Polymer Nanocomposites. Polymer 2014, 55, 5488–5499. [Google Scholar] [CrossRef]
- Christ, J.F.; Hohimer, C.J.; Aliheidari, N.; Ameli, A.; Mo, C.K.; Potschke, P. 3d Printing of Highly Elastic Strain Sensors Using Polyurethane/Multiwall Carbon Nanotube Composites. Sens. Smart Struct. Technol. Civ. Mech. Aerosp. Syst. 2017, 2017, 10168. [Google Scholar] [CrossRef]
- Yan, Y.; Sencadas, V.; Zhang, J.S.; Zu, G.Q.; Wei, D.B.; Jiang, Z.Y. Processing, Characterisation and Electromechanical Behaviour of Elastomeric Multiwall Carbon Nanotubes-Poly (Glycerol Sebacate) Nanocomposites for Piezoresistive Sensors Applications. Compos. Sci. Technol. 2017, 142, 163–170. [Google Scholar] [CrossRef]
- Drobny, J.G. Handbook of Thermoplastic Elastomers, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 1–441. [Google Scholar]
- Lozano-Perez, C.; Cauich-Rodriguez, J.V.; Aviles, F. Influence of Rigid Segment and Carbon Nanotube Concentration on the Cyclic Piezoresistive and Hysteretic Behavior of Multiwall Carbon Nanotube/Segmented Polyurethane Composites. Compos. Sci. Technol. 2016, 128, 25–32. [Google Scholar] [CrossRef]
- Zhou, S.B.; Xiao, A.G.; Huang, X.B.; Chen, Y.D.; Zhuang, Y.B.; Chen, Z.A. Mechanical Properties of Elastomeric Terpolymer Composites Containing Carbon Nanotubes. Polym. Plast. Technol. Eng. 2013, 52, 66–69. [Google Scholar] [CrossRef]
- Zhang, R.; Deng, H.; Valenca, R.; Jin, J.H.; Fu, Q.; Bilotti, E.; Peijs, T. Strain Sensing Behaviour of Elastomeric Composite Films Containing Carbon Nanotubes under Cyclic Loading. Compos. Sci. Technol. 2013, 74, 1–5. [Google Scholar] [CrossRef]
- Theravalappil, R.; Svoboda, P.; Vilcakova, J.; Poongavalappil, S.; Slobodian, P.; Svobodova, D. A Comparative Study on the Electrical, Thermal and Mechanical Properties of Ethylene–Octene Copolymer Based Composites with Carbon Fillers. Mater. Des. 2014, 60, 458–467. [Google Scholar] [CrossRef]
- Jha, V.; Hon, A.A.; Thomas, A.G.; Busfield, J.J.C. Modeling of the Effect of Rigid Fillers on the Stiffness of Rubbers. J. Appl. Polym. Sci. 2008, 107, 2572–2577. [Google Scholar] [CrossRef]
- Mandal, S.; Alam, S. Studies On the Mechanical, Thermal, and Morphological Properties of Poly(Ether Ether Ketone)/Poly(Ether Sulfone)/Barium Titanate Nanocomposites: Correlation of Experimental Results with Theoretical Predictive Models. J. Appl. Polym. Sci. 2012, 126, 724–733. [Google Scholar] [CrossRef]
- Rezende, C.A.; Braganca, F.C.; Doi, T.R.; Lee, L.T.; Galembeck, F.; Boue, F. Natural Rubber-Clay Nanocomposites: Mechanical and Structural Properties. Polymer 2010, 51, 3644–3652. [Google Scholar] [CrossRef]
- Wu, Y.P.; Jia, Q.X.; Yu, D.S.; Zhang, L.Q. Modeling Young’s Modulus of Rubber-Clay Nanocomposites Using Composite Theories. Polym. Test. 2004, 23, 903–909. [Google Scholar] [CrossRef]
- Dewey, J.M. Theory of Filler Reinforcement. J. Appl. Phys. 1945, 16, 55. [Google Scholar] [CrossRef]
- Hamid, Y.; Svoboda, P.; Svobodova, D. Influence of Electron Beam Irradiation on High-Temperature Mechanical Properties of Ethylene Vinyl Acetate/Carbon Fibers Composites. J. Vinyl Addit. Technol. 2020, 26, 325–335. [Google Scholar] [CrossRef]
- Dai, Z.H.; Gao, Y.; Liu, L.Q.; Potschke, P.; Yang, J.L.; Zhang, Z. Creep-Resistant Behavior of Mwcnt-Polycarbonate Melt Spun Nanocomposite Fibers at Elevated Temperature. Polymer 2013, 54, 3723–3729. [Google Scholar] [CrossRef]
- Hernandez-Estrada, Z.J.; Figueroa, J.D.C.; Rayas-Duarte, P.; Pena, R.J. Viscoelastic Characterization of Glutenins in Wheat Kernels Measured by Creep Tests. J. Food Eng. 2012, 113, 19–26. [Google Scholar] [CrossRef]
- Papanicolaou, G.C.; Lagas, G.P.; Zaoutsos, S.P. Viscoelastic Behavior of Hybrid Building Materials. J. Appl. Polym. Sci. 2015, 132, 41429. [Google Scholar] [CrossRef]
- Goodarzi, V.; Kokabi, M.; Kashani, M.R.; Bahramian, A.R. Prediction of Long-Term Mechanical Properties of Pvdf/Batio3 Nanocomposite. J. Appl. Polym. Sci. 2014, 131, 40596. [Google Scholar] [CrossRef]
- Wang, H.C.; Thompson, D.G.; Schoonover, J.R.; Aubuchon, S.R.; Palmer, R.A. Dma-Ftir Creep-Recovery Study of a Poly(Ester Urethane) Elastomer with Molecular-Level Viscoelastic Modeling. Macromolecules 2001, 34, 7084–7090. [Google Scholar] [CrossRef]
- Yang, J.L.; Zhang, Z.; Schlarb, A.K.; Friedrich, K. On the Characterization of Tensile Creep Resistance of Polyamide 66 Nanocomposites. Part II: Modeling and Prediction of Long-Term Performance. Polymer 2006, 47, 6745–6758. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, Y.; Chen, J.; Wu, D.; Qiu, Y.; Yao, X.; Zhou, Y.; Chen, C. Percolation Networks and Transient Rheology of Polylactide Composites Containing Graphite Nanosheets with Various Thicknesses. Polymer 2015, 67, 216–226. [Google Scholar] [CrossRef]
- Al Ahsan, M.; Tareq, M.S.H.; Hosur, M.; Tcherbi-Narteh, A. Thermo-Mechanical Analysis of Seawater-Conditioned Carbon/Polymer Composites Reinforced with Nanoclay/Graphene Nanoparticles. MRS Adv. 2021, 6, 369–377. [Google Scholar] [CrossRef]
- Anwer, M.A.S.; Naguib, H.E. Study on the Morphological, Dynamic Mechanical and Thermal Properties of Pla Carbon Nanofibre Composites. Compos. Part B Eng. 2016, 91, 631–639. [Google Scholar] [CrossRef]
- Mcnally, T.; Potschke, P.; Halley, P.; Murphy, M.; Martin, D.; Bell, S.E.J.; Brennan, G.P.; Bein, D.; Lemoine, P.; Quinn, J.P. Polyethylene Multiwalled Carbon Nanotube Composites. Polymer 2005, 46, 8222–8232. [Google Scholar] [CrossRef]
- Zeng, R.T.; Hu, W.; Wang, M.; Zhang, S.D.; Zeng, J.B. Morphology, Rheological and Crystallization Behavior in Non-Covalently Functionalized Carbon Nanotube Reinforced Poly(Butylene Succinate) Nanocomposites with Low Percolation Threshold. Polym. Test. 2016, 50, 182–190. [Google Scholar] [CrossRef]
- Fernandes, R.R.; Tamijani, A.Y.; Al-Haik, M. Mechanical Characterization of Additively Manufactured Fiber-Reinforced Composites. Aerosp. Sci. Technol. 2021, 113, 106653. [Google Scholar] [CrossRef]
- Durmus, A.; Woo, M.; Kasgoz, A.; Macosko, C.W.; Tsapatsis, M. Intercalated Linear Low Density Polyethylene (Lldpe)/Clay Nanocomposites Prepared with Oxidized Polyethylene as a New Type Compatibilizer: Structural, Mechanical and Barrier Properties. Eur. Polym. J. 2007, 43, 3737–3749. [Google Scholar] [CrossRef]
- Wang, S.K.; Chung, D.D.L. Piezoresistivity in Continuous Carbon Fiber Polymer-Matrix Composite. Polym. Compos. 2000, 21, 13–19. [Google Scholar] [CrossRef]
- Todoroki, A.; Yoshida, J. Electrical Resistance Change of Unidirectional Cfrp due to Applied Load. JSME Int. J. Ser. A Solid Mech. Mater. Eng. 2004, 47, 357–364. [Google Scholar] [CrossRef]
- Yan, X.; Bowen, C.R.; Yuan, C.; Hao, Z.; Pan, M. Carbon Fibre Based Flexible Piezoresistive Composites to Empower Inherent Sensing Capabilities for Soft Actuators. Soft Matter 2019, 15, 8001–8011. [Google Scholar] [CrossRef]
- Pan, M.; Yuan, C.G.; Anpalagan, H.; Plummer, A.; Zou, J.; Zhang, J.H.; Bowen, C. Soft Controllable Carbon Fibre-Based Piezoresistive Self-Sensing Actuators. Actuators 2020, 9, 79. [Google Scholar] [CrossRef]
- Wang, D.J.; Chung, D.D.L. Through-Thickness Piezoresistivity in a Carbon Fiber Polymer-Matrix Structural Composite for Electrical-Resistance-Based Through-Thickness Strain Sensing. Carbon 2013, 60, 129–138. [Google Scholar] [CrossRef]
- Biccai, S.; Boland, C.S.; O’driscoll, D.P.; Harvey, A.; Gabbett, C.; O’suilleabhain, D.R.; Griffin, A.J.; Li, Z.L.; Young, R.J.; Coleman, J.N. Negative Gauge Factor Piezoresistive Composites Based on Polymers Filled with Mos2 Nanosheets. ACS Nano 2019, 13, 6845–6855. [Google Scholar] [CrossRef]
- Alarifi, I.M. Investigation the Conductivity of Carbon Fiber Composites Focusing on Measurement Techniques under Dynamic and Static Loads. J. Mater. Res. Technol. 2019, 8, 4863–4893. [Google Scholar] [CrossRef]
- Birgin, H.B.; D’alessandro, A.; Corradini, A.; Laflamme, S.; Ubertini, F. Self-Sensing Asphalt Composite with Carbon Microfibers for Smart Weigh-in-Motion. Mater. Struct. 2022, 55, 138. [Google Scholar] [CrossRef]
- Slobodian, P.; Olejnik, R.; Matyas, J.; Babar, D.G. Improving Sensitivity of the Polyurethane/Cnt Laminate Strain Sensor by Controlled Mechanical Preload. IOP Conf. Ser. Mater. Sci. Eng. 2016, 108, 012022. [Google Scholar] [CrossRef]


| Average diameter | 150 nm |
| Average length | 15 μm |
| Aspect ratio | 10–500 |
| Density | 2.0 g/cm3 |
| Sample | Four-Parameter Model | ||||
|---|---|---|---|---|---|
| Em (MPa) | Ek (MPa) | ηm (MPa·s) | ηk (MPa·s) | R2 | |
| EOC | 6.7 | 142.6 | 67,114.7 | 3099.2 | 0.991 |
| EOC/10 wt% CF | 12.5 | 181.6 | 79,980.1 | 4501.2 | 0.993 |
| EOC/15 wt% CF | 14.3 | 175.1 | 76,050.2 | 4321.9 | 0.993 |
| EOC/20 wt% CF | 19.5 | 193.3 | 83,418.2 | 5017.1 | 0.992 |
| EOC/25 wt% CF | 24.1 | 222.2 | 92,440.7 | 6160.3 | 0.994 |
| EOC/30 wt% CF | 31.7 | 240.1 | 97,204.5 | 6803.7 | 0.994 |
| Sample | Six-Parameter Model | ||||||
|---|---|---|---|---|---|---|---|
| E0 (MPa) | η0 (MPa·s) | E1 (MPa) | η1 (MPa.s) | E2 (MPa) | η2 (MPa·s) | R2 | |
| EOC | 6.8 | 86,936.1 | 220.2 | 978.6 | 194.9 | 8612.1 | 0.9995 |
| EOC/10 wt% CF | 12.6 | 109,715.6 | 298.2 | 1964.3 | 244.6 | 13,323.8 | 0.9996 |
| EOC/15 wt% CF | 14.5 | 102,613.3 | 286.7 | 1684.1 | 231.4 | 12,130.8 | 0.9995 |
| EOC/20 wt% CF | 20.1 | 108,270.9 | 327.2 | 1480.5 | 239.9 | 11,713.2 | 0.9996 |
| EOC/25 wt% CF | 24.7 | 120,924.9 | 403.9 | 2206.1 | 271.9 | 14,217.2 | 0.9997 |
| EOC/30 wt% CF | 32.8 | 123,687.4 | 437.8 | 2034.5 | 286.3 | 14,497.8 | 0.9996 |
| wt.% CF | y0 | a | b | R2 |
|---|---|---|---|---|
| 15 | −98.82 | 111.8 | 41.96 | 0.9886 |
| 20 | −73.32 | 72.92 | 48.76 | 0.9876 |
| 25 | −49.85 | 45.36 | 41.06 | 0.9978 |
| wt.% CF | y0 | a | b | R2 |
|---|---|---|---|---|
| 15 | −15.52 | 13.81 | 7.619 | 0.9824 |
| 20 | −14.09 | 13.13 | 7.902 | 0.9841 |
| 25 | −7.252 | 6.008 | 9.577 | 0.9881 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nasr, A.; Mrhálek, O.; Svoboda, P. Elastic Electrically Conductive Composites Based on Vapor-Grown Carbon Fibers for Use in Sensors. Polymers 2023, 15, 2005. https://doi.org/10.3390/polym15092005
Nasr A, Mrhálek O, Svoboda P. Elastic Electrically Conductive Composites Based on Vapor-Grown Carbon Fibers for Use in Sensors. Polymers. 2023; 15(9):2005. https://doi.org/10.3390/polym15092005
Chicago/Turabian StyleNasr, Ahmed, Ondřej Mrhálek, and Petr Svoboda. 2023. "Elastic Electrically Conductive Composites Based on Vapor-Grown Carbon Fibers for Use in Sensors" Polymers 15, no. 9: 2005. https://doi.org/10.3390/polym15092005
APA StyleNasr, A., Mrhálek, O., & Svoboda, P. (2023). Elastic Electrically Conductive Composites Based on Vapor-Grown Carbon Fibers for Use in Sensors. Polymers, 15(9), 2005. https://doi.org/10.3390/polym15092005







