Kinetics and Mechanism of Liquid-State Polymerization of 2,4-Hexadiyne-1,6-diyl bis-(p-toluenesulfonate) as Studied by Thermal Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
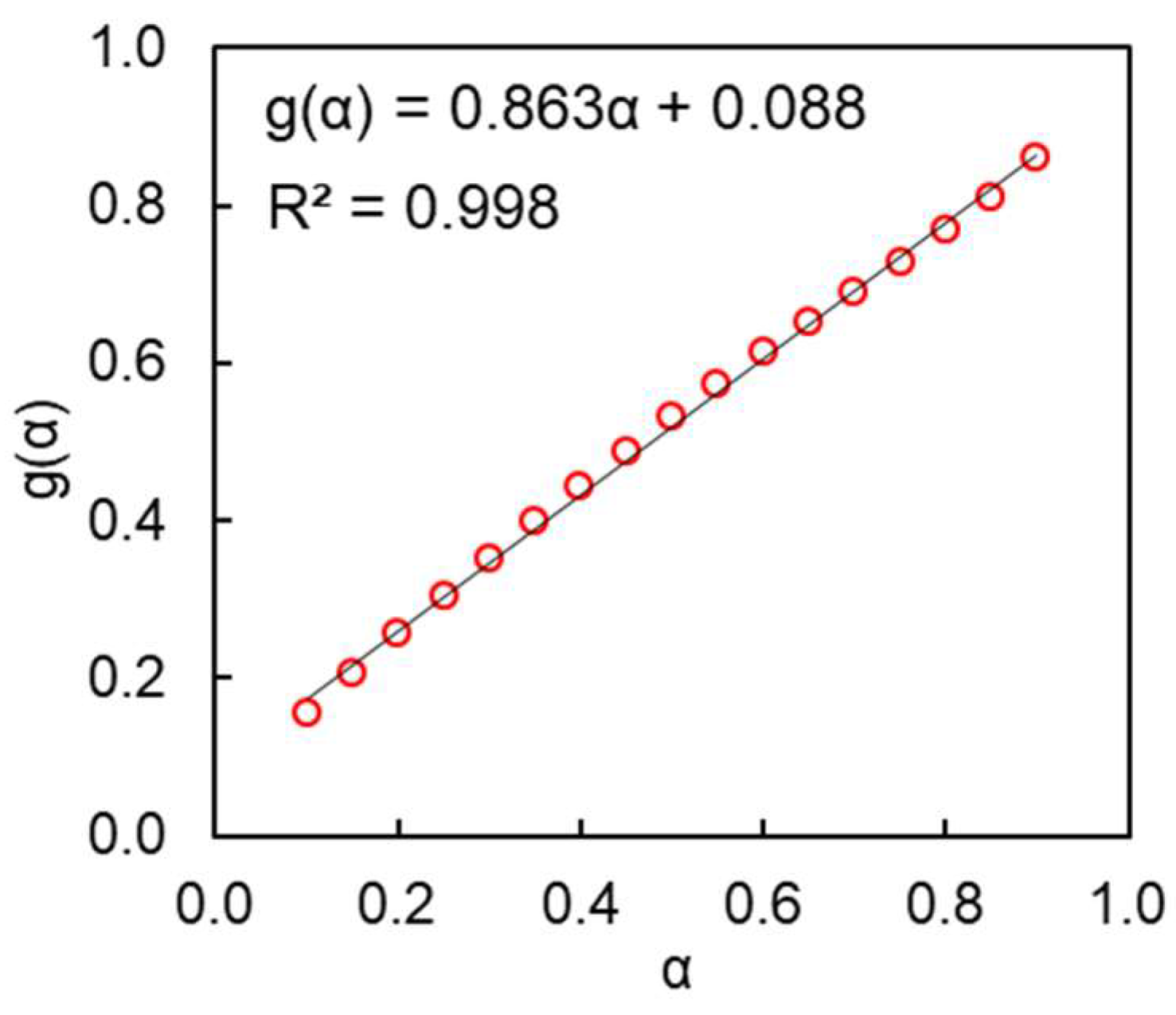
3. Calculations
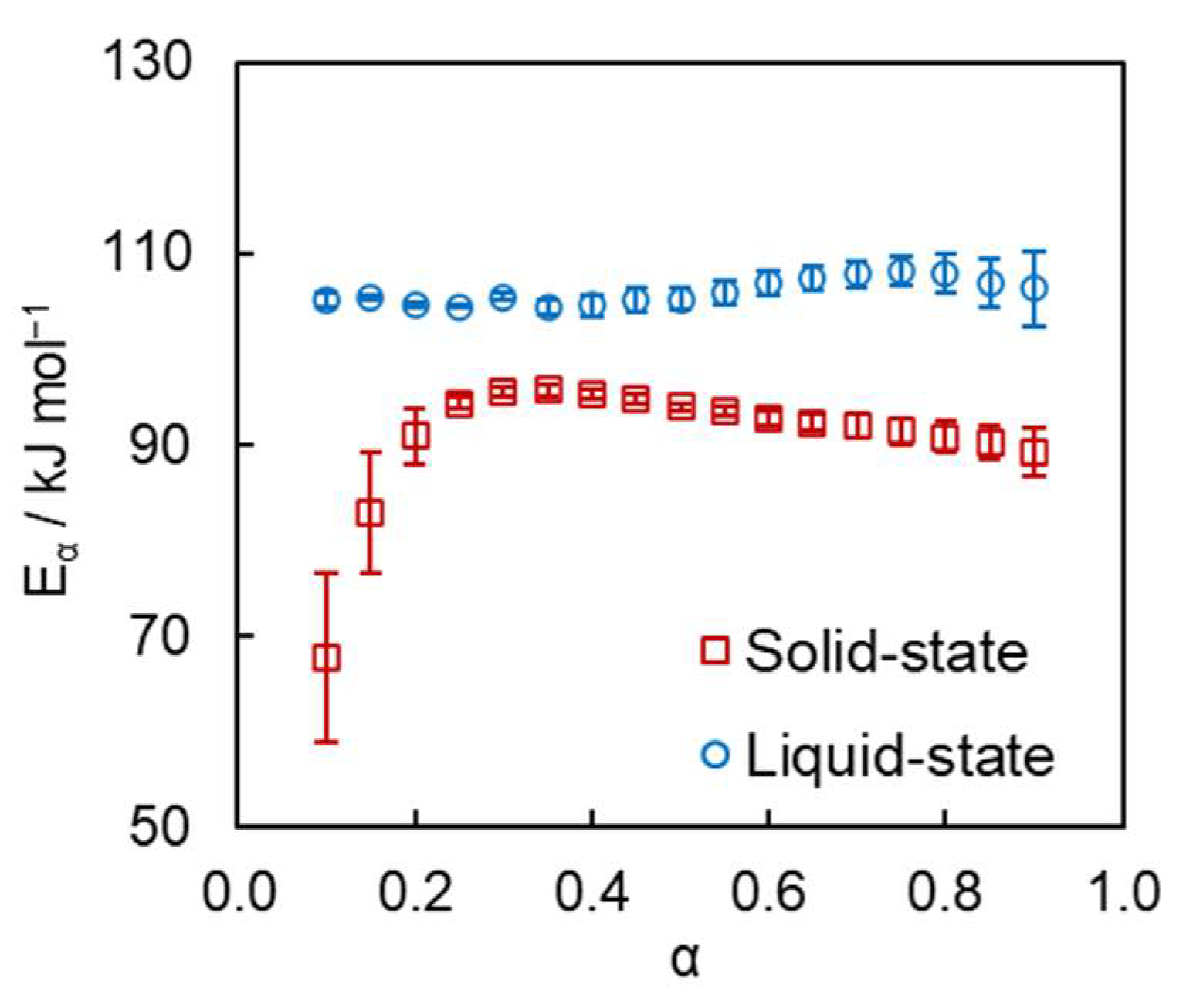
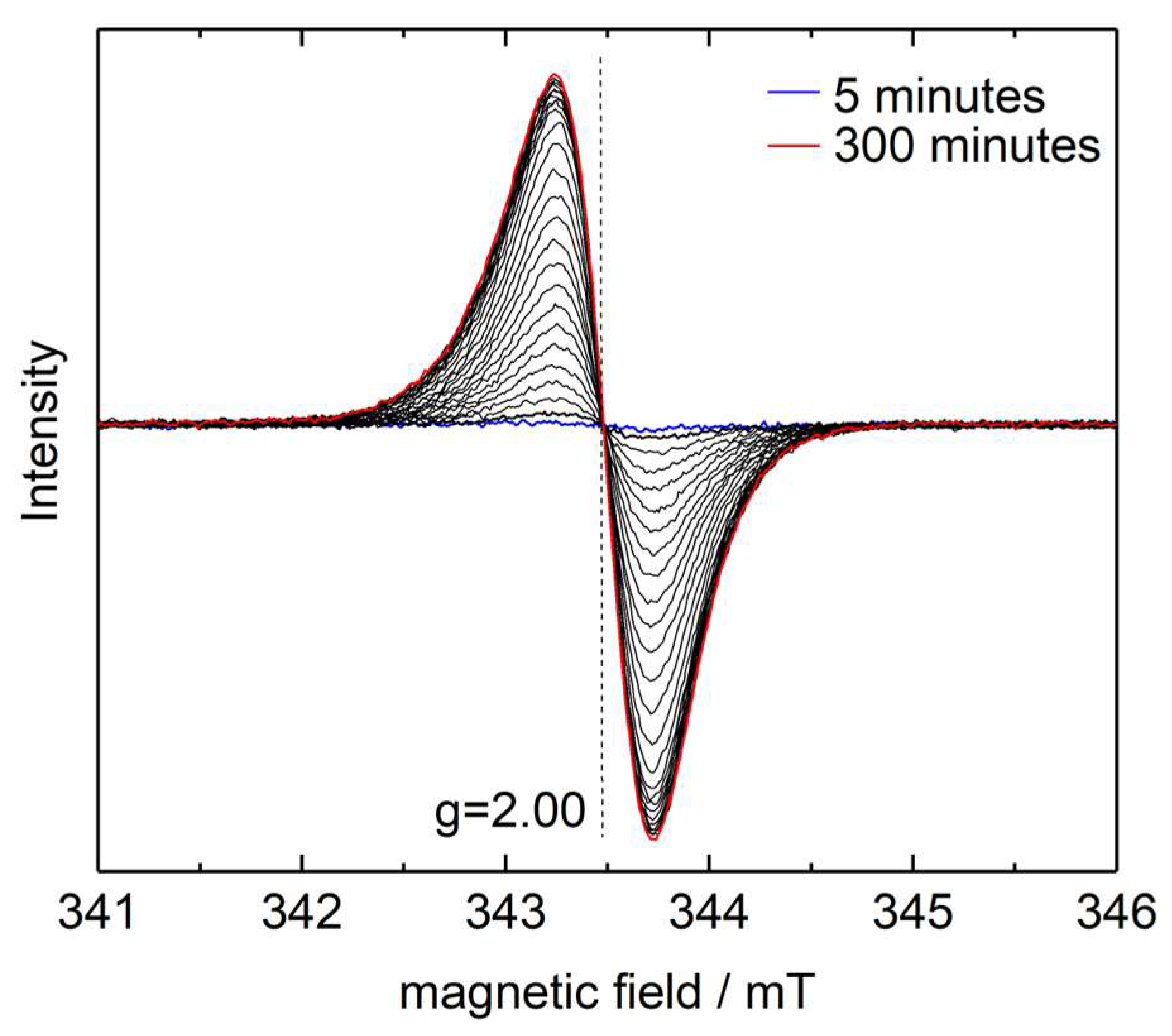
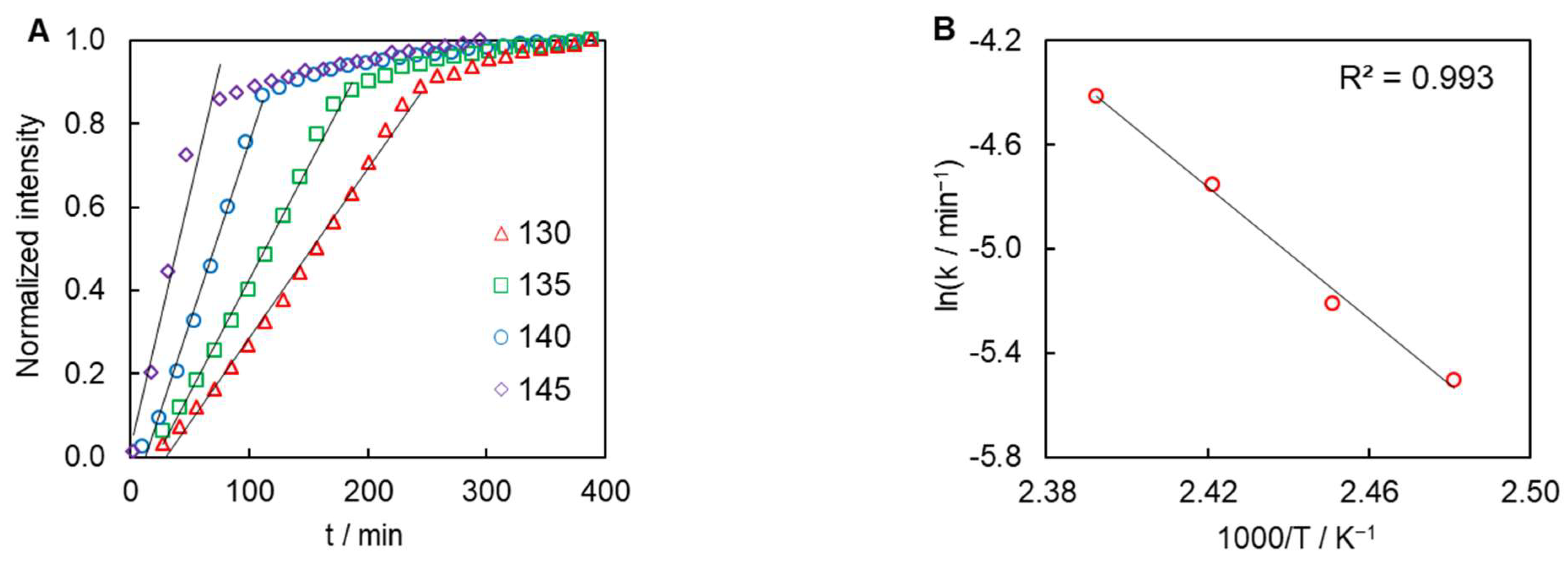
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Qian, X.; Städler, B. Recent Developments in Polydiacetylene-Based Sensors. Chem. Mater. 2019, 31, 1196–1222. [Google Scholar] [CrossRef]
- Park, D.-H.; Heo, J.-M.; Jeong, W.; Yoo, Y.H.; Park, B.J.; Kim, J.-M. Smartphone-Based VOC Sensor Using Colorimetric Polydiacetylenes. ACS Appl. Mater. Interfaces 2018, 10, 5014–5021. [Google Scholar] [CrossRef] [PubMed]
- Park, D.-H.; Kim, B.; Kim, J.-M. A Tetrahydrofuran-selective Optical Solvent Sensor Based on Solvatochromic Polydiacetylene. Bull. Korean Chem. Soc. 2016, 37, 793–794. [Google Scholar] [CrossRef]
- Wang, X.; Sun, X.; Hu, P.A.; Zhang, J.; Wang, L.; Feng, W.; Lei, S.; Yang, B.; Cao, W. Colorimetric Sensor Based on Self-Assembled Polydiacetylene/Graphene-Stacked Composite Film for Vapor-Phase Volatile Organic Compounds. Adv. Funct. Mater. 2013, 23, 6044–6050. [Google Scholar] [CrossRef]
- Chance, R.R.; Baughman, R.H.; Müller, H.; Eckhardt, C.J. Thermochromism in a polydiacetylene crystal. J. Chem. Phys. 2008, 67, 3616–3618. [Google Scholar] [CrossRef]
- Charoenthai, N.; Pattanatornchai, T.; Wacharasindhu, S.; Sukwattanasinitt, M.; Traiphol, R. Roles of head group architecture and side chain length on colorimetric response of polydiacetylene vesicles to temperature, ethanol and pH. J. Colloid Interface Sci. 2011, 360, 565–573. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Zhou, J.; Li, J. Tuned chromic process for polydiacetylenes vesicles: The influence of polymer matrices. Soft Matter 2011, 7, 6529–6531. [Google Scholar] [CrossRef]
- Tomioka, Y.; Tanaka, N.; Imazeki, S. Surface-pressure-induced reversible color change of a polydiacetylene monolayer at a gas–water interface. J. Chem. Phys. 1989, 91, 5694–5700. [Google Scholar] [CrossRef]
- Carpick, R.W.; Sasaki, D.Y.; Burns, A.R. First Observation of Mechanochromism at the Nanometer Scale. Langmuir 2000, 16, 1270–1278. [Google Scholar] [CrossRef]
- Feng, H.; Lu, J.; Li, J.; Tsow, F.; Forzani, E.; Tao, N. Hybrid Mechanoresponsive Polymer Wires Under Force Activation. Adv. Mater. 2013, 25, 1729–1733. [Google Scholar] [CrossRef]
- Enkelmann, V. Structural aspects of the topochemical polymerization of diacetylenes. Polydiacetylenes; Springer: Berlin/Heidelberg, Germany, 1984; pp. 91–136. [Google Scholar]
- Kollmar, C.; Sixl, H. Reaction kinetics of the solid state polymerization in diacetylene crystals. J. Chem. Phys. 1987, 87, 5541–5553. [Google Scholar] [CrossRef]
- McGhie, A.R.; Kalyanaraman, P.S.; Garito, A.F. Solid State Polymerization of a Diacetylene: 2,4-Hexadiyne-1,6-Diol bis (p-Toluenesulfonate) (PTS). Mol. Cryst. Liq. Cryst. 1979, 50, 287–299. [Google Scholar] [CrossRef]
- Njus, J.M.; Sandman, D.J. Solid-state NMR and the thermal polymerization of 2,4-hexadiyne-1,6-diol bis-(p-toluenesulfonate). Solid State Nucl. Magn. Reson. 2006, 29, 251–257. [Google Scholar] [CrossRef] [PubMed]
- Baughman, R.H. Solid-state reaction kinetics in single-phase polymerizations. J. Chem. Phys. 1978, 68, 3110–3121. [Google Scholar] [CrossRef]
- Patel, G.N.; Chance, R.R.; Turi, E.A.; Khanna, Y.P. Energetics and mechanism of the solid-state polymerization of diacetylenes. J. Am. Chem. Soc. 1978, 100, 6644–6649. [Google Scholar] [CrossRef]
- Chance, R.R.; Sowa, J.M. An examination of the thermal polymerization of a crystalline diacetylene using diffuse reflectance spectroscopy. J. Am. Chem. Soc. 1977, 99, 6703–6708. [Google Scholar] [CrossRef]
- Tsibouklis, J.; Werninck, A.R.; Shand, A.J.; Milburn, G.H.W. The Synthesis, Polymerization and Second Order Non-Linear Optical Properties of Novel, Conjugated, Unsymmetrical Diacetylenes Showing Liquid Crystal Behaviour. Liq. Cryst. 1988, 3, 1393–1400. [Google Scholar] [CrossRef]
- Schen, M.A.; Kotowski, K.; Cline, J. Rigid-rod derived amorphous polydiacetylenes. Polymer 1991, 32, 1843–1850. [Google Scholar] [CrossRef]
- Fomina, L.; Allier, H.; Fomine, S.; Salcedo, R.; Ogawa, T. Synthesis and Molten-State Polymerization of Some Novel Conjugated Diacetylenes. Polym. J. 1995, 27, 591–600. [Google Scholar] [CrossRef]
- Chance, R.R.; Patel, G.N. Solid-state polymerization of a diacetylene crystal: Thermal, ultraviolet, and γ-ray polymerization of 2,4-hexadiyne-1,6-diol bis-(p-toluene sulfonate). J. Polym. Sci. Polym. Phys. Ed. 1978, 16, 859–881. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Perez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Li, J.J. Name Reactions: A Collection of Detailed Reaction Mechanisms; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Vyazovkin, S. Modification of the integral isoconversional method to account for variation in the activation energy. J. Comput. Chem. 2001, 22, 178–183. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Wight, C.A. Estimating Realistic Confidence Intervals for the Activation Energy Determined from Thermoanalytical Measurements. Anal. Chem. 2000, 72, 3171–3175. [Google Scholar] [CrossRef] [PubMed]
- Liavitskaya, T.; Birx, L.; Vyazovkin, S. Thermal Stability of Malonic Acid Dissolved in Poly(vinylpyrrolidone) and Other Polymeric Matrices. Ind. Eng. Chem. Res. 2018, 57, 5228–5233. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. Part C Polym. Symp. 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Achilias, D.; Fernandez-Francos, X.; Galukhin, A.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for analysis of thermal polymerization kinetics. Thermochim. Acta 2022, 714, 179243. [Google Scholar] [CrossRef]
- Hoye, T.R.; Baire, B.; Niu, D.; Willoughby, P.H.; Woods, B.P. The hexadehydro-Diels–Alder reaction. Nature 2012, 490, 208–212. [Google Scholar] [CrossRef]
- Vyazovkin, S. Isoconversional Kinetics of Thermally Stimulated Processes; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; p. 236. [Google Scholar]
- Galukhin, A.; Nikolaev, I.; Nosov, R.; Vyazovkin, S. Solid-state polymerization of a novel cyanate ester based on 4-tert-butylcalix[6]arene. Polym. Chem. 2020, 11, 4115–4123. [Google Scholar] [CrossRef]
- Galukhin, A.; Vyazovkin, S. Cyanate Ester Polymerization: Overview of Mechanistic and Kinetic Aspects. Macromol. Chem. Phys. 2023, 224, 2200384. [Google Scholar] [CrossRef]
- Mechanism-Based Kinetics Simulator. Available online: https://www.stolaf.edu/depts/chemistry/courses/toolkits/126/js/kinetics/ (accessed on 27 October 2023).
- Vyazovkin, S. Determining Preexponential Factor in Model-Free Kinetic Methods: How and Why? Molecules 2021, 26, 3077. [Google Scholar] [CrossRef]
- Glasstone, S.; Laidler, K.; Eyring, H. The Theory of Rate Processes; Hammet, L., Ed.; McGRAW-Hizll Book Company, Inc.: New York, NY, USA; London, UK, 1941; p. 611. [Google Scholar]
- Benson, S. The Foundations of Chemical Kinetics, 1st ed.; McGraw Hill Book Company Inc.: New York, NY, USA, 1960. [Google Scholar]
- Galukhin, A.; Nikolaev, I.; Nosov, R.; Islamov, D.; Vyazovkin, S. Solvent-induced changes in the reactivity of tricyanate esters undergoing thermal polymerization. Polym. Chem. 2021, 12, 6179–6187. [Google Scholar] [CrossRef]
- Galukhin, A.; Aleshin, R.; Nosov, R.; Vyazovkin, S. Probing kinetic and mechanistic features of bulk azide–alkyne cycloaddition. Phys. Chem. Chem. Phys. 2023, 25, 10671–10677. [Google Scholar] [CrossRef] [PubMed]
- Salami, M.; Ezabadi, A. A caffeine-based ionic liquid as a novel and eco-friendly catalyst for the synthesis of 1,8-dioxo-octahydroxanthenes under solvent-free conditions. Res. Chem. Intermed. 2019, 45, 3673–3686. [Google Scholar] [CrossRef]
- Warta, R.; Sixl, H. Optical absorption and fluorescence spectroscopy of stable diacetylene oligomer molecules. J. Chem. Phys. 1988, 88, 95–99. [Google Scholar] [CrossRef]
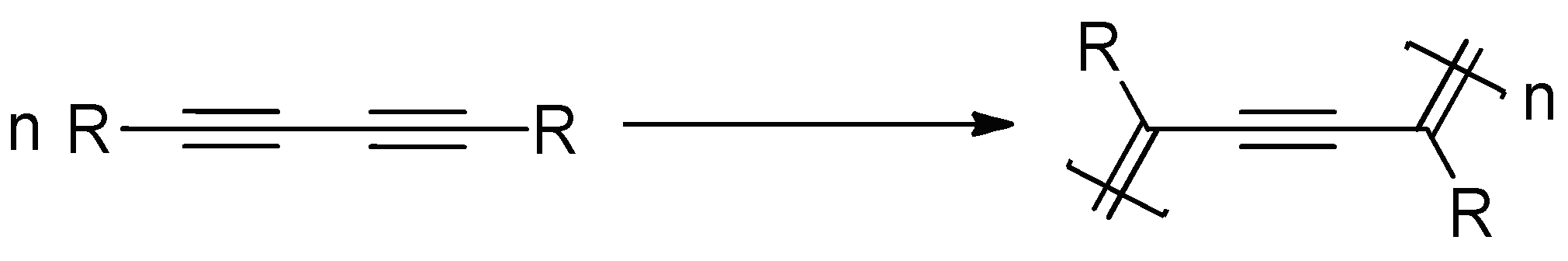



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galukhin, A.; Kachmarzhik, A.; Rodionov, A.; Mamin, G.; Gafurov, M.; Vyazovkin, S. Kinetics and Mechanism of Liquid-State Polymerization of 2,4-Hexadiyne-1,6-diyl bis-(p-toluenesulfonate) as Studied by Thermal Analysis. Polymers 2024, 16, 7. https://doi.org/10.3390/polym16010007
Galukhin A, Kachmarzhik A, Rodionov A, Mamin G, Gafurov M, Vyazovkin S. Kinetics and Mechanism of Liquid-State Polymerization of 2,4-Hexadiyne-1,6-diyl bis-(p-toluenesulfonate) as Studied by Thermal Analysis. Polymers. 2024; 16(1):7. https://doi.org/10.3390/polym16010007
Chicago/Turabian StyleGalukhin, Andrey, Alexander Kachmarzhik, Alexander Rodionov, Georgy Mamin, Marat Gafurov, and Sergey Vyazovkin. 2024. "Kinetics and Mechanism of Liquid-State Polymerization of 2,4-Hexadiyne-1,6-diyl bis-(p-toluenesulfonate) as Studied by Thermal Analysis" Polymers 16, no. 1: 7. https://doi.org/10.3390/polym16010007
APA StyleGalukhin, A., Kachmarzhik, A., Rodionov, A., Mamin, G., Gafurov, M., & Vyazovkin, S. (2024). Kinetics and Mechanism of Liquid-State Polymerization of 2,4-Hexadiyne-1,6-diyl bis-(p-toluenesulfonate) as Studied by Thermal Analysis. Polymers, 16(1), 7. https://doi.org/10.3390/polym16010007








