Estimation of the Shear Viscosity of Mixed-Polymer Materials for Screw Extrusion-Based Recycling Process Modeling
Abstract
1. Introduction
2. Materials and Methods
- Define several shear rate values for the calculation.
- Calculate the viscosity values of the pure polymers at the defined shear rate values.
- If needed, apply a viscosity model on the calculated viscosity of the mixture.
3. Results
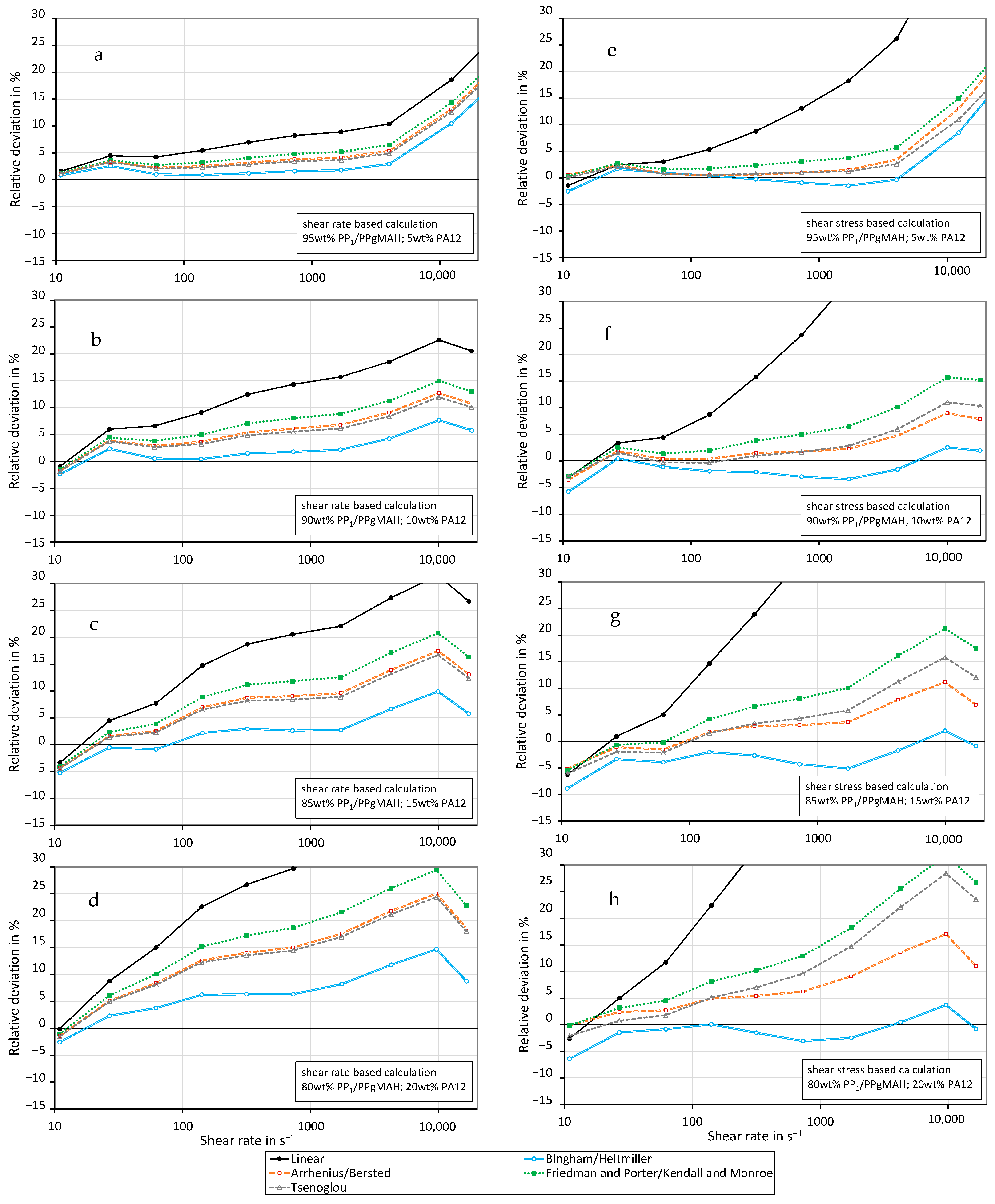
3.1. Shear Stress-Based Calculation of the Mixture Viscosity
- In the first step, several shear stress values for the calculation are defined. In this paper, the shear stress values of the mixtures from the rheological tests were used.
- The viscosity values of the pure polymers are calculated for those defined shear stresses. For this purpose, the basic relation between shear stress and shear rate is used. The shear rate value must be adapted until the calculated shear stress value equals the shear stress value that was defined in step 1. This can be done with a numerical solver, as presented in [6,54,55]
- After that, the mixing rules presented in the Introduction (linear mixing rule, Kendall and Monroe [42]/Friedman and Porter [41], Tsenoglou [37], Arrhenius [39]–Bersted et al. [40], Bingham [27]–Heitmiller et al. [28]) are employed to calculate the shear viscosity of the mixture as a function of the shear stress . The comparison of the results using the mixing models to the measured values is much more complicated for the shear stress-dependent calculation, as the shear rate must be calculated from the shear stress and the shear viscosity and deviates from the measured values. Thus, the next step is needed.
- The shear rate can now be calculated from the viscosity of the mixture and from the shear stress :The results of this calculation are several points that describe the viscosity of a mixture and the corresponding shear rate values for the different mixing rules.
- Then, a viscosity model is used to approximate the calculated viscosity values of the mixture considering the shear stress values obtained in step one and the shear rate value calculated in step four. In this paper, the simplified BCY (see Equation (9)) was used.
- To compare the results of the shear stress-dependent calculation, the viscosity models from step five must now be applied to calculate the viscosity of the mixture for the different models at the shear rates from the rheological tests.
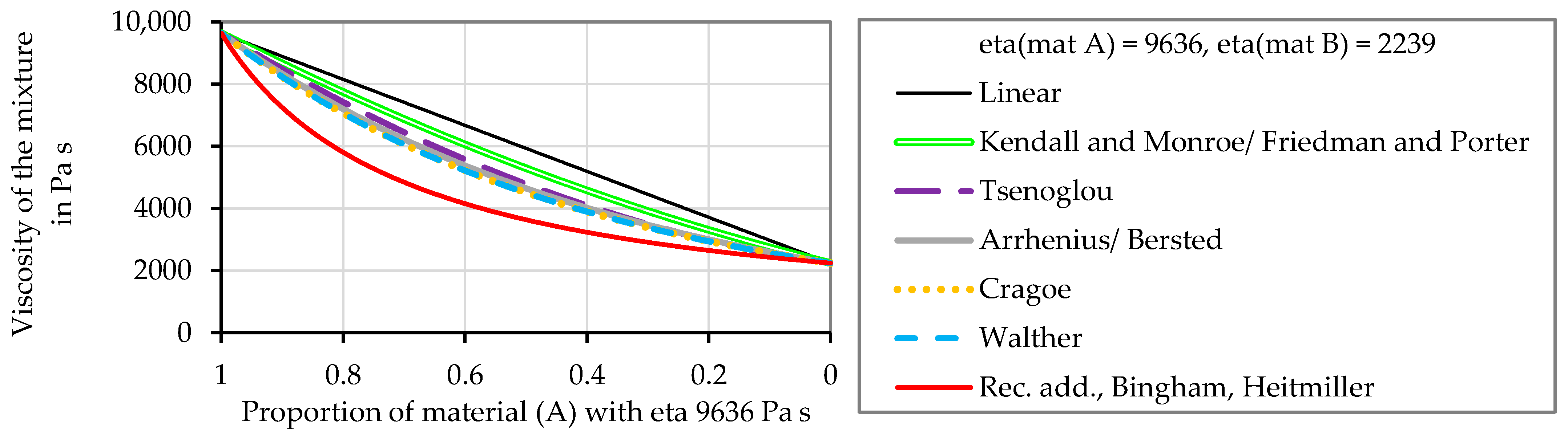
3.2. Comparison of the Mixing Models
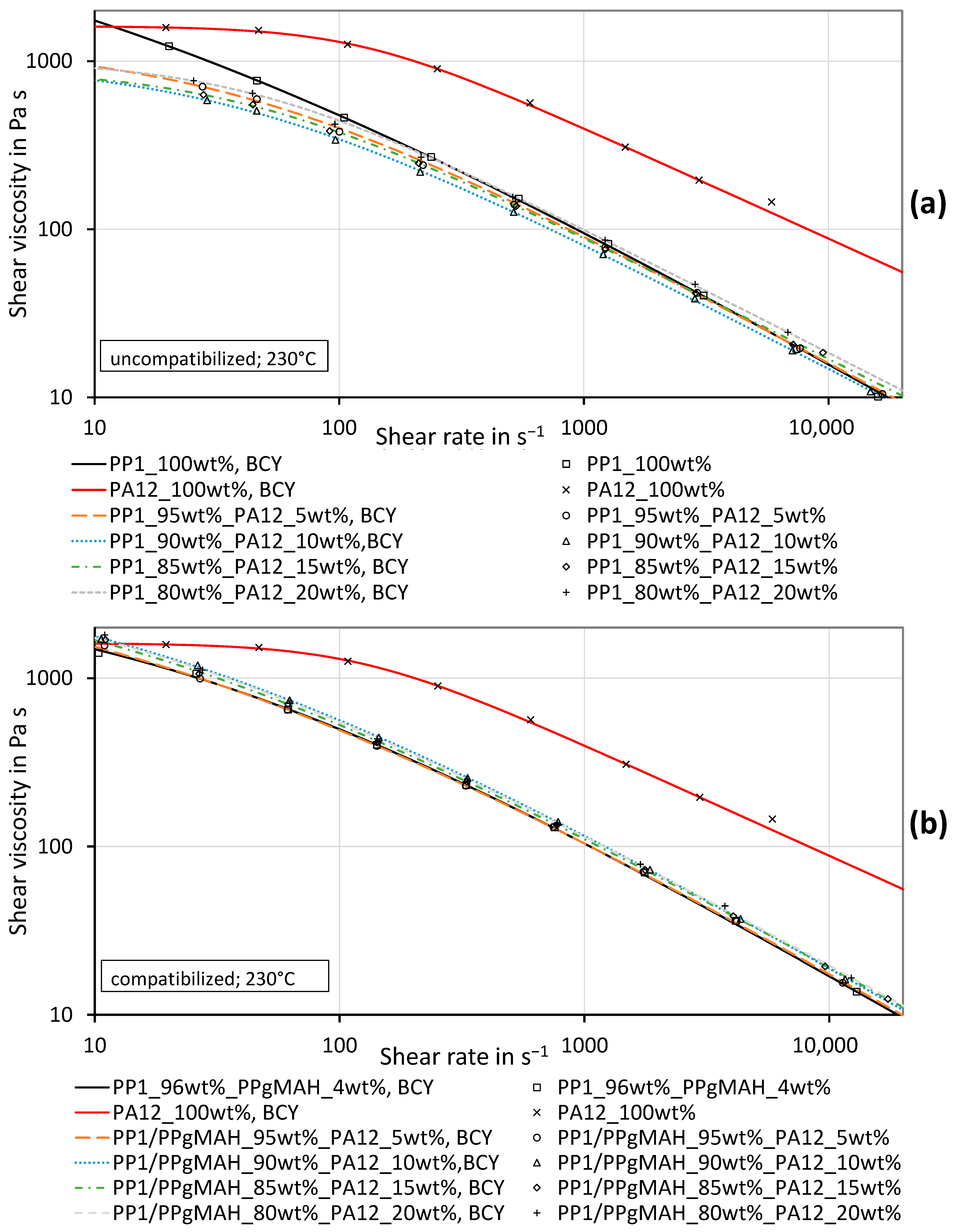
3.3. Shear Viscosity of PP Contaminated with a Different PP Grade
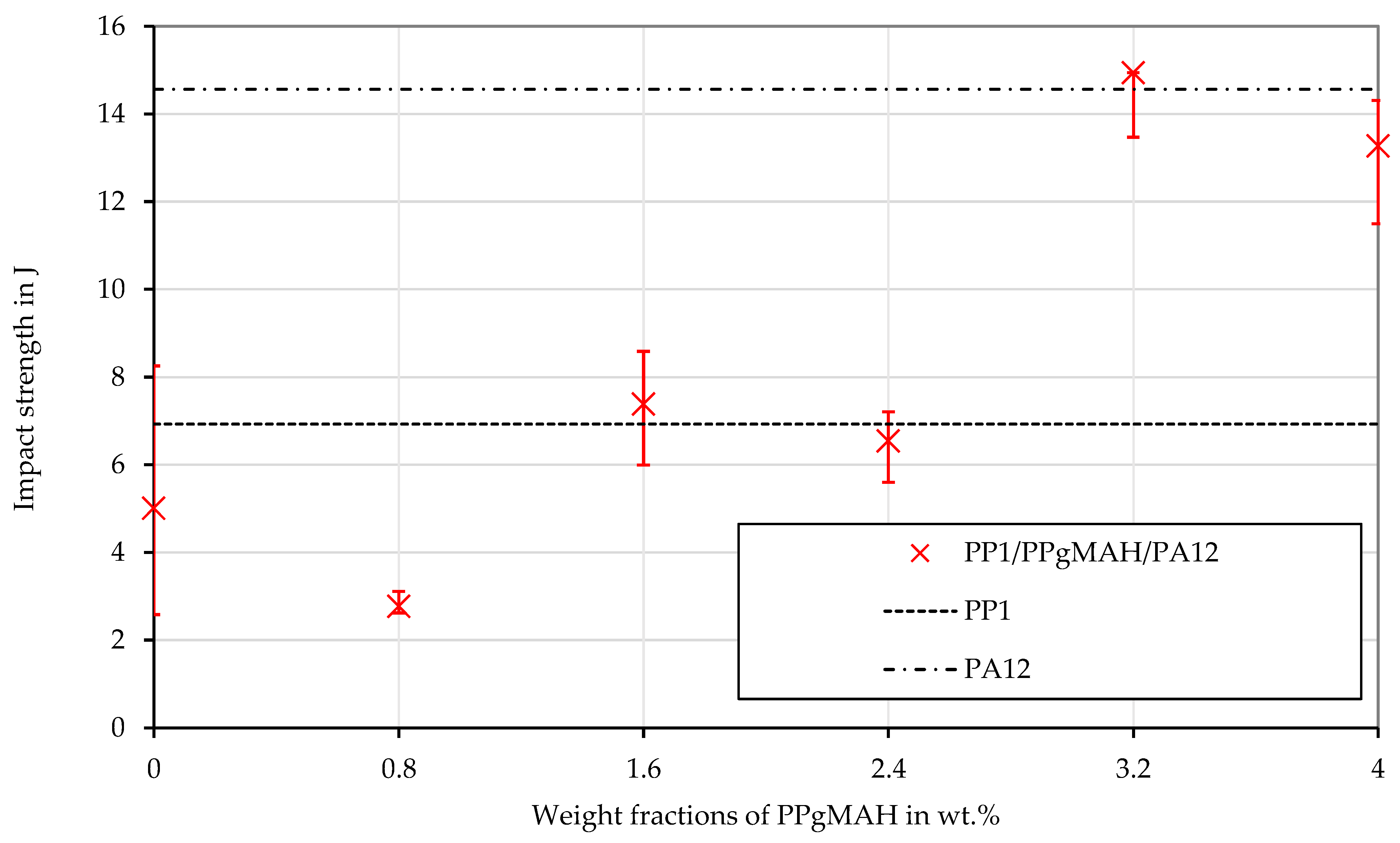
3.4. Shear Viscosity of PP Contaminated with PA12
4. Discussion
5. Conclusions
Author Contributions
Funding

Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Mixture | Temperature in C | in Pa s | in s | Deviation in % | ||
|---|---|---|---|---|---|---|
| 100% PP1 | 200 | 32,326.24 | 0.08 | 0.22 | 0.28 | 1.35 |
| 90% PP1; 10% PP2 | 200 | 12,443.06 | 0.15 | 0.18 | 0.38 | 1.35 |
| 70% PP1; 30% PP2 | 200 | 8374.55 | 0.19 | 0.17 | 0.46 | 1.86 |
| 50% PP1; 50% PP2 | 200 | 3070.17 | 0.21 | 0.06 | 0.69 | 2.04 |
| 30% PP1; 70% PP2 | 200 | 3509.35 | 0.15 | 0.04 | 0.44 | 1.13 |
| 10% PP1; 90% PP2 | 200 | 1177.96 | 0.24 | 0.02 | 0.92 | 0.68 |
| 100% PP2 | 200 | 2333.07 | 0.06 | 0.01 | 0.41 | 1.82 |
| MTSRate 100% PP₁ 0% PPgMAH 0% PA12 200 °C | MTVisc 100% PP₁ 0% PPgMAH 0% PA12 200 °C | MTSRate 90% PP₁ 0% PPgMAH 10% PA12 200 °C | MTVisc 90% PP₁ 0% PPgMAH 10% PA12 200 °C | MTSRate 70% PP₁ 0% PPgMAH 30% PA12 200 °C | MTVisc 70% PP₁ 0% PPgMAH 30% PA12 200 °C | MTSRate 50% PP₁ 0% PPgMAH 50% PA12 200 °C | MTVisc 50% PP₁ 0% PPgMAH 50% PA12 200 °C |
|---|---|---|---|---|---|---|---|
| 11.16 | 2232.93 | 22.88 | 1371.27 | 11.08 | 2036.03 | 10.99 | 1611.33 |
| 28.65 | 1284.30 | 62.20 | 765.16 | 29.18 | 1167.16 | 25.71 | 1066.53 |
| 66.05 | 783.48 | 147.80 | 443.14 | 65.29 | 710.51 | 60.79 | 723.14 |
| 153.17 | 452.61 | 337.98 | 253.31 | 147.19 | 434.26 | 144.73 | 418.97 |
| 341.96 | 260.99 | 776.74 | 141.21 | 337.98 | 247.99 | 331.32 | 243.59 |
| 802.71 | 142.49 | 1891.64 | 71.79 | 752.22 | 142.51 | 737.86 | 140.87 |
| 1964.28 | 70.55 | 4404.70 | 36.31 | 1803.28 | 75.34 | 1760.32 | 75.57 |
| 4413.11 | 36.85 | 12,867.65 | 14.71 | 4386.00 | 36.87 | 4342.20 | 36.75 |
| 9667.29 | 19.81 | 9910.65 | 19.08 | 10,085.44 | 18.48 | ||
| 16,904.08 | 13.21 | 17,179.09 | 12.78 | 17,565.97 | 12.24 |
| MTSRate 30% PP₁ 0% PPgMAH 70% PA12 200 °C | MTVisc 30% PP₁ 0% PPgMAH 70% PA12 200 °C | MTSRate 10% PP₁ 0% PPgMAH 90% PA12 200 °C | MTVisc 10% PP₁ 0% PPgMAH 90% PA12 200 °C | MTSRate 0% PP₁ 0% PPgMAH 100% PA12 200 °C | MTVisc 0% PP₁ 0% PPgMAH 100% PA12 200 °C |
|---|---|---|---|---|---|
| 22.30 | 975.10 | 22.31 | 794.66 | 10.51 | 967.74 |
| 57.64 | 621.41 | 55.52 | 568.03 | 24.67 | 738.95 |
| 135.50 | 387.95 | 133.94 | 355.43 | 56.13 | 530.42 |
| 316.94 | 228.79 | 311.27 | 210.94 | 130.53 | 349.94 |
| 738.55 | 128.72 | 734.70 | 119.15 | 308.89 | 208.92 |
| 1651.40 | 72.84 | 1700.51 | 64.73 | 736.65 | 116.15 |
| 3908.87 | 38.75 | 3835.44 | 35.59 | 1742.50 | 61.83 |
| 9402.64 | 19.19 | 9026.72 | 18.40 | 4085.47 | 32.17 |
| 16,691.30 | 12.67 | 16,470.85 | 11.85 | 9461.38 | 16.51 |
| 16,742.36 | 10.91 |
Appendix B
| Mixture | Temperature in °C | in Pa s | in s | Deviation in % | ||
|---|---|---|---|---|---|---|
| 100% PP1 | 230 | 10,995.94 | 0.15 | 0.19 | 0.38 | 2.02 |
| 95% PP1; 5% PA12 | 230 | 1262.94 | 0.22 | 0.02 | 0.77 | 2.18 |
| 90% PP1; 10% PA12 | 230 | 1013.39 | 0.24 | 0.02 | 0.80 | 1.31 |
| 85% PP1; 15% PA12 | 230 | 912.107 | 0.27 | 0.02 | 1.00 | 1.61 |
| 80% PP1; 20% PA12 | 230 | 1026.29 | 0.26 | 0.02 | 1.09 | 1.87 |
| 96% PP1; 4% PPgMAH | 230 | 3680.82 | 0.15 | 0.05 | 0.50 | 2.55 |
| 95% PP1–PPgMAH; 5% PA12 | 230 | 4988.348 | 0.15 | 0.06 | 0.44 | 1.86 |
| 90% PP1–PPgMAH; 10% PA12 | 230 | 5156.10 | 0.15 | 0.06 | 0.47 | 1.44 |
| 85% PP1–PPgMAH; 15% PA12 | 230 | 4746.50 | 0.19 | 0.08 | 0.51 | 1.02 |
| 80% PP1–PPgMAH; 20% PA12 | 230 | 4428 | 0.19 | 0.08 | 0.54 | 1.91 |
| 100% PA12 | 230 | 1614.30 | 0.34 | 0.00 | 1.67 | 2.50 |
| 100% PP1 | 250 | 20,863.15 | 0.04 | 0.11 | 0.25 | 2.88 |
| 95% PP1; 5% PA12 | 250 | 14,769.92 | 0.04 | 0.07 | 0.26 | 1.11 |
| 90% PP1; 10% PA12 | 250 | 14,645.04 | 0.04 | 0.07 | 0.26 | 2.26 |
| 85% PP1; 15% PA12 | 250 | 15,216.12 | 0.04 | 0.07 | 0.26 | 1.55 |
| 80% PP1; 20% PA12 | 250 | 14,560.54 | 0.03 | 0.06 | 0.25 | 1.85 |
| 96% PP1; 4% PPgMAH | 250 | 12,637.34 | 0.08 | 0.08 | 0.27 | 2.67 |
| 95% PP1–PPgMAH; 5% PA12 | 250 | 12,496.73 | 0.08 | 0.08 | 0.27 | 2.81 |
| 90% PP1–PPgMAH; 10% PA12 | 250 | 11,375.75 | 0.07 | 0.07 | 0.28 | 0.85 |
| 85% PP1–PPgMAH; 15% PA12 | 250 | 11,765.88 | 0.07 | 0.07 | 0.29 | 1.28 |
| 80% PP1–PPgMAH; 20% PA12 | 250 | 12,188 | 0.07 | 0.07 | 0.28 | 1.26 |
| 100% PA12 | 250 | 2849.27 | 0.14 | 0.00 | 0.55 | 2.66 |
| MTSRate 96% PP₁ 4% PPgMAH 0% PA12 230 °C | MTVisc 96% PP₁ 4% PPgMAH 0% PA12 230 °C | MTSRate 91.2% PP₁ 3.8% PPgMAH 5% PA12 230 °C | MTVisc 91.2% PP₁ 3.8% PPgMAH 5% PA12 230 °C | MTSRate 86.4% PP₁ 3.6% PPgMAH 10% PA12 230 °C | MTVisc 86.4% PP₁ 3.6% PPgMAH 10% PA12 230 °C |
|---|---|---|---|---|---|
| 10.38 | 1412.35 | 10.97 | 1564.79 | 10.64 | 1712.37 |
| 25.99 | 1064.44 | 26.95 | 993.20 | 26.36 | 1192.64 |
| 61.74 | 652.26 | 61.29 | 648.47 | 62.53 | 740.10 |
| 142.06 | 401.29 | 142.01 | 395.85 | 144.59 | 444.09 |
| 329.13 | 231.52 | 327.63 | 229.52 | 333.45 | 255.71 |
| 757.00 | 130.03 | 746.47 | 130.55 | 781.32 | 139.96 |
| 1762.59 | 70.03 | 1742.62 | 70.70 | 1852.57 | 72.75 |
| 4144.25 | 36.18 | 4183.34 | 35.84 | 4339.74 | 37.12 |
| 12,936.16 | 13.75 | 11,361.95 | 15.52 | 11,601.36 | 16.27 |
| 36,861.17 | 5.43 | 22,425.61 | 8.66 | 22,980.69 | 9.02 |
| MTSRate 81.6% PP₁ 3.4% PPgMAH 15% PA12, 230 °C | MTVisc 81.6% PP₁ 3.4% PPgMAH 15% PA12, 230 °C | MTSRate 76.8% PP₁ 3.2% PPgMAH 20% PA12, 230 °C | MTVisc 76.8% PP₁ 3.2% PPgMAH 20% PA12, 230 °C | MTSRate 0% PP₁ 0% PPgMAH 100% PA12, 230 °C | MTVisc 0% PP₁ 0% PPgMAH 100% PA12, 230 °C |
|---|---|---|---|---|---|
| 11.07 | 1691.22 | 10.99 | 1807.83 | 19.58 | 1585.16 |
| 26.70 | 1063.02 | 27.52 | 1119.55 | 46.85 | 1523.74 |
| 61.57 | 701.99 | 62.70 | 710.60 | 108.22 | 1261.41 |
| 143.60 | 418.52 | 142.68 | 435.84 | 251.82 | 899.55 |
| 330.80 | 242.57 | 332.36 | 250.91 | 603.50 | 565.40 |
| 770.16 | 134.08 | 773.87 | 137.79 | 1478.09 | 307.94 |
| 1773.18 | 72.34 | 1691.48 | 78.38 | 2957.63 | 195.87 |
| 4056.73 | 38.54 | 3752.81 | 44.31 | 5849.49 | 145.42 |
| 9610.83 | 19.42 | 12,319.38 | 16.63 | ||
| 17,343.03 | 12.45 | −100,932.70 | 4.75 |
| MTSRate 96% PP₁ 4% PPgMAH 0% PA12, 250 °C | MTVisc 96% PP₁ 4% PPgMAH 0% PA12, 250 °C | MTSRate 91.2% PP₁ 3.8% PPgMAH 5% PA12, 250 °C | MTVisc 91.2% PP₁ 3.8% PPgMAH 5% PA12, 250 °C | MTSRate 86.4% PP₁ 3.6% PPgMAH 10% PA12, 250 °C | MTVisc 86.4% PP₁ 3.6% PPgMAH 10% PA12, 250 °C |
|---|---|---|---|---|---|
| 10.80 | 1189.36 | 10.93 | 1322.41 | 11.02 | 1383.71 |
| 25.58 | 814.29 | 26.67 | 854.35 | 26.82 | 874.38 |
| 58.83 | 562.47 | 60.82 | 562.02 | 60.47 | 583.10 |
| 138.02 | 347.63 | 139.29 | 348.70 | 139.53 | 361.31 |
| 320.93 | 203.55 | 320.02 | 206.56 | 320.78 | 212.82 |
| 733.86 | 116.28 | 732.93 | 118.09 | 731.11 | 122.36 |
| 1676.36 | 64.87 | 1693.41 | 65.09 | 1707.39 | 66.82 |
| 4007.33 | 33.68 | 4024.87 | 33.77 | 4100.18 | 34.10 |
| 10,003.69 | 16.01 | 12,306.15 | 13.16 | 10,033.85 | 16.48 |
| 18,172.23 | 10.08 | 31,211.24 | 5.74 | 18,075.70 | 10.47 |
| MTSRate 81.6% PP₁ 3.4% PPgMAH 15% PA12, 250 °C | MTVisc 81.6% PP₁ 3.4% PPgMAH 15% PA12, 250 °C | MTSRate 76.8% PP₁ 3.2% PPgMAH 20% PA12, 250 °C | MTVisc 76.8% PP₁ 3.2% PPgMAH 20% PA12, 250 °C | MTSRate 0% PP₁ 0% PPgMAH 100% PA12, 250 °C | MTVisc 0% PP₁ 0% PPgMAH 100% PA12, 250 °C |
|---|---|---|---|---|---|
| 11.00 | 1451.30 | 10.96 | 1438.56 | 8.24 | 2148.32 |
| 26.73 | 923.44 | 26.89 | 917.96 | 17.71 | 1757.46 |
| 61.94 | 600.94 | 62.02 | 591.61 | 38.64 | 1385.98 |
| 142.24 | 362.84 | 140.62 | 363.69 | 84.95 | 1065.02 |
| 320.30 | 217.49 | 315.78 | 220.48 | 190.67 | 765.44 |
| 720.29 | 127.16 | 730.69 | 126.24 | 441.92 | 499.65 |
| 1718.32 | 68.64 | 1744.21 | 67.03 | 1071.40 | 285.17 |
| 4242.49 | 33.72 | 4248.64 | 33.41 | 2712.68 | 143.32 |
| 9871.78 | 16.98 | 9590.90 | 17.31 | 6487.90 | 71.19 |
| 17,178.96 | 11.33 | 16,460.06 | 11.87 |
References
- EU. European Commission Directive (Eu) 2018/852 of the European Parliament and of the Council of 30 May 2018 Amending Directive 94/62/EC on Packaging and Packaging Waste. Off. J. Eur. Union 2018, 61, 141–154. [Google Scholar]
- Giles, H.F.; Wagner, J.R.; Mount, E.M. Extrusion: The Definitive Processing Guide and Handbook; William Andrew Pub: Norwich, NY, USA, 2005; ISBN 0815514735. [Google Scholar]
- Gogos, C.G.; Tadmor, Z. Principles of Polymer Processing; Wiley-Interscience: Hoboken, NJ, USA, 2014; ISBN 978-0-470-35592-3. [Google Scholar]
- Rauwendaal, C. Polymer Extrusion, 5th ed.; Carl Hanser Verlag GmbH & Co. KG: München, Germany, 2014; ISBN 978-1-56990-516-6. [Google Scholar]
- Agassant, J.-F.; Avenas, P.; Carreau, P.J.; Vergnes, B.; Vincent, M. Polymer Processing: Principles and Modeling, 2nd ed.; Hamilton, C., Ed.; Hanser Publishers: Munich, Germany, 2017; ISBN 9781569906057. [Google Scholar]
- Kneidinger, C. Solids Conveying, Melting and Melt Conveying in Single Screw Extruders and Extrusion Dies. Doctoral Thesis, JKU Johannes Kepler University, Linz, Austria, 2021. [Google Scholar]
- DeLassus, P. Barrier Polymers. In Kirk-Othmer Encyclopedia of Chemical Technology; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Knudsen, M. Die Molekularströmung Der Gase Durch Offnungen Und Die Effusion. Ann. Phys. 1909, 333, 999–1016. [Google Scholar] [CrossRef]
- Knudsen, M. Experimentelle Bestimmung Des Druckes Gesättigter Quecksilberdämpfe Bei 0° und Höheren Temperaturen. Ann. Phys. 1909, 334, 179–193. [Google Scholar] [CrossRef]
- Knudsen, M. Die Gesetze Der Molekularströmung Und Der Inneren Reibungsströmung Der Gase Durch Röhren. Ann. Phys. 1909, 333, 75–130. [Google Scholar] [CrossRef]
- Valentas, K.J.; Rotstein, E.; Singh, R.P. Handbook of Food Engineering Practice; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Atkins, P.W.; de Paula, J.; Keeler, J. Atkins’ Physical Chemistry; Oxford University Press: Oxford, UK, 2023. [Google Scholar]
- Naderi Kalali, E.; Lotfian, S.; Entezar Shabestari, M.; Khayatzadeh, S.; Zhao, C.; Yazdani Nezhad, H. A Critical Review of the Current Progress of Plastic Waste Recycling Technology in Structural Materials. Curr. Opin. Green Sustain. Chem. 2023, 40, 100763. [Google Scholar] [CrossRef]
- Kaminsky, W. Thermal Recycling of Polymers. J. Anal. Appl. Pyrolysis 1985, 8, 439–448. [Google Scholar] [CrossRef]
- Samorì, C.; Pitacco, W.; Vagnoni, M.; Catelli, E.; Colloricchio, T.; Gualandi, C.; Mantovani, L.; Mezzi, A.; Sciutto, G.; Galletti, P. Recycling of Multilayer Packaging Waste with Sustainable Solvents. Resour. Conserv. Recycl. 2023, 190, 106832. [Google Scholar] [CrossRef]
- Koning, C. Strategies for Compatibilization of Polymer Blends. Prog. Polym. Sci. 1998, 23, 707–757. [Google Scholar] [CrossRef]
- Utracki, L.A. Compatibilization of Polymer Blends. Can. J. Chem. Eng. 2002, 80, 1008–1016. [Google Scholar] [CrossRef]
- Kallel, T.; Massardier-Nageotte, V.; Jaziri, M.; Gérard, J.F.; Elleuch, B. Compatibilization of PE/PS and PE/PP Blends. I. Effect of Processing Conditions and Formulation. J. Appl. Polym. Sci. 2003, 90, 2475–2484. [Google Scholar] [CrossRef]
- Palierne, J.F. Linear Rheology of Viscoelastic Emulsions with Interfacial Tension. Rheol. Acta 1990, 29, 204–214. [Google Scholar] [CrossRef]
- Bousmina, M. Effect of Interfacial Tension on Linear Viscoelastic Behavior of Immiscible Polymer Blends. Rheol. Acta 1999, 38, 251–254. [Google Scholar] [CrossRef]
- Yoo, S.J.; Lee, S.H.; Jeon, M.; Lee, H.S.; Kim, W.N. Effects of Compatibilizers on the Mechanical, Morphological, and Thermal Properties of Poly(Propylene Carbonate)/Poly(Methyl Methacrylate) Blends. Macromol. Res. 2013, 21, 1182–1187. [Google Scholar] [CrossRef]
- Kozlowski, M.; La Mantia, F.P. Study on Compatibilization of Polypropylene-Liquid Crystalline Polymer Blends. J. Appl. Polym. Sci. 1997, 66, 969–980. [Google Scholar] [CrossRef]
- Holsti-Miettinen, R.; Seppälä, J.; Ikkala, O.T. Effects of Compatibilizers on the Properties of Polyamide/Polypropylene Blends. Polym. Eng. Sci. 1992, 32, 868–877. [Google Scholar] [CrossRef]
- Kneidinger, C.; Schroecker, E.; Zitzenbacher, G.; Miethlinger, J. Melting Behavior of Heterogeneous Polymer Bulk Solids Related to Flood Fed Single Screw Extruders. Polymers 2020, 12, 2893. [Google Scholar] [CrossRef] [PubMed]
- Wilczyński, K.J.; Lewandowski, A.; Wilczyński, K. Experimental Study of Melting of Polymer Blends in a Starve Fed Single Screw Extruder. Polym. Eng. Sci. 2016, 56, 1349–1356. [Google Scholar] [CrossRef]
- Wilczyński, K.; Szymaniak, Z. Modeling and Experimental Studies for Polyblend Behaviour in Extrusion Process. J. Cent. South Univ. Technol. 2007, 14, 369–371. [Google Scholar] [CrossRef]
- Bingham, E.C. The Viscosity of Binary Mixtures. J. Phys. Chem. 1914, 18, 157–165. [Google Scholar] [CrossRef]
- Heitmiller, R.F.; Naar, R.Z.; Zabusky, H.H. Effect of Homogeneity on Viscosity in Capillary Extrusion of Polyethylene. J. Appl. Polym. Sci. 1964, 8, 873–880. [Google Scholar] [CrossRef]
- Lin, C.C. A Mathematical Model for Viscosity in Capillary Extrusion of Two-Component Polyblends. Polym. J. 1979, 11, 185–192. [Google Scholar] [CrossRef][Green Version]
- Lee, P.C.; Park, H.E.; Morse, D.C.; Macosko, C.W. Polymer-Polymer Interfacial Slip in Multilayered Films. J. Rheol. 2009, 53, 893–915. [Google Scholar] [CrossRef]
- Son, Y. Investigation of Interfacial Slip in Immiscible Polymer Blends. J. Polym. Res. 2011, 18, 2087–2092. [Google Scholar] [CrossRef]
- Komuro, R.; Sukumaran, S.K.; Sugimoto, M.; Koyama, K. Slip at the Interface between Immiscible Polymer Melts I: Method to Measure Slip. Rheol. Acta 2014, 53, 23–30. [Google Scholar] [CrossRef]
- Komuro, R.; Sukumaran, S.K.; Sugimoto, M.; Koyama, K. Slip at the Interface between Immiscible Polymer Melts II: Capillary Flow of Polymers with Unequal Viscosities. Nihon Reoroji Gakkaishi 2014, 42, 151–156. [Google Scholar] [CrossRef][Green Version]
- Schrenk, W.J.; Bradley, N.L.; Alfrey, T.; Maack, H. Interfacial Flow Instability in Multilayer Coextrusion. Polym. Eng. Sci. 1978, 18, 620–623. [Google Scholar] [CrossRef]
- Agassant, J.F.; Demay, Y. Investigation of the Polymer Coextrusion Process: A Review. Polymers 2022, 14, 1309. [Google Scholar] [CrossRef]
- Han, C.D.; Shetty, R. Studies on Multilayer Film Coextrusion II. Interfacial Instability in Flat Film Coextrusion. Polym. Eng. Sci. 1978, 18, 180–186. [Google Scholar] [CrossRef]
- Tsenoglou, C. Viscoelasticity of Binary Homopolymer Blends. ASC Polym. Prepr. 1987, 28, 185–186. [Google Scholar]
- Aydogan, A.; Kneidinger, C.; Zitzenbacher, G. Characterization of the Rheological Behavior of Mixed Miscible Polymers Derived from Recycling Processes. AIP Conf. Proc. 2024. under review. [Google Scholar]
- Arrhenius, S. On the Internal Friction of Dilute Aqueous Solutions—Original Title “Über Die Innere Reibung Verdünnter Wässeriger Lösungen”. Z. Für Phys. Chem. 1887, 1, 285–298. [Google Scholar] [CrossRef]
- Bersted, B.H.; Slee, J.D.; Richter, C.A. Prediction of Rheological Behavior of Branched Polyethylene from Molecular Structure. J. Appl. Polym. Sci. 1981, 26, 1001–1014. [Google Scholar] [CrossRef]
- Friedman, E.M.; Porter, R.S. Polymer viscosity-molecular weight distribution correlations via blending: For high molecular weight poly(dimethyl siloxanes) and for polystyrenes. Trans. Soc. Rheol. 1975, 19, 493–508. [Google Scholar] [CrossRef]
- Kendall, J.; Monroe, K.P. The viscosity of liquids. II. the viscosity-composition curve for ideal liquid mixtures 1. J. Am. Chem. Soc. 1917, 39, 1787–1802. [Google Scholar] [CrossRef]
- Haley, J.C.; Lodge, T.P. A Framework for Predicting the Viscosity of Miscible Polymer Blends. J. Rheol. 2004, 48, 463–486. [Google Scholar] [CrossRef]
- Haley, J.C.; Lodge, T.P. Viscosity Predictions for Model Miscible Polymer Blends: Including Self-Concentration, Double Reptation, and Tube Dilation. J. Rheol. 2005, 49, 1277–1302. [Google Scholar] [CrossRef]
- Walther, C. The Evaluation of Viscosity Data. Erdol. Teer 1931, 7, 382–384. [Google Scholar]
- Gao, Y.; Li, K. New Models for Calculating the Viscosity of Mixed Oil. Fuel 2012, 95, 431–437. [Google Scholar] [CrossRef]
- Cragoe, C.S. Changes in the Viscosity of Liquids with Temperature, Pressure and Composition. In Proceedings of the World Petroleum Congress Proceedings, London, UK, 18–24 July 1933; Volume 1933. [Google Scholar]
- Utracki, L.A.; Wilkie, C.A. Polymer Blends Handbook, 2nd ed.; Utracki, L.A., Wilkie, C.A., Eds.; Springer Science + Business Media, LLC: Boston, MA, USA, 2014; ISBN 978-94-007-6063-9. [Google Scholar]
- DIN EN ISO 20753:2019; Plastics—Test Specimens. Original title: Kunststoffe-Probekörper; Beuth: Berlin, Germany, 2019.
- DIN EN ISO 179-2; Charpy Impact Strength and Charpy Notched Impact Strength of Plastics. Original Title: Charpy Schlagzähigkeit und Charpy Kerbschlagzähigkeit von Kunststoffen; Austrian Standards International: Vienna, Austria, 2023.
- Bagley, E.B. End Corrections in the Capillary Flow of Polyethylene. J. Appl. Phys. 1957, 28, 624–627. [Google Scholar] [CrossRef]
- Rabinowitsch, B. Über Die Viskosität Und Elastizität von Solen. Z. Für Phys. Chem. 1929, 145A, 1–26. [Google Scholar] [CrossRef]
- Yasuda, K. Investigation of the Analogies between Viscometric and Linear Viscoelastic Properties of Polystyrene Fluids. Ph.D. Thesis, MIT—Massachusetts Institute of Technology, Cambridge, MA USA, 1979. [Google Scholar]
- Kneidinger, C. How to Apply Carreaus Approach without CFD-Tools. AIP Conf. Proc. 2023, 2607, 160001. [Google Scholar] [CrossRef]
- Kneidinger, C.; Laengauer, M.; Mayrhofer, E.; Zitzenbacher, G.; Miethlinger, J. Simulation of Asymmetrical Multilayer Flat Film Coextrusion Regarding Slip at the Wall and Interfacial Slip at the Polymer-Polymer Interface. AIP Conf. Proc. 2019, 2055, 040004. [Google Scholar] [CrossRef]
- Zhao, R.; Macosko, C.W. Slip at Polymer–Polymer Interfaces: Rheological Measurements on Coextruded Multilayers. J. Rheol. 2002, 46, 145–167. [Google Scholar] [CrossRef]
- Lam, Y.C.; Jiang, L.; Yue, C.Y.; Tam, K.C.; Li, L.; Hu, X. Interfacial Slip between Polymer Melts Studied by Confocal Microscopy and Rheological Measurements. J. Rheol. 2003, 47, 795–807. [Google Scholar] [CrossRef]
- Lee, P.C.; Park, H.E.; Macosko, C.W.; Co, A.; Leal, G.L.; Colby, R.H.; Giacomin, A.J. Direct and Indirect Polymer-Polymer Interfacial Slip Measurements in Multilayered Films. AIP Conf. Proc. 2008, 1027, 1072–1074. [Google Scholar]
- Lo, T.S.; Mihajlovic, M.; Shnidman, Y.; Li, W.; Gersappe, D. Interfacial Slip in Sheared Polymer Blends. Phys. Rev. E 2005, 72, 040801. [Google Scholar] [CrossRef]
- Zhang, J.; Lodge, T.P.; Macosko, C.W. Interfacial Slip Reduces Polymer-Polymer Adhesion during Coextrusion. J. Rheol. 2006, 50, 41–57. [Google Scholar] [CrossRef]








| Grade | Abbreviation | MFR/MVR 1 | Processing Temperature 1 |
|---|---|---|---|
| PP HB600TF | PP1 | 2 g/10 min (230 °C/2.16 kg) | 200–260 °C |
| PP HD234CF | PP2 | 8 g/10 min (230 °C/2.16 kg) | N.A. |
| PA12 Grilamid L25 | PA12 | 20 cm3/10 min (275 °C/5 kg) | 230–250 °C |
| Orevac CA 100 | PPgMAH | 10 g/10 min (190 °C/0.325 kg) | Wide range |
| Base Polymer | Concentration Base Polymer (wt%) | Contaminating Polymer | Concentration Contaminating Polymer (wt%) | Coupling Agent | Concentration Coupling Agent (wt%) |
|---|---|---|---|---|---|
| PP1 | 79.2 | PA12 | 20 | PPgMAH | 0.8 |
| PP1 | 78.4 | PA12 | 20 | PPgMAH | 1.6 |
| PP1 | 77.6 | PA12 | 20 | PPgMAH | 2.4 |
| PP1 | 76.8 | PA12 | 20 | PPgMAH | 3.2 |
| PP1 | 76.0 | PA12 | 20 | PPgMAH | 4.0 |
| Base Polymer | Concentration Base Polymer (wt%) | Contaminating Polymer | Concentration Contaminating Polymer (wt%) | Coupling Agent | Concentration Coupling Agent (wt%) |
|---|---|---|---|---|---|
| PP1 | 100 | - | - | - | - |
| PP1 | 90 | PP2 | 10 | - | - |
| PP1 | 80 | PP2 | 20 | - | - |
| PP1 | 70 | PP2 | 30 | - | - |
| PP1 | 50 | PP2 | 50 | - | - |
| PP1 | 30 | PP2 | 70 | - | - |
| PP1 | 10 | PP2 | 90 | - | - |
| PP2 | 100 | - | - | - | - |
| PP1 | 95 | PA12 | 5 | - | - |
| PP1 | 90 | PA12 | 10 | - | - |
| PP1 | 85 | PA12 | 15 | - | - |
| PP1 | 80 | PA12 | 20 | - | - |
| PP1 | 96 | - | - | PPgMAH | 4.00 |
| PP1 * | 91.20 | PA12 | 5 | PPgMAH | 3.80 |
| PP1 * | 86.40 | PA12 | 10 | PPgMAH | 3.60 |
| PP1 * | 81.60 | PA12 | 15 | PPgMAH | 3.40 |
| PP1 * | 76.80 | PA12 | 20 | PPgMAH | 3.20 |
| PA12 | 100 | - | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kneidinger, C.; Wagner, E.; Längauer, M.; Zitzenbacher, G. Estimation of the Shear Viscosity of Mixed-Polymer Materials for Screw Extrusion-Based Recycling Process Modeling. Polymers 2024, 16, 1339. https://doi.org/10.3390/polym16101339
Kneidinger C, Wagner E, Längauer M, Zitzenbacher G. Estimation of the Shear Viscosity of Mixed-Polymer Materials for Screw Extrusion-Based Recycling Process Modeling. Polymers. 2024; 16(10):1339. https://doi.org/10.3390/polym16101339
Chicago/Turabian StyleKneidinger, Christian, Emil Wagner, Manuel Längauer, and Gernot Zitzenbacher. 2024. "Estimation of the Shear Viscosity of Mixed-Polymer Materials for Screw Extrusion-Based Recycling Process Modeling" Polymers 16, no. 10: 1339. https://doi.org/10.3390/polym16101339
APA StyleKneidinger, C., Wagner, E., Längauer, M., & Zitzenbacher, G. (2024). Estimation of the Shear Viscosity of Mixed-Polymer Materials for Screw Extrusion-Based Recycling Process Modeling. Polymers, 16(10), 1339. https://doi.org/10.3390/polym16101339










