Prediction of Short- to Long-Term Cyclic Deformation Behavior and Fatigue Life of Polymers
Abstract
1. Introduction
2. Material and Methods
Tests
- -
- cyclic fatigue tests at Hz (sinusoidal, force-control) until rupture at the stress ratios , , and 0.5. The maximum stresses were 25, 35, and 50% of the rupture (ultimate) stress, 60 MPa, for , 15, 37.5, 50, 75, 90, and 97% for , and 37.5, 50, 75, 90, and 97% for .
3. Theory-Modeling
3.1. Kinematics and Constitutive Theory
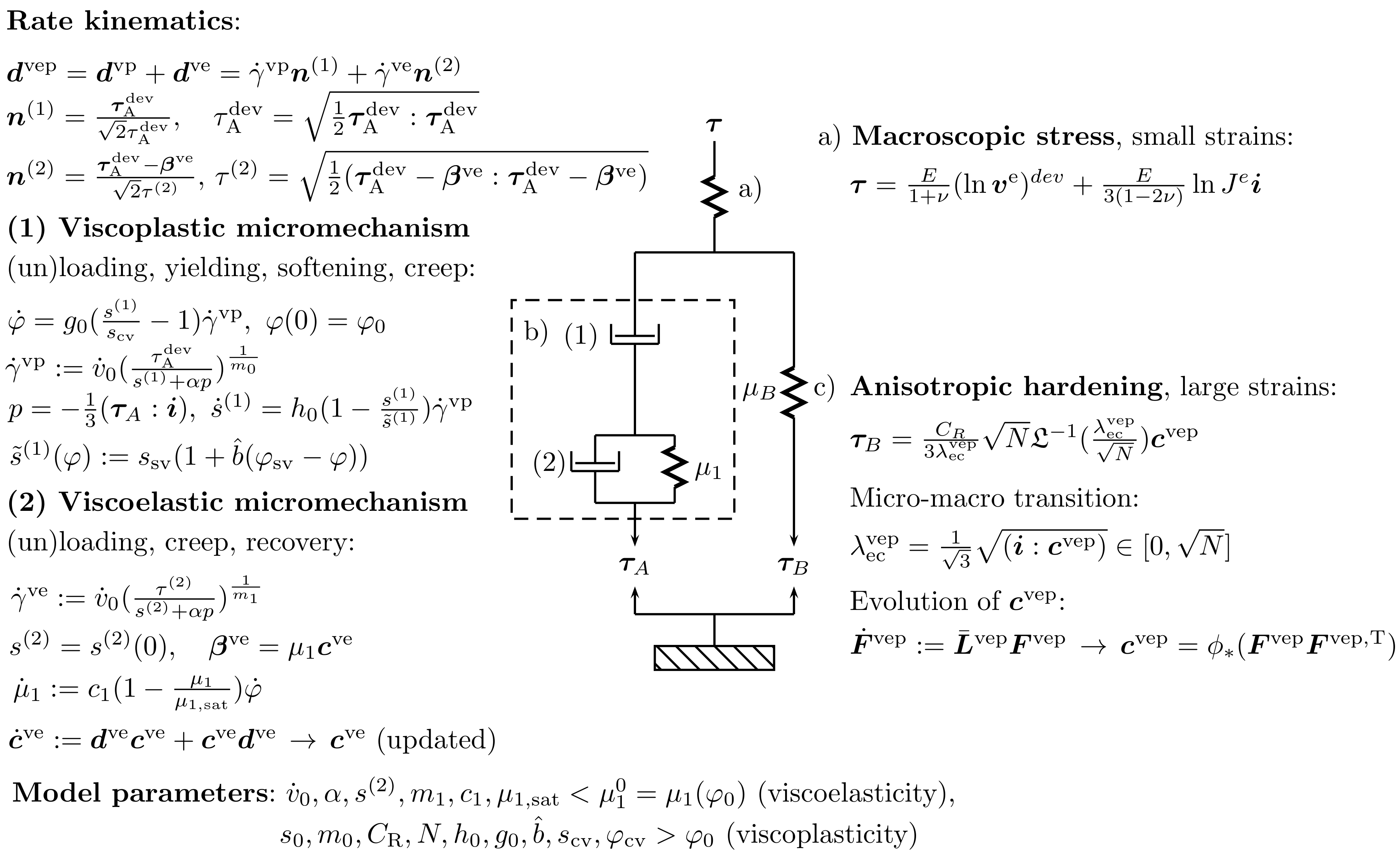
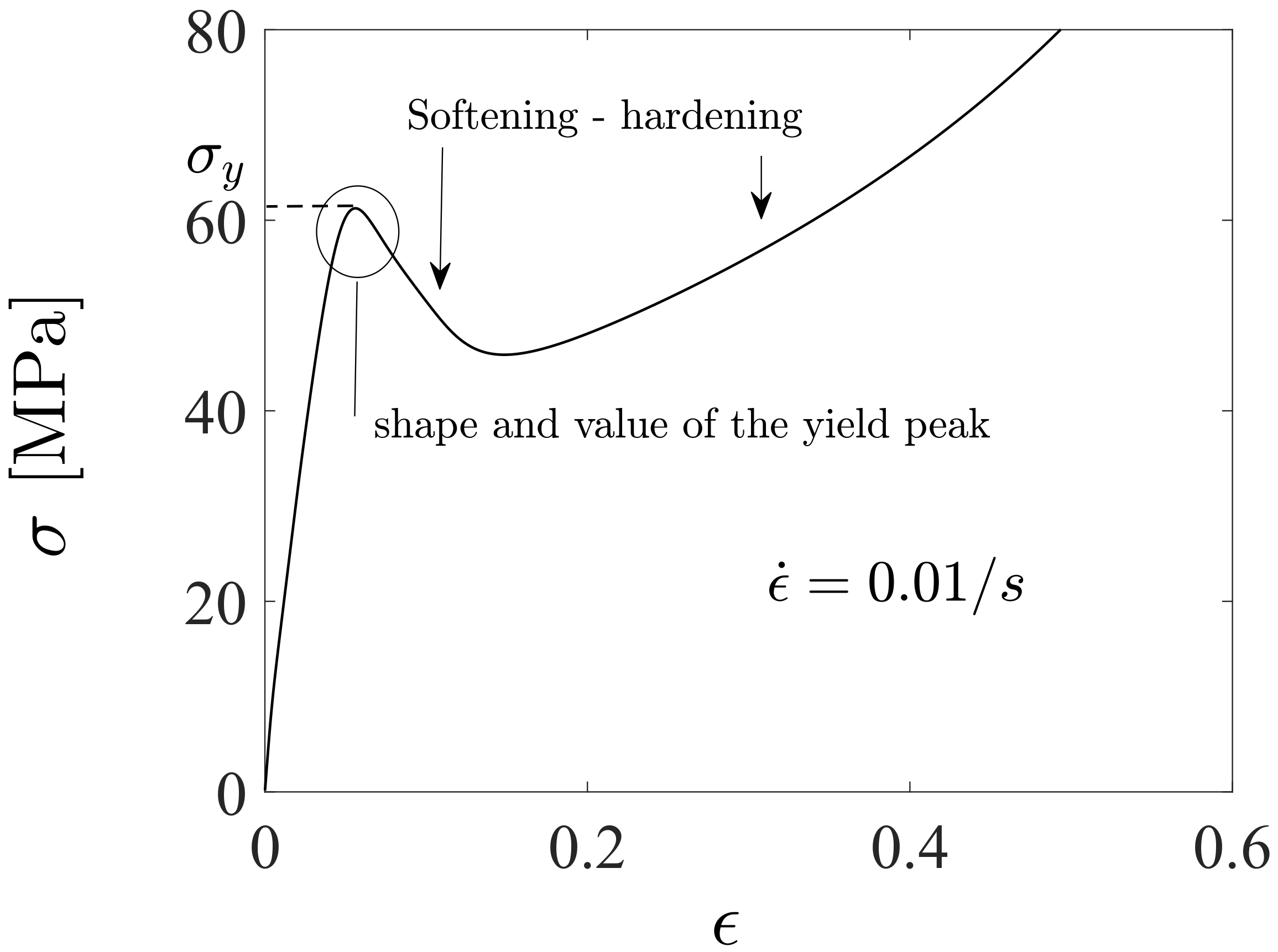
3.2. Prediction of Fatigue Life
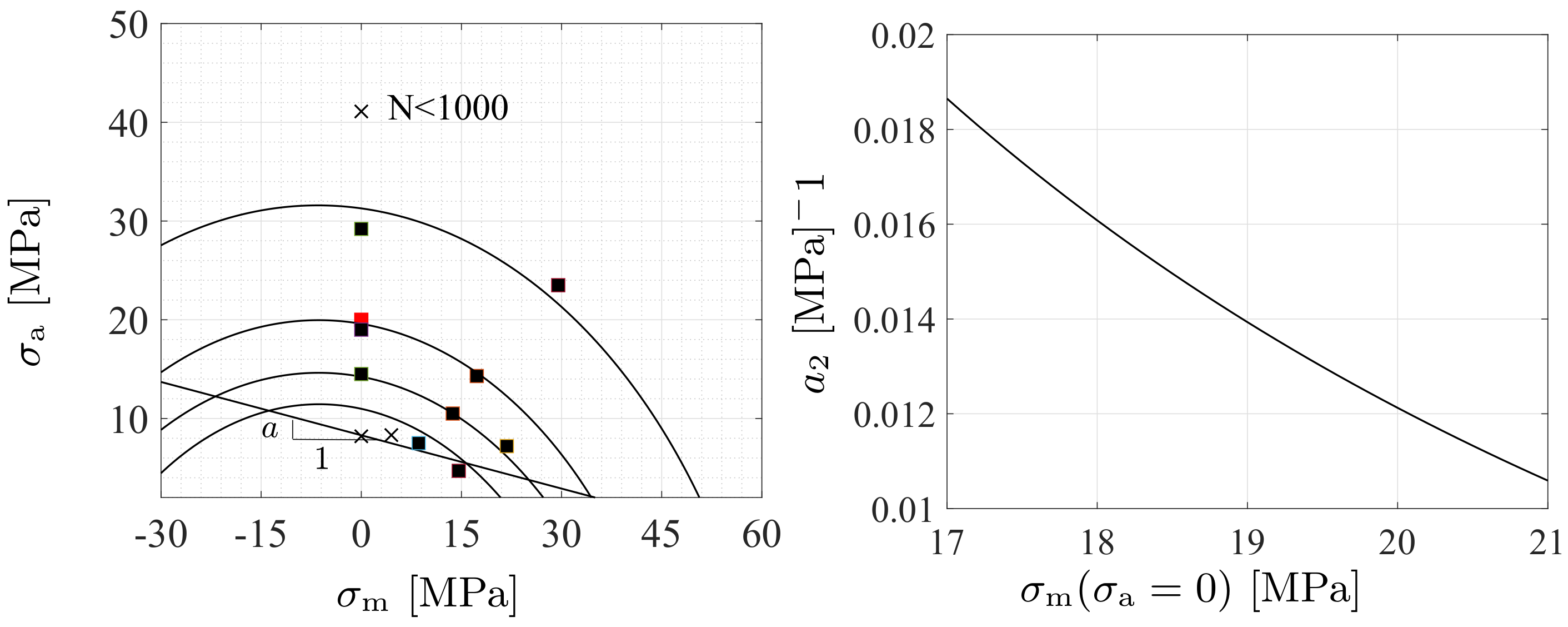
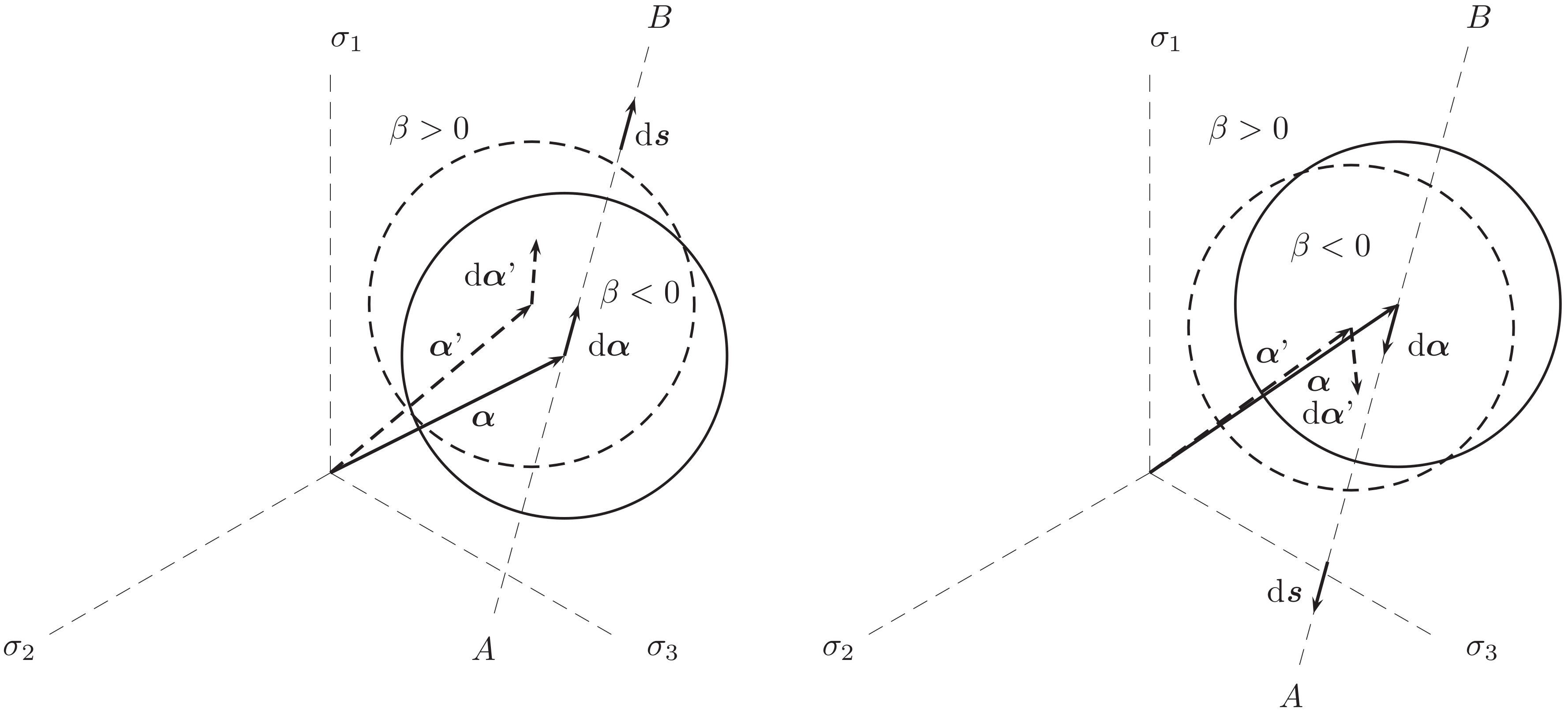
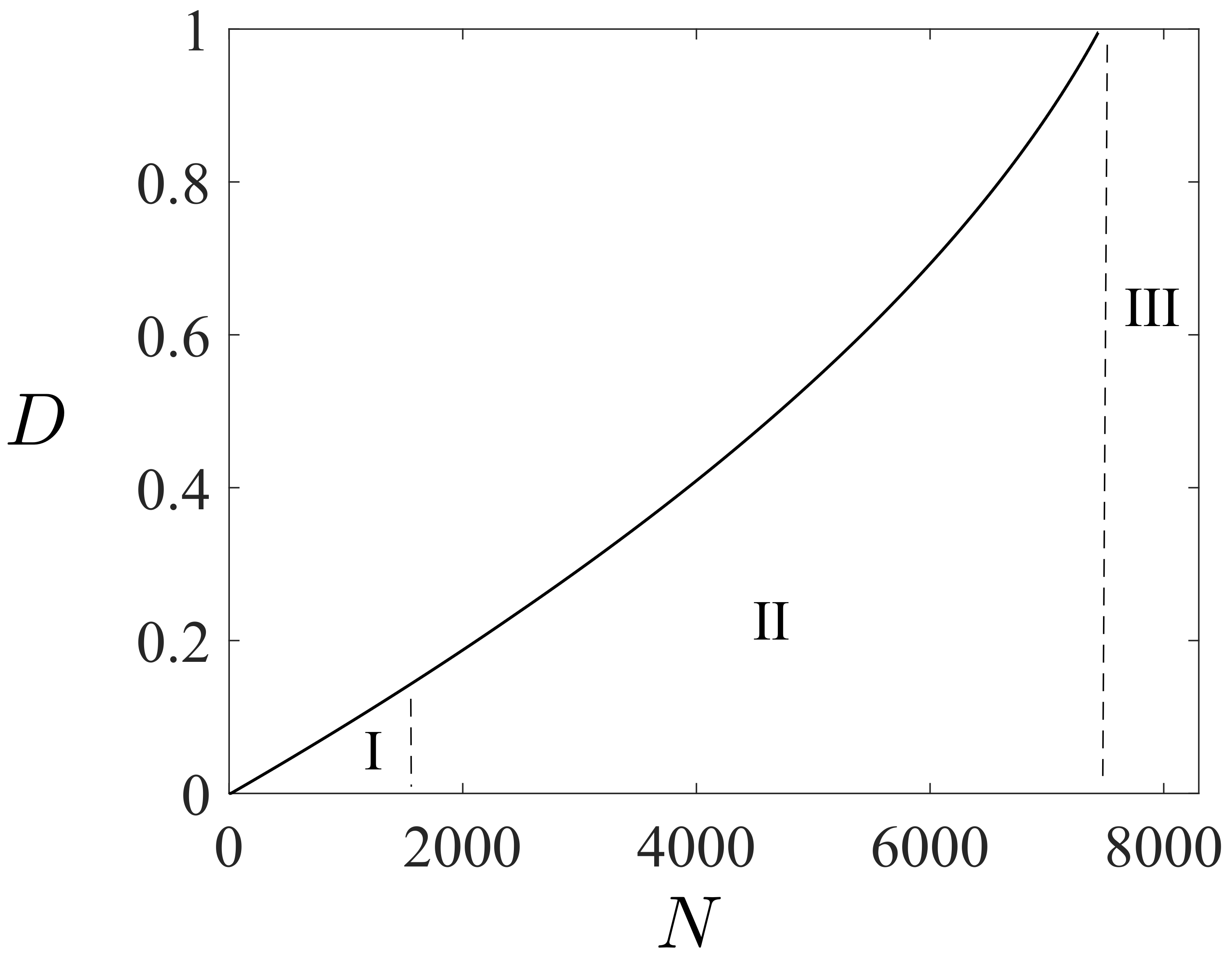
Fatigue Damage Evolution
3.3. Model Calibration
3.3.1. Constitutive Model Parameters
3.3.2. Fatigue Model Parameters
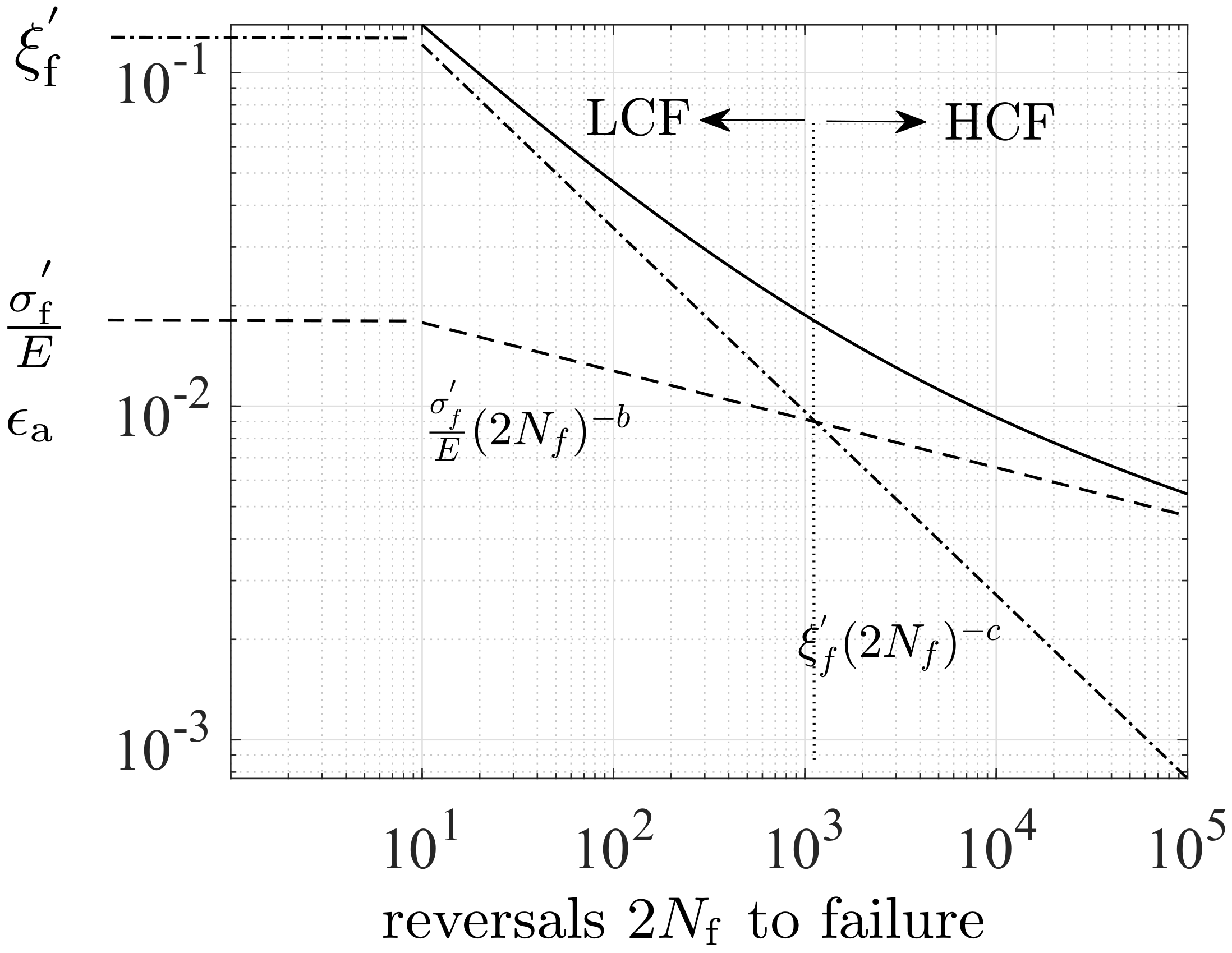
Polymer vs. Metal Fatigue Parameters
HCF Region
LCF Region
4. Results
4.1. Fatigue Parameter Values and Sensitivity

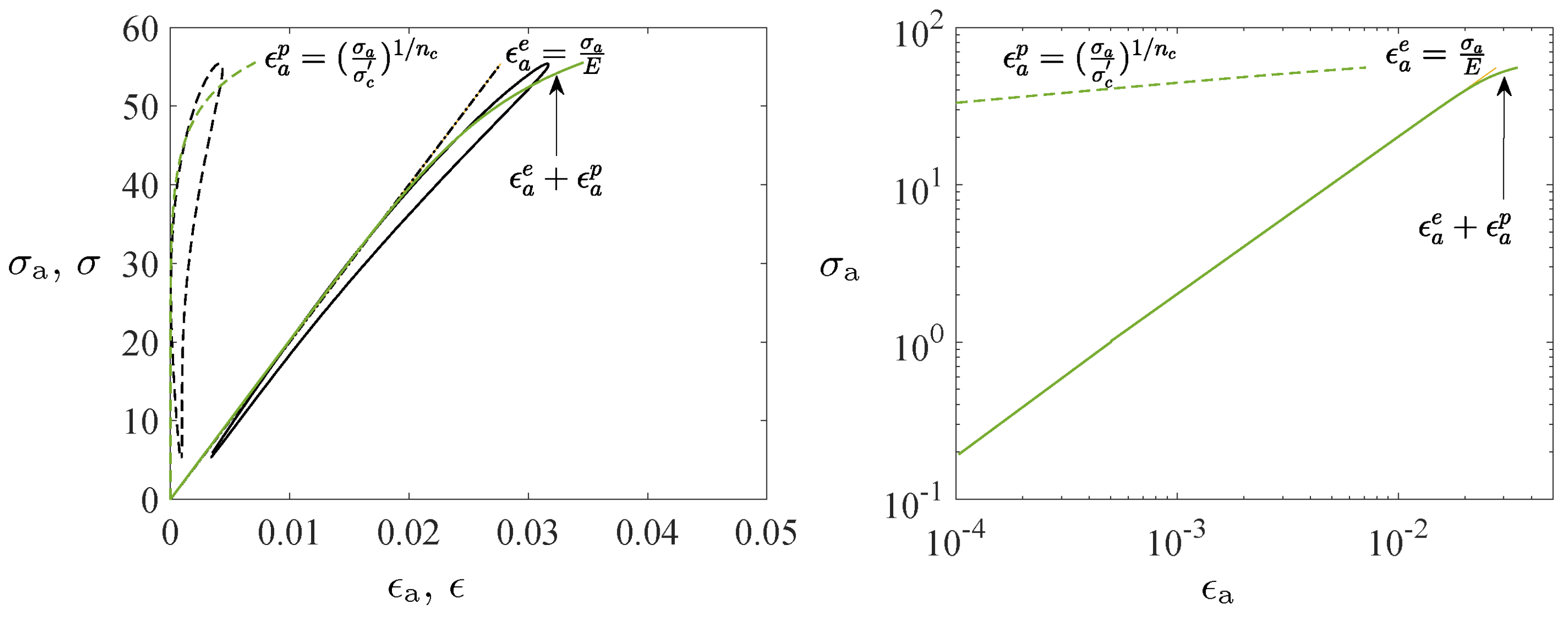
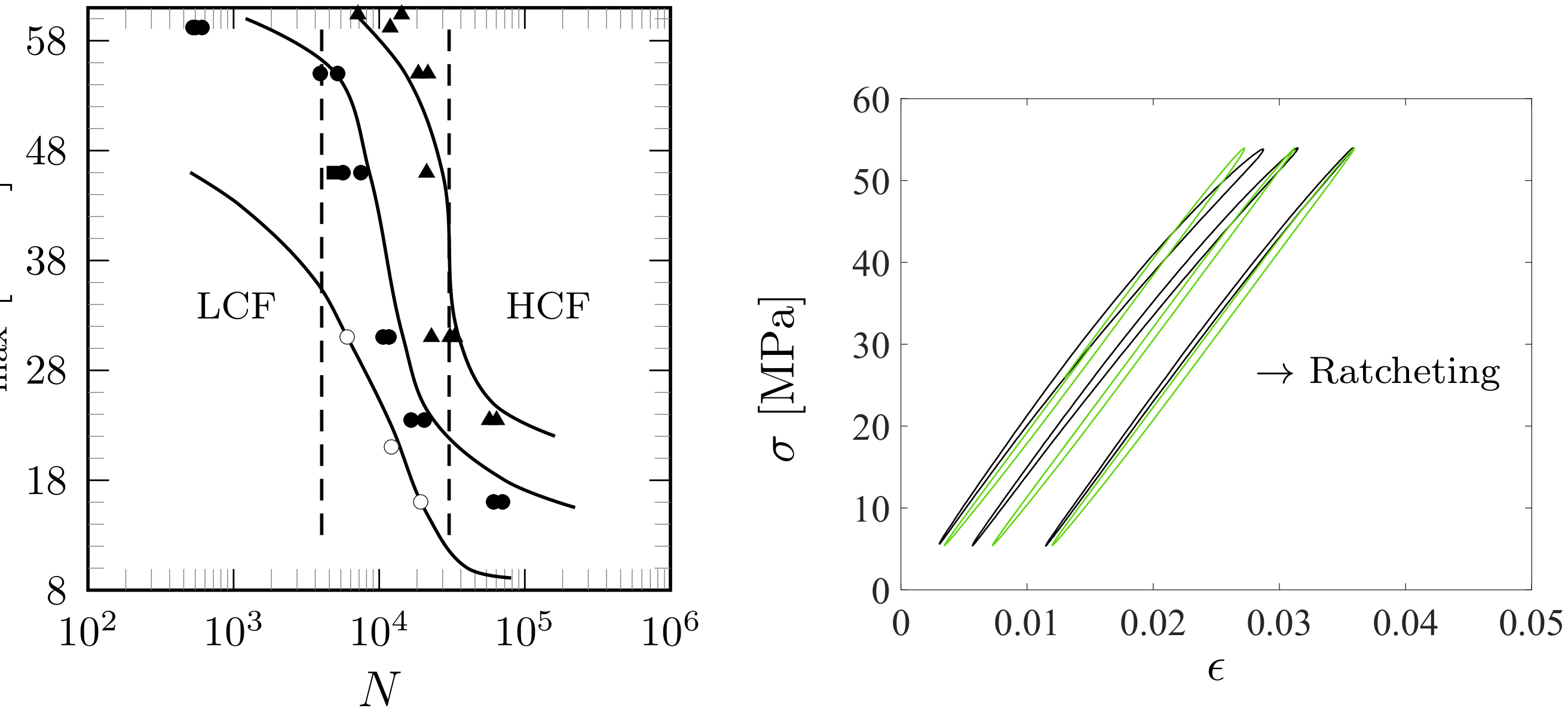
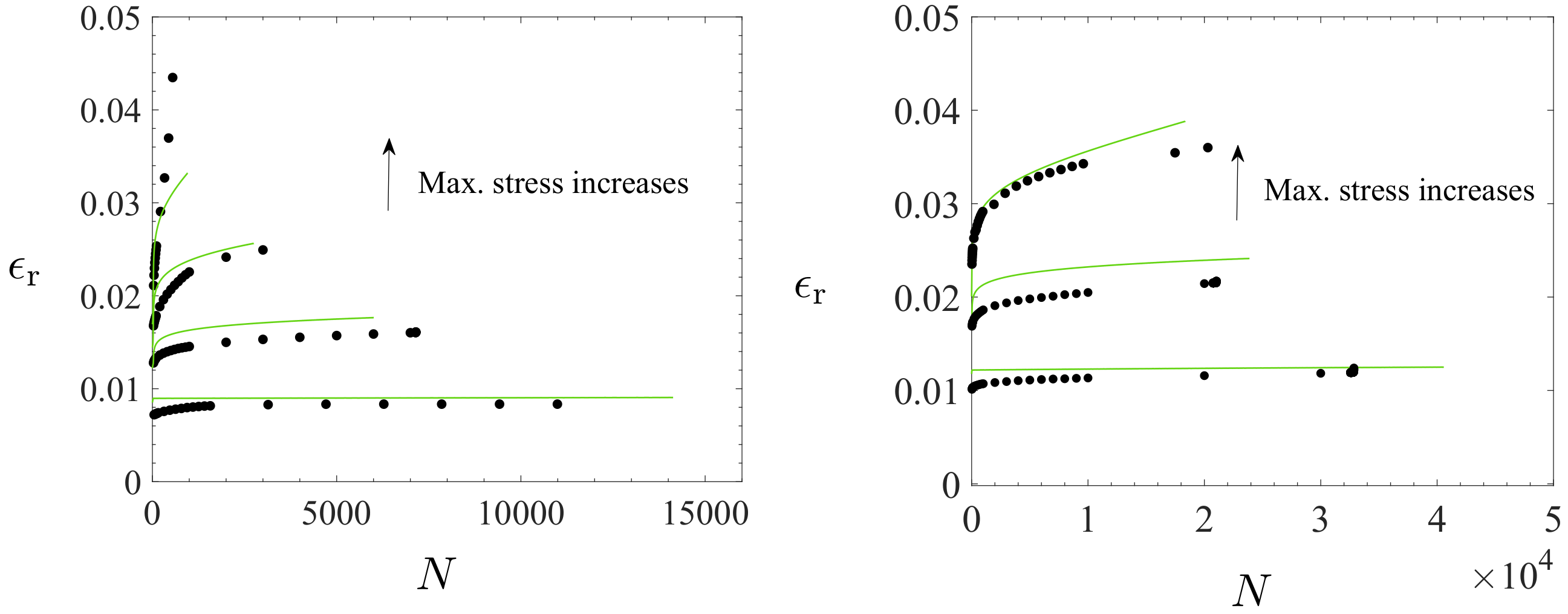
4.2. Macrostructural Aspects
4.3. Microstructural Aspects
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| uniaxial strain | |
| F | deformation gradient |
| stress and its deviatoric component | |
| true stress range vs. number of cycles N to failure | |
| peak yield stress | |
| ultimate tensile strength | |
| stress amplitude | |
| mean stress | |
| endurance function | |
| equivalent stress | |
| fatigue variable (kinematic) | |
| model (material) parameter | |
| fatigue strengths for alternating and pulsating uniaxial loads | |
| function in for the mean stress | |
| first stress invariant | |
| slope parameters of the Haigh diagram for low and high values of | |
| D | fatigue damage |
| HCF, LCF | high-cycle fatigue, low-cycle fatigue |
| fatigue damage parameters for HCF | |
| fatigue damage parameters for LCF | |
| stress ratio | |
| stress ratio | |
| parameters of Basquin equation | |
| parameters of Coffin-Manson formula | |
| parameters of Ramberg-Osgood formula | |
| ratcheting strain | |
| SBs | Shear bands |
Appendix A. Integration of the Fatigue Model
References
- SkyQuest. Global Polymer Market; Technical Report, Report ID: SQSG15E2004; SkyQuest Technology Consulting Pvt. Ltd.: London, UK, 2022. [Google Scholar]
- Beesley, R.; Chen, H.; Hughes, M. A novel simulation for the design of a low cycle fatigue experimental testing programme. Comput. Struct. 2017, 178, 105–118. [Google Scholar] [CrossRef]
- Liaw, P.K.; Chen, P.; Lee, C.; Wang, S.Y.; Seifi, M.; Lewandowski, J.J.; Dahmen, K.A. Fatigue behavior of high-entropy alloys: A review. Sci. China Technol. Sci. 2018, 61, 168–178. [Google Scholar]
- Ritchie, R.O. Mechanisms of fatigue-crack propagation in ductile and brittle solids. Int. J. Fract. 1999, 100, 55–83. [Google Scholar] [CrossRef]
- Acharya, P.; Ebrahimian, H.; Moustafa, M.A. Behavior study of commercial polyurea under monotonic, rate dependent, cyclic, and fatigue tensile loading for potential structural applications. Polymers 2022, 14, 1878. [Google Scholar] [CrossRef] [PubMed]
- Gawel, A.; Kuciel, S.; Liber-Kneé, A.; Mierzwiáski, D. Examination of low-cyclic fatigue tests and poisson’s ratio depending on the different infill density of polylactide (PLA) produced by the fused deposition modeling method. Polymers 2023, 15, 1651. [Google Scholar] [CrossRef] [PubMed]
- Barriere, T.; Gabrion, X.; Holopainen, S.; Jokinen, J. Testing and analysis of solid polymers under large monotonic and long-term cyclic deformation. Int. J. Plast. 2020, 135, 102781. [Google Scholar] [CrossRef]
- Chen, K.; Kang, G.; Yu, C.; Jiang, H. Effect of crystalline content on ratchetting of ultra-high molecular weight polyethylene polymers: Experimental investigation and constitutive model. Mech. Mater. 2019, 113, 37–54. [Google Scholar] [CrossRef]
- Holopainen, S.; Barriere, T. Modeling of mechanical behavior of amorphous solids undergoing fatigue loadings, with application to polymers. Comput. Struct. 2018, 199, 57–73. [Google Scholar] [CrossRef]
- Qi, Z.; Hu, N.; Li, G.; Zeng, D.; Su, X. Constitutive modeling for the elastic-viscoplastic behavior of high density polyethylene under cyclic loading. Int. J. Plast. 2019, 113, 125–144. [Google Scholar] [CrossRef]
- Zhu, D.; Zhang, W.; Ding, Z. A modified fatigue damage model considering loading sequence effect. Int. J. Damage Mech. 2022, 31, 1027–1056. [Google Scholar] [CrossRef]
- Alves, A.F.C.; Ferreira, B.P.; Pires, F. A constitutive model for amorphous thermoplastics from low to high strain rates: Formulation and computational aspects. Int. J. Plast. 2023, 169, 103712. [Google Scholar] [CrossRef]
- Chudnovsky, A.; Zhou, Z.; Zhang, H.; Sehanobish, K. Lifetime assessment of engineering thermoplastics. Int. J. Eng. Sci. 2012, 59, 108–139. [Google Scholar] [CrossRef]
- Khaleghi, H.; Amiri-Rad, A.; Mashayekhi, M. A thermodynamically consistent continuum damage model for time-dependent failure of thermoplastic polymers. Int. J. Plastic. 2022, 154, 103278. [Google Scholar] [CrossRef]
- Lan, T.; Jiang, Y.; Wu, P. A thermodynamically-based constitutive theory for amorphous glassy polymers at finite deformations. Int. J. Plast. 2022, 158, 103415. [Google Scholar] [CrossRef]
- Laschuetza, T.; Seelig, T. A continuum-micromechanical model for crazing in glassy polymers under cyclic loading. Mech. Mater. 2024, 189, 104901. [Google Scholar] [CrossRef]
- Song, R.; Muliana, A.; Rajagopa, K. A thermodynamically consistent model for viscoelastic polymers undergoing microstructural changes. Int. J. Eng. Sci. 2019, 142, 106–124. [Google Scholar] [CrossRef]
- Wang, J.; Peng, L.F.; Deng, Y.J.; Lai, X.M.; Fu, M.W.; Ni, J. A finite strain thermodynamically-based constitutive modeling and analysis of viscoelastic-viscoplastic deformation behavior of glassy polymers. Int. J. Plast. 2019, 122, 135–163. [Google Scholar] [CrossRef]
- Shojaei, A.K.; Volgers, P. A coupled hyperelastic-plastic-continuum damage model for studying cyclic behavior of unfilled engineering polymers. Int. J. Fatigue 2018, 107, 33–39. [Google Scholar] [CrossRef]
- Salazar, A.; Cano, A.J.; Rodríguez, J. Mechanical and fatigue behaviour of polyamide 12 processed via injection moulding and selective laser sintering: Analysis based on Kitagawa-Takahashi diagrams. Eng. Fract. Mech. 2022, 275, 108825. [Google Scholar] [CrossRef]
- Anand, L.; Ames, N.M. On modeling the micro-indentation response of an amorphous polymer. Int. J. Plast. 2006, 22, 1123–1170. [Google Scholar] [CrossRef]
- Barriere, T.; Gabrion, X.; Holopainen, S. A compact constitutive model to describe the viscoelastic-plastic behaviour of glassy polymers: Comparison with monotonic and cyclic experiments and state-of-the-art models. Int. J. Plast. 2019, 122, 31–48. [Google Scholar] [CrossRef]
- Janssen, R.P.M.; Govaert, L.E.; Meijer, H.E.H. An analytical method to predict fatigue life of thermoplastics in uniaxial loading: Sensitivity to wave type, frequency, and stress amplitude. Macromolecules 2008, 41, 2531–2540. [Google Scholar] [CrossRef]
- Jiang, C.K.; Jiang, H.; Zhang, J.W.; Kang, G.Z. A viscoelasticplastic constitutive model for uniaxial ratcheting behaviors of polycarbonate. Polym. Eng. Sci. 2015, 55, 2559–2565. [Google Scholar] [CrossRef]
- Fatemi, A.; Yang, L. Cumulative fatigue damage and life prediction theories: A survey of the state of the art for homogeneous materials. Int. J. Fatigue 1998, 20, 9–34. [Google Scholar] [CrossRef]
- Zengah, S.; Aid, A.; Benguediab, M. Comparative study of fatigue damage models using different number of classes combined with the rainflow method. Eng. Technol. Appl. Sci. Res. 2013, 3, 446–451. [Google Scholar] [CrossRef]
- Elkin, A.; Gaibel, V.; Dzhurinskiy, D.; Sergeichev, I. A multiaxial fatigue damage model based on constant life diagrams for polymer fiber-reinforced laminates. Polymers 2022, 14, 4985. [Google Scholar] [CrossRef] [PubMed]
- Ottosen, N.; Stenström, R.; Ristinmaa, M. Continuum approach to high-cycle fatigue modeling. Int. J. Fatigue 2008, 30, 996–1006. [Google Scholar] [CrossRef]
- Lampman, S.R. ASM Handbook: Fatigue and Fracture, 1st ed.; ASM International: Almere, The Netherlands, 1996. [Google Scholar]
- Murakami, Y. Metal Fatigue: Effects of Small Defects and Nonmetallic Inclusions; Elsevier: Amsterdam, The Netherlands; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Huang, J.S.; Lin, J.Y. Fatigue of cellular materials. Acta Mater. 1996, 44, 289–296. [Google Scholar] [CrossRef]
- Chen, G.; Liang, H.Q.; Wang, L.; Mei, Y.H.; Chen, X. Multiaxial ratcheting-fatigue interaction on acrylonitrile-butadiene-styrene terpolymer. Polym. Eng. Sci. 2015, 55, 664–671. [Google Scholar] [CrossRef]
- Hughes, J.M.; Lugo, M.; Bouvard, J.L.; McIntyre, T.; Horstemeyer, M.F. Cyclic behavior and modeling of small fatigue cracks of a polycarbonate polymer. Int. J. Fatigue 2017, 99, 78–86. [Google Scholar] [CrossRef]
- Lugo, M.; Fountain, J.E.; Hughes, J.M.; Bouvard, J.L.; Horstemayer, M.F. Microstructure-based fatigue modeling of an acrylonitrile butadiene styrene (abs) copolymer. J. Appl. Polym. Sci. 2014, 131, 1–12. [Google Scholar] [CrossRef]
- Hofmann, D.C.; Suh, J.Y.; Wiest, A.; Duan, G.; Lind, M.L.; Demetriou, M.D.; Johnson, W.L. Designing metallic glass matrix composites with high toughness and tensile ductility. Nature 2008, 451, 1085. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.; Lee, H.; Lee, H.; Kim, N. A methodology to predict the fatigue life under multi-axial loading of carbon fiber-reinforced polymer composites considering anisotropic mechanical behavior. Materials 2023, 16, 1952. [Google Scholar] [CrossRef] [PubMed]
- Holzweber, J.; Müllerb, J.; Çakmaka, U.D.; Major, Z. Characterization and modeling of the fatigue behavior of TPU. Mater. Today Proc. 2018, 5, 26572–26577. [Google Scholar] [CrossRef][Green Version]
- Barriere, T.; Bernard, F.; Gabrion, X.; Carbillet, S.; Holopainen, S.; Niang, N.; Pelletier, J.M.; Wang, W.H. Super ductile metallic glasses for energy-saving solid-state processing. Mater. Des. 2023, 232, 112112. [Google Scholar] [CrossRef]
- Mao, H.; Mahadevan, S. Fatigue damage modelling of composite materials. Compos. Struct. 2002, 58, 405–410. [Google Scholar] [CrossRef]
- ASTM D638; Designation: D 638-03. Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshohocken, PA, USA, 2003; pp. 1–15.
- ASTM E2207; Standard Practice for Strain-Controlled Axial-Torsional Fatigue Testing with Thin- Walled Tubular Specimens. ASTM International: West Conshohocken, PA, USA, 2002; pp. 1–8.
- ASTM D2990; Standard Test Methods for Tensile, Compressive, and Flexural Creep and Creep- Rupture of Plastics. ASTM International: West Conshohocken, PA, USA, 2001; pp. 1–20.
- Anand, L.; Gurtin, M.E. A theory of amorphous solids undergoing large deformations with application to polymer glasses. Int. J. Solids Struct. 2003, 40, 1465–1487. [Google Scholar] [CrossRef]
- Venkatesan, S.; Basu, S. Investigations into crazing in glassy amorphous polymers through molecular dynamics simulations. J. Mech. Phys. Solids 2015, 77, 123–145. [Google Scholar] [CrossRef]
- Zirak, N.; Tcharkhtchi, A. Fatigue life prediction for amorphous glassy polymers based on cumulative evolution of micro-defects. Int. J. Fatigue 2023, 167, 107360. [Google Scholar] [CrossRef]
- Barriere, T.; Gabrion, X.; Imane, N.; Holopainen, S. Mechanical degradation and fatigue life of amorphous polymers. Procedia Struct. Integr. 2024, 52, 105–110. [Google Scholar] [CrossRef]
- Bowman, A.L.; Mun, S.; Nouranian, S.; Huddleston, B.; Gwaltney, S.; Baskes, M.; Horstemeyer, M. Free volume and internal structural evolution during creep in model amorphous polyethylene by Molecular Dynamics simulations. Polymers 2019, 170, 85–100. [Google Scholar] [CrossRef]
- Haward, R.N.; Thackray, G. The use of a mathematical model to describe isothermal stress-strain curves in glassy thermoplastics. Proc. Roy. Soc. A 1968, 302, 453–472. [Google Scholar]
- Boyce, M.C.; Weber, G.G.; Parks, D.M. On the kinematics of finite strain plasticity. J. Mech. Phys. Solids 1989, 37, 647–665. [Google Scholar] [CrossRef]
- Kermajani, M.; Ghaini, F.M.; Miresmaeili, R.; Baghi-abadi, M.K.; Mousavi-nasab, M. Damage mechanisms in the ultra-low cycle fatigue loading. Eng. Fract. Mech. 2020, 223, 106772. [Google Scholar] [CrossRef]
- Lampman, S.R. Properties and Selection: Irons, Steels, and High-Performance Alloys, 10th ed.; ASM International: Almere, The Netherlands, 1990. [Google Scholar]
- Dong, Q.; Shi, X.; Tong, D.; Liu, F.; Wang, L.; Zhao, L. Crack initiation life model for compression-compression low cycle fatigue based on damage mechanics. Int. J. Fatigue 2023, 169, 107495. [Google Scholar] [CrossRef]
- Ramkumar, A.; Kannan, K.; Gnanamoorthy, R. Experimental and theoretical investigation of a polymer subjected to cyclic loading conditions. Int. J. Eng. Sci. 2010, 48, 101–110. [Google Scholar] [CrossRef]
- Chaboche, J.L. Thermodynamic formulation of constitutive equations and application to the viscoplasticity and viscoelasticity of metals and polymers. Int. J. Solids Struct. 1997, 34, 2239–2254. [Google Scholar] [CrossRef]
- Holopainen, S.; Barriere, T.; Cheng, G.; Kouhia, R. Continuum approach for modeling fatigue in amorphous glassy polymers. applications to the investigation of damage-ratcheting interaction in polycarbonate. Int. J. Plast. 2017, 91, 109–133. [Google Scholar] [CrossRef]
- Lu, Z.; Feng, B.; Loh, C. Fatigue behaviour and mean stress effect of thermoplastic polymers and composites. Frattura ed Integrità Strutturale 2018, 46, 150–157. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Ellingwood, B. Continuum damage mechanics analysis of fatigue crack initiation. Int. J. Fatigue 1998, 20, 631–639. [Google Scholar] [CrossRef]
- Janssen, R.P.M.; Kanter, D.K.; Govaert, L.E.; Meijer, H.E.H. Fatigue life predictions for glassy polymers: A constitutive approach. Macromolecules 2008, 41, 2520–2530. [Google Scholar] [CrossRef]
- Marissen, R.; Schudy, D.; Kemp, A.V.J.M.; Coolen, S.M.H.; Duijzings, W.G.; der Pol, A.V.; Gulick, A.J.V. The effect of material defects on the fatigue behaviour and the fracture strain of ABS. J. Mater. Sci. 2001, 36, 4167–4180. [Google Scholar] [CrossRef]
- Launeya, M.E.; Hofmann, D.C.; Johnson, W.L.; Ritchie, R.O. Solution to the problem of the poor cyclic fatigue resistance of bulk metallic glasses. Proc. Natl. Acad. Sci. USA 2009, 106, 4986–4991. [Google Scholar] [CrossRef] [PubMed]
- Chaboche, J.L.; Lesne, P.M. A non-linear continuous fatigue damage model. Fatigue Fract. Engng Mater. Struct. 1988, 11, 1–17. [Google Scholar] [CrossRef]
- Lemaitre, J.; Chaboche, J.L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Marc, M.; Jean, L.; Christophe, P.; Ludovic, V.; Nathalie, B.; Pierre-Olivier, B. Impact of strain rate sensitivity on the identification of the material parameters scattering and on the formability of zinc sheet. Int. J. Mater. Form. 2020, 13, 203–218. [Google Scholar]
- Ferreira, B.P.; Alves, A.F.C.; Pires, F. An efficient finite strain constitutive model for amorphous thermoplastics: Fully implicit computational implementation and optimization-based parameter calibration. Comput Struct. 2023, 281, 107007. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C.; Quintus-Bosz, H. Effects of initial anisotropy on the finite strain deformation behavior of glassy polymers. Int. J. Plast. 1993, 9, 783–811. [Google Scholar] [CrossRef]
- Nieslony, A.; Dsoki, C.E.; Kaufmann, H.; Krug, P. New method for evaluation of the Manson-Coffin-Basquin and Ramberg-Osgood equations with respect to compatibility. Int. J. Fatigue 2008, 30, 1967–1977. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, G.; Gao, Y.; Niu, P.; Li, Y. Development of improved Manson-Coffin model considering the effect of yield stress under asymmetrical cyclic loading. J. Mech. Sci. Technol. 2021, 35, 5415–5424. [Google Scholar] [CrossRef]
- Lesser, A.J. Fatigue behavior of polymers. In Encyclopedia of Polymer Science and Technology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002; Volume 6. [Google Scholar]
- Ashby, M.; Hugh, S.; David, C. Materials: Engineering, Science, Processing and Design, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2007. [Google Scholar]
- Barriere, T.; Cherouat, A.; Gabrion, X.; Holopainen, S. Short- to long-term deformation behavior, failure, and service life of amorphous polymers under cyclic torsional and multiaxial loadings. Int. J. Plast. 2021, 147, 103106. [Google Scholar] [CrossRef]
- Losi, G.; Knauss, W.G. Free volume theory and nonlinear thermoviscoelasticity. Polym. Eng. Sci. 1992, 32, 542–557. [Google Scholar] [CrossRef]
- Francis, D.K.; Bouvard, J.L.; Hammi, Y.; Horstemeyer, M.F. Formulation of a damage internal state variable model for amorphous glassy polymers. Int. J. Solids Struct. 2014, 51, 2765–2776. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, Z.; Chudnovsky, A. Applying the crack-layer concept to modeling of slow crack growth in polyethylene. Int. J. Eng. Sci. 2014, 83, 42–56. [Google Scholar] [CrossRef]
- James, M.N.; Lu, Y.; Christopher, C.J.; Patterson, E.A. Crack path support for deformation mechanisms in fatigue of polycarbonate. Eng. Fract. Mech. 2013, 108, 89–97. [Google Scholar] [CrossRef]
- Pastukhov, L.V.; Kanters, M.J.W.; Engels, T.A.P.; Govaert, L.E. Physical background of the endurance in poly(ether ether ketone). J. Polym. Sci. 2020, 47, 1–21. [Google Scholar] [CrossRef]
- Jones, D.; Snider, C.; Nassehi, A.; Yon, J.; Hicks, B. Characterising the digital twin: A systematic literature review. CIRP J. Manuf. Sci. Technol. 2020, 29, 36–52. [Google Scholar] [CrossRef]




| Parameter | E | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Unit | MPa | MPa | MPa | MPa | MPa | ||||
| Value | 2000 | 0.37 | 0.031 | 0.204 | 0.19 | 12 | 4.5 | 2500 | 8000 |
| Parameter | N | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Unit | MPa | MPa | MPa | MPa | |||||
| Value | 28.0 | 0.037 | 14.0 | 1.65 | 3500 | 600 | 0.015 | 26.5 | 0.0013 |
| Source | [MPa] | a | [MPa]−1 | C | K | L | B | ||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | 8.3 | 0.18 | 0.014 | 0.75 | 4.0 | 1.1 | 160 | 18 | 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barriere, T.; Carbillet, S.; Gabrion, X.; Holopainen, S. Prediction of Short- to Long-Term Cyclic Deformation Behavior and Fatigue Life of Polymers. Polymers 2024, 16, 1640. https://doi.org/10.3390/polym16121640
Barriere T, Carbillet S, Gabrion X, Holopainen S. Prediction of Short- to Long-Term Cyclic Deformation Behavior and Fatigue Life of Polymers. Polymers. 2024; 16(12):1640. https://doi.org/10.3390/polym16121640
Chicago/Turabian StyleBarriere, Thierry, Stani Carbillet, Xavier Gabrion, and Sami Holopainen. 2024. "Prediction of Short- to Long-Term Cyclic Deformation Behavior and Fatigue Life of Polymers" Polymers 16, no. 12: 1640. https://doi.org/10.3390/polym16121640
APA StyleBarriere, T., Carbillet, S., Gabrion, X., & Holopainen, S. (2024). Prediction of Short- to Long-Term Cyclic Deformation Behavior and Fatigue Life of Polymers. Polymers, 16(12), 1640. https://doi.org/10.3390/polym16121640








