Lagrangian Split-Step Method for Viscoelastic Flows
Abstract
1. Introduction
2. Governing Equations
2.1. Solvent Viscous Stress
2.2. Polymeric Stress
3. Numerical Procedure
3.1. Lagrangian Splitting Scheme
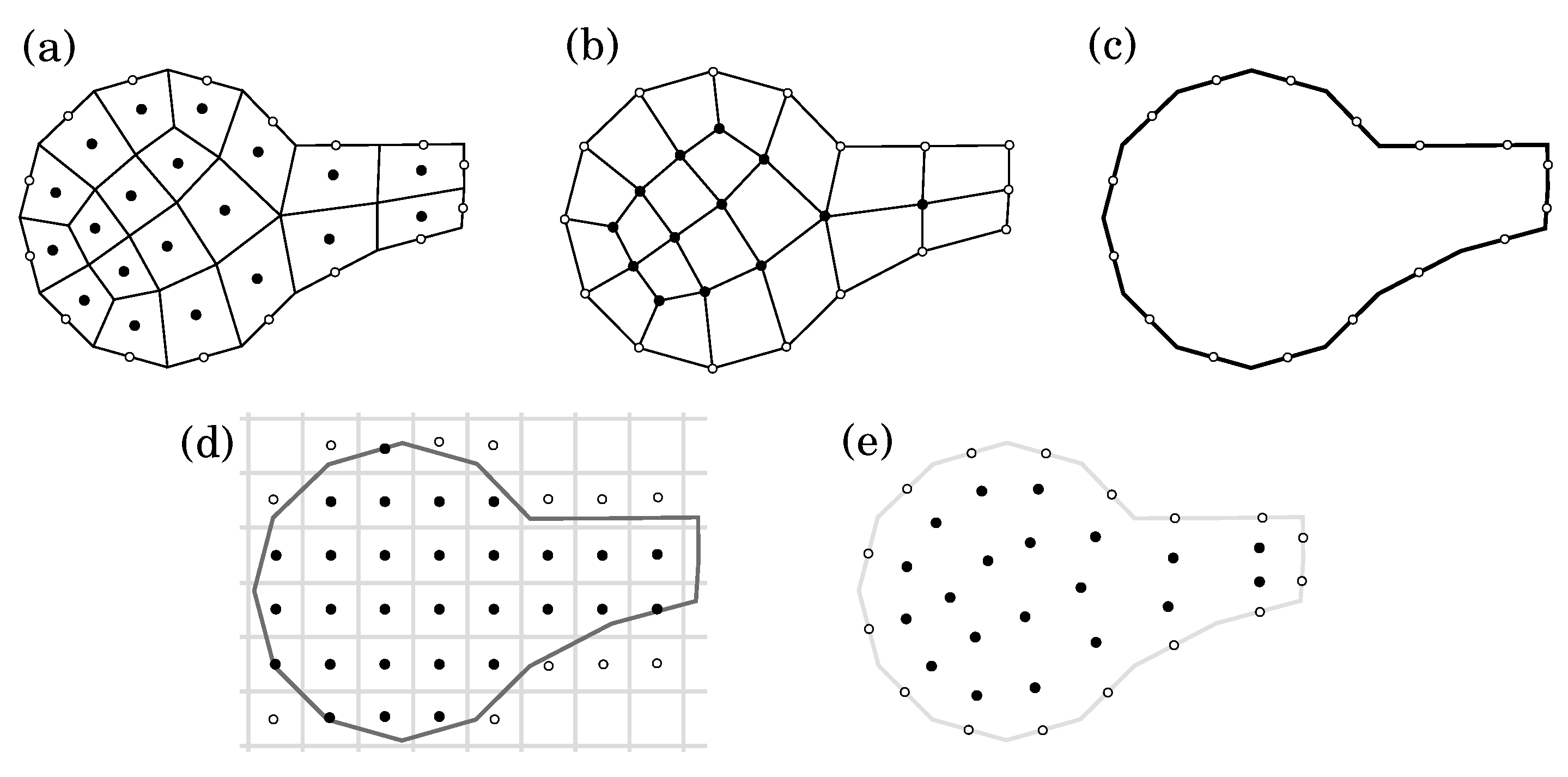
3.2. Spatial Discretization
3.3. Temporal Discretization
3.3.1. Momentum Equation
3.3.2. Advection
3.3.3. Extra-Stress Evolution
3.4. Final Algorithm
- Advect particles and reorder their positions, as described in Section 3.3.2.
- Generate boundary particles on walls by projecting closest fluid particles into walls, as described in [6].
- Solve the pressure equation, as described in Section 3.1.
- Solve for velocity, as described in Section 3.3.1.
- Calculate the viscoelasticity tensor, as described in Section 3.3.3.
- Calculate the next allowable time-step size according to (22).
4. Results and Discussion
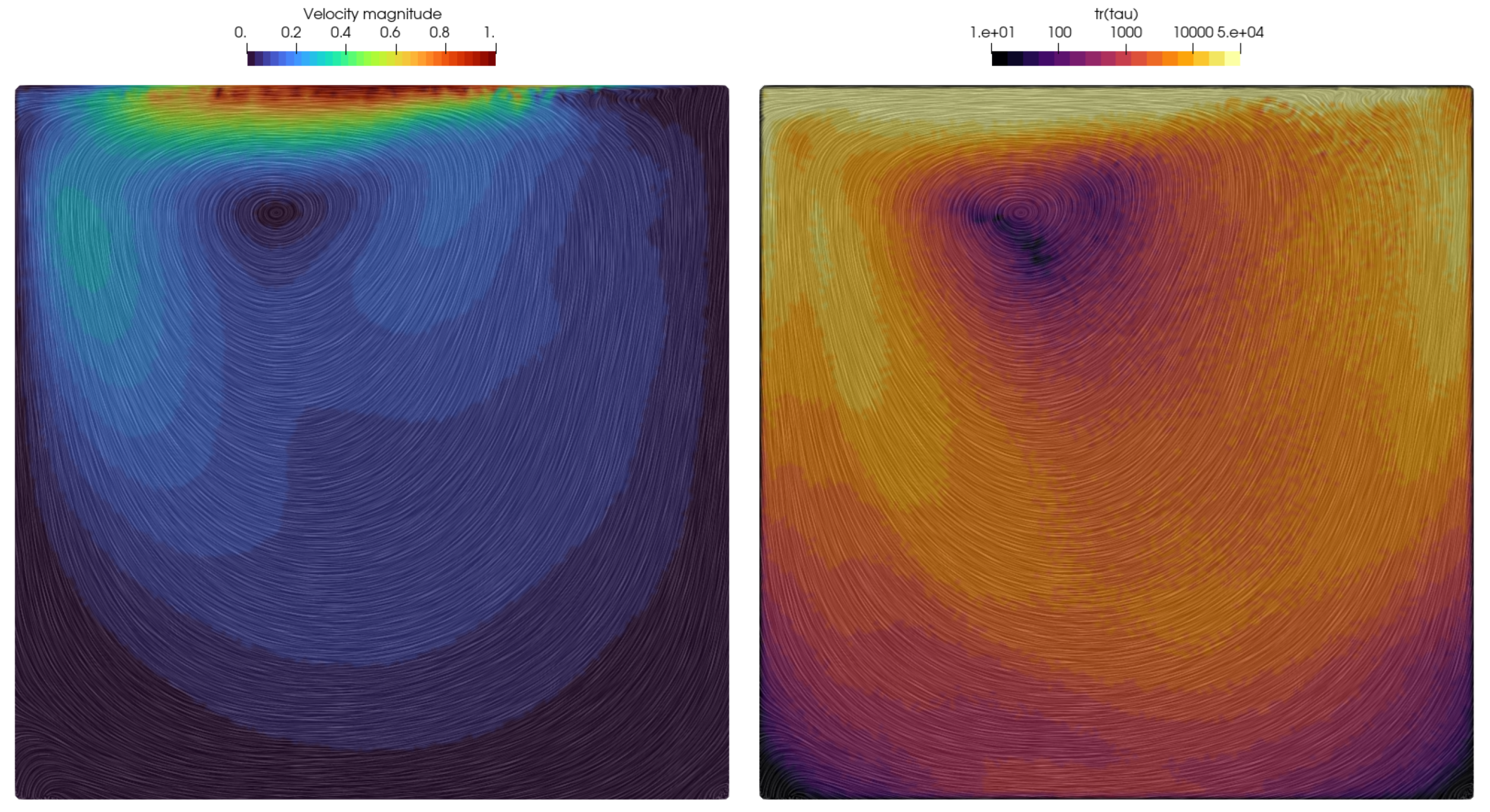
4.1. Lid-Driven Cavity
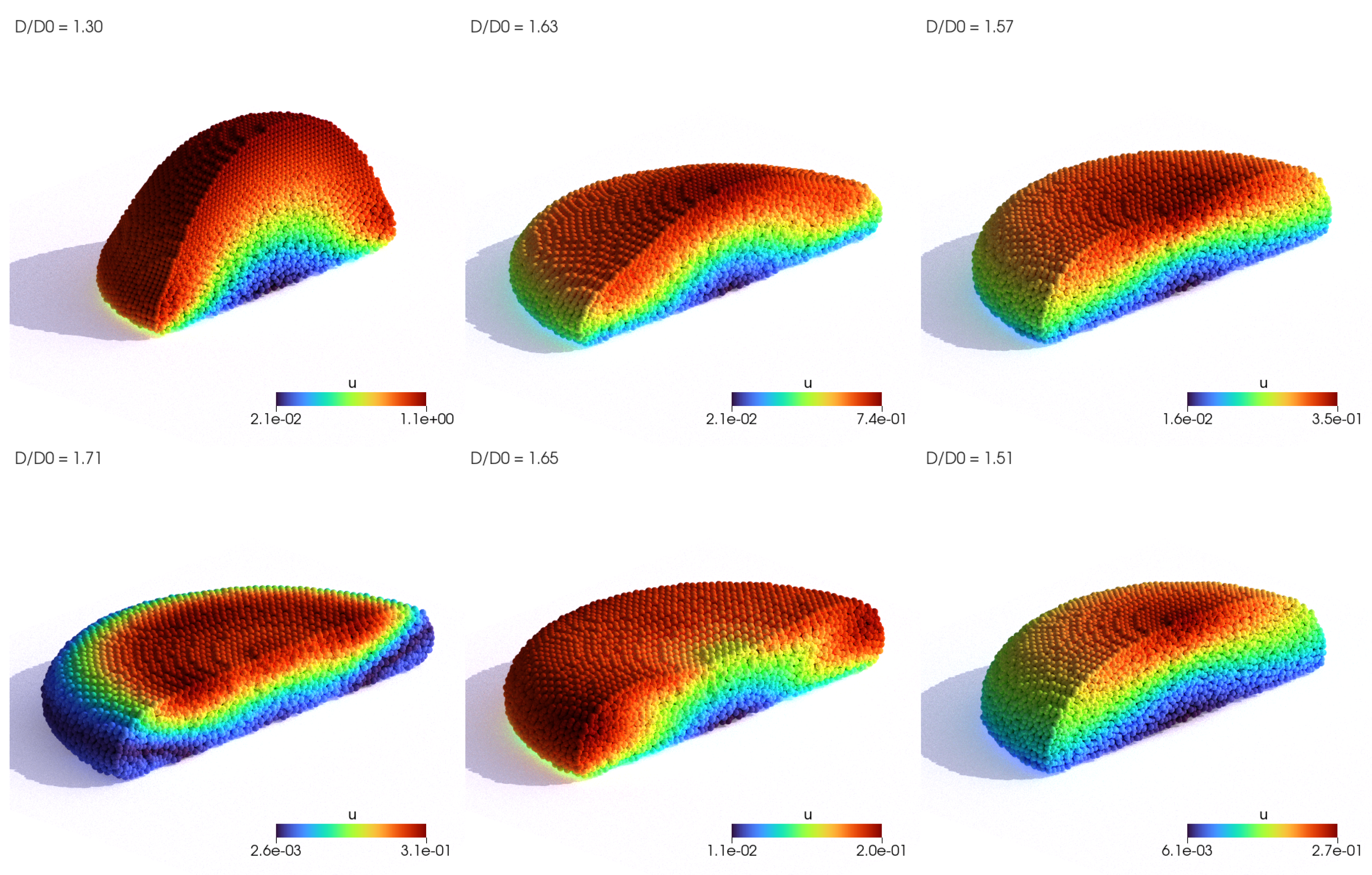
4.2. Droplet Impact
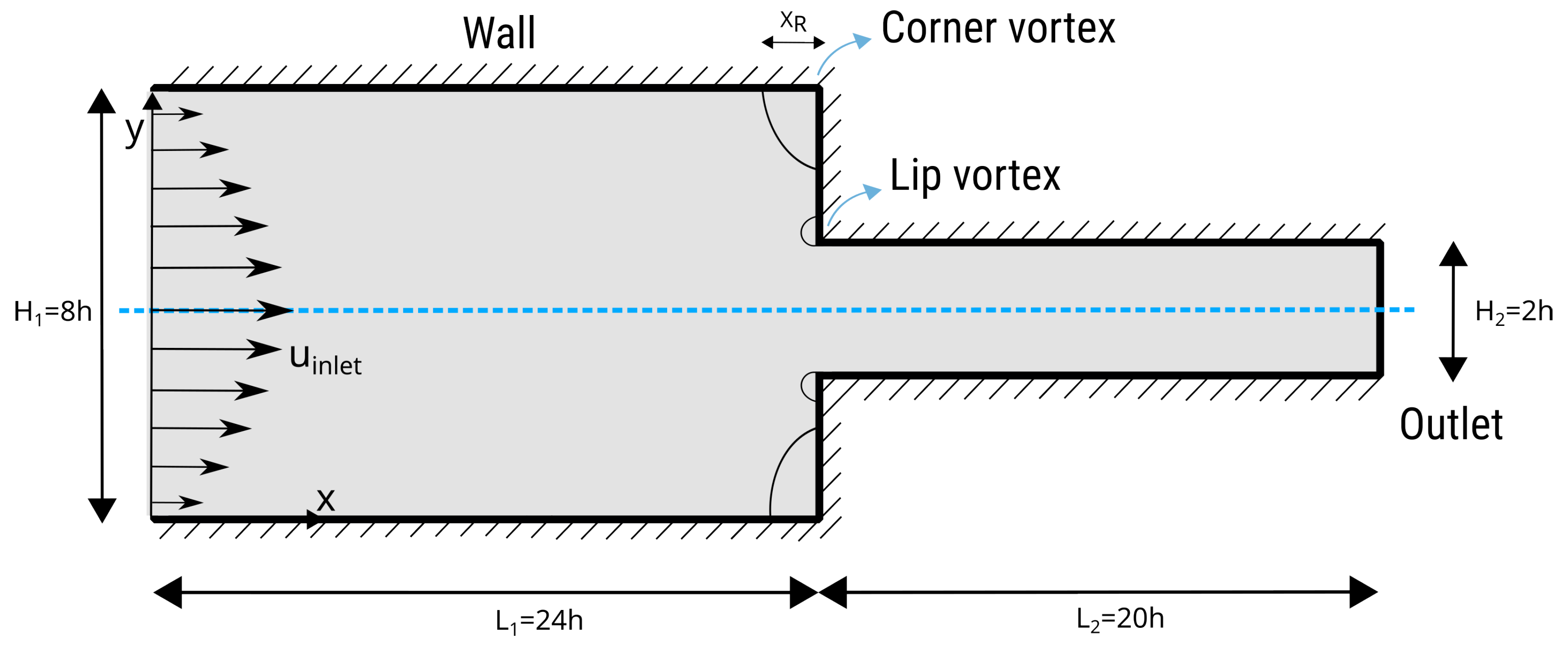
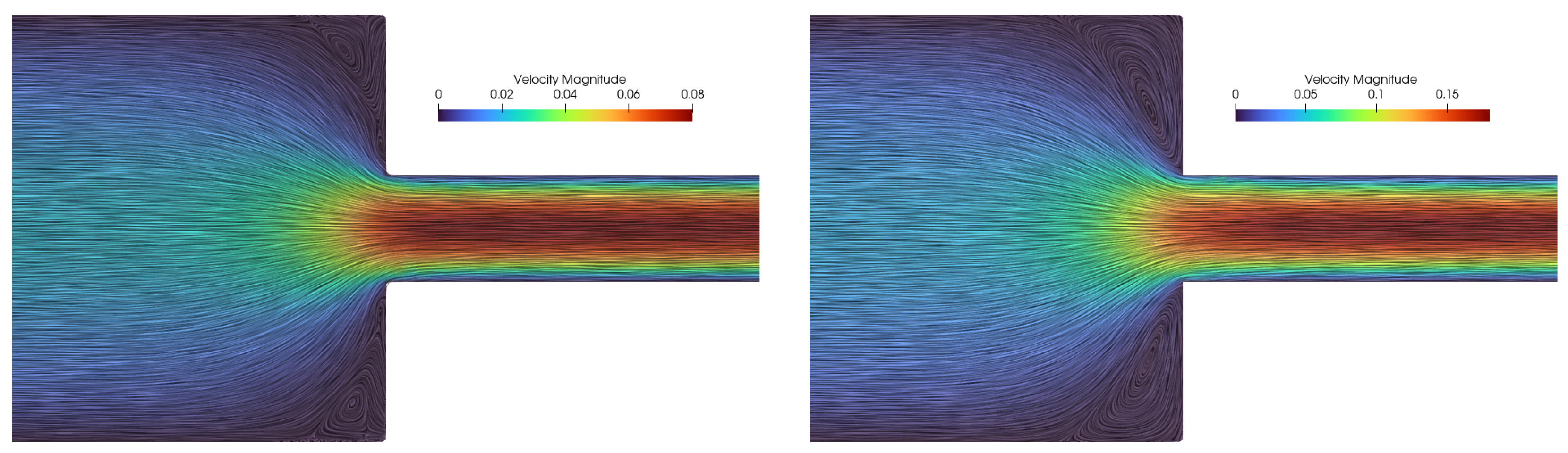
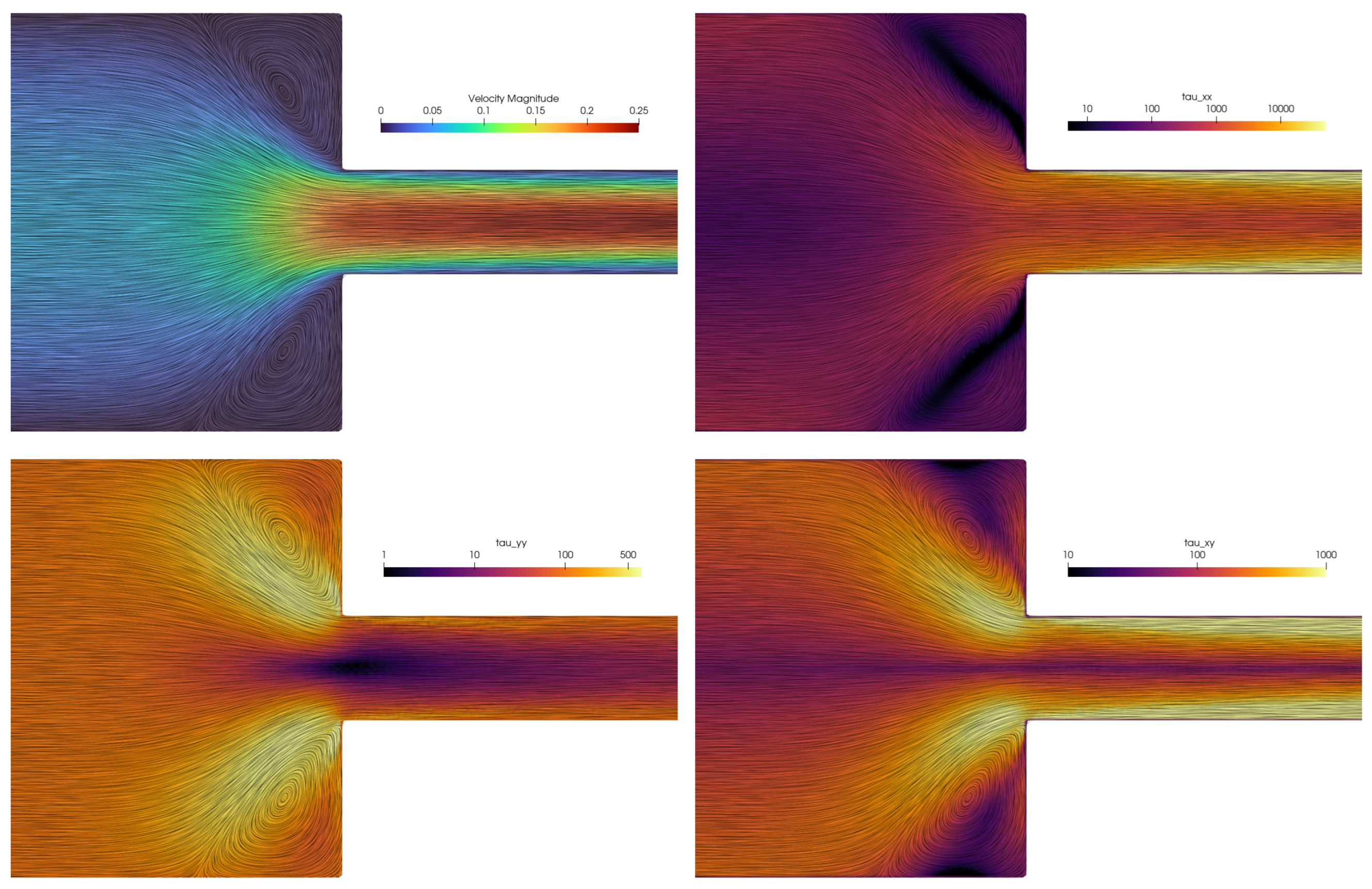
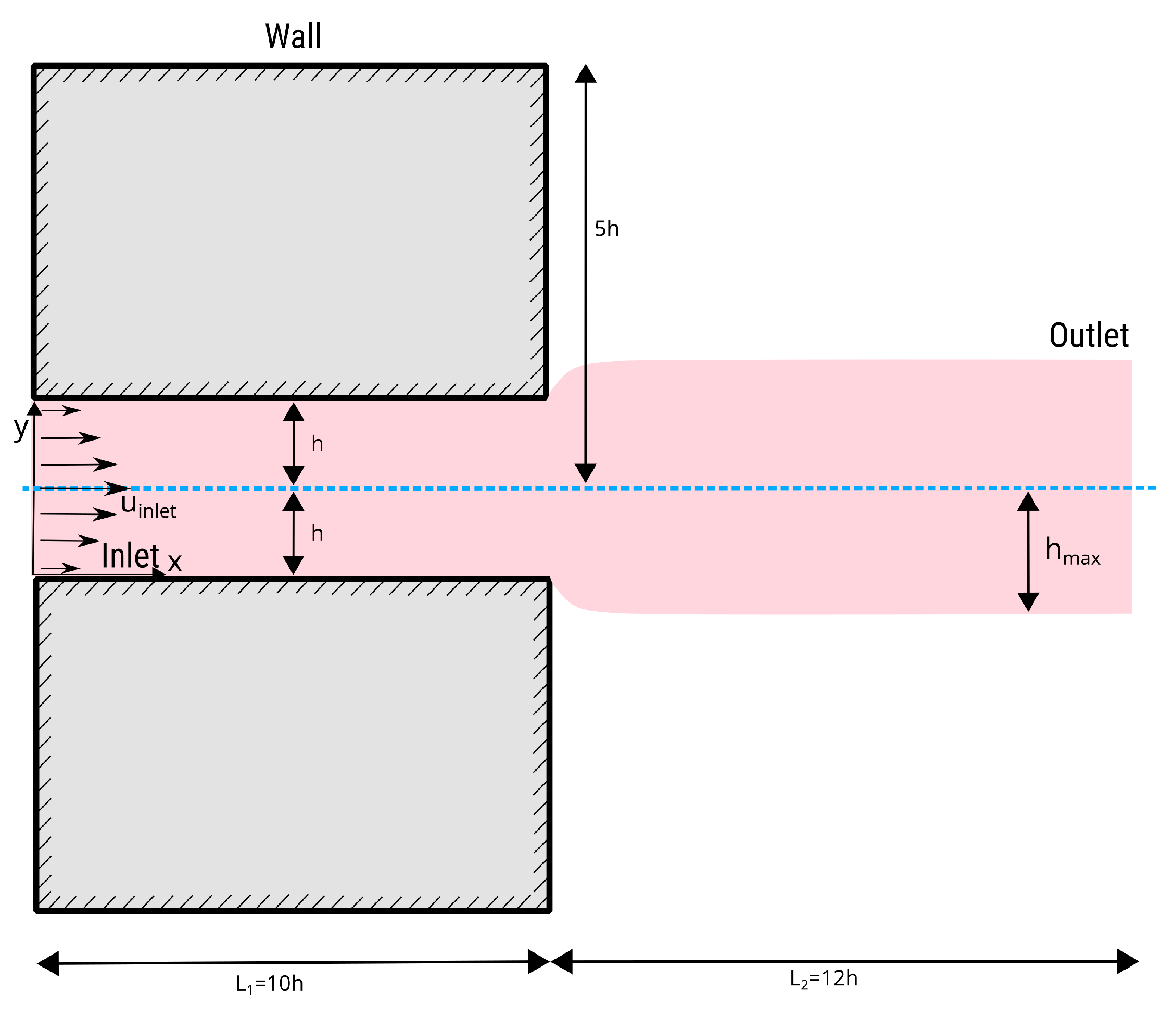
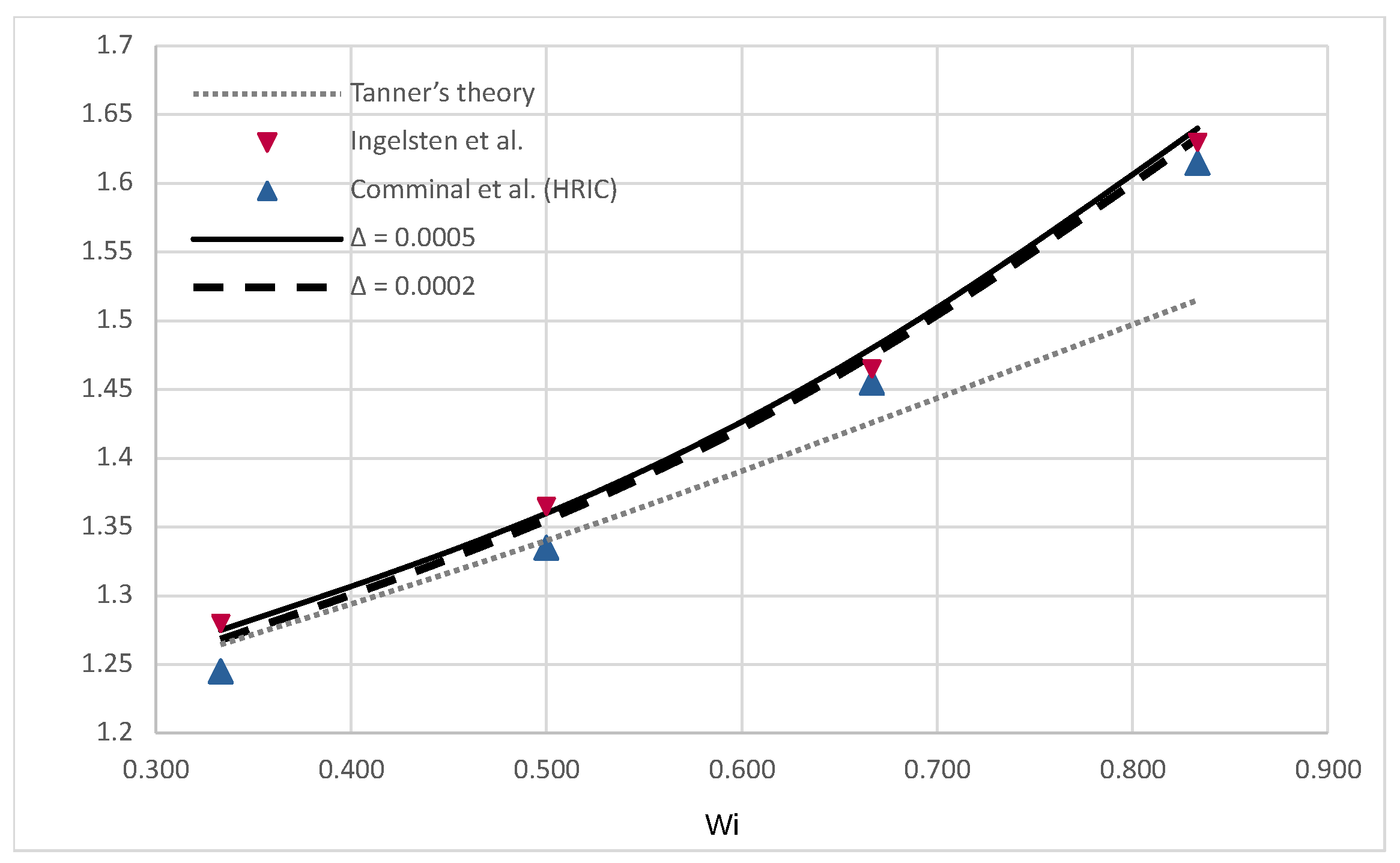
4.3. 4:1 Planar Contraction
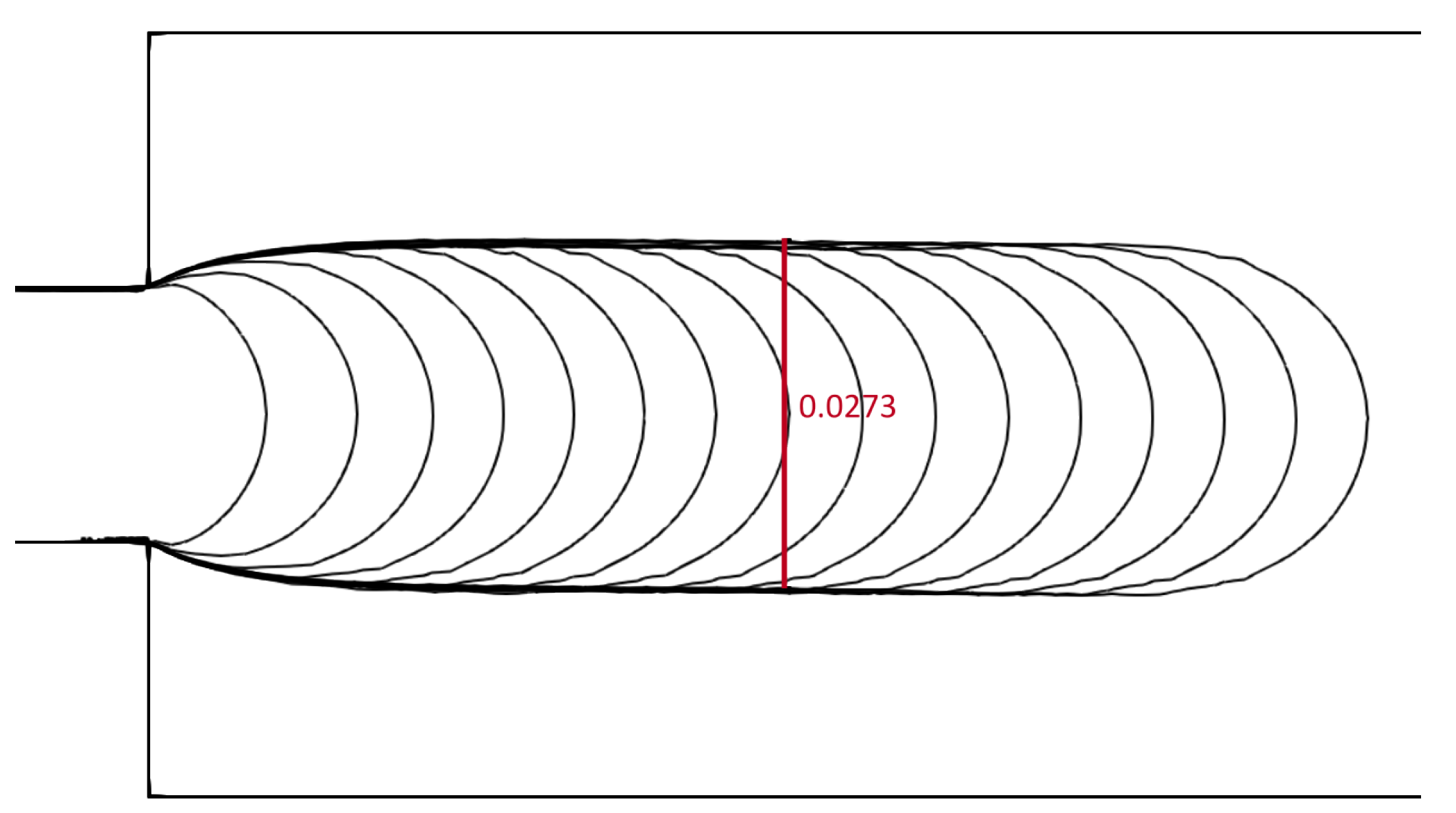
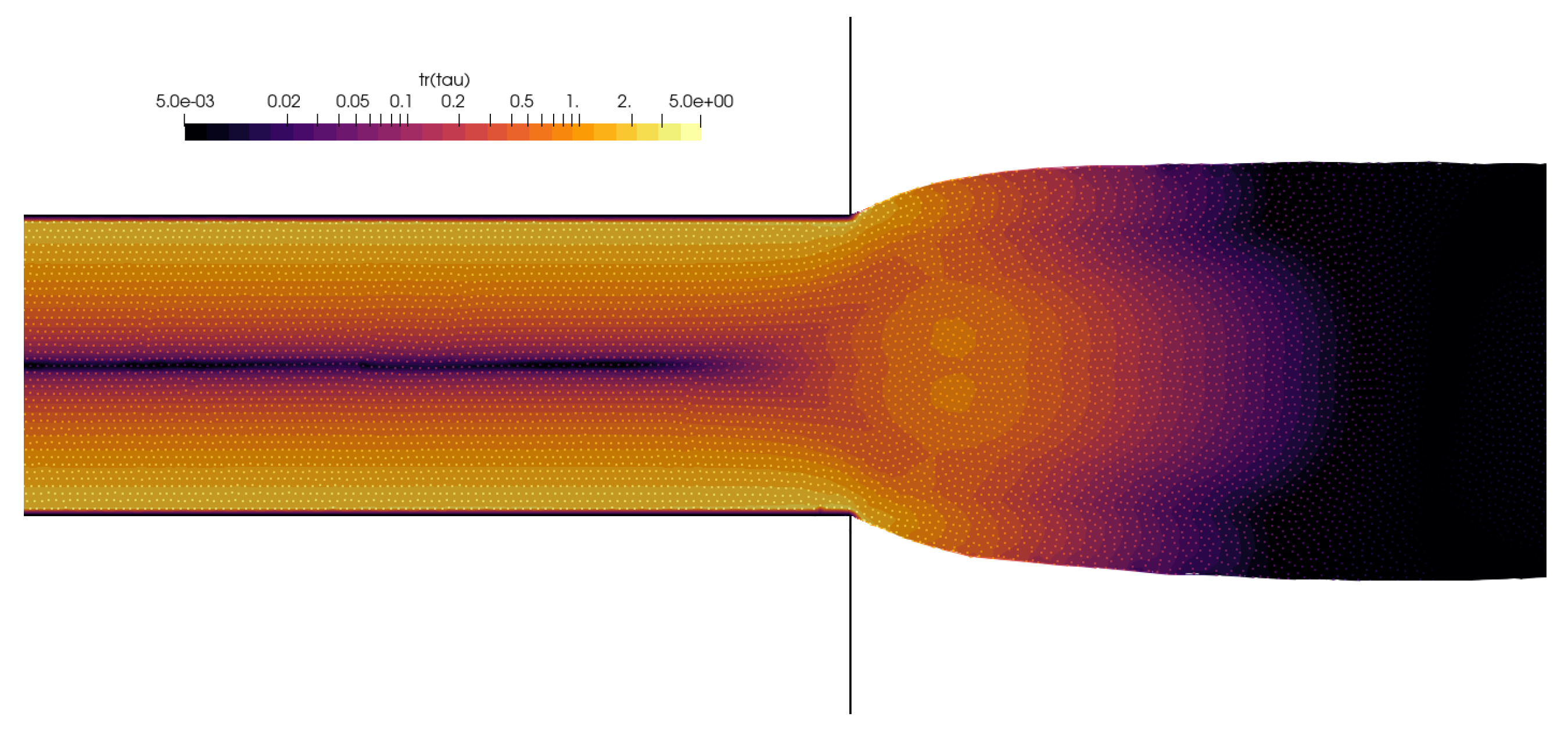
4.4. Die Swelling
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LDD | Lagrangian Differencing Dynamics |
| CFD | Computational Fluid Dynamics |
| ODE | Ordinary Differential Equation |
| PDE | Partial Differential Equation |
| HWNP | high Weissenberg Number Problem |
| SPH | Smoothed Particle Hydrodynamics |
| UCM | Upper-convected Maxwell |
| DNS | Direct Numerical Simulation |
| LST | Linear Stability Theory |
| NSE | Navier–Stokes equations |
| BDF2 | Backward Differencing Formula of the Second Order |
| PSD | Principal Stress Difference |
| FIB | flow-induced Birefringence |
Appendix A. Divergence of the Diffusive Stress
Appendix B. Divergence of the Divergence of the Extra Stress
References
- Comminal, R.; Spangenberg, J.; Hattel, J.H. Robust simulations of viscoelastic flows at high Weissenberg numbers with the streamfunction/log-conformation formulation. J. Non-Newton. Fluid Mech. 2015, 223, 37–61. [Google Scholar] [CrossRef]
- Snoeijer, J.H.; Pandey, A.; Herrada, M.A.; Eggers, J. The relationship between viscoelasticity and elasticity. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20200419. [Google Scholar] [CrossRef] [PubMed]
- Alves, M.; Oliveira, P.; Pinho, F. Numerical Methods for Viscoelastic Fluid Flows. Annu. Rev. Fluid Mech. 2021, 53, 509–541. [Google Scholar] [CrossRef]
- Oldroyd, J.G. On the formulation of rheological equations of state. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1950, 200, 523–541. [Google Scholar] [CrossRef]
- Castillo Sánchez, H.A.; Jovanović, M.R.; Kumar, S.; Morozov, A.; Shankar, V.; Subramanian, G.; Wilson, H.J. Understanding viscoelastic flow instabilities: Oldroyd-B and beyond. J. Non-Newton. Fluid Mech. 2022, 302, 104742. [Google Scholar] [CrossRef]
- Bašić, J.; Degiuli, N.; Blagojević, B.; Ban, D. Lagrangian differencing dynamics for incompressible flows. J. Comput. Phys. 2022, 462, 111198. [Google Scholar] [CrossRef]
- Fattal, R.; Kupferman, R. Constitutive laws for the matrix-logarithm of the conformation tensor. J. Non-Newton. Fluid Mech. 2004, 123, 281–285. [Google Scholar] [CrossRef]
- Hulsen, M.A.; Fattal, R.; Kupferman, R. Flow of viscoelastic fluids past a cylinder at high Weissenberg number: Stabilized simulations using matrix logarithms. J. Non-Newton. Fluid Mech. 2005, 127, 27–39. [Google Scholar] [CrossRef]
- Pimenta, F.; Alves, M.A. Stabilization of an open-source finite-volume solver for viscoelastic fluid flows. J. Non-Newton. Fluid Mech. 2017, 239, 85–104. [Google Scholar] [CrossRef]
- Habla, F.; Tan, M.W.; Haßlberger, J.; Hinrichsen, O. Numerical simulation of the viscoelastic flow in a three-dimensional lid-driven cavity using the log-conformation reformulation in OpenFOAM®. J. Non-Newton. Fluid Mech. 2014, 212, 47–62. [Google Scholar] [CrossRef]
- Fernandes, C. A Fully Implicit Log-Conformation Tensor Coupled Algorithm for the Solution of Incompressible Non-Isothermal Viscoelastic Flows. Polymers 2022, 14, 4099. [Google Scholar] [CrossRef] [PubMed]
- Fattal, R.; Kupferman, R. Time-dependent simulation of viscoelastic flows at high Weissenberg number using the log-conformation representation. J. Non-Newton. Fluid Mech. 2005, 126, 23–37. [Google Scholar] [CrossRef]
- Verbeeten, W.M.; Peters, G.W.; Baaijens, F.P. Numerical simulations of the planar contraction flow for a polyethylene melt using the XPP model. J. Non-Newton. Fluid Mech. 2004, 117, 73–84. [Google Scholar] [CrossRef]
- Meburger, S.; Niethammer, M.; Bothe, D.; Schäfer, M. Numerical simulation of non-isothermal viscoelastic flows at high Weissenberg numbers using a finite volume method on general unstructured meshes. J. Non-Newton. Fluid Mech. 2021, 287, 104451. [Google Scholar] [CrossRef]
- Fernandes, C.; Araujo, M.S.B.; Ferrás, L.L.; Miguel Nóbrega, J. Improved both sides diffusion (iBSD): A new and straightforward stabilization approach for viscoelastic fluid flows. J. Non-Newton. Fluid Mech. 2017, 249, 63–78. [Google Scholar] [CrossRef]
- Giorgi, C.; Morro, A. Nonlinear Models of Thermo-Viscoelastic Materials. Materials 2021, 14, 7617. [Google Scholar] [CrossRef] [PubMed]
- Brandi, A.C.; Mendonça, M.T.; Souza, L.F. DNS and LST stability analysis of Oldroyd-B fluid in a flow between two parallel plates. J. Non-Newton. Fluid Mech. 2019, 267, 14–27. [Google Scholar] [CrossRef]
- Faroughi, S.A.; Roriz, A.I.; Fernandes, C. A Meta-Model to Predict the Drag Coefficient of a Particle Translating in Viscoelastic Fluids: A Machine Learning Approach. Polymers 2022, 14, 430. [Google Scholar] [CrossRef]
- Phillips, T.N.; Williams, A.J. Viscoelastic flow through a planar contraction using a semi-Lagrangian finite volume method. J. Non-Newton. Fluid Mech. 1999, 87, 215–246. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, B.; Chen, J.; Zhou, X.; Chen, W. The simulation of sediment transport and erosion caused by free-surface flow based on two-phase SPH model with the improved Shields criterion. Ocean Dyn. 2022, 72, 169–186. [Google Scholar] [CrossRef]
- Bhattacharya, K.; Jana, T.K.; Shaw, A.; Ramachandra, L.S.; Mehera, V. An adaptive approach to remove tensile instability in SPH for weakly compressible fluids. arXiv 2023, arXiv:2307.05960. [Google Scholar] [CrossRef]
- Xu, X.; Yu, P. A technique to remove the tensile instability in weakly compressible SPH. Comput. Mech. 2018, 62, 963–990. [Google Scholar] [CrossRef]
- Castelo, A.; Afonso, A.M.; De Souza Bezerra, W. A Hierarchical Grid Solver for Simulation of Flows of Complex Fluids. Polymers 2021, 13, 3168. [Google Scholar] [CrossRef] [PubMed]
- Bašić, J.; Degiuli, N.; Malenica, Š.; Ban, D. Lagrangian finite-difference method for predicting green water loadings. Ocean Eng. 2020, 209, 107533. [Google Scholar] [CrossRef]
- Bašić, M.; Blagojević, B.; Peng, C.; Bašić, J. Lagrangian Differencing Dynamics for Time-Independent Non-Newtonian Materials. Materials 2021, 14, 6210. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.; Bašić, M.; Blagojević, B.; Bašić, J.; Wu, W. A Lagrangian differencing dynamics method for granular flow modeling. Comput. Geotech. 2021, 137, 104297. [Google Scholar] [CrossRef]
- Fan, X.J.; Tanner, R.I.; Zheng, R. Smoothed particle hydrodynamics simulation of non-Newtonian moulding flow. J. Non-Newton. Fluid Mech. 2010, 165, 219–226. [Google Scholar] [CrossRef]
- Fang, J.; Owens, R.G.; Tacher, L.; Parriaux, A. A numerical study of the SPH method for simulating transient viscoelastic free surface flows. J. Non-Newton. Fluid Mech. 2006, 139, 68–84. [Google Scholar] [CrossRef]
- Xu, X.; Ouyang, J.; Yang, B.; Liu, Z. SPH simulations of three-dimensional non-Newtonian free surface flows. Comput. Methods Appl. Mech. Eng. 2013, 256, 101–116. [Google Scholar] [CrossRef]
- Basic, J.; Basic, M.; Blagojevic, B. Strong formulations of the generalised Navier-Stokes momentum equation. arXiv 2022, arXiv:2210.15724. [Google Scholar]
- Chupin, L. Global Strong Solutions for Some Differential Viscoelastic Models. SIAM J. Appl. Math. 2018, 78, 2919–2949. [Google Scholar] [CrossRef]
- Coussot, P.; Rogers, S.A. Oldroyd’s model and the foundation of modern rheology of yield stress fluids. J. Non-Newton. Fluid Mech. 2021, 295, 104604. [Google Scholar] [CrossRef]
- Paulo, J.; Oliveira, F.T.P. Numerical procedure for the computation of fluid flow with arbitrary stress-strain relationships. Numer. Heat Transf. Part B Fundam. 1999, 35, 295–315. [Google Scholar] [CrossRef]
- Basic, J.; Degiuli, N.; Ban, D. A class of renormalised meshless Laplacians for boundary value problems. J. Comput. Phys. 2018, 354, 269–287. [Google Scholar] [CrossRef]
- Henshaw, W.D.; Petersson, N.A. A Split-Step Scheme for the Incompressible Navier-Stokes Equations. In Numerical Simulations of Incompressible Flows; World Scientific: Half Moon Bay, CA, USA, 2003; pp. 108–125. [Google Scholar] [CrossRef]
- Johnston, H.; Liu, J.G. Accurate, stable and efficient Navier-Stokes solvers based on explicit treatment of the pressure term. J. Comput. Phys. 2004, 199, 221–259. [Google Scholar] [CrossRef]
- Vreman, A. The projection method for the incompressible Navier-Stokes equations: The pressure near a no-slip wall. J. Comput. Phys. 2014, 263, 353–374. [Google Scholar] [CrossRef]
- Shirokoff, D.; Rosales, R. An efficient method for the incompressible Navier-Stokes equations on irregular domains with no-slip boundary conditions, high order up to the boundary. J. Comput. Phys. 2011, 230, 8619–8646. [Google Scholar] [CrossRef][Green Version]
- Henshaw, W.D. A Fourth-Order Accurate Method for the Incompressible Navier-Stokes Equations on Overlapping Grids. J. Comput. Phys. 1994, 113, 13–25. [Google Scholar] [CrossRef]
- Pacheco, D.R.; Schussnig, R.; Fries, T.P. An efficient split-step framework for non-Newtonian incompressible flow problems with consistent pressure boundary conditions. Comput. Methods Appl. Mech. Eng. 2021, 382, 113888. [Google Scholar] [CrossRef]
- Kumar, M.; Guasto, J.S.; Ardekani, A.M. Lagrangian stretching reveals stress topology in viscoelastic flows. Proc. Natl. Acad. Sci. USA 2023, 120, e2211347120. [Google Scholar] [CrossRef]
- Johnston, H.; Liu, J.G. Finite Difference Schemes for Incompressible Flow Based on Local Pressure Boundary Conditions. J. Comput. Phys. 2002, 180, 120–154. [Google Scholar] [CrossRef]
- Pacheco, D.R.Q.; Castillo, E. Consistent splitting schemes for incompressible viscoelastic flow problems. Int. J. Numer. Methods Eng. 2023, 124, 1908–1927. [Google Scholar] [CrossRef]
- Cottet, G.H. Semi-Lagrangian particle methods for high-dimensional Vlasov–Poisson systems. J. Comput. Phys. 2018, 365, 362–375. [Google Scholar] [CrossRef]
- Suchde, P.; Kuhnert, J. Point Cloud Movement For Fully Lagrangian Meshfree Methods. J. Comput. Appl. Math. 2017, 340, 89–100. [Google Scholar] [CrossRef]
- Macklin, M.; Müller, M. Position based fluids. ACM Trans. Graph. 2013, 32, 104. [Google Scholar] [CrossRef]
- Ingelsten, S.; Mark, A.; Kádár, R.; Edelvik, F. A Backwards-Tracking Lagrangian-Eulerian Method for Viscoelastic Two-Fluid Flows. Appl. Sci. 2021, 11, 439. [Google Scholar] [CrossRef]
- Sousa, R.G.; Poole, R.J.; Afonso, A.M.; Pinho, F.T.; Oliveira, P.J.; Morozov, A.; Alves, M.A. Lid-driven cavity flow of viscoelastic liquids. J. Non-Newton. Fluid Mech. 2016, 234, 129–138. [Google Scholar] [CrossRef]
- Bui, C.M.; Ho, A.N.T.; Nguyen, X.B. Flow Behaviors of Polymer Solution in a Lid-Driven Cavity. Polymers 2022, 14, 2330. [Google Scholar] [CrossRef] [PubMed]
- Mokhtari, O.; Davit, Y.; Latché, J.C.; Quintard, M. A staggered projection scheme for viscoelastic flows. ESAIM Math. Model. Numer. Anal. 2023, 57, 1747–1793. [Google Scholar] [CrossRef]
- Renardy, M. A comment on smoothness of viscoelastic stresses. J. Non-Newton. Fluid Mech. 2006, 138, 204–205. [Google Scholar] [CrossRef]
- Figueiredo, R.A.; Oishi, C.M.; Afonso, A.M.; Tasso, I.V.M.; Cuminato, J.A. A two-phase solver for complex fluids: Studies of the Weissenberg effect. Int. J. Multiph. Flow 2016, 84, 98–115. [Google Scholar] [CrossRef]
- Wang, W.; Wang, L. An Experimental Investigation of Viscoelastic Flow in a Contraction Channel. Polymers 2021, 13, 1876. [Google Scholar] [CrossRef] [PubMed]
- Moreno, L.; Codina, R.; Baiges, J.; Castillo, E. Logarithmic conformation reformulation in viscoelastic flow problems approximated by a VMS-type stabilized finite element formulation. Comput. Methods Appl. Mech. Eng. 2019, 354, 706–731. [Google Scholar] [CrossRef]
- Afonso, A.M.; Oliveira, P.J.; Pinho, F.T.; Alves, M.A. Dynamics of high-Deborah-number entry flows: A numerical study. J. Fluid Mech. 2011, 677, 272–304. [Google Scholar] [CrossRef]
- Wittschieber, S.; Demkowicz, L.; Behr, M. Stabilized finite element methods for a fully-implicit logarithmic reformulation of the Oldroyd-B constitutive law. J. Non-Newton. Fluid Mech. 2022, 306, 104838. [Google Scholar] [CrossRef]
- Niethammer, M.; Marschall, H.; Kunkelmann, C.; Bothe, D. A numerical stabilization framework for viscoelastic fluid flow using the finite volume method on general unstructured meshes. Int. J. Numer. Methods Fluids 2018, 86, 131–166. [Google Scholar] [CrossRef]
- Hooshyar, S.; Germann, N. Shear Banding in 4:1 Planar Contraction. Polymers 2019, 11, 417. [Google Scholar] [CrossRef]
- Comminal, R.; Pimenta, F.; Hattel, J.H.; Alves, M.A.; Spangenberg, J. Numerical simulation of the planar extrudate swell of pseudoplastic and viscoelastic fluids with the streamfunction and the VOF methods. J. Non-Newton. Fluid Mech. 2018, 252, 1–18. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bašić, M.; Blagojević, B.; Klarin, B.; Peng, C.; Bašić, J. Lagrangian Split-Step Method for Viscoelastic Flows. Polymers 2024, 16, 2068. https://doi.org/10.3390/polym16142068
Bašić M, Blagojević B, Klarin B, Peng C, Bašić J. Lagrangian Split-Step Method for Viscoelastic Flows. Polymers. 2024; 16(14):2068. https://doi.org/10.3390/polym16142068
Chicago/Turabian StyleBašić, Martina, Branko Blagojević, Branko Klarin, Chong Peng, and Josip Bašić. 2024. "Lagrangian Split-Step Method for Viscoelastic Flows" Polymers 16, no. 14: 2068. https://doi.org/10.3390/polym16142068
APA StyleBašić, M., Blagojević, B., Klarin, B., Peng, C., & Bašić, J. (2024). Lagrangian Split-Step Method for Viscoelastic Flows. Polymers, 16(14), 2068. https://doi.org/10.3390/polym16142068







