Modeling of the Time-Dependent H2 Emission and Equilibrium Time in H2-Enriched Polymers with Cylindrical, Spherical and Sheet Shapes and Comparisons with Experimental Investigations
Abstract
:1. Introduction
2. Modeling Background
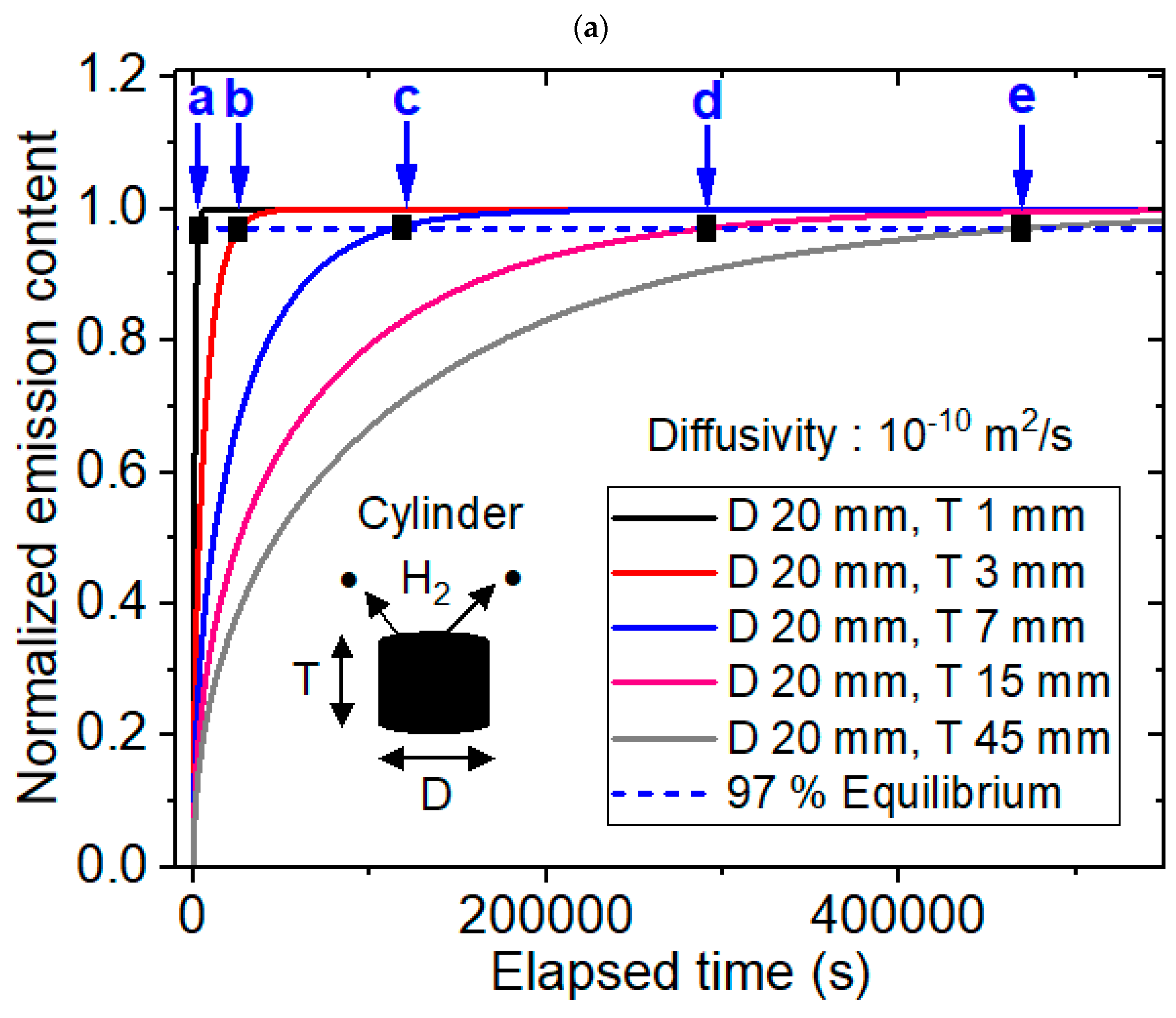
Modeling Background for Determining the Sorption Equilibrium Time
3. Modeling for Three Shaped Specimens and Comparison with Experiment
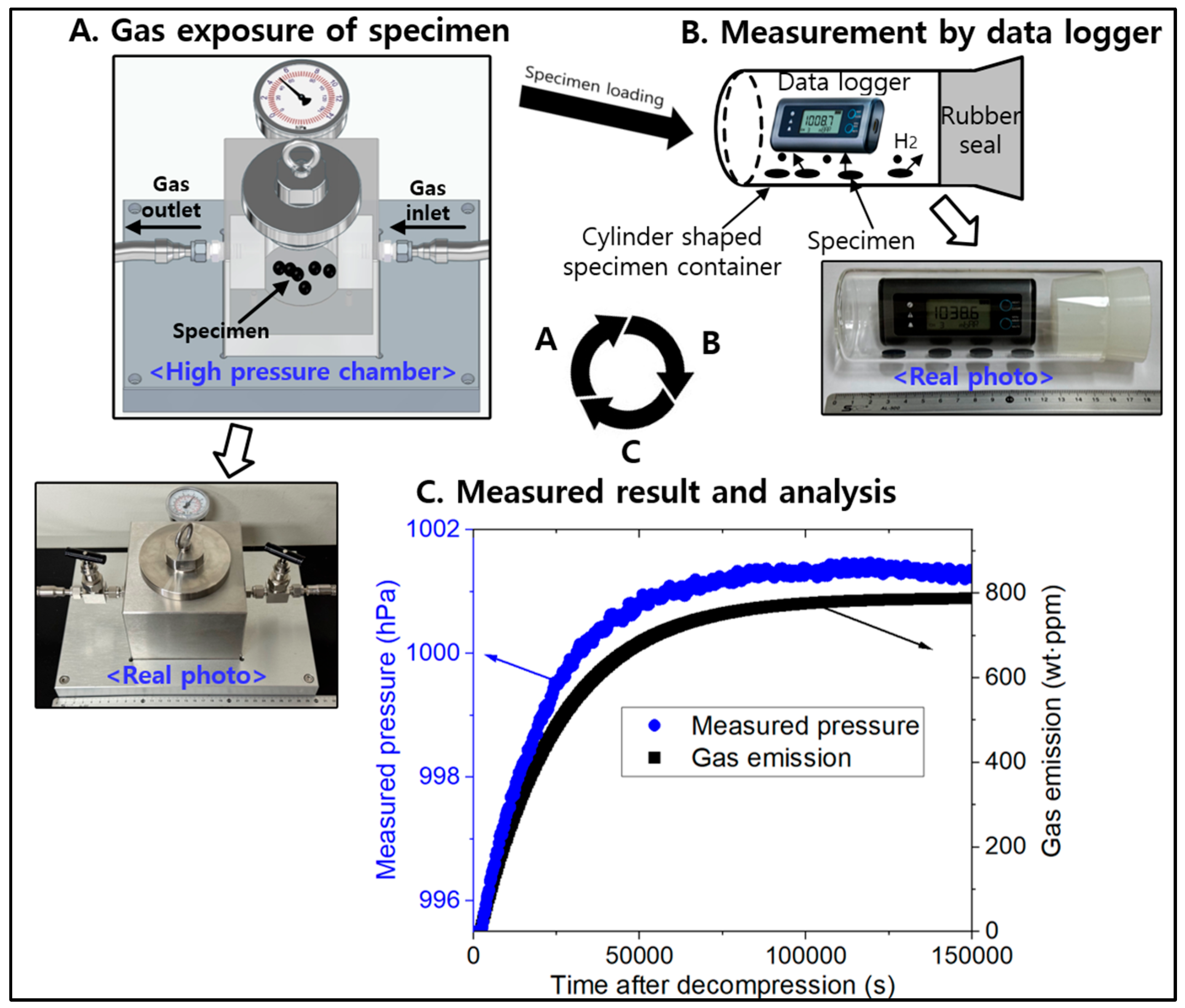
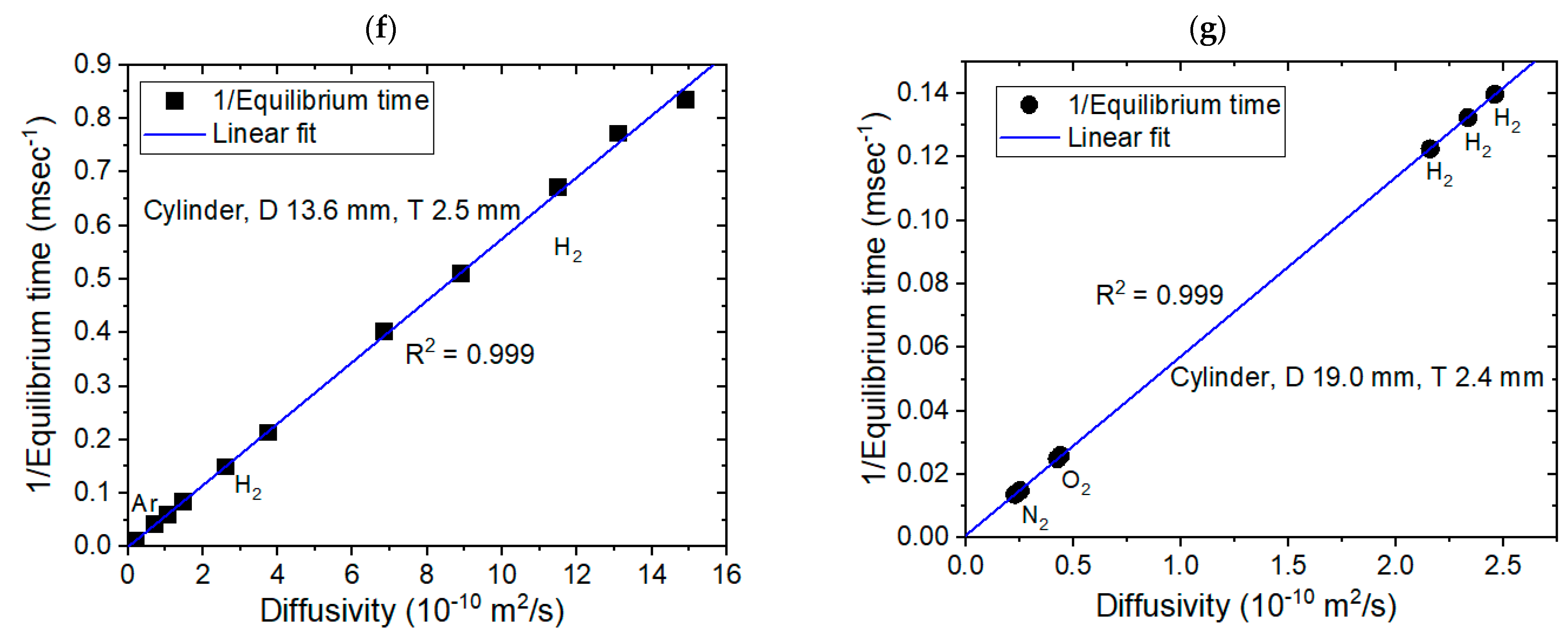
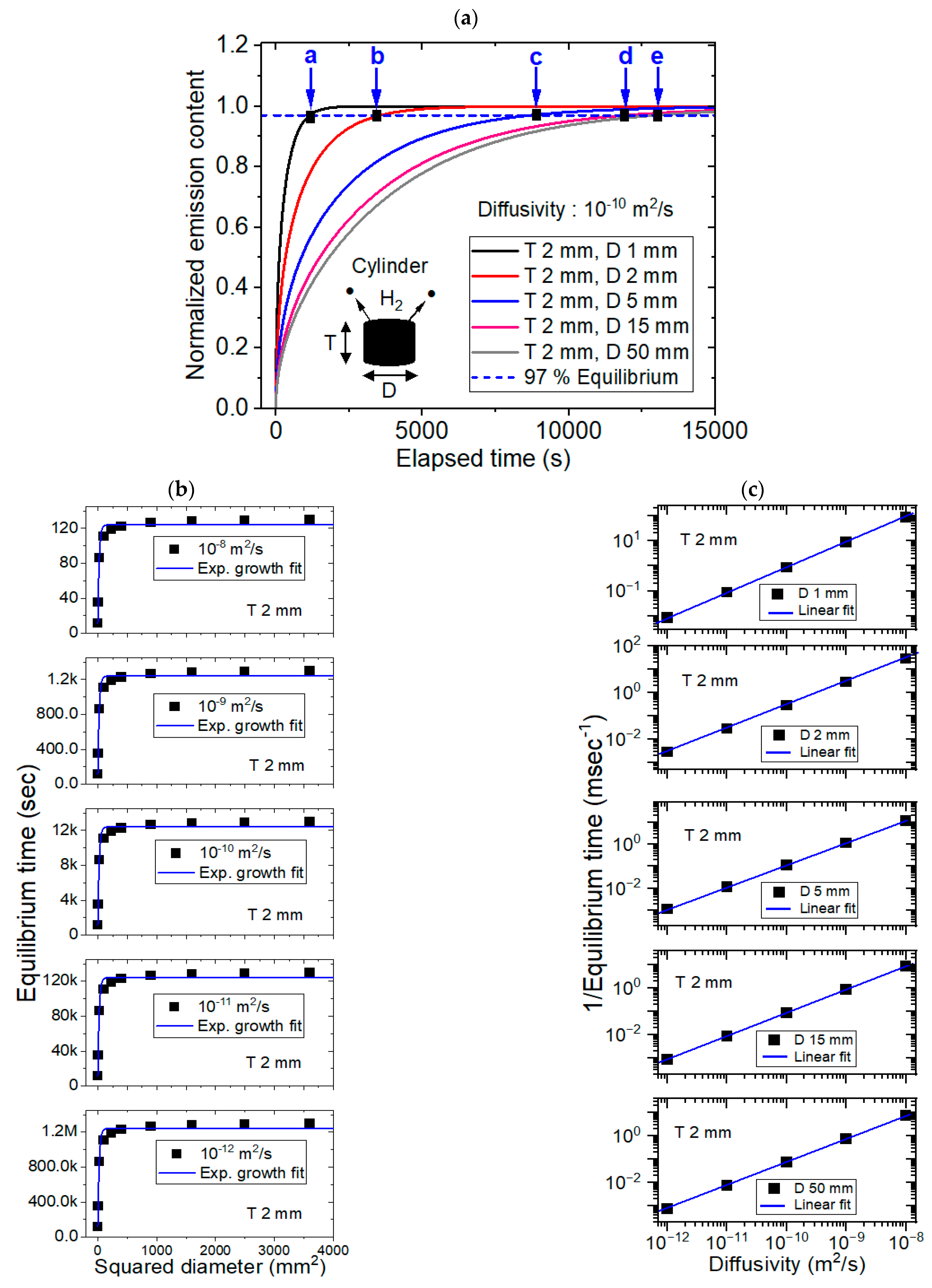
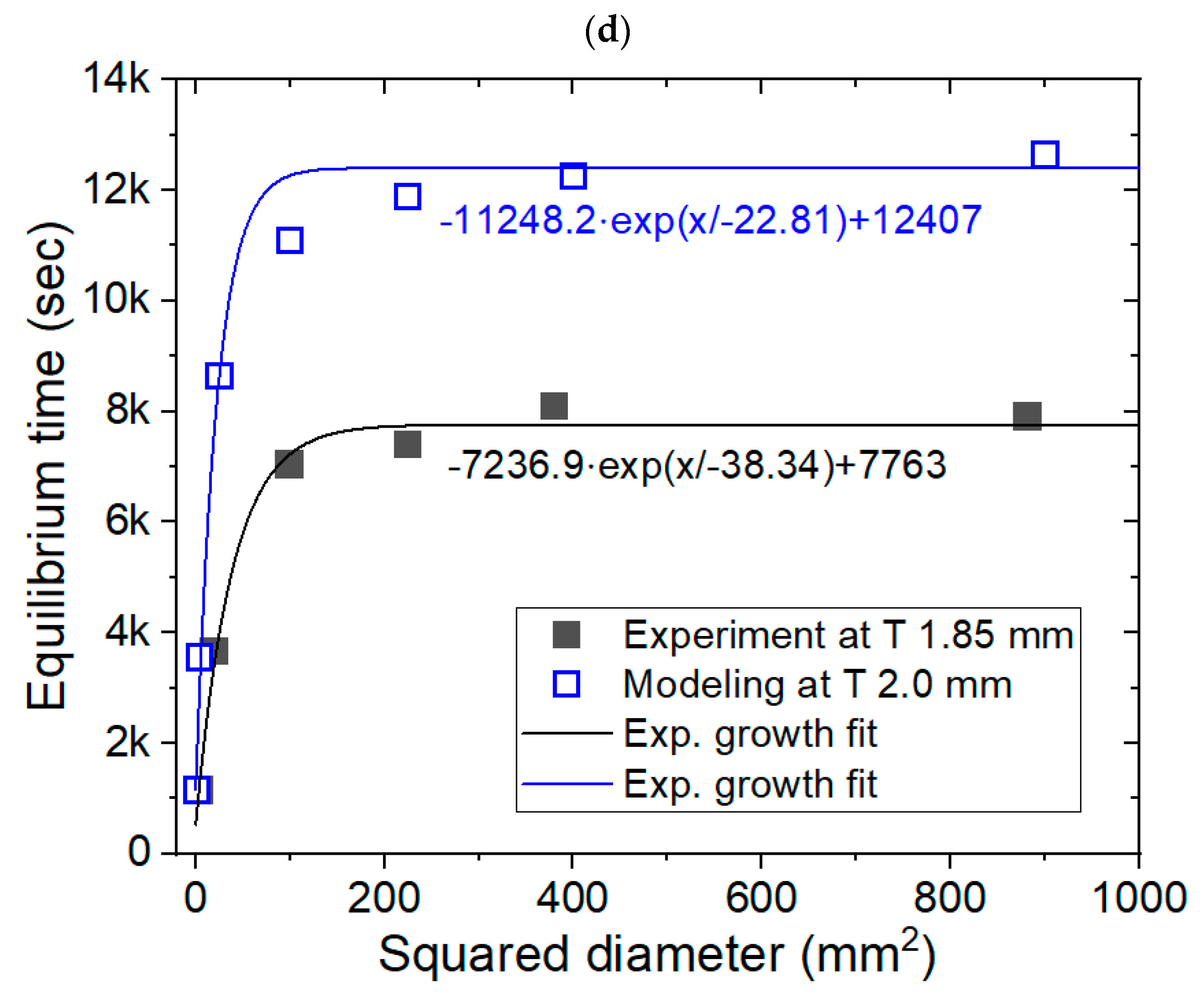
3.1. Modeling for the Cylinder-Shaped Polymer Specimens and Comparison with Experimental Results
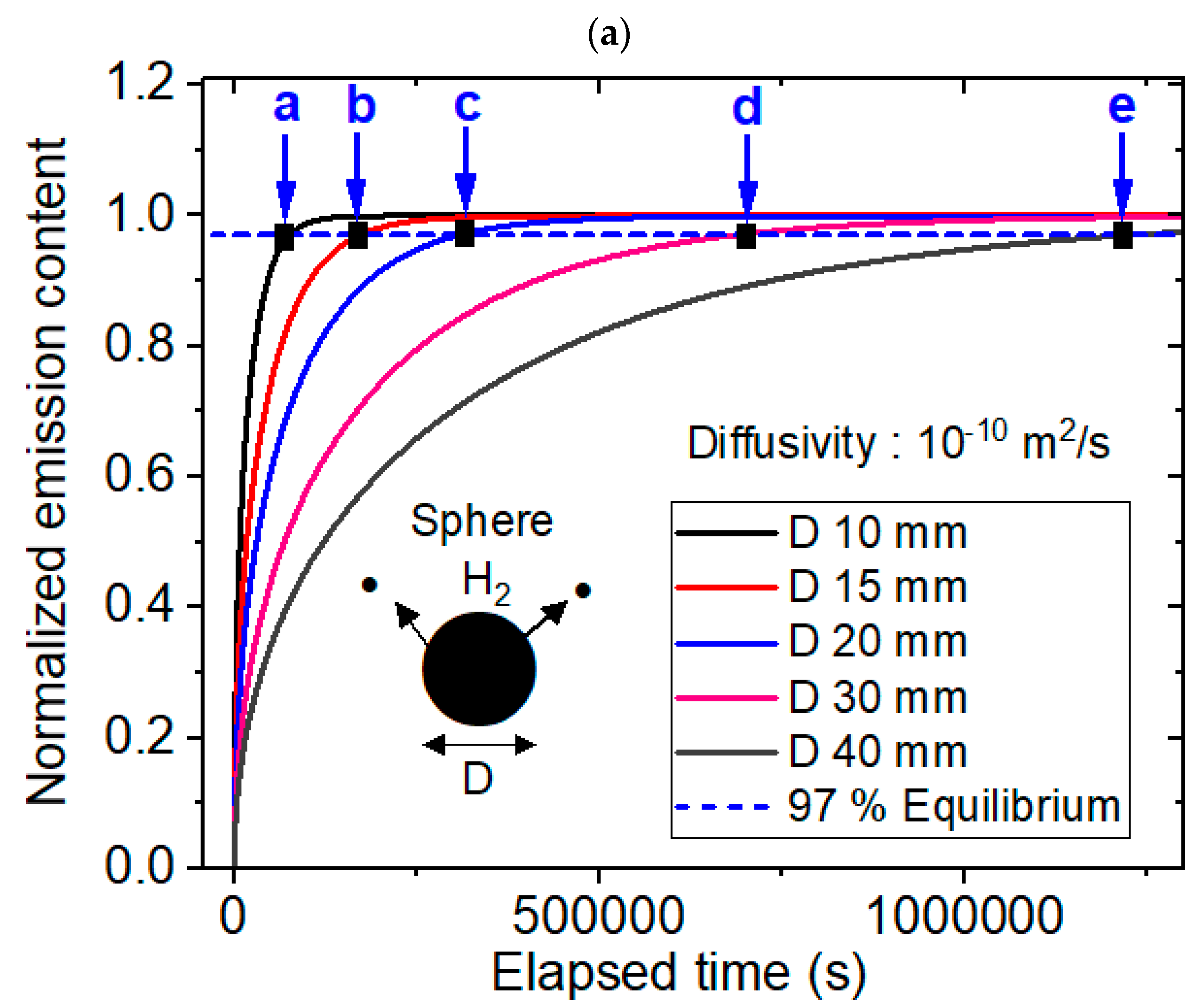
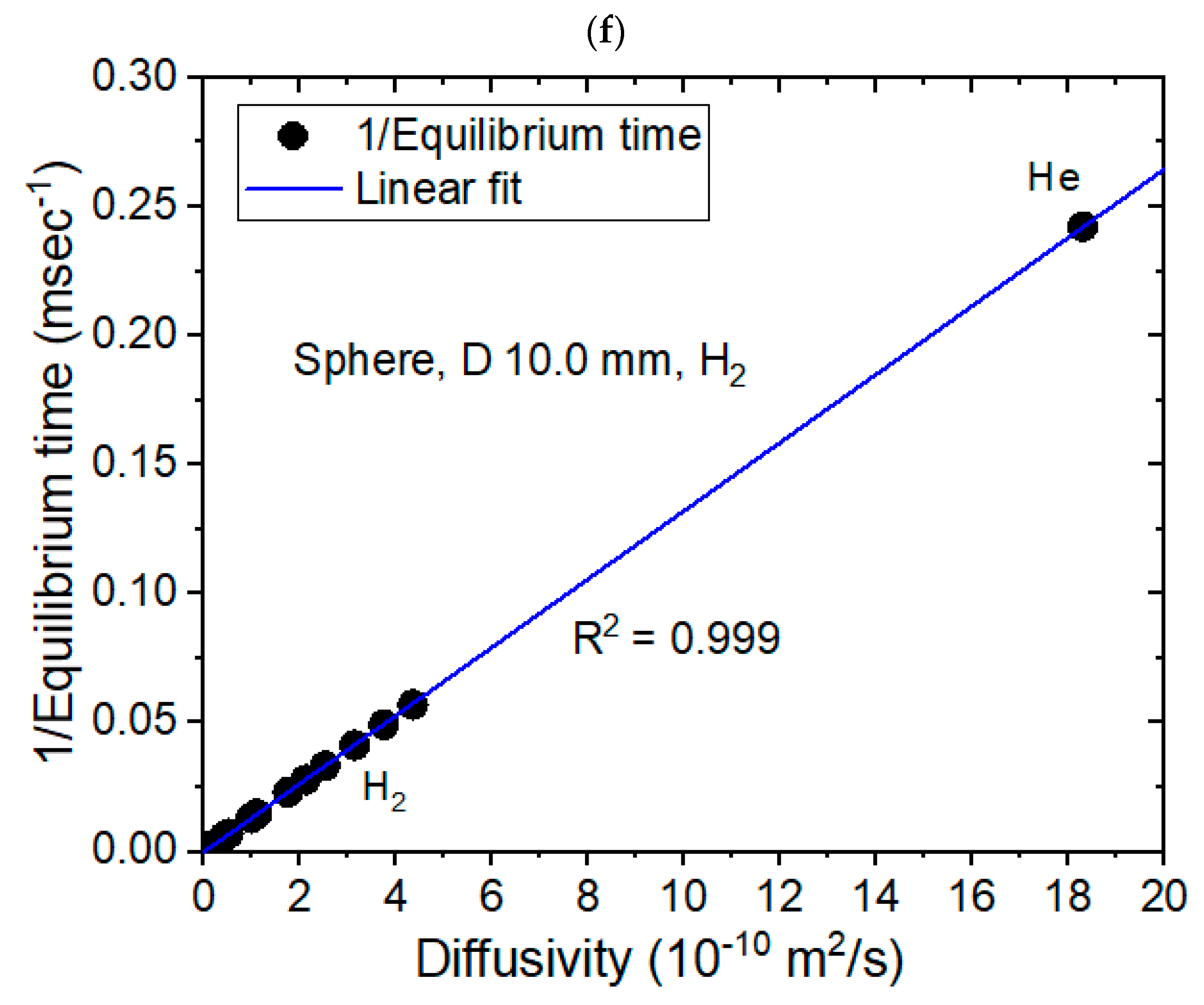
3.2. Modeling for the Sphere-Shaped Polymer Specimens and Comparison with Experimental Results
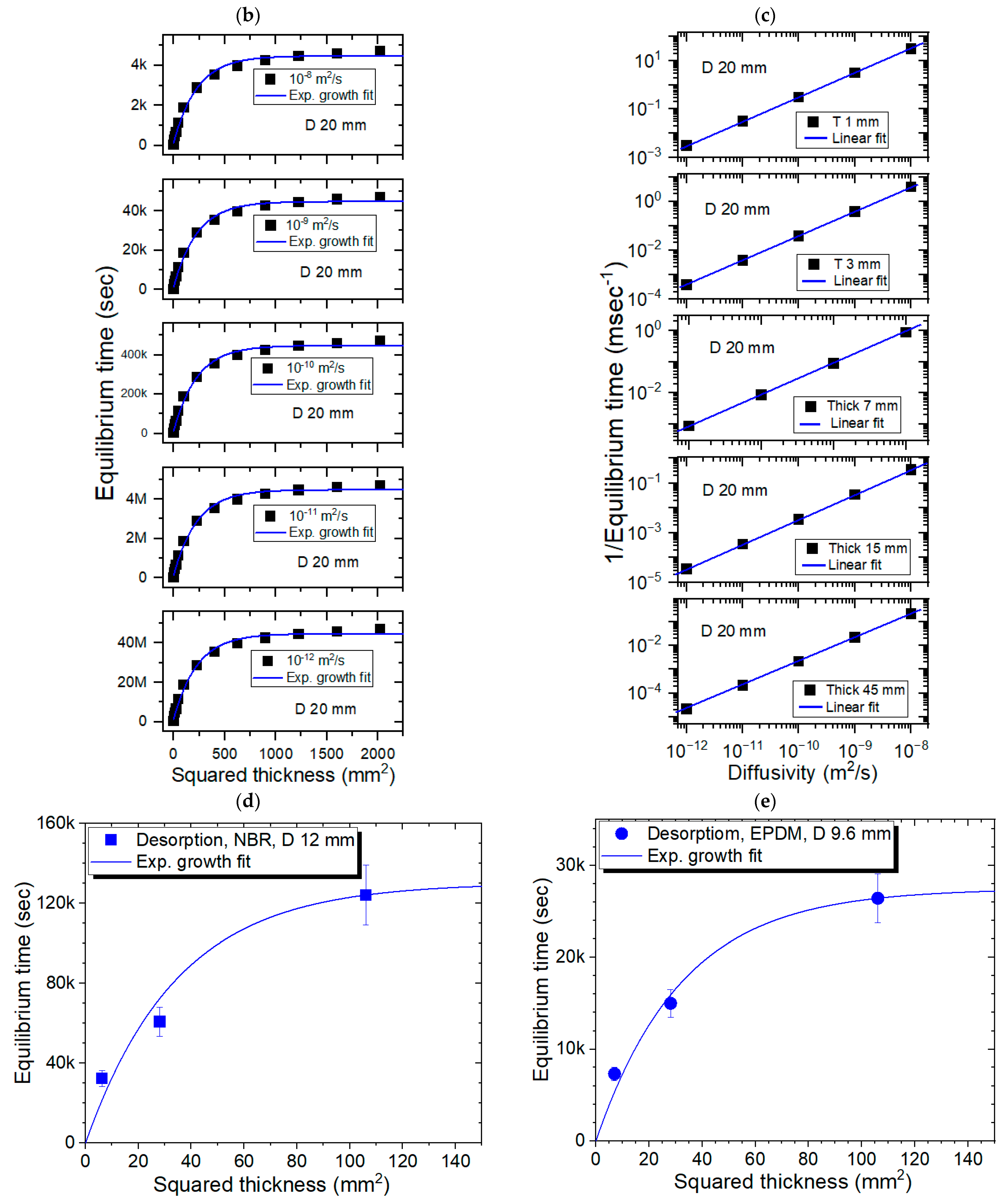
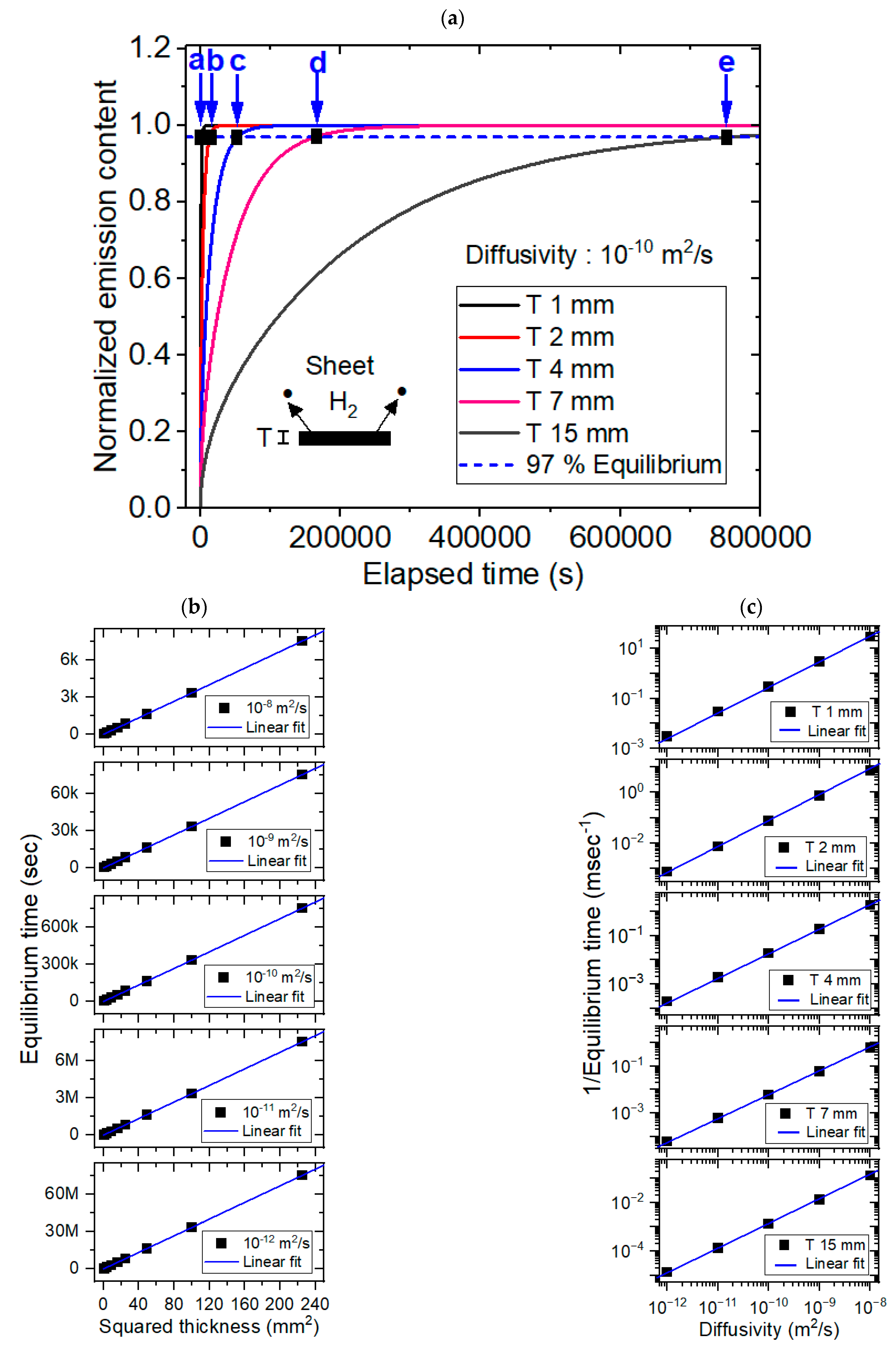
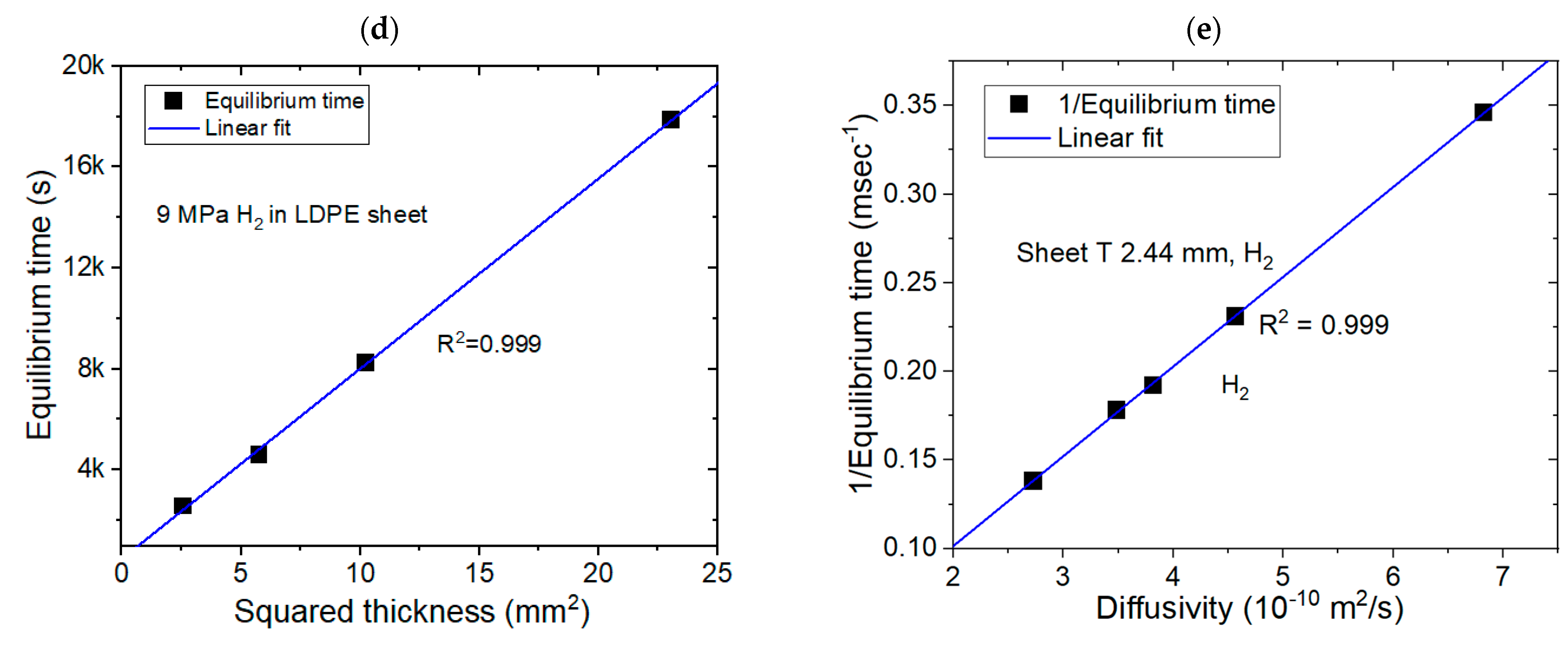
3.3. Modeling for the Sheet-Shaped Polymer Specimens and Comparison with Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
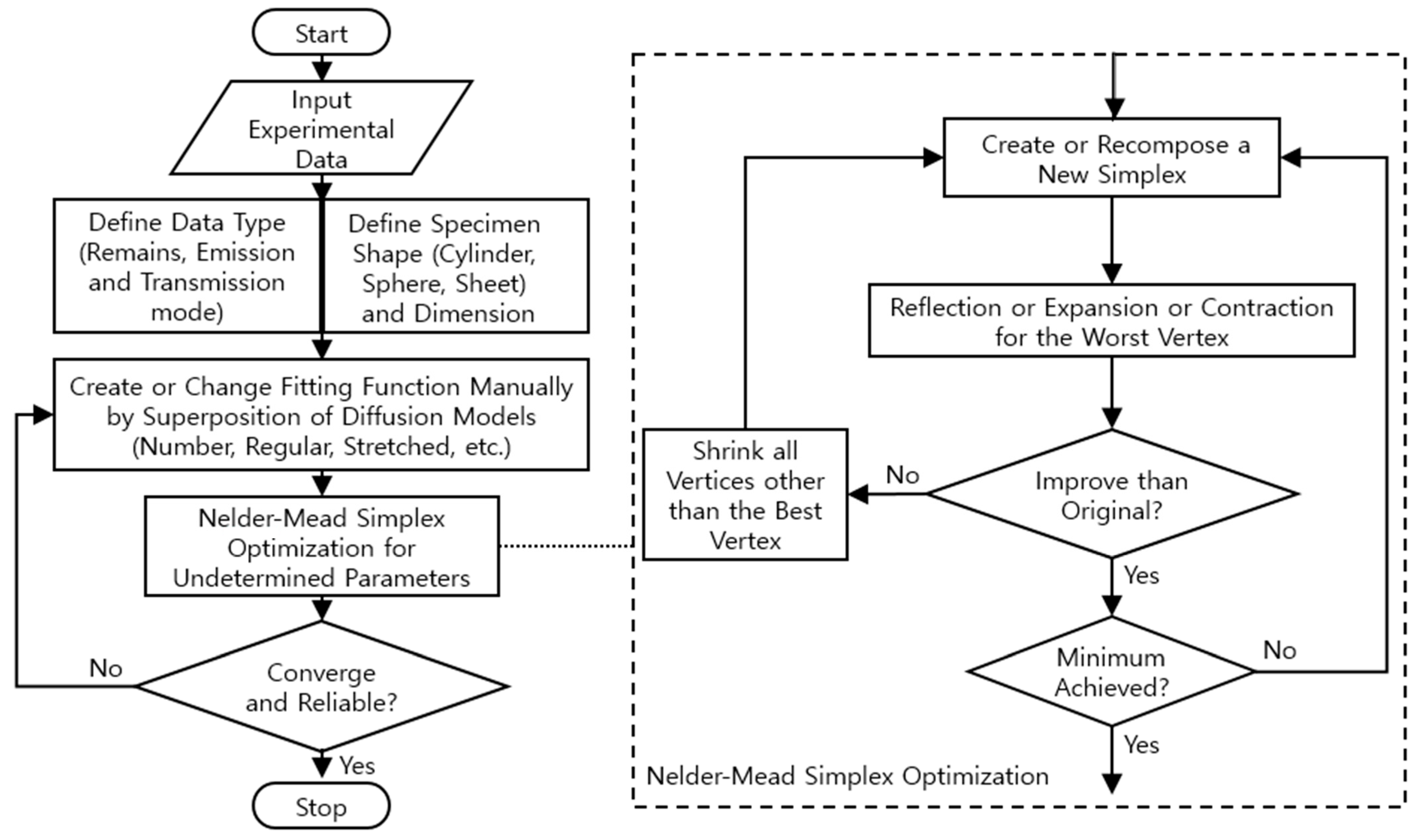
Appendix A. Flowchart, Application Example and Code for Diffusion Analysis Program
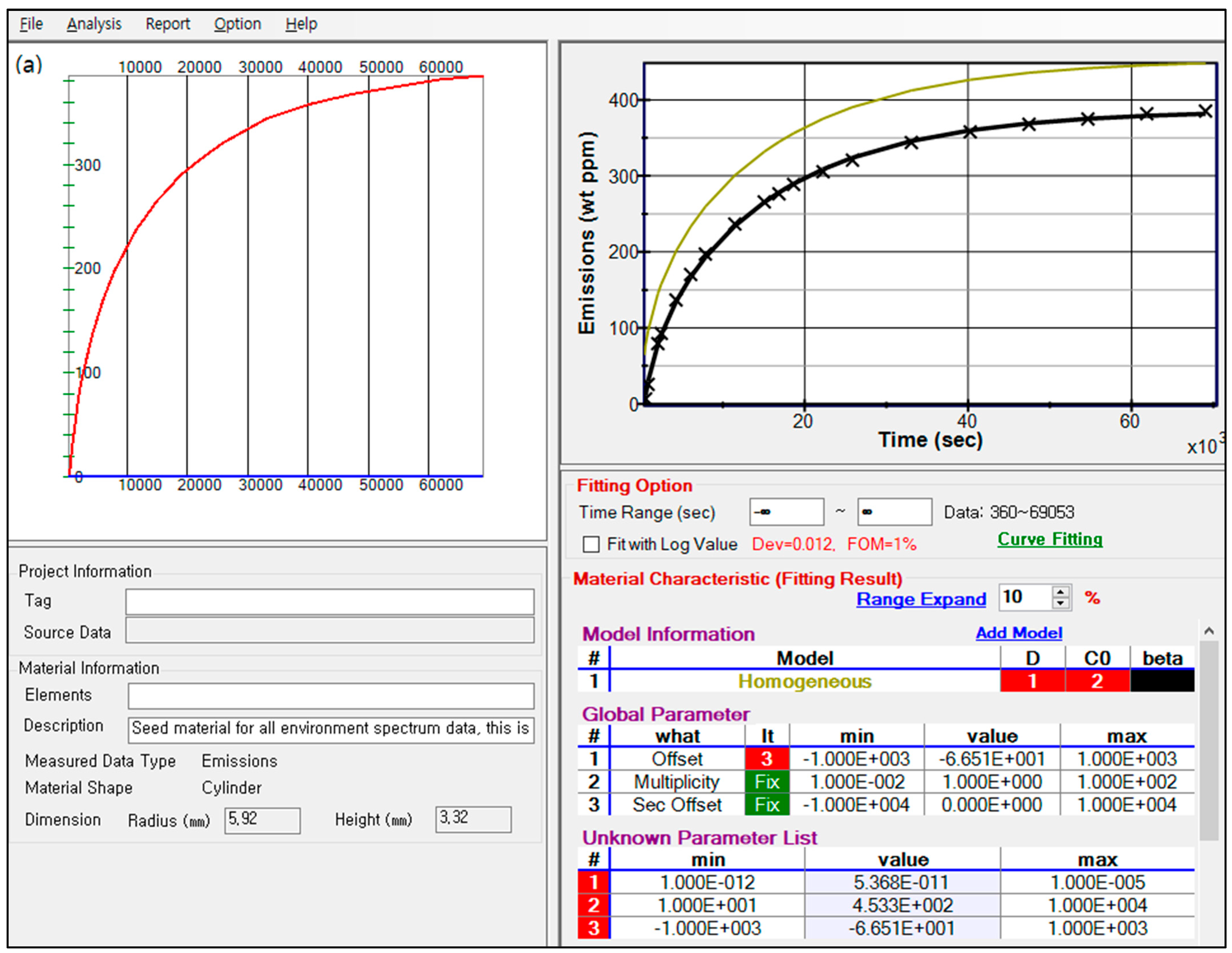
| <Coding of sheet, sphere- and cylinder-shaped specimen in the emission mode> | ||||||
| // Total amount of diffusing gas which has entered the sheet at time t | ||||||
| // Ref: Crank et.al. The Mathematics of Diffusion (1975) p. 47, Equation (4.18) [24] | ||||||
| // D: Diffusion coefficient, L: Sheet thickness | ||||||
| // M: Emitted total amount by diffusion at infinite time. | ||||||
| public double Ftn_Sheet(double t) { | ||||||
| double pi2 = Math.PI × Math.PI; | ||||||
| double zSum = 0; | ||||||
| for (int n = 0; n < 50; ++n) { | ||||||
| int n21 = (2 × n + 1) × (2 × n + 1); | ||||||
| double add = Math.Exp(−D × n21 × pi2 × t/(L × L))/n21; | ||||||
| double zSumAdded = zSum + add; | ||||||
| if (zSum >= zSumAdded) break; // When convergence achieved | ||||||
| zSum = zSumAdded; | ||||||
| } | ||||||
| return M − 8/pi2 × (M × zSum); | ||||||
| } | ||||||
| // Total amount of diffusing gas which has entered the sphere at time t. | ||||||
| // Ref: Crank et.al. The Mathematics of Diffusion (1975) p. 91, Equation (6.20) [24] | ||||||
| // D: Diffusion Coefficient, a: Radius of sphere. | ||||||
| // M: Emitted total amount by diffusion at infinite time. | ||||||
| public double Ftn_Sphere(double t) { | ||||||
| double pi2 = Math.PI × Math.PI; | ||||||
| double zSum = 0; | ||||||
| for (int n = 1; n < 100; ++n) { | ||||||
| int n2 = n × n; | ||||||
| double add = Math.Exp(−D × n2 × pi2 × t/(a × a))/n2; | ||||||
| double zSumAdded = zSum + add; | ||||||
| if (zSum >= zSumAdded) break; // When convergence achieved | ||||||
| zSum = zSumAdded; | ||||||
| } | ||||||
| return M − 6/pi2 × (M × zSum); | ||||||
| } | ||||||
| // Total amount of diffusing gas which has entered the cylinder at time t. | ||||||
| // Ref: Al Demarez, et. al., Acta Metallurgica (1954), Equation (5) [28] | ||||||
| // D: Diffusion Coefficient, a: Radius of cylinder, L: Length of cylinder | ||||||
| // M: Emitted total amount by diffusion at infinite time. | ||||||
| public double Ftn_Cylinder(double t) { | ||||||
| double pi2 = Math.PI × Math.PI; | ||||||
| double zSum = 0; | ||||||
| for (int n = 0; n < 100; ++n) { | ||||||
| int n2 = (2 × n + 1) × (2 × n + 1); | ||||||
| double add = Math.Exp(−n2 × pi2 × D × t/(L × L))/n2; | ||||||
| double zSumAdded = zSum + add; | ||||||
| if (zSum >= zSumAdded) break; // When convergence achieved | ||||||
| zSum = zSumAdded; | ||||||
| } | ||||||
| double rSum = 0; | ||||||
| for (int n = 1; n <= 50; ++n) { | ||||||
| double b = Bessel0root[n − 1]; | ||||||
| double add = Math.Exp(−D × b × b × t/(a × a))/(b × b); | ||||||
| double rSumAdded = rSum + add; | ||||||
| if (rSum >= rSumAdded) break; // When convergence achieved | ||||||
| rSum = rSumAdded; | ||||||
| } | ||||||
| return M − 32/pi2 × (M × zSum × rSum); | ||||||
| } | ||||||
| // Zeros of first kind Bessel function J_0(x) | ||||||
| public static double[] bessel0root = | ||||||
| new double[] {2.40482556, 5.52007811, 8.65372791, 11.79153444, 14.93091771, | ||||||
| 18.07106397, 21.21163663, 24.35247153, 27.49347913, 30.63460647, | ||||||
| 33.77582021, 36.91709835, 40.05842576, 43.19979171, 46.34118837, | ||||||
| 49.4826099, 52.62405184, 55.76551076, 58.90698393, 62.04846919, | ||||||
| 65.1899648, 68.33146933, 71.4729816, 74.61450064, 77.75602563, | ||||||
| 80.89755587, 84.03909078, 87.18062984, 90.32217264, 93.46371878, | ||||||
| 96.605267951, 99.74681986, 102.88837425, 106.02993092, 109.17148965, | ||||||
| 112.3130503, 115.45461265, 118.59617663, 121.73774209, 124.87930891, | ||||||
| 128.020877, 131.1624463, 134.3040166, 137.445588, 140.5871604, | ||||||
| 143.7287336, 146.8703076, 150.0118825, 153.153458, 156.2950343}; | ||||||
| // Nelder-Mead Simplex Optimization. | ||||||
| // Return value is fit error | ||||||
| // Optima(class): Manage all optimization procedure and calc. error and FOM etc. | ||||||
| // Simplex(Class): Polytope of N + 1 vertices in N dim. undetermined param. space. | ||||||
| // Vertex(Class): One of N + 1 vertices of Simplex. | ||||||
| // Coord(Class): Having coord. of vertex and methods, reflect(), expand(), … | ||||||
| // simplexProtocol: ExpFactor = 2.0, ConFactor = 0.5, PrcntInitCoef = 5.0, … | ||||||
| public double Iterate(double[] unknowns) { | ||||||
| int b, w; | ||||||
| int loop = 0; // # of loops | ||||||
| int dim = unknowns.Length; | ||||||
| Simplex simplex = new Simplex(unknowns, simplexProtocol.PrcntInitCoef); | ||||||
| // Calculate errors for each vertexes. | ||||||
| for (int i = 0; i < dim + 1; ++i) | ||||||
| simplex.s[i].error = optima.ErrorF(simplex.s[i].coord); | ||||||
| do { // start iteration | ||||||
| b = simplex.bestVertex(); // find best and worst vertices | ||||||
| w = simplex.worstVertex(); | ||||||
| // calculate the midPoint of the non-worst values for later calc’s | ||||||
| double[] mp = simplex.midPoint(w); | ||||||
| Vertex refl_vrtx = new Vertex(simplex.s[w]); // save the old values | ||||||
| Coord.reflect(mp, refl_vrtx.coord); // first try a reflection | ||||||
| refl_vrtx.error = optima.ErrorF(refl_vrtx.coord); | ||||||
| // is the new vertex better or equal to the old best vertex | ||||||
| if (refl_vrtx.error < simplex.s[b].error) { | ||||||
| // try to expand the reflected vertex next | ||||||
| Vertex expd_vrtx = new Vertex(refl_vrtx); | ||||||
| Coord.expand(mp, expd_vrtx.coord, simplexProtocol.ExpFactor); | ||||||
| expd_vrtx.error = optima.ErrorF(expd_vrtx.coord); | ||||||
| // if the expanded vertex is not as good or better than the best | ||||||
| // revert to the reflected vertex | ||||||
| if (expd_vrtx.error <= refl_vrtx.error) simplex.s[w] = expd_vrtx; | ||||||
| else simplex.s[w] = refl_vrtx; | ||||||
| } else { | ||||||
| if (refl_vrtx.error <= simplex.s[w].error) simplex.s[w] = refl_vrtx; | ||||||
| else { | ||||||
| Vertex cont_vrtx = new Vertex(simplex.s[w]); | ||||||
| Coord.contract(mp, cont_vrtx.coord, simplexProtocol.ConFactor); | ||||||
| cont_vrtx.error = optima.ErrorF(cont_vrtx.coord); | ||||||
| if (cont_vrtx.error <= simplex.s[w].error) simplex.s[w] = cont_vrtx; | ||||||
| else { | ||||||
| simplex.contract_all(b, simplexProtocol.ConFactor); | ||||||
| for (int i = 0; i < dim + 1; ++i) | ||||||
| simplex.s[i].error = otima.ErrorF(simplex.s[i].coord); | ||||||
| }; // else | ||||||
| }; // else | ||||||
| }; | ||||||
| ++loop; | ||||||
| } while (!(simplex.s[b].error <= simplexProtocol.Tolerance || | ||||||
| loop >= simplexProtocol.InternalLoop)); | ||||||
| // return best result | ||||||
| for (int i = 0; i < dim; ++i) unknowns[i] = simplex.s[b].coord[i]; | ||||||
| return simplex.s[b].error; | ||||||
| } | ||||||
References
- Zheng, Y.; Tan, Y.; Zhou, C.; Chen, G.; Li, J.; Liu, Y.; Liao, B.; Zhang, G. A review on effect of hydrogen on rubber seals used in the high-pressure hydrogen infrastructure. Int. J. Hydrogen Energy 2020, 45, 23721–23738. [Google Scholar] [CrossRef]
- Nishimura, S. Rubbers and elastomers for high-pressure hydrogen seal. Soc. Polym. Sci. 2015, 64, 356–357. [Google Scholar]
- Lipiäinen, S.; Lipiäinen, K.; Ahola, A.; Vakkilainen, E. Use of existing gas infrastructure in European hydrogen economy. Int. J. Hydrogen Energy 2023, 48, 31317–31329. [Google Scholar] [CrossRef]
- Sahin, H.; Gondal, I.; Sahir, M. Prospects of natural gas pipeline infrastructure in hydrogen transportation. Int. J. Energy Res. 2012, 36, 1338–1345. [Google Scholar] [CrossRef]
- Dou, X.; Zhu, T.; Wang, Z.; Sun, W.; Lai, Y.; Sui, K.; Tan, Y.; Zhang, Y.; Yuan, W.Z. Color-tunable, excitation-dependent, and time-dependent afterglows from pure organic amorphous polymers. Adv. Mater. 2020, 32, 2004768. [Google Scholar] [CrossRef]
- Singh, S.B.; De, M. Thermally exfoliated graphene oxide for hydrogen storage. Mater. Chem. Phys. 2020, 239, 122102. [Google Scholar] [CrossRef]
- Pan, M.; Pan, C.; Li, C.; Zhao, J. A review of membranes in proton exchange membrane fuel cells: Transport phenomena, performance and durability. Renew. Sustain. Energy Rev. 2021, 141, 110771. [Google Scholar] [CrossRef]
- Ravera, F.; Dziza, K.; Santini, E.; Cristofolini, L.; Liggieri, L. Emulsification and emulsion stability: The role of the interfacial properties. Adv. Colloid Interface Sci. 2021, 288, 102344. [Google Scholar] [CrossRef]
- Briottet, L.; Moro, I.; Lemoine, P. Quantifying the hydrogen embrittlement of pipeline steels for safety considerations. Int. J. Hydrogen Energy 2012, 37, 17616–17623. [Google Scholar] [CrossRef]
- Huang, Q.; Li, X.; Li, J.; Liu, Y.; Li, X.; Zhu, C. Overview of standards on pressure cycling test for on-board composite hydrogen storage cylinders. In Proceedings of the Volume 1: Codes and Standards; ASME: Nevada, CA, USA, 2022; p. 7. [Google Scholar]
- Tanioka, A.; Oobayashi, A.; Kageyama, Y.; Miyasaka, K.; Ishikawa, K. Effects of carbon filler on sorption and diffusion of gases through rubbery materials. J. Polym. Sci. Polym. Phys. Ed. 1982, 20, 2197–2208. [Google Scholar] [CrossRef]
- Sereda, L.; Mar López-González, M.; Yuan Visconte, L.L.; Nunes, R.C.R.; Guimarães Furtado, C.R.; Riande, E. Influence of silica and black rice husk ash fillers on the diffusivity and solubility of gases in silicone rubbers. Polymer 2003, 44, 3085–3093. [Google Scholar] [CrossRef]
- Wang, Z.F.; Wang, B.; Qi, N.; Zhang, H.F.; Zhang, L.Q. Influence of fillers on free volume and gas barrier properties in styrene-butadiene rubber studied by positrons. Polymer 2005, 46, 719–724. [Google Scholar] [CrossRef]
- Barrer, R.M.; Chio, H.T. Solution and diffusion of gases and vapors in silicone rubber membranes. J. Polym. Sci. C Polym. Symp. 1965, 10, 111–138. [Google Scholar] [CrossRef]
- Robeson, L.M.; Liu, Q.; Freeman, B.D.; Paul, D.R. Comparison of transport properties of rubbery and glassy polymers and the relevance to the upper bound relationship. J. Membr. Sci. 2015, 476, 421–431. [Google Scholar] [CrossRef]
- Jung, J.K.; Kim, I.G.; Jeon, S.K.; Kim, K.-T.; Baek, U.B.; Nahm, S.H. Volumetric analysis technique for analyzing the transport properties of hydrogen gas in cylindrical-shaped rubbery polymers. Polym. Test. 2021, 99, 107147. [Google Scholar] [CrossRef]
- Jung, J.K.; Kim, I.G.; Kim, K.T.; Ryu, K.S.; Chung, K.S. Evaluation techniques of hydrogen permeation in sealing rubber materials. Polym. Test. 2021, 93, 107016. [Google Scholar] [CrossRef]
- Jung, J.K. Review of developed methods for measuring gas uptake and diffusivity in polymers enriched by pure gas under high pressure. Polymers 2024, 16, 723. [Google Scholar] [CrossRef] [PubMed]
- Fujiwara, H.; Nishimura, S. Evaluation of hydrogen dissolved in rubber materials under high-pressure exposure using nuclear magnetic resonance. Polym. J. 2012, 44, 832–837. [Google Scholar] [CrossRef]
- Müller, M.; Mishra, R.K.; Šleger, V.; Pexa, M.; Čedík, J. Elastomer-based sealing o-rings and their compatibility with methanol, ethanol, and hydrotreated vegetable oil for fueling internal combustion engines. Materials 2024, 17, 430. [Google Scholar] [CrossRef] [PubMed]
- Philibert, J. One and a half century of diffusion: Fick, Einstein, before and beyond. Diffus. Fundam. 2005, 2, 1.1–1.10. [Google Scholar] [CrossRef]
- Conlisk, A.T. Essentials of Micro-and Nanofluidics: With Applications to the Biological and Chemical Sciences; Cambridge University Press: Cambridge, UK, 2012; p. 43. [Google Scholar]
- Sander, R. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmos. Chem. Phys. 2015, 15, 4399–4981. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Yamabe, J.; Nishimura, S. Influence of fillers on hydrogen penetration properties and blister fracture of rubber composites for O-ring exposed to high-pressure hydrogen gas. Int. J. Hydrogen Energy 2009, 34, 1977–1989. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, S. Estimation and modeling of pressure-dependent gas diffusion coefficient for coal: A fractal theory-based approach. Fuel 2019, 253, 588–606. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Demarez, A.; Hock, A.G.; Meunier, F.A. Diffusion of hydrogen in mild steel. Acta Metallurgica 1954, 2, 214–223. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, J.K.; Lee, J.H.; Park, J.Y.; Jeon, S.K. Modeling of the Time-Dependent H2 Emission and Equilibrium Time in H2-Enriched Polymers with Cylindrical, Spherical and Sheet Shapes and Comparisons with Experimental Investigations. Polymers 2024, 16, 2158. https://doi.org/10.3390/polym16152158
Jung JK, Lee JH, Park JY, Jeon SK. Modeling of the Time-Dependent H2 Emission and Equilibrium Time in H2-Enriched Polymers with Cylindrical, Spherical and Sheet Shapes and Comparisons with Experimental Investigations. Polymers. 2024; 16(15):2158. https://doi.org/10.3390/polym16152158
Chicago/Turabian StyleJung, Jae Kap, Ji Hun Lee, Jae Yeong Park, and Sang Koo Jeon. 2024. "Modeling of the Time-Dependent H2 Emission and Equilibrium Time in H2-Enriched Polymers with Cylindrical, Spherical and Sheet Shapes and Comparisons with Experimental Investigations" Polymers 16, no. 15: 2158. https://doi.org/10.3390/polym16152158
APA StyleJung, J. K., Lee, J. H., Park, J. Y., & Jeon, S. K. (2024). Modeling of the Time-Dependent H2 Emission and Equilibrium Time in H2-Enriched Polymers with Cylindrical, Spherical and Sheet Shapes and Comparisons with Experimental Investigations. Polymers, 16(15), 2158. https://doi.org/10.3390/polym16152158





