Effect of Hydrothermal Aging on Damping Properties in Sisal Mat-Reinforced Polyester Composites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Compounding and Processing
2.3. Hydrothermal Aging
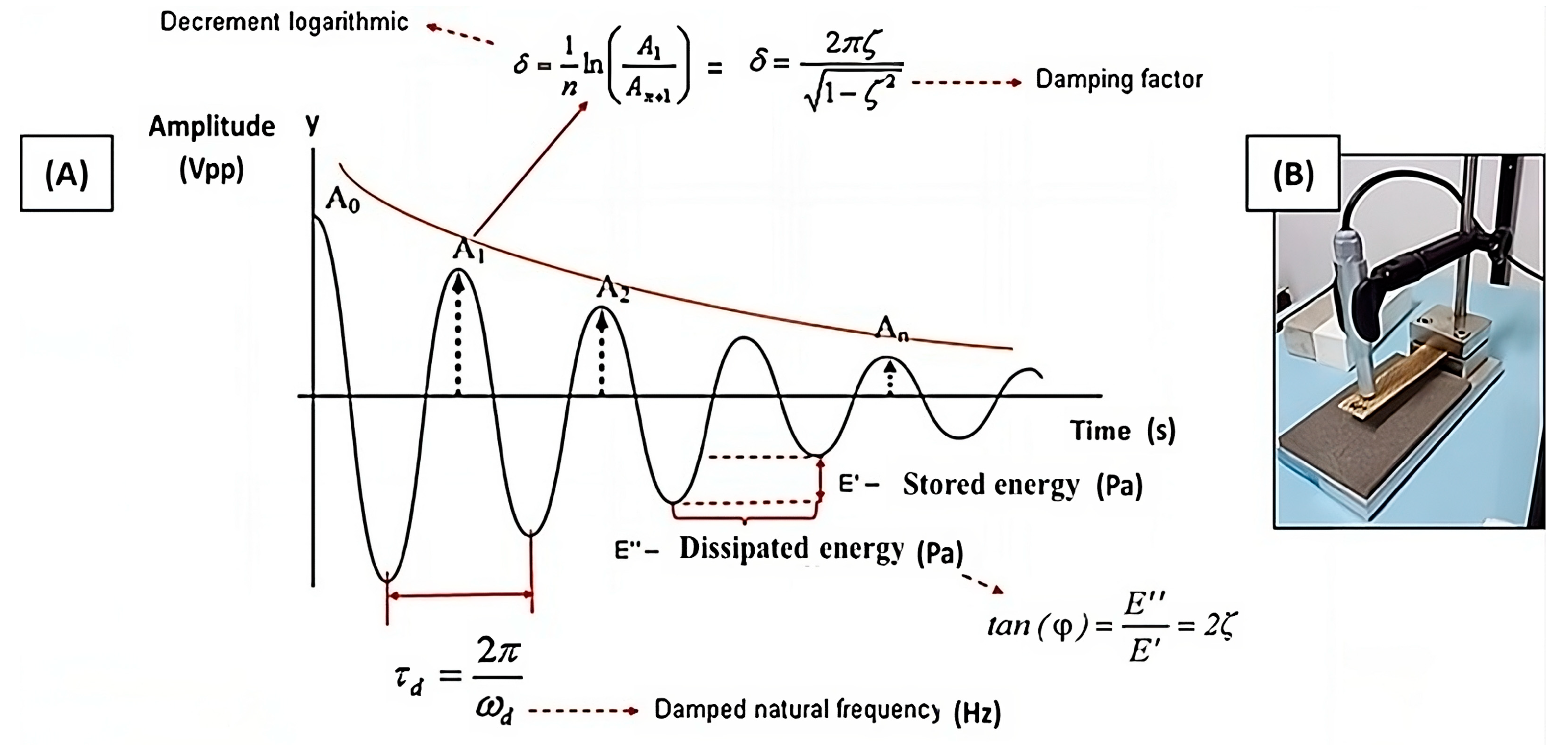
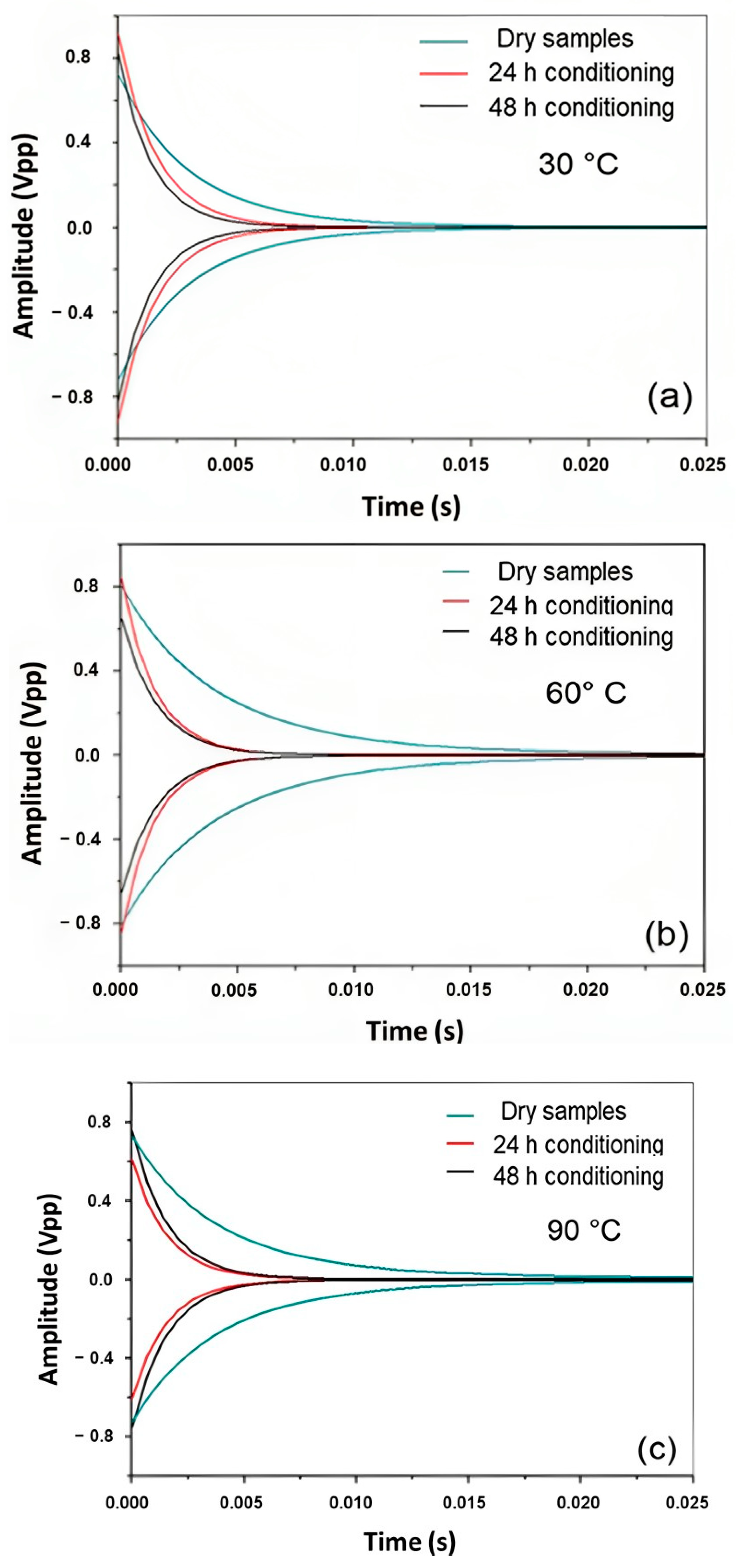
2.4. Damping Analysis
2.5. Scanning Electron Microscopy (SEM)
3. Results and Discussion
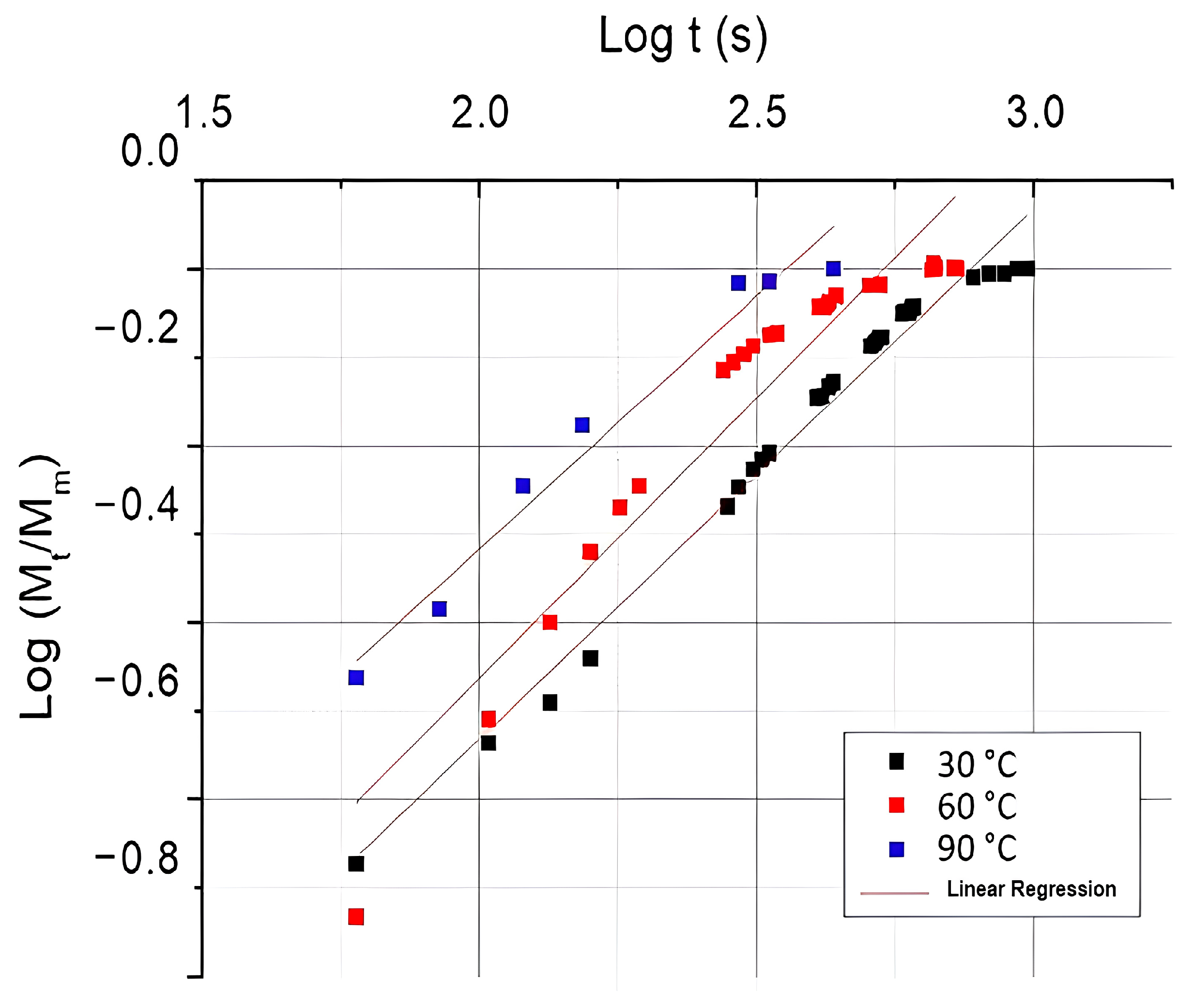
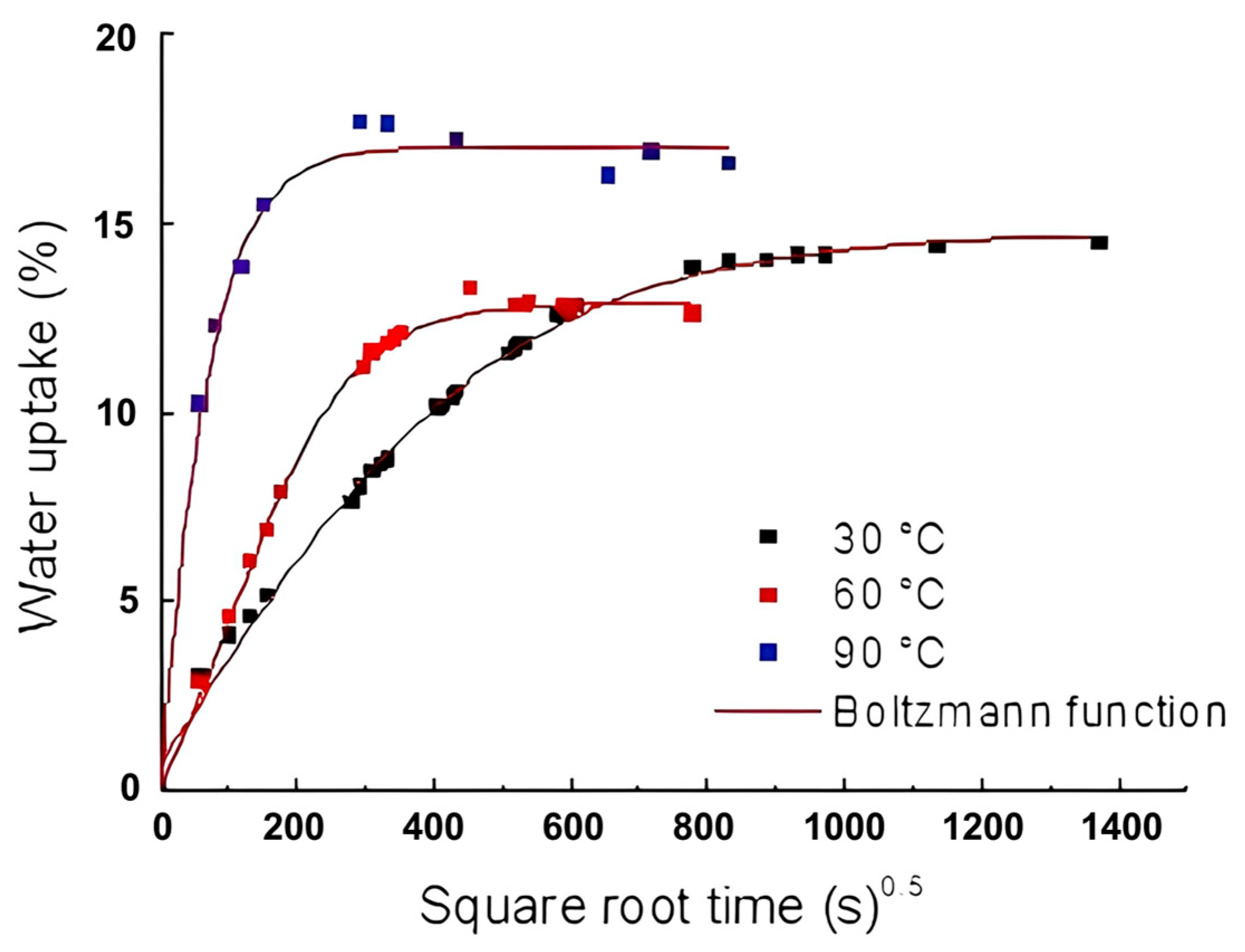
3.1. Water Sorption Kinetics
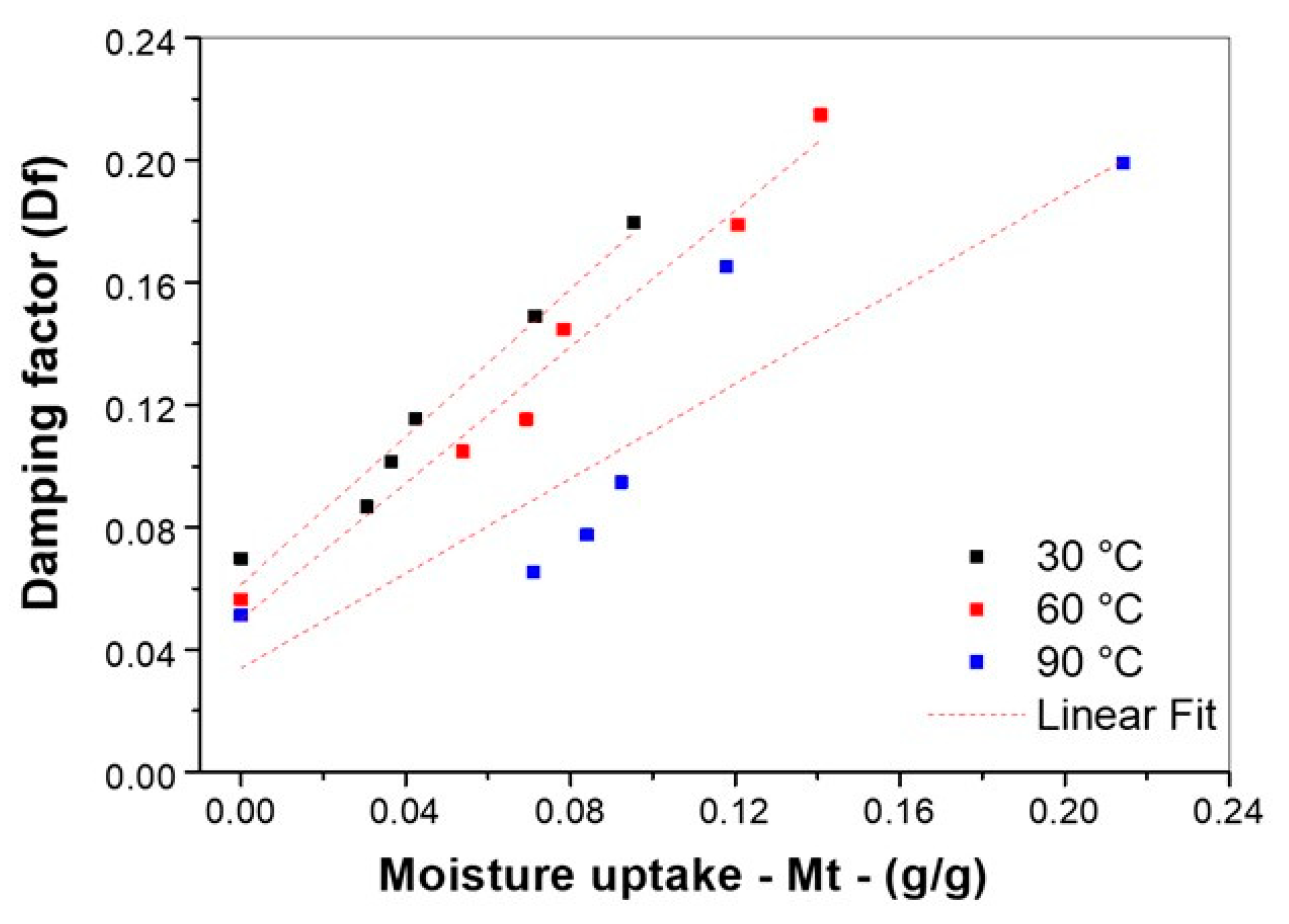
3.2. Damping Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, P.S.S.; Allamraju, K.V. A Review of Natural Fiber Composites [Jute, Sisal, Kenaf]. Mater. Today Proc. 2019, 18, 2556–2562. [Google Scholar] [CrossRef]
- Peças, P.; Carvalho, H.; Salman, H.; Leite, M. Natural Fibre Composites and Their Applications: A Review. J. Compos. Sci. 2018, 2, 66. [Google Scholar] [CrossRef]
- David-West, O. Water Absorption and Effect of Temperature on the Characteristics of Flax/Hemp Hybrid Composites. Mater. Today Proc. 2020, 31, S227–S231. [Google Scholar] [CrossRef]
- Chilali, A.; Zouari, W.; Assarar, M.; Kebir, H.; Ayad, R. Effect of Water Ageing on the Load-Unload Cyclic Behaviour of Flax Fibre-Reinforced Thermoplastic and Thermosetting Composites. Compos. Struct. 2018, 183, 309–319. [Google Scholar] [CrossRef]
- Parvez, Y.A.; Abuthakeer, S.S. Damping Research in Fibre Reinforced Composites—A Review. Mater. Today Proc. 2021, 44, 1794–1799. [Google Scholar] [CrossRef]
- Sridhar, I.; Venkatesha, C.S. Variation of Damping Property of Polymer Composite under Saline Water Treatment. Int. J. Innov. Eng. Technol. (IJIET) 2013, 2, 420–423. [Google Scholar]
- Berges, M.; Léger, R.; Placet, V.; Person, V.; Corn, S.; Gabrion, X.; Rousseau, J.; Ramasso, E.; Ienny, P.; Fontaine, S. Influence of Moisture Uptake on the Static, Cyclic and Dynamic Behaviour of Unidirectional Flax Fibre-Reinforced Epoxy Laminates. Compos. Part A Appl. Sci. Manuf. 2016, 88, 165–177. [Google Scholar] [CrossRef]
- Cheour, K.; Assarar, M.; Scida, D.; Ayad, R.; Gong, X.-L. Effect of Water Ageing on the Mechanical and Damping Properties of Flax-Fibre Reinforced Composite Materials. Compos. Struct. 2016, 152, 259–266. [Google Scholar] [CrossRef]
- Senthilkumar, K.; Siva, I.; Chandrasekar, M.; Rajini, N.; Kalusuraman, G.; Karthikeyan, S.; Vishnuteja, B.; Mallikarjuna, B. Influence of Curing Temperature on the Mechanical and Free Vibration Properties of Sisal Fiber Reinforced Polyester Composites. AIP Conf. Proc. 2019, 2057, 020066. [Google Scholar] [CrossRef]
- Zai, B.A.; Park, M.K.; Choi, H.S.; Mehboob, H.; Ali, R. Effect of Moisture Absorption on Damping and Dynamic Stiffness of Carbon Fiber/Epoxy Composites. J. Mech. Sci. Technol. 2009, 23, 2998–3004. [Google Scholar] [CrossRef]
- Venkataravanappa, R.Y.; Lakshmikanthan, A.; Kapilan, N.; Chandrashekarappa, M.P.G.; Der, O.; Ercetin, A. Physico-Mechanical Property Evaluation and Morphology Study of Moisture-Treated Hemp–Banana Natural-Fiber Reinforced Green Composites. J. Compos. Sci. 2023, 7, 266. [Google Scholar] [CrossRef]
- Duc, F.; Bourban, P.; Månson, J.-A. The Role of Twist and Crimp on the Vibration Behaviour of Flax Fibre Composites. Compos. Sci. Technol. 2014, 102, 94–99. [Google Scholar] [CrossRef]
- Tang, X.; Yan, X. A Review on the Damping Properties of Fiber Reinforced Polymer Composites. J. Ind. Text. 2020, 49, 693–721. [Google Scholar] [CrossRef]
- Standard Test Method for Water Absorption of Plastics. Available online: https://www.astm.org/d0570-22.html (accessed on 10 June 2023).
- Scida, D.; Assarar, M.; Poilâne, C.; Ayad, R. Influence of Hygrothermal Ageing on the Damage Mechanisms of Flax-Fibre Reinforced Epoxy Composite. Compos. Part B Eng. 2013, 48, 51–58. [Google Scholar] [CrossRef]
- Ghasemi, I.; Kord, B. Long-Term Water Absorption Behaviour of Polypropylene/Wood Flour/Organoclay Hybrid Nanocomposite. Iran. Polym. J. 2009, 18, 683–691. [Google Scholar]
- Standard Test Method for Measuring Vibration-Damping Properties of Materials. Available online: https://www.astm.org/e0756-05r17.html (accessed on 10 June 2023).
- Panthapulakkal, S.; Sain, M. Studies on the Water Absorption Properties of Short Hemp—Glass Fiber Hybrid Polypropylene Composites. J. Compos. Mater. 2007, 41, 1871–1883. [Google Scholar] [CrossRef]
- Kumari, Y.R.; Ramanaiah, K.; Prasad, A.R.; Reddy, K.H.; Sanaka, S.P.; Prudhvi, A.K. Experimental Investigation of Water Absorption Behaviour of Sisal Fiber Reinforced Polyester and Sisal Fiber Reinforced Poly Lactic Acid Composites. Mater. Today: Proc. 2021, 44, 935–940. [Google Scholar] [CrossRef]
- Mazur, K.; Kuciel, S. Mechanical and Hydrothermal Aging Behaviour of Polyhydroxybutyrate-Co-Valerate (PHBV) Composites Reinforced by Natural Fibres. Molecules 2019, 24, 3538. [Google Scholar] [CrossRef]
- Dhakal, H.; Zhang, Z.; Richardson, M. Effect of Water Absorption on the Mechanical Properties of Hemp Fibre Reinforced Unsaturated Polyester Composites. Compos. Sci. Technol. 2007, 67, 1674–1683. [Google Scholar] [CrossRef]
- Yorseng, K.; Mavinkere Rangappa, S.; Parameswaranpillai, J.; Siengchin, S. Influence of accelerated weathering on the mechanical, fracture morphology, thermal stability, contact angle, and water absorption properties of natural fiber fabric-based epoxy hybrid composites. Polymers 2020, 12, 2254. [Google Scholar] [CrossRef]
- Sreekumar, P.; Thomas, S.P.; Saiter, J.M.; Joseph, K.; Unnikrishnan, G.; Thomas, S. Effect of Fiber Surface Modification on the Mechanical and Water Absorption Characteristics of Sisal/Polyester Composites Fabricated by Resin Transfer Molding. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1777–1784. [Google Scholar] [CrossRef]
- Assarar, M.; Scida, D.; EL Mahi, A.; Poilâne, C.; Ayad, R. Influence of Water Ageing on Mechanical Properties and Damage Events of Two Reinforced Composite Materials: Flax-Fibres and Glass-Fibres. Mater. Des. 2011, 32, 788–795. [Google Scholar] [CrossRef]
- Brito MK, T.D.; Santos WR, G.D.; Correia BR, D.B.; Queiroz RA, D.; Tavares FV, D.S.; Oliveira Neto GL, D.; Lima AG, B.D. Moisture Absorption in Polymer Composites Reinforced with Vegetable Fiber: A Three-Dimensional Investigation via Langmuir Model. Polymers 2019, 11, 1847. [Google Scholar] [CrossRef] [PubMed]
- Vilaseca, F.; Mendez, J.; Pèlach, A.; Llop, M.; Cañigueral, N.; Gironès, J.; Turon, X.; Mutjé, P. Composite Materials Derived from Biodegradable Starch Polymer and Jute Strands. Process Biochem. 2007, 42, 329–334. [Google Scholar] [CrossRef]
- Gudayu, A.D.; Steuernagel, L.; Meiners, D.; Gideon, R. Effect of surface treatment on moisture absorption, thermal, and mechanical properties of sisal fiber. J. Ind. Text. 2022, 51 (Suppl. S2), 2853S–2873S. [Google Scholar] [CrossRef]
- Hill, C.A.S.; Norton, A.; Newman, G. The Water Vapor Sorption Behavior of Natural Fibers. J. Appl. Polym. Sci. 2009, 112, 1524–1537. [Google Scholar] [CrossRef]
- Kandola, B.K.; Mistik, S.I.; Pornwannachai, W.; Horrocks, A.R. Effects of Water and Chemical Solutions Ageing on the Physical, Mechanical, Thermal and Flammability Properties of Natural Fibre-Reinforced Thermoplastic Composites. Molecules 2021, 26, 4581. [Google Scholar] [CrossRef]
- Botelho, E.C.; Pardini, L.C.; Rezende, M.C. Hygrothermal Effects on Damping Behavior of Metal/Glass Fiber/Epoxy Hybrid Composites. Mater. Sci. Eng. A 2005, 399, 190–198. [Google Scholar] [CrossRef]
- Shakeri, A.; Ghasemian, A. Water Absorption and Thickness Swelling Behavior of Polypropylene Reinforced with Hybrid Recycled Newspaper and Glass Fiber. Appl. Compos. Mater. 2010, 17, 183–193. [Google Scholar] [CrossRef]
- Gurunathan, T.; Mohanty, S.; Nayak, S.K. A review of the recent developments in biocomposites based on natural fibres and their application perspectives. Compos. Part A Appl. Sci. Manuf. 2015, 77, 1–25. [Google Scholar] [CrossRef]

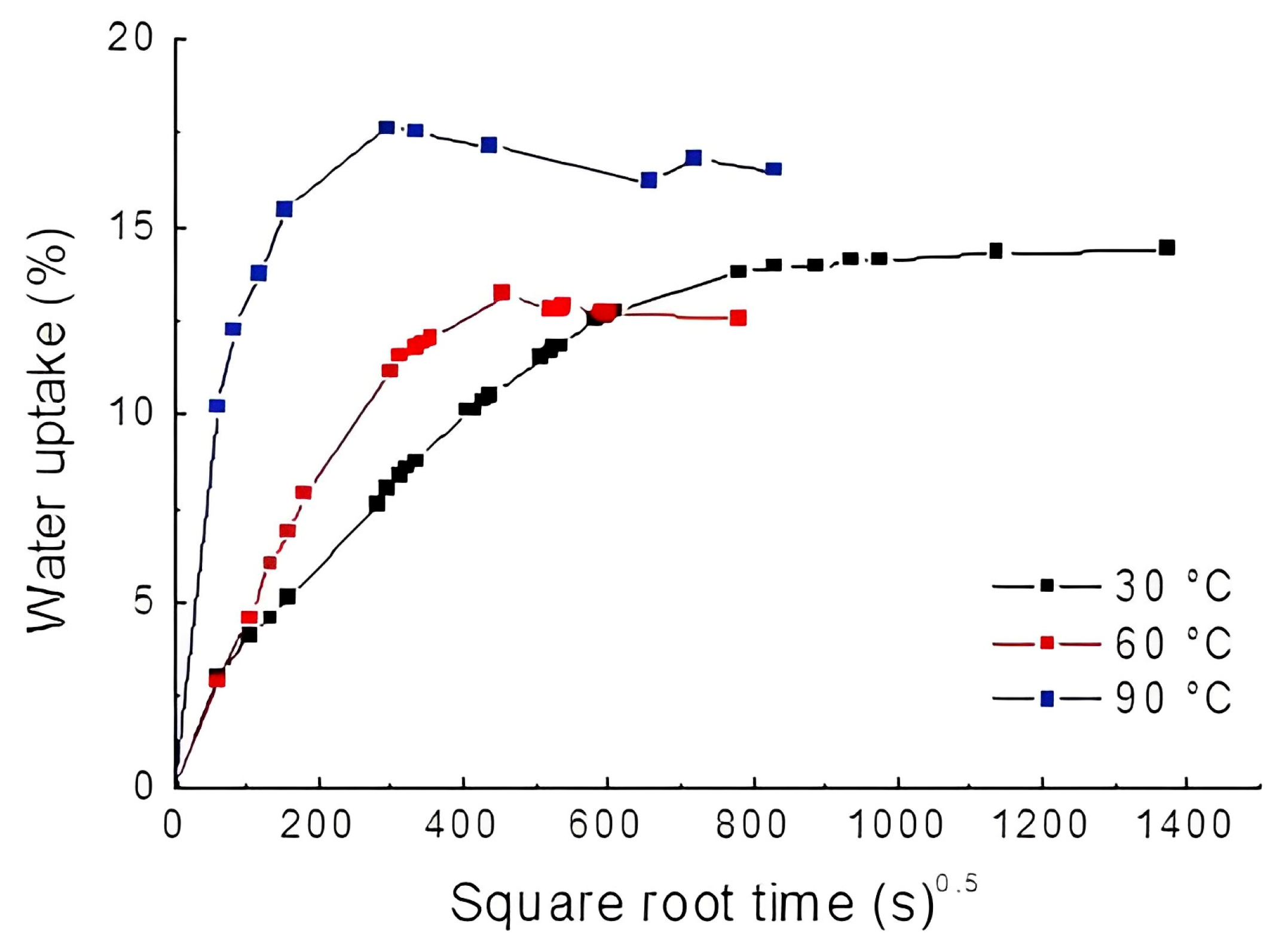

| Temperature (°C) | Equilibrium Moisture (%) | Saturation Time (h) | Diffusion Coefficient (mm2·s−1) |
|---|---|---|---|
| 30 ± 2 | 13.83 ± 0.29 | 264 | 6.01 · 10−6 ± 5.19 · 10−7 |
| 60 ± 2 | 12.85 ± 0.08 | 75 | 1.91 · 10−5 ± 7.16 · 10−7 |
| 90 ± 2 | 16.79 ± 0.28 | 31 | 1.27 · 10−4 ± 1.47 · 10−5 |
| Equation | log (Mt/M∞) = log (k) + n log (t) | ||
|---|---|---|---|
| Temperature | 30 °C | 60 °C | 90 °C |
| R2 | 0.96 | 0.90 | 0.97 |
| n | 0.59 ± 0.017 | 0.63 ± 0.042 | 0.57 ± 0.045 |
| k | 0.0181 | 0.0185 | 0.035 |
| Equation | y = A2 + (A1 − A2)/(1 + exp((x−x0)/dx))) | ||
|---|---|---|---|
| Temperature | 30 °C | 60 °C | 90 °C |
| Correlation (R2) | 0.99 | 0.99 | 0.98 |
| Initial (A1) | −12.97 ± 4.79 | −3.78 ± 0.96 | −105.13 ± 425.88 |
| Final (A2) = M∞ | 14.75 ± 0.18 | 12.85 ± 0.08 | 16.98 ± 0.25 |
| x0 | 6.63 ± 78.16 | 103.49 ± 11.32 | −111.94 ± 281.97 |
| Dx | 246.38 ± 21.86 | 88.48 ± 5.71 | 61.36 ± 19.10 |
| T (°C) | Control Sample | 24 h | 48 h | |||
|---|---|---|---|---|---|---|
| Damping (ζ) × 10−2 | Tan φ × 10−2 | Damping (ζ) × 10−2 | Tan φ × 10−2 | Damping (ζ) × 10−2 | Tan φ × 10−2 | |
| 30 | 7 ± 0.9 | 14 ± 1.8 | 14.9 ± 1.0 | 29.8 ± 2.1 | 18 ± 1.3 | 35.9 ± 2.6 |
| 60 | 2.7 ± 0.9 | 5.4 ± 1.8 | 18.9 ± 2.6 | 37.8 ± 5.3 | 21.4 ± 1.9 | 42.9 ± 3.9 |
| 90 | 6.1 ± 0.7 | 12.3 ± 1.5 | 18.7 ± 1.2 | 37.4 ± 2.5 | 19.9 ± 0.9 | 39.8 ± 1.8 |
| Temperature | Equation | Correlation Coefficient (R2) |
|---|---|---|
| 30 °C | Df = 1.207 × Mt + 0.0613 | 0.964 |
| 60 °C | Df = 1.113 × Mt + 0.0499 | 0.971 |
| 90 °C | Df = 0.775 × Mt + 0.0339 | 0.786 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, M.F.E.; Silva, B.R.; Marques, A.N.; Mattedi, S.; Carvalho, R.F. Effect of Hydrothermal Aging on Damping Properties in Sisal Mat-Reinforced Polyester Composites. Polymers 2024, 16, 166. https://doi.org/10.3390/polym16020166
Silva MFE, Silva BR, Marques AN, Mattedi S, Carvalho RF. Effect of Hydrothermal Aging on Damping Properties in Sisal Mat-Reinforced Polyester Composites. Polymers. 2024; 16(2):166. https://doi.org/10.3390/polym16020166
Chicago/Turabian StyleSilva, Moisés F. E., Beatriz R. Silva, Adrielle N. Marques, Silvana Mattedi, and Ricardo F. Carvalho. 2024. "Effect of Hydrothermal Aging on Damping Properties in Sisal Mat-Reinforced Polyester Composites" Polymers 16, no. 2: 166. https://doi.org/10.3390/polym16020166
APA StyleSilva, M. F. E., Silva, B. R., Marques, A. N., Mattedi, S., & Carvalho, R. F. (2024). Effect of Hydrothermal Aging on Damping Properties in Sisal Mat-Reinforced Polyester Composites. Polymers, 16(2), 166. https://doi.org/10.3390/polym16020166









