Experimental and Numerical Analysis of Bolted Repair for Composite Laminates with Delamination Damage
Abstract
:1. Introduction
2. Theoretical Background
2.1. Basic Formulations
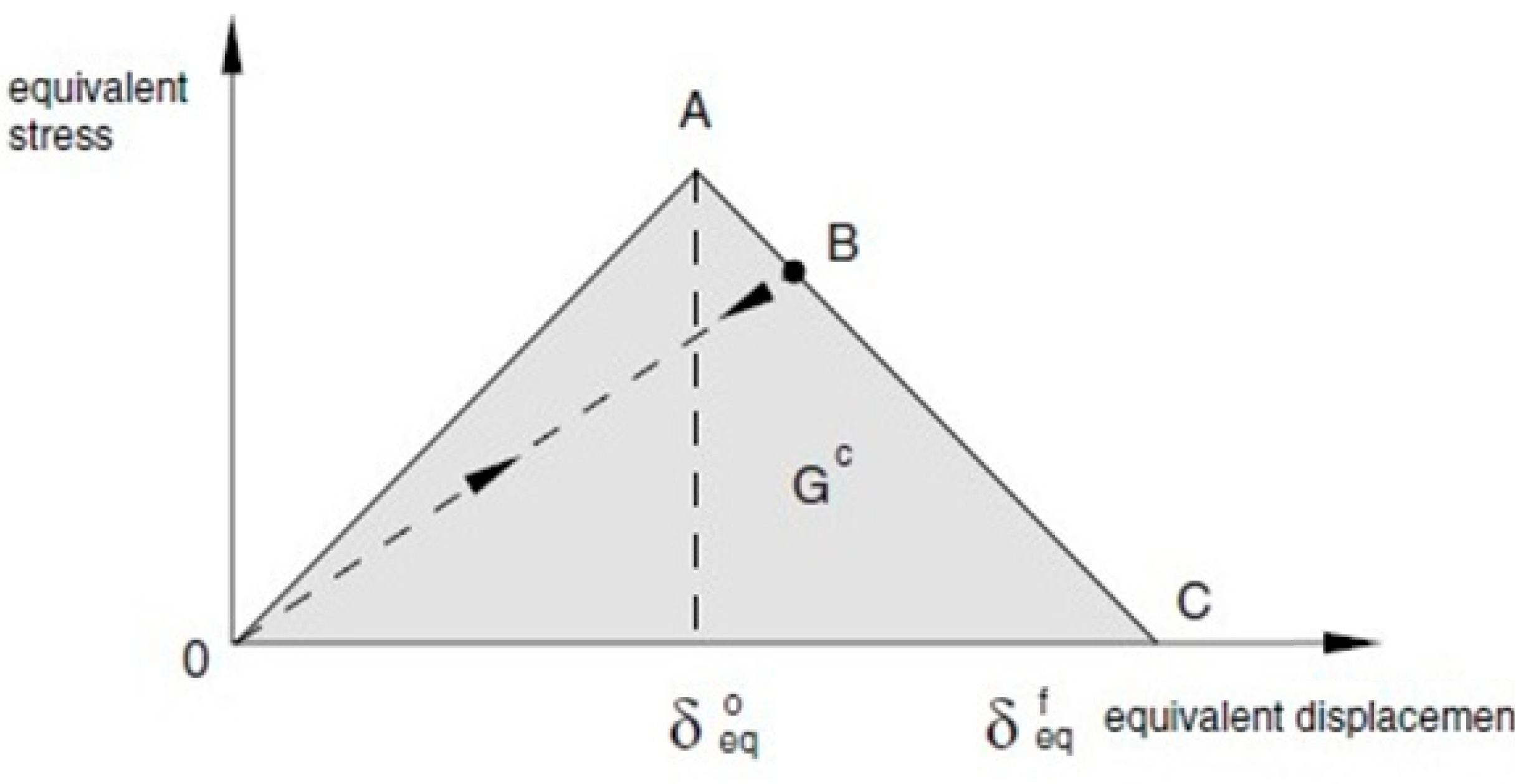
2.2. Progressive Damage Analysis
- Matrix tensile failure
- Matrix compression failure
- Fiber tensile failure
- Fiber compression failure
- Shear failure of fiber matrix
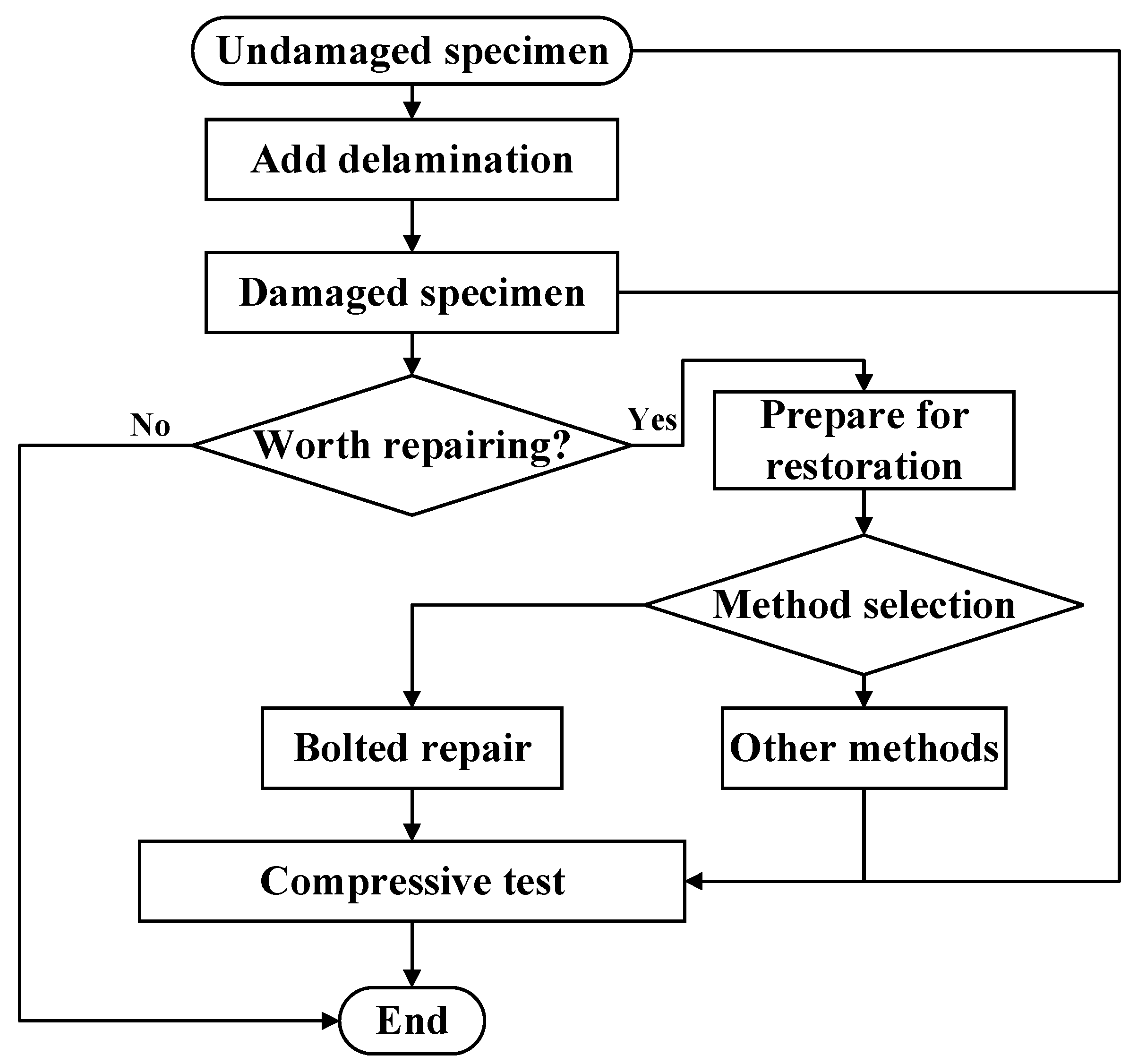
3. Experiment and Simulation Preparation
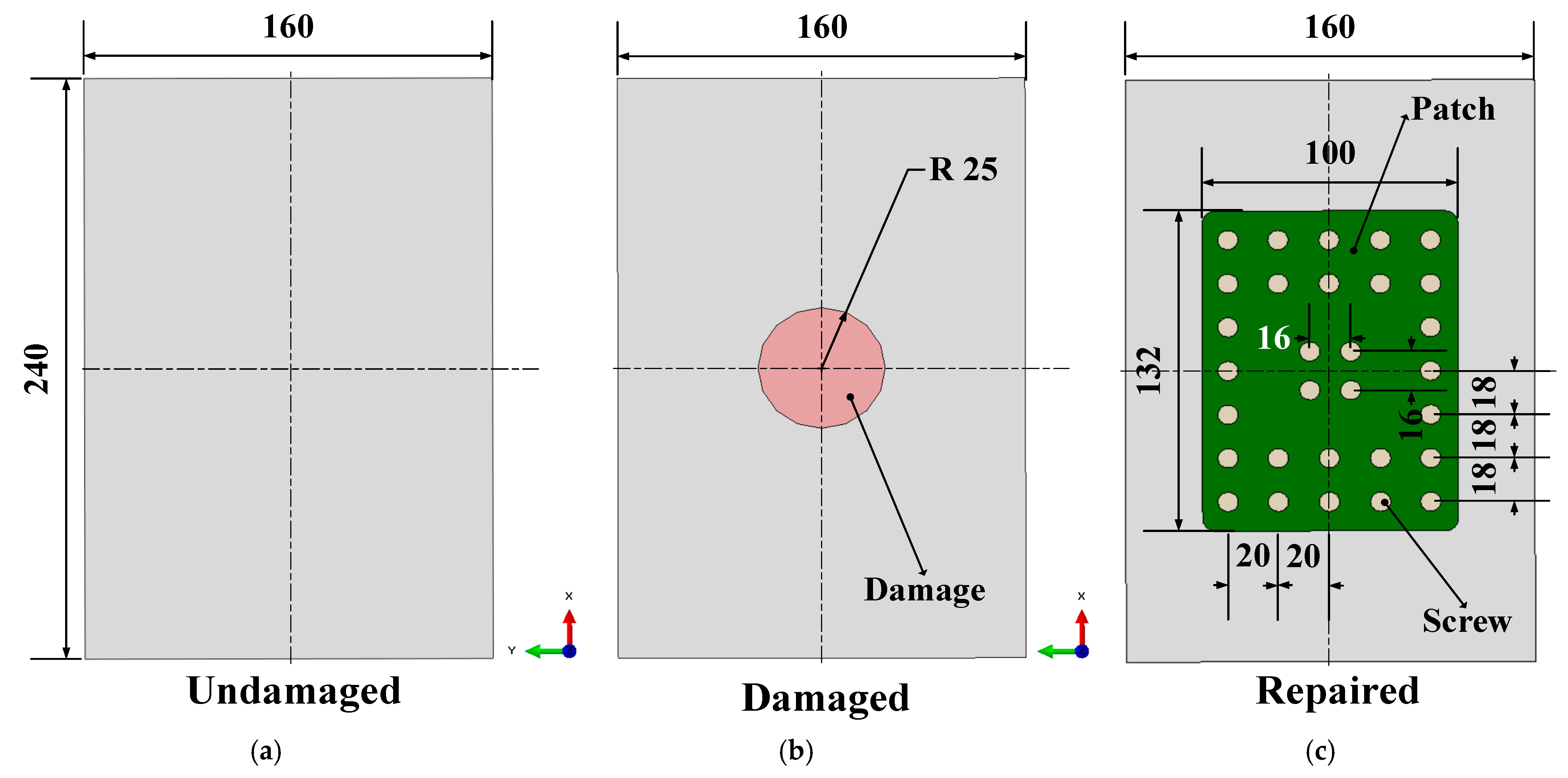
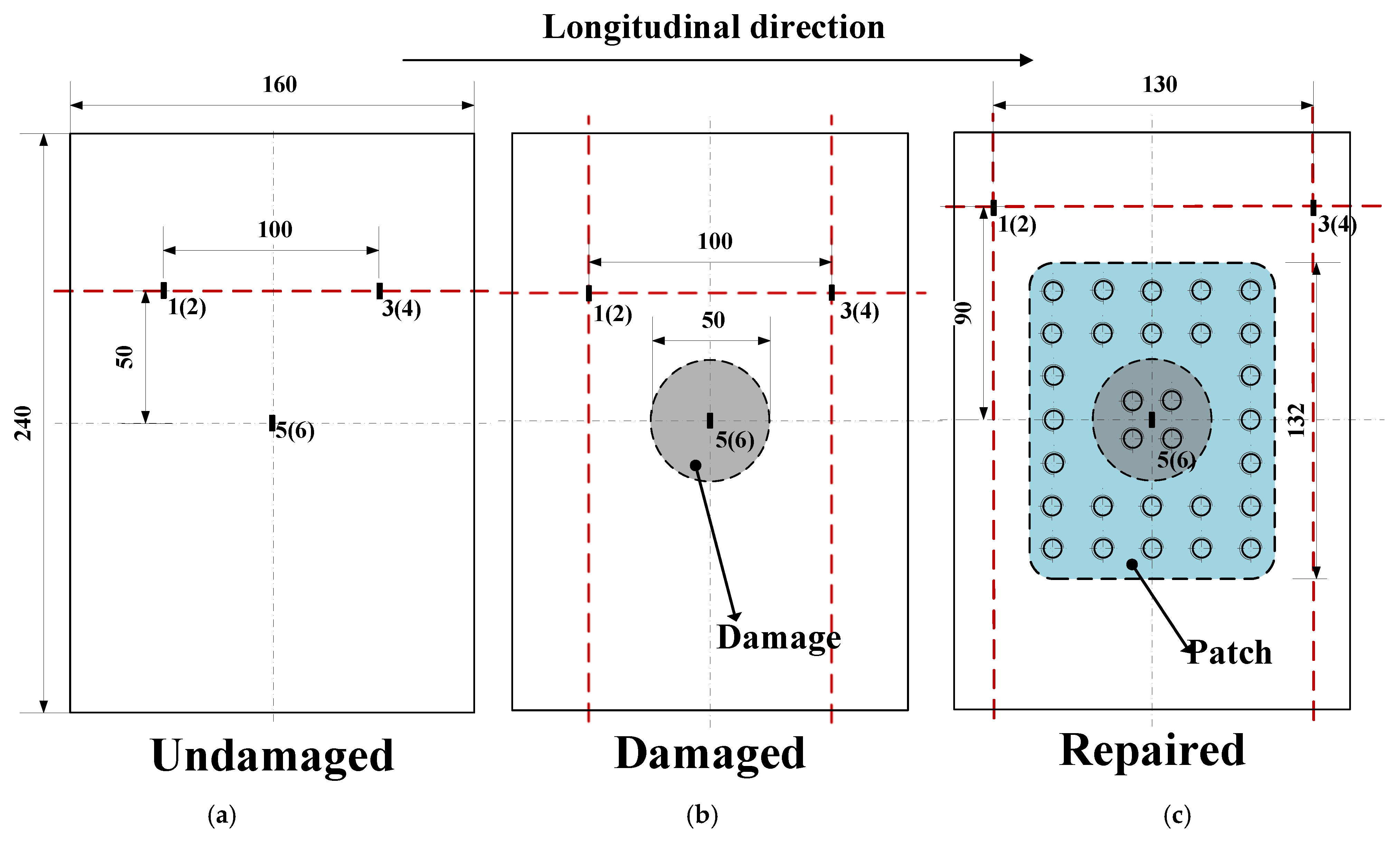
3.1. Specimen Description
3.2. Experimental Setup
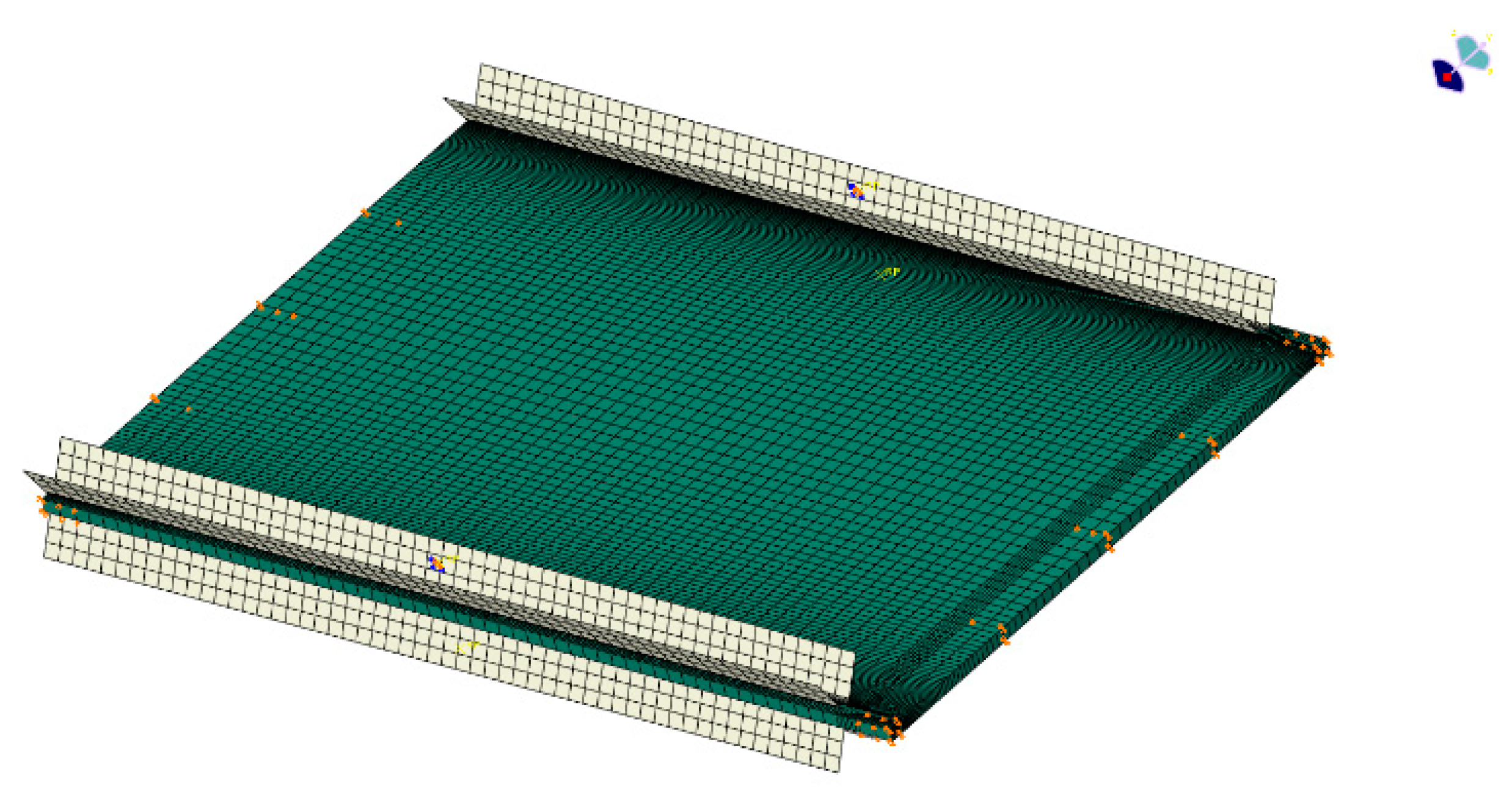
3.3. Finite Element Model
4. Results and Discussion
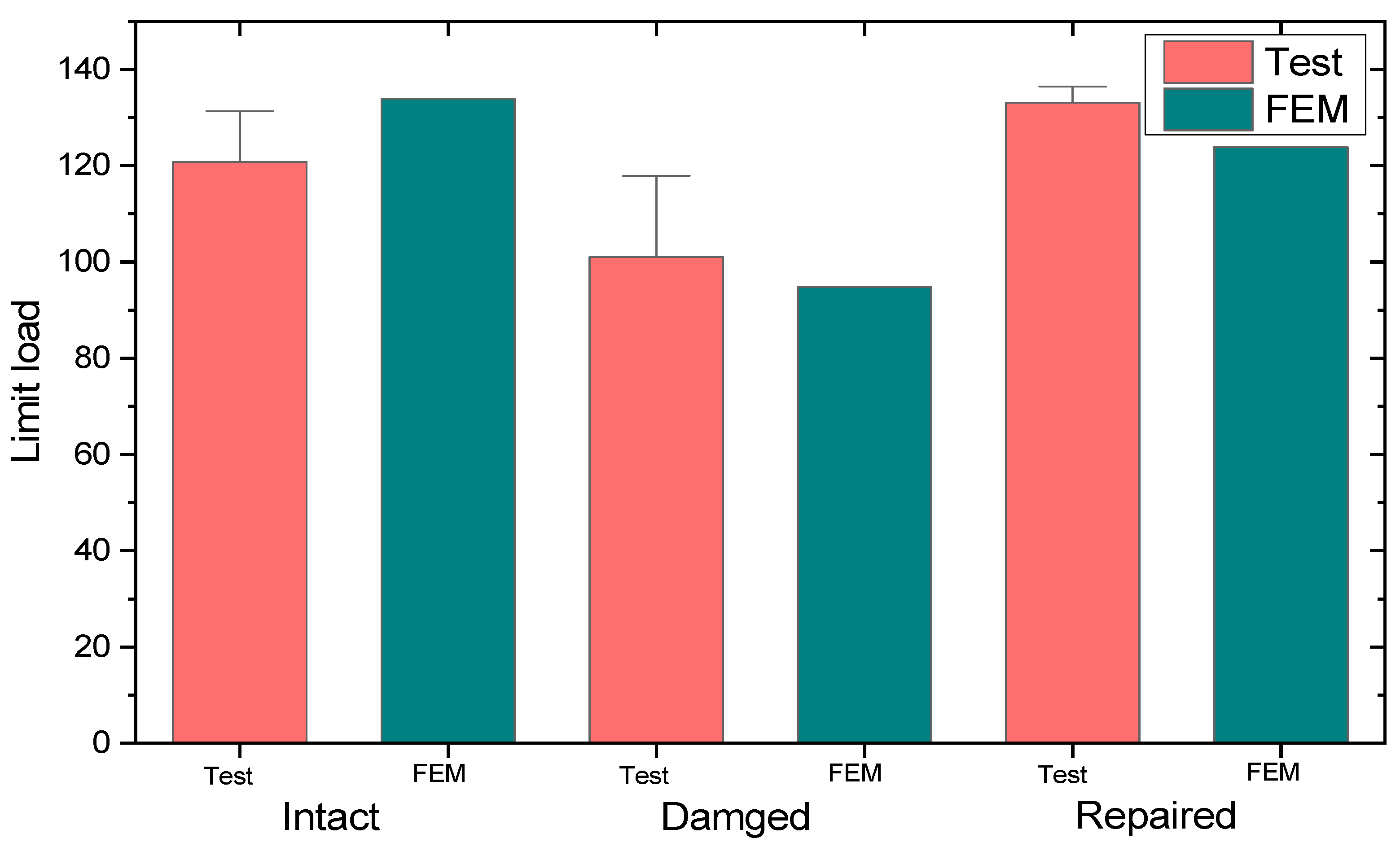
4.1. Comparative Analysis of Limit Load
4.1.1. Intact Composite Laminate
4.1.2. Damaged Composite Laminate
4.1.3. Repaired Composite Laminate
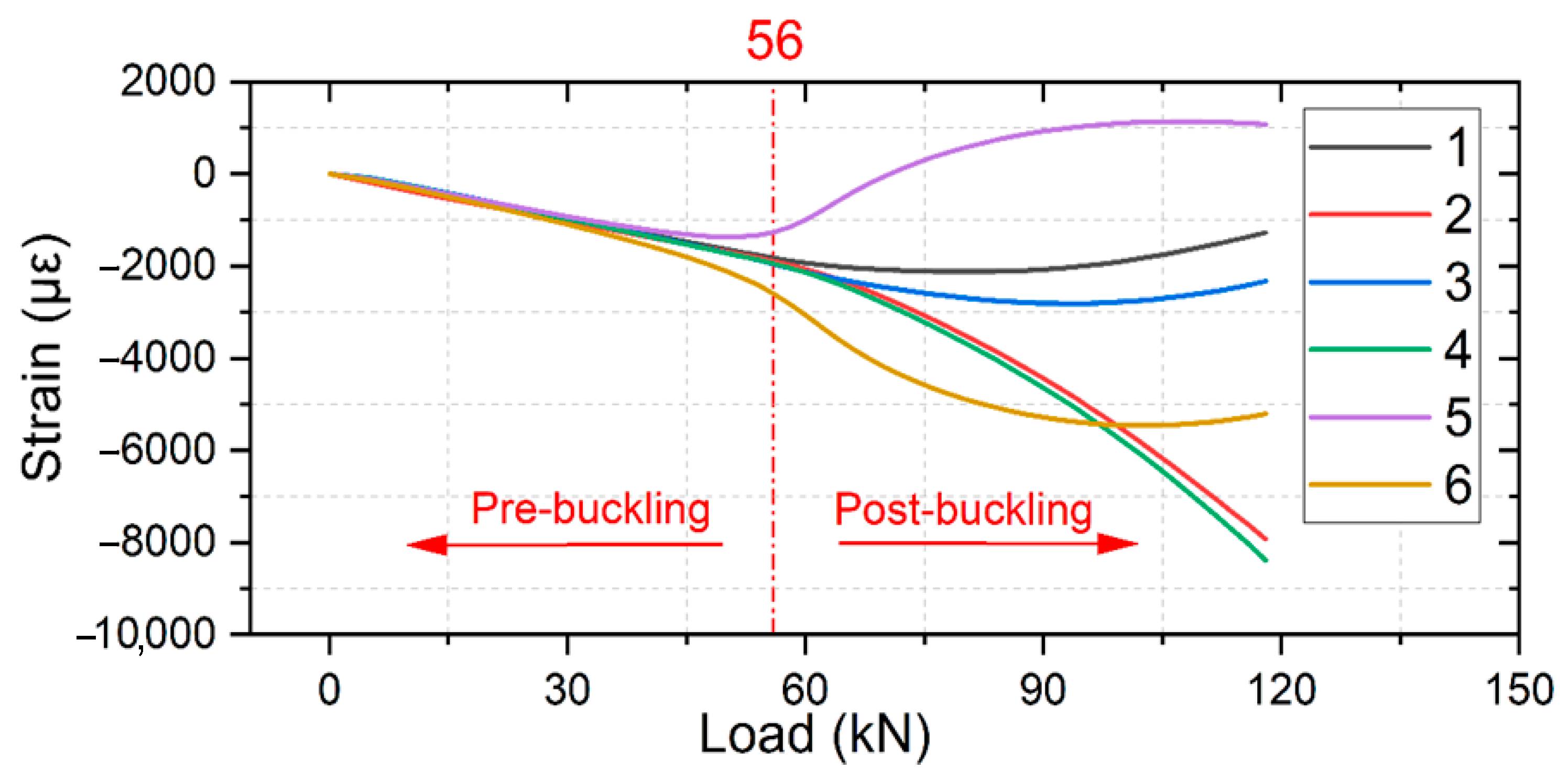
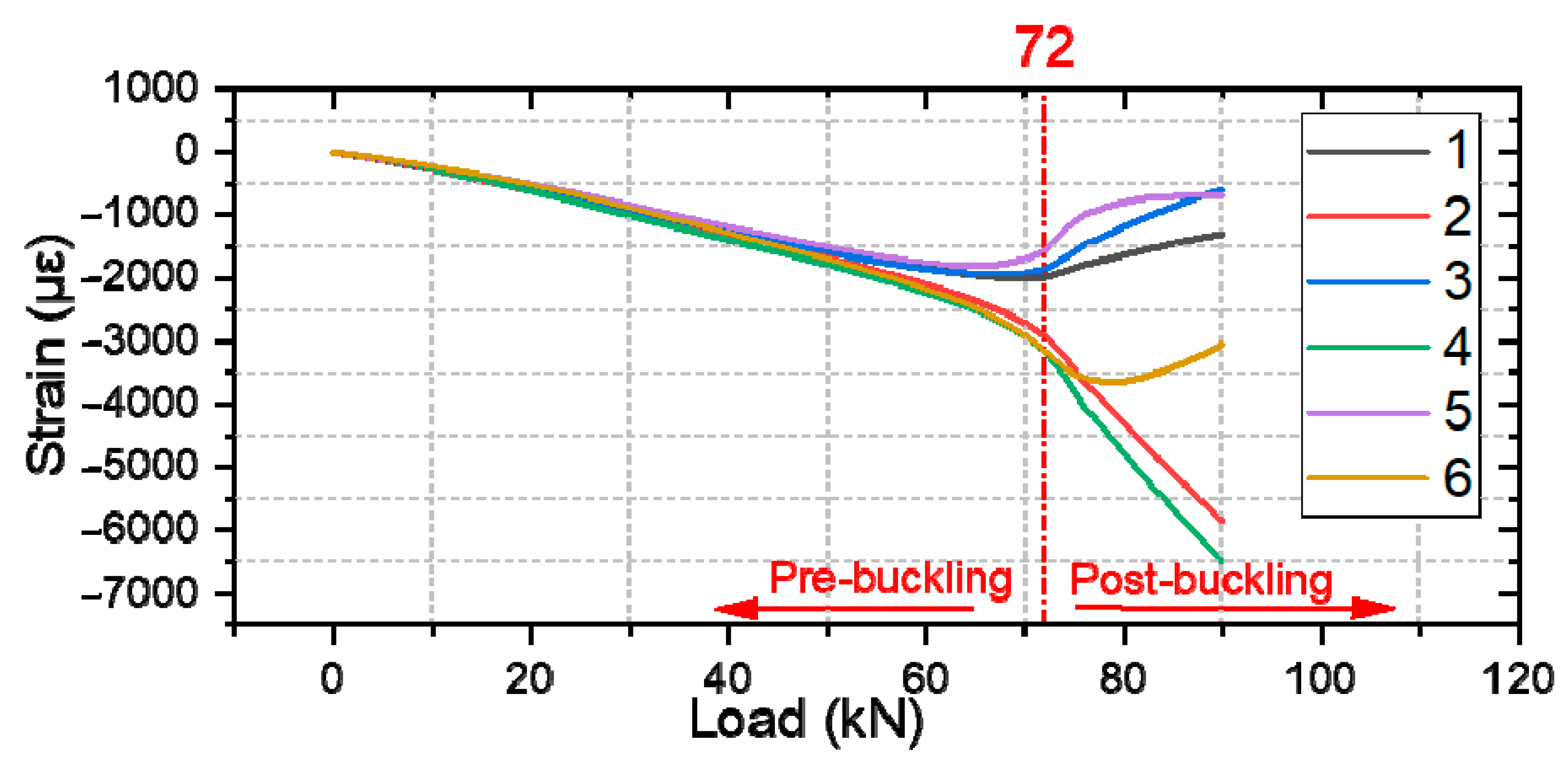
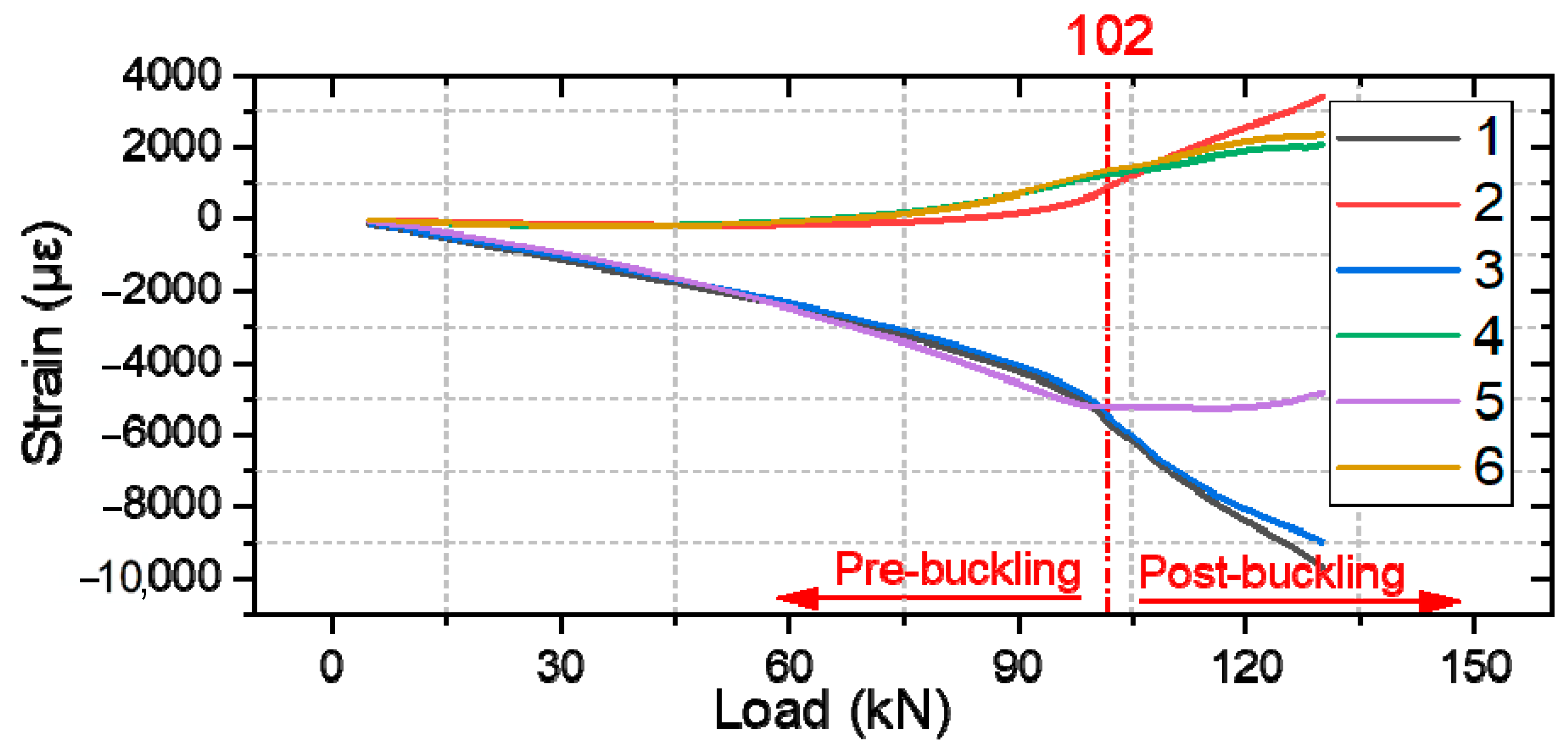
4.2. Comparative Analysis of Strain
4.3. Failure Analysis
4.3.1. Intact Composite Laminate
4.3.2. Damaged Composite Laminate
4.3.3. Repaired Composite Laminate
5. Conclusions
- In the static compression tests of composite laminates, the pre-existing single delamination can cause an 18.4% decrease in strength. After bolt repair, 107% strength recovery is achieved, indicating that the repair is effective.
- The damage mechanism of composite laminates is revealed. Delamination in both intact and damaged laminates can propagate freely, and in damaged laminates, it is easier due to the presence of prefabricated delamination. In bolt-repaired laminates, the damage propagation must bypass the bolt, which changes the damage mechanism and allows them to carry greater loads.
- The results of the finite element analysis show that the maximum prediction error for the strength of all specimens is not more than 7.9%. In addition, the failure modes and locations predicted by the finite element model are consistent with the experimental results. These results show that the modeling method used in this paper is reliable.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Obradovic, J.; Boria, S.; Belingardi, G. Lightweight design and crash analysis of composite frontal impact energy absorbing structures. Compos. Struct. 2012, 94, 423–430. [Google Scholar] [CrossRef]
- Liu, Q.; Lin, Y.Z.; Zong, Z.J.; Sun, G.Y.; Li, Q. Lightweight design of carbon twill weave fabric composite body structure for electric vehicle. Compos. Struct. 2013, 97, 231–238. [Google Scholar] [CrossRef]
- Shanmugasundram, H.; Jayamani, E.; Soon, K.H. A comprehensive review on dielectric composites: Classification of dielectric composites. Renew. Sustain. Energy Rev. 2022, 157, 24. [Google Scholar] [CrossRef]
- Guo, Q.; Yao, W.J.; Li, W.B.; Gupta, N. Constitutive models for the structural analysis of composite materials for the finite element analysis: A review of recent practices. Compos. Struct. 2021, 260, 14. [Google Scholar] [CrossRef]
- Chen, Y.L.; Ma, Y.; Yin, Q.F.; Pan, F.; Cui, C.J.; Zhang, Z.Q.; Liu, B. Advances in mechanics of hierarchical composite materials. Compos. Sci. Technol. 2021, 214, 13. [Google Scholar] [CrossRef]
- Albat, A.M. Thermal residual stresses in bonded composite repairs on cracked metal structures. Mater. Technol. 2000, 15, 299–308. [Google Scholar] [CrossRef]
- Baker, A. Bonded composite repair of fatigue-cracked primary aircraft structure. Compos. Struct. 1999, 47, 431–443. [Google Scholar] [CrossRef]
- Umamaheswar, T.; Singh, R. Modelling of a patch repair to a thin cracked sheet. Eng. Fract. Mech. 1999, 62, 267–289. [Google Scholar] [CrossRef]
- Clark, R.J. Damage Tolerance of Bonded Composite Aircraft Repairs for Metallic Structures. Ph.D. Thesis, University of British Columbia, Kelowna, BC, Canada, 2007. [Google Scholar]
- Naboulsi, S.; Mall, S. Nonlinear analysis of bonded composite patch repair of cracked aluminum panels. Compos. Struct. 1998, 41, 303–313. [Google Scholar] [CrossRef]
- Ali, M.; Israr, A.; Ahmed, A.; Ikram, R. Effect of Patch Repair on the Physical and Mechanical Properties of Carbon Bidirectional Reinforced Composites. Iran. J. Sci. Technol. Trans. Mech. Eng. 2023, 47, 569–581. [Google Scholar] [CrossRef]
- Caliskan, U.; Ekici, R.; Bayazit, A.Y.; Apalak, M.K. Numerical model for composite patch repair of notched aluminum plates under impact loading. Proc. Inst. Mech. Eng. Pt. L-J. Mater.-Des. Appl. 2021, 235, 958–973. [Google Scholar] [CrossRef]
- Makwana, A.H.; Vyas, N.; Barot, R.S. Numerical investigation of composite patch repair of inclined cracked panel using XFEM. In Proceedings of the 2nd International Conference on Aspects of Materials Science and Engineering (ICAMSE), Chandigarh, India, 5–6 March 2021; Elsevier: Amsterdam, The Netherlands; pp. 5128–5133. [Google Scholar] [CrossRef]
- Mohammadi, S. The effect of disbond on the efficiency and durability of a composite patch repair in mode I and mixed mode considering different patch materials. Polym. Polym. Compos. 2022, 30, 12. [Google Scholar] [CrossRef]
- Zhou, W.; Ji, X.L.; Yang, S.; Liu, J.; Ma, L.H. Review on the performance improvements and non-destructive testing of patches repaired composites. Compos. Struct. 2021, 263, 20. [Google Scholar] [CrossRef]
- Amari, K.; Berrahou, M. Experimental and Numerical Study of the Effect of Patch Shape for Notched Cracked Composite Structure Repaired by Composite Patching. J. Fail. Anal. Prev. 2022, 22, 1040–1049. [Google Scholar] [CrossRef]
- Sun, C.; Zhao, W.; Zhou, J.; Altenaiji, M.; Cantwell, W.J.; Wang, Q.Y.; Guan, Z.W. Mechanical behaviour of composite laminates repaired with a stitched scarf patch. Compos. Struct. 2021, 255, 10. [Google Scholar] [CrossRef]
- Sonat, E.; Özerinç, S. Failure behavior of scarf-bonded woven fabric CFRP laminates. Compos. Struct. 2021, 258, 11. [Google Scholar] [CrossRef]
- Bendemra, H.; Compston, P.; Crothers, P.J. Optimisation study of tapered scarf and stepped-lap joints in composite repair patches. Compos. Struct. 2015, 130, 1–8. [Google Scholar] [CrossRef]
- Sadowski, T.; Golewski, P. Numerical study of the prestressed connectors and their distribution on the strength of a single lap, a double lap and hybrid joints subjected to uniaxial tensile test. Arch. Metall. Mater. 2013, 58, 579–585. [Google Scholar] [CrossRef]
- Ascione, F.; Feo, L.; Maceri, F. An experimental investigation on the bearing failure load of glass fibre/epoxy laminates. Compos. Pt. B-Eng. 2009, 40, 197–205. [Google Scholar] [CrossRef]
- Minghini, F.; Tullini, N.; Ascione, F.; Feo, L. Numerical failure analysis of built-up columns composed of closely spaced pultruded FRP channels. Compos. Struct. 2019, 207, 478–487. [Google Scholar] [CrossRef]
- Chen, S. Composite Structure Repair Manual; Aeronautic Industry Press: Beijing, China, 2001. [Google Scholar]
- Hu, J.S.; Mi, S.Q.; Yang, Z.Y.; Wang, C.R.; Yang, Y.H.; Tian, W. An experimental investigation on bearing behavior and failure mechanism of bolted composite interference-fit joints under thermal effects. Eng. Fail. Anal. 2022, 131, 16. [Google Scholar] [CrossRef]
- Caliskan, M. Evaluation of bonded and bolted repair techniques with finite element method. Mater. Des. 2006, 27, 811–820. [Google Scholar] [CrossRef]
- Hashin, Z. Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Khan, T.A.; Kim, H.; Kim, H.J. Fatigue delamination of carbon fiber-reinforced polymer-matrix composites. In Failure Analysis in Biocomposites, Fibre-Reinforced Composites and Hybrid Composites; Woodhead Publishing: Cambridge, UK, 2019; pp. 1–28. [Google Scholar]
- Zou, J.; Lei, Z.; Liu, D.; Hong, X.; Shang, Y.; Bai, R. Rapid prediction of compression after impact properties of composite structures: An equivalent strategy for impact damage. Compos. Struct. 2023, 307, 116655. [Google Scholar] [CrossRef]
- Kumar, S.B.; Sivashanker, S.; Bag, A.; Sridhar, I. Failure of aerospace composite scarf-joints subjected to uniaxial compression. Mater. Sci. Eng. A 2005, 412, 117–122. [Google Scholar] [CrossRef]
- ASTM D6641/D6641M; Standard Test Method for Compressive Properties of Polymer Matrix Composite Materials Using a Combined Loading Compression (CLC) Test Fixture. ASTM International: West Conshohocken, PA, USA, 2016.









| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Longitudinal elastic modulus | E1 | 135 | GPa |
| Transverse and normal elastic modulus | E2, E3 | 8.8 | GPa |
| Poisson’s ratio | ν12 | 0.33 | - |
| Shear modulus | G12, G13, G23 | 4.47 | GPa |
| Longitudinal tensile strength | XT | 1548 | MPa |
| Longitudinal compressive strength | XC | 1226 | MPa |
| Transverse tensile strength | YT | 55.5 | MPa |
| Transverse compressive strength | YC | 110.5 | MPa |
| Shear strength | S12, S23 | 89.9 | MPa |
| Specimen | Test Results/kN | FEM Results/kN | Error | |||
|---|---|---|---|---|---|---|
| Buckling Load | Average | Limit Load | Average | |||
| WSC1 | 56 | 60.7 | 118.50 | 124.04 | 133.91 | 7.9% |
| WSC2 | 54 | 122.32 | ||||
| WSC3 | 72 | 131.30 | ||||
| Specimen | Test Results/kN | FEM Results/kN | Error | |||
|---|---|---|---|---|---|---|
| Buckling Load | Average | Limit Load | Average | |||
| YSC1 | 72 | 68.7 | 90.70 | 100.97 | 94.75 | 6.2% |
| YSC2 | 68 | 117.82 | ||||
| YSC3 | 66 | 94.39 | ||||
| Specimen | Test Results/kN | FEM Results/kN | Error | |||
|---|---|---|---|---|---|---|
| Buckling Load | Average | Limit Load | Average | |||
| XLC1 | 102 | 109.3 | 131.13 | 133.07 | 123.84 | 7.45% |
| XLC2 | 114 | 136.41 | ||||
| XLC3 | 112 | 131.67 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, S.; Huang, M.; Xu, Z.; Yang, Y.; Du, S. Experimental and Numerical Analysis of Bolted Repair for Composite Laminates with Delamination Damage. Polymers 2024, 16, 2918. https://doi.org/10.3390/polym16202918
Xiao S, Huang M, Xu Z, Yang Y, Du S. Experimental and Numerical Analysis of Bolted Repair for Composite Laminates with Delamination Damage. Polymers. 2024; 16(20):2918. https://doi.org/10.3390/polym16202918
Chicago/Turabian StyleXiao, Shan, Mingxuan Huang, Zhonghai Xu, Yusong Yang, and Shanyi Du. 2024. "Experimental and Numerical Analysis of Bolted Repair for Composite Laminates with Delamination Damage" Polymers 16, no. 20: 2918. https://doi.org/10.3390/polym16202918
APA StyleXiao, S., Huang, M., Xu, Z., Yang, Y., & Du, S. (2024). Experimental and Numerical Analysis of Bolted Repair for Composite Laminates with Delamination Damage. Polymers, 16(20), 2918. https://doi.org/10.3390/polym16202918







