Moisture Absorption and Mechanical Degradation of Polymer Systems Incorporated with Layered Double Hydroxide Particles
Abstract
1. Introduction
2. Analytical and Numerical Solutions of the Sorption Process in Single- and Multilayered Plates
2.1. Absorption Process in Monolayer Plates
2.2. Calculation of the Moisture Concentration Field in Multilayered Structures
2.2.1. Mathematical Model of Sorption
2.2.2. Transport of Moisture at the Interface of the Layers
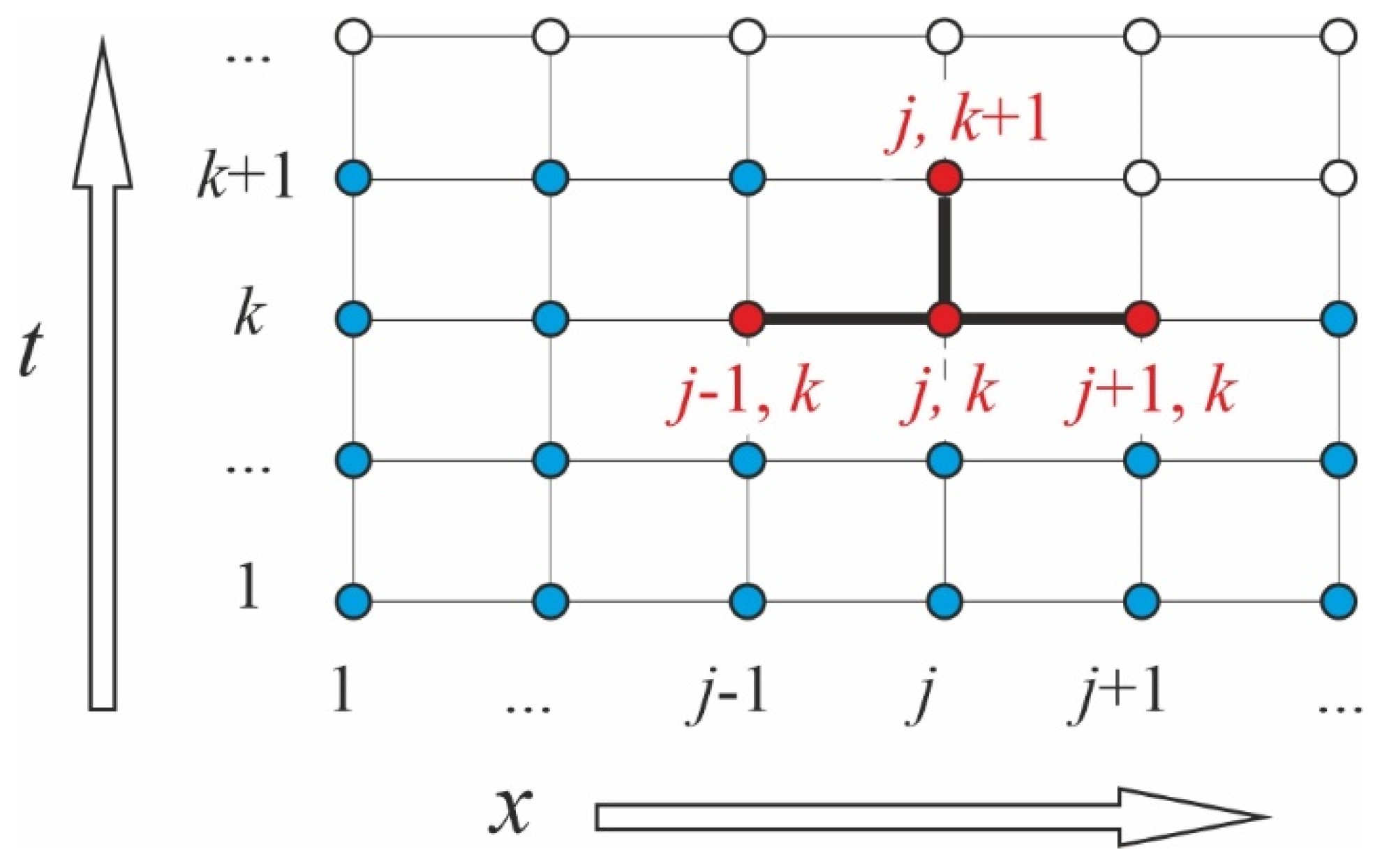
2.2.3. Algorithm for Numerical Solution of the Problem
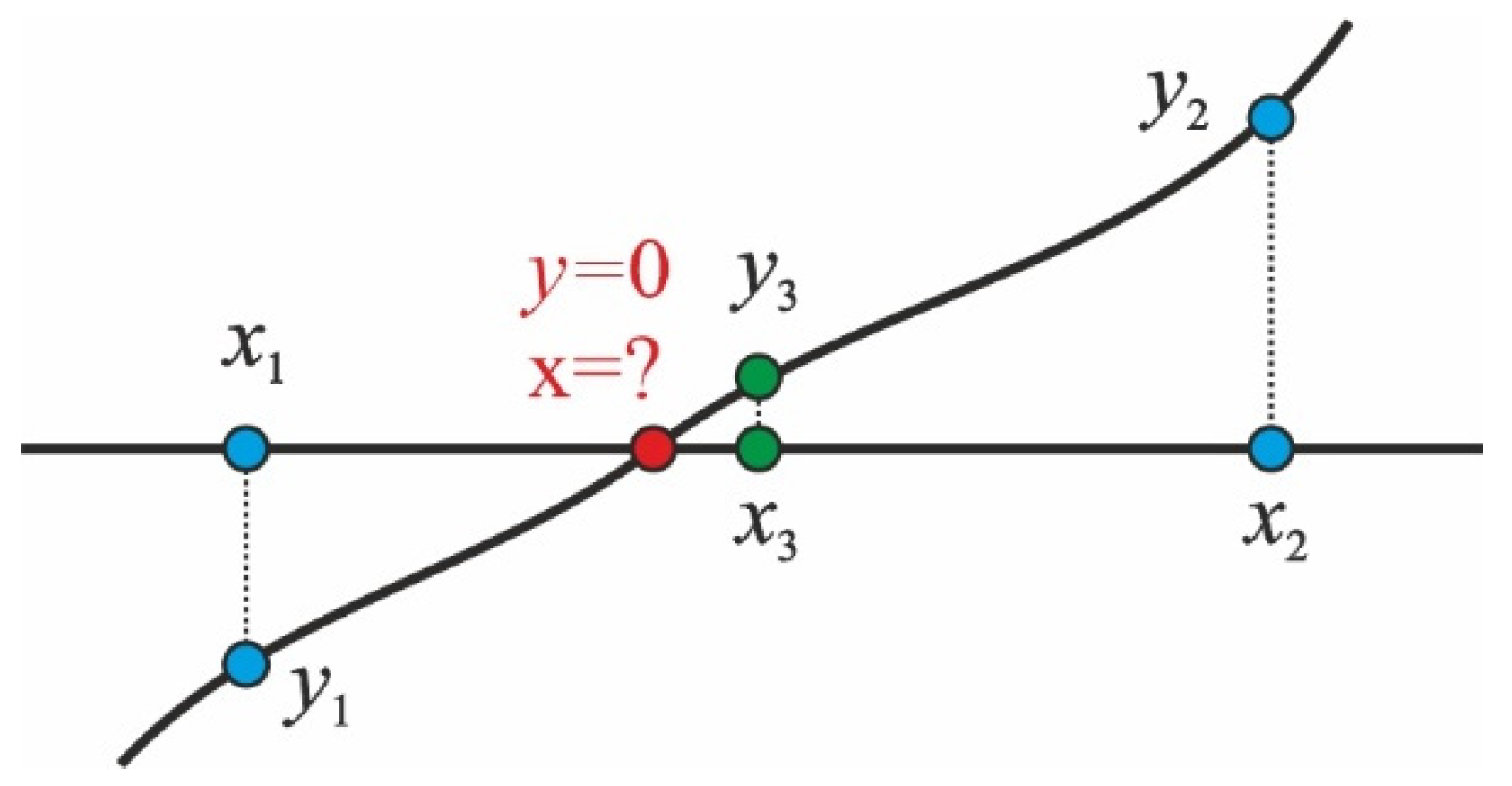
2.2.4. Interface Jump of the Concentration
2.2.5. Flowchart
3. Materials and Methodology
3.1. Compound Preparation
3.1.1. Epoxy/LDH Nanocomposites with Xylene
3.1.2. Epoxy/LDH Nanocomposites with BYK
3.1.3. Direct Incorporation Without BYK or Xylene
3.2. Specimens
3.3. Mechanical Testing
3.4. Absorption Measurement Procedure
4. Characterisation
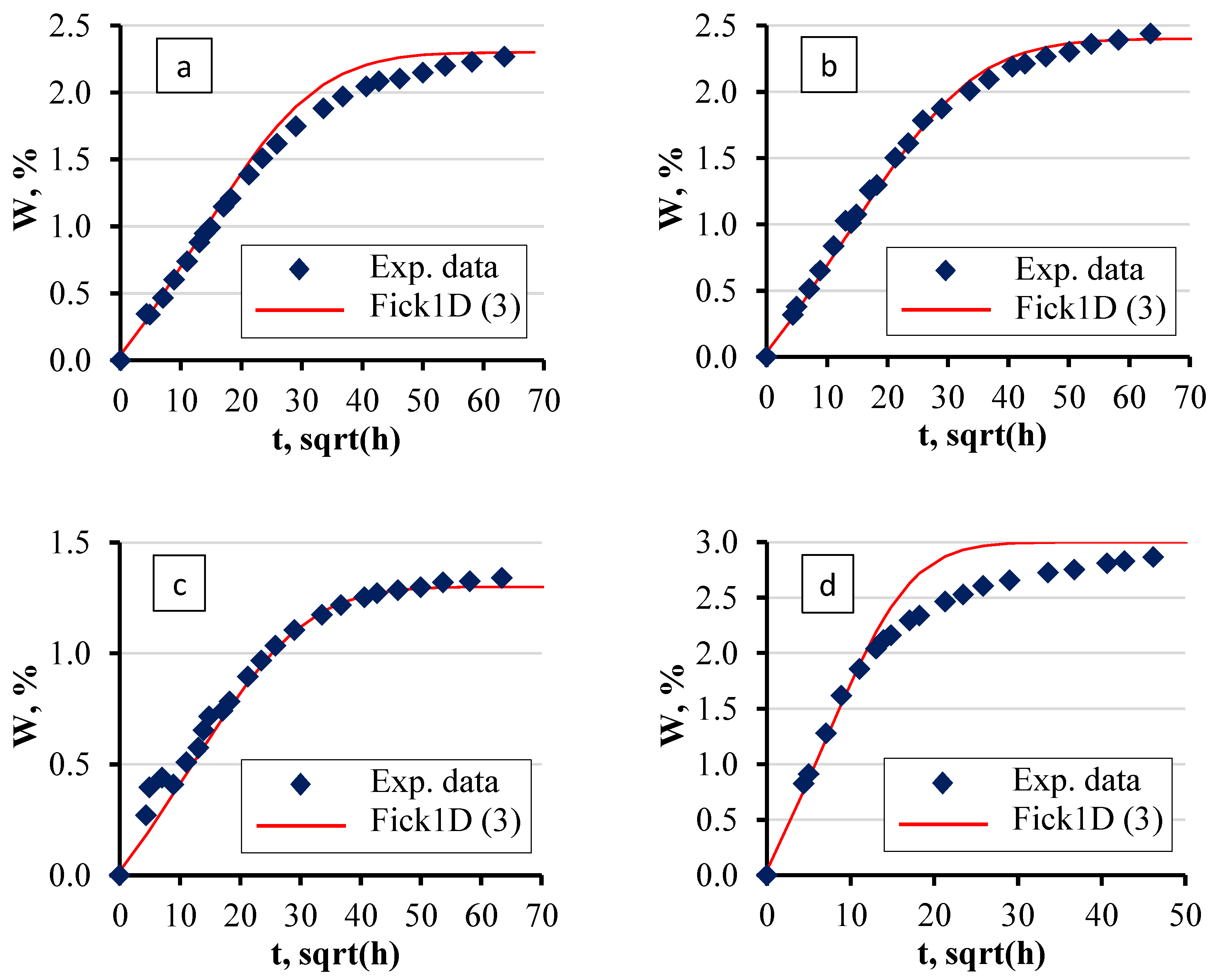
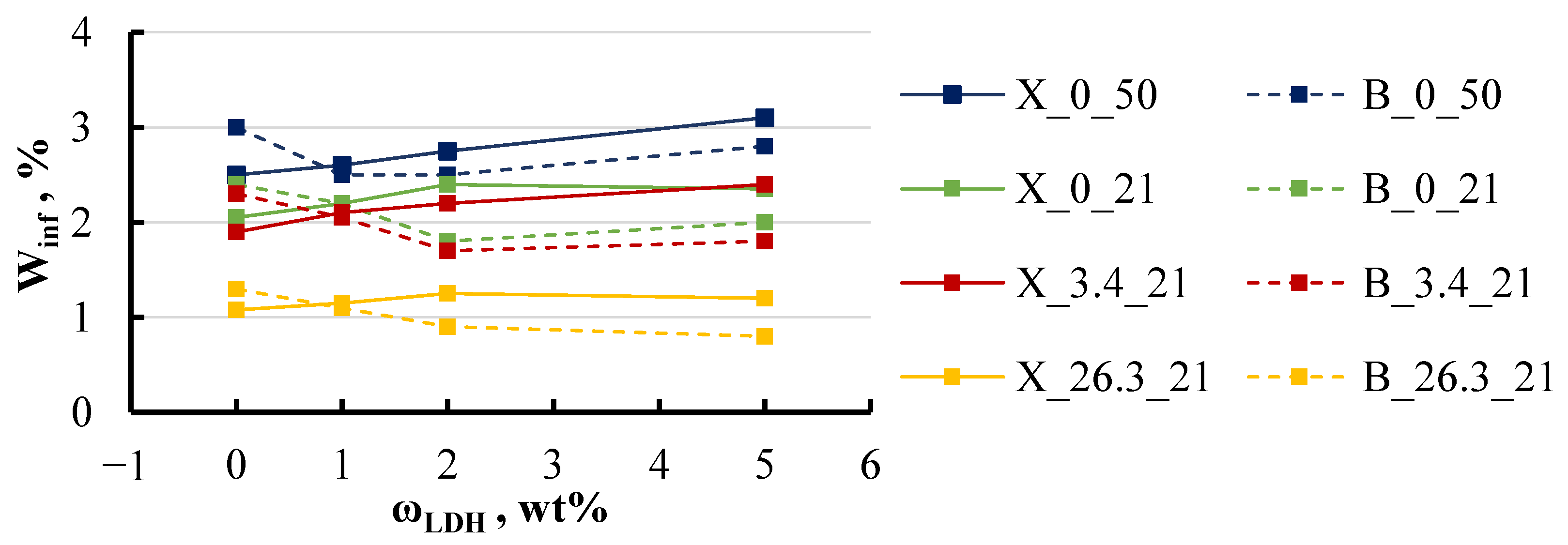
4.1. Sorption Parameters
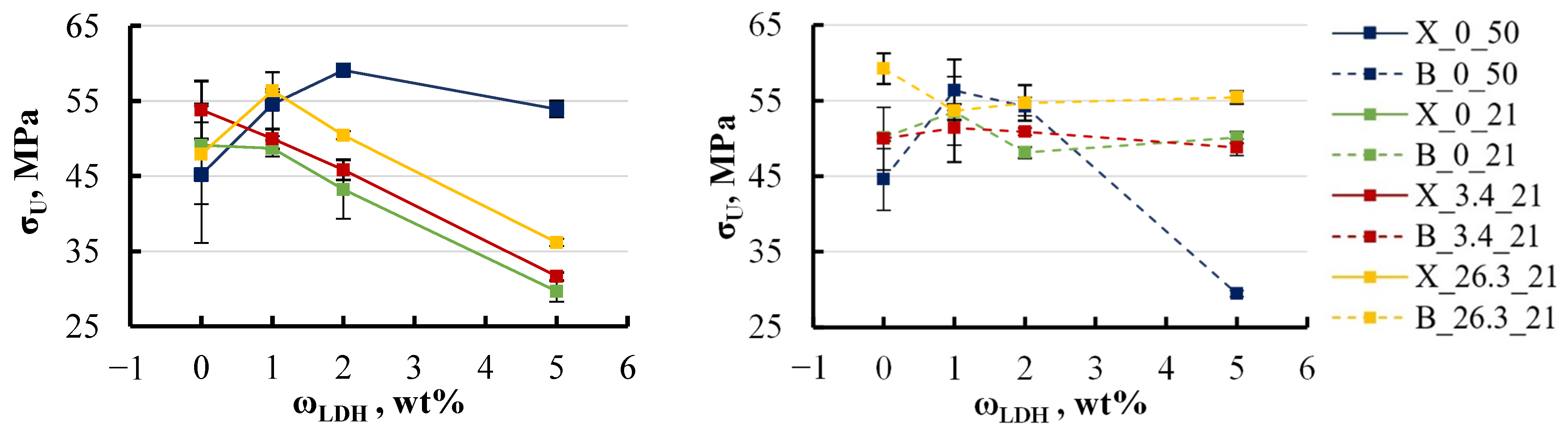
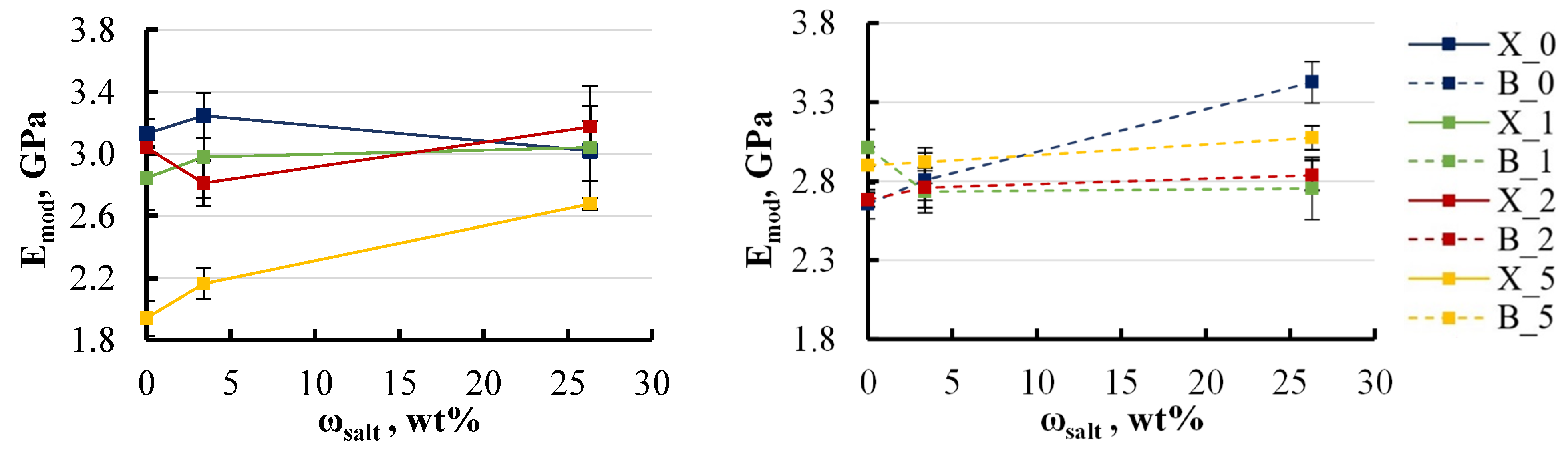
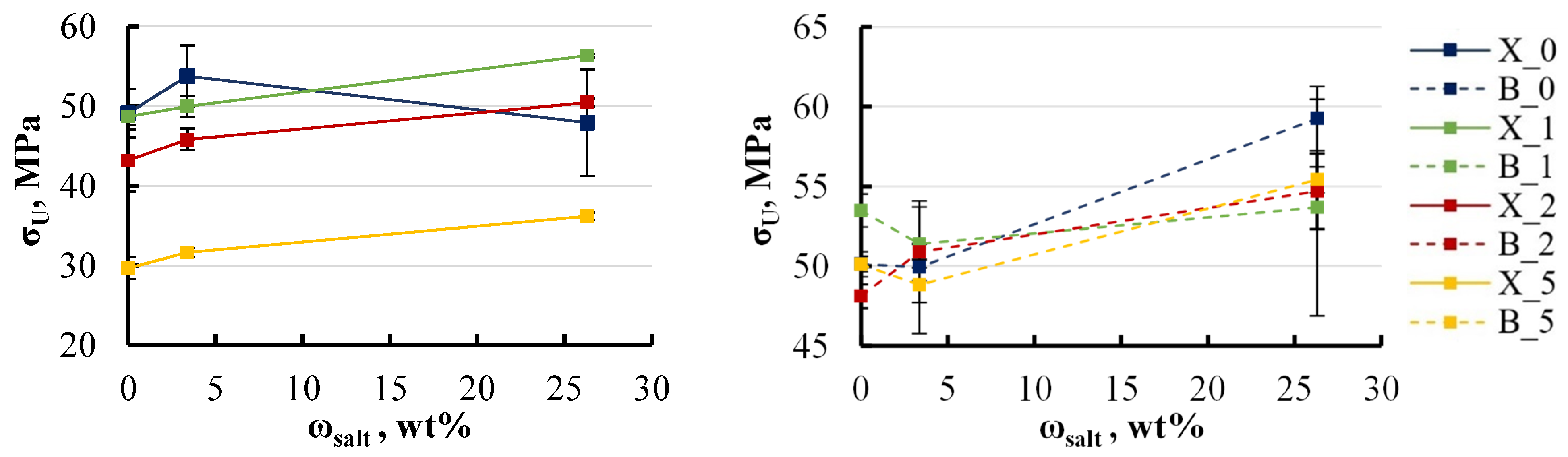
4.2. Mechanical Tests and Degradation
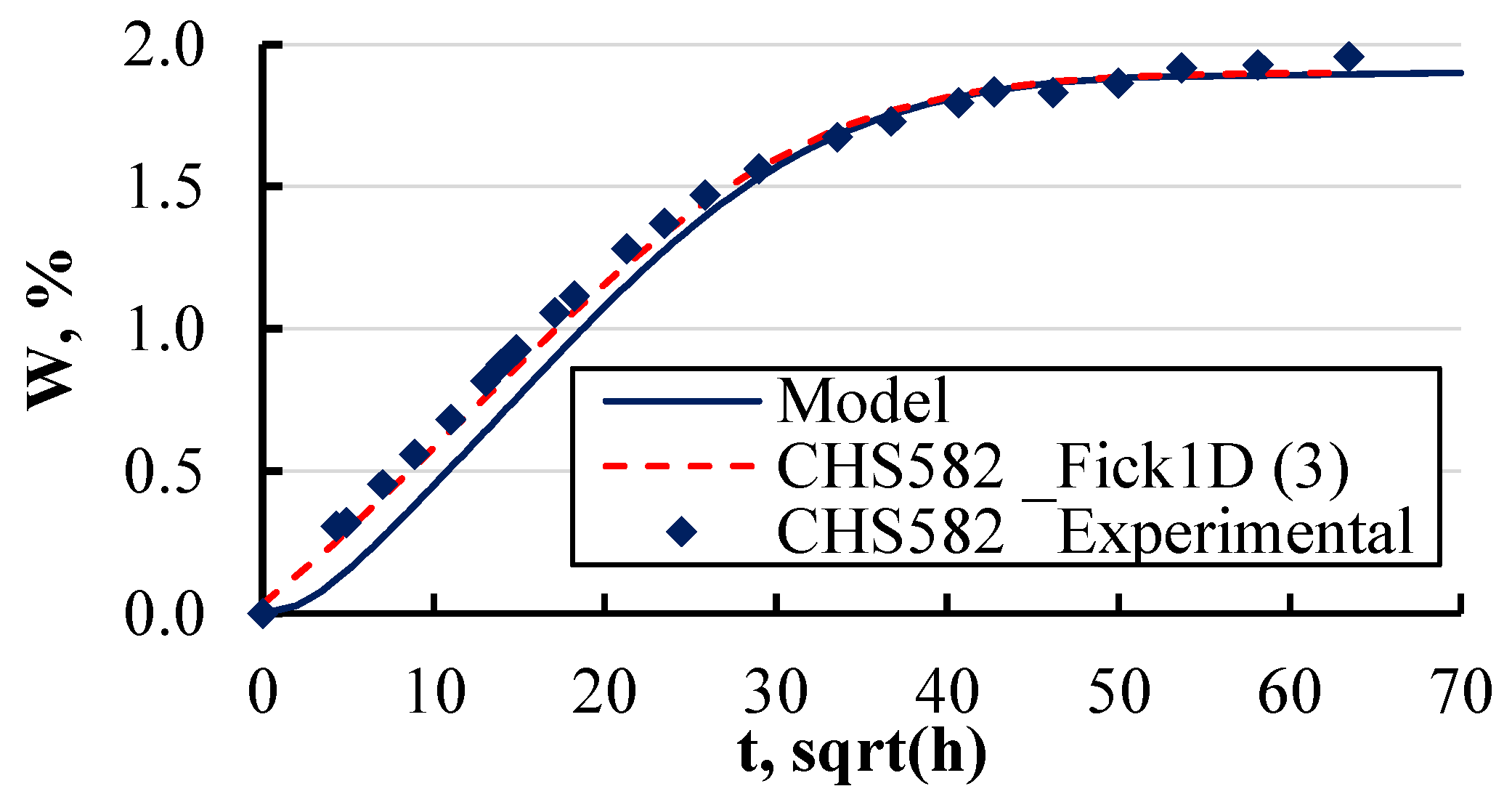
5. Validation
6. Conclusions
- This study highlights that moisture absorption in epoxy/LDH nanocomposites is significantly influenced by environmental factors, such as temperature and salinity. Sorption curves indicate a gradual increase in equilibrium moisture content over time, which could be attributed to material degradation or leaching effects. Temperature was found to have a particularly strong impact, with the diffusion coefficient doubling when the temperature increased to 50 °C for most specimen groups. Additionally, an increase in salt concentration to 26 wt% led to a 50% reduction in equilibrium moisture content.
- This study reveals a degradation in mechanical properties when epoxy/LDH nanocomposites are exposed to aqueous environments, especially at elevated temperatures. The elastic modulus decreased by approximately 5–8% with the addition of LDH up to 2 wt%, while the ultimate strength exhibited a more pronounced decline, dropping by 10–50% following immersion, particularly in hot water. Varying the LDH filler content from 0 to 5 wt% had minimal impact on the elastic modulus but did lead to a 5–10% reduction in ultimate strength. The study also examined the impact of base components, finding that xylene-modified specimens without LDH experienced a 10–15% reduction in ultimate strength. BYK-modified specimens showed greater stability.
- The developed numerical model, designed to calculate moisture concentration fields in single- and multilayer materials, was rigorously validated against experimental and analytical data. The model effectively predicted moisture distribution over time, showing strong agreement with experimental observations. However, the model demonstrated limitations in predicting sorption curves at elevated temperatures, similarly to analytical methods. This validation process confirms the model’s reliability in simulating moisture absorption behaviour at near-room temperatures in complex, multilayered systems.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Presuel, F.; Jakab, M.; Tailleart, N.; Goldman, M.; Scully, J. Corrosion-resistant metallic coatings. Mater. Today 2008, 11, 14–23. [Google Scholar] [CrossRef]
- Zheng, S.; Bellido-Aguilar, D.A.; Hu, J.; Huang, Y.; Zhao, X.; Wang, Z.; Zeng, X.; Zhang, Q.; Chen, Z. Waterborne bio-based epoxy coatings for the corrosion protection of metallic substrates. Prog. Org. Coat. 2019, 136, 105265. [Google Scholar] [CrossRef]
- Lu, T.; Solis-Ramos, E.; Yi, Y.; Kumosa, M. UV degradation model for polymers and polymer matrix composites. Polym. Degrad. Stab. 2018, 154, 203–210. [Google Scholar] [CrossRef]
- Neǐman, M.; Kovarskaya, B.; Golubenkova, L.; Strizhkova, A.; Levantovskaya, I.; Akutin, M. The thermal degradation of some epoxy resins. J. Polym. Sci. 2003, 56, 383–389. [Google Scholar] [CrossRef]
- Cao, Q.; Oluwoye, I.; Pojtanabuntoeng, T.; Farhat, H.; Iannuzzi, M. Evaluation of epoxy-based coating degradation under thermal insulation at elevated temperatures on different steel substrates. Prog. Org. Coat. 2023, 180, 107544. [Google Scholar] [CrossRef]
- Yang, H.-Q.; Zhang, Q.; Li, Y.-M.; Liu, G.; Huang, Y. Effects of mechanical stress on protective properties of a marine coating on mild steel substrate. Corros. Sci. 2020, 177, 108986. [Google Scholar] [CrossRef]
- Wegmann, A. Chemical resistance of waterborne epoxy/amine coatings. Prog. Org. Coat. 1997, 32, 231–239. [Google Scholar] [CrossRef]
- Walter, G.W. A critical review of the protection of metals by paints. Corros. Sci. 1986, 26, 27–38. [Google Scholar] [CrossRef]
- Schmelter, D.; Langry, A.; Koenig, A.; Keil, P.; Leroux, F.; Hintze-Bruening, H. Inhibition of Steel Corrosion and Alkaline Zinc Oxide Dissolution by Dicarboxylate Bola-Amphiphiles: Self-Assembly Supersedes Host-Guest Conception. Sci. Rep. 2017, 7, 2785. [Google Scholar] [CrossRef]
- Tedim, J.; Poznyak, S.K.; Kuznetsova, A.; Raps, D.; Hack, T.; Zheludkevich, M.L.; Ferreira, M.G.S. Enhancement of Active Corrosion Protection via Combination of Inhibitor-Loaded Nanocontainers. ACS Appl. Mater. Interfaces 2010, 2, 1528–1535. [Google Scholar] [CrossRef]
- Wilhelm, M.; Quevedo, M.C.; Sushkova, A.; Galvão, T.L.P.; Bastos, A.; Ferreira, M.; Tedim, J. Hexacyanoferrate-Intercalated Layered Double Hydroxides as Nanoadditives for the Detection of Early-Stage Corrosion of Steel: The Revival of Prussian blue. Eur. J. Inorg. Chem. 2020, 2020, 2063–2073. [Google Scholar] [CrossRef]
- Kameliya, J.; Verma, A.; Dutta, P.; Arora, C.; Vyas, S.; Varma, R.S. Layered Double Hydroxide Materials: A Review on Their Preparation, Characterization, and Applications. Inorganics 2023, 11, 121. [Google Scholar] [CrossRef]
- Hou, L.; Li, Y.; Sun, J.; Zhang, S.H.; Wei, H.; Wei, Y. Enhancement corrosion resistance of MgAl layered double hydroxides films by anion-exchange mechanism on magnesium alloys. Appl. Surf. Sci. 2019, 487, 101–108. [Google Scholar] [CrossRef]
- Ayemi, G.J.; Blivet, C.; Marcelin, S.; Thérias, S.; Leroux, F.; Normand, B. Efficiency of layered double hydroxides in epoxy coating as corrosion inhibitor reservoirs for carbon steel. Appl. Clay Sci. 2024, 258, 107510. [Google Scholar] [CrossRef]
- Zhao, X.; Yuan, Y.; Wei, Y.; Zhang, Z.; Zhang, Y. LDH-Based “Smart” Films for Corrosion Sensing and Protection. Materials 2023, 16, 3483. [Google Scholar] [CrossRef]
- Zimmermann, C.; Koslowski, L.; Araújo, M.; Silveira, M. The influence of soluble salts content on the performance of an epoxy coating system via accelerated corrosion tests. Matéria 2020, 25, e-12648. [Google Scholar] [CrossRef]
- Rudawska, A. The Effect of the Salt Water Aging on the Mechanical Properties of Epoxy Adhesives Compounds. Polymers 2020, 12, 843. [Google Scholar] [CrossRef]
- Glaskova, T.I.; Guedes, R.M.; Morais, J.J.; Aniskevich, A.N. A comparative analysis of moisture transport models as applied to an epoxy binder. Mech. Compos. Mater. 2007, 43, 377–388. [Google Scholar] [CrossRef]
- Mintzas, A.; Guedes, R.M.; Aniskevich, A. Stress–strain analysis of specimens subjected to tensile loading during moisture uptake. Int. J. Automot. Compos. 2015, 1, 205–222. [Google Scholar] [CrossRef]
- Shen, C.-H.; Springer, G.S. Moisture Absorption and Desorption of Composite Materials. J. Compos. Mater. 1976, 10, 2–20. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Aniskevich, A.N.; Ivanov, Y.V. Calculation of the moisture concentration field in a multilayered plate. Mech. Compos. Mater. 1995, 30, 364–370. [Google Scholar] [CrossRef]
- Aniskevich, A.N.; Yanson, Y.O. Study of moisture absorption by an organoplastic. Mech. Compos. Mater. 1991, 26, 455–462. [Google Scholar] [CrossRef]
- Lykov, A.V.; Mikhailov, Y.A. Theory of Heat and Mass Transfer; IPST: Jerusalem, Israel, 1968. [Google Scholar]
- Samarskii, A.A. The Theory of Difference Schemes, 1st ed.; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Zhang, Z.; Qin, J.; Zhang, W.; Pan, Y.-T.; Wang, D.-Y.; Yang, R. Synthesis of a novel dual layered double hydroxide hybrid nanomaterial and its application in epoxy nanocomposites. Chem. Eng. J. 2020, 381, 122777. [Google Scholar] [CrossRef]
- Becker, C.M.; Gabbardo, A.D.; Wypych, F.; Amico, S.C. Mechanical and flame-retardant properties of epoxy/Mg–Al LDH composites. Compos. Part A Appl. Sci. Manuf. 2011, 42, 196–202. [Google Scholar] [CrossRef]
- Millero, F.J.; Feistel, R.; Wright, D.G.; McDougall, T.J. The composition of Standard Seawater and the definition of the Reference-Composition Salinity Scale. Deep Sea Res. Part I Oceanogr. Res. Pap. 2008, 55, 50–72. [Google Scholar] [CrossRef]







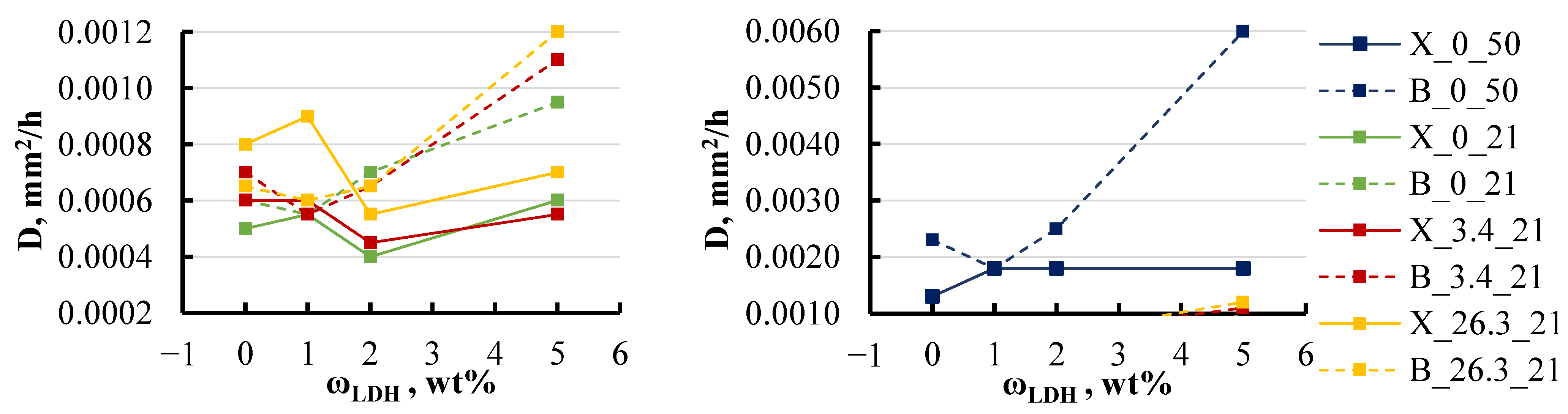







| Method | Comp. Nr. | LDH % | Epoxy % | Hardener % | Xylene (X) % | BYK 180 (B) % |
|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 80.0 | 20.0 | - | - |
| 2 | 0 | 68.0 | 17.0 | 15.0 | - | |
| 3 | 1 | 78.5 | 19.6 | 0.9 | - | |
| 4 | 2 | 76.9 | 19.2 | 1.9 | - | |
| 5 | 5 | 64.0 | 16.0 | 15.0 | - | |
| 2 | 6 | 0 | 79.3 | 19.8 | - | 0.9 |
| 7 | 1 | 78.9 | 19.7 | - | 0.4 | |
| 8 | 2 | 77.7 | 19.4 | - | 0.9 | |
| 9 | 5 | 74.3 | 18.6 | - | 2.2 | |
| 3 | 10 | 1 | 79.2 | 19.8 | - | - |
| 11 | 2 | 78.4 | 19.6 | - | - | |
| 12 | 5 | 76.0 | 19.0 | - | - |
| Material Name | Diffusion Coefficient | Layer Thickness | Density | Initial Relative Moisture Content | Sorption Isotherms | Number of Grid Points | |
|---|---|---|---|---|---|---|---|
| ai | bi | ||||||
| 10−6, cm2/h | cm | g/cm3 | % | n | |||
| CHS582 | 6.00 | 0.2 | 1.106 | 0.0 | 0.01900 | 1.00 | 10 |
| Reinforced plastic | 1.93 | 0.2 | 1.2 | 0.0 | 0.0471 | 1.51 | 10 |
| CHS582 | 6.00 | 0.2 | 1.106 | 0.0 | 0.01900 | 1.00 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stankevich, S.; Zeleniakiene, D.; Sevcenko, J.; Bulderberga, O.; Zetkova, K.; Tedim, J.; Aniskevich, A. Moisture Absorption and Mechanical Degradation of Polymer Systems Incorporated with Layered Double Hydroxide Particles. Polymers 2024, 16, 3388. https://doi.org/10.3390/polym16233388
Stankevich S, Zeleniakiene D, Sevcenko J, Bulderberga O, Zetkova K, Tedim J, Aniskevich A. Moisture Absorption and Mechanical Degradation of Polymer Systems Incorporated with Layered Double Hydroxide Particles. Polymers. 2024; 16(23):3388. https://doi.org/10.3390/polym16233388
Chicago/Turabian StyleStankevich, Stanislav, Daiva Zeleniakiene, Jevgenijs Sevcenko, Olga Bulderberga, Katerina Zetkova, Joao Tedim, and Andrey Aniskevich. 2024. "Moisture Absorption and Mechanical Degradation of Polymer Systems Incorporated with Layered Double Hydroxide Particles" Polymers 16, no. 23: 3388. https://doi.org/10.3390/polym16233388
APA StyleStankevich, S., Zeleniakiene, D., Sevcenko, J., Bulderberga, O., Zetkova, K., Tedim, J., & Aniskevich, A. (2024). Moisture Absorption and Mechanical Degradation of Polymer Systems Incorporated with Layered Double Hydroxide Particles. Polymers, 16(23), 3388. https://doi.org/10.3390/polym16233388









