Study on the Gelation Process and Mechanical Properties of Organic Polymer Grouting Materials Applied to Fissure Sealing in Underground Mines
Abstract
:1. Introduction
2. Materials and Methods
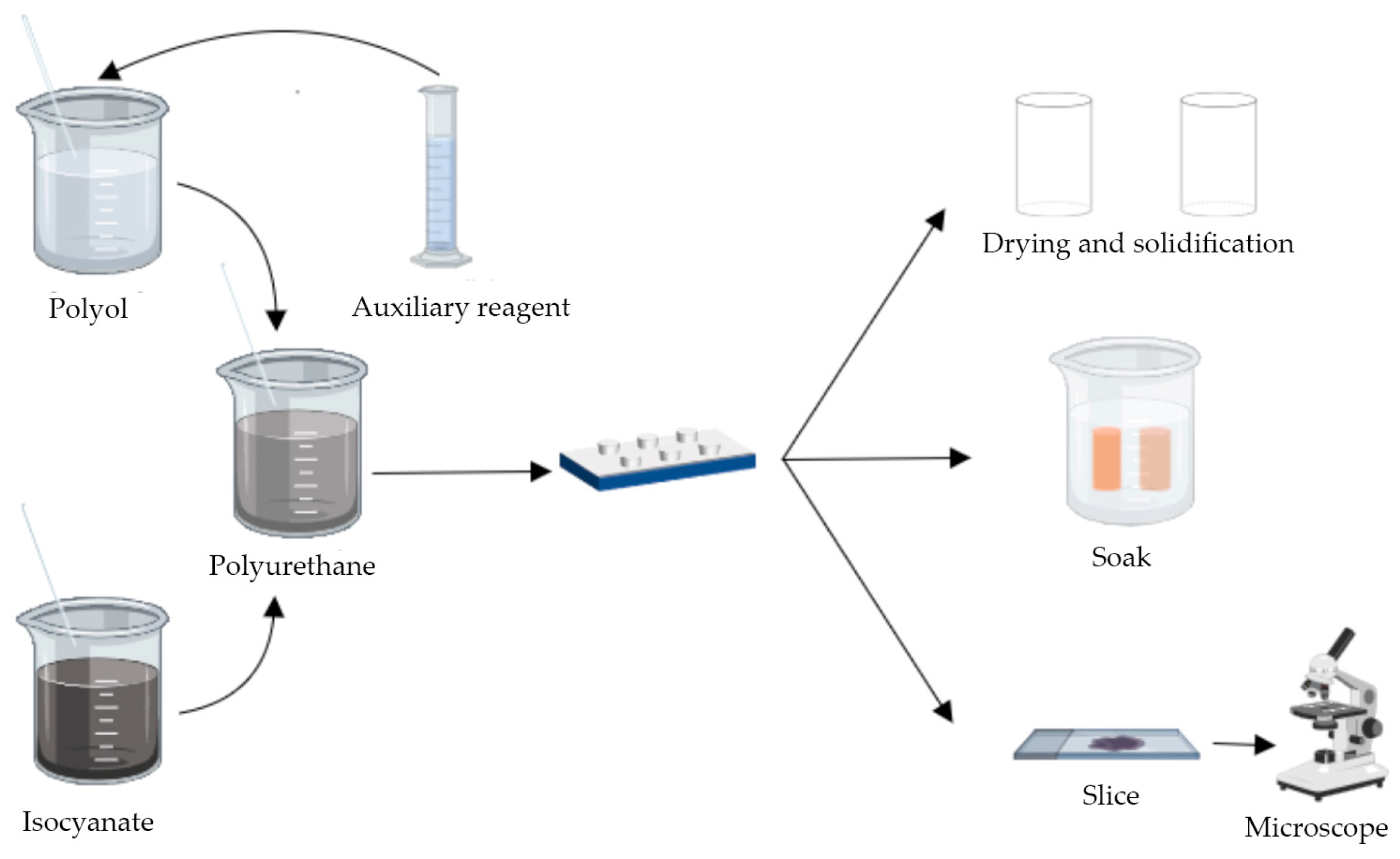
2.1. Grouting Ingredients
2.2. Specimen Preparation
2.3. Characterization and Mechanical Tests
3. Results and Discussion
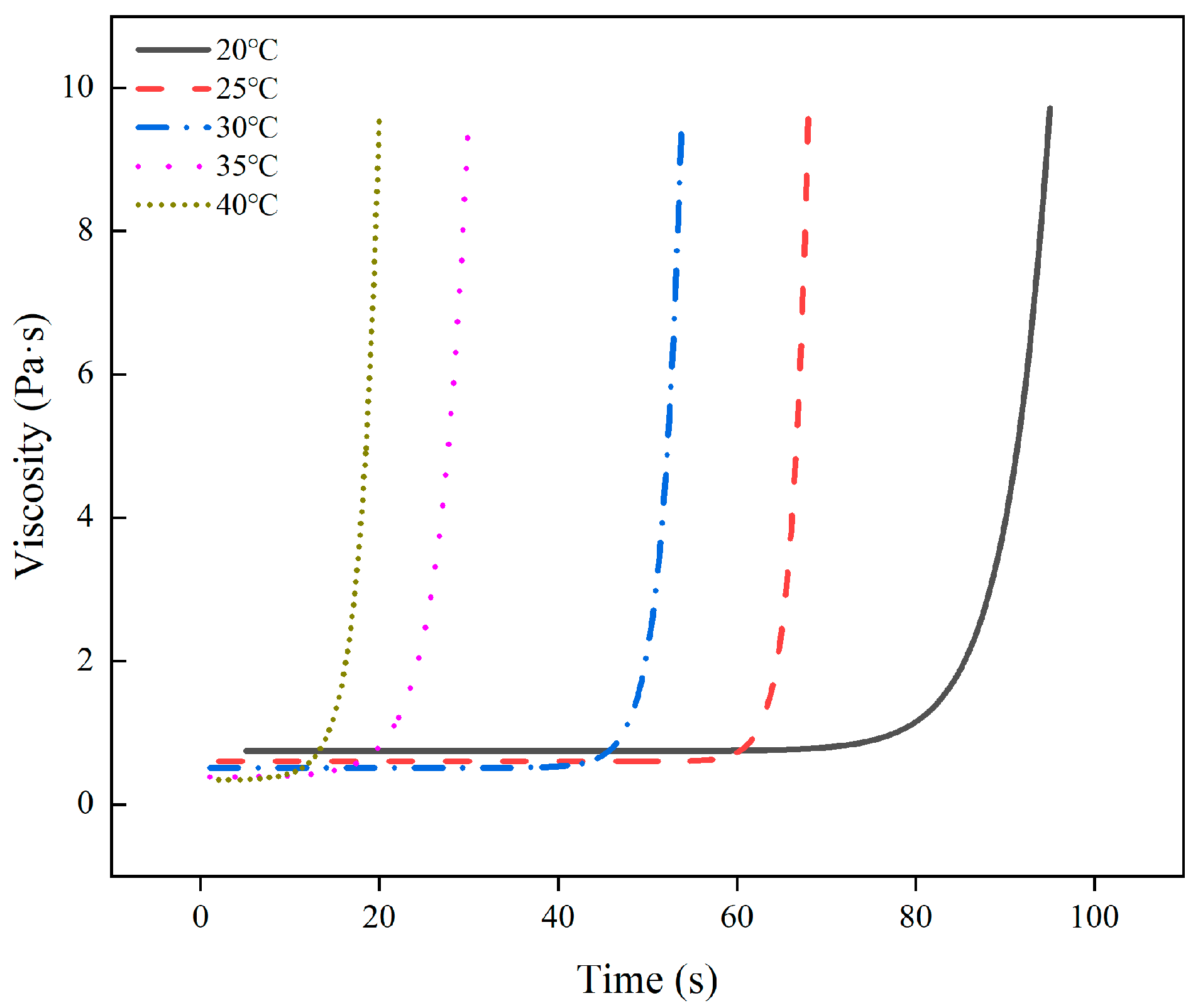
3.1. Viscosity Tests of Polyurethane Slurry
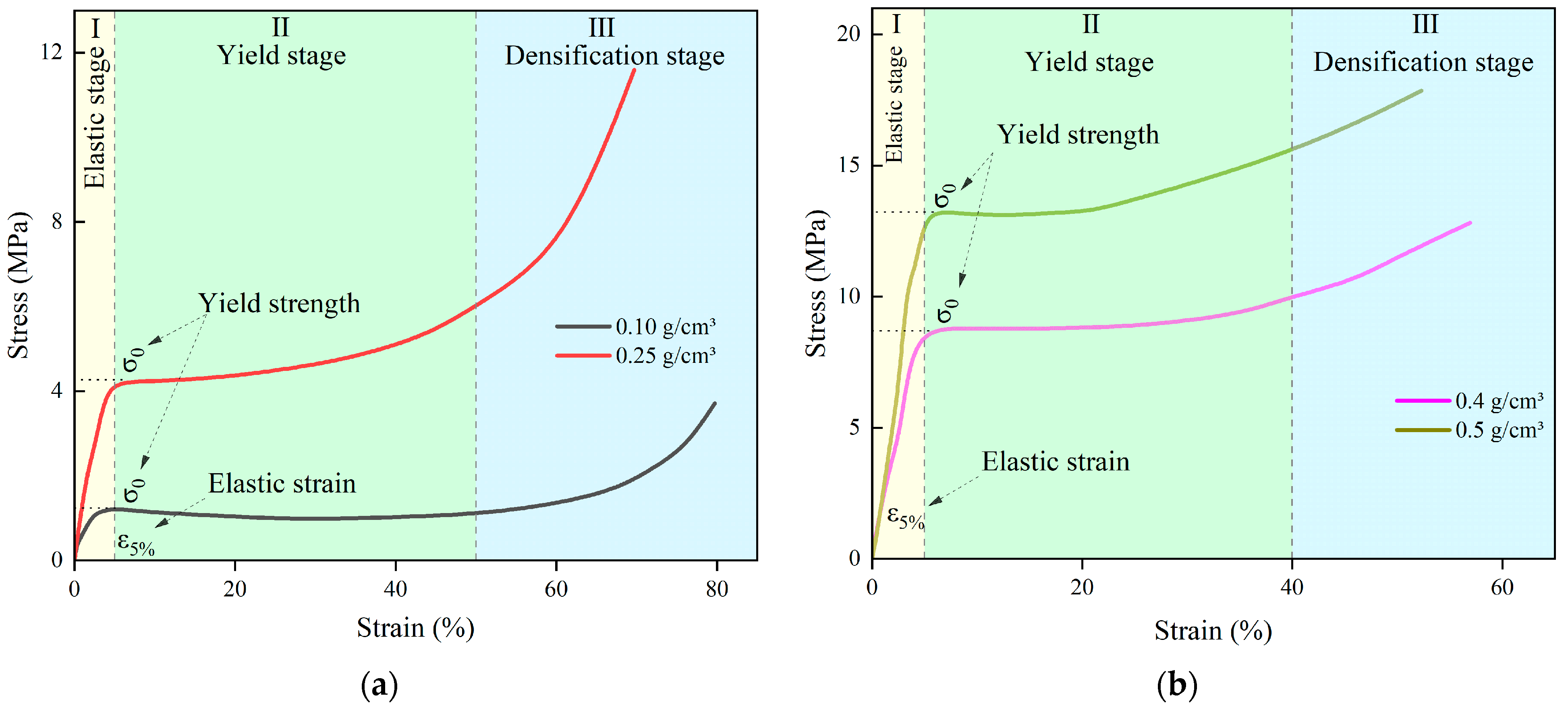
3.2. Mechanical Properties of Polymers
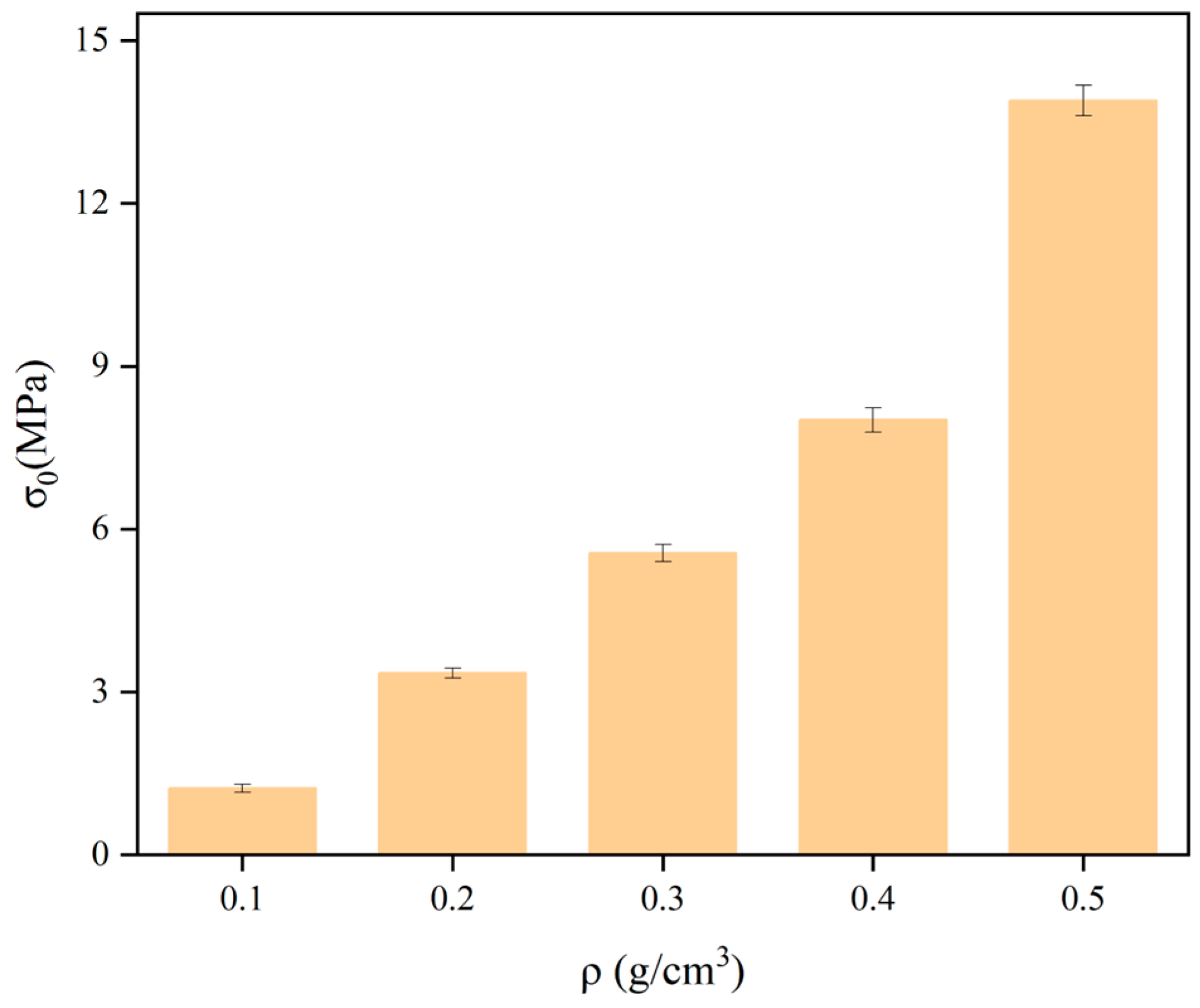
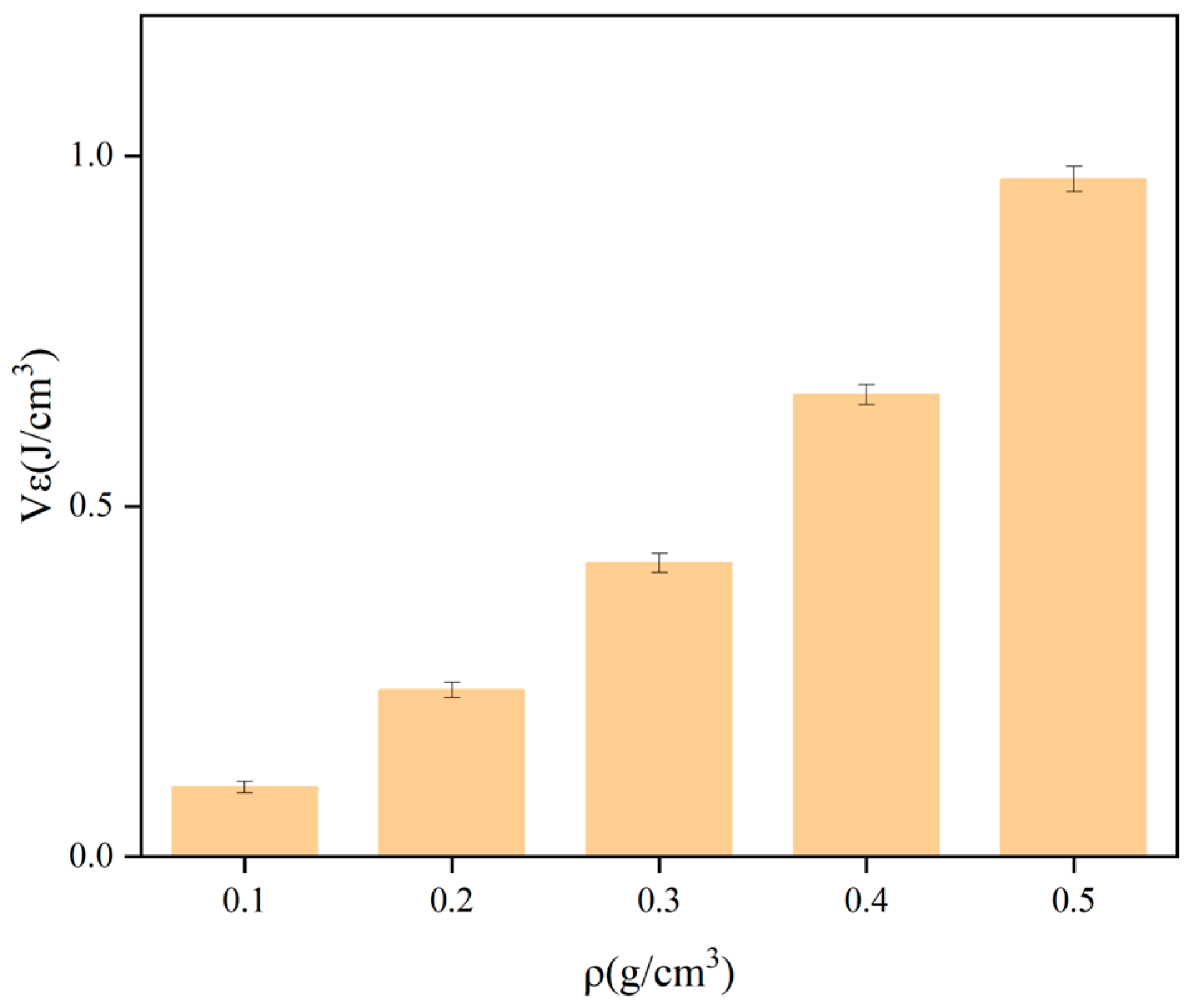
3.2.1. Effect of Density on Compressive Properties of Polymers
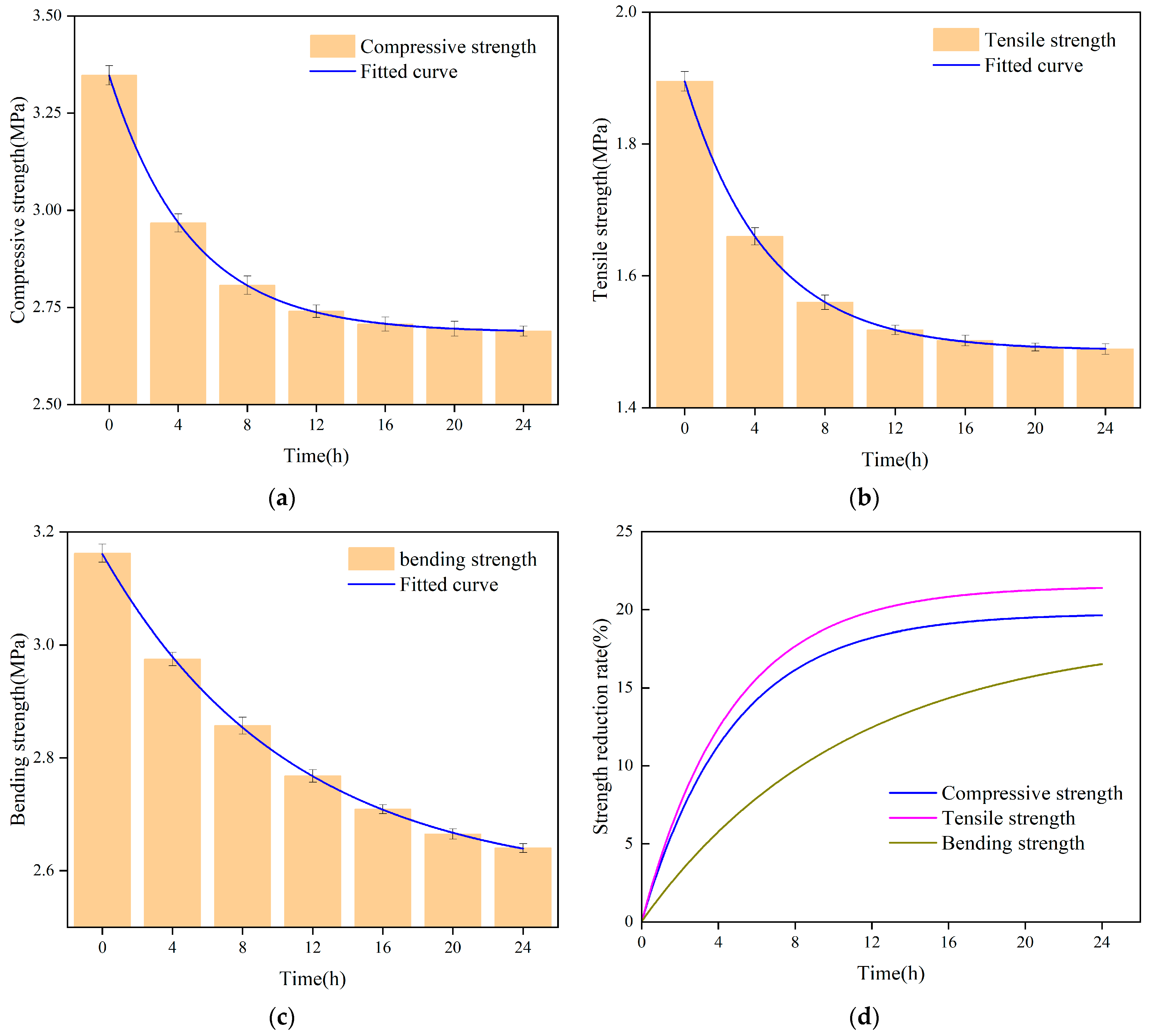
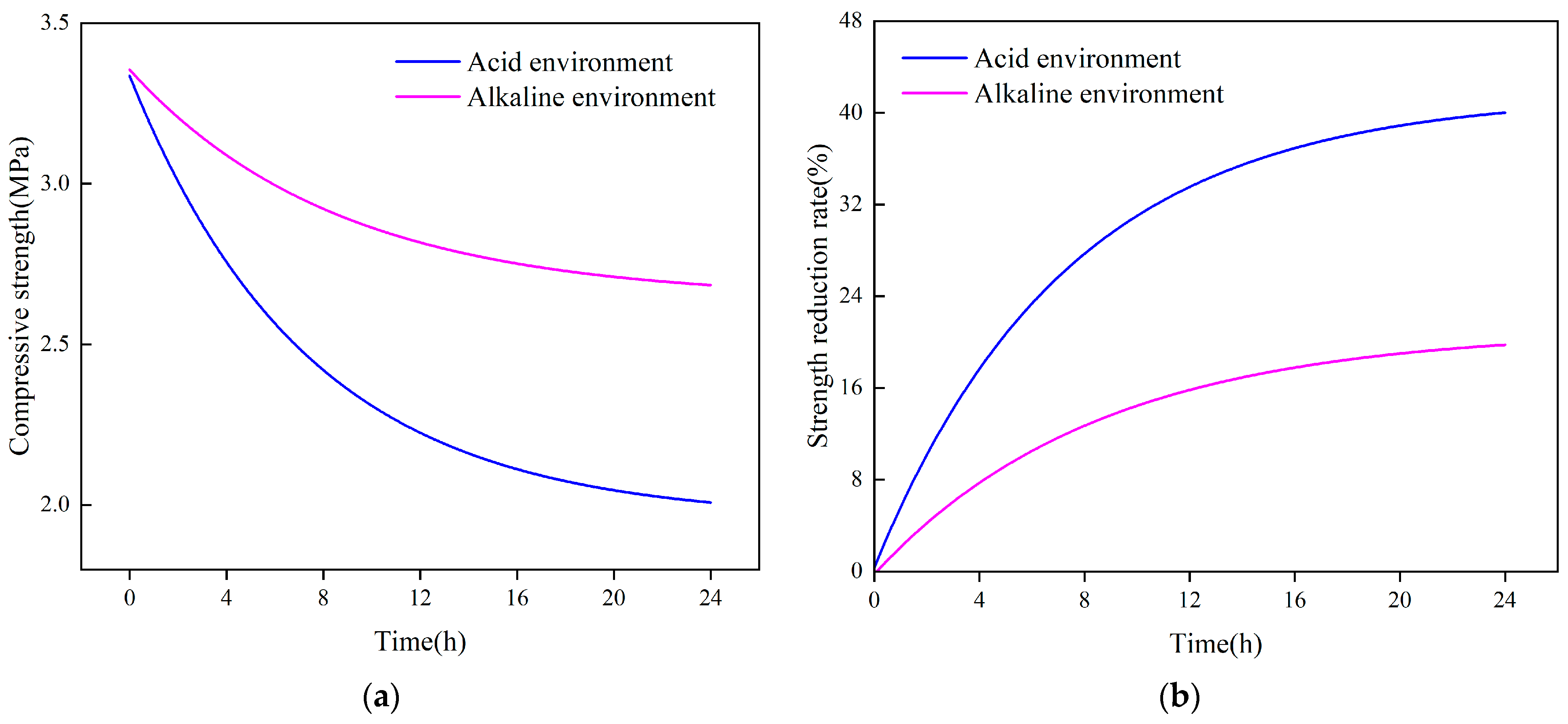
3.2.2. Effect of Soaking Time on Polymer Strength
3.3. Microscopic Characteristics of Polymers
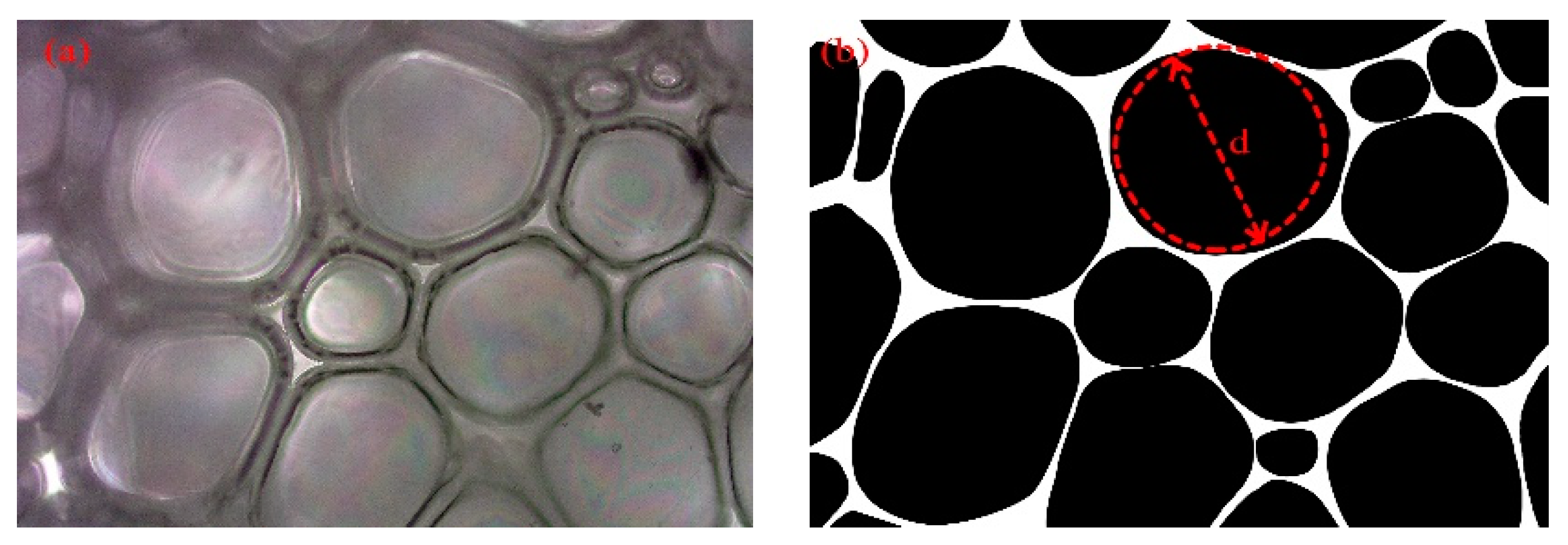
3.3.1. SEM Images of the Polymer
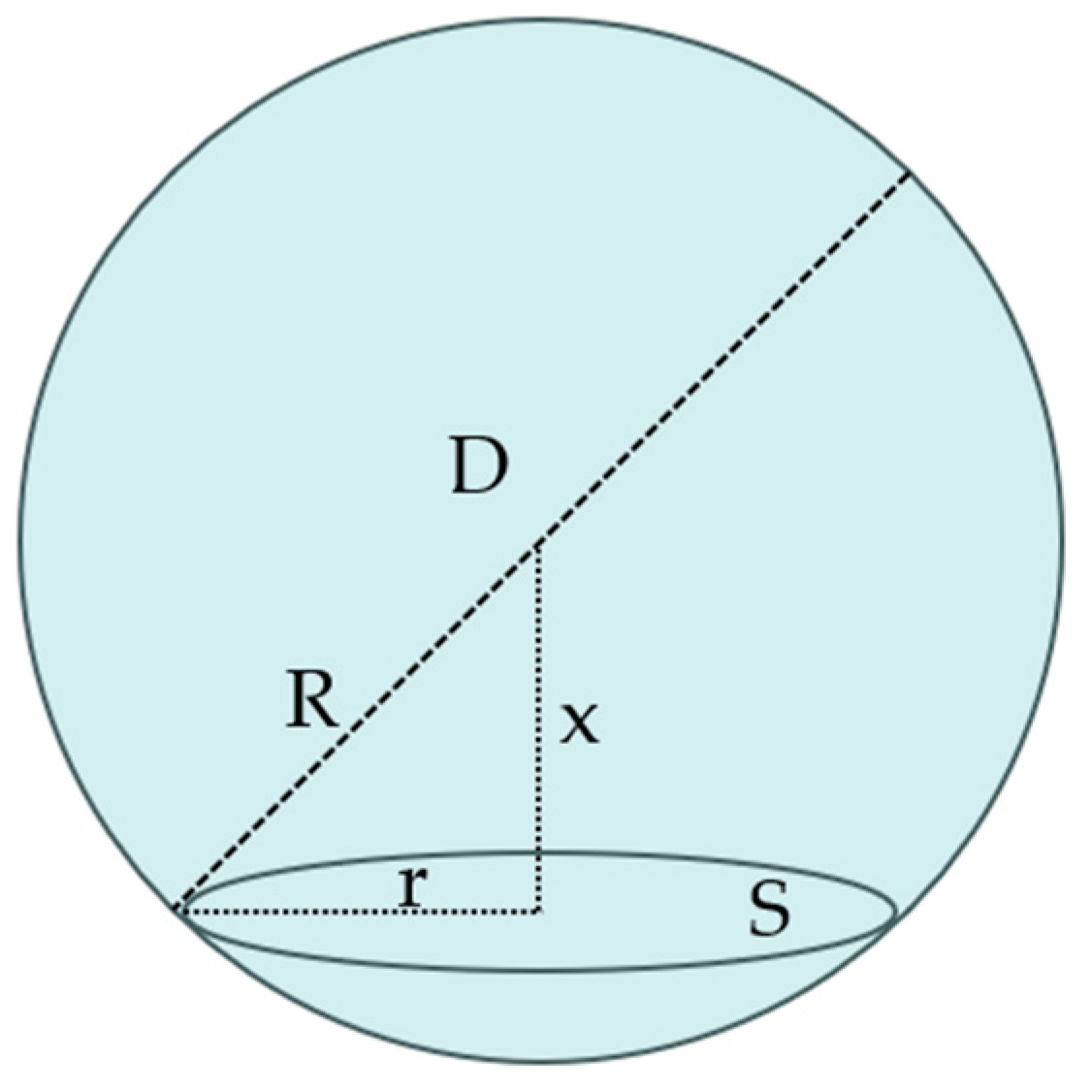
3.3.2. Characteristic Parameters of Polymer Cell
3.4. Model of Compressive Strength
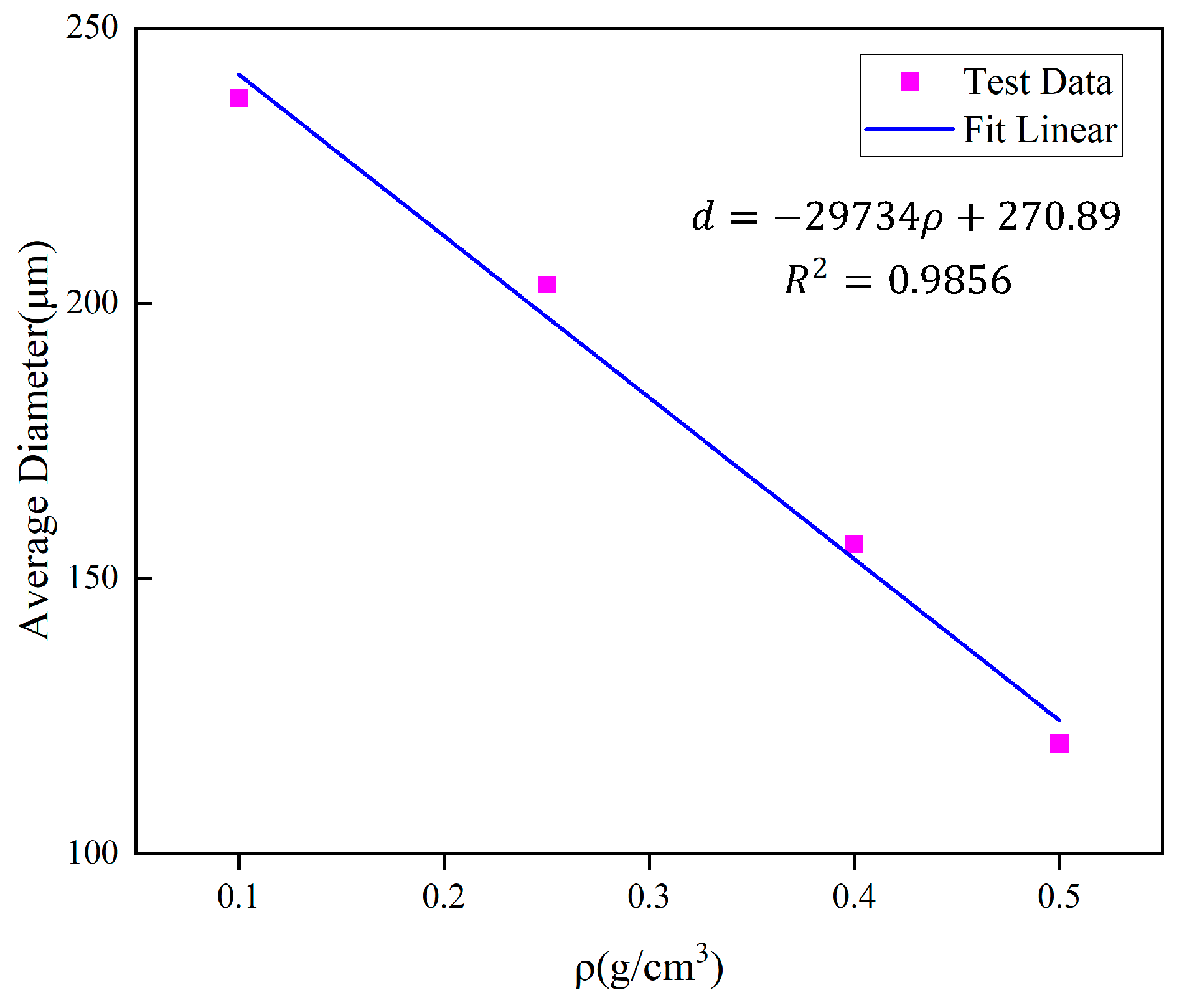
3.4.1. Modeling of Strength–Density Relationship
3.4.2. Validation of the Model
4. Conclusions
- The initial viscosity and gel time of the polyurethane slurry decreased significantly with the increase of the initial temperature, and the change rule of viscosity with time is not linear. The viscosity of the polyurethane slurry is almost unchanged before the gel time point is reached, and when the gel time point is reached, there is a substantial increase in the viscosity of the slurry, and the gel is cured in a short period;
- Under uniaxial loading, the stress–strain curve of polymers is divided into three stages: elastic deformation stage, plateau stage, and densification stage. The yield strength, Young’s modulus, and strain energy of the polymers increase with increasing density. In both water and corrosive environments, the mechanical strength of the specimens decreased with increasing immersion time and stabilized after the immersion time reached 16 h;
- Polyurethanes have a porous structure and the internal cells are approximately spherical. The structural parameters of the polymer cell are statistically determined by graphical processing techniques to establish a link between cell diameter and density.
- Based on the Gibson–Ashby equation, the modeling equations that can predict the yield strength of polymers from their densities are derived in conjunction with the structural parameters of the cell, making the application of polymers more efficient. These studies help to support and guide the application of polyurethane in mine engineering.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lei, Y.; Cui, N.; Pan, D. Economic and Social Effects Analysis of Mineral Development in China and Policy Implications. Resour. Policy 2013, 38, 448–457. [Google Scholar] [CrossRef]
- Prior, T.; Giurco, D.; Mudd, G.; Mason, L.; Behrisch, J. Resource Depletion, Peak Minerals and the Implications for Sustainable Resource Management. Glob. Environ. Change 2012, 22, 577–587. [Google Scholar] [CrossRef]
- Xue, Y.; Kong, F.; Li, S.; Qiu, D.; Su, M.; Li, Z.; Zhou, B. Water and Mud Inrush Hazard in Underground Engineering: Genesis, Evolution and Prevention. Tunn. Undergr. Space Technol. 2021, 114, 103987. [Google Scholar] [CrossRef]
- Wu, Q.; Fan, S.; Zhou, W.; Liu, S. Application of the Analytic Hierarchy Process to Assessment of Water Inrush: A Case Study for the No. 17 Coal Seam in the Sanhejian Coal Mine, China. Mine Water Environ. 2013, 32, 229–238. [Google Scholar] [CrossRef]
- Sha, F.; Lin, C.; Li, Z.; Liu, R. Reinforcement Simulation of Water-Rich and Broken Rock with Portland Cement-Based Grout. Constr. Build. Mater. 2019, 221, 292–300. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, X.; Liu, X.; Guan, X.; Zhang, C.; Niu, Y. Flexible and Stretchable Polyurethane/Waterglass Grouting Material. Constr. Build. Mater. 2017, 138, 240–246. [Google Scholar] [CrossRef]
- Fang, H.; Zhao, P.; Zhang, C.; Pan, W.; Yu, Z.; Cai, K.; Wang, C.; Wang, J.; Du, M.; He, W.; et al. A Cleaner Polyurethane Elastomer Grouting Material with High Hardening Strain for the Fundamental Rehabilitation: The Comprehensive Mechanical Properties Study. Constr. Build. Mater. 2022, 318, 125951. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, X.; Wu, M.; Zhao, Y.; Yu, C. Effects of Different Catalysts on the Structure and Properties of Polyurethane/Water Glass Grouting Materials. J. Appl. Polym. Sci. 2018, 135, 46460. [Google Scholar] [CrossRef]
- He, Z.; Li, Q.; Wang, J.; Yin, N.; Jiang, S.; Kang, M. Effect of Silane Treatment on the Mechanical Properties of Polyurethane/Water Glass Grouting Materials. Constr. Build. Mater. 2016, 116, 110–120. [Google Scholar] [CrossRef]
- Wang, C.; Guo, C.; Du, X.; Shi, M.; Liu, Q.; Xia, Y. Reinforcement of Silty Soil with Permeable Polyurethane by Penetration Injection. Constr. Build. Mater. 2021, 310, 124829. [Google Scholar] [CrossRef]
- Lee, G.; Cui, M.; Yoon, Y.; Khim, J.; Jang, M. Passive Treatment of Arsenic and Heavy Metals Contaminated Circumneutral Mine Drainage Using Granular Polyurethane Impregnated by Coal Mine Drainage Sludge. J. Clean. Prod. 2018, 186, 282–292. [Google Scholar] [CrossRef]
- Luo, Z.; Hong, R.Y.; Xie, H.D.; Feng, W.G. One-Step Synthesis of Functional Silica Nanoparticles for Reinforcement of Polyurethane Coatings. Powder Technol. 2012, 218, 23–30. [Google Scholar] [CrossRef]
- Saleh, S.; Yunus, N.Z.M.; Ahmad, K.; Ali, N. Improving the Strength of Weak Soil Using Polyurethane Grouts: A Review. Constr. Build. Mater. 2019, 202, 738–752. [Google Scholar] [CrossRef]
- Peper, S.; Dohrn, R.; Konejung, K. Methods for the Prediction of Thermophysical Properties of Polyurethane Raw Material Mixtures. Fluid. Phase Equilibria 2016, 424, 137–151. [Google Scholar] [CrossRef]
- Zhou, K.; Gong, K.; Zhou, Q.; Zhao, S.; Guo, H.; Qian, X. Estimating the Feasibility of Using Industrial Solid Wastes as Raw Material for Polyurethane Composites with Low Fire Hazards. J. Clean. Prod. 2020, 257, 120606. [Google Scholar] [CrossRef]
- Kim, H.-M.; Lee, J.-W.; Yazdani, M.; Tohidi, E.; Nejati, H.R.; Park, E.-S. Coupled Viscous Fluid Flow and Joint Deformation Analysis for Grout Injection in a Rock Joint. Rock. Mech. Rock. Eng. 2018, 51, 627–638. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, F.; Gao, X.; Zhong, Y. Microstructure and Fatigue Performance of Polyurethane Grout Materials under Compression. J. Mater. Civ. Eng. 2017, 29, 04017101. [Google Scholar] [CrossRef]
- Shi, L.; Li, Z. Morphology Development of High-density Rigid Polyurethane Foam upon Compression by On-line Scanning Electronic Microscope. J. Appl. Polym. Sci. 2007, 105, 2008–2011. [Google Scholar] [CrossRef]
- Liu, K.; Liang, W.; Ren, F.; Ren, J.; Wang, F.; Ding, H. The Study on Compressive Mechanical Properties of Rigid Polyurethane Grout Materials with Different Densities. Constr. Build. Mater. 2019, 206, 270–278. [Google Scholar] [CrossRef]
- Linul, E.; Şerban, D.A.; Marsavina, L.; Sadowski, T. Assessment of Collapse Diagrams of Rigid Polyurethane Foams under Dynamic Loading Conditions. Arch. Civ. Mech. Eng. 2017, 17, 457–466. [Google Scholar] [CrossRef]
- Wu, J.; He, Y.; Yu, Z. Failure Mechanism of Rigid Polyurethane Foam under High Temperature Vibration Condition by Experimental and Finite Element Method. J. Appl. Polym. Sci. 2020, 137, 48343. [Google Scholar] [CrossRef]
- He, Y.; Wu, J.; Qiu, D.; Yu, Z. Experimental and Numerical Analyses of Thermal Failure of Rigid Polyurethane Foam. Mater. Chem. Phys. 2019, 233, 378–389. [Google Scholar] [CrossRef]
- Gustafson, G.; Stille, H. Stop Criteria for Cement Grouting. Felsbau 2005, 23, 62–68. [Google Scholar]
- Wang, Y.; Han, M. Optimal Design of Slope Reinforcement by a New Developed Polymer Micro Anti-Slide Pile in Case of Emergency and Disaster Relief. Nat. Hazards 2022, 112, 899–917. [Google Scholar] [CrossRef]
- Aktaş, M.; Karakuzu, R. Determination of mechanical properties of glass-epoxy composites in high temperatures. Polym. Compos. 2009, 30, 1437–1441. [Google Scholar] [CrossRef]
- Mohaghegh, S.M.S.; Barikani, M.; Entezami, A.A. The Effect of Grafted Poly(Ethylene Glycol Monomethyl Ether) on Particle Size and Viscosity of Aqueous Polyurethane Dispersions. Colloids Surf. A Physicochem. Eng. Asp. 2006, 276, 95–99. [Google Scholar] [CrossRef]
- Meincken, M.; Klash, A.; Seboa, S.; Sanderson, R. Influence of the Viscosity and the Substrate on the Surface Hydrophobicity of Polyurethane Coatings. Appl. Surf. Sci. 2006, 253, 805–809. [Google Scholar] [CrossRef]
- Ren, B.; Shen, J.; Liu, W.; Cao, Q. Fracture Characteristics of Polyurethane Grouting Materials Based on Acoustic Emission Monitoring. Shock Vib. 2021, 2021, 8888691. [Google Scholar] [CrossRef]
- Xiang, X.J.; Qian, J.W.; Yang, W.Y.; Fang, M.H.; Qian, X.Q. Synthesis and Properties of Nanosilica-Reinforced Polyurethane for Grouting. J. Appl. Polym. Sci. 2006, 100, 4333–4337. [Google Scholar] [CrossRef]
- Sebastian, G.C.A. Construction and Building Materials. Constr. Build. Mater. 2001, 15, 465–471. [Google Scholar]
- Li, M.; Du, M.; Wang, F.; Xue, B.; Fang, H. Study on the Mechanical Properties of Polyurethane (PU) Grouting Material of Different Geometric Sizes under Uniaxial Compression. Constr. Build. Mater. 2020, 259, 119797. [Google Scholar] [CrossRef]
- Li, M.; Fang, H.; Zhang, C.; Du, M.; Wang, F. Study on the New Polyurethane Material Suitable for Foaming in Water. Constr. Build. Mater. 2022, 354, 129163. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]




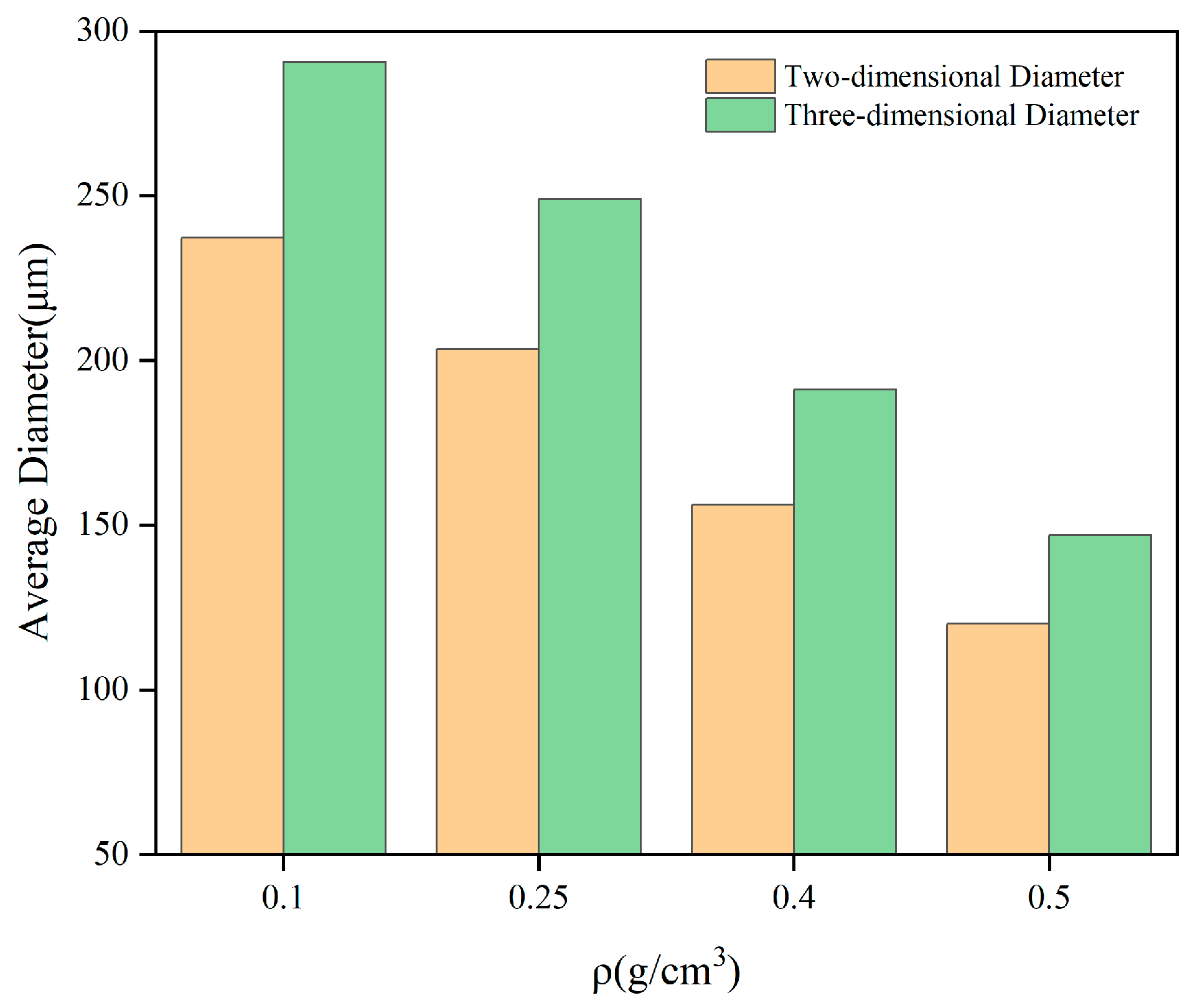
| Raw Material | Type | Proportion (%) |
|---|---|---|
| Isocyanate | MDI | 47 |
| Polyether Polyol | GE-220 | 47 |
| Catalyst | DBTDL | 1–5 |
| Foam Stabilizer | PMX-200 | 0.5–2 |
| Chain Extender | BOP | 0.5–1 |
| Plasticizer | DOP | 0.5–1 |
| T/°C | η0/Pa s | K1 | t1 |
|---|---|---|---|
| 20 | 0.744 | 2.756 × 10−8 | −4.847 |
| 25 | 0.598 | 1.390 × 10−15 | −1.867 |
| 30 | 0.511 | 2.949 × 10−10 | −2.229 |
| 35 | 0.379 | 9.318 × 10−4 | −3.258 |
| 40 | 0.341 | 8.768 × 10−4 | −2.157 |
| ρ/g/cm3 | d/μm | D/μm |
|---|---|---|
| 0.1 | 237.25 | 290.57 |
| 0.25 | 203.39 | 249.10 |
| 0.4 | 156.18 | 191.28 |
| 0.5 | 120.06 | 147.04 |
| Density/g/cm3 | Test Strength/MPa | Predicted Strength/MPa | Error/% |
|---|---|---|---|
| 0.1 | 1.226 | 1.207 | 1.5 |
| 0.2 | 3.347 | 3.277 | 3.6 |
| 0.3 | 5.598 | 5.963 | 6.5 |
| 0.4 | 8.517 | 9.174 | 7.7 |
| 0.5 | 14.197 | 15.247 | 7.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wang, E. Study on the Gelation Process and Mechanical Properties of Organic Polymer Grouting Materials Applied to Fissure Sealing in Underground Mines. Polymers 2024, 16, 446. https://doi.org/10.3390/polym16040446
Zhang X, Wang E. Study on the Gelation Process and Mechanical Properties of Organic Polymer Grouting Materials Applied to Fissure Sealing in Underground Mines. Polymers. 2024; 16(4):446. https://doi.org/10.3390/polym16040446
Chicago/Turabian StyleZhang, Xuanning, and Ende Wang. 2024. "Study on the Gelation Process and Mechanical Properties of Organic Polymer Grouting Materials Applied to Fissure Sealing in Underground Mines" Polymers 16, no. 4: 446. https://doi.org/10.3390/polym16040446
APA StyleZhang, X., & Wang, E. (2024). Study on the Gelation Process and Mechanical Properties of Organic Polymer Grouting Materials Applied to Fissure Sealing in Underground Mines. Polymers, 16(4), 446. https://doi.org/10.3390/polym16040446





