Elasto-Static Analysis of Composite Restorations in a Molar Tooth: A Meshless Approach
Abstract
:1. Introduction
2. Meshless Methods
3. Material and Model Specification
| Human Tooth | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Identification | Material | (GPa) | (MPa) | (MPa) | |||||
| 1 | Dentine | [28] | 0.31 [28] | Avg.: 24 [29] | Avg.: 310 [29] | ||||
| 2 | Enamel | [28] | 0.30 [28] | Avg.: 108 [29] | Avg.: 279 [29] | ||||
| 3 | Pulp | [28] | 0.45 [28] | - | - | ||||
| 4 | Periodontal ligament | [30] | 0.45 [30] | - | - | ||||
| 5 | Cortical bone | [30] | 0.30 [30] | min: 133 [29] | - | ||||
| 6 | Cancellous bone | [30] | 0.30 [30] | min: 75 [29] | - | ||||
| 7 | Fictitious material | 0.30 | - | - | |||||
| Composite restorations | |||||||||
| Material | Manufacturer | Type | Composition | Filler | |||||
| 3M™ Filtek™ Z250TM | 3M ESPE | Microhybrid | Matrix: BisGMA, UDMA, TEGDMA Filler: Zerconia, silica | 60% | 11.0 | 0.31 | 85 | 405 | |
| 3M™ Z100™ | 3M ESPE | Microhybrid | Matrix: BisGMA, TEGDMA Filler: Zerconia, silica | 66% | 14.5 | 0.30 | 105 | 470 | |
| Herculite XRV UltraTM | Kerr | Nanohybrid | Matrix: BisGMA, TEGDMA Filler: PPF, barium glass, silica nanofiller | 59% | 8.2 | 0.30 | 137 | 349 | |
4. Numerical Modelling
- Occlusal right vertical (ORV);
- Occlusal left vertical (OLV);
- Bruxism right vertical (BRV);
- Bruxism left vertical (BLV).
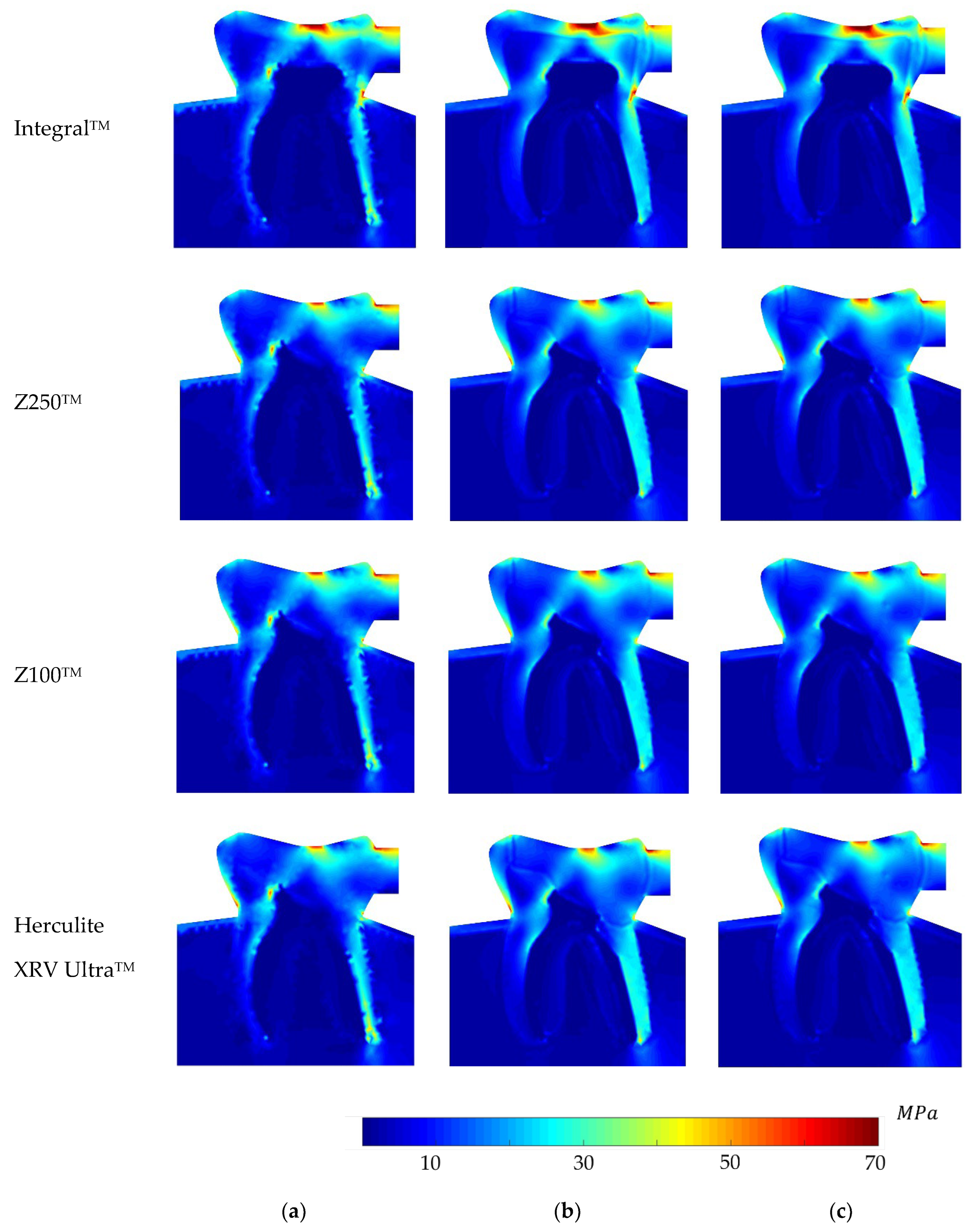
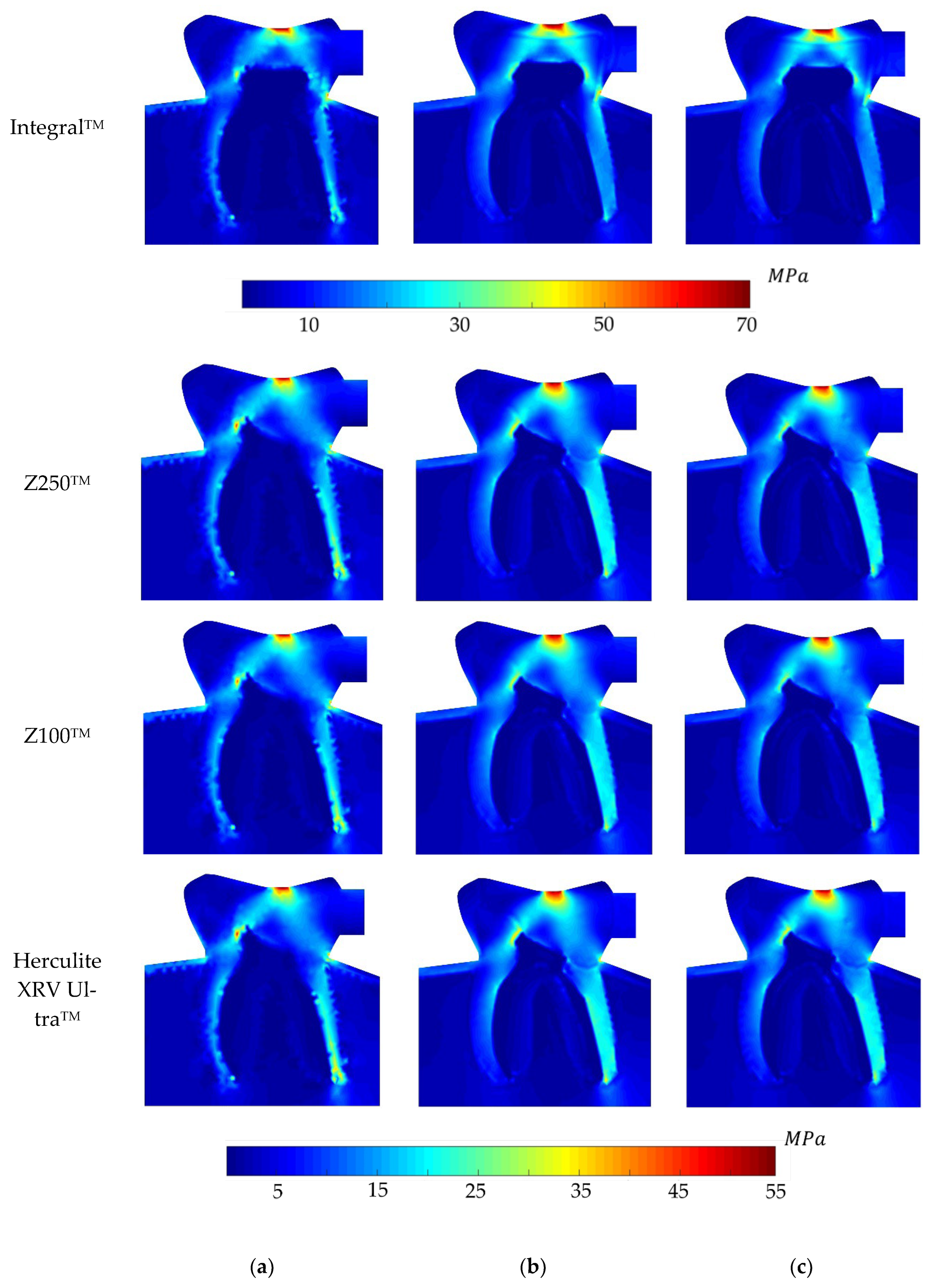
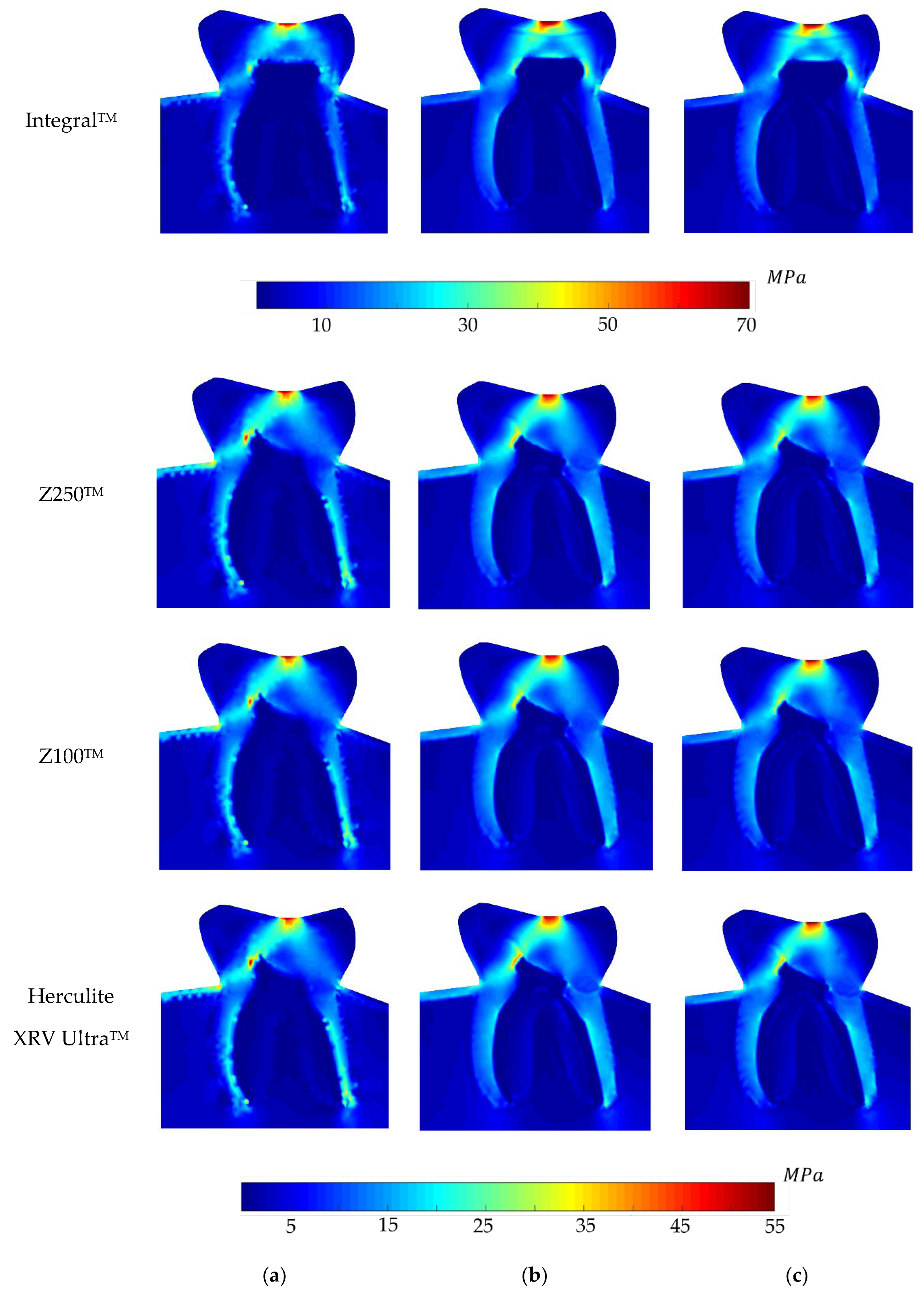
5. Analysis and Results
6. Discussion on the Results
7. Conclusions
- The non-restored tooth is characterised by enamel rather than composite restoration. Enamel exhibits the highest Young’s modulus compared to the composites. Consequently, an integral tooth demonstrates a greater ability to withstand forces compared to composite restorations. It means that the stiffness of enamel is higher than that of the restorative materials.
- The ranking on the local stress analysis can be rationalised based on the superior mechanical properties of Z100TM, including its elevated Young’s modulus, notably higher tensile and compressive strength compared to other composite materials. This implies that dental restoration using Z100TM results in increased stiffness and rigidity in the treated tooth. It owns the highest percentage of fillers, 66%, which implies higher hardness.
- Herculite XRV UltraTM exhibited the weakest response in terms of elasto-static analysis. One potential reason could be attributed to its lower Young’s modulus and consequently, the lowest hardness, which may be influenced by the presence of barium glass filler in this composite. Conversely, the Zirconia Filler in Z100TM and Filtek Z250TM might account for the improved physical properties observed in these two composites.
- In the depicted stress profiles of the BLV load case, where there is no tooth on the left side of the model (no essential boundary condition), the stress distribution shows higher value on critical regions, mostly close to the boundaries. The absence of essential boundary conditions on the left side of the 2D model in the BLV and OLV load cases leads the applied force to produce a higher level of stress on the borders and critical spots. In this regard, the global stress distribution maps obtained with the meshless methods clearly show the potential rupture lines. This study shows the importance of the neighbour tooth to prevent a potential fracture.
- There is an acceptable verification between the FEM and meshless results. However, in some cases, in the points close to more complex curves, FEA yields a far different value from the ones calculated by meshless methods.
- Within the restrictions of the numerical methods, the computational simulations implemented in this work have the capacity to improve and refine the results until they are closer to clinical implications. Performing these simulations with denser meshes could potentially lead to better results. Furthermore, future composite materials for dental restorations perhaps will possess better mechanical properties, especially a higher Young’s modulus. Thus, mechanical improvement on composites will eventually lead them to withstand critical loads of bruxism. It is undeniable that deeper research on this topic would allow increases in the quality of patients’ life.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| 2D | Two-dimensional | RPIM | Radial point interpolation method |
| 3D | Three-dimensional | RPI | Radial point interpolation |
| BisGMA | Bisphenol A-glycidyl methacrylate | TEGDMA | Triethylene glycol dimethacrylate |
| BRV | Bruxism right vertical | UDMA | Urethane dimethacrylate |
| BLV | Bruxism left vertical | Young’s modulus | |
| CNS | Central nervous system | Applied force | |
| FEA | Finite element analysis | Poisson’s ratio | |
| FEM | Finite element method | Stress tensor | |
| NNRPIM | Natural neighbour RPIM | Compressive strength | |
| OLV | Occlusal left vertical | Tensile strength | |
| ORV | Occlusal right vertical | Equivalent von Mises effective stress |
References
- Eskandarizadeh, A.; Elm-Amooz, N.; Rahimi, F.; Baharlooyi, K.; Naeimi-Jamal, M.-R. The Effect of Aging on Nano-Hardness and Modulus of Elasticity of Four Types of Composites: An in-vitro Study. J. Dent. Mater. Tech. 2016, 5, 162–171. [Google Scholar] [CrossRef]
- Thayer, M.L.T.; Ali, R. The dental demolition derby: Bruxism and its impact—Part 1: Background. Br. Dent. J. 2022, 232, 515–521. [Google Scholar] [CrossRef] [PubMed]
- Borges, A.L.S.; Grangeiro, M.T.V.; de Andrade, G.S.; de Melo, R.M.; Baroudi, K.; Silva-Concilio, L.R.; Tribst, J.P.M. Stress Concentration of Endodontically Treated Molars Restored with Transfixed Glass Fiber Post: 3D-Finite Element Analysis. Materials 2021, 14, 4249. [Google Scholar] [CrossRef] [PubMed]
- Sellan, P.L.B.; Campaner, L.M.; Tribst, J.P.M.; Dal Piva, A.M.d.O.; de Andrade, G.S.; Borges, A.L.S.; Bresciani, E.; Lanzotti, A.; Ausiello, P. Functional or Nonfunctional Cusps Preservation for Molars Restored with Indirect Composite or Glass-Ceramic Onlays: 3D FEA Study. Polymers 2021, 13, 3831. [Google Scholar] [CrossRef]
- Syed, A.U.Y.; Rokaya, D.; Shahrbaf, S.; Martin, N. Three-Dimensional Finite Element Analysis of Stress Distribution in a Tooth Restored with Full Coverage Machined Polymer Crown. Appl. Sci. 2021, 11, 1220. [Google Scholar] [CrossRef]
- Al-Zordk, W.; Saudi, A.; Abdelkader, A.; Taher, M.; Ghazy, M. Fracture Resistance and Failure Mode of Mandibular Molar Restored by Occlusal Veneer: Effect of Material Type and Dental Bonding Surface. Materials 2021, 14, 6476. [Google Scholar] [CrossRef]
- Young, F.A.; Williams, K.R.; Draughn, R.; Strohaver, R. Design of prosthetic cantilever bridgework supported by osseointegrated implants using the finite element method. Dent. Mater. 1998, 14, 37–43. [Google Scholar] [CrossRef] [PubMed]
- Bandela, V.; Kanaparthi, S. Finite Element Analysis and Its Applications in Dentistry. In Finite Element Methods and Their Applications; Baccouch, M., Ed.; IntechOpen: Rijeka, Croatia, 2020; p. 316. [Google Scholar] [CrossRef]
- Romanyk, D.L.; Vafaeian, B.; Addison, O.; Adeeb, S. The use of finite element analysis in dentistry and orthodontics: Critical points for model development and interpreting results. Semin. Orthod. 2020, 26, 162–173. [Google Scholar] [CrossRef]
- Jorge, M.; Vaz, M.; Lopes, J.; Ustrell-Torrent, J.-M.; Farahani, B.; Ponces, M.-J. Biomechanical effects of Teuscher activator in hyperdivergent Class II malocclusion treatment: A finite element analysis. J. Clin. Exp. Dent. 2021, 13, e1124–e1130. [Google Scholar] [CrossRef]
- Ritthiti, A.; Sattabanasuk, V.; Karunratanakul, K.; Senawongse, P. Effect of Stress Generated by Occlusal Cyclic Force on Class I Bulk-Fill Composite Restoration Microleakage. Eur. J. Dent. 2022, 16, 307–314. [Google Scholar] [CrossRef]
- Singhal, S.; Gurtu, A.; Singhal, A.; Bansal, R.; Mohan, S. Effect of Different Composite Restorations on the Cuspal Deflection of Premolars Restored with Different Insertion Techniques—An In vitro Study. J. Clin. Diagn. Res. 2017, 11, ZC67–ZC70. [Google Scholar] [CrossRef]
- Sakhabutdinova, L.; Kamenskikh, A.A.; Kuchumov, A.G.; Nosov, Y.; Baradina, I. Numerical Study of the Mechanical Behaviour of Wedge-Shaped Defect Filling Materials. Materials 2022, 15, 7387. [Google Scholar] [CrossRef]
- Brailko, N.N.; Tkachenko, I.M.; Kovalenko, V.V.; Lemeshko, A.V.; Fenko, A.G.; Kozak, R.V.; Kalashnikov, D.V. Investigation of Stress-Strain State of ‘Restoration & Tooth’ System in Wedge-Shaped Defects by Computed Modeling Method. Wiadomości Lekarskie 2021, 74, 2112–2117. [Google Scholar] [CrossRef]
- Dikova, T.; Vasilev, T.; Hristova, V.; Panov, V. Finite element analysis of V-shaped tooth defects filled with universal nanohybrid composite using incremental technique. J. Mech. Behav. Biomed. Mater. 2021, 118, 104425. [Google Scholar] [CrossRef]
- Belinha, J. Meshless Methods in Biomechanics: Bone Tissue Remodelling Analysis; Springer: Dordrecht, The Netherlands, 2014; Volume 16. [Google Scholar]
- Liu, G.R.; Gu, Y.T. A point interpolation method for two-dimensional solids. Int. J. Numer Methods Eng. 2001, 50, 937–951. [Google Scholar] [CrossRef]
- Wang, J.G.; Liu, G.R. A point interpolation meshless method based on radial basis functions. Numer. Methods Eng. 2002, 54, 1623–1648. [Google Scholar] [CrossRef]
- Braun, J.; Sambridge, M. A numerical method for solving partial differential equations on highly irregular evolving grids. Nature 1995, 376, 655–660. [Google Scholar] [CrossRef]
- Idelsohn, S.R.; Del Pin, F.; Oñate, E.; Calvo, N.; Del Pin, F. The meshless finite element method. Int. J. Numer. Methods Eng. 2003, 58, 893–912. [Google Scholar] [CrossRef]
- Baghini, E.G.; Toufigh, M.M.; Toufigh, V. Analysis of pile foundations using natural element method with disturbed state concept. Comput. Geotech. 2018, 96, 178–188. [Google Scholar] [CrossRef]
- Doblaré, M.; Cueto, E.; Calvo, B.; Martínez, M.A.; Garcia, J.M.; Cegoñino, J. On the employ of meshless methods in biomechanics. Comput. Methods Appl. Mech. Eng. 2005, 194, 801–821. [Google Scholar] [CrossRef]
- Wittek, A.; Joldes, G.R.; Miller, K. Meshless Algorithms for Computational Biomechanics of the Brain BT—Biomechanics of the Brain. In Biomechanics of the Brain; Miller, K., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 273–301. [Google Scholar] [CrossRef]
- Chen, Y.; Lee, J.; Eskandarian, A. Meshless Methods in Solid Mechanics, 1st ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Chung, S.M.; Yap, A.U.J.; Koh, W.K.; Tsai, K.T.; Lim, C.T. Measurement of Poisson’s ratio of dental composite restorative materials. Biomaterials 2004, 25, 2455–2460. [Google Scholar] [CrossRef] [PubMed]
- Biron, M. 7—Mechanical Properties. In Material Selection for Thermoplastic Parts; Biron, M., Ed.; William Andrew Publishing: Oxford, UK, 2016; pp. 261–337. [Google Scholar] [CrossRef]
- MatWeb: Online Materials Information Resource. Available online: http://www.matweb.com (accessed on 4 February 2024).
- Jang, Y.; Hong, H.T.; Roh, B.D. Influence of apical root resection on the biomechanical response of a single-rooted tooth: A 3-dimensional finite element analysis. J. Endod. 2014, 40, 1489–1493. [Google Scholar] [CrossRef] [PubMed]
- Celik, H.K.; Koc, S.; Kustarci, A.; Rennie, A.E.W. A literature review on the linear elastic material properties assigned in finite element analyses in dental research. Mater. Today Commun. 2022, 30, 103087. [Google Scholar] [CrossRef]
- Vanlıoğlu, B.; Özkan, K.; Uçankale, M.; Cansız, E.; Kayabaşı, O. Effect of post material, cement and amount of coronal destruction on stress distribution: 3D FEA study. Balk. J. Stomatol. 2013, 17, 18–25. [Google Scholar]
- Carey, J.P.; Craig, M.; Kerstein, R.B.; Radke, J. Determining a relationship between applied occlusal load and articulating paper mark area. Open Dent. J. 2007, 1, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Vasudeva, G.; Bogra, P. The effect of occlusal restoration and loading on the development of abfraction lesions: A finite element study. J. Conserv. Dent. Endod. 2008, 11, 117–120. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Zhou, Z.R.; Zhang, J.; Li, H.; Yu, H.Y. On the friction and wear behaviour of human tooth enamel and dentin. Wear 2003, 255, 967–974. [Google Scholar] [CrossRef]
- Sofiani, F.M.; Farahani, B.V.; Belinha, J. Fracture Toughness Determination on an SCB Specimen by Meshless Methods. Appl. Sci. 2022, 12, 2633. [Google Scholar] [CrossRef]
- Farahani, B.V.; Berardo, J.M.; Drgas, R.; de Sá, J.M.A.C.; Ferreira, A.J.M.; Belinha, J. The Axisymmetric Analysis of Circular Plates Using the Radial Point Interpolation Method. Int. J. Comput. Methods Eng. Sci. Mech. 2015, 16, 336–353. [Google Scholar] [CrossRef]
- Sofiani, F.M.; Chaudhuri, S.; Elahi, S.A.; Hectors, K.; De Waele, W. Quantitative analysis of the correlation between geometric parameters of pits and stress concentration factors for a plate subject to uniaxial tensile stress. Theor. Appl. Fract. Mech. 2023, 127, 104081. [Google Scholar] [CrossRef]
- Curtis, A.R.; Shortall, A.C.; Marquis, P.M.; Palin, W.M. Water uptake and strength characteristics of a nanofilled resin-based composite. J. Dent. 2008, 36, 186–193. [Google Scholar] [CrossRef] [PubMed]
- Stanford, J.W.; Weigel, K.V.; Paffenbarger, G.C.; Sweeney, W.T. Compressive properties of hard tooth tissues and some restorative materials. J. Am. Dent. Assoc. 1960, 60, 746–756. [Google Scholar] [CrossRef] [PubMed]
- Morozova, S.Y.; Holik, P.; Ctvrtlik, R.; Tomastik, J.; Foltasova, L.; Harcekova, A. Tooth Wear—Fundamental Mechanisms and Diagnosis. IOSR J. Dent. Med. Sci. 2016, 15, 84–91. [Google Scholar]
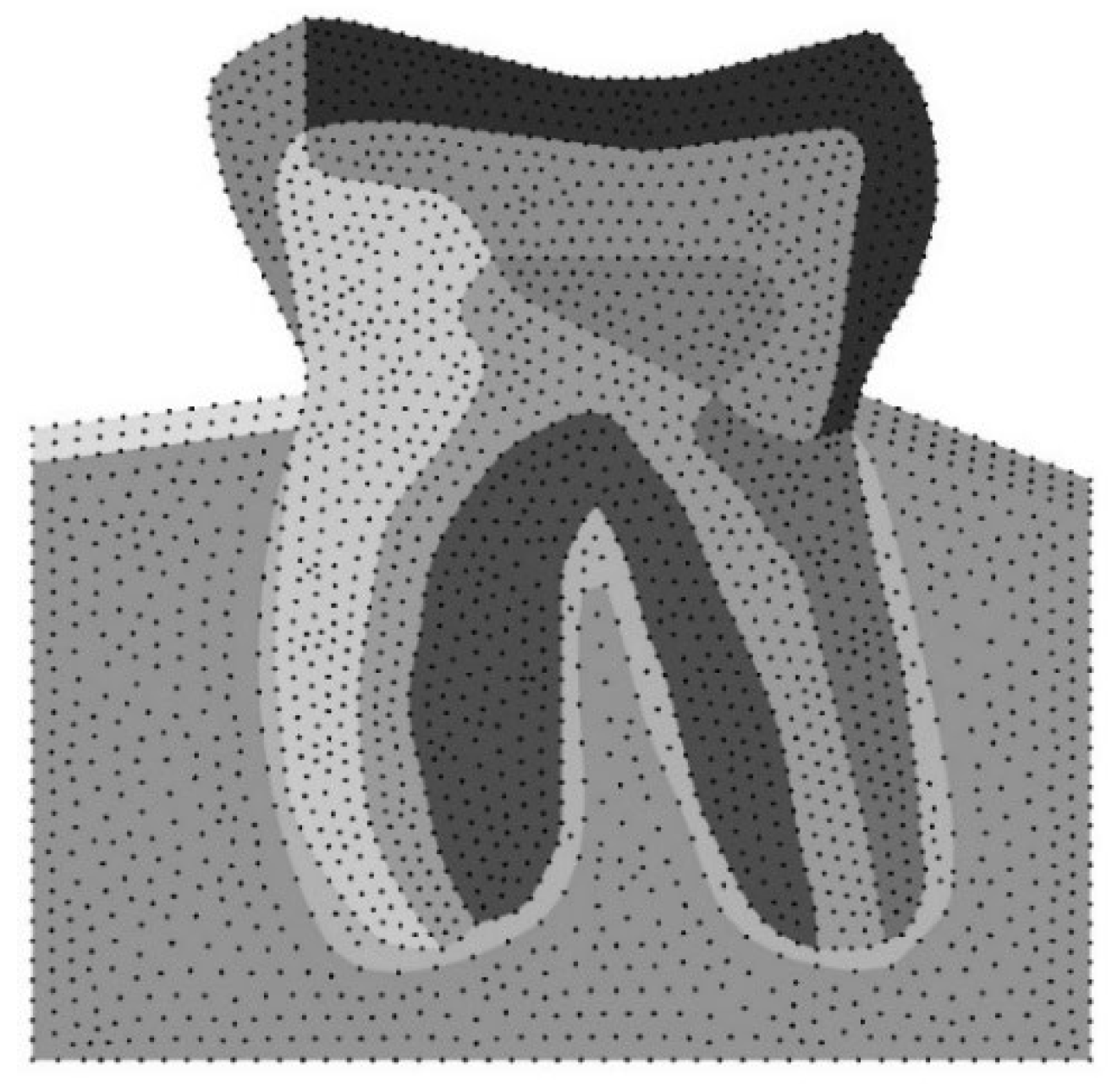
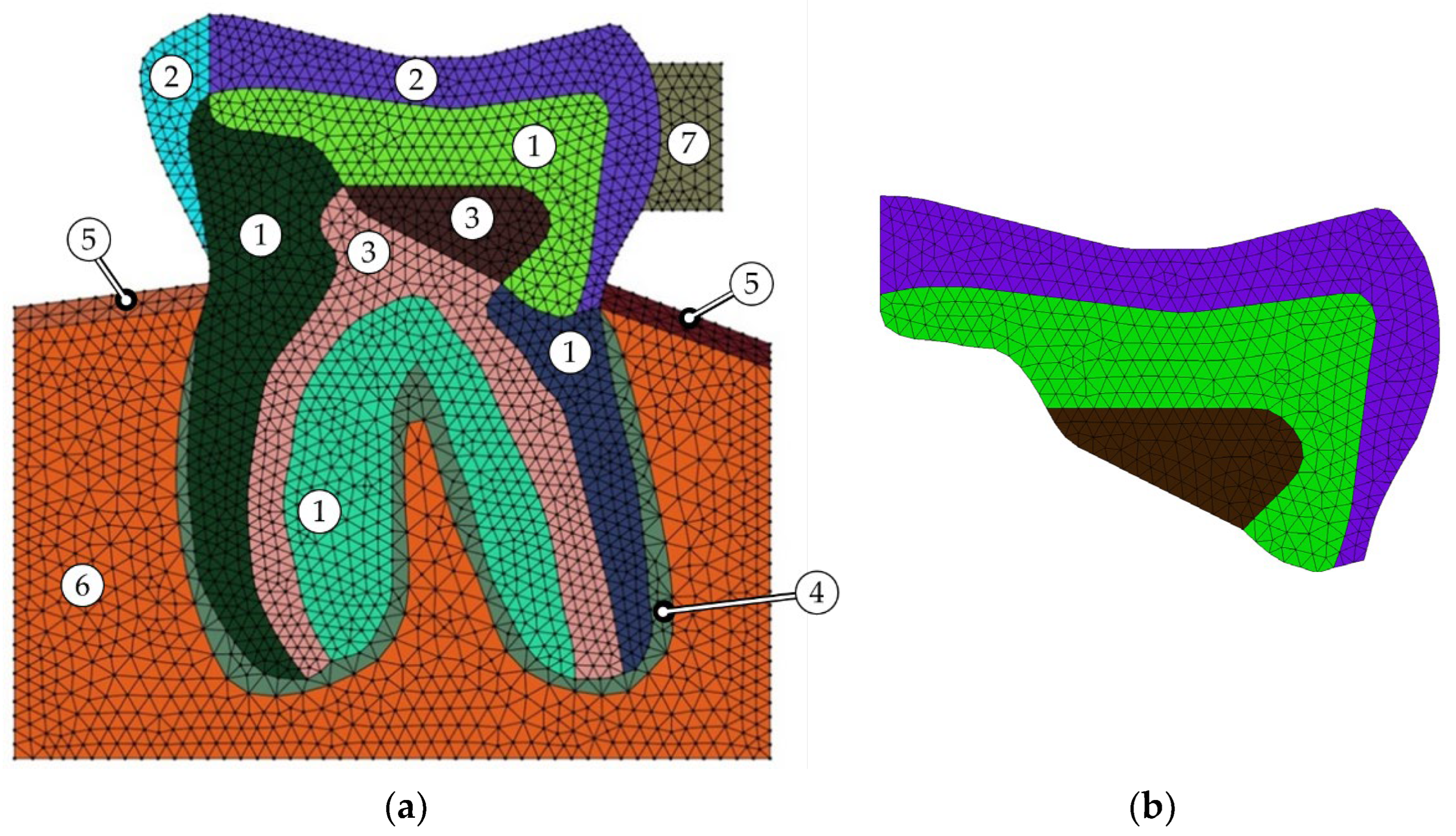
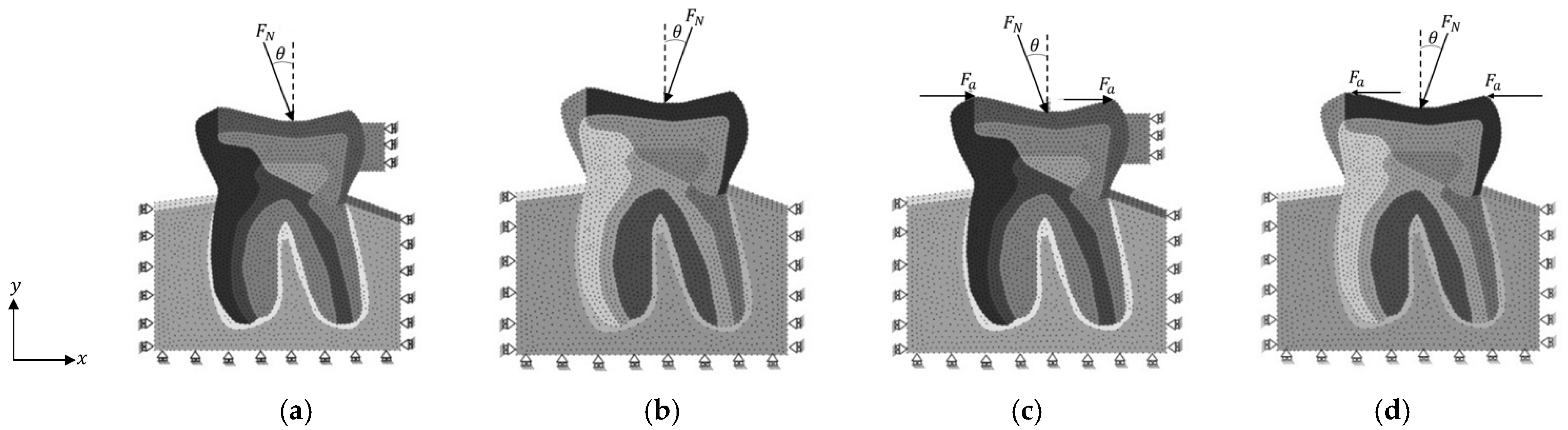
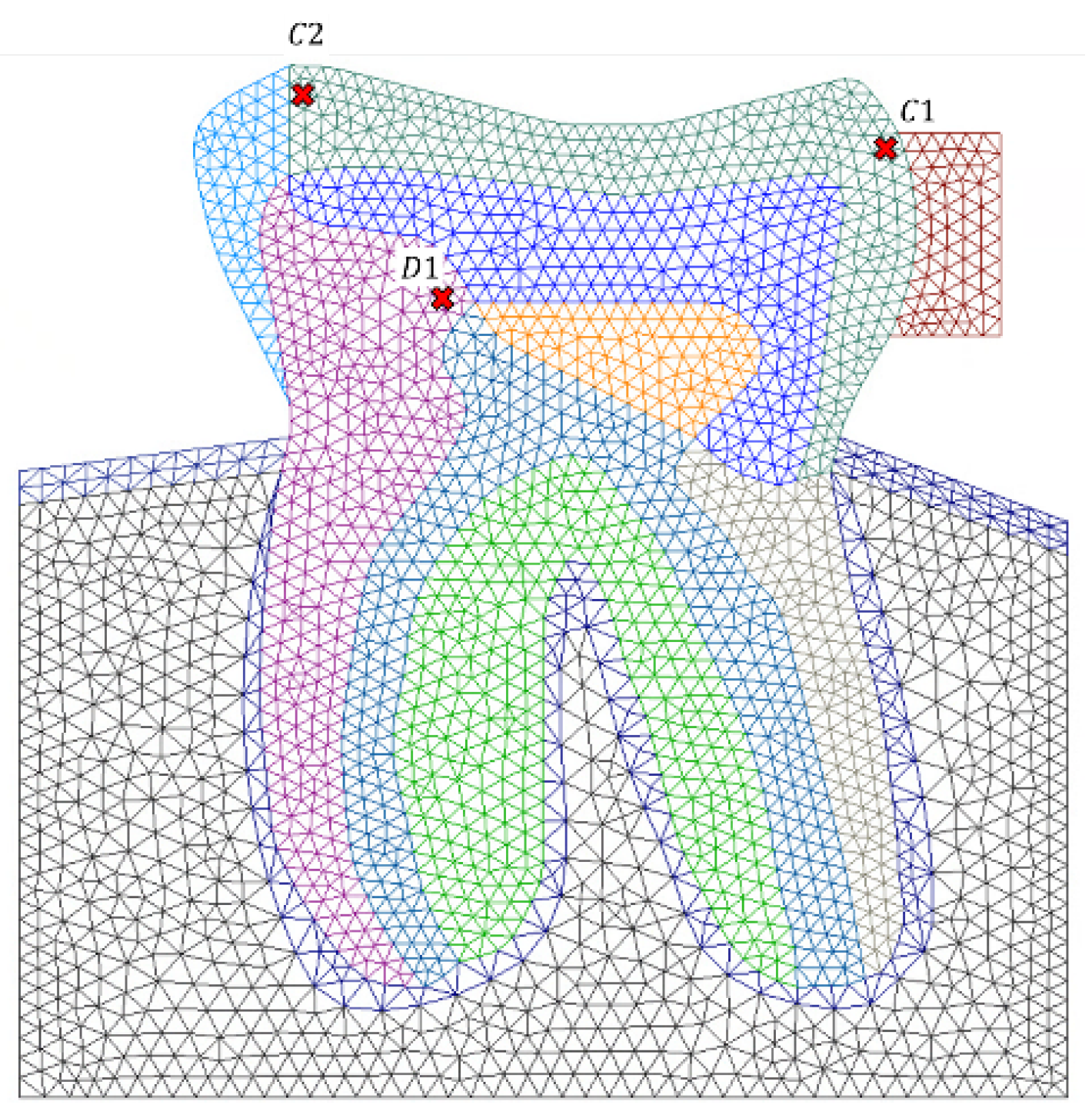

| Load Case | Force Magnitude (N) |
|---|---|
| ORV | 225 |
| OLV | 225 |
| BRV | 405 |
| BLV | 405 |
| (MPa) | |||||
|---|---|---|---|---|---|
| Point | Method | Integral | Z100TM | Z250TM | Herculite XRV UltraTM |
| C1 | FEM | 5.59 | 8.21 | 7.43 | 6.59 |
| RPIM | 3.19 | 6.04 | 5.15 | 4.25 | |
| NNRPIM | 3.06 | 5.68 | 4.86 | 4.03 | |
| C2 | FEM | 3.00 | 1.57 | 1.55 | 1.53 |
| RPIM | 2.93 | 1.24 | 1.17 | 1.11 | |
| NNRPIM | 2.75 | 1.15 | 1.08 | 1.03 | |
| D1 | FEM | 16.47 | 20.59 | 20.34 | 20.19 |
| RPIM | 23.95 | 22.46 | 21.43 | 20.33 | |
| NNRPIM | 26.73 | 23.68 | 22.59 | 21.45 | |
| (MPa) | |||||
|---|---|---|---|---|---|
| Point | Method | Integral | Z100TM | Z250TM | Herculite XRV UltraTM |
| C1 | FEM | 39.71 | 38.62 | 37.91 | 37.01 |
| RPIM | 38.36 | 38.50 | 37.11 | 35.58 | |
| NNRPIM | 36.86 | 36.24 | 34.73 | 33.08 | |
| C2 | FEM | 25.35 | 22.18 | 21.38 | 20.50 |
| RPIM | 29.96 | 22.51 | 20.83 | 19.13 | |
| NNRPIM | 27.03 | 19.99 | 18.34 | 16.64 | |
| D1 | FEM | 17.81 | 21.34 | 20.92 | 20.54 |
| RPIM | 23.74 | 21.03 | 19.63 | 18.09 | |
| NNRPIM | 26.48 | 22.39 | 20.89 | 19.25 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehri Sofiani, F.; Farahani, B.V.; Belinha, J. Elasto-Static Analysis of Composite Restorations in a Molar Tooth: A Meshless Approach. Polymers 2024, 16, 458. https://doi.org/10.3390/polym16040458
Mehri Sofiani F, Farahani BV, Belinha J. Elasto-Static Analysis of Composite Restorations in a Molar Tooth: A Meshless Approach. Polymers. 2024; 16(4):458. https://doi.org/10.3390/polym16040458
Chicago/Turabian StyleMehri Sofiani, Farid, Behzad V. Farahani, and Jorge Belinha. 2024. "Elasto-Static Analysis of Composite Restorations in a Molar Tooth: A Meshless Approach" Polymers 16, no. 4: 458. https://doi.org/10.3390/polym16040458
APA StyleMehri Sofiani, F., Farahani, B. V., & Belinha, J. (2024). Elasto-Static Analysis of Composite Restorations in a Molar Tooth: A Meshless Approach. Polymers, 16(4), 458. https://doi.org/10.3390/polym16040458








