Enhancing the Thermal Performance of Shape Memory Polymers: Designing a Minichannel Structure
Abstract
:1. Introduction
2. Material and Model
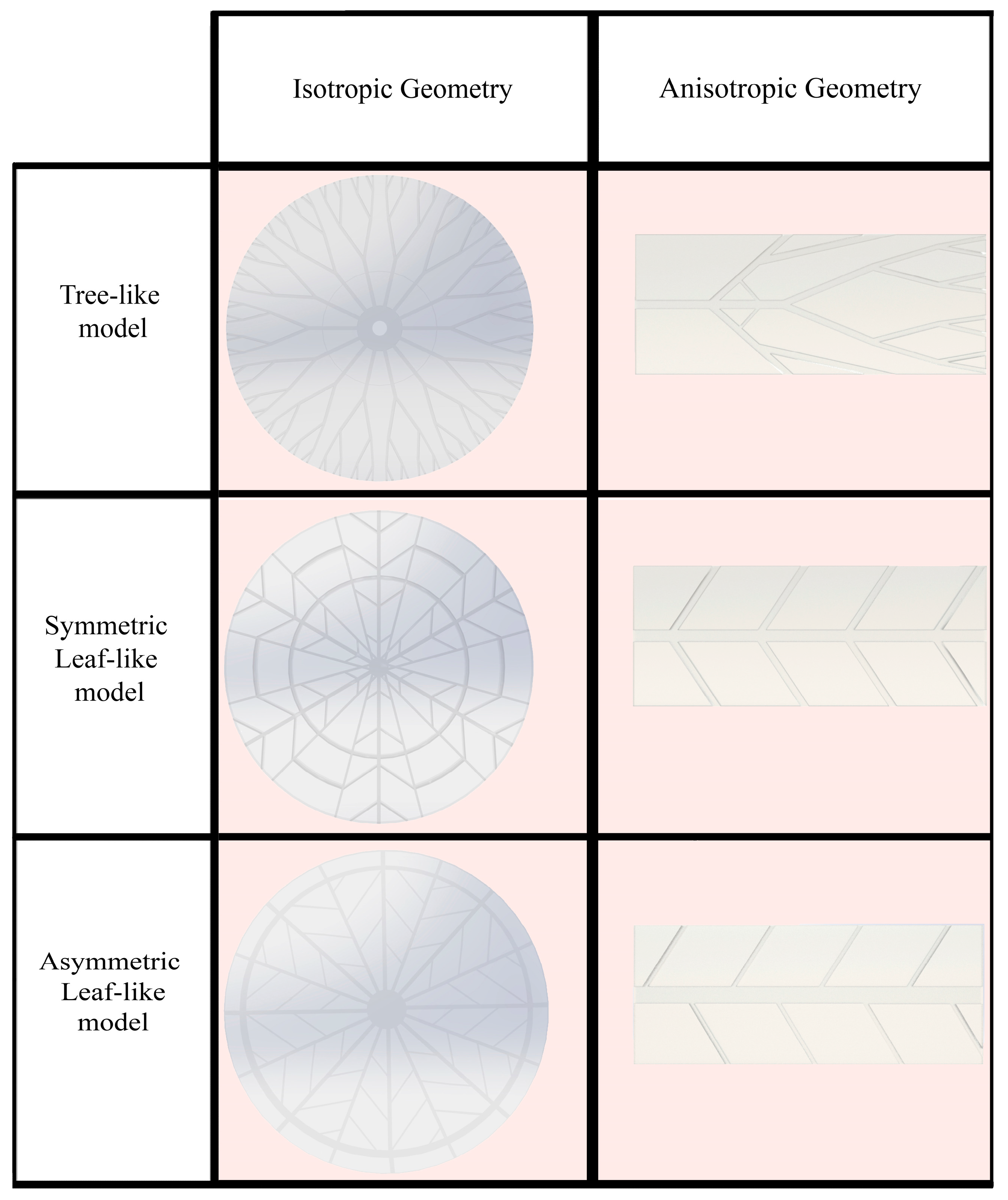
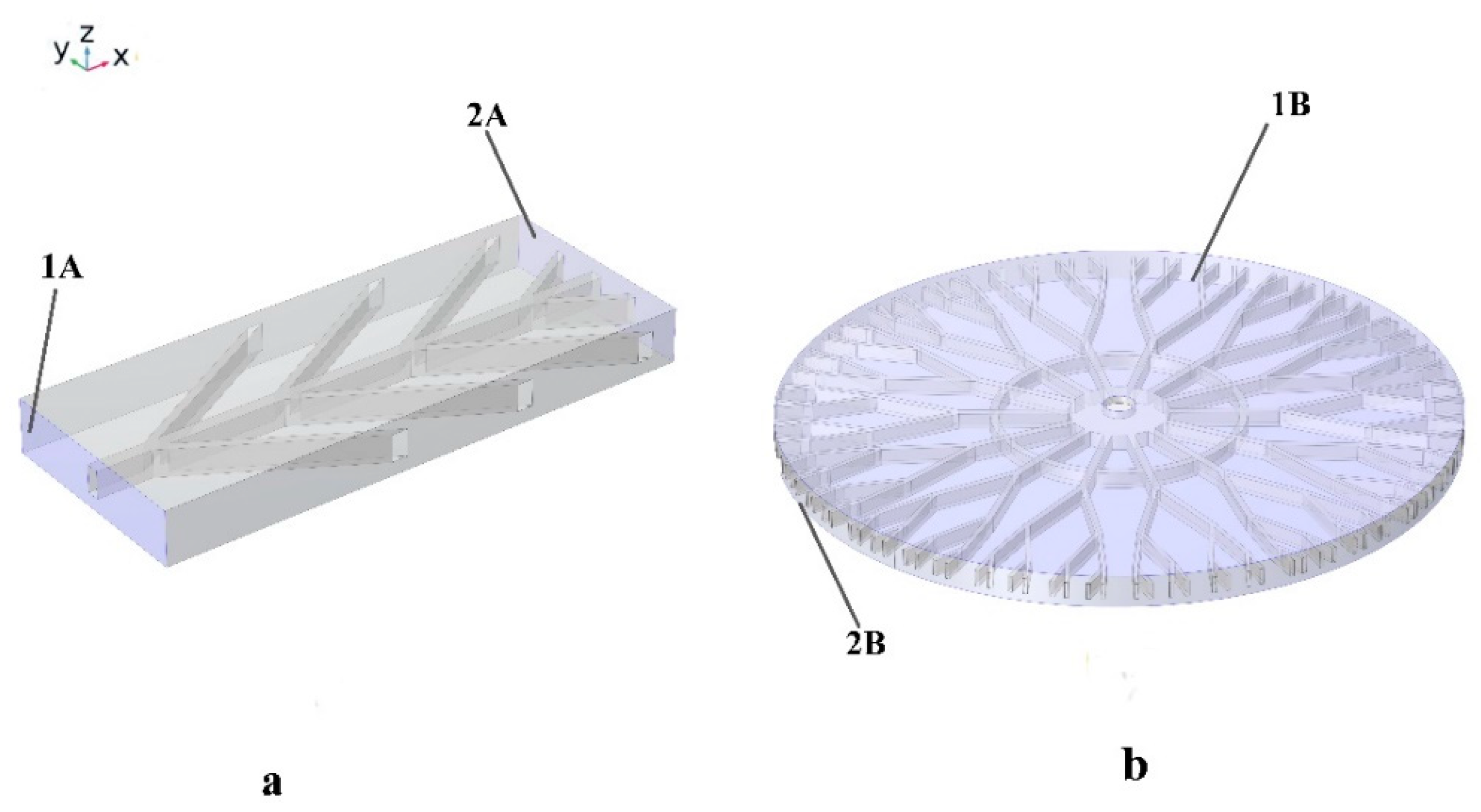
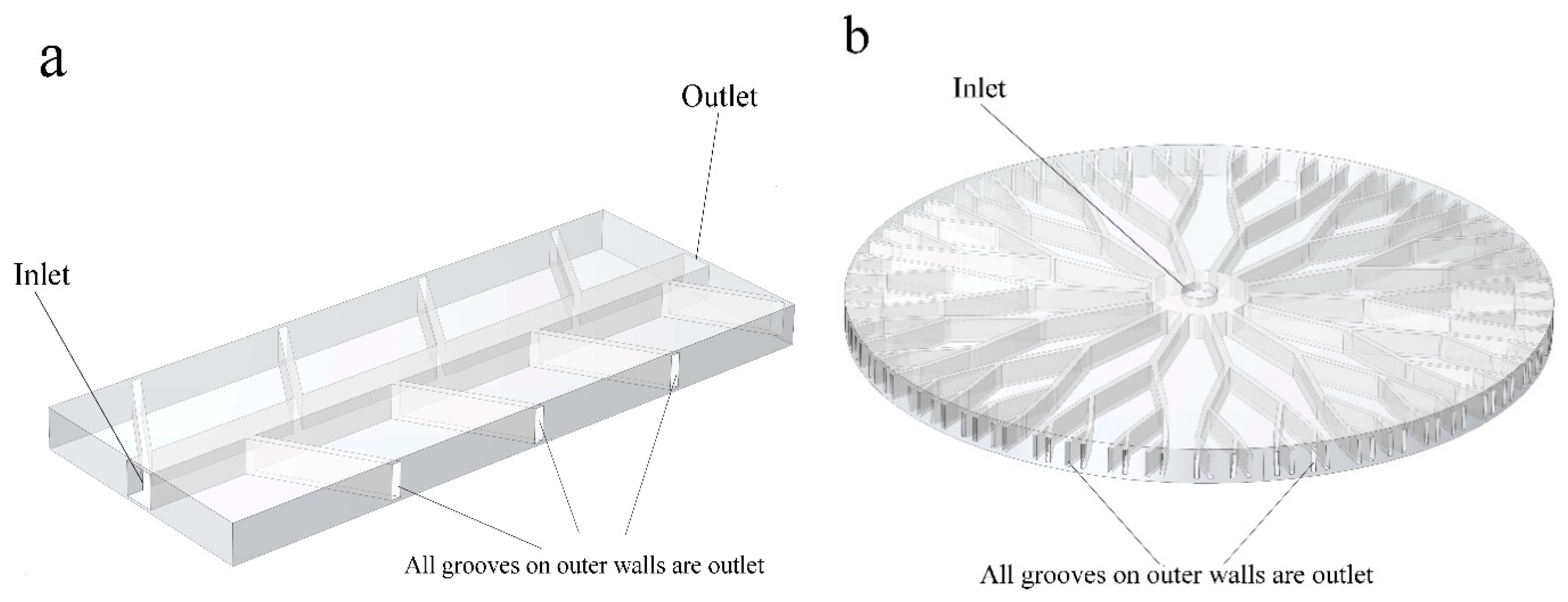
2.1. Designing the Structure
- The total surface area exposed to convective heat transfer fluid is fixed for each flow network.
- The inlet cross-section area at the loading step is the same for various structures.
2.2. Structural Model of the SMPs
2.3. Fluid-Structure Interaction- SMP Model Coupling
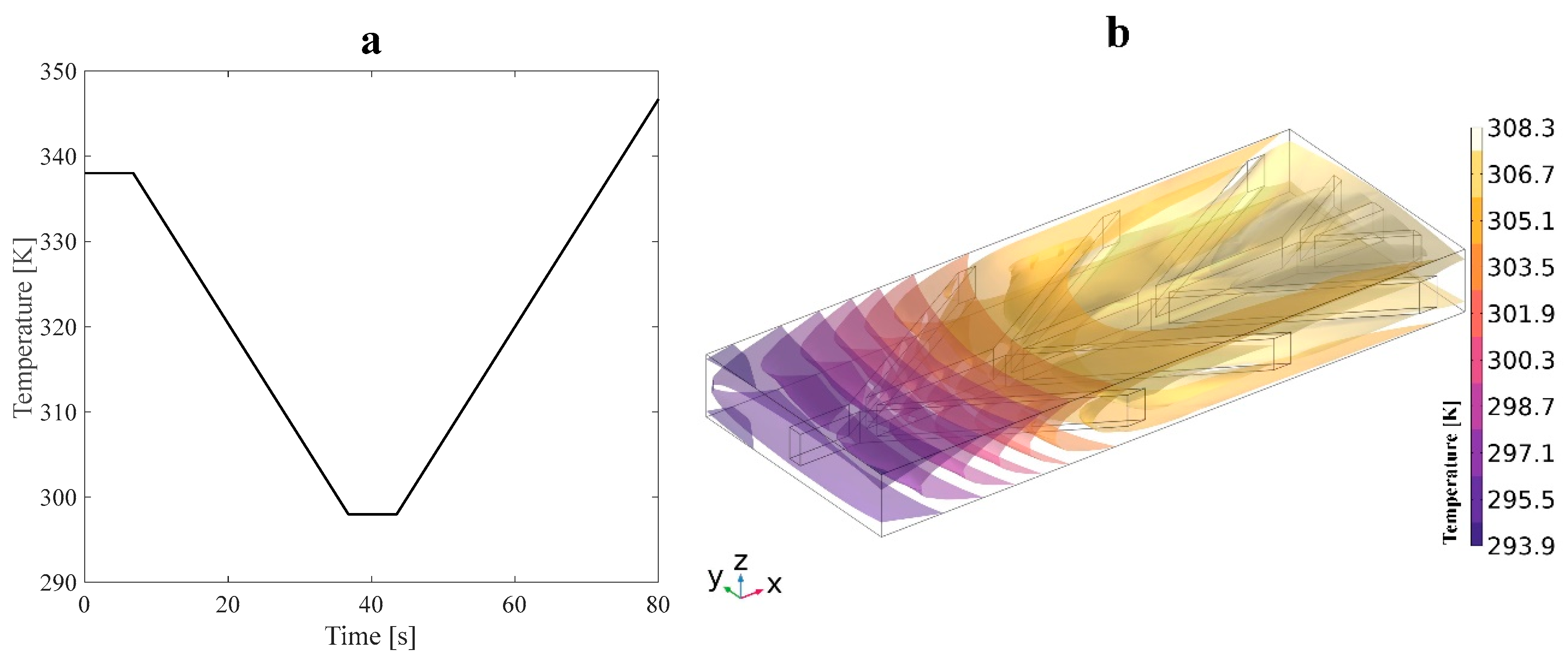
2.4. Thermal Boundary Conditions
3. Results and Discussions
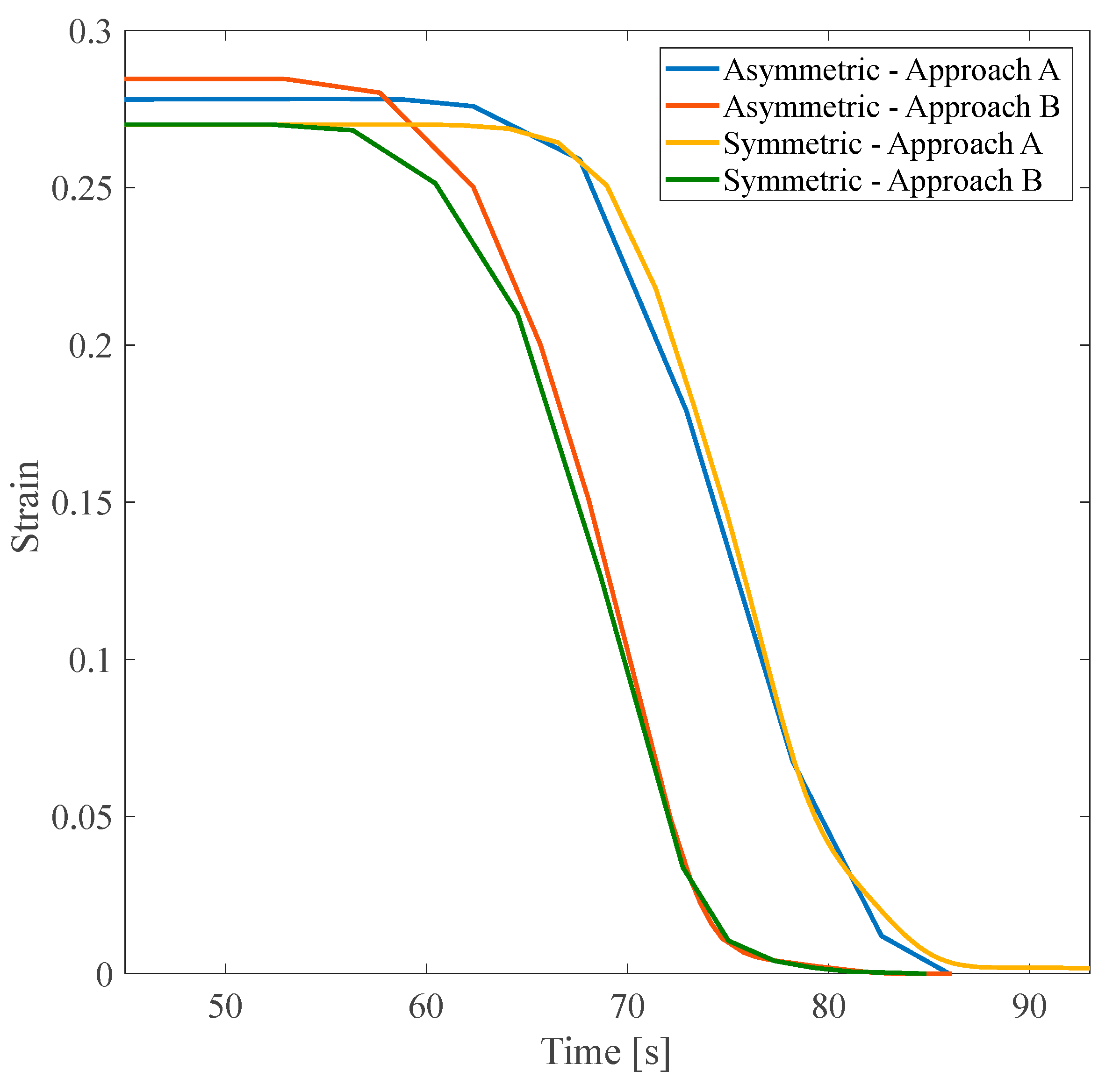
3.1. Anisotropic Structures
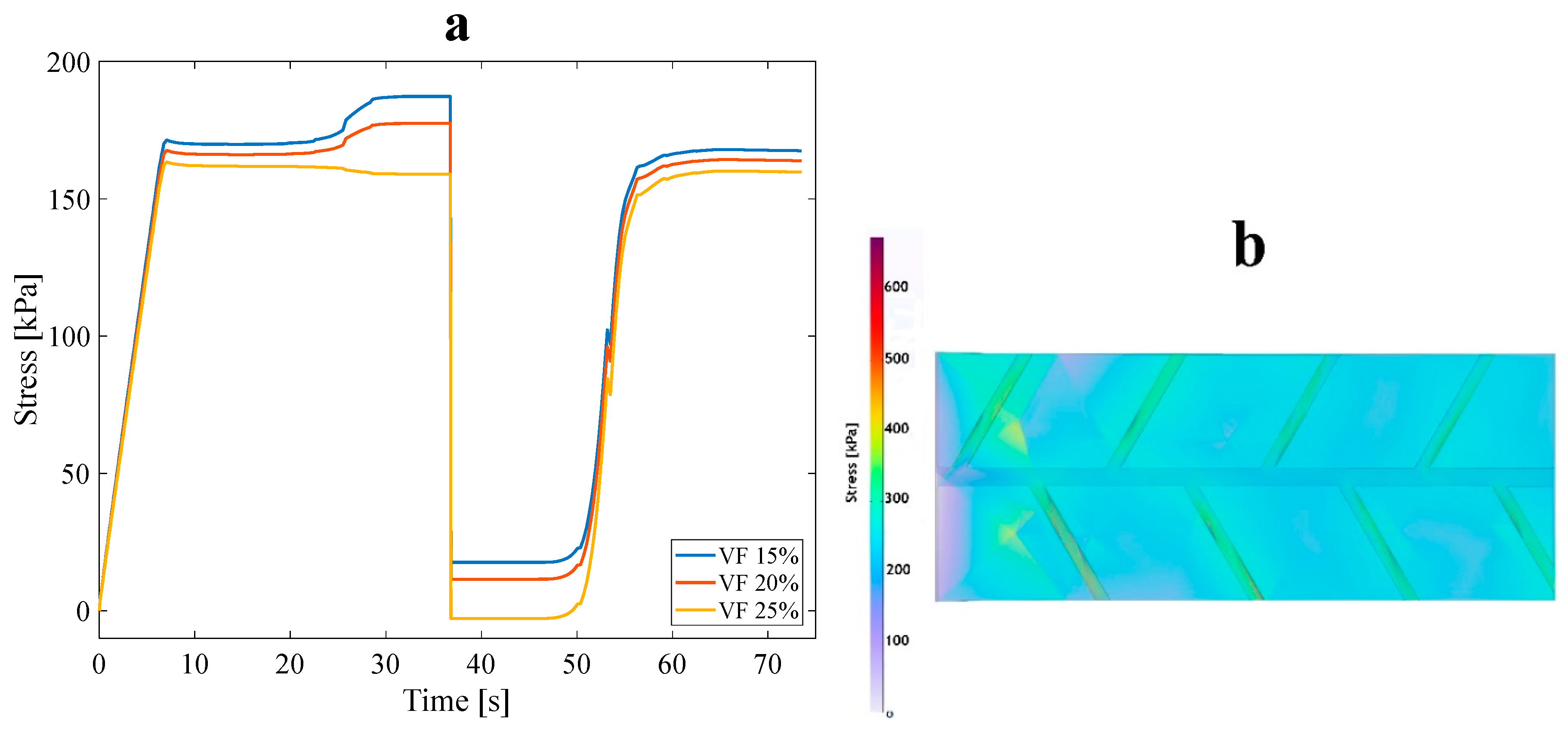
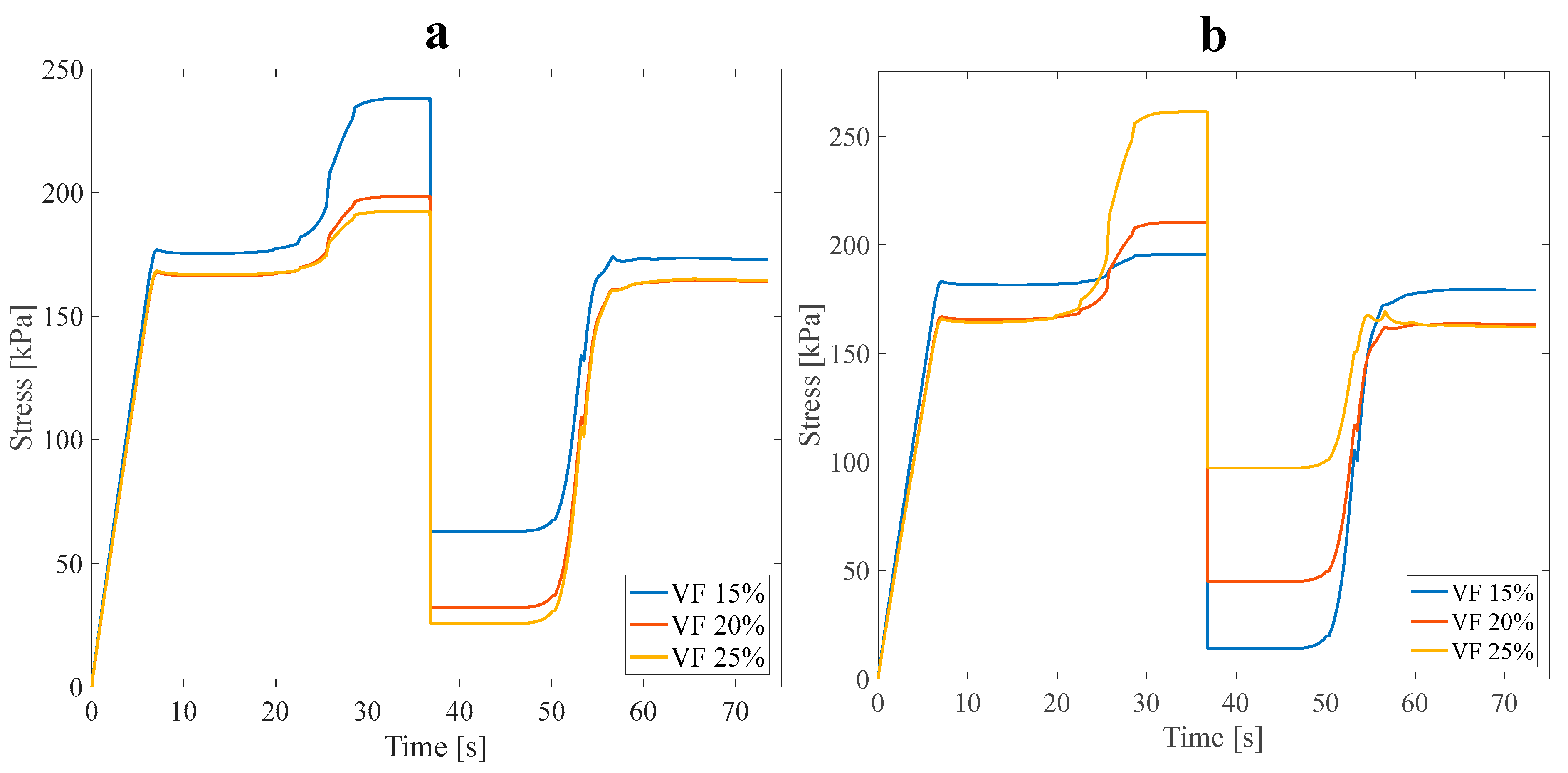
3.1.1. Effect of VF
3.1.2. Effect of Design Angle
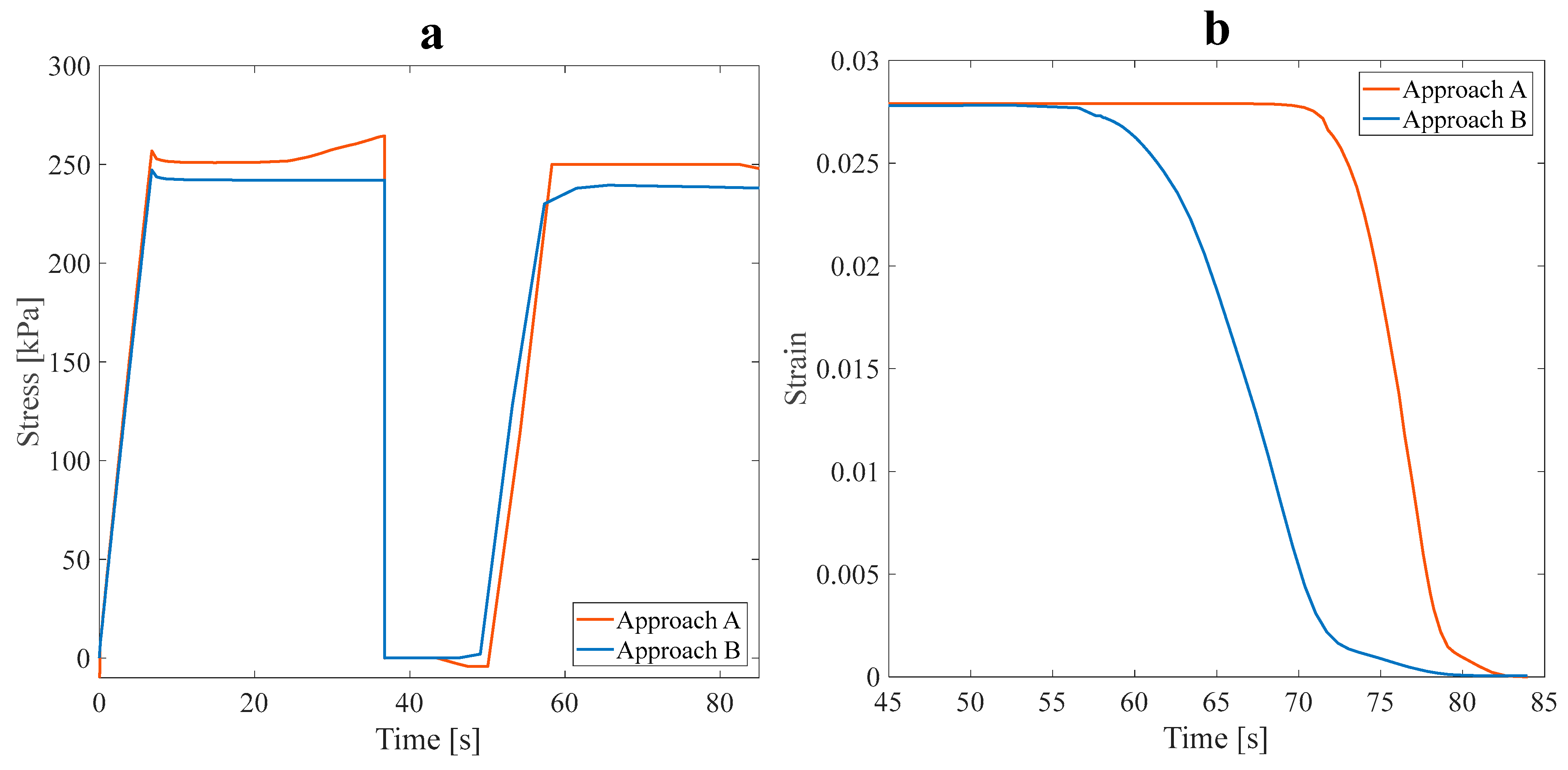
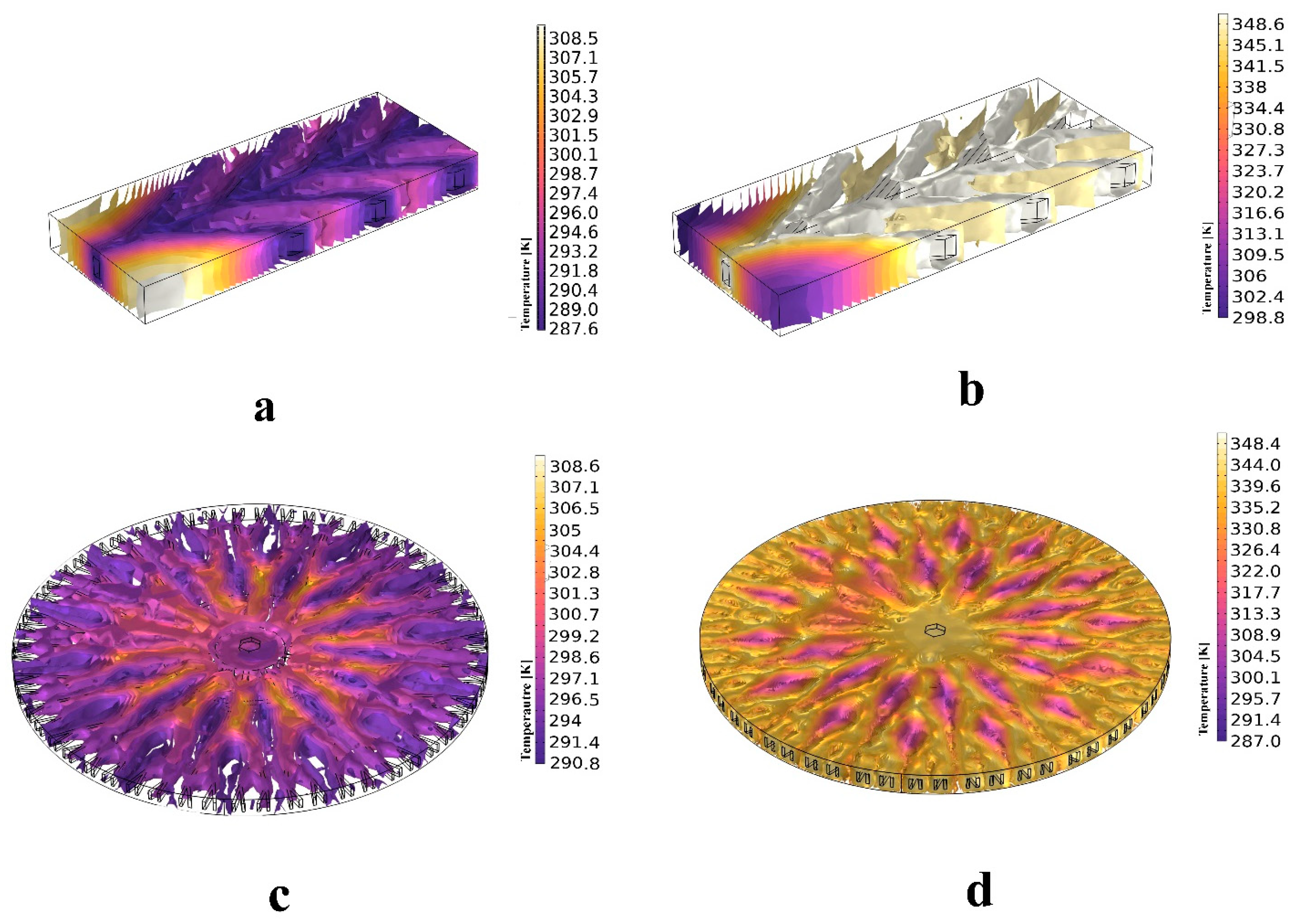
3.1.3. The FSI Simulation and Coupling the Structure with Fluid Flow Effects
3.2. Isotropic Structures
FSI Simulation
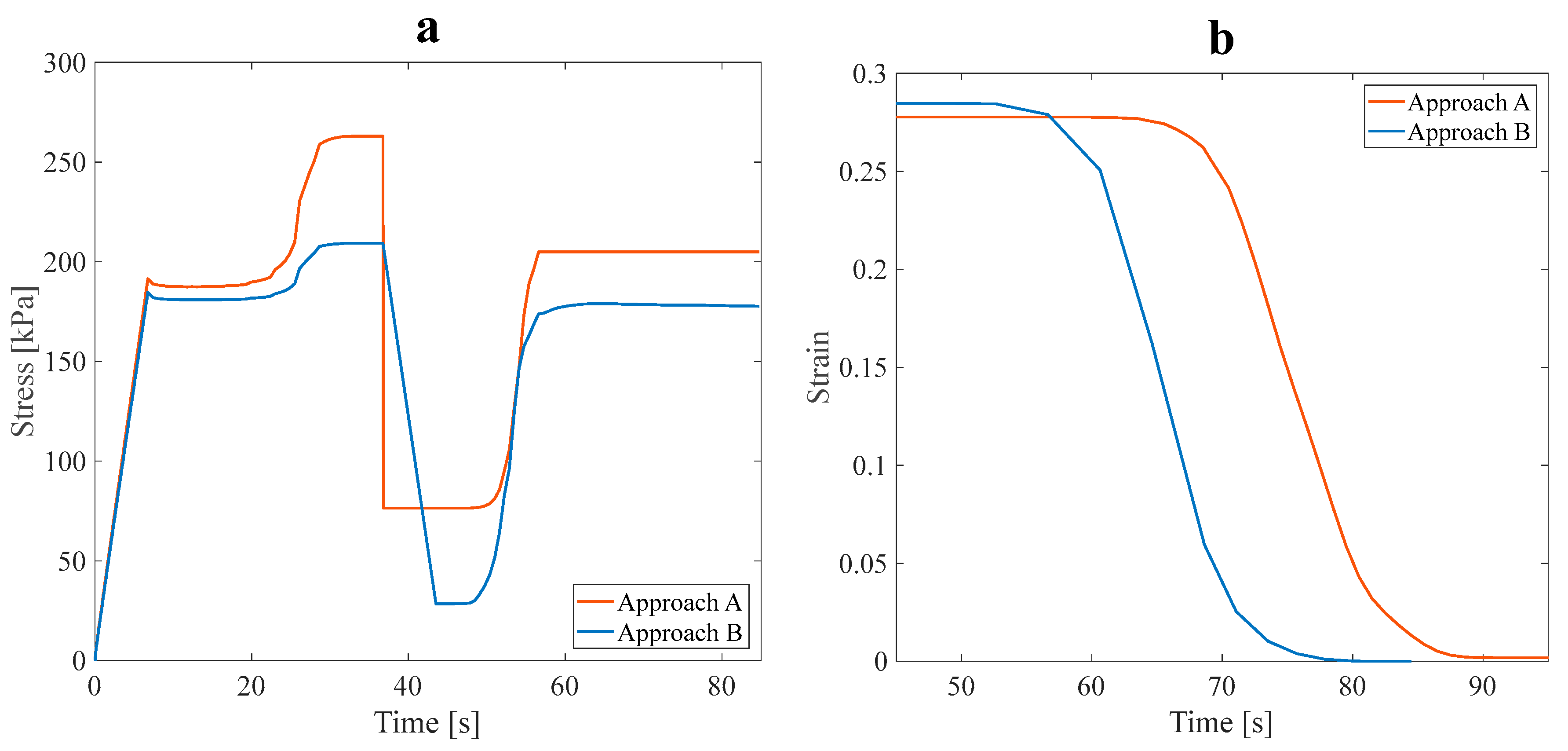
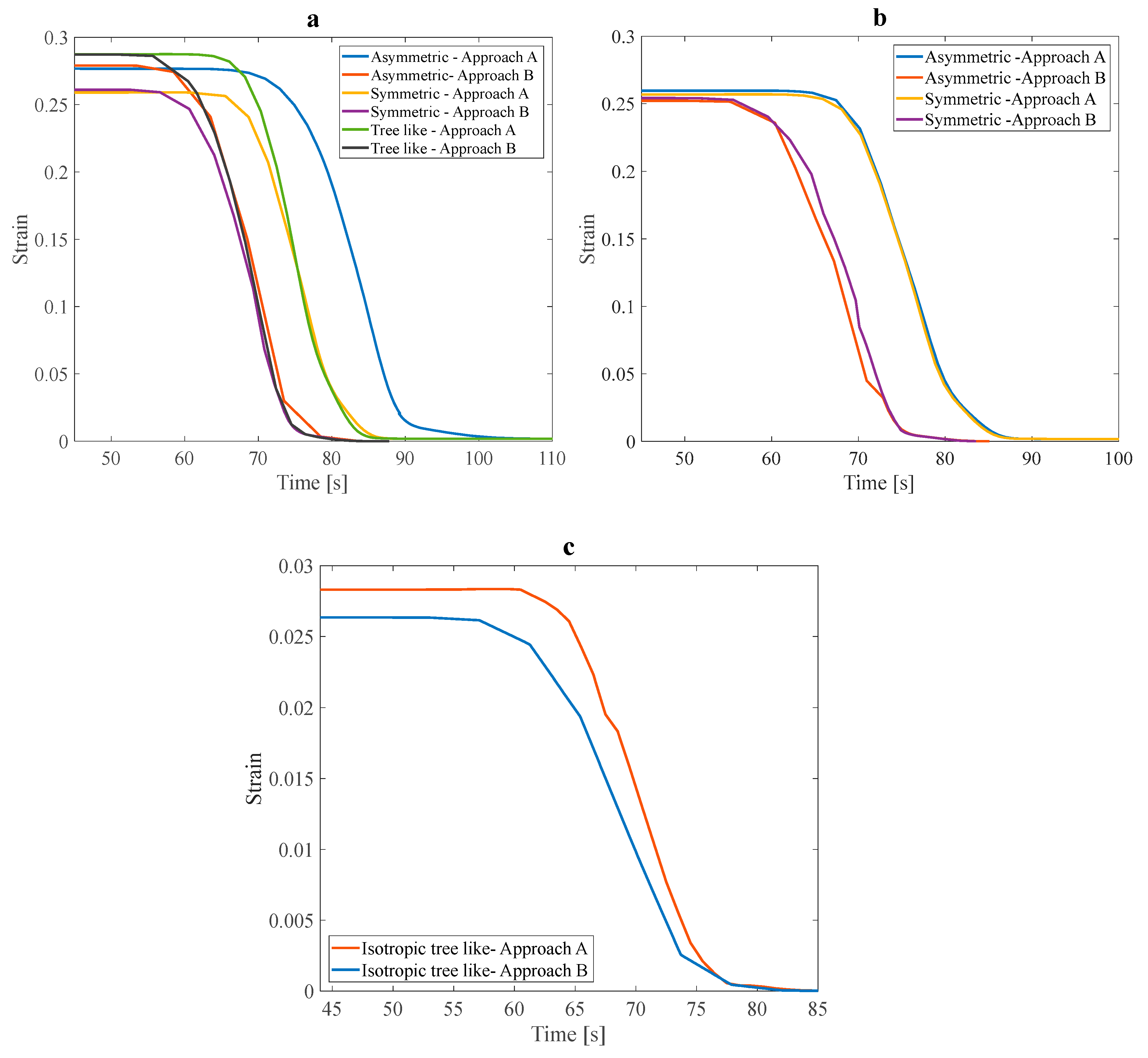
3.3. Shape Recovery in Optimal Structures
4. Summary and Conclusions
- The recovery ratio and parameter (α) were computed for all isotropic and anisotropic structures.
- Anisotropic structures with a 25% VF demonstrated the highest recovery ratio when coupled with water.
- Anisotropic structures with a 30° angle between the main branch and sub-branches exhibited a much lower temperature for shape recovery in the coupled state with the fluid.
- Isotropic structures have a higher recovery speed and exhibit better heat transfer and thermal response when coupled with fluid.
- The effect of the VF of networks on the strength and mechanical properties of the structures was investigated, and structures with a lower VF demonstrated more satisfactory thermal properties.
- Decreasing the angle between the main branch and sub-branches can enhance the thermal properties of a structure.
- The implemented methods in this study did not cause a significant decrease in the mechanical properties of the structures.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, S.; Brigham, J.C. A computational framework for the optimal design of morphing processes in locally activated smart material structures. Smart Mater. Struct. 2012, 21, 105016. [Google Scholar] [CrossRef]
- Qiang, J.; Furman, M.A.; Ryne, R.D. Parallel Particle-In-Cell Simulation of Colliding Beams in High Energy Accelerators. In Proceedings of the BT—SC2003: Igniting Innovation, Phoenix, AZ, USA, 15–21 November 2003; Available online: http://www.sc-conference.org/sc2003/inter_cal/inter_cal_detail.php?eventid=10694#2 (accessed on 10 October 2022).
- Dayyoub, T.; Maksimkin, A.V.; Filippova, O.V.; Tcherdyntsev, V.V.; Telyshev, D.V. Shape Memory Polymers as Smart Materials: A Review. Polymers 2022, 14, 3511. [Google Scholar] [CrossRef] [PubMed]
- Farahani, M.M.; Bakhtiyari, A.; Beshkoofe, S.; Kajbafzadeh, A.; Kiani, A.; Eskandari, A.H.; Baniassadi, M.; Baghani, M. Numerical simulation of the effect of geometric parameters on silicone airway stent migration. Front. Mech. Eng. 2023, 9, 1215895. [Google Scholar] [CrossRef]
- Peterson, G.I.; Dobrynin, A.V.; Becker, M.L. Biodegradable Shape Memory Polymers in Medicine. Adv. Healthc. Mater. 2017, 6, 1700694. [Google Scholar] [CrossRef] [PubMed]
- Sabahi, N.; Chen, W.; Wang, C.-H.; Kruzic, J.J.; Li, X. A Review on Additive Manufacturing of Shape-Memory Materials for Biomedical Applications. JOM 2020, 72, 1229–1253. [Google Scholar] [CrossRef]
- Robertson, J.M.; Rodriguez, R.X.; Holmes, L.R.; Mather, P.T.; Wetzel, E.D. Thermally driven microfluidic pumping via reversible shape memory polymers. Smart Mater. Struct. 2016, 25, 085043. [Google Scholar] [CrossRef]
- Beshkoofe, S.; Baghani, M.; Baniassadi, M.; Shahsavari, H. An investigation on an SMA valve in micro-channel through FSI approach. Int. J. Appl. Mech. 2024. [Google Scholar] [CrossRef]
- Kim, H.; Ahn, S.-K.; Mackie, D.M.; Kwon, J.; Kim, S.H.; Choi, C.; Moon, Y.H.; Lee, H.B.; Ko, S.H. Shape morphing smart 3D actuator materials for micro soft robot. Mater. Today 2020, 41, 243–269. [Google Scholar] [CrossRef]
- Zhang, F.; Xia, Y.; Liu, Y.; Leng, J. Nano/microstructures of shape memory polymers: From materials to applications. Nanoscale Horiz. 2020, 5, 1155–1173. [Google Scholar] [CrossRef] [PubMed]
- Park, B.; Jung, Y.; Ko, J.S.; Park, J.; Cho, H. Self-Restoring Capacitive Pressure Sensor Based on Three-Dimensional Porous Structure and Shape Memory Polymer. Polymers 2021, 13, 824. [Google Scholar] [CrossRef] [PubMed]
- Zeng, L.; Deng, D.; Zhong, N.; Zheng, G. Thermal and flow performance in microchannel heat sink with open-ring pin fins. Int. J. Mech. Sci. 2021, 200, 106445. [Google Scholar] [CrossRef]
- Yang, S.H.; Park, J.; Youn, J.R.; Song, Y.S. Programmable microfluidic logic device fabricated with a shape memory polymer. Lab a Chip 2018, 18, 2865–2872. [Google Scholar] [CrossRef]
- Gall, K.; Kreiner, P.; Turner, D.; Hulse, M. Shape-Memory Polymers for Microelectromechanical Systems. J. Microelectromechanical Syst. 2004, 13, 472–483. [Google Scholar] [CrossRef]
- Roudbarian, N.; Baniasadi, M.; Ansari, M.; Baghani, M. An experimental investigation on structural design of shape memory polymers. Smart Mater. Struct. 2019, 28, 095017. [Google Scholar] [CrossRef]
- Rousseau, I.A. Challenges of shape memory polymers: A review of the progress toward overcoming SMP’s limitations. Polym. Eng. Sci. 2008, 48, 2075–2089. [Google Scholar] [CrossRef]
- Zhou, B.; Liu, Y.; Leng, J. A macro-mechanical constitutive model for shape memory polymer. Sci. China Phys. Mech. Astron. 2010, 53, 2266–2273. [Google Scholar] [CrossRef]
- Teng, J.; Wang, Z.; Liu, J.; Sun, X. Thermodynamic and shape memory properties of TPI/HDPE hybrid shape memory polymer. Polym. Test. 2020, 81, 106257. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Z. A novel constitutive model of shape memory polymers combining phase transition and viscoelasticity. Polymer 2018, 143, 298–308. [Google Scholar] [CrossRef]
- Tobushi, H.; Hashimoto, T.; Hayashi, S.; Yamada, E. Thermomechanical Constitutive Modeling in Shape Memory Polymer of Polyurethane Series. J. Intell. Mater. Syst. Struct. 1997, 8, 711–718. [Google Scholar] [CrossRef]
- Diani, J.; Gilormini, P.; Frédy, C.; Rousseau, I. Predicting thermal shape memory of crosslinked polymer networks from linear viscoelasticity. Int. J. Solids Struct. 2012, 49, 793–799. [Google Scholar] [CrossRef]
- Westbrook, K.K.; Kao, P.H.; Castro, F.; Ding, Y.; Qi, H.J. A 3D finite deformation constitutive model for amorphous shape memory polymers: A multi-branch modeling approach for nonequilibrium relaxation processes. Mech. Mater. 2011, 43, 853–869. [Google Scholar] [CrossRef]
- Arrieta, J.S.; Diani, J.; Gilormini, P. Experimental and modelling studies of the shape memory properties of amorphous polymer network composites. Smart Mater. Struct. 2014, 23, 095009. [Google Scholar] [CrossRef]
- Zhang, L.; Du, H.; Liu, L.; Liu, Y.; Leng, J. Analysis and design of smart mandrels using shape memory polymers. Compos. Part B Eng. 2014, 59, 230–237. [Google Scholar] [CrossRef]
- Hasan, S.M.; Nash, L.D.; Maitland, D.J. Porous shape memory polymers: Design and applications. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 1300–1318. [Google Scholar] [CrossRef]
- Siva, V.M.; Pattamatta, A.; Das, S.K. Effect of flow maldistribution on the thermal performance of parallel microchannel cooling systems. Int. J. Heat Mass Transf. 2014, 73, 424–428. [Google Scholar] [CrossRef]
- Bejan, A.; Errera, M.R. Deterministic Tree Networks for Fluid Flow: Geometry for Minimal Flow Resistance Between a Volume and One Point. Fractals 1997, 5, 685–695. [Google Scholar] [CrossRef]
- Wang, X.-Q.; Xu, P.; Mujumdar, A.S.; Yap, C. Flow and thermal characteristics of offset branching network. Int. J. Therm. Sci. 2010, 49, 272–280. [Google Scholar] [CrossRef]
- Kang, X.; Jia, S.; Peng, J.; Yu, H.; Zhou, X. Electromagnetic-driven electrocaloric cooling device based on ternary ferroelectric composites. Compos. Part B Eng. 2021, 227, 109391. [Google Scholar] [CrossRef]
- Deng, C.; Kim, H.; Ki, H. Fabrication of functionally-graded yttria-stabilized zirconia coatings by 355 nm picosecond dual-beam pulsed laser deposition. Compos. Part B Eng. 2019, 160, 498–504. [Google Scholar] [CrossRef]
- Bakhtiyari, A.; Baghani, M.; Sohrabpour, S. An investigation on multilayer shape memory polymers under finite bending through nonlinear thermo-visco-hyperelasticity. Appl. Math. Mech. 2022, 44, 73–88. [Google Scholar] [CrossRef]
- Holzapfel, G.A. On large strain viscoelasticity: Continuum formulation and finite element applications to elastomeric structures. Int. J. Numer. Methods Eng. 1996, 39, 3903–3926. Available online: https://onlinelibrary.wiley.com/doi/10.1002/(SICI)1097-0207(19961130)39:22%3C3903::AID-NME34%3E3.0.CO;2-C (accessed on 26 November 2022). [CrossRef]
- Holzapfel, G.A. Nonlinear Solid Mechanics: A Continuum Approach for Engineering; John Wiley & Sons: Chichester, UK, 2000; p. 455. Available online: https://www.wiley.com/en-us/Nonlinear+Solid+Mechanics%3A+A+Continuum+Approach+for+Engineering-p-9780471823193 (accessed on 26 November 2022).
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-forming Liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Arrieta, S.; Diani, J.; Gilormini, P. Experimental characterization and thermoviscoelastic modeling of strain and stress recoveries of an amorphous polymer network. Mech. Mater. 2014, 68, 95–103. [Google Scholar] [CrossRef]
- Rafiee, M.M.; Baniassadi, M.; Wang, K.; Baniasadi, M.; Baghani, M. Mechanical properties improvement of shape memory polymers by designing the microstructure of multi-phase heterogeneous materials. Comput. Mater. Sci. 2021, 196, 110523. [Google Scholar] [CrossRef]
- Guo, F.; Zheng, X.; Liang, C.; Jiang, Y.; Xu, Z.; Jiao, Z.; Liu, Y.; Wang, H.T.; Sun, H.; Ma, L.; et al. Millisecond Response of Shape Memory Polymer Nanocomposite Aerogel Powered by Stretchable Graphene Framework. ACS Nano 2019, 13, 5549–5558. [Google Scholar] [CrossRef]




| Viscoelastic Properties | ||||||
| Energy factor () | 5.862759 522 | 101.590 4875 | 1.379170 492 | 0.095327 903 | 0.004518 184 | 0.010219 807 |
| Relaxation time () | 0.00141 | 0.0000428 | 0.0208 | 0.74 | 46 | 100,000 |
| Hyperelastic Properties | ||||||
| Strain energy potential | Neo-Hookean | |||||
| Incompressible | µ (Pa) 1,919,999.996 4 | |||||
| WLF | ||||||
| 80 | 6.9 | 87.9 | ||||
| Silicone | ||||||
| Strain energy potential | Neo-Hookean | |||||
| Incompressible | µ (Pa) 400,000 | |||||
| Material Properties | |
|---|---|
| Density (ρ) | |
| Thermal conductivity (λ) | |
| Specific heat capacity (Cp) | |
| Dynamic viscosity |
| Anisotropic Structures | VF of Branches | (kPa) | (kPa) | |
|---|---|---|---|---|
| 15% | 169.952 | 168.0 | 98.85 | |
| Tree-like | 20% | 166.271 | 164.290 | 98.80 |
| 25% | 162.105 | 160.126 | 98.77 | |
| 15% | 182.0 | 180.0 | 98.90 | |
| Symmetric leaf-like | 20% | 166.0 | 164.0 | 98.79 |
| 25% | 164.485 | 162.291 | 98.66 | |
| 15% | 175.411 | 173.610 | 98.97 | |
| Asymmetric leaf-like | 20% | 166.970 | 165.0 | 98.82 |
| 25% | 166.490 | 164.607 | 98.86 |
| Anisotropic Structures | Angle of Branches | (kPa) | (kPa) | |
|---|---|---|---|---|
| 30° | 173.328 | 171.151 | 98.74 | |
| Symmetric leaf-like | 45° | 183.203 | 180.922 | 98.75 |
| 60° | 195.546 | 193.280 | 98.84 | |
| 30° | 143.124 | 141.330 | 98.74 | |
| Asymmetric leaf-like | 45° | 149.434 | 147.769 | 98.88 |
| 60° | 175.411 | 173.610 | 98.94 |
| Anisotropic Structure | Approaches | (kPa) | (kPa) | |
|---|---|---|---|---|
| Asymmetric leaf-like (VF15% and angle 45°) | B | 184.736 | 170.658 | 93.37 |
| A | 175.411 | 173.610 | 98.97 |
| Isotropic Structures | (Pa) | (Pa) | |
|---|---|---|---|
| Symmetric leaf-like | 83.7 | 83.2 | 99.40 |
| Asymmetric leaf-like | 183 | 185 | 98.91 |
| Tree-like | 223 | 227 | 98.69 |
| Solid disk | 254 | 253.6 | 99.84 |
| Isotropic Structure | Approaches | (kPa) | (kPa) | |
|---|---|---|---|---|
| B | 247.229 | 239.492 | 96.87 | |
| Symmetric leaf-like | ||||
| A | 83.7 | 83.2 | 99.40 |
| Geometric Design | Structure Name | Shape Recovery Temperature (Approach B) [K] | Initial Shape Recovery Temperature [K] | Recovery Ratio (Approach B) % | Recovery Ratio (Approach A) % |
|---|---|---|---|---|---|
| Asymmetric leaf-like/VF25% | 351.32 | 358.44 | 79.29 | 9.74 | |
| Symmetric leaf-like/VF25% | 351.81 | 367.31 | 73.82 | 20.01 | |
| Tree-like/VF25% | 357.05 | 367.80 | 73.81 | 5.78 | |
| Anisotropic | Asymmetric leaf-like/VF15% | 343.5 | 366.65 | 79.06 | 13.04 |
| Symmetric leaf-like/angle 30° | 351.36 | 368.23 | 66.69 | 11.65 | |
| Symmetric leaf-like/angle 60° | 353.13 | 367.05 | 87.45 | 19.23 | |
| Asymmetric leaf-like/angle 60° | 352.86 | 355.59 | 65.70 | 35.63 | |
| Asymmetric leaf-like/angle 30° | 353.42 | 370.53 | 64.61 | 10.87 | |
| Isotropic | Symmetric leaf-like | 344.6 | 350 | 82.38 | 25.08 |
| Tree-like | 347.32 | 352.65 | 62.65 | 43.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beshkoofe, S.; Baniassadi, M.; Mahdavi Nejad, A.; Sheidaei, A.; Baghani, M. Enhancing the Thermal Performance of Shape Memory Polymers: Designing a Minichannel Structure. Polymers 2024, 16, 500. https://doi.org/10.3390/polym16040500
Beshkoofe S, Baniassadi M, Mahdavi Nejad A, Sheidaei A, Baghani M. Enhancing the Thermal Performance of Shape Memory Polymers: Designing a Minichannel Structure. Polymers. 2024; 16(4):500. https://doi.org/10.3390/polym16040500
Chicago/Turabian StyleBeshkoofe, Saed, Majid Baniassadi, Alireza Mahdavi Nejad, Azadeh Sheidaei, and Mostafa Baghani. 2024. "Enhancing the Thermal Performance of Shape Memory Polymers: Designing a Minichannel Structure" Polymers 16, no. 4: 500. https://doi.org/10.3390/polym16040500
APA StyleBeshkoofe, S., Baniassadi, M., Mahdavi Nejad, A., Sheidaei, A., & Baghani, M. (2024). Enhancing the Thermal Performance of Shape Memory Polymers: Designing a Minichannel Structure. Polymers, 16(4), 500. https://doi.org/10.3390/polym16040500







