Effect of Water Absorption on Electric Properties of Temperature-Resistant Polymers
Abstract
:1. Introduction
2. Experimental Procedures
2.1. Samples
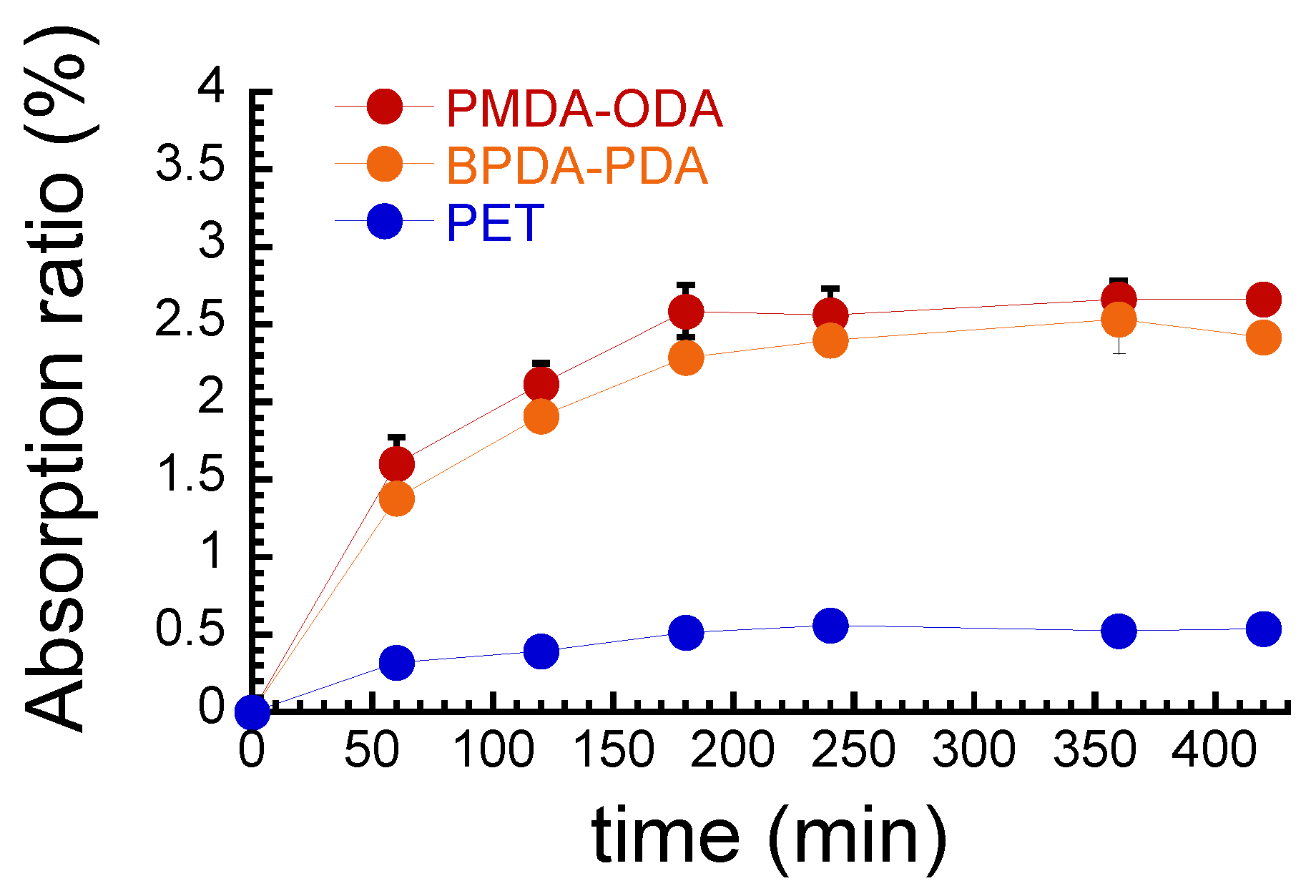
2.2. Water Absorption Measurements
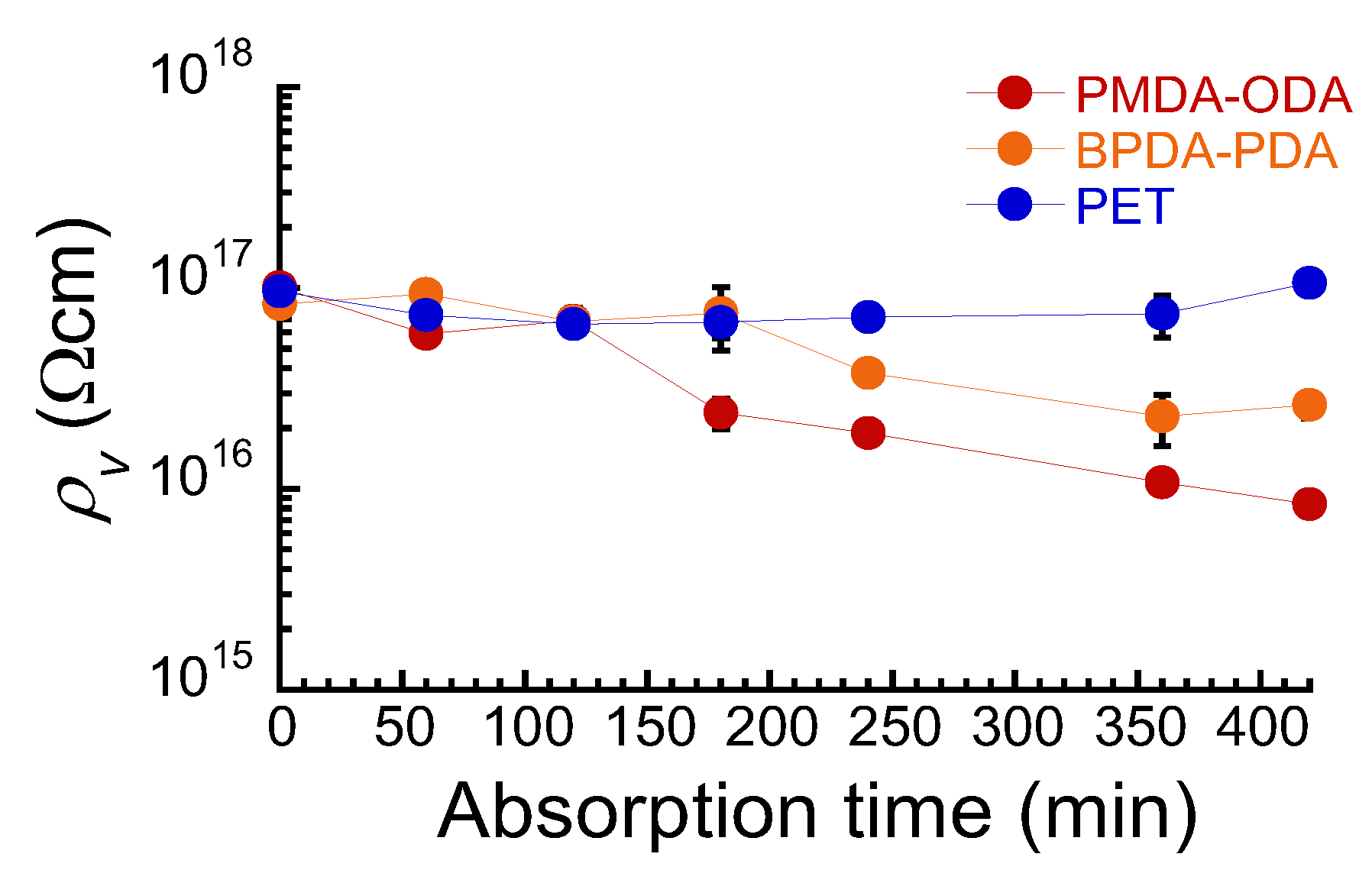
2.3. Electric Resistance Measurements
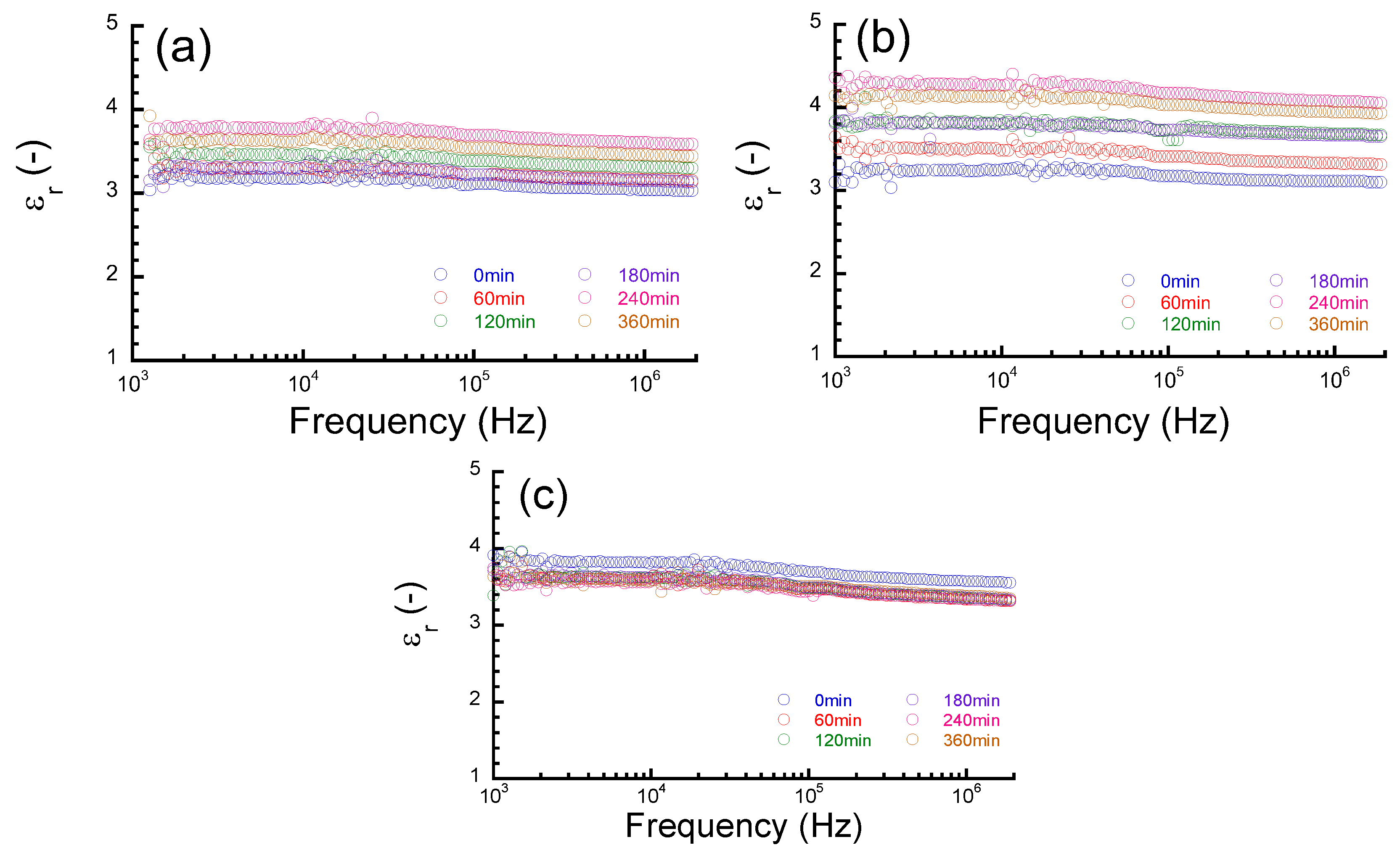
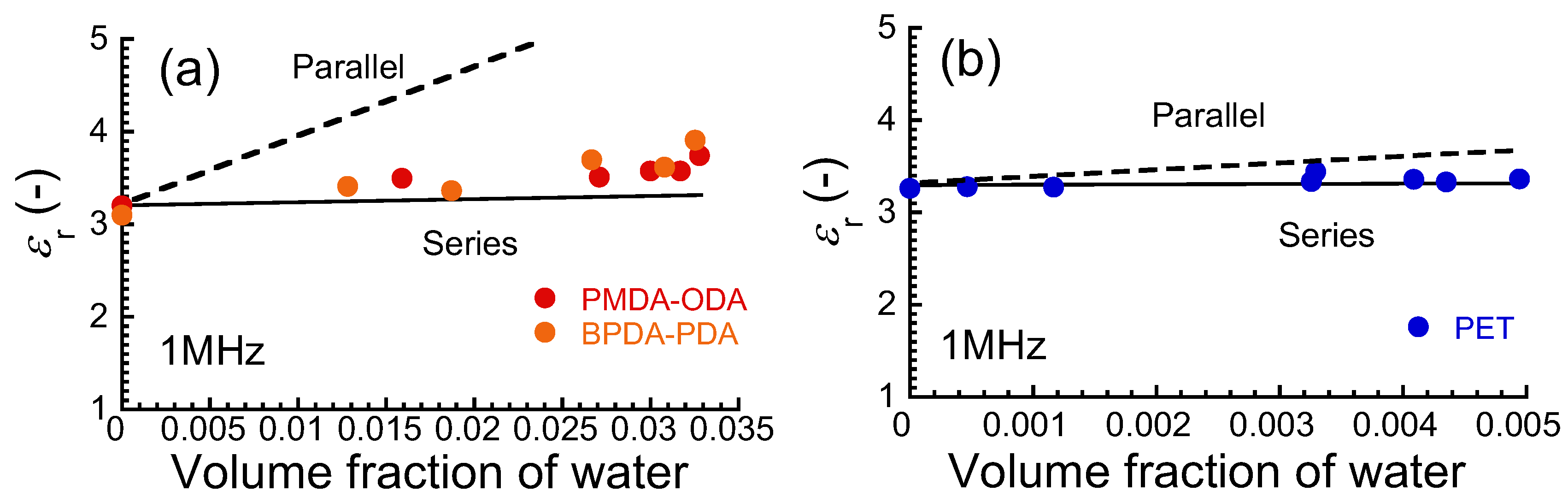
2.4. Capacitance Measurements
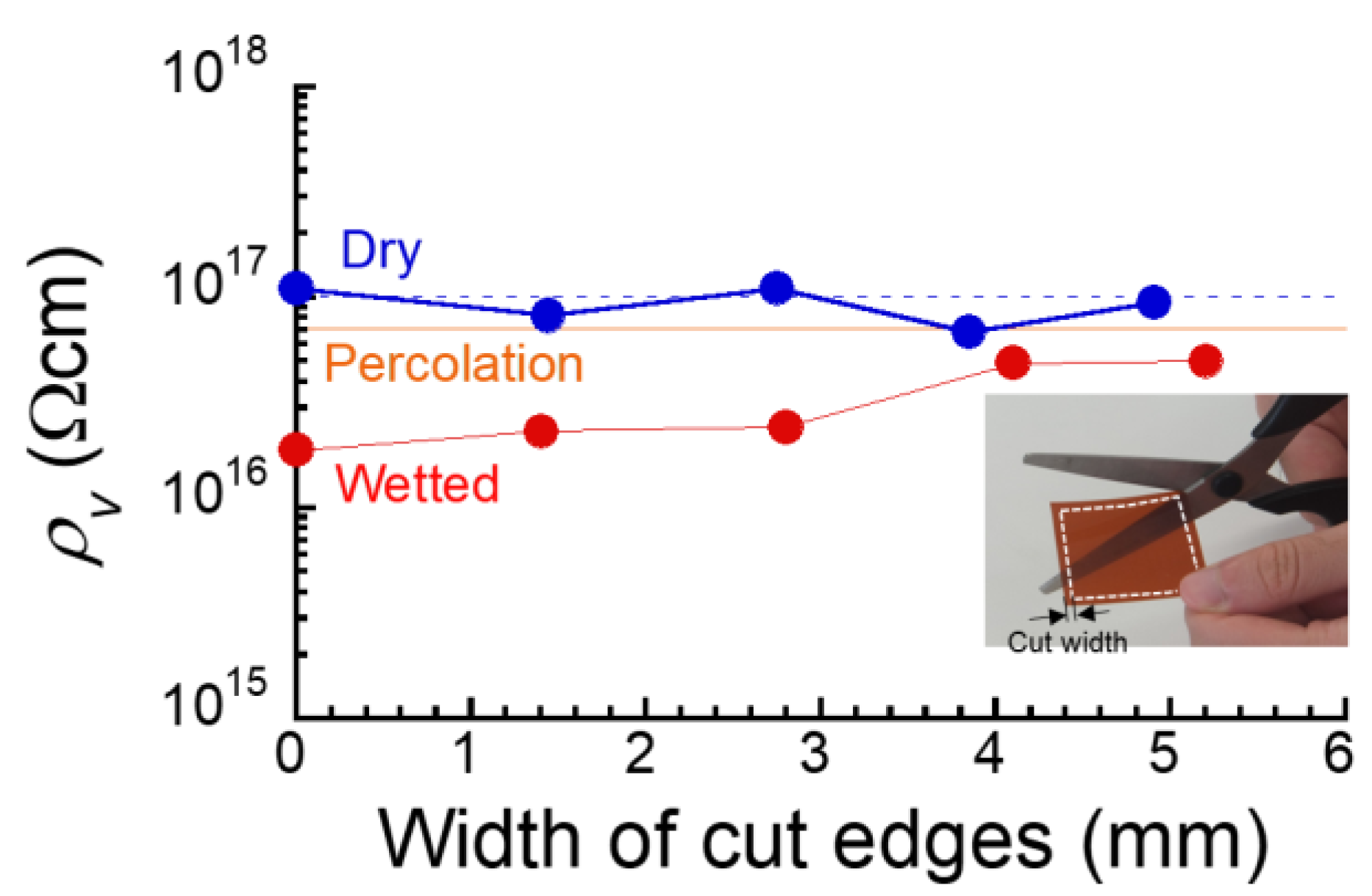
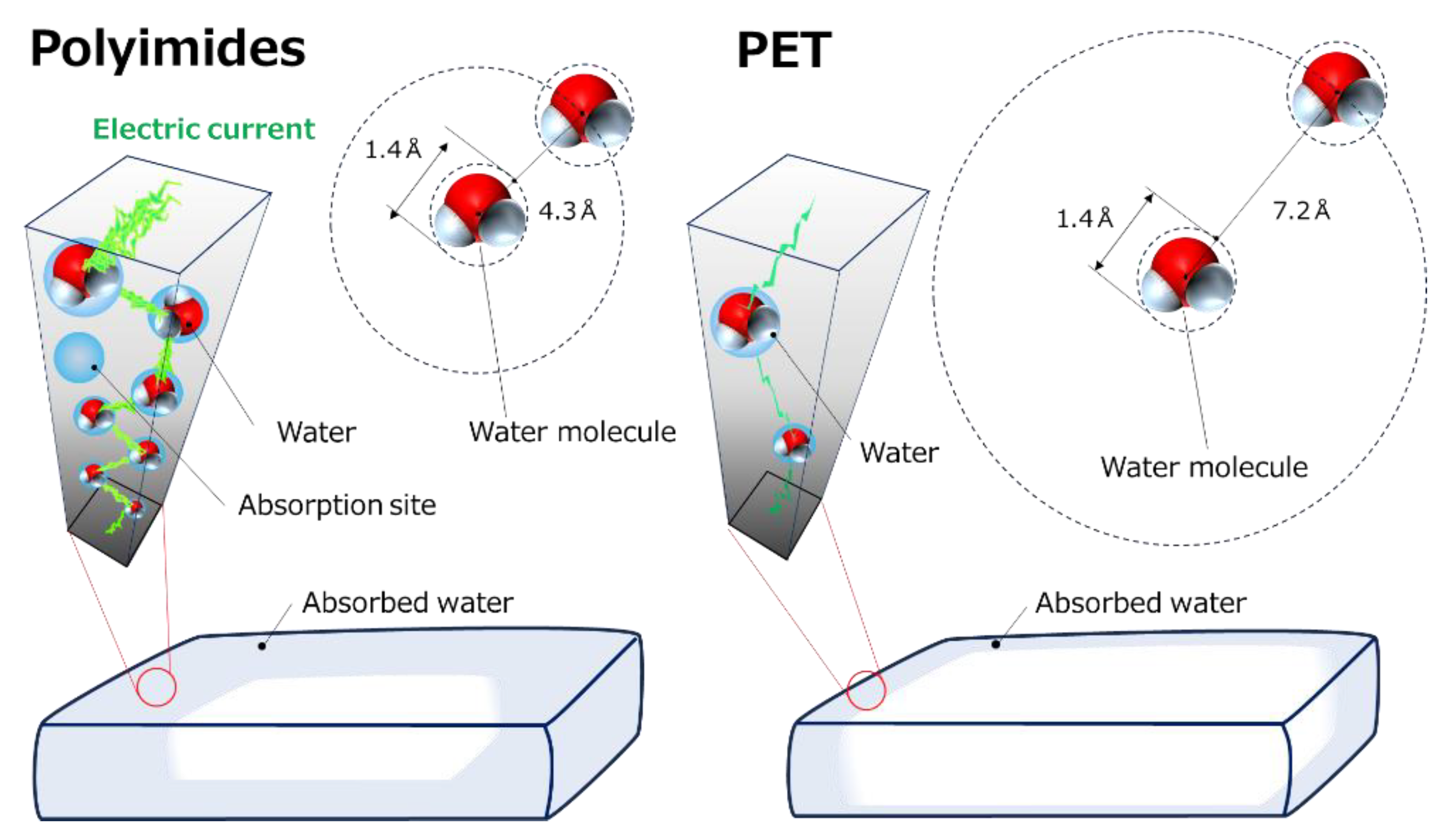
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cassidy, P.E. History of Heat-Resistant Polymers. J. Macromol. Sci.-Chem. 1981, A15, 1435–1460. [Google Scholar] [CrossRef]
- Luo, H.; Li, W.; Yuan, R.; Huang, Y.; Chen, J.Z.; Yang, L.; Chang, G.J. A Heat-Resistant Polymer Based on the Reversible Change in Polymer Skeleton Structure for Self-Anticounterfeiting. Macromol. Rapid Commun. 2023, 2300516. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.X.; Zhang, Z.Z.; Gao, F.B.; Zhou, P.; Liu, Y.; Hou, Y.Q.; An, C.W.; Wang, J.Y.; Wu, B.D. New TKX-55-based heat resistant microspheres. Propellants Explos Pyrotech. 2023, 48, e202300057. [Google Scholar] [CrossRef]
- Mashhadikhan, S.; Ahmadi, R.; Amooghin, A.E.; Sanaeepur, H.; Aminabhavi, T.M.; Rezakazemi, M. Breaking temperature barrier: Highly thermally heat resistant polymeric membranes for sustainable water and wastewater treatment. Renew. Sustain. Energy Rev. 2024, 189, 113902. [Google Scholar] [CrossRef]
- He, L.L.; An, T.F.; He, M.; Fan, Q.; Yang, J.F.; Liu, Y.F.; Qin, S.H.; Yu, J. Achieving anti-moisture absorption and high thermal properties in bio-based polyamide 56/F-based heat-resistant agent composites through crystal regulation. J. Appl. Polym. Sci. 2023, 140, e54301. [Google Scholar] [CrossRef]
- Qiu, Z.L.; Chen, C.; Huang, Z.Q.; Fu, P.; Zhang, X.M.; Zhao, W.; Qiao, X.G.; Pang, X.C.; Liu, M.Y.; Chen, S.; et al. New insights into contribution of aromatic ring versus aliphatic ring to thermal transition temperatures of heat resistant polyamides: A comparison study of PA 10T and t-PA 10C. Polymer 2023, 267, 125701. [Google Scholar] [CrossRef]
- Lin, M.F.; Shu, Y.C. Modification of nylon-6 with poly(m-phenylene isophthalamide) via MDI as a chain extender. J. Mater. Sci. 1993, 28, 4862–4867. [Google Scholar] [CrossRef]
- Patel, A.; Wilcox, K.; Li, Z.; George, I.; Juneja, R.; Lollar, C.; Lazar, S.; Grunlan, J.; Tenhaeff, W.E.; Lutkenhaus, J.L. High Modulus, Thermally Stable, and Self-Extinguishing Aramid Nanofiber Separators. ACS Appl. Mater. Interfaces 2020, 12, 25756–25766. [Google Scholar] [CrossRef]
- Liaw, D.J.; Wang, K.L.; Huang, Y.C.; Lee, K.R.; Lai, J.Y.; Ha, C.S. Advanced polyimide materials: Syntheses, physical properties and applications. Progr. Polym. Sci. 2012, 37, 907–974. [Google Scholar] [CrossRef]
- Srinivas, S.; Caputo, F.E.; Graham, M.; Gardner, S.; Davis, R.M.; McGrath, J.E.; Wilkes, G.L. Semicrystalline Polyimides Based on Controlled Molecular Weight Phthalimide End-Capped 1,3-Bis(4-aminophenoxy)benzene and 3,3′,4,4′-Biphenyltetracarboxylic Dianhydride: Synthesis, Crystallization, Melting, and Thermal Stability. Macromolecules 1997, 30, 1012–1022. [Google Scholar] [CrossRef]
- Han, Y.H.; Ma, Y.Y.; Zhang, J.M.; Yao, S.; Xu, K.Z. Overall Improvement in Dielectric, Water Resistance and Mechanical Properties of Polyimide Film via Synergy between GO and Sandwich-type Porous Structure. Chem. Asian J. 2023, 18, e202201130. [Google Scholar] [CrossRef]
- Lee, C.; Shul, Y.; Han, H. Dielectric Properties of Oxydianiline-Based Polyimide Thin Films According to the Water Uptake. Polym. Phys. 2002, 40, 2190–2198. [Google Scholar] [CrossRef]
- Feng, Q.K.; Liu, D.F.; Zhang, Y.X.; Pei, J.Y.; Zhong, S.L.; Hu, H.Y.; Wang, X.J.; Dang, Z.M. Significantly improved high-temperature charge-discharge efficiency of all-organic polyimide composites by suppressing space charges. Nano Energy 2022, 99, 107410. [Google Scholar] [CrossRef]
- Dang, Z.M.; Ma, L.J.; Zha, J.W.; Yao, S.H.; Xie, D.; Chen, Q.; Duan, X. Origin of ultralow permittivity in polyimide/mesoporous silicate nanohybrid films with high resistivity and high breakdown strength. J. Appl. Phys. 2009, 105, 044104. [Google Scholar] [CrossRef]
- Frederickson, A.R.; Benson, C.E.; Bockman, J.F. Measurement of charge storage and leakage in polyimides. Nucl. Instrum. Methods Phys. Res. Sect. B 2003, 208, 454–460. [Google Scholar] [CrossRef]
- Vila, F.; Sessler, G.M.; Sykja, H. The influence of electron-beam irradiation on the volume resistivity of polyethylene and Kapton. J. Electrost. 2005, 63, 749–754. [Google Scholar] [CrossRef]
- Kato, S.; Yusof, F.A.A.; Harimoto, T.; Takada, K.; Kaneko, T.; Kawai, M.; Mitsumata, T. Electric Volume Resistivity for Biopolyimide Using 4,4’-Diamino-α-truxillic acid and 1,2,3,4-Cyclobutanetetracarboxylic dianhydride. Polymers 2019, 11, 1552. [Google Scholar] [CrossRef]
- Yusof, F.A.A.; Noda, T.; Takada, K.; Kaneko, T.; Kawai, M.; Mitsumata, T. Critical Electric Field and Activation Energy for Electric Conductivity for Biopolyimide Using 4,4’-Diamino-α-truxillic Acid and 1,2,3,4-Cyclobutanetetracarboxylic Dianhydride. Chem. Lett. 2020, 49, 929–931. [Google Scholar] [CrossRef]
- Bulletti, A.; Capineri, L.; Dunn, B.D.; Bruzzi, M. Investigation of Resistivity Variation of Printed Circuit Board Laminates Due to Aging. IEEE Trans. Compon. Packag. Manuf. Technol. 2012, 2, 2001–2006. [Google Scholar] [CrossRef]
- Lim, B.S.; Nowick, A.S.; Lee, K.W.; Viehbeck, A. Sorption of water and organic solutes in polyimide films and its effects on dielectric properties. J. Polym. Sci. B Polym. Phys. 1993, 31, 545–555. [Google Scholar] [CrossRef]
- Zeng, L.; Zhao, T.S.; An, L.; Zhao, G.; Yan, X.H. Physicochemical properties of alkaline doped polybenzimidazole membranes for anion exchange membrane fuel cells. J. Membr. Sci. 2015, 493, 340–348. [Google Scholar] [CrossRef]
- Korkees, F.; Swart, R.; Barsoum, I. Diffusion mechanism and properties of chemical liquids and their mixtures in 977-2 epoxy resin. Polym. Eng. Sci. 2022, 62, 1582–1592. [Google Scholar] [CrossRef]
- Pei, S.X.; Han, Y.; Guo, Y.; Liu, J.S.; Ding, J.N.; Li, Y.C.; Zhou, H.; Zhao, T. Thermal and water absorption properties of cyanate ester resins modified by fluoride-containing and silicone-containing components. Polym. Adv. Technol. 2020, 31, 1245–1255. [Google Scholar] [CrossRef]
- Wu, T.B.; Ke, Y.C. The absorption and thermal behaviors of PET-SiO2 nanocomposite films. Polym. Degrad. Stab. 2006, 91, 2205–2212. [Google Scholar] [CrossRef]
- Diez-Pascual, A.M.; Diez-Vicente, A.L. High-Performance Aminated Poly(phenylene sulfide)/ZnO Nanocomposites for Medical Applications. ACS Appl. Mater. Interfaces 2014, 6, 10132–10145. [Google Scholar] [CrossRef]
- Jia, M.C.; Li, Y.J.; He, C.Q.; Huang, X.Y. Soluble Perfluorocyclobutyl Aryl Ether-Based Polyimide for High-Performance Dielectric Material. ACS Appl. Mater. Interfaces 2016, 8, 26352–26358. [Google Scholar] [CrossRef]
- Gong, C.; Zhao, Y.S.; Zhang, S.; Zhang, Z.Y.; Ding, L.J.; Zhang, H.D.; Li, X. Improving the insulating performance of epoxy resin in humid environments by HTPDMS modification. J. Appl. Polym. Sci. 2022, 139, e51754. [Google Scholar] [CrossRef]
- Gonon, P.; Hong, T.P.; Lesaint, O.; Bourdelais, S.; Debruyne, H. Influence of high levels of water absorption on the resistivity and dielectric permittivity of epoxy composites. Polym. Test. 2005, 24, 799–804. [Google Scholar] [CrossRef]
- Buchhold, R.; Nakladal, A.; Gerlach, G.; Sahre, K.; Muller, M.; Eichhorn, K.J.; Herold, M.; Gauglitz, G. A study on the microphysical mechanisms of adsorption in polyimide layers for microelectronic applications. J. Electrochem. Soc. 1998, 145, 11. [Google Scholar] [CrossRef]
- Li, S.Z.; Pak, Y.S.; Adamic, K.; Greenbaum, S.G.; Lim, B.S.; Xu, G.; Nowick, A.S. Diffusion and Deuteron Nuclear Magnetic Resonance Study of the Distribution of Water Molecules in Polyimide Films. J. Electrochem. Soc. 1992, 139, 662–667. [Google Scholar] [CrossRef]
- JIS K6911; Testing Methods for Thermosetting Plastics. JIS Handbook: Tokyo, Japan, 2021.
- JIS K6271; Rubber, Vulcanized or Thermoplastic Determination of Resistivity, Part 1: Guarded Electrode System. Rubber and Elastomer Handbook: Tokyo, Japan, 2015.
- IEC 61340-2-3 2000; Electrostatics, Part 2-3: Methods of Test for Determining the Resistance and Resistivity of Solid Planar Materials Used to Avoid Electrostatic Charge Accumulation. IEC: Tokyo, Japan, 2015.
- Qian, G.T.; Chen, H.Q.; Song, G.L.; Yao, J.N.; Hu, M.J.; Chen, C.H. Synthesis of polyimides with lower H2O-absorption and higher thermal properties by incorporation of intramolecular H-bonding. J. Polym. Sci. 2020, 58, 969–976. [Google Scholar] [CrossRef]
- Zhuang, Y.B.; Liu, X.Y.; Gu, Y. Molecular packing and properties of poly(benzoxazole-benzimidazole-imide) copolymers. Polym. Chem. 2012, 3, 1517. [Google Scholar] [CrossRef]
- Lian, M.; Lu, X.M.; Lu, Q.H. Synthesis of Superheat-Resistant Polyimides with High Tg and Low Coefficient of Thermal Expansion by Introduction of Strong Intermolecular Interaction. Macromolecules 2018, 51, 10127. [Google Scholar] [CrossRef]
- Tomlin, D.W.; Fratini, A.V.; Hunsaker, M.; Adams, W.W. The role of hydrogen bonding in rigid-rod polymers: The crystal structure of a polybenzobisimidazole model compound. Polymer 2000, 41, 9003. [Google Scholar] [CrossRef]
- Lamb, D.R. Electrical Conduction Mechanisms in Thin Insulating Films; Methuen: London, UK, 1967. [Google Scholar]
- Passi, J.; Nurmi, S.; Vuorinen, R.; Strengell, S.; Maijala, P. Performance of ESD protective materials at low relative humidity. J Electrost. 2001, 51–52, 429–434. [Google Scholar] [CrossRef]
- Wang, W.; Sain, M.; Cooper, P.A. Study of moisture absorption in natural fiber plastic composites. Compos. Sci. Technol. 2006, 66, 379–386. [Google Scholar] [CrossRef]
- Perets, Y.; Matzui, L.; Vovchenko, L.; Ovsiienko, I.; Yakovenko, O.; Lazarenko, O.; Zhuravkov, A.; Brusylovets, O. Influence of Ultraviolet/Ozonolysis Treatment of Nanocarbon Filler on the Electrical Resistivity of Epoxy Composites. Nanoscale Res. Lett. 2016, 11, 370. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory Revised Second Edition; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Connor, M.T.; Ray, S.; Ezquerre, T.A.; Balta, F.J. Broadband ac conductivity of conductor-polymer composites. Phys. Rev. B 1998, 57, 2286. [Google Scholar] [CrossRef]
- Kirkpatrick, S. Percolation and conduction. Rev. Mod. Phys. 1973, 45, 574. [Google Scholar] [CrossRef]
- Weber, M.; Kamal, M.R. Estimation of the volume resistivity of electrically conductive composites. Polym. Compos. 1997, 18, 711–725. [Google Scholar] [CrossRef]
- Sokolowska, D.; Krol-Otwinowska, A.; Bialecka, M.; Fiedor, L.; Szczygiel, M.; Moscicki, J.K. Water-network percolation transition in hydrated blue-green algae in vivo. J. Non-Cryst. Solids. 2007, 353, 4541–4545. [Google Scholar] [CrossRef]
- Nowak, J.; Dziob, D.; Rutkowska, M.; Chmielarz, L.; Gorska, U.; Sokolowska, D.; Moscicki, J.K. DC conductivity percolation on drying moistened mesoporous silica SBA-15. Microporous Mesoporous Mater. 2015, 206, 202–206. [Google Scholar] [CrossRef]
- Sokolowska, D.; Krol-Otwinowska, A.; Moscicki, J.K. Water-network percolation transitions in hydrated yeast. Phys. Rev. E 2004, 70, 052901. [Google Scholar] [CrossRef] [PubMed]
- Feng, Q.K.; Zhang, Y.X.; Liu, D.F.; Song, Y.H.; Huang, L.; Dang, Z.M. Dielectric and energy storage properties of all-organic sandwich-structured films used for high-temperature film capacitors. Mater. Today Energy 2022, 29, 101132. [Google Scholar] [CrossRef]
- Kudus, M.H.A.; Akil, H.M.; Zakaria, M.R.; Othman, M.B.H. Effect of Water Absorption on Dielectric Constant of TMD Cured of Carbonaceous Filled Epoxy Composites. J. Phys. Sci. 2019, 30, 101–107. [Google Scholar] [CrossRef]
- Breck, D.W. Zeolite Molecular Sieves: Structure, Chemistry, and Use; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Sharma, B.L.; Pillai, P.K.C. Electrical conduction in Kapton polyimide film at high electrical fields. Polymer 1982, 23, 17–20. [Google Scholar] [CrossRef]
- Sharma, B.L.; Pillai, P.K.C. Photoconduction in Kapton Polyimide Film at High Electric-Fields. Phys. Status. Solidi A 1982, 71, 583–588. [Google Scholar]
- Sawa, G.; Nakamura, S.; Iida, K.; Ieda, M. Electrical Conduction of Polypyromellitimide Films at Temperatures of 120–180 °C. Jpn. J. Appl. Phys. 1980, 19, 453–458. [Google Scholar] [CrossRef]
- Kim, T.Y.; Kim, W.J.; Lee, T.H.; Kim, J.E.; Yoon, H.G.; Suh, K.S. Electrical conduction of polyimide films prepared from polyamic acid (PAA) and pre-imidized polyimide (PI) solution. Express Polym. Lett. 2007, 1, 427–432. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watanabe, K.; Kaneko, M.; Zhong, X.; Takada, K.; Kaneko, T.; Kawai, M.; Mitsumata, T. Effect of Water Absorption on Electric Properties of Temperature-Resistant Polymers. Polymers 2024, 16, 521. https://doi.org/10.3390/polym16040521
Watanabe K, Kaneko M, Zhong X, Takada K, Kaneko T, Kawai M, Mitsumata T. Effect of Water Absorption on Electric Properties of Temperature-Resistant Polymers. Polymers. 2024; 16(4):521. https://doi.org/10.3390/polym16040521
Chicago/Turabian StyleWatanabe, Kaito, Masahiro Kaneko, Xianzhu Zhong, Kenji Takada, Tatsuo Kaneko, Mika Kawai, and Tetsu Mitsumata. 2024. "Effect of Water Absorption on Electric Properties of Temperature-Resistant Polymers" Polymers 16, no. 4: 521. https://doi.org/10.3390/polym16040521
APA StyleWatanabe, K., Kaneko, M., Zhong, X., Takada, K., Kaneko, T., Kawai, M., & Mitsumata, T. (2024). Effect of Water Absorption on Electric Properties of Temperature-Resistant Polymers. Polymers, 16(4), 521. https://doi.org/10.3390/polym16040521







