Comparison of the Bending Behavior of Cylindrically Shaped Lattice Specimens with Radially and Orthogonally Arranged Cells Made of ABS
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specification of Samples
2.2. Material and Fabrication
2.3. Experimental Conditions and Methodology of Evaluation
- push thorn radius—5 mm;
- cross-head speed—20 mm/min;
- distance of supports—170 mm.
3. Results and Discussion
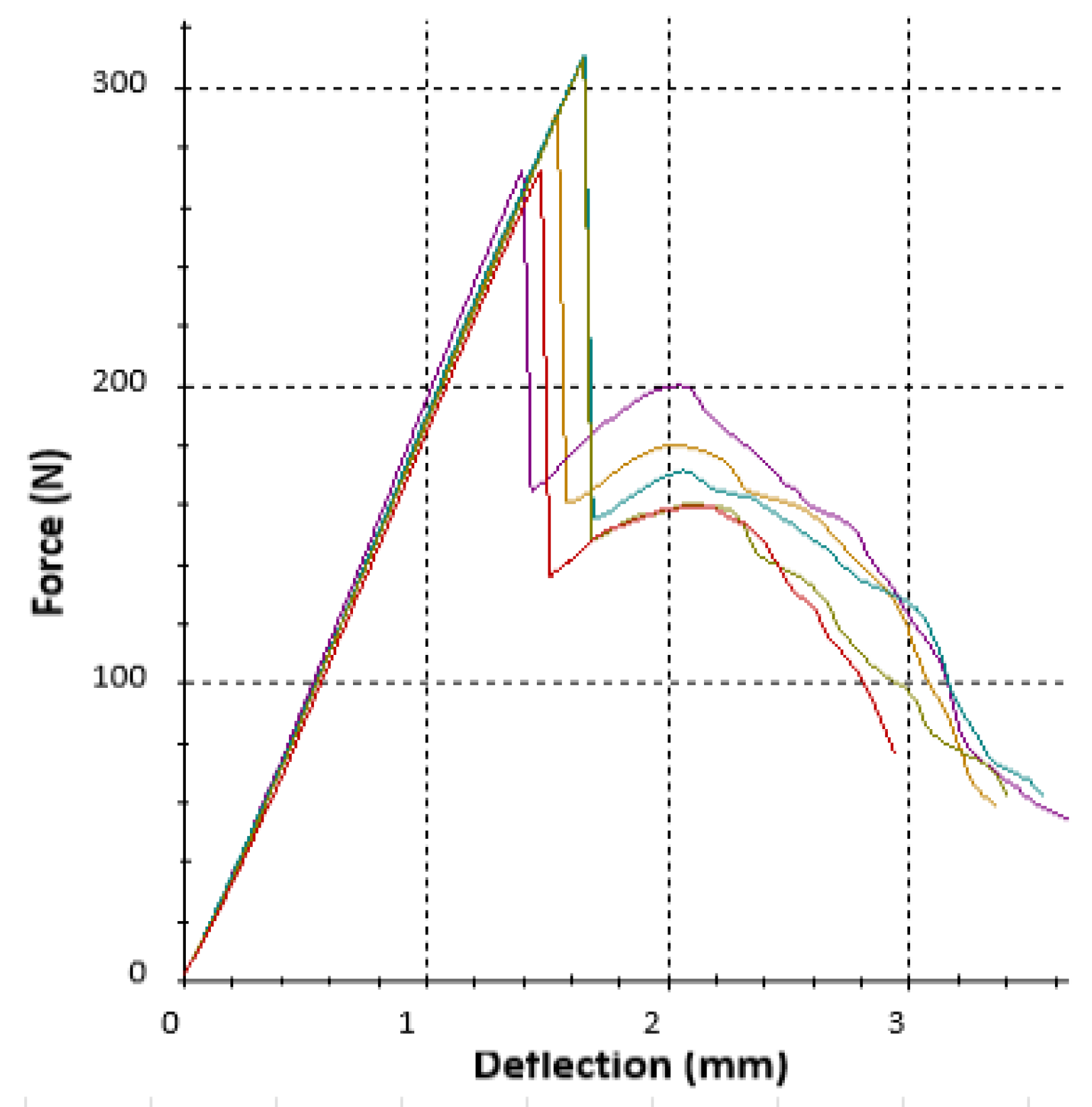
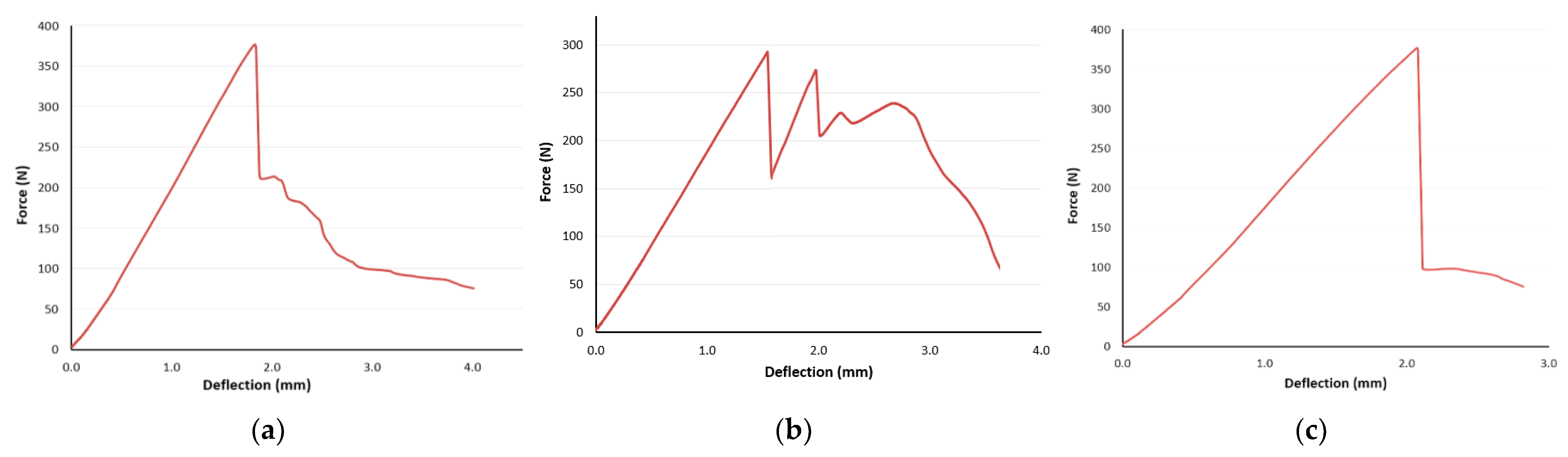
3.1. Bending Stress Evaluation
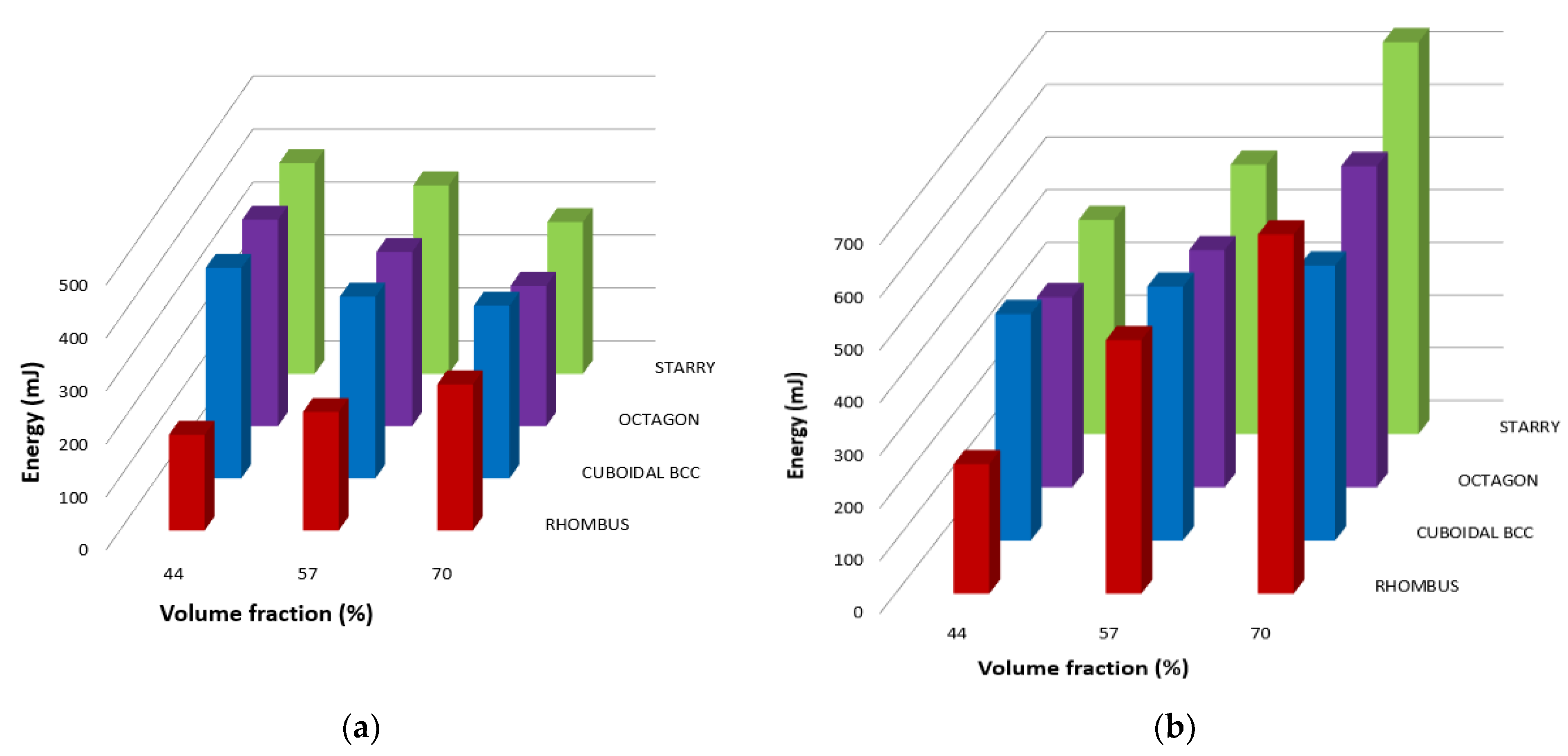
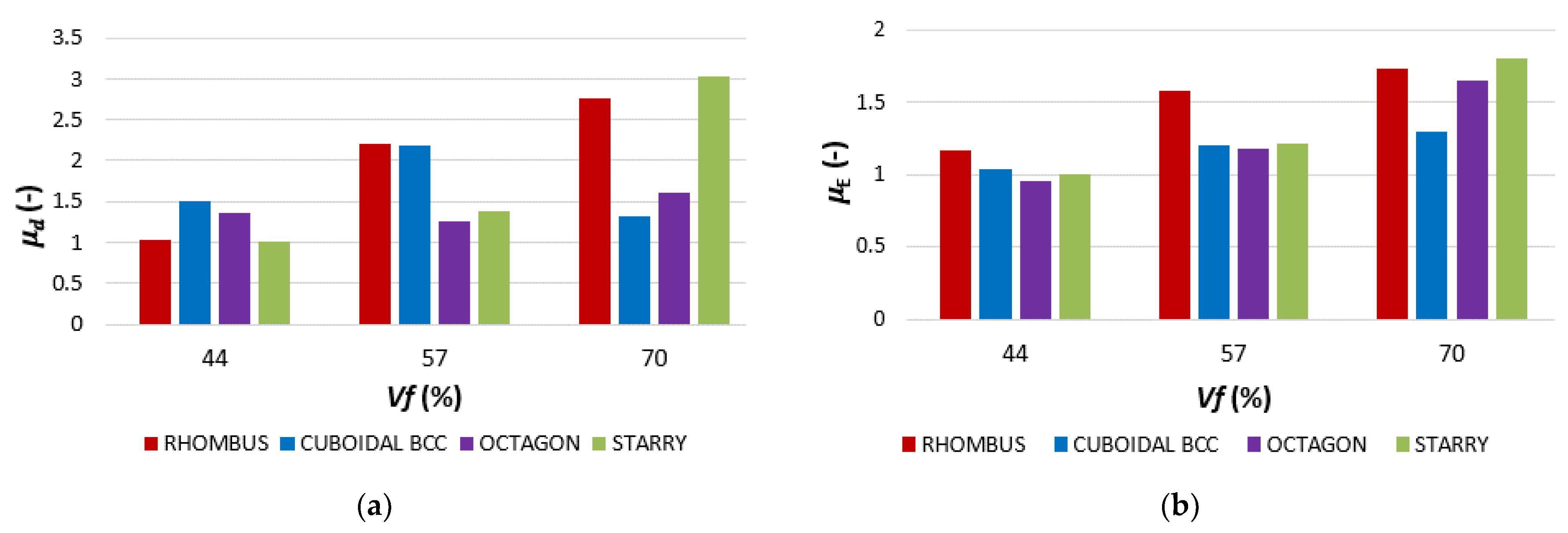
3.2. Energy Absorption and Ductility Assesment
- -
- Wtot is the total energy absorbed by the sample during bending (J);
- -
- We is the elastic energy (fraction of total) absorbed by the sample up to the elastic limit (J).
4. Conclusions
- The results showed that the Starry structure reached the highest values of stress in all volume fractions Vf and it can absorb the highest amount of energy.
- When the structure types were arranged according to their bending properties in descending order (best to worst), it could be seen that structures with a radial distribution alternate in position with orthogonally distributed structures. It means that the hypothesis about the influence of the radial or orthogonal distribution of the basic cell on the behavior of the lattice structures in bending was not confirmed.
- The samples with lattice structures made from ABS material by FFF technology used for the research showed mostly a brittle fracture behavior, while the failure propagation differs and it is affected by their topology (a combination of geometry, material volume fraction Vf, and cell distribution).
- In addition, the results showed that technology plays a significant role, since no difference (or very little) was visible in the obtained values when comparing the bending properties of the tube-shaped sample without structure and with structure (at Vf = 44%), and no difference (or really very small) in the obtained values was visible.
- Ductility indices µd (based on the deflection value at the proportionality limit) and µE (expressed as the quotient of the total and elastic energy) were also evaluated. Based on the obtained ductility indices, it can be concluded that the Rhombus structure appears to be the best; however, the structure showed the lowest values of bending stresses. Therefore, from a synergic point of view of both factors, stress and ductility, the Starry structure appears to be the most suitable for application in rotating components stressed by bending.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar Mishra, A.; Kumar, A. Performance of asymmetric octet lattice structures under compressive and bending loads. Eng. Fail. Anal. 2023, 154, 107669. [Google Scholar] [CrossRef]
- Liu, Y. Mechanical properties of a new type of plate–lattice structures. Int. J. Mech. Sci. 2020, 192, 106141. [Google Scholar] [CrossRef]
- Mahbod, M.; Asgari, M. Elastic and plastic characterization of a new developed additively manufactured functionally graded porous lattice structure: Analytical and numerical models. Int. J. Mech. Sci. 2019, 155, 248–266. [Google Scholar] [CrossRef]
- Günaydın, K.; Sala, G.; Türkmen, H.S.; Grande, A.M. Failure analysis of auxetic lattice structures under crush load. Procedia Struct. Integr. 2022, 35, 237–246. [Google Scholar] [CrossRef]
- Raghavendra, S.; Molinari, A.; Fontanari, V.; Luchin, V.; Zappini, G.; Benedetti, M. Effect of Porosity and Cell Topology on Elastic-Plastic Behavior of Cellular Structures. Procedia Struct. Integr. 2019, 18, 93–100. [Google Scholar] [CrossRef]
- Zhang, C.; Nie, G.; Dai, J.; Zhi, X. Experimental studies of the seismic behavior of double-layer lattice space structures I: Experimental verification. Eng. Fail. Anal. 2016, 64, 85–96. [Google Scholar] [CrossRef]
- Della Ripa, M.; Paolino, D.S.; Amorese, A.; Tridello, A. Numerical modelling of the mechanical response of lattice structures produced through AM. Procedia Struct. Integr. 2021, 33, 714–723. [Google Scholar] [CrossRef]
- Baranowski, P.; Płatek, P.; Antolak-Dudka, A.; Sarzyński, M.; Kucewicz, M.; Durejko, T.; Małachowski, J.; Janiszewski, J.; Czujko, T. Deformation of honeycomb cellular structures manufactured with Laser Engineered Net Shaping (LENS) technology under quasi-static loading: Experimental testing and simulation. Addit. Manuf. 2019, 25, 307–316. [Google Scholar] [CrossRef]
- Benedetti, M.; du Plessis, A.; Ritchie, R.O.; Dallago, M.; Razavi, N.; Berto, F. Architected cellular materials: A review on their mechanical properties towards fatigue-tolerant design and fabrication. Mater. Sci. Eng. R Rep. 2021, 144, 100606. [Google Scholar] [CrossRef]
- Monkova, K.; Monka, P.P.; Hricová, R.; Hausnerova, B.; Knapčíková, L. Tensile Properties of Four Types of ABS Lattice Structures—A Comparative Study. Polymers 2023, 15, 4090. [Google Scholar] [CrossRef]
- Li, Y.; Pavier, M.; Coules, H. Fracture behaviour of octet-truss lattices in different orientations. Procedia Struct. Integr. 2022, 37, 49–56. [Google Scholar] [CrossRef]
- Vazdirvanidis, A.; Bouzouni, M.; Pantazopoulos, G. Failure and Fracture analysis of a high-alloy Ni-Al bronze chain connector of a tube drawing machine. Eng. Fail. Anal. 2020, 110, 104432. [Google Scholar] [CrossRef]
- Monkova, K.; Vasina, M.; Zaludek, M.; Monka, P.P.; Tkac, J. Mechanical Vibration Damping and Compression Properties of a Lattice Structure. Materials 2021, 14, 1502. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Ziegler, H.; Zhang, Z.; Atre, S.; Chen, Y. Bending behavior of 3D printed mechanically robust tubular lattice metamaterials. Addit. Manuf. 2022, 50, 102565. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, H.; Xing, S. Mechanical performances of metal-polymer sandwich structures with 3D-printed lattice cores subjected to bending load. Arch. Civ. Mech. Eng. 2020, 20, 89. [Google Scholar] [CrossRef]
- Gullapalli, H.; Masood, S.H.; Riza, S.; Ponnusamy, P. Flexural Behaviour of 2D Cellular Lattice Structures Manufactured by Fused Deposition Modelling; Lecture Notes on Multidisciplinary Industrial Engineering; Springer: Singapore, 2020; pp. 109–117. [Google Scholar]
- Catana, D.; Pop, M.-A.; Brus, D.-I. Comparison between the Test and Simulation Results for PLA Structures 3D Printed, Bending Stressed. Molecules 2021, 26, 3325. [Google Scholar] [CrossRef] [PubMed]
- Eryildiz, M. Experimental investigation and simulation of 3D printed sandwich structures with novel core topologies under bending loads. Int. Polym. Process. 2023, 38, 277–289. [Google Scholar] [CrossRef]
- Pirouzfar, S.; Zeinedini, A. Effect of geometrical parameters on the flexural properties of sandwich structures with 3D-printed honeycomb core and E-glass/epoxy Face-sheets. Structures 2021, 33, 2724–2738. [Google Scholar] [CrossRef]
- Öteyaka, M.Ö.; Çakir, F.H.; Sofuoğlu, M.A. Effect of infill pattern and ratio on the flexural and vibration damping characteristics of FDM printed PLA specimens. Mater. Today Commun. 2022, 33, 104912. [Google Scholar] [CrossRef]
- Fongsamootr, T.; Suttakul, P.; Tippayawong, N.; Nanakorn, P.; Cappellini, C. Bending behavior of 2D periodic plates with different unit cells: Numerical and experimental investigations. Mater. Today Commun. 2022, 31, 103774. [Google Scholar] [CrossRef]
- Pantazopoulos, G.A. Failure Mechanisms in Alloys. Metals 2020, 10, 117. [Google Scholar] [CrossRef]
- Bellini, C.; Borrelli, R.; Di Caprio, F.; Di Cocco, V.; Franchitti, S.; Iacoviello, F.; Mocanu, L.P.; Sorrentino, L. Manufacturing process effect on the bending characteristics of titanium-lattice/FRP hybrid structures. Procedia Struct. Integr. 2022, 42, 196–201. [Google Scholar] [CrossRef]
- Le, C.; Kolasangiani, K.; Nayyeri, P.; Bougherara, H. Experimental and numerical investigation of 3D-Printed bone plates under four-point bending load utilizing machine learning techniques. J. Mech. Behav. Biomed. Mater. 2023, 143, 105885. [Google Scholar] [CrossRef]
- Lampropoulos, A.D.; Markopoulos, A.P.; Manolakos, D.E. Modeling of Ti6Al4V alloy orthogonal cutting with smooth particle hydrodynamics: A parametric analysis on formulation and particle density. Metals 2019, 9, 388. [Google Scholar] [CrossRef]
- Grbović, A.; Kastratović, G.; Božić, Ž.; Božić, I.; Obradović, A.; Sedmak, A.; Sedmak, S. Experimental and numerical evaluation of fracture characteristics of composite material used in the aircraft engine cover manufacturing. Eng. Fail. Anal. 2022, 137, 106286. [Google Scholar] [CrossRef]
- Mushtaq, R.T.; Wang, Y.; Bao, C.; Chen, X.; Anwar, S.; Sharma, S.; Khan, A.M.; Sharma, K.; Bisht, Y.S.; Abbas, M.; et al. Multi-objective optimization of laser polishing parameters for enhanced mechanical properties, sustainability, and surface finish of 3D-Printed industrial ABS polymers using response surface methodology (RSM). J. Mater. Res. Technol. 2024, 29, 3168–3184. [Google Scholar] [CrossRef]
- Tkac, J.; Samborski, S.; Monkova, K.; Debski, H. Analysis of mechanical properties of a lattice structure produced with the additive technology. Compos. Struct. 2020, 242, 112138. [Google Scholar] [CrossRef]
- Kessler, J.; Balc, N.; Gebhardt, A. Basic research on lattice structures focused on the reliance of the cross sectional area and additional coatings. MATEC Web. Conf. 2017, 94, 03008. [Google Scholar] [CrossRef]
- Vanca, J. Research of Properties of Complex Cell Structures Produced by Additive Technology. Ph.D. Thesis, Technical University of Kosice, Faculty of Manufacturing Technologies with a seat in Presov, Presov, Slovakia, 2019. [Google Scholar]
- Kadkhodapour, J.; Montazerian, H.; Darabi, A.C.; Anaraki, A.P.; Ahmadi, S.M.; Zadpoor, A.A.; Schmauder, S. Failure mechanisms of additively manufactured porous biomaterials. J. Mech. Behav. Biomed. Mater. 2015, 50, 180–191. [Google Scholar] [CrossRef]
- Frank, L.; Weihe, S. Component tests and numerical investigations to determine the lifetime and failure behavior of end stage blades. Procedia Struct. Integr. 2023, 46, 3–9. [Google Scholar] [CrossRef]
- Hric, S. Research of Possibilities Application of Components of Technical Systems Made by Additive Technology. Ph.D. Thesis, Technical University of Kosice, Faculty of Manufacturing Technologies with a seat in Presov, Presov, Slovakia, 2019. [Google Scholar]
- ISO 527-1/-2; Determination of Tensile Properties. ISO: Geneva, Switzerland, 2012.
- Technical Datasheet White EasyABS, Prusa Polymers by Josef Prusa; Prusa Research, a. s.: Prague, Czech Republic, 2023.
- ISO 178:2019 Standard; Plastics Determination of Flexural Properties. ISO: Geneva, Switzerland, 2019.
- Kožar, I.; Bede, N.; Mrakovčić, S.; Božić, Ž. Verification of a fracture model for fiber reinforced concrete beams in bending. Eng. Fail. Anal. 2022, 138, 106378. [Google Scholar] [CrossRef]
- Pantazopoulos, G.A. A Short Review on Fracture Mechanisms of Mechanical Components Operated under Industrial Process Conditions: Fractographic Analysis and Selected Prevention Strategies. Metals 2019, 9, 148. [Google Scholar] [CrossRef]
- Kahraman, M.F.; İriç, S.; Genel, K. Comparative failure behavior of metal honeycomb structures under bending: A finite element-based study. Eng. Fail. Anal. 2024, 157, 107963. [Google Scholar] [CrossRef]
- Dell’ Isola, F.; Ruta, G.C. Generalizing Jouravski Formulas by Techniques from Differential Geometry. Math. Mech. Solids 1997, 2, 307–319. [Google Scholar] [CrossRef]
- Arowojolu, O.; Ibrahim, A.; Almakrab, A.; Saras, N.; Nielsen, R. Influence of Shear Span-to-Effective Depth Ratio on Behavior of High-Strength Reinforced Concrete Beams. Int. J. Concr. Struct. Mater. 2021, 15, 14. [Google Scholar] [CrossRef]
- Sudheer, R.L.; Ramana, R.N.V.; Gunneswara, R.T.D. Shear resistance of high strength concrete beams without shear reinforcement. Int. J. Civ. Struct. Eng. 2010, 1, 101–113. [Google Scholar]
- Huber, T.; Huber, P.; Kollegger, J. Influence of aggregate interlock on the shear resistance of reinforced concrete beams without stirrups. Eng. Struct. 2019, 186, 26–42. [Google Scholar] [CrossRef]
- Hu, B.; Wu, Y.F. Effect of shear span-to-depth ratio on shear strength components of RC beams. Eng. Struct. 2018, 168, 770–783. [Google Scholar] [CrossRef]
- Kožar, I.; Sulovsky, T.; Plovanić, M.; Božić, Ž. Verification of a displacement model for three-point bending test. Procedia Struct. Integr. 2023, 46, 143–148. [Google Scholar] [CrossRef]
- Li, J.; Cui, Y.; Xiong, D.; Lu, Z.; Dong, X.; Zhang, H.; Cui, F.; Zhou, T. Experimental Study on the Bending Resistance of Hollow Slab Beams Strengthened with Prestressed Steel Strand Polyurethane Cement Composite. Coatings 2023, 13, 458. [Google Scholar] [CrossRef]
- Tong, K.; Zhou, J.; Zhou, S.; Zhang, Y.; Chen, R.; Li, S.; Zhao, R. Investigation of the relationship between bending capacity and SMFL intensity of existing reinforced concrete hollow slab beams. Measurement 2024, 228, 114331. [Google Scholar] [CrossRef]
- Haedir, J.; Bambach, M.R.; Zhao, X.-L.; Grzebieta, R.H. Strength of circular hollow sections (CHS) tubular beams externally reinforced by carbon FRP sheets in pure bending. Thin-Walled Struct. 2009, 47, 1136–1147. [Google Scholar] [CrossRef]
- Daud, S.A.; Daud, R.A.; Al-Azzawi, A.A. Behavior of reinforced concrete solid and hollow beams that have additional reinforcement in the constant moment zone. Ain Shams Eng. J. 2020, 12, 31–36. [Google Scholar] [CrossRef]
- Vanca, J.; Monkova, K.; Žaludek, M.; Monka, P.P.; Koroľ, M.; Kozak, D.; Beno, P.; Ferroudji, F. Investigation of the Influence of Orientation on the Tensile Properties of 3D Printed Samples with Gyroid Structure. In Proceedings of the 13th International Conference on Mechanical and Aerospace Engineering, Bratislava, Slovakia, 20–22 July 2022; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2022; pp. 526–531, ISBN 978-1-6654-7234-0. [Google Scholar]
- Monkova, K.; Monka, P.P.; Žaludek, M.; Beňo, P.; Hricová, R.; Šmeringaiová, A. Experimental Study of the Bending Behaviour of the Neovius Porous Structure Made Additively from Aluminium Alloy. Aerospace 2023, 10, 361. [Google Scholar] [CrossRef]
- Campagnolo, A.; Berto, F.; Leguillon, D. Mode II loading in sharp V-notched components: A comparison among some recent criteria for brittle fracture assessment. Procedia Struct. Integr. 2016, 2, 1845–1852. [Google Scholar] [CrossRef]
- Marsavina, L.; Negru, R.; Serban, D.; Marghitas, M.; Popa, C. The notch effect on additive manufactured polymers. Procedia Struct. Integr. 2023, 47, 744–748. [Google Scholar] [CrossRef]
- Arrieta, S.; Cicero, S.; Sánchez, M.; Castanon-Jano, L. Estimation of fracture loads in 3D printed PLA notched specimens using the ASED criterion. Procedia Struct. Integr. 2023, 47, 13–21. [Google Scholar] [CrossRef]
- Subhani, M.; Globa, A.; Al-Ameri, R.; Moloney, J. Flexural strengthening of LVL beam using CFRP. Constr. Build. Mater. 2017, 150, 480–489. [Google Scholar] [CrossRef]
- Nabavi-Kivi, A.; Ayatollahi, M.R.; Schmauder, S.; Khosravani, M.R. Fracture analysis of a 3D-printed ABS specimen: Effects of raster angle and layer orientation. Fiz. Mezomekhanika 2022, 25, 26–39. [Google Scholar] [CrossRef]
- Birro, T.V.; Aufray, M.; Paroissien, E.; Lachaud, F. Assessment of interface failure behaviour for brittle adhesive using the three-point bending test. Int. J. Adhes. Adhes. 2021, 110, 102891. [Google Scholar] [CrossRef]
- Roche, A.; Behme, A.; Solomon, J. A three-point flexure test configuration for improved sensitivity to metal/adhesive interfacial phenomena. Int. J. Adhes. Adhes. 1982, 2, 249–254. [Google Scholar] [CrossRef]
- Kim, T.-K.; Park, J.-S. Evaluation of the Performance and Ductility Index of Concrete Structures Using Advanced Composite Material Strengthening Methods. Polymers 2021, 13, 4239. [Google Scholar] [CrossRef] [PubMed]

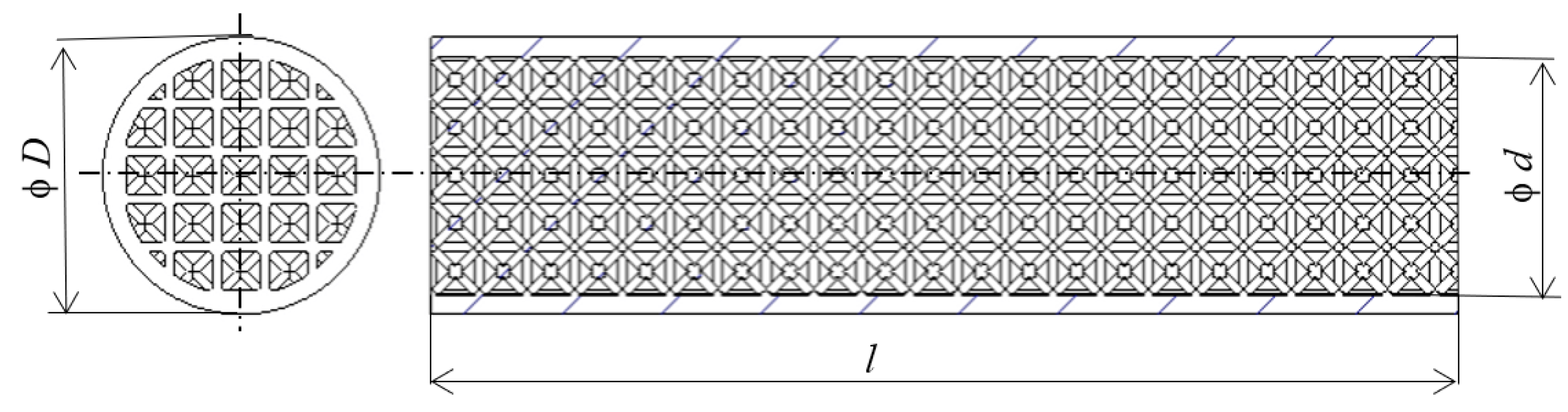



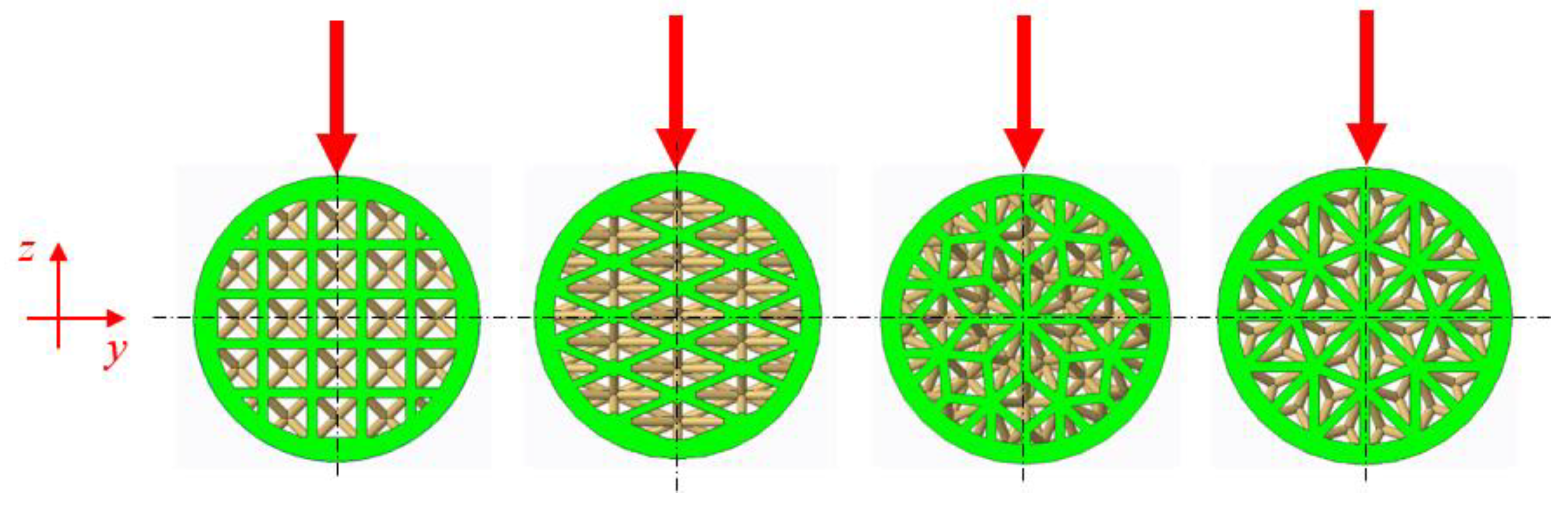




| Structure Type | Volume Fraction Vf (%) | Sample Designation | Cell Sizes * (mm) | Strut Diameter (mm) | Number of Pieces |
|---|---|---|---|---|---|
| Tube type | 25 | T_25 | - | - | 6 |
| Cuboidal BCC | 44 | C_44 | x, y, z = 5 mm | 1 | 6 |
| Rhombus | R_44 | x = 7 mm; y = 7 mm; z = 5.5 mm; φ = 45° | 6 | ||
| Starry | S_44 | x = 5 mm; y = 9 mm; z = 7.5 | 6 | ||
| Octagon | O_44 | x = 5 mm; y = 7 mm; z = 6 mm | 6 | ||
| Cuboidal BCC | 57 | C_57 | x, y, z = 5 mm | 1.4 | 6 |
| Rhombus | R_57 | x = 7 mm; y = 7 mm; z = 5.5 mm; φ = 45° | 6 | ||
| Starry | S_57 | x = 5 mm; y = 9 mm; z = 7.5 | 6 | ||
| Octagon | O_57 | x = 5 mm; y = 7 mm; z = 6 mm | 6 | ||
| Cuboidal BCC | 70 | C_70 | x, y, z = 5 mm | 1.8 | 6 |
| Rhombus | R_70 | x = 7 mm; y = 7 mm; z = 5.5 mm; φ = 45° | 6 | ||
| Starry | S_70 | x = 5 mm; y = 9 mm; z = 8 | 6 | ||
| Octagon | O_70 | x = 5 mm; y = 7 mm; z = 5.5 mm | 6 | ||
| Bar-type | 100 | B_100 | - | - | 6 |
| Characteristics | Designation | Unit | Value |
|---|---|---|---|
| Ultimate tensile strength | Rm | MPa | 43 |
| Young’s modulus | E | MPa | 2140 |
| Poisson number | ν | 0.394 | |
| Density | ρ | g/cm3 | 1.05 |
| Sample | Section Moduli (mm3) |
|---|---|
| C_44 | 1212.29 |
| C_57 | 1352.12 |
| C_70 | 1542.77 |
| R_44 | 1463.70 |
| R_57 | 1691.13 |
| R_70 | 1937.27 |
| S_44 | 1260.66 |
| S_57 | 1578.53 |
| S_70 | 1773.23 |
| O_44 | 1390.69 |
| O_57 | 1608.98 |
| O_70 | 1968.59 |
| B_100 | 2394.38 |
| T_25 | 1071.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monkova, K.; Monka, P.P.; Vodilka, A. Comparison of the Bending Behavior of Cylindrically Shaped Lattice Specimens with Radially and Orthogonally Arranged Cells Made of ABS. Polymers 2024, 16, 979. https://doi.org/10.3390/polym16070979
Monkova K, Monka PP, Vodilka A. Comparison of the Bending Behavior of Cylindrically Shaped Lattice Specimens with Radially and Orthogonally Arranged Cells Made of ABS. Polymers. 2024; 16(7):979. https://doi.org/10.3390/polym16070979
Chicago/Turabian StyleMonkova, Katarina, Peter Pavol Monka, and Adrián Vodilka. 2024. "Comparison of the Bending Behavior of Cylindrically Shaped Lattice Specimens with Radially and Orthogonally Arranged Cells Made of ABS" Polymers 16, no. 7: 979. https://doi.org/10.3390/polym16070979







