Method Development for the Prediction of Melt Quality in the Extrusion Process
Abstract
:1. Introduction
1.1. Screw Performance Index (SPI)
- SPI: Screw performance index;
- : Minimum and maximum processing temperatures of the polymer;
- : Degree of melting;
- : Back pressure fluctuation;
- : Difference between the max. pressure and the back pressure;
- : Melt temperature;
- : Temperature fluctuation;
- : Thermal homogeneity;
- : Degree of efficiency;
- : Change in the melt flow rate.
1.2. Simulation of the Extrusion Process
- The principle of the simple model.
- The principle of mathematical clarity of model solutions.
- The principle of mathematically closed solutions, even if rigorous simplifications are necessary.
- The principle of linearization of intermediate results in semi-logarithmic or double-logarithmic representation in order to obtain a closed solution for a sequence of differential equations to obtain a closed solution.
- The principle of approximation of numerical solutions when exact solutions are no longer possible.
- The principle of describing stochastic processes as well as possible by well-defined distribution functions.
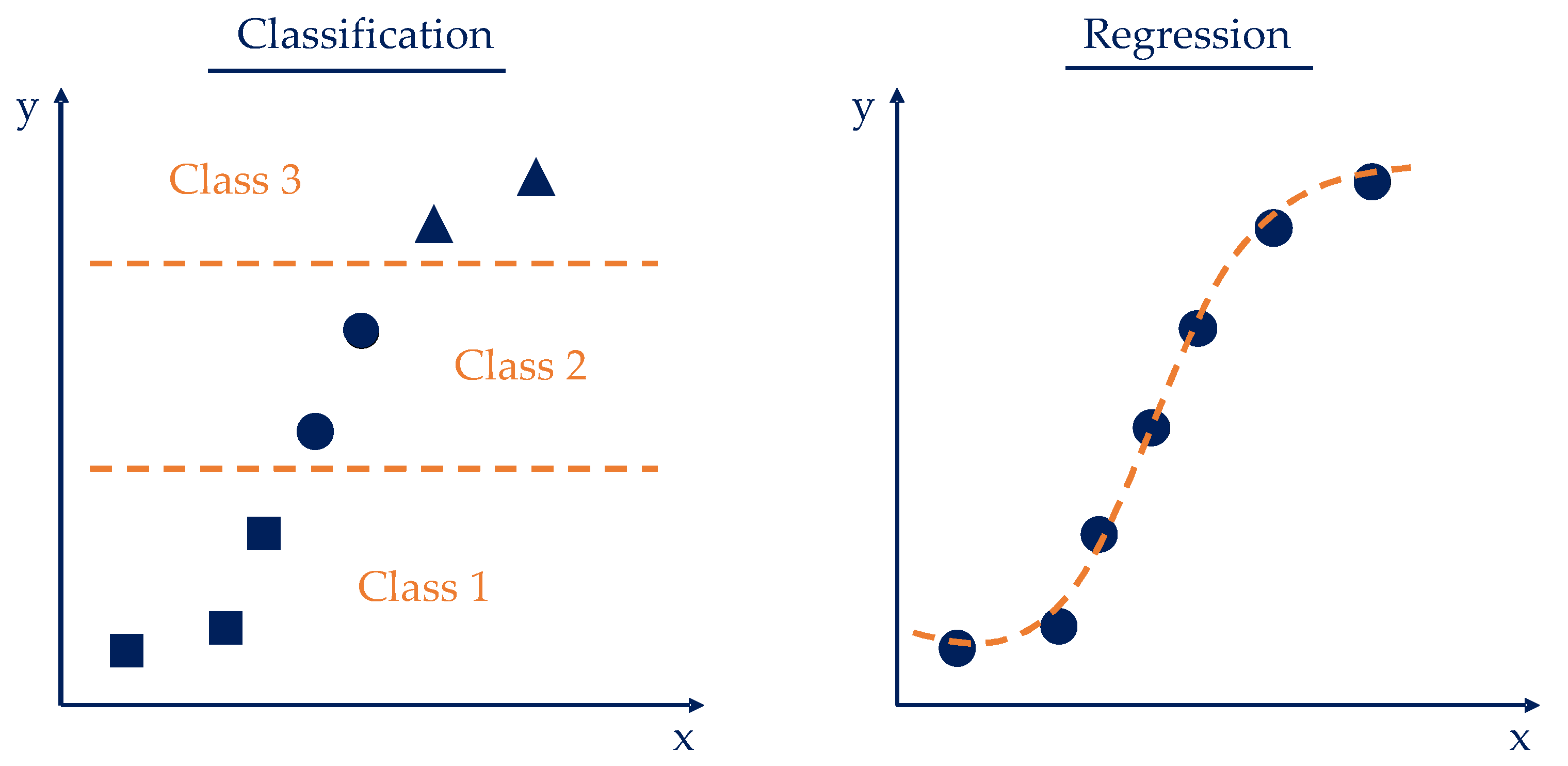
1.3. Machine Learning (Comparison Classification and Regression)
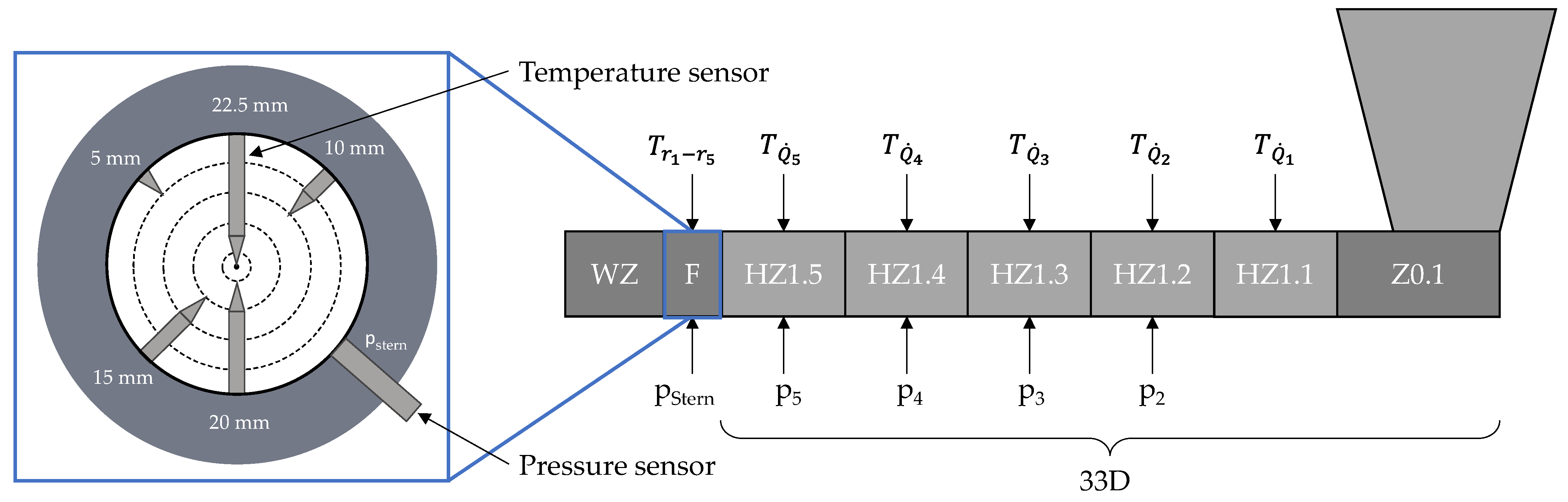
2. Experimental Setup
3. Method
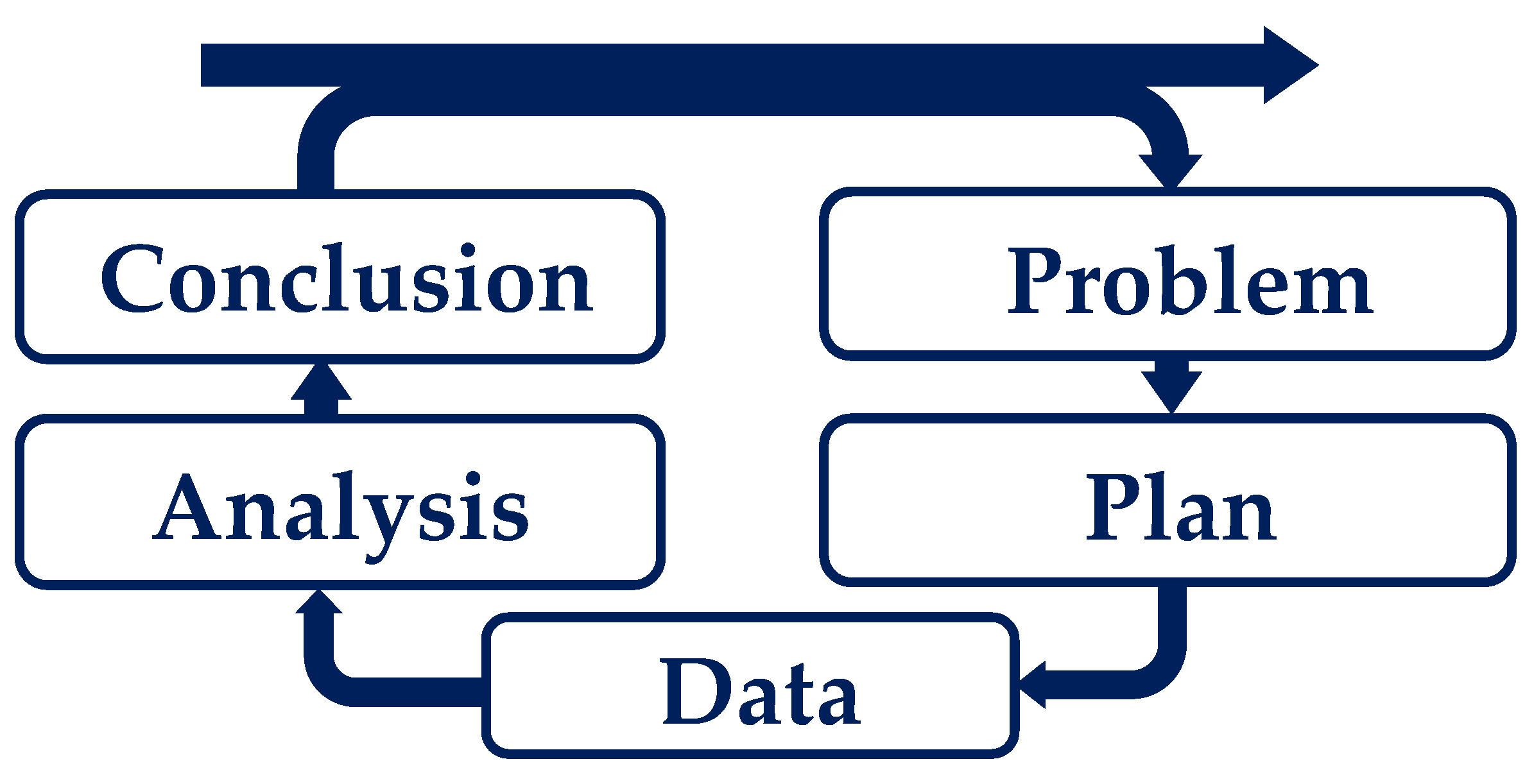
3.1. PPDAC
- According to [23,25], the Problem analysis phase focuses on identifying the system dynamics and understanding and defining the problem. The following question can be used as a problem definition: How can melt quality be predicted by simulation? The analysis of this question showed that current simulation software can generate simulative parameters and that the SPI evaluation index can evaluate melt quality through experiments. However, both aspects show deficiencies in the ability to predict melt quality on a simulative basis.
- The Data collection phase focuses on collecting, managing, and cleaning the data. It is important to have access to valid and reliable data in order to draw sound and reliable conclusions [23,25]. The data collection includes the SPI data and the problem definition characteristics of the simulation software. The labeled data are used to generate a model for simulating melt quality using machine learning.
- The Analysis phase involves a series of steps, including organizing data in a structured way, creating tables and graphs to analyze data and calculate predictions, examining data in depth, identifying patterns, conducting planned and unplanned analyses, and formulating hypotheses [23]. In the analysis step, the available data set must be transformed into a processable structure and divided into training and test data. The decision was made to use 10-fold cross-validation, which will be discussed in more detail in the following Section 3.2.
3.2. Cross-Validation Statistics
3.3. Labelling
4. Model Training and Assessment
4.1. Regression, Cross-Validation, and Significance Analysis by Lasso Regression
- Ridge regression, which adds the square of the regression coefficients to the regression equation. This stabilizes the coefficients and prevents them from taking on very large values. Equation (5) shows the calculation, where the left term is the squared error between the observed and predicted values, and the right regularization term limits the size of the regression coefficients. The larger α is, the stronger the regularization applied [35]:
- Lasso regression, in which the absolute value of the regression coefficients is added to the regression equation. An advantage of lasso regression is that it can reduce coefficients to zero. Automatic feature selection is performed by eliminating the irrelevant variables. The calculation of lasso regression is shown in Equation (6), where the variables are the same as in ridge regression. The difference is in the regularization term, where the absolute values of all regression coefficients are summed [35].
4.2. Model Development Challenges
4.3. Results
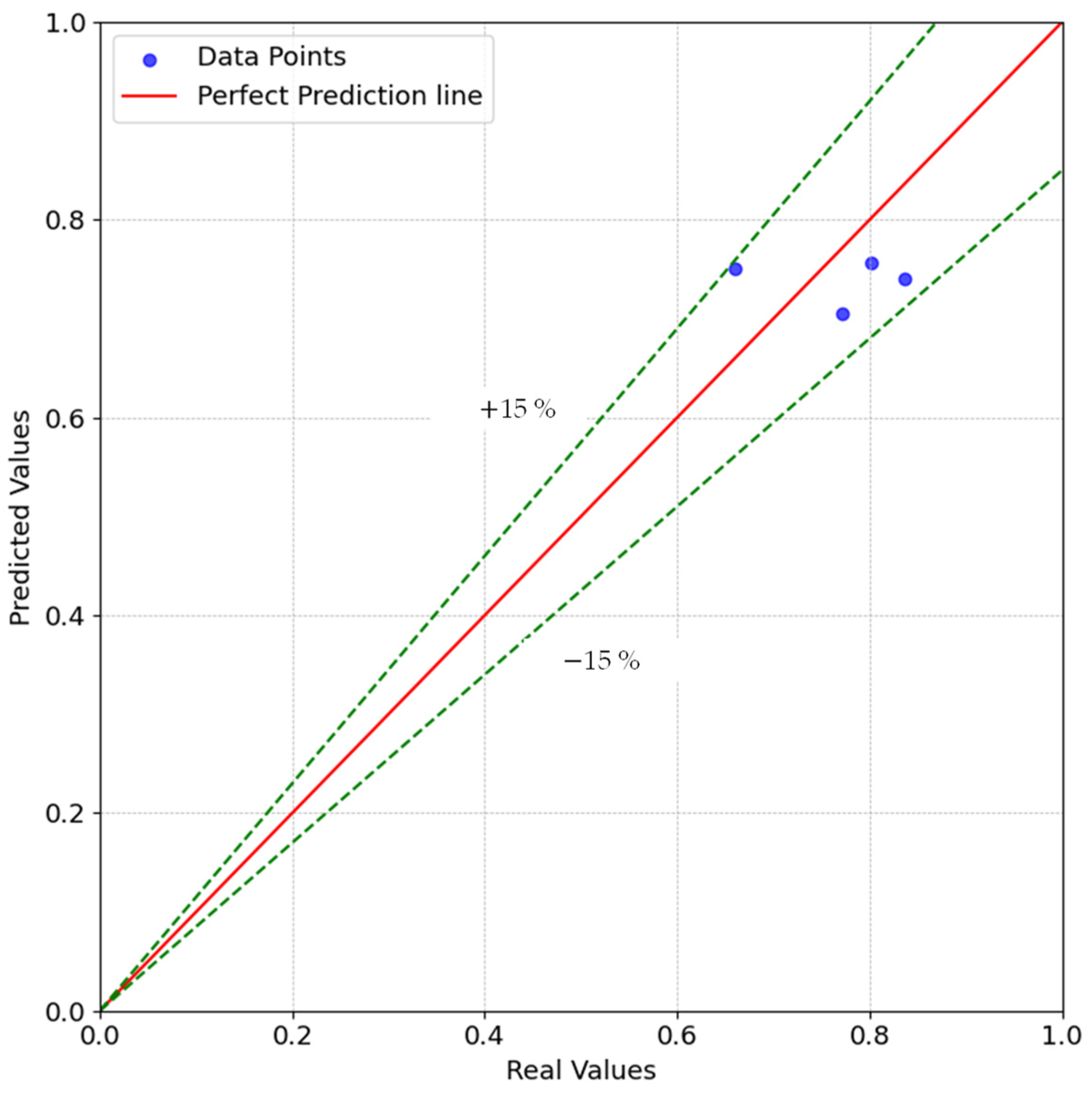
5. Validation
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Chung, C.I. Extrusion of Polymers: Theory and Practice, 3rd ed.; Carl Hanser Verlag: München, Germany, 2019; ISBN 978-1-56990-609-5. [Google Scholar]
- Abeykoon, C.; Li, K.; McAfee, M.; Martin, P.J.; Niu, Q.; Kelly, A.L.; Deng, J. A new model based approach for the prediction and optimisation of thermal homogeneity in single screw extrusion. Control Eng. Pract. 2011, 19, 862–874. [Google Scholar] [CrossRef]
- Rauwendaal, C. Polymer Extrusion, 5th ed.; Hanser Publication: Munich, Germany; Cincinnati, OH, USA, 2014; ISBN 978-1-56990-539-5. [Google Scholar]
- Dörner, M. Wave-Schnecken in der Einschneckenextrusion. Ph.D. Thesis, Universität Paderborn, Paderborn, Germany, 2022. [Google Scholar]
- Schöppner, V. Verfahrenstechnische Auslegung von Extrusionsanlagen; VDI: Paderborn, Germany, 2001. [Google Scholar]
- Resonnek, V.; Schöppner, V. Self-Optimizing Barrel Temperature Setting Control of Single Screw Extruders for Improving the Melt Quality. In Proceedings of the 34th International Conference of the Polymer Processing Society (PPS), Taiwan, China, 21–25 May 2018. [Google Scholar]
- Schall, C. Materialschonende Verarbeitung von Thermoplasten auf Wave-Schnecken. Ph.D. Thesis, Universität Paderborn, Paderborn, Germany, 2023. [Google Scholar]
- DIN EN ISO 9000:2015-11; Qualitätsmanagementsysteme—Grundlagen und Begriffe (ISO_9000:2015). International Organization for Standardization: Geneva, Switzerland, 2015.
- Gorczyca, P. Analyse und Optimierung von Einschneckenextrudern mit Schnelldrehenden Schnecken. Ph.D. Thesis, Universität Duisburg-Essen, Essen, Germany, 2011. [Google Scholar]
- Abeykoon, C.; Pérez, P.; Kelly, A.L. The effect of materials’ rheology on process energy consumption and melt thermal quality in polymer extrusion. Polym. Eng. Sci. 2020, 60, 1244–1265. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, D.; Cai, J. Model prediction and numerical simulation on melt temperature distribution in process of polymer extrusion. In Proceedings of the 2009 IEEE International Conference on Intelligent Computing and Intelligent Systems, Shanghai, China, 20–22 November 2009; pp. 808–812. [Google Scholar]
- Chen, T.-F.; Nguyen, K.T.; Wen, S.-S.L.; Jen, C.-K. Temperature measurement of polymer extrusion by ultrasonic techniques. Meas. Sci. Technol. 1999, 10, 139–145. [Google Scholar] [CrossRef]
- Dörner, M.; Schöppner, V.; Marschik, C. Analysis of the advantageous process and mixing behaviour of wave-dispersion screws in single screw extrusion. In SPE ANTEC 2020: The Virtual Edition; Society of Plastics Engineers: Brookfield, CT, USA, 2020. [Google Scholar]
- Epple, S.; Grünschloss, E.; Bonten, C. Mischergebnisse im Einschneckenextruder. Kunststoffe-Munchen 2012, 102, 58. [Google Scholar]
- Trienens, D.; Schöppner, V. Investigation of the influence of screw geometry on the resulting melt quality for cast film extrusion. In Proceedings of the 38th International Conference of the Polymer Processing Society, St. Gallen, Switzerland, 22–26 May 2023. [Google Scholar]
- Trienens, D.; Schöppner, V.; Bunse, R. Determination of Correlations between Melt Quality and the Screw Performance Index in the Extrusion Process. Polymers 2023, 15, 3427. [Google Scholar] [CrossRef] [PubMed]
- Potente, H.; Schöppner, V. Rechnergestützte Extruderauslegung (REX); Skript; Universität Paderborn: Paderborn, Germany, 1992. [Google Scholar]
- Buxmann, P.; Schmidt, H. Künstliche Intelligenz; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Matzka, S. Künstliche Intelligenz in den Ingenieurwissenschaften; Springer: Wiesbaden, Germany, 2021. [Google Scholar]
- Raschka, S.; Mirjalili, V. 2. aktualisierte und erweiterte Auflage. In Machine Learning mit Python und Scikit-Learn und TensorFlow: Das Umfassende Praxis-Handbuch für Data Science, Deep Learning und Predictive Analytics; MITP: Frechen, Germany, 2018; ISBN 3958457339. [Google Scholar]
- Westfall, P.H.; Arias, A.L. Understanding Regression Analysis: A Conditional Distribution Approach; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2020; ISBN 978-0-367-49351-6. [Google Scholar]
- Trienens, D.; Schöppner, V. Investigation Regarding the Correlation of the Relative Influences during the Extrusion Process of Cast Films on the Resulting Melt Quality; Ilmenau University of Technology: Ilmenau, Germany, 2023. [Google Scholar]
- Arnold, P.; Pfannkuch, M. On being Data Detectives: Developing Novice Statisticians Using the Statistical Enquiry Cycle. J. Issue 2020, 1. [Google Scholar] [CrossRef]
- Walter, C. Statistische Untersuchungen Planen; Springer: Wiesbaden, Germany, 2020. [Google Scholar]
- Boßow-Thies, S.; Krol, B. Quantitative Forschung in Masterarbeiten; Springer: Wiesbaden, Germany, 2022. [Google Scholar]
- Wasserstein, R.L.; Schirm, A.L.; Lazar, N.A. Moving to a World Beyond “p < 0.05”. Am. Stat. 2019, 73, 1–19. [Google Scholar] [CrossRef]
- Albers, S. Methodik der Empirischen Forschung, 2nd ed.; Springer: Wiesbaden, Germany, 2007; ISBN 978-3-8349-0469-0. [Google Scholar]
- Liu, L.; Tamer Özsu, M. Encyclopedia of Database Systems; Springer: New York, NY, USA, 2009; ISBN 978-0-387-35544-3. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013. [Google Scholar]
- Paper, D. Hands-on Scikit-Learn for Machine Learning Applications: Data Science Fundamentals with Python, 1st ed.; Apress: Boston, MA, USA, 2019. [Google Scholar]
- Alhorn, K. Optimale Versuchsplanung für Model-Averaging Schätzer. Ph.D. Thesis, Technische Universität Dortmund, Dortmund, Germany, 2019. [Google Scholar]
- Gehrau, V.; Maubach, K.; Fujarski, S. Einfache Datenauswertung mit R; Springer: Wiesbaden, Germany, 2022. [Google Scholar]
- Bolón-Canedo, V.; Remeseiro, B. Feature selection in image analysis: A survey. Artif. Intell. Rev. 2020, 53, 2905–2931. [Google Scholar] [CrossRef]
- Kabir, H.; Garg, N. Machine learning enabled orthogonal camera goniometry for accurate and robust contact angle measurements. Sci. Rep. 2023, 13, 1497. [Google Scholar] [CrossRef] [PubMed]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Multivariate Statistical Machine Learning Methods for Genomic Prediction, 1st ed.; Springer International Publishing: Berlin/Heidelberg, Germany; Imprint Springer: Cham, Switzerland, 2022. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Statist. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trienens, D.; Schöppner, V.; Krause, P.; Bäck, T.; Tsi-Nda Lontsi, S.; Budde, F. Method Development for the Prediction of Melt Quality in the Extrusion Process. Polymers 2024, 16, 1197. https://doi.org/10.3390/polym16091197
Trienens D, Schöppner V, Krause P, Bäck T, Tsi-Nda Lontsi S, Budde F. Method Development for the Prediction of Melt Quality in the Extrusion Process. Polymers. 2024; 16(9):1197. https://doi.org/10.3390/polym16091197
Chicago/Turabian StyleTrienens, Dorte, Volker Schöppner, Peter Krause, Thomas Bäck, Seraphin Tsi-Nda Lontsi, and Finn Budde. 2024. "Method Development for the Prediction of Melt Quality in the Extrusion Process" Polymers 16, no. 9: 1197. https://doi.org/10.3390/polym16091197
APA StyleTrienens, D., Schöppner, V., Krause, P., Bäck, T., Tsi-Nda Lontsi, S., & Budde, F. (2024). Method Development for the Prediction of Melt Quality in the Extrusion Process. Polymers, 16(9), 1197. https://doi.org/10.3390/polym16091197







