Phase-Retrieval Algorithm for Hololens Resolution Analysis in a Sustainable Photopolymer
Abstract
1. Introduction
2. Materials and Methods
2.1. Photopolymer Preparation
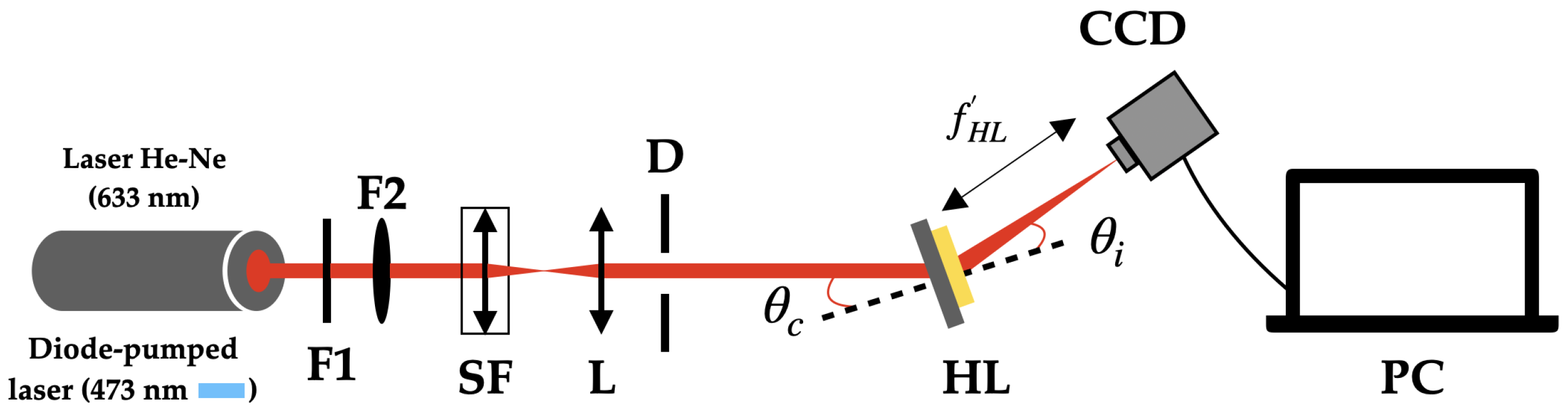
2.2. Holographic Experimental Setup for Writing and Reading
2.3. Experimental Setup to Analyze the Intensity Distribution in the Image Plane with a CCD Sensor
3. Computing Framework
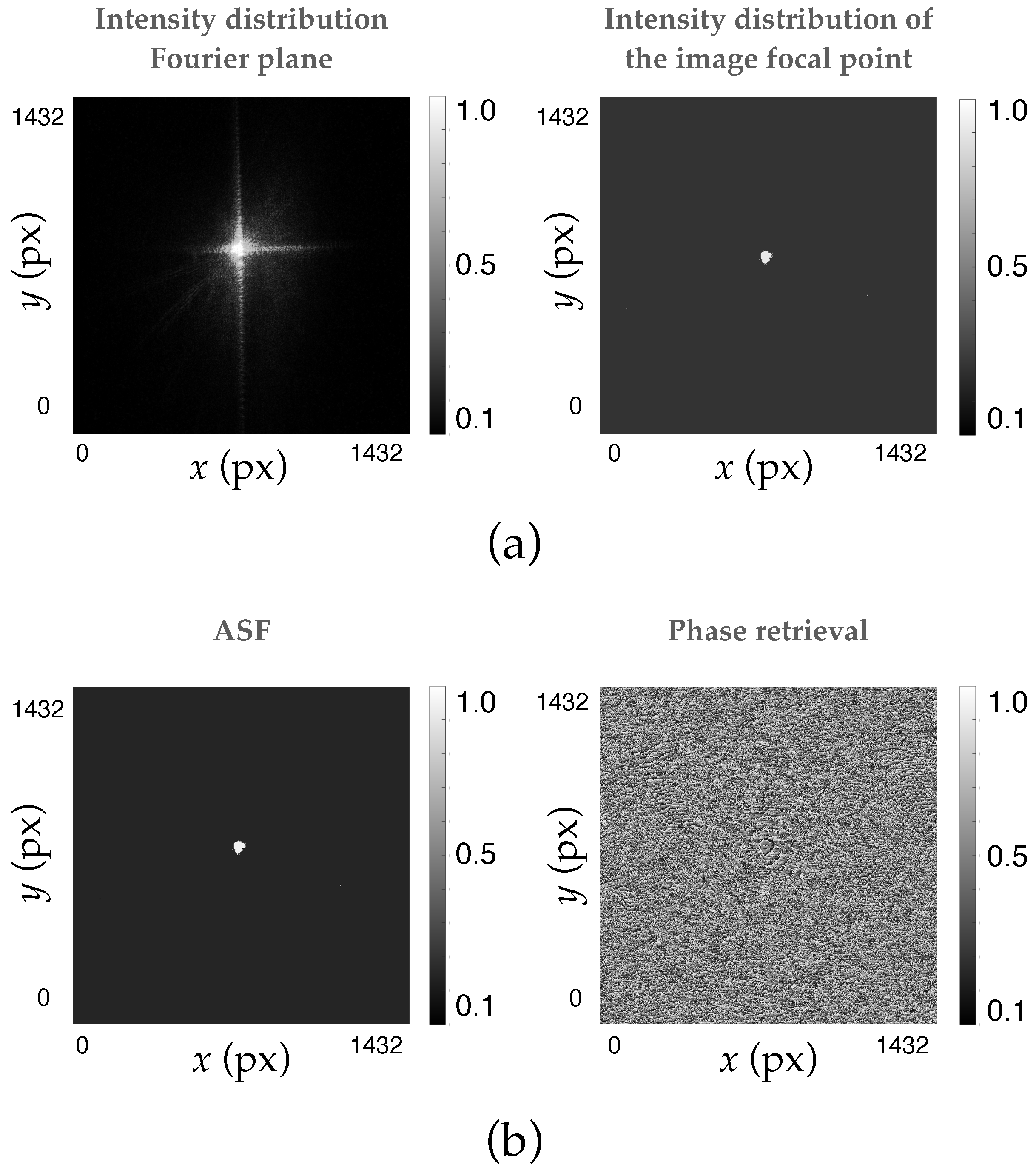
3.1. Convolution Theorem and Amplitude Spread Function
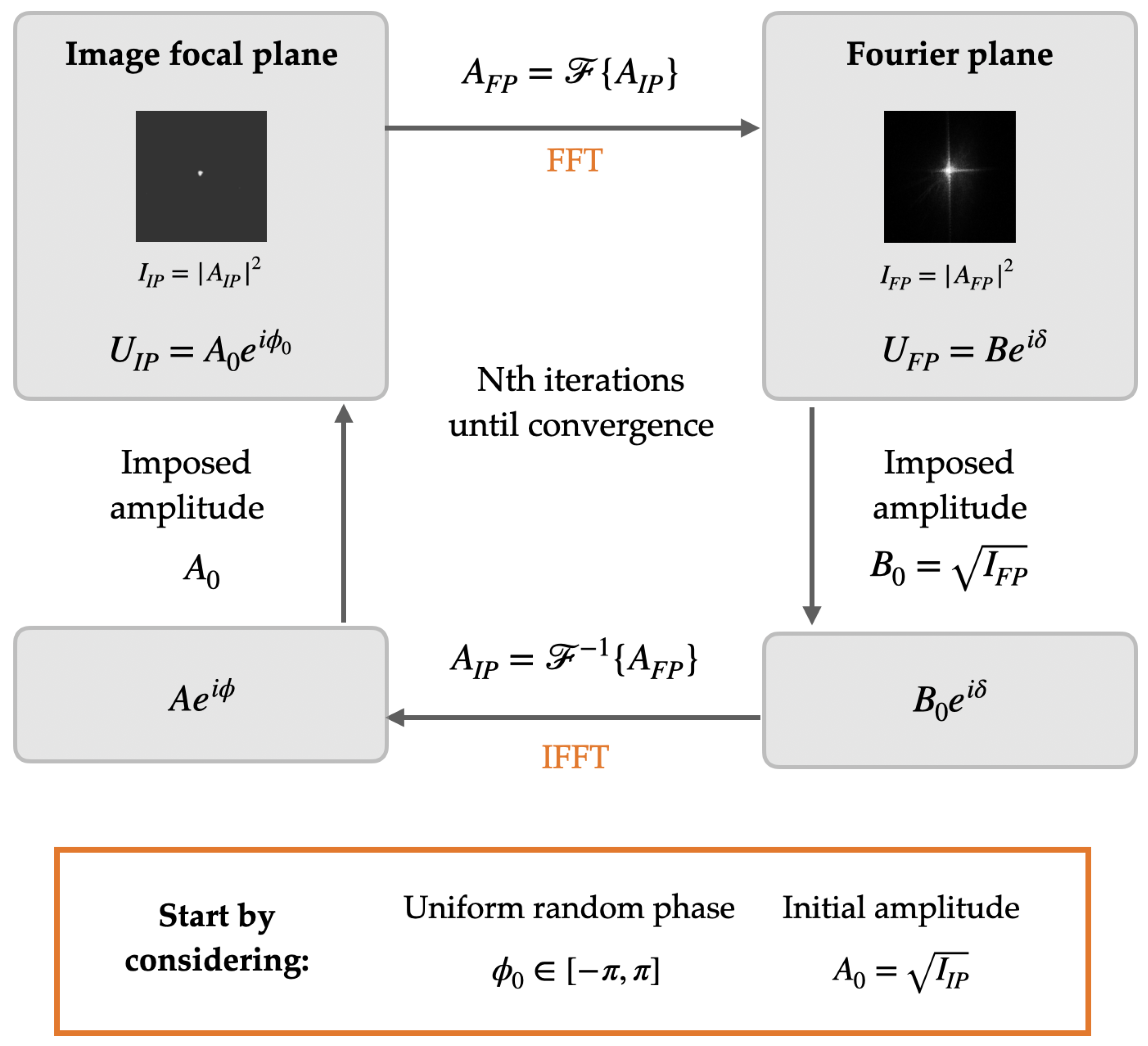
3.2. Gerchberg–Saxton (GS) Iterative Phase-Retrieval Algorithm
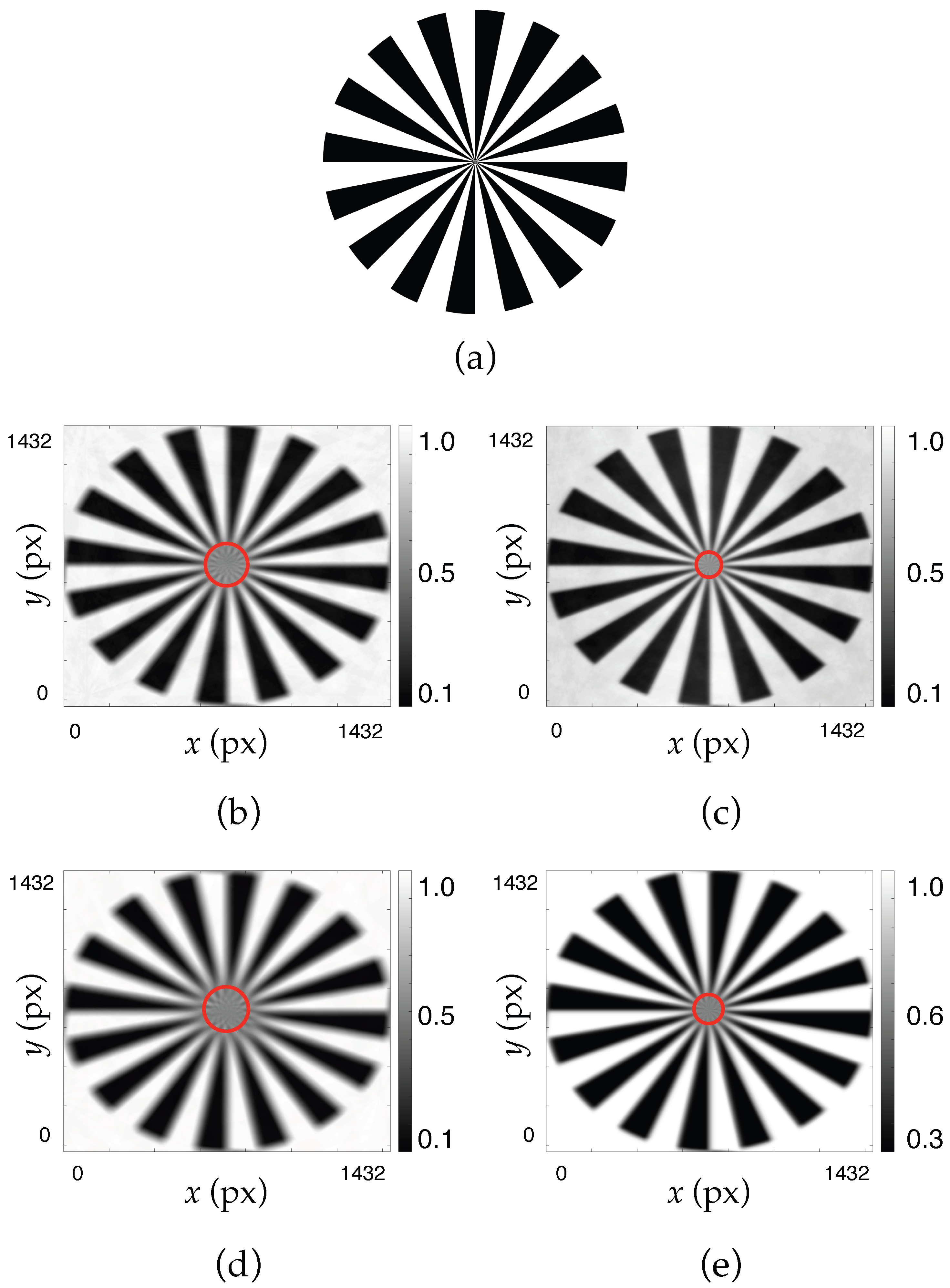
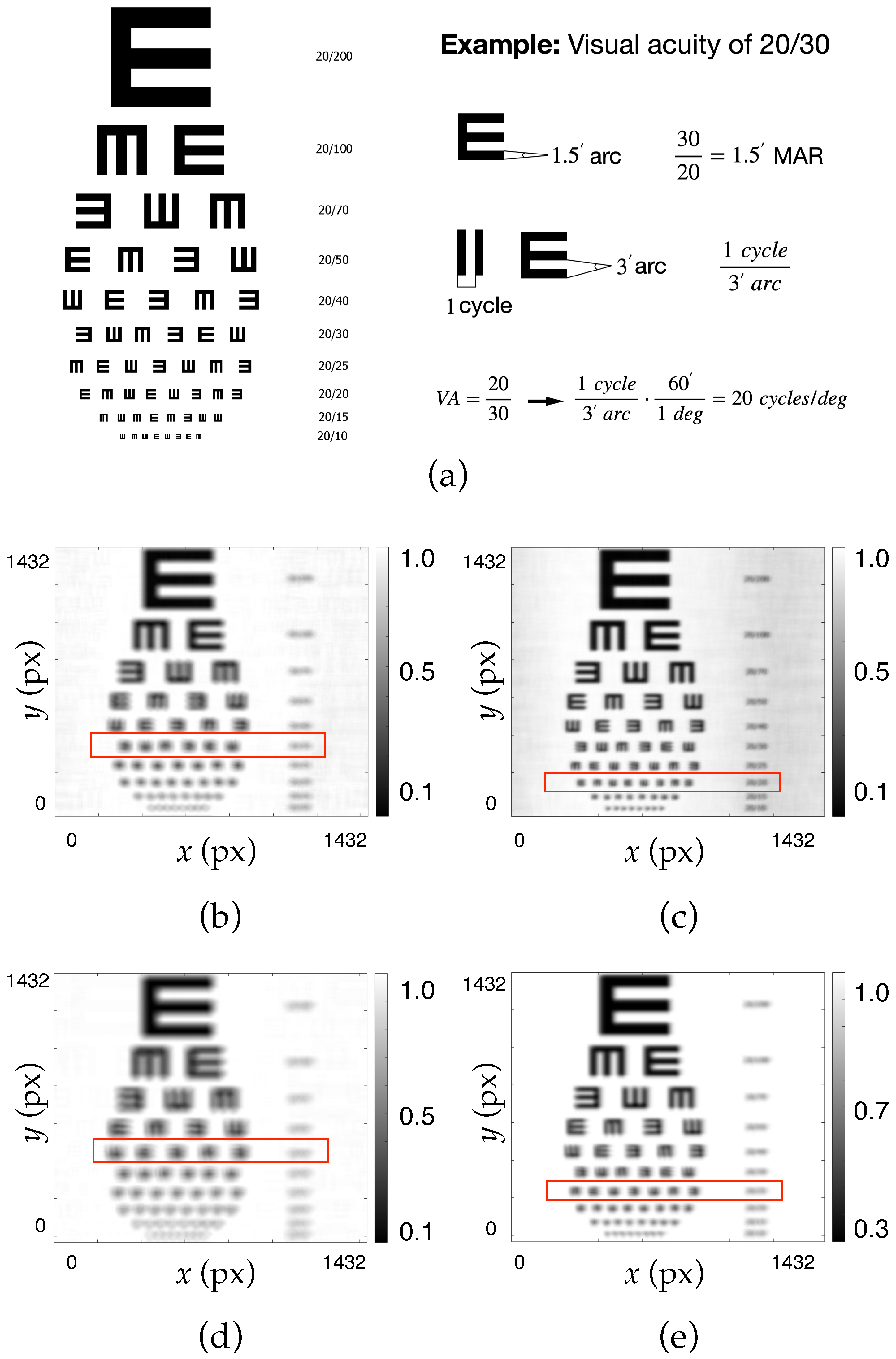
3.3. Resolution Using a Siemens Star Chart and a Visual Acuity Test
4. Results
4.1. Objective Evaluation of Optical Resolution Using the Siemens Star Chart
4.2. Perceptual Evaluation of Angular Resolution Capacity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| HL | Hololens |
| HOE | Holographic optical element |
| PVA | Polyvinyl alcohol |
| NaOA | Sodium acrylate |
| TEA | Triethanolamine |
| RF | Riboflavin -monophosphate sodium salt |
| GS | Gerchberg–Saxton iterative phase-retrieval algorithm |
| CCD | Charge-coupled device |
| CMOS | Complementary metal oxide semiconductor |
| ASF | Amplitude spread function |
| PSF | Point spread function |
| MTF | Modulation transfer function |
| VA | Visual acuity |
Appendix A. Relationship Between VA and Resolution for the Random E Chart Visual Acuity Test
| Visual Acuity (Snellen Fraction) | Spatial Resolution (c/deg) |
|---|---|
| 20/10 | 60 |
| 20/15 | 40 |
| 20/20 | 30 |
| 20/25 | 24 |
| 20/30 | 20 |
| 20/40 | 15 |
| 20/50 | 12 |
| 20/70 | 8.57 |
| 20/100 | 6 |
| 20/200 | 3 |
References
- Gabor, D. A New Microscopi Prinnciple. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef]
- Gabor, D. Microscopy by Reconstructed Wave Fronts: II. Proc. Phys. Soc. Sect. B 1951, 64, 449. [Google Scholar] [CrossRef]
- Gabor, D. Holography. 1948–1971. Nobel Lecture, The Nobel Foundation. 1971. Available online: https://www.nobelprize.org/prizes/physics/1971/gabor/lecture/ (accessed on 29 July 2025).
- Close, D.; Jacobson, A.; Margerum, J.; Brault, R.; McClung, F. Hologram recording on photopolymer materials. Appl. Phys. Lett. 1969, 14, 159–160. [Google Scholar] [CrossRef]
- Sheridan, J.T.; Kostuk, R.K.; Gil, A.F.; Wang, Y.; Lu, W.; Zhong, H.; Tomita, Y.; Neipp, C.; Francés, J.; Pascual, I.; et al. Roadmap on holography. J. Opt. 2020, 22, 123002. [Google Scholar] [CrossRef]
- Schwar, M.; Pandya, T.; Weinberg, F. Point holograms as optical elements. Nature 1967, 215, 239–241. [Google Scholar] [CrossRef]
- Denisyuk, Y.N. Photographic reconstruction of the optical properties of an object in its own scattered radiation field. Sov. Phys. Dokl. 1962, 7, 543. [Google Scholar]
- Kostuk, R.; Russo, J.; Zhang, D.; Castro, J.; Vorndran, S. Holographic Applications in Solar-Energy-Conversion Processes; SPIE: Philadelphia, PA, USA, 2016. [Google Scholar]
- Hariharan, P. Basics of Holography; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Syms, R.R.A. Practical Volume Holography; Oxford Engineering Science Series; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Kress, B.; Cummings, W. 11-1: Invited Paper: Towards the Ultimate Mixed Reality Experience: HoloLens Display Architecture Choices. SID Symp. Dig. Tech. Pap. 2017, 48, 127–131. [Google Scholar] [CrossRef]
- Tseng, E.; Kuo, G.; Baek, S.H.; Matsuda, N.; Maimone, A.; Schiffers, F.; Chakravarthy, P.; Fu, Q.; Heidrich, W.; Lanman, D.; et al. Neural étendue expander for ultra-wide-angle high-fidelity holographic display. Nat. Commun. 2024, 15, 2907. [Google Scholar] [CrossRef]
- Lin, W.K.; Matoba, O.; Lin, B.S.; Su, W.C. Astigmatism and deformation correction for a holographic head-mounted display with a wedge-shaped holographic waveguide. Appl. Opt. 2018, 57, 7094–7101. [Google Scholar] [CrossRef]
- Li, G.; Lee, D.; Jeong, Y.; Cho, J.; Lee, B. Holographic display for see-through augmented reality using mirror-lens holographic optical element. Opt. Lett. 2016, 41, 2486–2489. [Google Scholar] [CrossRef]
- Guo, H.; Xie, Y.; Lu, D.; Liao, Y.; Zhou, X.; Li, Z.; Peng, H.; Xie, X. Reliable Holographic Plastic for Augmented Reality Display. Adv. Opt. Mater. 2025, 13, 2500612. [Google Scholar] [CrossRef]
- Kaczorowski, A. Holography and Its Applications in Augmented Reality; Springer: Berlin/Heidelberg, Germany, 2025; pp. 1–39. [Google Scholar] [CrossRef]
- Haegel, N.; Verlinden, P.; Victoria, M.; Altermatt, P.; Atwater, H.; Barnes, T.; Case, C.; De Wolf, S.; Deline, C.; Dharmrin, M.; et al. Photovoltaics at multi-terawatt scale: Waiting is not an option. Science 2023, 380, 39–42. [Google Scholar] [CrossRef]
- Anctil, A.; Beattie, M.N.; Case, C.; Chaudhary, A.; Chrysler, B.D.; Debije, M.G.; Essig, S.; Ferry, D.K.; Ferry, V.E.; Freitag, M.; et al. Status report on emerging photovoltaics. J. Photonics Energy 2023, 13, 042301. [Google Scholar] [CrossRef]
- Lloret, T.; Morales-Vidal, M.; Nieto-Rodríguez, B.; García-Vázquez, J.C.; Beléndez, A.; Pascual, I. Building-Integrated Concentrating Photovoltaics based on a low-toxicity photopolymer. J. Phys. Energy 2024, 6, 015017. [Google Scholar] [CrossRef]
- Morales-Vidal, M.; Lloret, T.; Ramírez, M.G.; Beléndez, A.; Pascual, I. Green and wide acceptance angle solar concentrators. Opt. Express 2022, 30, 25366–25379. [Google Scholar] [CrossRef] [PubMed]
- Lloret, T.; Navarro-Fuster, V.; Ramírez, M.G.; Ortuño, M.; Neipp, C.; Beléndez, A.; Pascual, I. Holographic lenses in an environment-friendly photopolymer. Polymers 2018, 10, 302. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Cui, Y. Limit of resolution for holographic lenses. In Proceedings of the Holography, Diffractive Optics, and Applications, Shanghai, China, 15–17 October 2002; Volume 4924, pp. 39–45. [Google Scholar]
- Zhu, L.; Cui, Y. Abnormal phenomena in resolution limit of holographic lens. In Proceedings of the Applications of Photonic Technology 5, Shanghai, China, 15–17 October 2003; Volume 4833, pp. 342–347. [Google Scholar]
- Lloret, T.; Navarro-Fuster, V.; Ramirez, M.; Morales-Vidal, M.; Beléndez, A.; Pascual, I. Aberration-Based Quality Metrics in Holographic Lenses. Polymers 2020, 12, 993. [Google Scholar] [CrossRef]
- Yeom, J.; Jeong, J.; Hong, J.; Choi, K.s. Analysis on image quality of a holographic lens with a non-converging signal wave for compact near-eye displays. Opt. Express 2022, 30, 36632–36643. [Google Scholar] [CrossRef]
- Lloret, T.; Morales-Vidal, M.; Navarro-Fuster, V.; Ramirez, M.; Beléndez, A.; Pascual, I. Holographic Lens Resolution Using the Convolution Theorem. Polymers 2022, 14, 5426. [Google Scholar] [CrossRef]
- Lloret, T.; Navarro-Fuster, V.; Morales-Vidal, M.; Ramírez, M.G.; Márquez, A.; Beléndez, A.; Pascual, I. CCD and Hartmann-Shack wavefront sensor to analyse holographic lens resolution. In Proceedings of the Holography: Advances and Modern Trends VIII, Prague, Czech Republic, 24–25 April 2023; Volume 12574, p. 125740Z. [Google Scholar]
- Calixto, S.; Alfaro-Gomez, M. Dichromated Gelatin in Optics. Gels 2025, 11, 298. [Google Scholar] [CrossRef]
- Blanche, P.A. Holographic recording media and devices. In Optical Holography; Elsevier: Amsterdam, The Netherlands, 2020; pp. 41–60. [Google Scholar]
- Berramdane, K.; Lucío, M.I.; Ramírez, M.G.; Navarro-Fuster, V.; Bañuls, M.J.; Maquieira, Á.; Morales-Vidal, M.; Belendez, A.; Pascual, I. Storage Optimization of Transmission Holographic Gratings in Photohydrogels. ACS Appl. Mater. Interfaces 2024, 16, 48187–48202. [Google Scholar] [CrossRef] [PubMed]
- Friedman, M. Chemistry, Biochemistry, and Safety of Acrylamide. A Review. J. Agric. Food Chem. 2003, 51, 4504–4526. [Google Scholar] [CrossRef] [PubMed]
- Ortuño, M.; Fernández, E.; Gallego, S.; Beléndez, A.; Pascual, I. New photopolymer holographic recording material with sustainable design. Opt. Express 2007, 15, 12425–12435. [Google Scholar] [CrossRef]
- Ortuño, M.; Gallego, S.; Márquez, A.; Neipp, C.; Pascual, I.; Beléndez, A. Biophotopol: A Sustainable Photopolymer for Holographic Data Storage Applications. Materials 2012, 5, 772–783. [Google Scholar] [CrossRef] [PubMed]
- Champagne, E.B. Nonparaxial Imaging, Magnification, and Aberration Properties in Holography∗. J. Opt. Soc. Am. 1967, 57, 51–55. [Google Scholar] [CrossRef]
- Latta, J.N. Computer-Based Analysis of Hologram Imagery and Aberrations II: Aberrations Induced by a Wavelength Shift. Appl. Opt. 1971, 10, 609–618. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics; W. H. Freeman: New York, NY, USA, 2017. [Google Scholar]
- Mahajan, V.N. Aberration Theory Made Simple; SPIE Tutorial Texts; SPIE Optical Engineering Press: Philadelphia, PA, USA, 1991. [Google Scholar]
- Dubois, F.; Schockaert, C.; Callens, N.; Yourassowsky, C. Focus plane detection criteria in digital holography microscopy by amplitude analysis. Opt. Express 2006, 14, 5895–5908. [Google Scholar] [CrossRef]
- Gao, P.; Yao, B.; Rupp, R.; Min, J.; Guo, R.; Ma, B.; Zheng, J.; Lei, M.; Yan, S.; Dan, D.; et al. Autofocusing based on wavelength dependence of diffraction in two-wavelength digital holographic microscopy. Opt. Lett. 2012, 37, 1172–1174. [Google Scholar] [CrossRef]
- Hennelly, B.M.; Kelly, D.P.; Pandey, N.; Monaghan, D.S. Review of Twin Reduction and Twin Removal Techniques in Holography. In Proceedings of the China-Ireland Information and Communications Technologies Conference, Maynooth, Ireland, 19–21 August 2009. [Google Scholar]
- Gerchberg, R.W. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Perucho, B.; Micó, V. Wavefront holoscopy: Application of digital in-line holography for the inspection of engraved marks in progressive addition lenses. J. Biomed. Opt. 2014, 19, 016017. [Google Scholar] [CrossRef]
- Vila-Andrés, R.; Esteve-Taboada, J.J.; Micó, V. Soft Contact Lens Engraving Characterization by Wavefront Holoscopy. Sensors 2024, 24, 3492. [Google Scholar] [CrossRef]
- Merchán Price, M.S.; Acosta Yepes, N.F.; Gonzales Rodríguez, M.L.; Cortés Rodríguez, D.C. Snellen visual acuity versus spatial frequency of preferential looking test. Cienc. Tecnología Para Salud Vis. Ocul. 2010, 8, 117–127. [Google Scholar] [CrossRef]
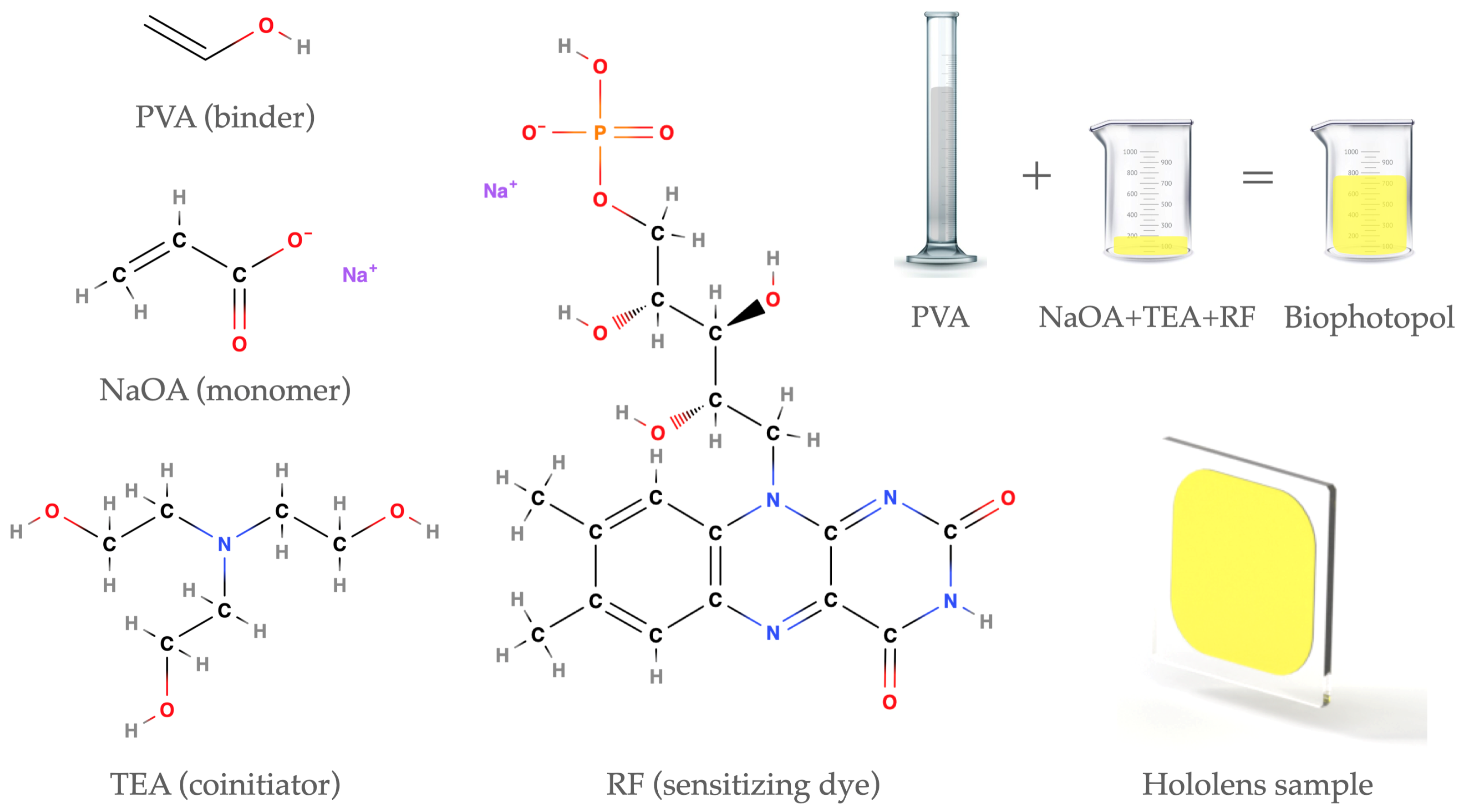


| PVA (wt/V %) | NaAO (M) | TEA (M) | RF (M) |
|---|---|---|---|
| 13.5 | 0.39 | 9.0 | 1.0 |
| Amplitude | |
| Intensity |
(nm) | (lp/mm) | Resolution Before GS (lp/mm) | Resolution After GS (lp/mm) |
|---|---|---|---|
| 473 | 67.7 | 4.9 | 8.8 |
| 633 | 68.2 | 4.5 | 8.1 |
(nm) | (c/deg) | Resolution Before GS (c/deg) | Resolution After GS (c/deg) |
|---|---|---|---|
| 473 | 110.7 | 20 | 30 |
| 633 | 82.7 | 15 | 24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lloret, T.; Navarro-Fuster, V.; Morales-Vidal, M.; Pascual, I. Phase-Retrieval Algorithm for Hololens Resolution Analysis in a Sustainable Photopolymer. Polymers 2025, 17, 2732. https://doi.org/10.3390/polym17202732
Lloret T, Navarro-Fuster V, Morales-Vidal M, Pascual I. Phase-Retrieval Algorithm for Hololens Resolution Analysis in a Sustainable Photopolymer. Polymers. 2025; 17(20):2732. https://doi.org/10.3390/polym17202732
Chicago/Turabian StyleLloret, Tomás, Víctor Navarro-Fuster, Marta Morales-Vidal, and Inmaculada Pascual. 2025. "Phase-Retrieval Algorithm for Hololens Resolution Analysis in a Sustainable Photopolymer" Polymers 17, no. 20: 2732. https://doi.org/10.3390/polym17202732
APA StyleLloret, T., Navarro-Fuster, V., Morales-Vidal, M., & Pascual, I. (2025). Phase-Retrieval Algorithm for Hololens Resolution Analysis in a Sustainable Photopolymer. Polymers, 17(20), 2732. https://doi.org/10.3390/polym17202732









