Investigation of Constitutive Models for Pressure Monitoring of Viscoelastic–Hyperelastic Composite Structures
Abstract
1. Introduction
2. Materials and Methods
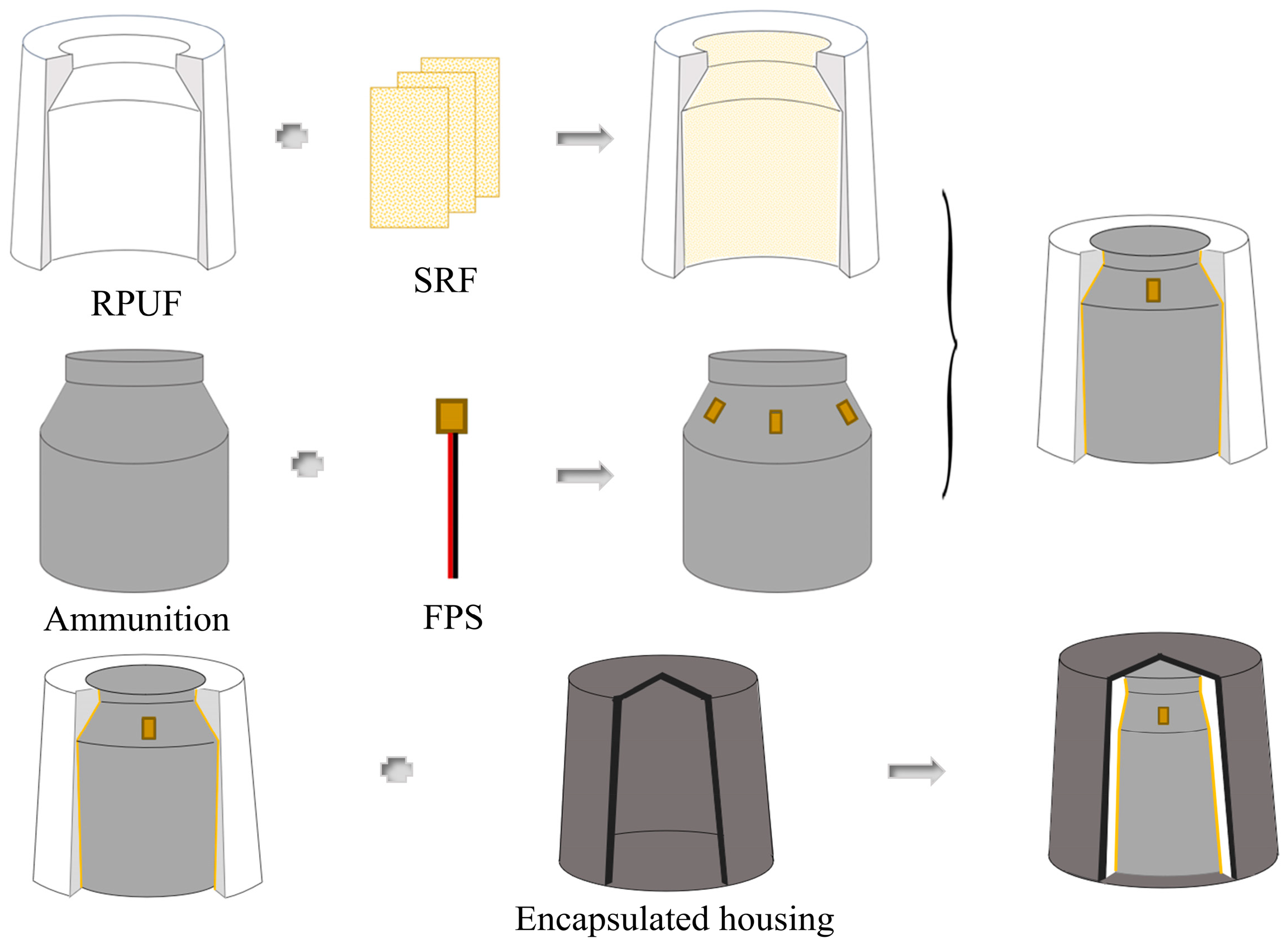
2.1. Materials
2.2. Experimental Methods
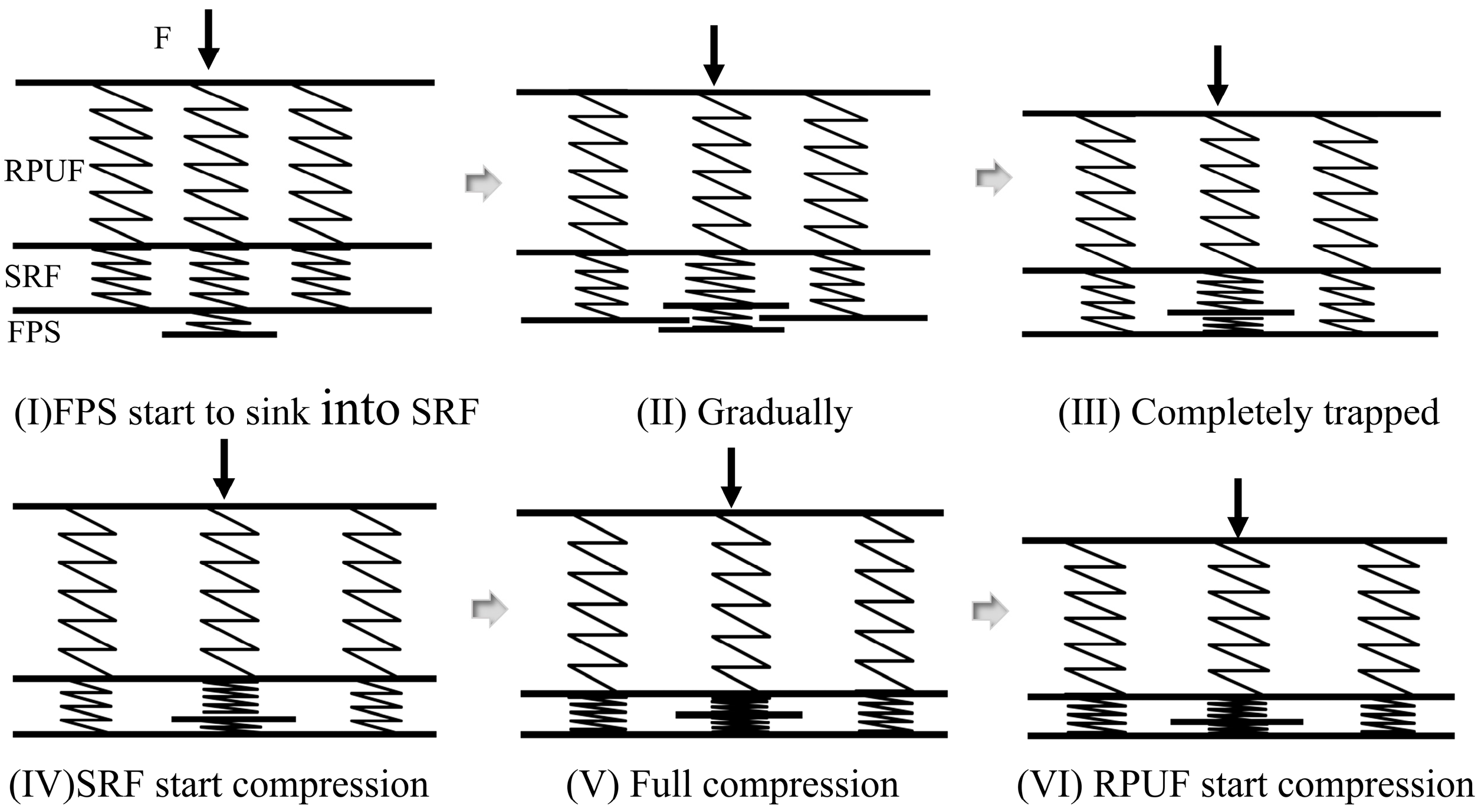
2.3. Stability of the FPS
3. Constitutive Model
3.1. Model Description
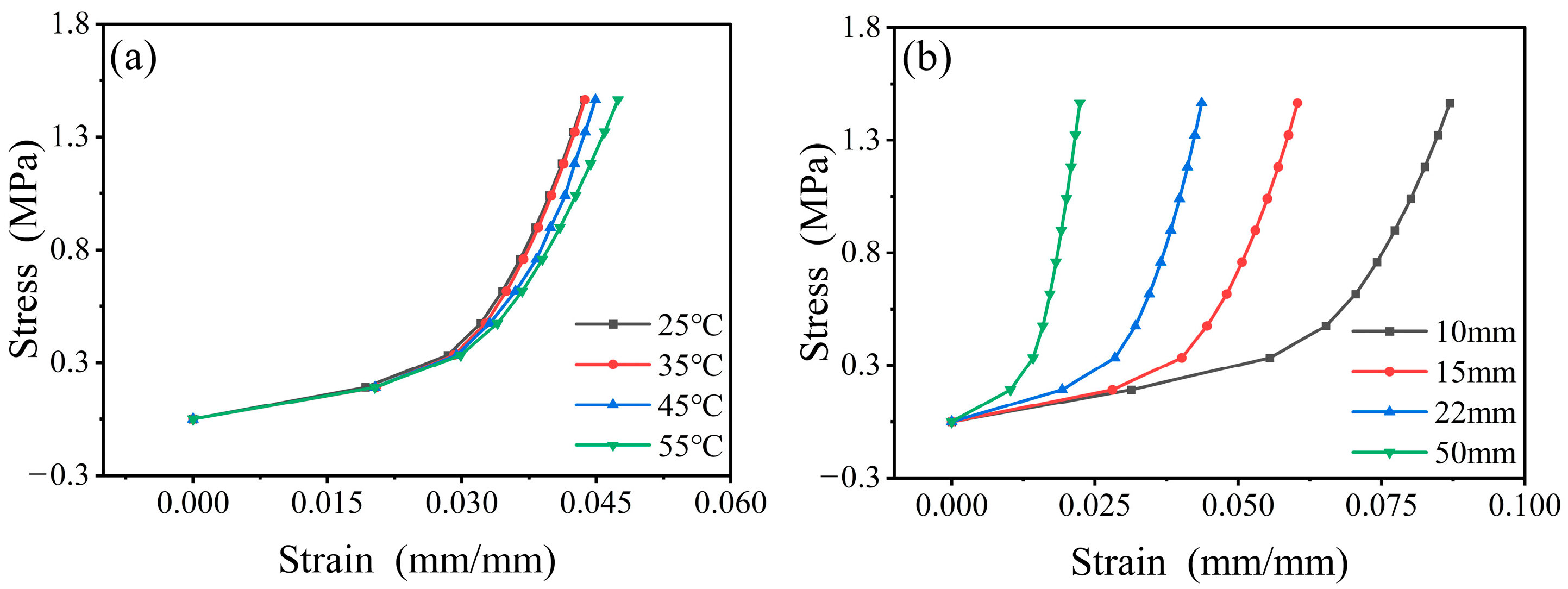
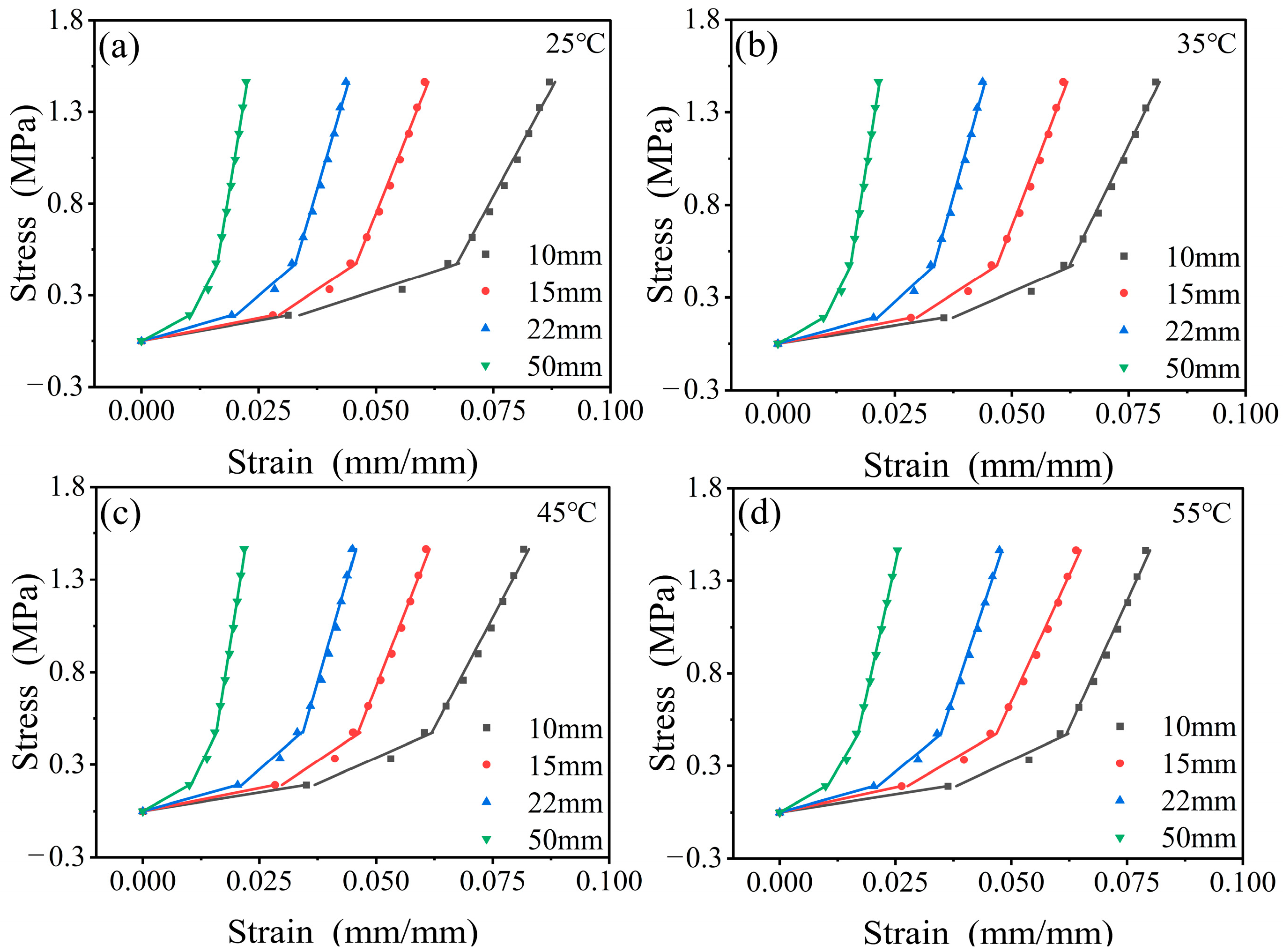
3.2. Parameter Determination
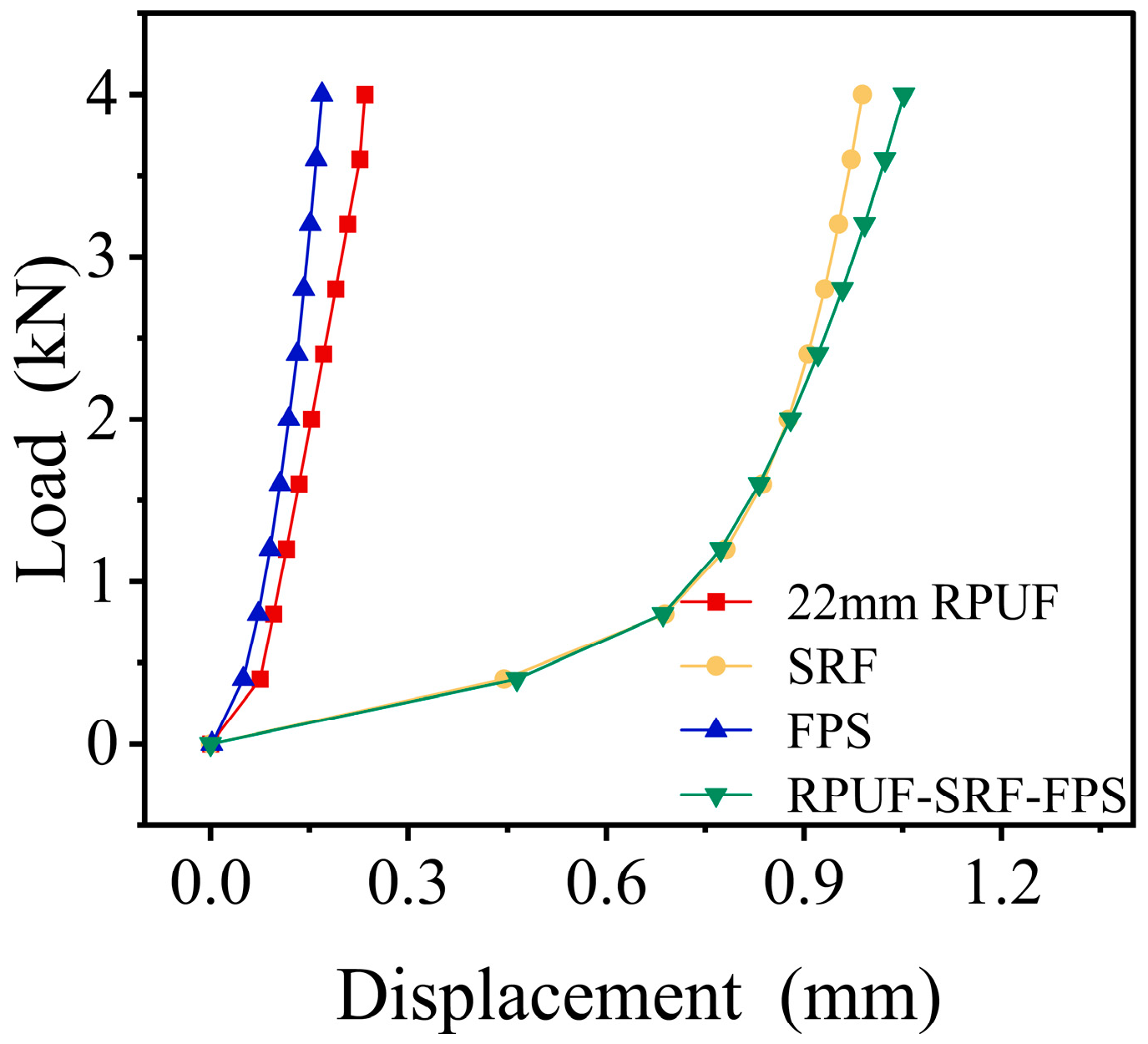
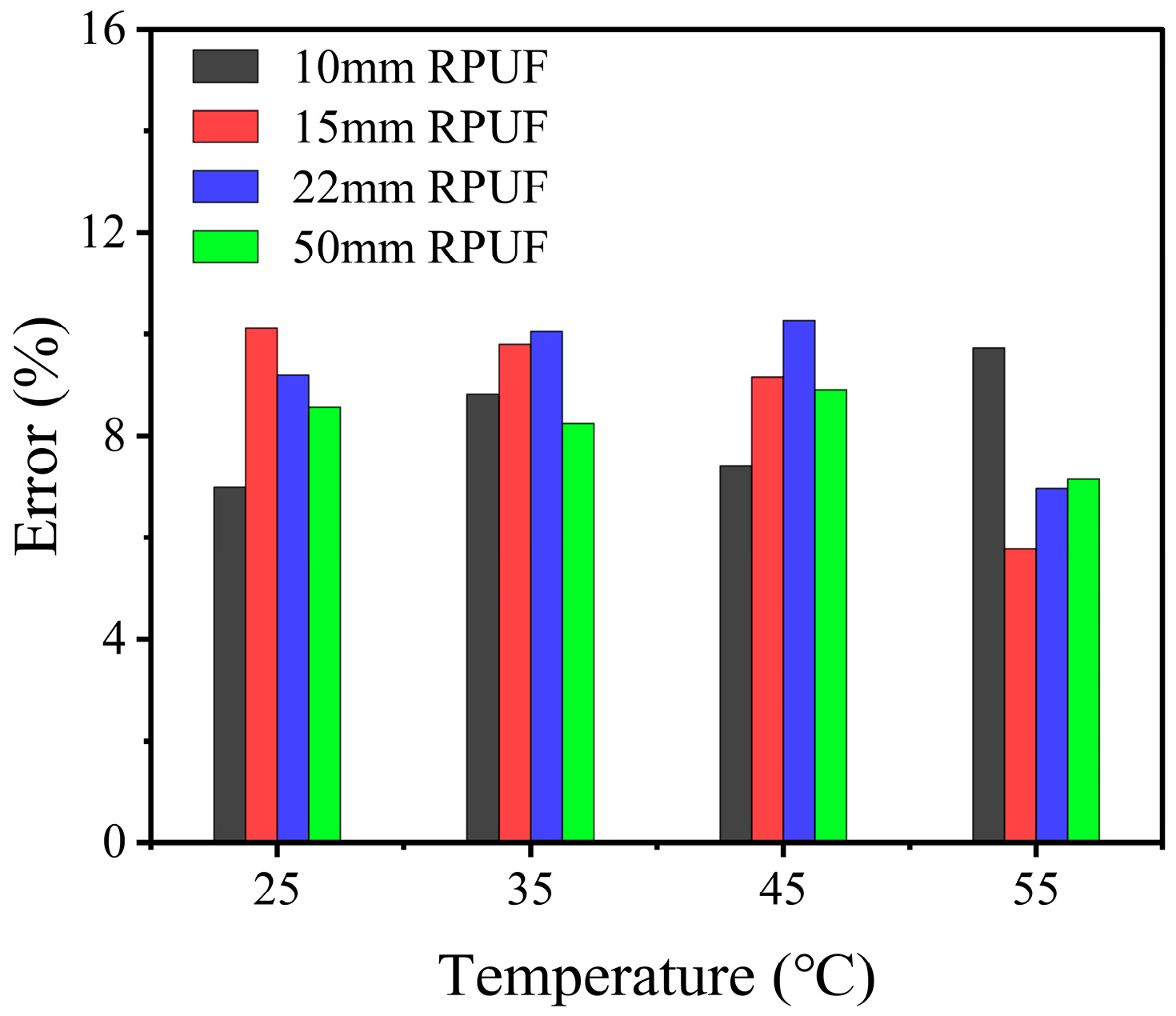
3.3. Model Verification
4. Application of Stress Monitoring Systems
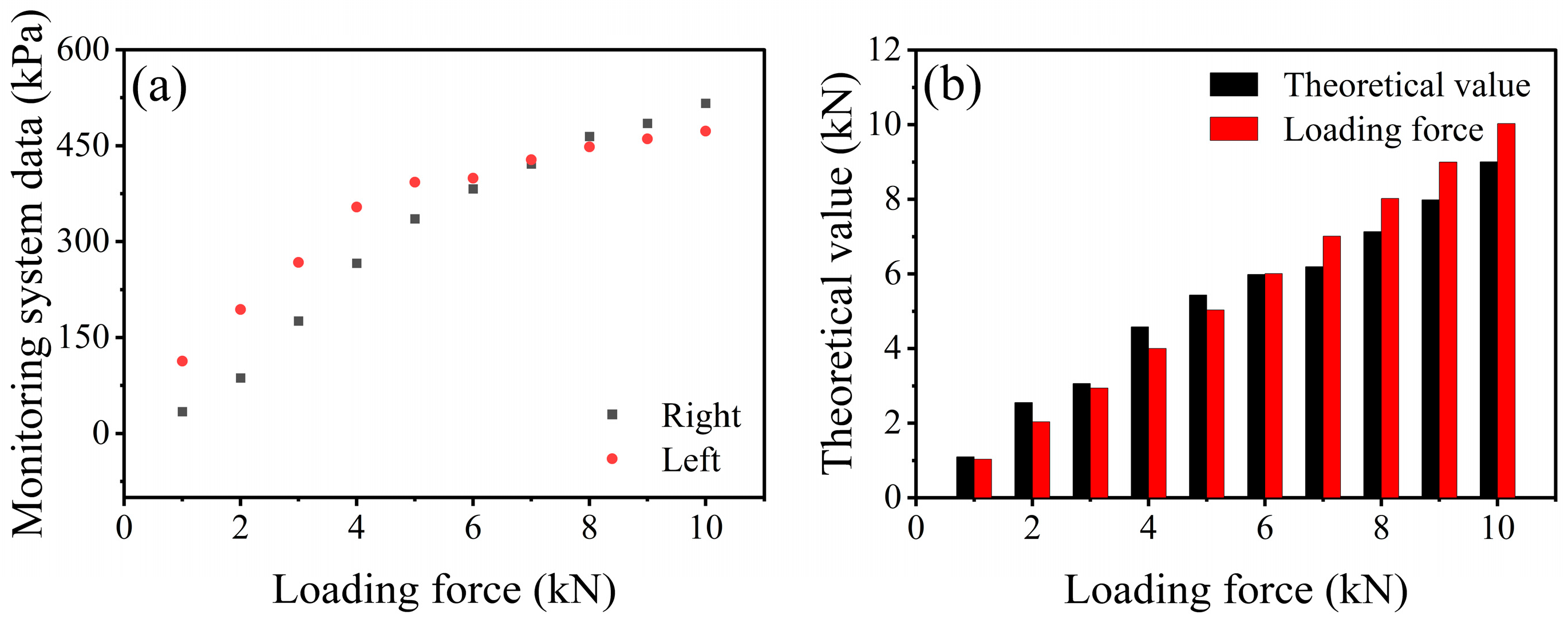
4.1. Analysis of Pressure Monitoring Results
4.2. Multi-Channel Pressure Monitoring System Applications
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
DURC Statement
- Explanation of Potential Risks: Our paper investigates the mechanical properties of viscoelastic–hyperelastic material composite structures. This study is confined to providing theoretical and experimental support for the development of multilayer polymer material composite structures and does not pose any threat to public health or national security.
- Evaluation of Benefits to the General Public: Our research is limited to the academic field, which is beneficial to the development of material science. There is no risk to the general public.
- Compliance With Laws: As an ethical responsibility, we strictly adhere to relevant national and international laws about dual-use research. And, we have considered and adhered to these regulations in our paper.
Conflicts of Interest
References
- Guo, X.; Cai, X.; Huo, Y.; Wang, H. Nuclear safety characterisation of PBX explosives under low-velocity impact conditions. Ann. Nucl. Energy 2025, 211, 110984. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Zou, G.; Dong, H.; Huo, Y. Pressure relief of underground ammunition storage under missile accidental ignition. Def. Technol. 2021, 17, 1081–1093. [Google Scholar] [CrossRef]
- Zan, Y.; Wang, H.; Zheng, Y.; Guo, H. Damage behavior of the KKV direct hit against fluid-filled submunition payload. Def. Technol. 2022, 18, 2052–2064. [Google Scholar] [CrossRef]
- Xiao, Y.; Pei, K.; Zou, Y.; Han, Y.; Gong, T.; Xiao, X.; Sun, Y. Dynamic damage and non-shock ignition behavior of polymer bonded explosive under lower velocity impact. Propellants Explos. Pyrotech. 2024, 49, 00016. [Google Scholar] [CrossRef]
- Akshay, D.; Marisol, K. Effect of particle proximity and surface properties on the response of PBX under vibration. Comput. Mater. Sci. 2021, 192, 11034. [Google Scholar] [CrossRef]
- Wang, L.; Kong, D.; Zhang, C. Research on the suppression method of sensor impact vibration parasitic effects in surface reflection pressure measurement. Rev. Sci. Instrum. 2024, 95, 015108. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Qiu, C.; Ni, L.; Ye, H.; Zou, H.; Luo, Y.; Liang, M. Cell structure control and performance of rigid polyurethane foam with lightweight, good mechanical, thermal insulation and sound insulation. Constr. Build. Mater. 2024, 447, 138068. [Google Scholar] [CrossRef]
- Wen, Y.; Lai, Z.; Ma, J.; Liu, H.; Wang, Y.; Chi, H.; Huang, R. A dynamic constitutive model for high-density rigid polyurethane foam subjected to impact loading. Constr. Build. Mater. 2023, 387, 131642. [Google Scholar] [CrossRef]
- Sun, M.; Wang, L.; Lu, H.; Xiong, Z.; Xie, M.; Xu, B. The Numerical Study on the Blast Resistance Performance of Protection Armor with I-Core Sandwich. Ijst T Civ. Eng. 2023, 48, 895–908. [Google Scholar] [CrossRef]
- Kerche, E.F.; Bock, D.N.; Delucis, R.A.; Magalhães, W.L.E.; Amico, S.C. Micro fibrillated cellulose reinforced bio-based rigid high-density polyurethane foams. Cellulose 2021, 28, 4313–4326. [Google Scholar] [CrossRef]
- Șerban, D.A.; Emanoil, L. Fatigue behaviour of closed-cell polyurethane rigid foams. Eng. Fail. Anal. 2023, 154, 107728. [Google Scholar] [CrossRef]
- Yang, Z.; Wen, J.; Zhang, G.; Tang, C.; Deng, Q.; Ling, J.; Hu, H. Mechanical Characteristics of Multi-Level 3D-Printed Silicone Foams. Materials 2024, 17, 4097. [Google Scholar] [CrossRef] [PubMed]
- Soydan, A.S.; Var, C. Assessment of a unique reinforcement construction on mechanical behaviour of composite structures. J. Text. Inst. 2024, 115, 341–349. [Google Scholar] [CrossRef]
- Cho, S.; Ma, J.; Yakimenko, O.A. Aerial multi-spectral AI-based detection system for unexploded ordnance. Def. Technol. 2023, 27, 24–37. [Google Scholar] [CrossRef]
- Hou, T.; Tong, J.; Wang, Y.; Cui, M.; Yan, Y.; Xin, Y. An overpressure monitoring system based on PVDF integrated electronic sensor with enhanced noise attenuation capability. Measurement 2024, 228, 114297. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhong, W.; Chen, J.; Luo, J. Compressive properties and energy absorption of rigid polyurethane foam. J. Phys. Conf. Ser. 2022, 2368, 1742–6596. [Google Scholar] [CrossRef]
- Klimm, W.; Kwok, K. Mechanism of resistance relaxation and hysteresis in viscoelastic piezoresistive polymer nanocomposites. Int. J. Mech. Mater. Des. 2022, 18, 769–783. [Google Scholar] [CrossRef]
- Xiao, Y.; Yin, J.; Zhang, X.; An, X.; Xiong, Y.; Sun, Y. Mechanical performance and cushioning energy absorption characteristics of rigid polyurethane foam at low and high strain rates. Polym. Test. 2022, 109, 107531. [Google Scholar] [CrossRef]
- Lu, F.; Gao, D. Quasi-static and Impact Responses of Multi-layered Corrugated Paperboard Cushion by Virtual Mass Method. Packag. Technol. Sci. 2014, 27, 867–881. [Google Scholar] [CrossRef]
- Ji, X.J.; Han, S.Y.; Zhang, H.H. A constitutive relation of hierarchical composite fibrous materials. Int. J. Fracture 2021, 229, 215–227. [Google Scholar] [CrossRef]
- Merzhievskii, A.L.; Voronin, S.M. Modeling of Shock-Wave Deformation of Polymethyl Metacrylate. Combust. Explos. Shock Waves 2012, 48, 226–235. [Google Scholar] [CrossRef]
- Popova, T.V.; Mayer, A.E.; Khishchenko, K.V. Evolution of shock compression pulses in polymethylmethacrylate and aluminum. J. Appl. Phys. 2018, 123, 235902. [Google Scholar] [CrossRef]
- Qian, C.; Liang, C.; He, Z.; Ji, W. Effect of Layer Thickness in Layered Aluminum Matrix Syntactic Foam. Materials 2019, 12, 4172. [Google Scholar] [CrossRef] [PubMed]
- Çıbıkçı, K.C.; Yaman, M. Experimental investigation of compressive behavior and vibration properties of layered hybrid foam formed by aluminum foam/EPS-filled syntactic foam. J. Mater. Sci. 2024, 59, 3636–3651. [Google Scholar] [CrossRef]
- Salehi, M.; Mirbagheri, S.M.H.; Ramiani, A.J. Experimental, Theoretical, and Numerical Investigations into the Compressive Behavior of Multi-layer Metallic Foam Filled Tubes. J. Mater. Eng. Perform. 2022, 31, 3723–3740. [Google Scholar] [CrossRef]
- Gupta, V.; Kidane, A. Designing density-graded cellular materials for tailored constitutive response. Compos. Part B Eng. 2024, 287, 111793. [Google Scholar] [CrossRef]
- Yang, J.; Chen, S.; Liu, X.; Lin, Z.; Yang, L.; Schröder, K.U.; Schmidt, R. Dynamic crushing behavior of multi-layered hybrid foam-filled composite graded lattice sandwich panels. Mech. Adv. Mater. Struc. 2022, 29, 6694–6704. [Google Scholar] [CrossRef]
- Hashin, Z. Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture Characteristics of Three Metals Subjected to Various Strains, Strain Rates, Temperatures and Pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Pathipaka, R.K.; Namala, K.K.; Sunkara, N.; Bandaru, C.R. Damage characterization of sandwich composites subjected to impact loading. J. Sandw. Struct. Mater. 2020, 22, 2125–2138. [Google Scholar] [CrossRef]
- Hu, W.; Wang, B.; Luo, B.; Bao, W.; Fan, H. Foam-Filled Double-Layer Woven Lattice Truss Sandwich Panels: Manufacturing, Testing and Composite Effects. Appl. Compos. Mater. 2023, 31, 313–327. [Google Scholar] [CrossRef]
- Iqbal, N.; Mubashar, A.; Ahmed, S.; Arif, N.; Din, E.U. Investigating relative density effects on quasi-static response of high-density Rigid Polyurethane Foam (RPUF). Mater. Today. Commun. 2022, 31, 103320. [Google Scholar] [CrossRef]
- Lou, W.; Xie, C.; Guan, X. Thermal-aging constitutive model for a silicone rubber foam under compression. Polym. Degrad. Stabil. 2022, 198, 109873. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, B.; Li, K.; Zhang, T.; Yang, X. A wide linearity range and high sensitivity flexible pressure sensor with hierarchical microstructures via laser marking. J. Mater. Chem. C. 2020, 8, 3088–3096. [Google Scholar] [CrossRef]
- Guo, Y.; Ji, M.; Fu, Y.; Pan, D.; Wang, X.; Kang, J. Cushioning energy absorption of composite layered structures including paper corrugation, paper honeycomb and expandable polyethylene. J. Strain. Anal. Eng. Des. 2019, 54, 176–191. [Google Scholar] [CrossRef]
- Burmister, D.M. The General Theory of Stresses and Displacements in Layered Soil Systems. II. J. Appl. Phys. 1945, 16, 126–127. [Google Scholar] [CrossRef]
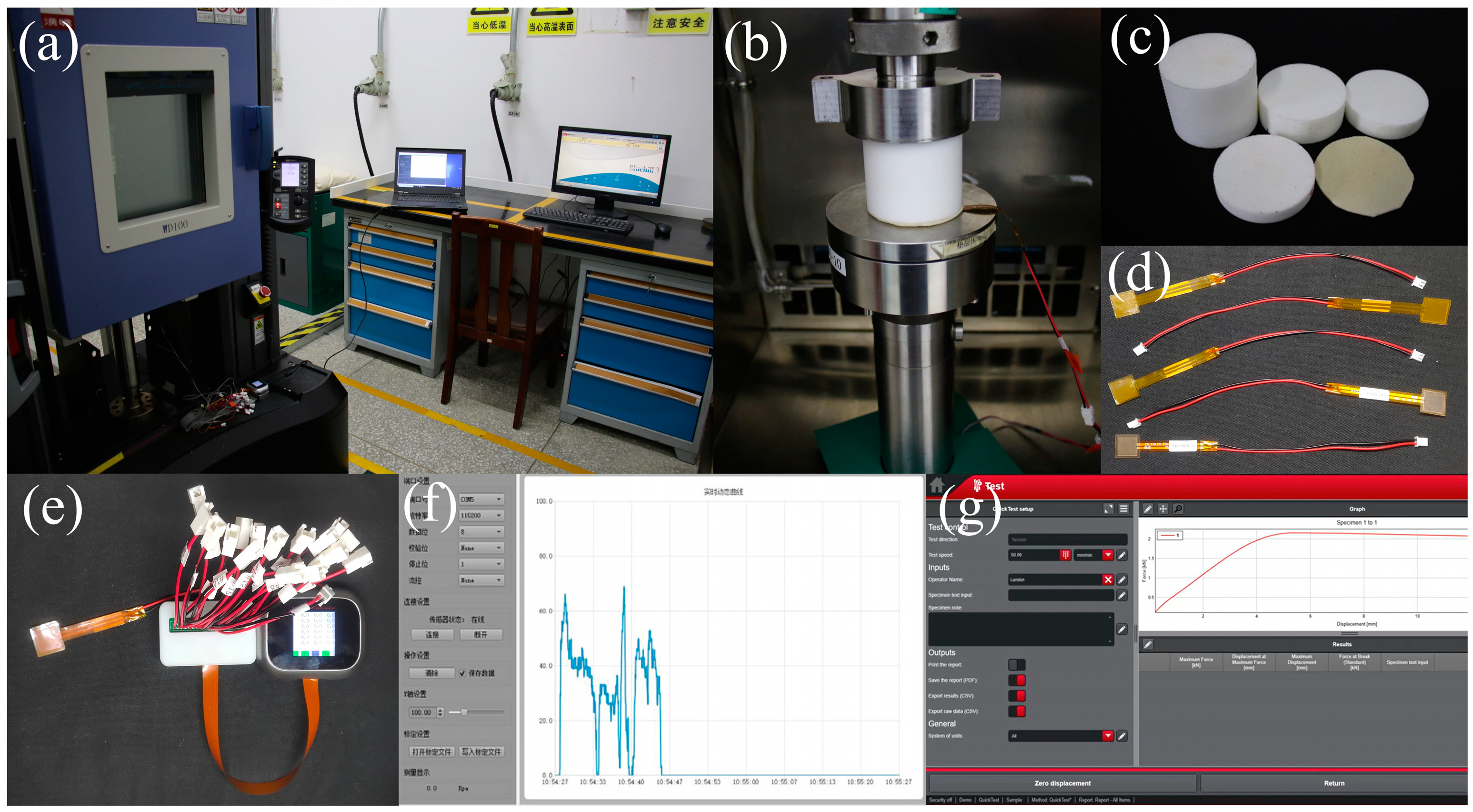




| Style Number | Thickness (mm) | Diameter (mm) |
|---|---|---|
| 1 | 10 | 60 |
| 2 | 15 | 60 |
| 3 | 22 | 60 |
| 4 | 50 | 60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, L.; Li, P.; Yuan, H.; Tian, C.; Qiang, X.; Fu, T. Investigation of Constitutive Models for Pressure Monitoring of Viscoelastic–Hyperelastic Composite Structures. Polymers 2025, 17, 647. https://doi.org/10.3390/polym17050647
Ai L, Li P, Yuan H, Tian C, Qiang X, Fu T. Investigation of Constitutive Models for Pressure Monitoring of Viscoelastic–Hyperelastic Composite Structures. Polymers. 2025; 17(5):647. https://doi.org/10.3390/polym17050647
Chicago/Turabian StyleAi, Lijia, Peng Li, Hongwei Yuan, Chunrong Tian, Xiaolian Qiang, and Tao Fu. 2025. "Investigation of Constitutive Models for Pressure Monitoring of Viscoelastic–Hyperelastic Composite Structures" Polymers 17, no. 5: 647. https://doi.org/10.3390/polym17050647
APA StyleAi, L., Li, P., Yuan, H., Tian, C., Qiang, X., & Fu, T. (2025). Investigation of Constitutive Models for Pressure Monitoring of Viscoelastic–Hyperelastic Composite Structures. Polymers, 17(5), 647. https://doi.org/10.3390/polym17050647







