The Role of Polyisobutylene-Bis-Succinimide (PIBSI) Dispersants in Lubricant Oils on the Deposit Control Mechanism
Abstract
:1. Introduction
2. Materials and Methods
2.1. Molecular Modeling Methods
2.1.1. Density Functional Theory Calculations
2.1.2. All-Atom MD Simulations
2.1.3. Insoluble Sludge Nanoparticle Model
2.1.4. Validation of Computational Method and Force Field Approach
2.1.5. All-Atom Molecular Dynamics Simulation Procedure
2.2. Coarse-Grained MD Simulations
2.2.1. Construction of the Coarse-Grained Models
2.2.2. Coarse-Grained Simulation Procedure
3. Results and Discussion
3.1. Density Functional Theory Calculation Results
3.2. Solubility Parameter Calculations
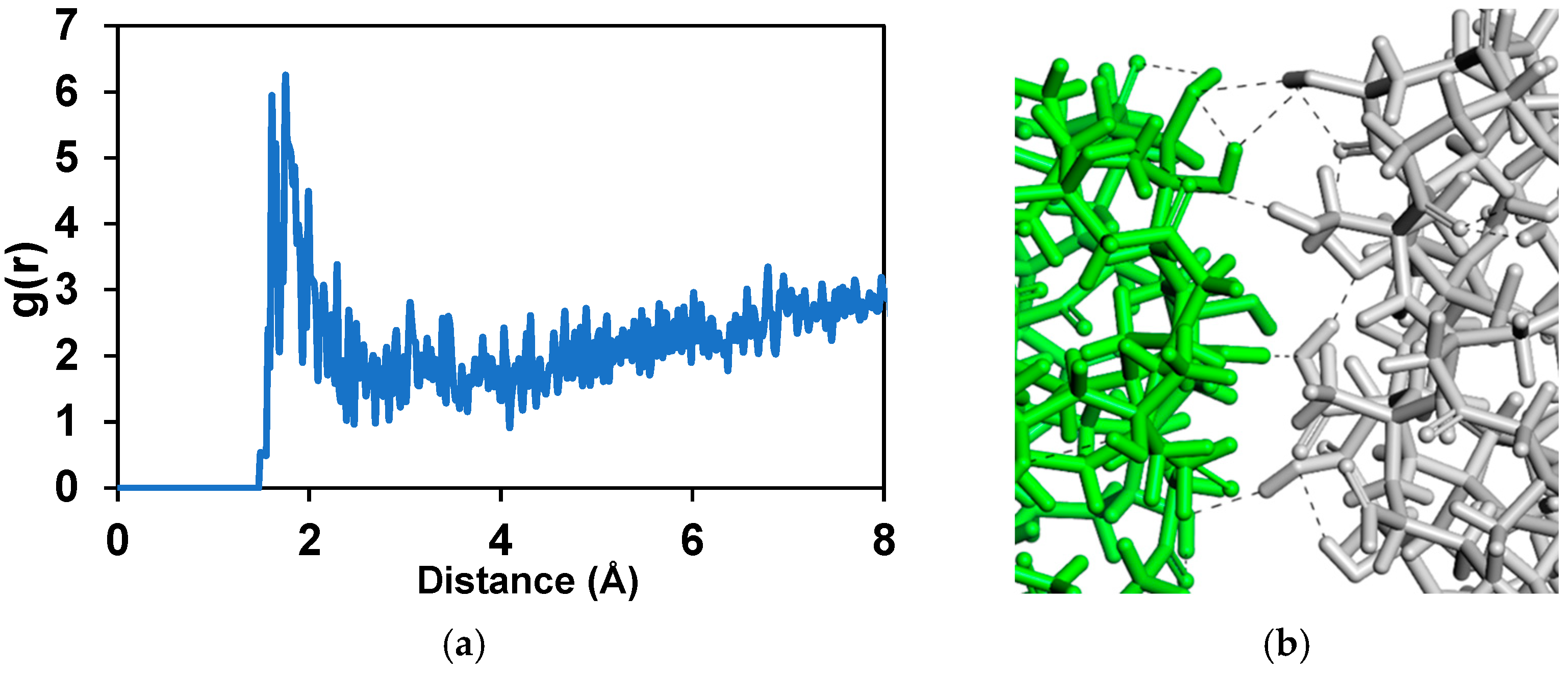
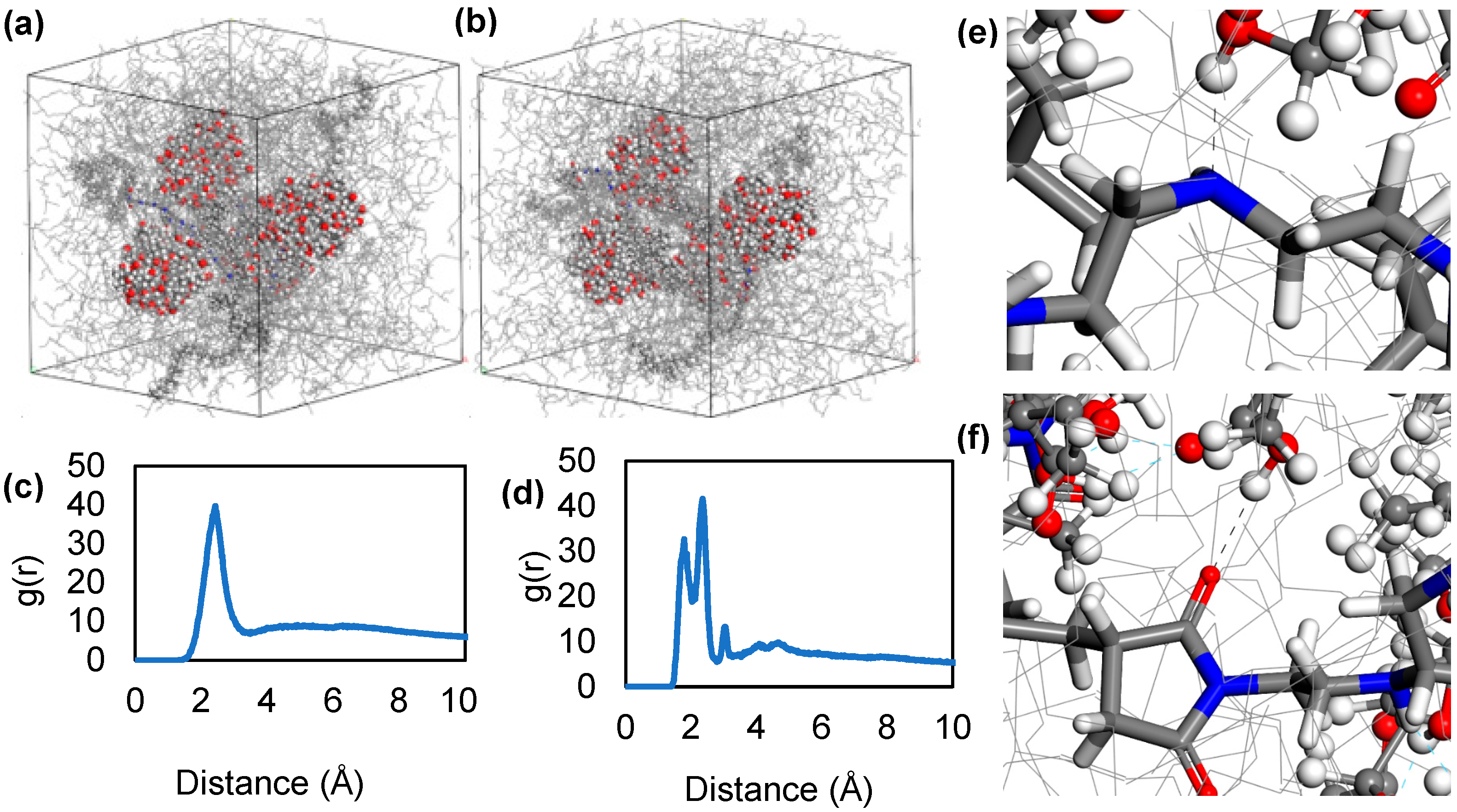
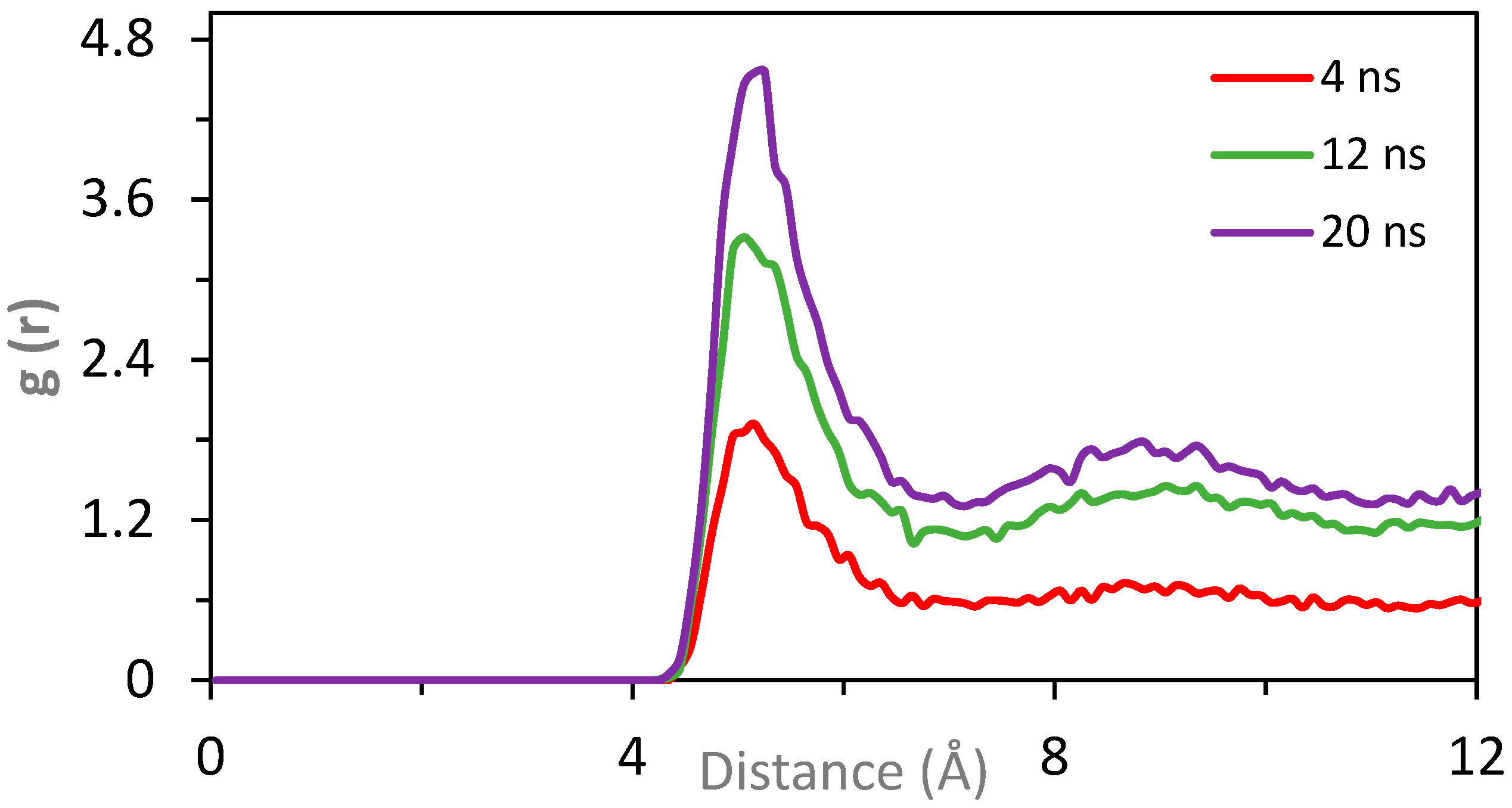
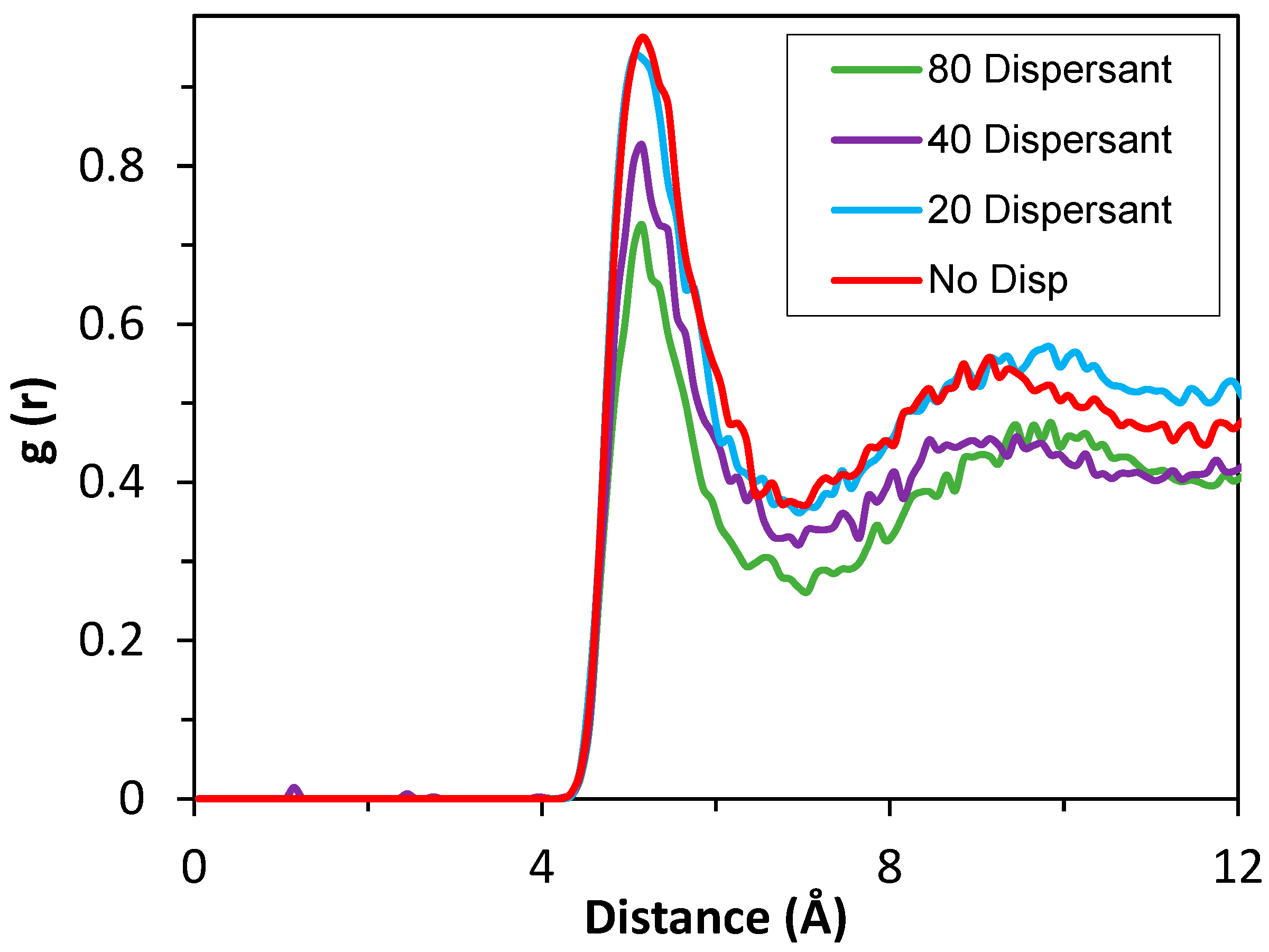
3.3. Molecular Dynamics Simulations
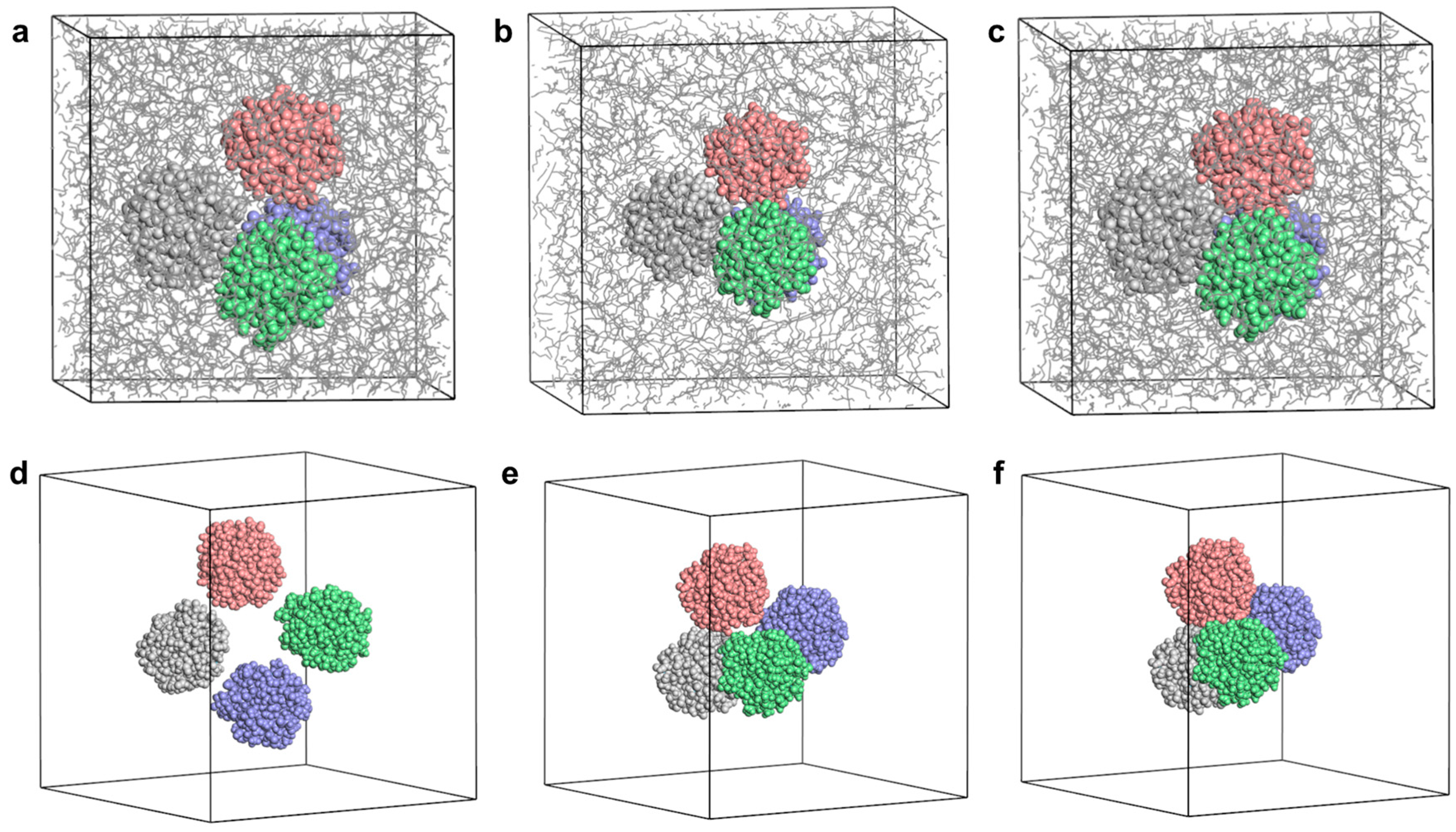
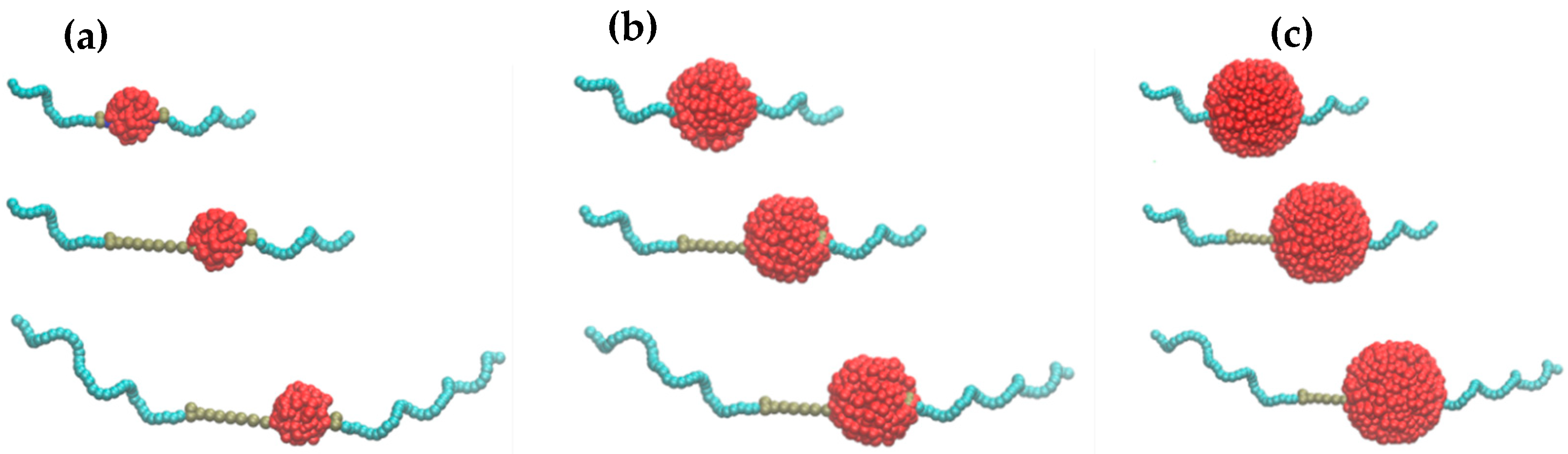
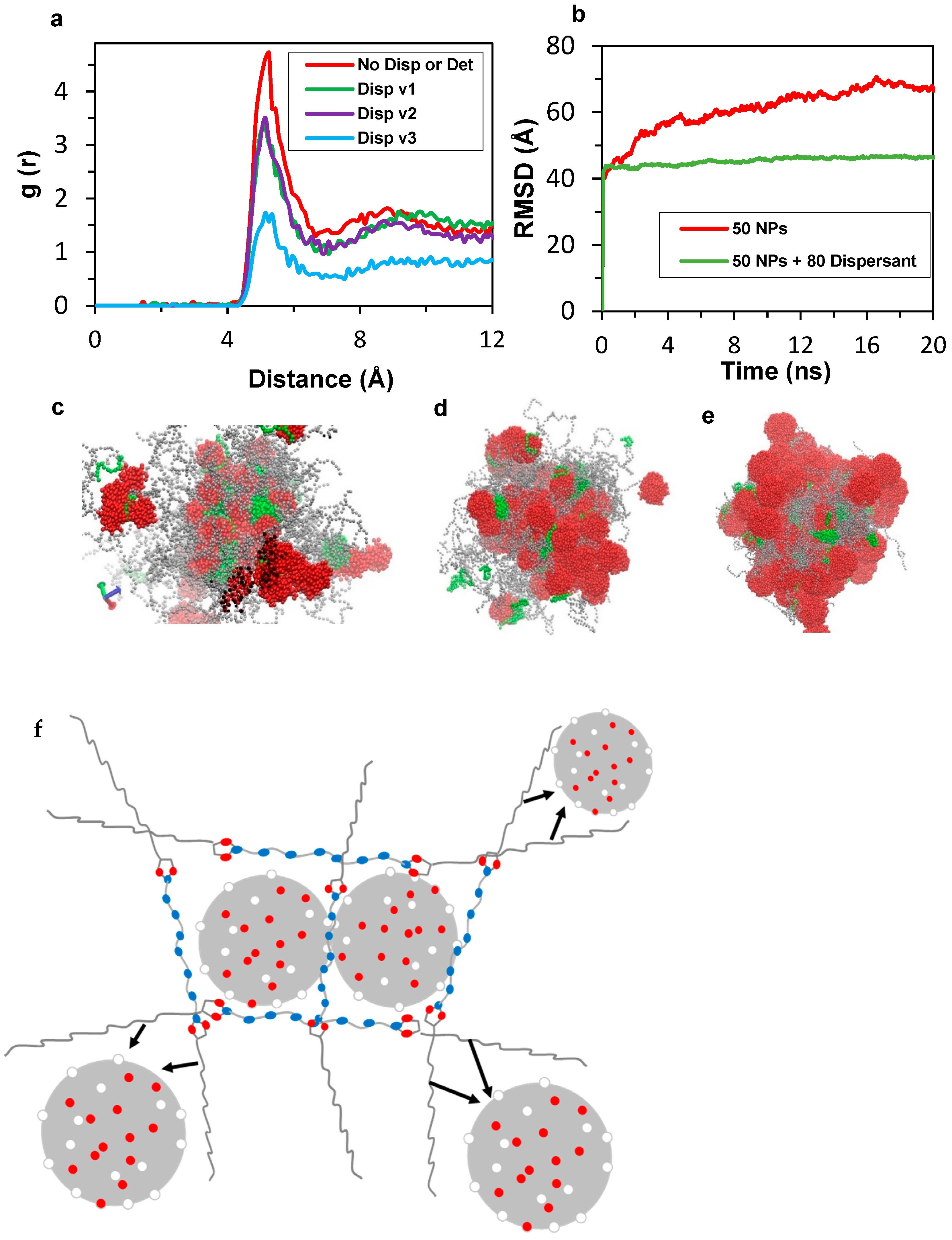
3.4. Coarse-Grained (CG) Simulations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PIBSI | Polyisobutylene–bis-succinimide |
| DFT | Density functional theory |
| MD | Molecular dynamics |
| CG | Coarse-grained |
| PIB | Polyisobutylene |
| PCFF | Polymer consistent force field |
| LJ | Lennard–Jones |
| PPPM | Particle–particle mesh solver |
| PBC | Periodic boundary condition |
| ESP | Electrostatic potential surface |
| SASA | Solvent accessible surface area |
| TPSA | Total polar surface area |
| TASA | Total apolar surface area |
| RPSA | Relative polar surface area |
| RASA | Relative apolar surface area |
| RDF | Radial pair distribution function |
References
- Herguth, W.R.; Warne, T.M. Turbine Lubrication in the 21st Century; ASTM International: West Conshohocken, PA, USA, 2001. [Google Scholar] [CrossRef]
- Brown, S.F. Base Oil Groups: Manufacture, Properties, and Performance. Tribol. Lubr. Technol. 2015, 71, 32–35. [Google Scholar]
- Havet, L.; Blouet, J.; Robbe Valloire, F.; Brasseur, E.; Slomka, D. Tribological Characteristics of Some Environmentally Friendly Lubricants. Wear 2001, 248, 140–146. [Google Scholar] [CrossRef]
- Rizvi, A.; Syed, Q. Lubricant Additives: Chemistry and Applications; Rudnick, L., Ed.; CRC Press: New York, NY, USA, 2010; ISBN 1420059653. [Google Scholar]
- Seddon, E.J.; Friend, C.L.; Roski, J.P. Detergents and Dispersants. In Chemistry and Technology of Lubricants; Springer: Amsterdam, The Netherlands, 1997; pp. 213–236. [Google Scholar]
- Kunc, J.F., Jr.; Hamer, J.P. Hamer Lubricants—The Surface Savers. SAE Trans. 1953, 61, 378–385. [Google Scholar]
- Smiechowski, M.F.; Lvovich, V.F. Characterization of Non-Aqueous Dispersions of Carbon Black Nanoparticles by Electrochemical Impedance Spectroscopy. J. Electroanal. Chem. 2005, 577, 67–78. [Google Scholar] [CrossRef]
- Smith, G.W. Kinetic Aspects of Diesel Soot Coagulation. In Soot in Combustion Systems and Its Toxic Properties; NATO Conference Series; Lahaye, J., Prado, G., Eds.; Springer: Boston, MA, USA, 1983; Volume 7, pp. 163–170. [Google Scholar] [CrossRef]
- Lashkhi, V.L.; Leimeter, T.; Nemsadze, G.G.; Smirnov, K.Y.; Shor, G.I.; Evseev, A.A. Theoretical Principles of Lube Oil Qualimetry. Chem. Technol. Fuels Oils 2003, 39, 197–200. [Google Scholar] [CrossRef]
- Dörr, N.; Agocs, A.; Besser, C.; Ristić, A.; Frauscher, M. Engine Oils in the Field: A Comprehensive Chemical Assessment of Engine Oil Degradation in a Passenger Car. Tribol. Lett. 2019, 67, 68. [Google Scholar] [CrossRef]
- Singh, A.K.; Singh, R.K. A Search for Ecofriendly Detergent/Dispersant Additives for Vegetable-Oil Based Lubricants. J. Surfactants Deterg. 2012, 15, 399–409. [Google Scholar] [CrossRef]
- Burrington, J.D.; Pudelski, J.K.; Roski, J.P. Challenges in Detergents and Dispersants for Engine Oils. In Practical Advances in Petroleum Processing; Hsu, C.S., Robinson, P.R., Eds.; Springer: New York, NY, USA, 2006; pp. 579–595. ISBN 978-0-387-25789-1. [Google Scholar]
- Ahmed, N.S.; Nassar, A.M. Lubricating Oil Additives Based on Polyalkylpolyamines. Int. J. Polym. Mater. Polym. Biomater. 2009, 58, 178–190. [Google Scholar] [CrossRef]
- Pawlak, Z. Role of Detergent & Dispersant. In Tribochemistry of Lubricating Oils; Elsevier: Amsterdam, The Netherlands, 2003; p. 25. [Google Scholar]
- Colyer, C.C.; Gergel, W.C. Detergents/Dispersants. In Chemistry and Technology of Lubricants; Mortier, R.M., Orszulik, S.T., Eds.; Springer: Boston, MA, USA, 1992; pp. 62–82. ISBN 978-1-4615-3272-9. [Google Scholar]
- Sarpal, A.S.; Sastry, M.I.S.; Bansal, V.; Singh, I.; Mazumdar, S.K.; Basu, B. Correlation of Structure and Properties of Groups I to III Base Oils. Lubr. Sci. 2012, 24, 199–215. [Google Scholar] [CrossRef]
- Menon, A.; Gupta, C.; Perkins, K.M.; Decost, B.L.; Budwal, N.; Rios, R.T.; Zhang, K.; Póczos, B.; Washburn, N.R. Elucidating Multi-Physics Interactions in Suspensions for the Design of Polymeric Dispersants: A Hierarchical Machine Learning Approach. Mol. Syst. Des. Eng. 2017, 2, 263–273. [Google Scholar] [CrossRef]
- Dimkovski, Z.; Bååth, L.; Rosén, S.; Ohlsson, R.; Rosén, B.G. Interference Measurements of Deposits on Cylinder Liner Surfaces. Wear 2011, 270, 247–251. [Google Scholar] [CrossRef]
- Ahmed, N.S.; Nassar, A.M.; Abdel-Azim, A.A.A. Synthesis and Evaluation of Some Detergent/Dispersant Additives for Lube Oil. Int. J. Polym. Mater. Polym. Biomater. 2008, 57, 114–124. [Google Scholar] [CrossRef]
- Abramo, G.P.; Blain, D.A.; Cardis, A.B. Modified Succinimides as Dispersants and Detergents and Lubricant and Fuel Compositions Containing Same. US5486301A, 23 January 1996. [Google Scholar]
- Tomlinson, A.; Danks, T.N.; Heyes, D.M.; Taylor, S.E.; Moreton, D.J. Interfacial Characterization of Succinimide Surfactants. Langmuir 1997, 13, 5881–5893. [Google Scholar] [CrossRef]
- Nassar, A.M.; Ahmed, N.S.; Abd El-Aziz, K.I.; Abdel Azim, A.A.A.; El-Kafrawy, A.F. Synthesis and Evaluation of Detergent/Dispersant Additives from Polyisobutylene Succinimides. Int. J. Polym. Mater. Polym. Biomater. 2006, 55, 703–713. [Google Scholar] [CrossRef]
- Pirouz, S.; Wang, Y.; Chong, J.M.; Duhamel, J. Chemical Modification of Polyisobutylene Succinimide Dispersants and Characterization of Their Associative Properties. J. Phys. Chem. B 2015, 119, 12202–12211. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Yu, S.; Feng, J.; Liu, S. Multifunctional Lubricant Additive Derived from Polyisobutylene Succinimide Dispersant. J. Dispers. Sci. Technol. 2021, 42, 396–406. [Google Scholar] [CrossRef]
- Özdemir, E.; Kan, E.; Guo, B.; Pashkovski, E.; Agiral, A.; Yildirim, E. Multiscale Modeling Approach to Understand Mechanism of Deposit Control by Sulfonate-Based Lubricant Detergents. ACS Omega 2024, 9, 38753–38768. [Google Scholar] [CrossRef]
- Ke-Cheng, W.; Dong-Yun, L.; Han, Z.; Wei, X.; Hao, W.; Zhi-Hong, X. Mesoscale Simulation for Succinimide Dispersant Systems. Acta Phys. Chim. Sin. 2004, 20, 602–607. [Google Scholar] [CrossRef]
- Tsagkaropoulou, G.; Warrens, C.P.; Camp, P.J. Interactions between Friction Modifiers and Dispersants in Lubricants: The Case of Glycerol Monooleate and Polyisobutylsuccinimide-Polyamine. ACS Appl. Mater. Interfaces 2019, 11, 28359–28369. [Google Scholar] [CrossRef]
- Zhang, W.; Du, Y.; Gao, Z.; Yu, F.; He, Y.-P. Recyclable Multifunctional PSOGs for Rapid Removal of Wastewater Pollutants (Oily and Dye). Adv. Mater. Interfaces 2025, 12, 2400525. [Google Scholar] [CrossRef]
- Shen, Y.; Duhamel, J. Micellization and Adsorption of a Series of Succinimide Dispersants. Langmuir 2008, 24, 10665–10673. [Google Scholar] [CrossRef] [PubMed]
- Benmansour, M.; Afanasiev, P.; Galipaud, J.; Vacher, B.; Trillaud, V.; Joly-Pottuz, L.; Dassenoy, F. Influence of a Succinimide Dispersant on the Tribological Performance of MoS2 Nanoparticles. Tribol. Lett. 2023, 72, 15. [Google Scholar] [CrossRef]
- Shi, J.; Yi, X.; Wang, J.; Jin, G.; Lu, Y.; Wu, H.; Fan, X. Carbonaceous Soot Dispersion Characteristic and Mechanism in Lubricant with Effect of Dispersants by Molecular Dynamics Simulation and Experimental Studies. Carbon N. Y. 2022, 200, 253–263. [Google Scholar] [CrossRef]
- Rudnick, L.R. Lubricant Additives: Chemistry and Applications. In Lubricant Additives: Chemistry and Applications, 3rd ed.; CRC Press: New York, NY, USA, 2018; pp. 1–694. ISBN 9781498731744. [Google Scholar]
- Ghose, A.K.; Crippen, G.M. Atomic Physicochemical Parameters for Three-Dimensional Structure-Directed Quantitative Structure-Activity Relationships I. Partition Coefficients as a Measure of Hydrophobicity. J. Comput. Chem. 1986, 7, 565–577. [Google Scholar] [CrossRef]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; De Vries, A.H. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef]
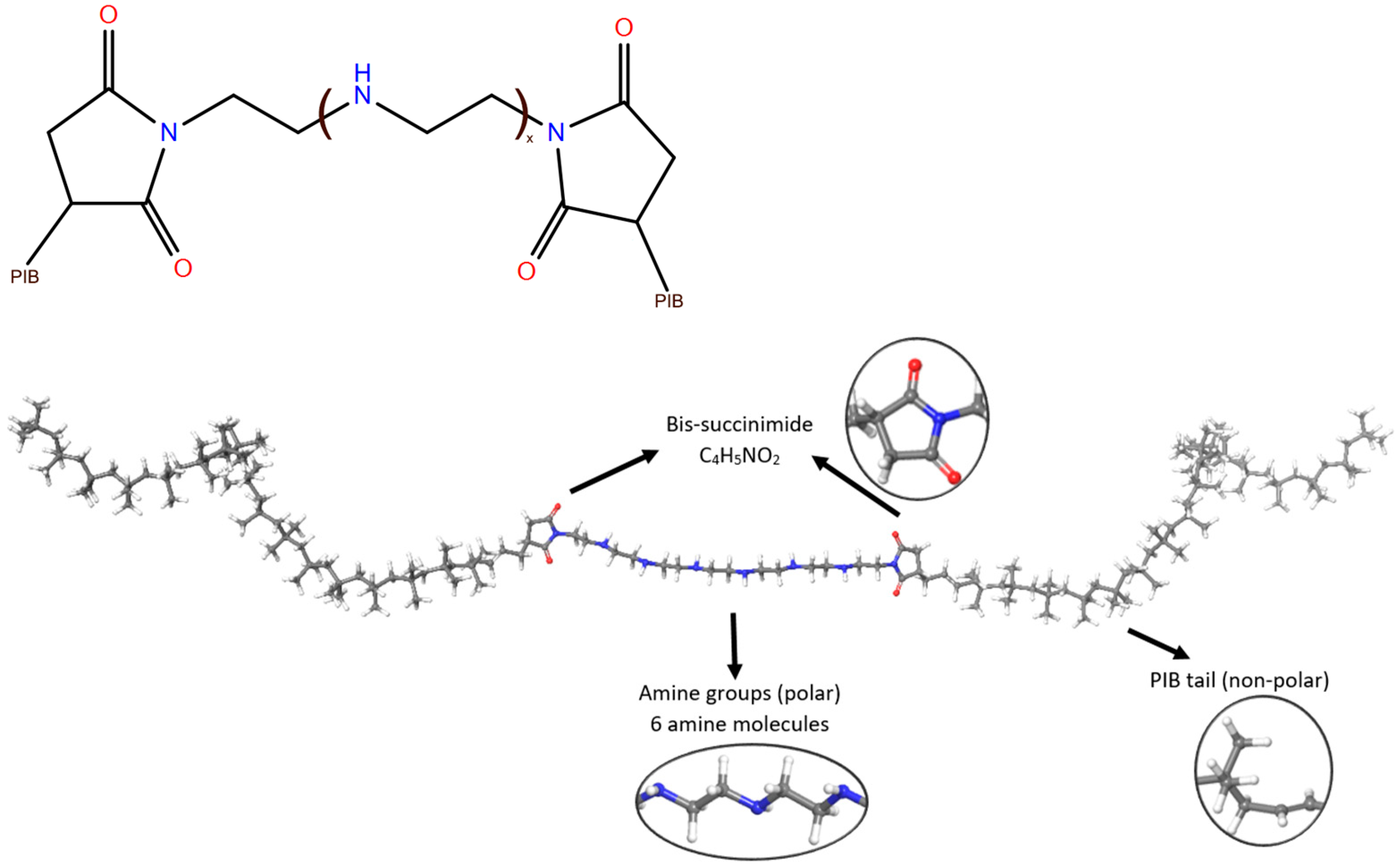



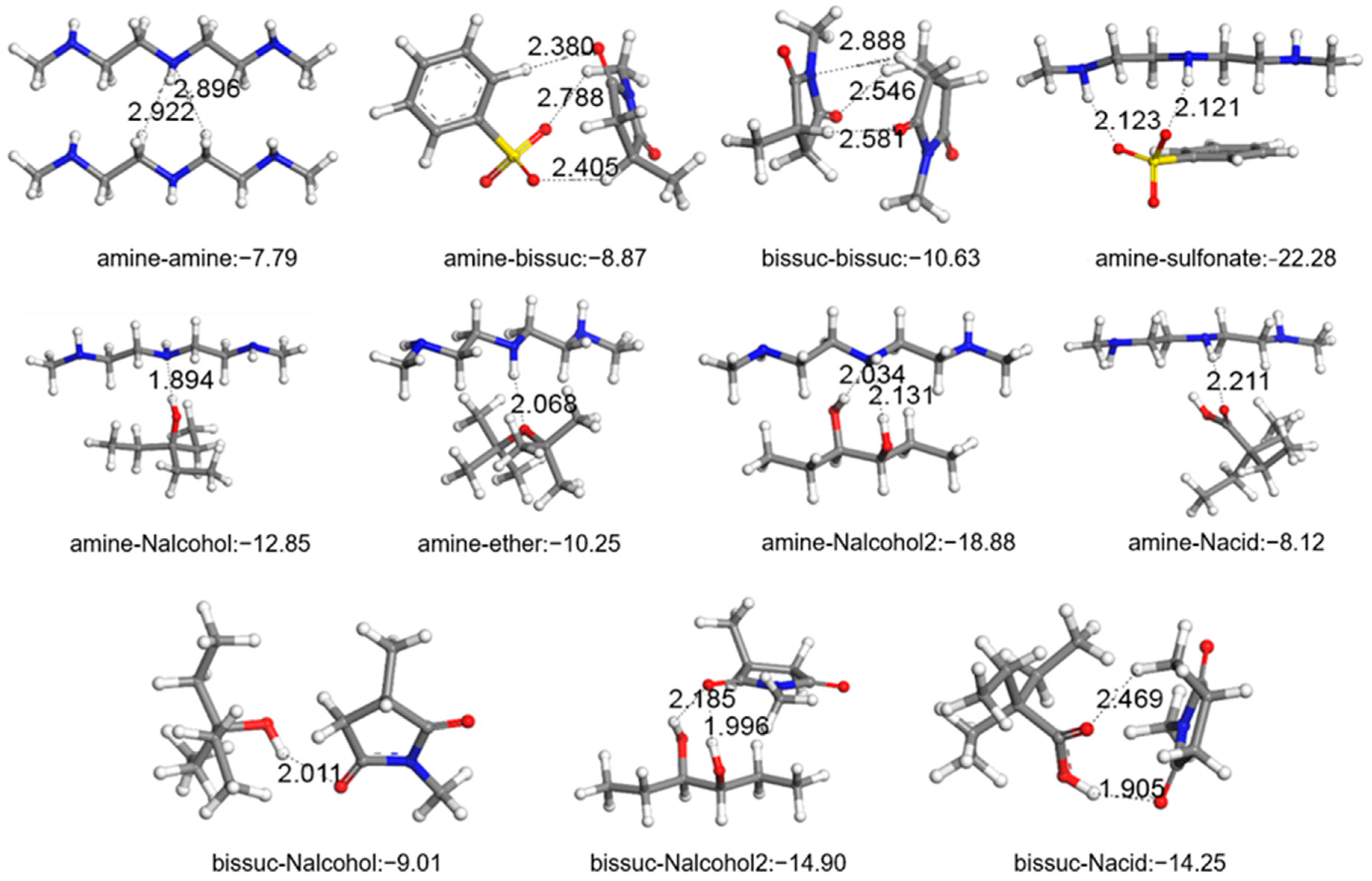



| i | j | ΔEij (kcal/mol) | i | j | ΔEij (kcal/mol) |
|---|---|---|---|---|---|
| PIB | R-COH | −6.44 | PIB | R-(OH)2 | −7.09 |
| PIB | amine | −8.56 | PIB | R=O | −6.54 |
| PIB | bis-suc | −6.62 | PIB | R-O-R | −5.65 |
| PIB | R-COOH | −6.82 | PIB | PIB | −7.05 |
| PIB | R-OH | −6.99 | PIB | sulfonate | −12.88 |
| amine | R-COH | −7.27 | amine | R-O-R | −10.25 |
| amine | R-COOH | −8.12 | amine | alkyl | −5.76 |
| amine | R-OH | −12.85 | amine | amine | −7.79 |
| amine | R-(OH)2 | −18.88 | amine | sulfonate | −22.28 |
| amine | R=O | −7.60 | |||
| bis-suc | R-COH | −9.29 | bis-suc | R=O | −10.41 |
| bis-suc | bis-suc | −10.63 | bis-suc | R-O-R | −8.20 |
| bis-suc | R-COOH | −14.25 | bis-suc | amine | −8.87 |
| bis-suc | R-OH | −9.01 | bis-suc | sulfonate | −20.68 |
| Van Der Waals Solubility Parameter ((J/cm3)0.5) | Electrostatic Solubility Parameter ((J/cm3)0.5) | Total Solubility Parameter ((J/cm3)0.5) | |
|---|---|---|---|
| Base oil [25] | 17.013 | 0.874 | 17.407 |
| Dispersant (polar center) | 20.341 | 11.233 | 23.637 |
| Dispersant (non-polar PIB tail) | 12.304 | 0.414 | 12.671 |
| Structures | AlogP [33] | SASA | TPSA | TASA | RPSA | RASA |
|---|---|---|---|---|---|---|
| Oil molecule [25] | 10.47 | 794.41 | 0.00 | 794.41 | 0.00 | 1.00 |
| CH3COOH | −0.20 | 212.70 | 122.97 | 89.74 | 0.58 | 0.42 |
| CH3OH | −0.36 | 170.74 | 69.06 | 101.68 | 0.40 | 0.60 |
| Nacid | 2.71 | 346.28 | 76.50 | 269.77 | 0.22 | 0.78 |
| Nketone | 2.15 | 314.80 | 47.36 | 267.44 | 0.15 | 0.85 |
| Nalcohol | 2.14 | 323.00 | 29.06 | 293.94 | 0.09 | 0.91 |
| Nalcohol2 | 1.41 | 317.06 | 68.40 | 248.66 | 0.22 | 0.78 |
| Amine center | −1.50 | 738.57 | 131.62 | 606.95 | 0.18 | 0.82 |
| Amine monomer | −0.22 | 209.51 | 39.09 | 170.41 | 0.19 | 0.81 |
| Bis-succinimide | 0.40 | 322.74 | 103.50 | 219.24 | 0.32 | 0.68 |
| PIB18 | 25.50 | 1523.92 | 0.00 | 1523.92 | 0.00 | 1.00 |
| PIB monomer | 2.20 | 260.08 | 0.00 | 260.08 | 0.00 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Özdemir, E.; Kan, E.; Guo, B.; Pashkovski, E.; Agiral, A.; Yildirim, E. The Role of Polyisobutylene-Bis-Succinimide (PIBSI) Dispersants in Lubricant Oils on the Deposit Control Mechanism. Polymers 2025, 17, 1041. https://doi.org/10.3390/polym17081041
Özdemir E, Kan E, Guo B, Pashkovski E, Agiral A, Yildirim E. The Role of Polyisobutylene-Bis-Succinimide (PIBSI) Dispersants in Lubricant Oils on the Deposit Control Mechanism. Polymers. 2025; 17(8):1041. https://doi.org/10.3390/polym17081041
Chicago/Turabian StyleÖzdemir, Erhan, Esra Kan, Binbin Guo, Eugene Pashkovski, Anil Agiral, and Erol Yildirim. 2025. "The Role of Polyisobutylene-Bis-Succinimide (PIBSI) Dispersants in Lubricant Oils on the Deposit Control Mechanism" Polymers 17, no. 8: 1041. https://doi.org/10.3390/polym17081041
APA StyleÖzdemir, E., Kan, E., Guo, B., Pashkovski, E., Agiral, A., & Yildirim, E. (2025). The Role of Polyisobutylene-Bis-Succinimide (PIBSI) Dispersants in Lubricant Oils on the Deposit Control Mechanism. Polymers, 17(8), 1041. https://doi.org/10.3390/polym17081041







