Prediction of Rheological Properties of PVA Fiber and Nano-SiO2-Reinforced Geopolymer Mortar Based on Back Propagation Neural Network Model Optimized by Genetic Algorithm
Abstract
1. Introduction
2. Experiment Program
3. Model Establishment
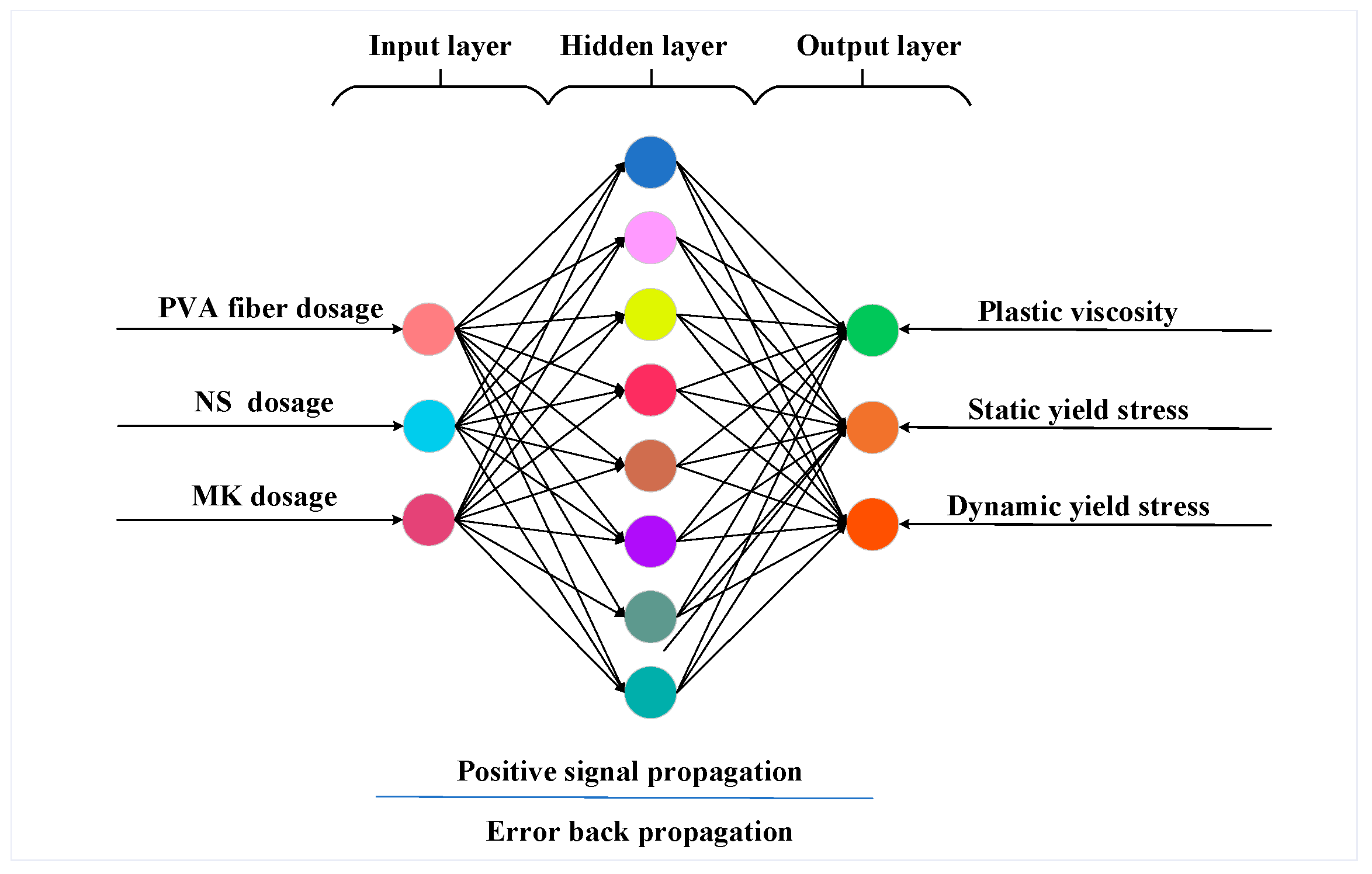
3.1. BP Neural Network
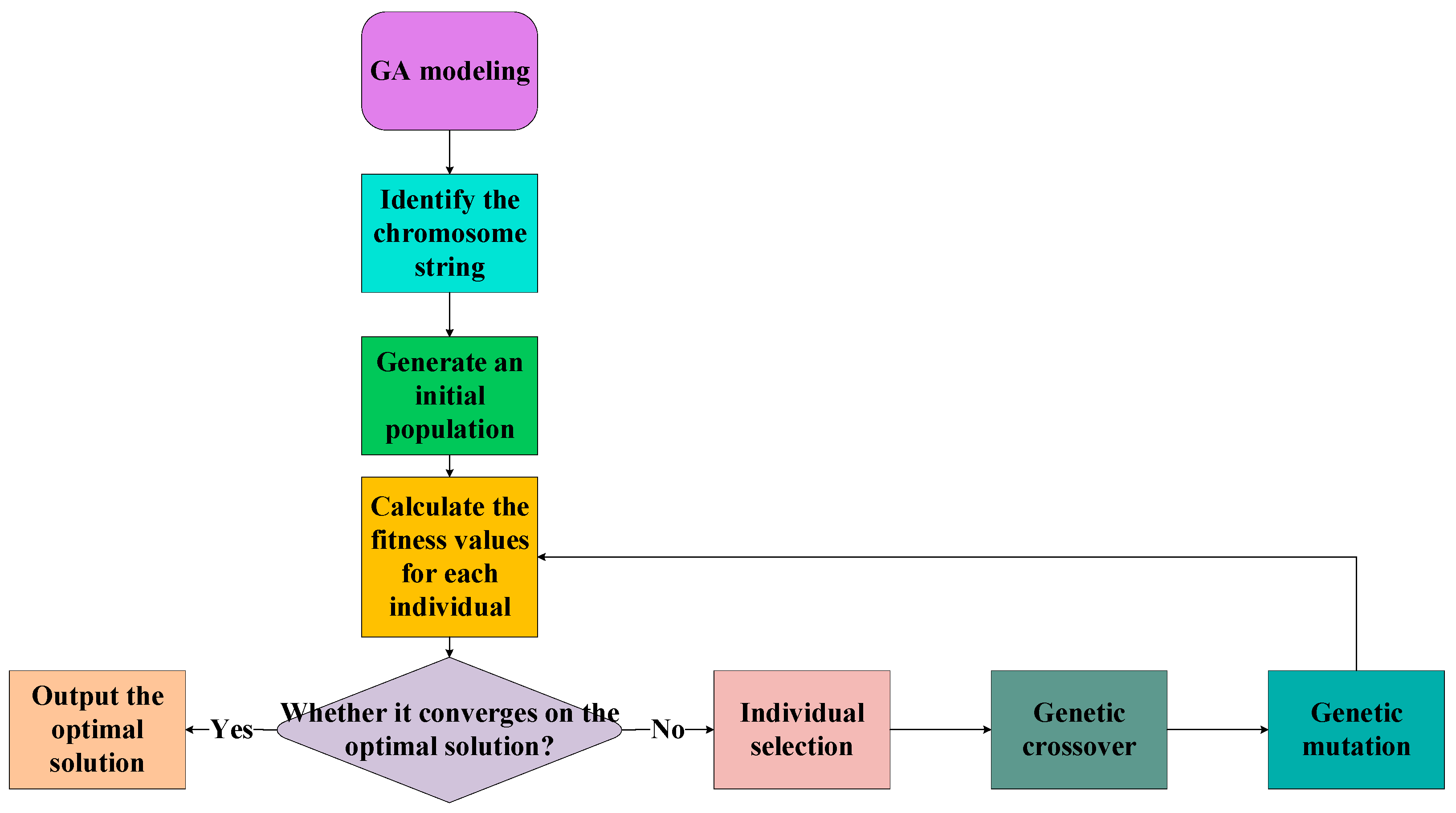
3.2. The Genetic Algorithm
3.3. GA–BP Neural Network
4. Discussion
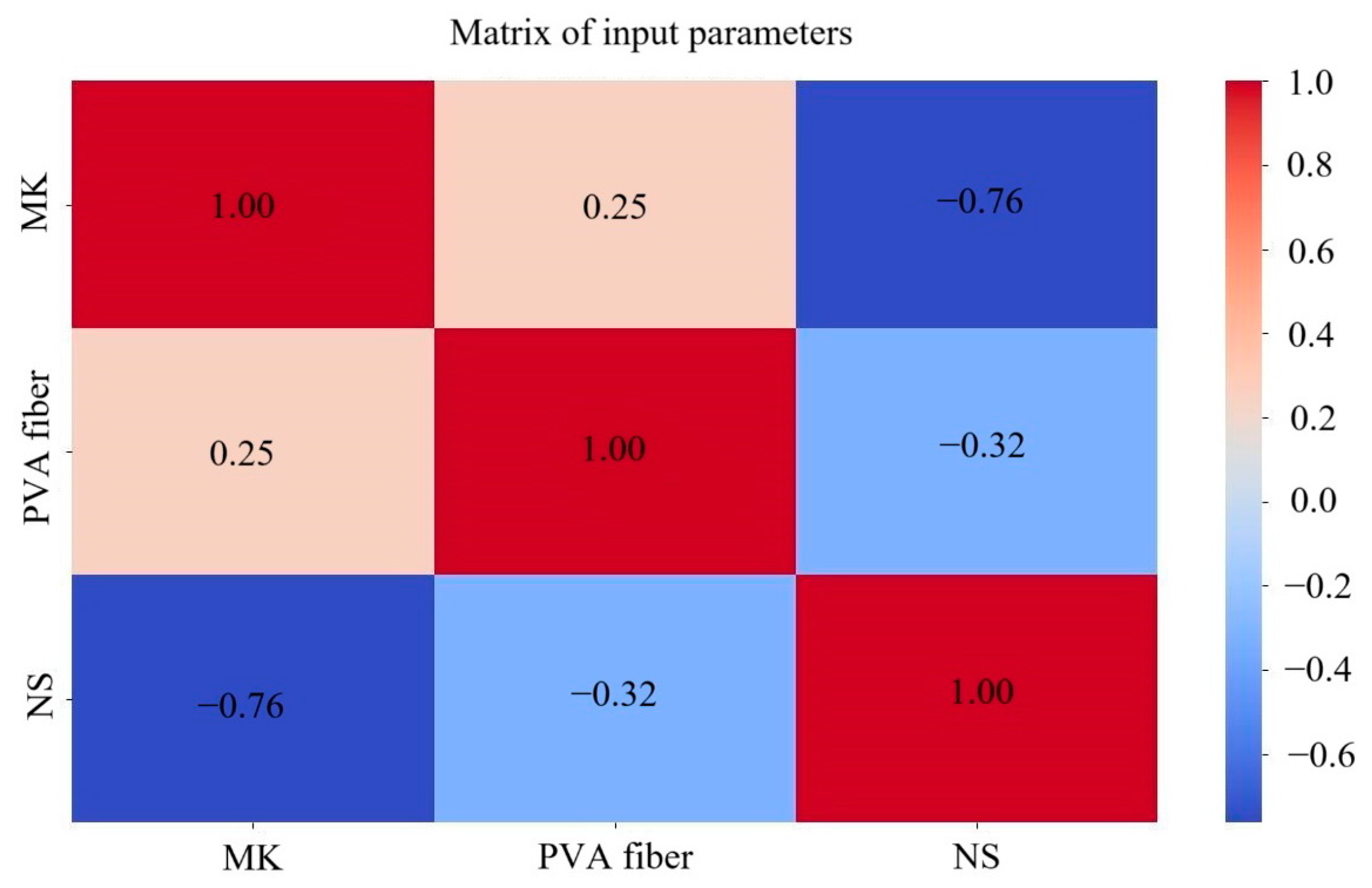
4.1. Normalization and Correlation Analysis
4.2. Experimental Results and Analysis
5. Conclusions
- (1)
- Through correlation analysis, the correlation coefficients of NS, PVA fiber and MK content are all less than 0.8, so those three parameters are unrelated to one another. Consequently, there will not be a multicollinearity problem when predicting the rheological properties of NS- and PVA-fiber-reinforced GM using these three factors as input parameters.
- (2)
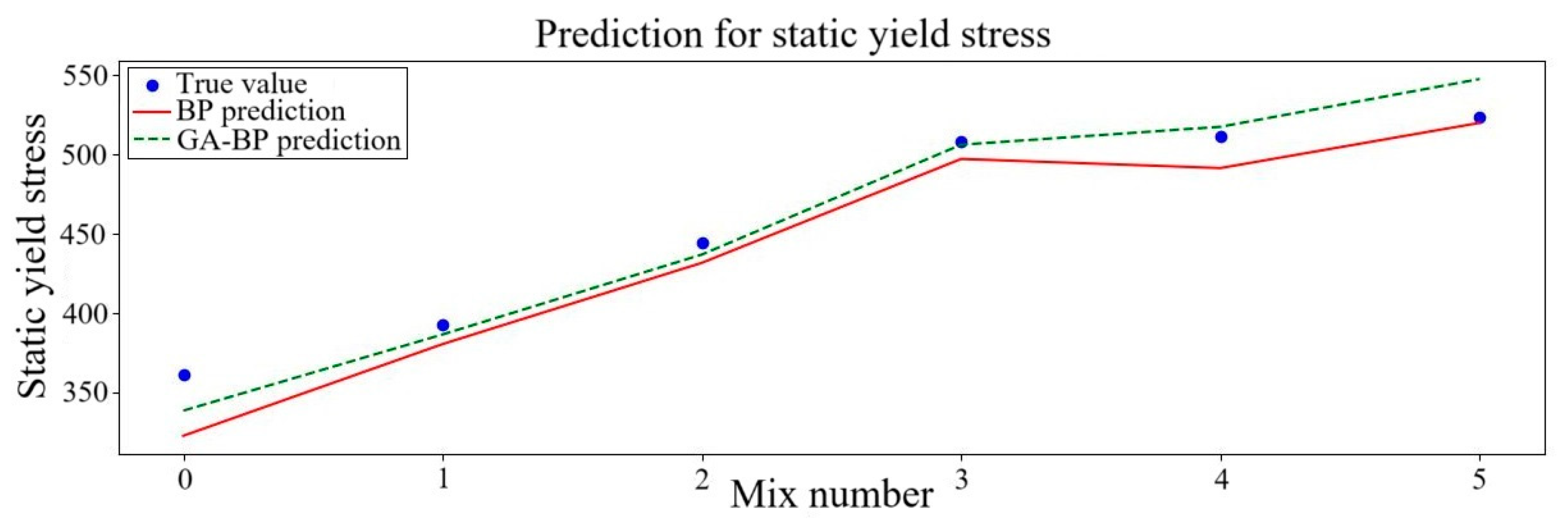
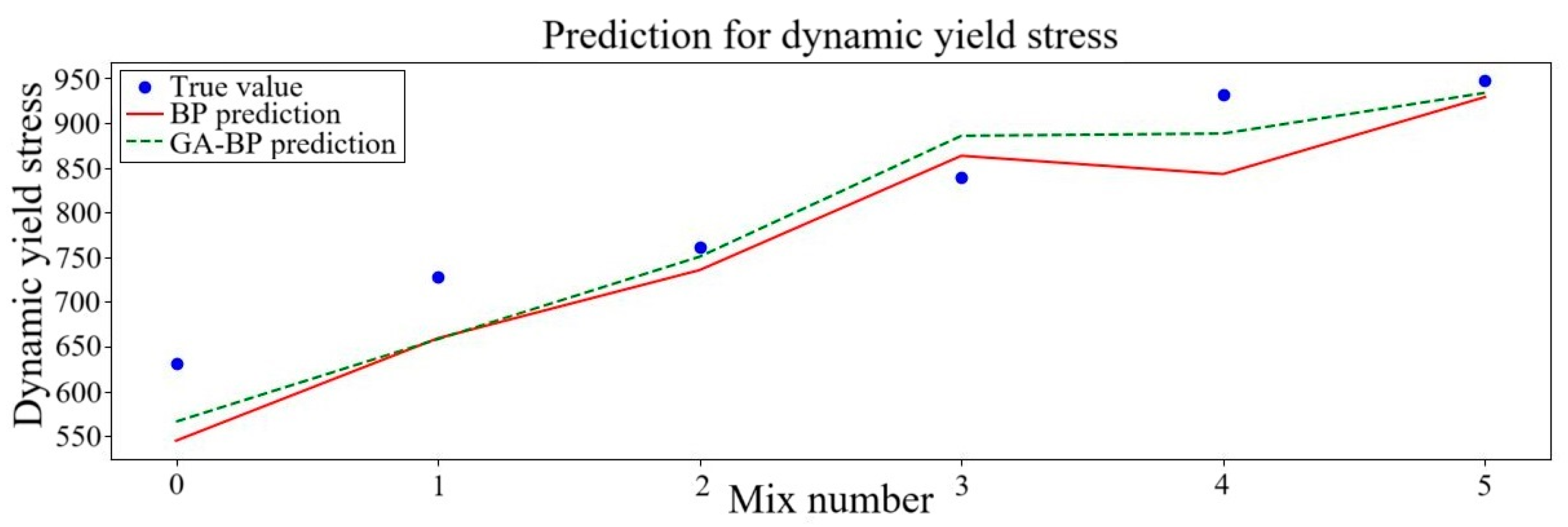
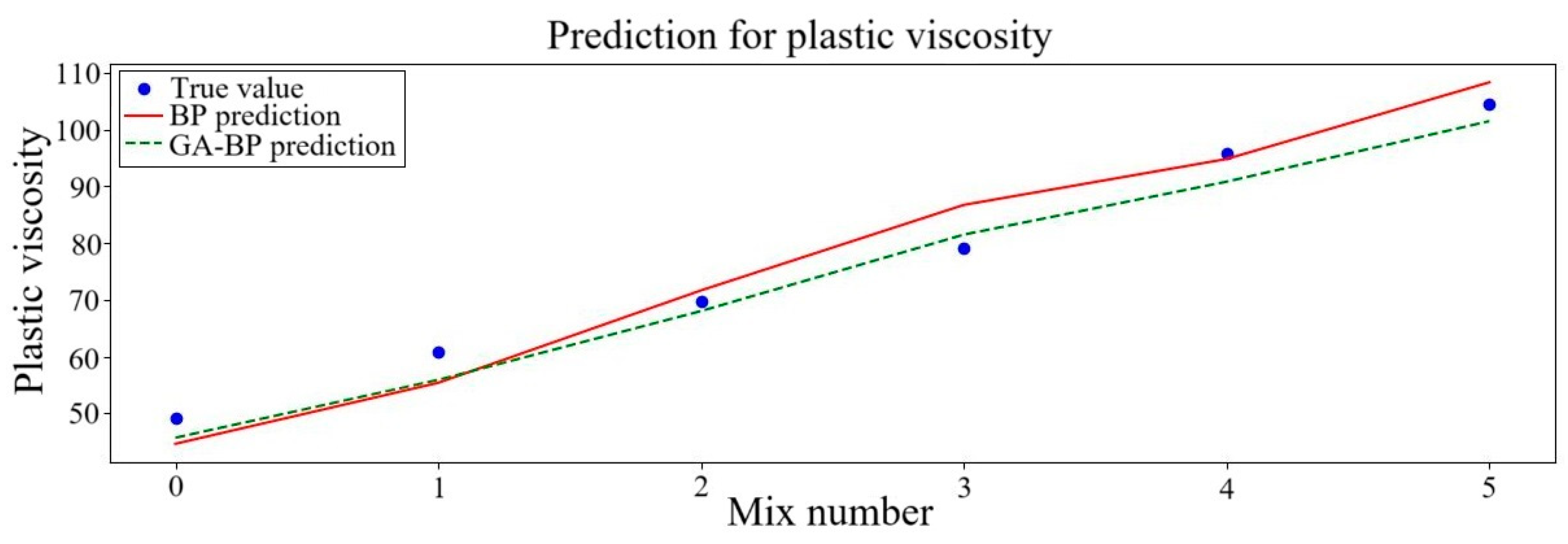
- The findings of the analysis show that there is a concordance between the experimental and predicted rheological parameters for the rheological parameters of NS- and PVA-fiber-reinforced GM. The R2 of the plastic viscosity, dynamic yield stress and static yield stress increased by 2.11%, 15.28% and 4.40%, respectively, when the GA–BP neural network was employed instead of the BP neural network. As a result, the predictive capacity of the GA–BP neural network outperforms the BP neural network.
- (3)
- The GA–BP neural network can simplify the prediction of rheological properties for NS- and PVA-fiber-reinforced GM by capturing the complex nonlinear mappings between the rheological properties and the mix proportions of the mortar. Furthermore, this model can effectively optimize the mix proportions of NS- and PVA-fiber-reinforced GM, whose predictions could be employed in composite mix proportion testing to enhance the efficiency of the testing process.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bourzik, O.; Akkouri, N.; Baba, K.; Haddaji, Y.; Nounah, A.; Assafi, M.; Bazzar, K. Study of the effects of drinking water treatment sludge on the properties of Class F fly ash-based geopolymer. Environ. Sci. Pollut. 2022, 29, 87668–87679. [Google Scholar] [CrossRef]
- Mao, Y.; Zhang, P.; Gao, Z.; Zheng, Y.; Zheng, M. Durability and microstructure of waste slurry based geopolymer concrete. J. Mater. Res. Technol. 2025, 34, 1468–1481. [Google Scholar] [CrossRef]
- Bhutta, A.; Farooq, M.; Zanotti, C.; Banthia, N. Pull-out behavior of different fibers in geopolymer mortars: Effects of alkaline solution concentration and curing. Mater. Struct. 2017, 50, 80. [Google Scholar] [CrossRef]
- Zhang, P.; Mao, Y.; Gao, Z.; Guo, J.; Zheng, M. Efficient utilization of waste drilling mud to prepare material stabilized with fly ash/slag based geopolymer for subgrade engineering. J. Environ. Manage 2025, 373, 123600. [Google Scholar] [CrossRef]
- Sheshadri, A.; Marathe, S.; Sadowski, L. Development of sustainable, high strength slag based alkali activated pavement quality concrete using agro-industrial wastes: Properties and life cycle analysis. Int. J. Pavement Eng. 2024, 25, 2410953. [Google Scholar] [CrossRef]
- Conversano, A.; Sogni, D.; Lombardelli, G.; Di Bona, D.; Vigano, F.; Consonni, S. Energy and environmental assessment of solid recovered fuels valorisation: Waste-to-Chemicals options vs co-combustion in cement plants. Waste Manage 2024, 190, 432–442. [Google Scholar] [CrossRef]
- Davidovits, J. Geopolymers and geopolymeric materials. J. Therm. Anal. Calorim. 1989, 35, 429–441. [Google Scholar] [CrossRef]
- Amran, Y.H.M.; Alyousef, R.; Alabduljabbar, H.; El-Zeadani, M. Clean production and properties of geopolymer concrete; A review. J. Clean. Prod. 2020, 251, 119679. [Google Scholar] [CrossRef]
- Leong, H.Y.; Ong, D.E.L.; Sanjayan, J.G.; Nazari, A. Suitability of Sarawak and Gladstone fly ash to produce geopolymers: A physical, chemical, mechanical, mineralogical and microstructural analysis. Ceram. Int. 2016, 42, 9613–9620. [Google Scholar] [CrossRef]
- Bourzik, O.; Baba, K.; Akkouri, N. Eco-friendly geopolymer mortar prepared from geopolymer waste: Mechanical and thermal properties. Environ. Qual. Manag. 2024, 33, 411–419. [Google Scholar] [CrossRef]
- Khalil, M.Y.; Merz, E. Immobizization of intermediate-level wastes in geopolymers. J. Nucl. Mater. 1994, 211, 141–148. [Google Scholar] [CrossRef]
- Pelisser, F.; Guerrino, E.L.; Menger, M.; Michel, M.D.; Labrincha, J.A. Micromechanical characterization of metakaolin-based geopolymers. Constr. Build. Mater. 2013, 49, 547–553. [Google Scholar] [CrossRef]
- Sate, V.; Sathonsaowaphak, A.; Chindaprasirt, P. Resistance of lignite bottom ash geopolymer mortar to sulfate and sulfuric acid attack. Cem. Concr. Comp. 2012, 34, 700–708. [Google Scholar] [CrossRef]
- Szostak, B.; Golewski, G.L. Rheology of Cement Pastes with Siliceous Fly Ash and the CSH Nano-Admixture. Materials 2021, 14, 3640. [Google Scholar] [CrossRef]
- Wu, L.; Lu, Z.; Zhuang, C.; Chen, Y.; Hu, R. Mechanical Properties of Nano SiO2 and Carbon Fiber Reinforced Concrete after Exposure to High Temperatures. Materials 2019, 12, 3373. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, W.; Guo, J.; Zheng, Y. Abrasion resistance and damage mechanism of hybrid fiber-reinforced geopolymer concrete containing nano-SiO2. J. Clean. Prod. 2025, 494, 144971. [Google Scholar] [CrossRef]
- Wang, L.; Guo, F.; Yang, H.; Wang, Y.; Tang, S. Comparison of fly ash, PVA fiber, MgO and shrinkage-reducing admixture on the frost resistance of face slab concrete via pore structural and fractal analysis. Fractals 2021, 29, 2140002. [Google Scholar] [CrossRef]
- Zhang, P.; Sun, Y.; Wu, J.; Hong, J.; Gao, Z. Mechanical properties and microstructure of nano-modified geopolymer concrete containing hybrid fibers after exposure to elevated temperature. Constr. Build. Mater. 2023, 409, 134044. [Google Scholar] [CrossRef]
- Szostak, B.; Golewski, G.L. Improvement of Strength Parameters of Cement Matrix with the Addition of Siliceous Fly Ash by Using Nanometric C-S-H Seeds. Energies 2020, 13, 6734. [Google Scholar] [CrossRef]
- Szostak, B.; Golewski, G.L. Effect of Nano Admixture of CSH on Selected Strength Parameters of Concrete Including Fly Ash. IOP Conf. Ser. Mater. Sci. Eng. 2018, 416, 012105. [Google Scholar] [CrossRef]
- Alomayri, T.; Raza, A.; Shaikh, F. Effect of nano SiO2 on mechanical properties of micro-steel fibers reinforced geopolymer composites. Ceram Int. 2021, 47, 33444–33453. [Google Scholar] [CrossRef]
- Zidi, Z.; Ltifi, M.; Zafar, I. Synthesis and attributes of nano-SiO2 local metakaolin based-geopolymer. J. Build. Eng. 2021, 33, 101586. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Chen, Q. Neural network and particle swarm optimization for predicting the unconfined compressive strength of cemented paste backfill. Constr. Build. Mater. 2018, 159, 473–478. [Google Scholar] [CrossRef]
- Zhang, P.; Ding, J.; Dai, X.; Zheng, Y.; Zheng, M. Mechanical properties of geopolymer concrete solidified with waste materials. Constr. Build. Mater. 2025, 460, 139835. [Google Scholar] [CrossRef]
- Ali, S.; Sheikh, M.N.; NS Hadi, M. Behavior of axially loaded plain and fiber-reinforced geopolymer concrete columns with glass fiber-reinforced polymer cages. Struct Conceret. 2021, 22, 1800–1816. [Google Scholar] [CrossRef]
- Darvishan, E.; Adabi, M.; Amani, A. Investigation of Mechanical and Durability Properties of Alkali-Activated Concrete Prepared with Ternary Blended Ground Granulated Blast Furnace Slag, Fly Ash, and Jajrood Trass. J. Mater. Civil. Eng. 2023, 35, 15144. [Google Scholar] [CrossRef]
- Wang, S.L.; Zhu, B.L. Influence of nano-SiO2 on the mechanical properties of recycled aggregate concrete with and without polyvinyl alcohol (PVA) fiber. Materials 2021, 14, 1446. [Google Scholar] [CrossRef]
- Zhang, P.; Feng, Z.; Guo, J.; Zheng, Y.; Yuan, P. Mechanical behavior and microscopic damage mechanism of hybrid fiber-reinforced geopolymer concrete at elevated temperature. Ceram. Int. 2024, 50, 53851–53866. [Google Scholar] [CrossRef]
- Xu, F.; Deng, X.; Peng, C.; Zhu, J.; Chen, J. Mix design and flexural toughness of PVA fiber reinforced fly ash-geopolymer composites. Constr. Build. Mater. 2017, 150, 179–189. [Google Scholar] [CrossRef]
- Tanyildizi, H.; Yonar, Y. Mechanical properties of geopolymer concrete containing polyvinyl alcohol fiber exposed to high temperature. Constr. Build. Mater. 2016, 126, 381–387. [Google Scholar] [CrossRef]
- Feng, Z.; Zhang, P.; Guo, J.; Zheng, Y.; Hu, S. Single and synergistic effects of nano-SiO2 and hybrid fiber on rheological property and compressive strength of geopolymer concrete. Constr. Build. Mater. 2025, 472, 140945. [Google Scholar] [CrossRef]
- Xu, S.; Malik, M.A.; Qi, Z.; Huang, B.; Li, Q.; Sarkar, M. Influence of the PVA fibers and SiO2 NPs on the structural properties of fly ash based sustainable geopolymer. Constr. Build. Mater. 2018, 164, 238–245. [Google Scholar] [CrossRef]
- Zhang, P.; Wen, Z.; Han, X.; Guo, J.; Hu, S. A state-of-the-art review on frost resistance of fiber-reinforced geopolymer composites. Sustain. Chem. Pharm. 2025, 45, 102006. [Google Scholar] [CrossRef]
- Anh-Duc, P.; Nhat-Duc, H.; Quang-Trung, N. Predicting Compressive Strength of High-Performance Concrete Using Metaheuristic-Optimized Least Squares Support Vector Regression. J. Comput. Civil. Eng. 2016, 30, 06015002. [Google Scholar]
- Khoa Tan, N.; Quang Dang, N.; Tuan Anh, L.; Shin, J.; Lee, K. Analyzing the compressive strength of green fly ash based geopolymer concrete using experiment and machine learning approaches. Constr. Build. Mater. 2020, 247, 118581. [Google Scholar]
- Dong Van, D.; Hai-Bang, L.; Son Hoang, T.; Tien-Thinh, L.; Binh Thai, P. Artificial Intelligence Approaches for Prediction of Compressive Strength of Geopolymer Concrete. Materials 2019, 12, 983. [Google Scholar] [CrossRef] [PubMed]
- Bagheri, A.; Nazari, A.; Sanjayan, J. The use of machine learning in boron-based geopolymers: Function approximation of compressive strength by ANN and GP. Measurement 2019, 141, 241–249. [Google Scholar] [CrossRef]
- Awoyera, P.O.; Kirgiz, M.S.; Viloria, A.; Ovallos-Gazabon, D. Estimating strength properties of geopolymer self-compacting concrete using machine learning techniques. J. Mater. Res. Techonl. 2020, 9, 9016–9028. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, P.; Yuan, W.; Hu, S. Durability prediction of geopolymer mortar reinforced with nanoparticles and PVA fiber using particle swarm optimized BP neural network. Nanotechnol. Rev. 2024, 13, 20230241. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Liu, X.; Zhang, J.; Wang, W.; Xu, H. Prediction of Mechanical Properties of Cotton Fibers by a BP Neural Network Model Optimized by Genetic Algorithm. J. Nat. Fibers. 2024, 21, 2389161. [Google Scholar] [CrossRef]
- Kaya, M.; Ilkentapar, S.; Durak, U.; Atabey, I.I.; Celikten, S. Physical Mechanical and Microstructural Properties of Kaolin-Based Fly Ash-Added Geopolymer Mortars. Iran. J. Sci. Technol. Trans. Civ. Eng. 2024, 48, 3559–3572. [Google Scholar] [CrossRef]
- Sun, S. Adjustment and calculation of water glass modulus. Mine. Construct. Technol. 1984, 2, 26–29. [Google Scholar]
- Zhang, P.; Sun, Y.; Wu, J.; Guo, Z.; Wang, C. Properties of road subbase materials manufactured with geopolymer solidified waste drilling mud. Constr. Build. Mater. 2024, 430, 136509. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, P.; Guo, J.; Hu, S. Effects of PVA fibers and nano-SiO2 on rheological properties of geopolymer mortar. Nanotechnol. Rev. 2024, 13, 20240103. [Google Scholar] [CrossRef]
- Zhang, P.; Gao, Z.; Wang, J.; Guo, J.; Wang, T. Influencing factors analysis and optimized prediction model for rheology and flowability of nano-SiO2 and PVA fiber reinforced alkali-activated composites. J. Clean. Prod. 2022, 366, 132988. [Google Scholar] [CrossRef]
- Zhang, P.; Han, X.; Zheng, Y.; Wan, J.; Hui, D. Effect of PVA fiber on mechanical properties of fly ash-based geopolymer concrete. Rev. Adv. Mater. Sci. 2021, 60, 418–437. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, P.; Dai, X.; Zheng, Y.; Hu, S. Workability of self-compacting geopolymer concrete: The effect of nano-SiO2 and steel-polyvinyl alcohol hybrid fiber. Constr. Build. Mater. 2025, 460, 139849. [Google Scholar] [CrossRef]
- Ani, K.A. Predictive comparison and assessment of ANFIS and ANN, as efficient tools in modeling degradation of total petroleum hydrocarbon (TPH). Clean. Waste Syst. 2023, 6, 100052. [Google Scholar]
- Congro, M.; de Alencar Monteiro, V.M.; Brandao, A.L.T.; dos Santos, B.F.; Roehl, D.; Silva, F.d.A. Prediction of the residual flexural strength of fiber reinforced concrete using artificial neural networks. Constr. Build. Mater. 2021, 303, 124502. [Google Scholar] [CrossRef]
- Liu, W.; Chao, W.; Jin, Y.; Yang, F.; Fan, L.; Zhang, W.; Wu, L.; Song, C. Study on GA-ANN-Based Prediction of Paving Time of Cement-Stabilized Layer above Ultra-High-Filled Subgrade. J. Build. Eng. 2024, 14, 2312. [Google Scholar] [CrossRef]
- Amiri, M.; Hatami, F. Prediction of mechanical and durability characteristics of concrete including slag and recycled aggregate concrete with artificial neural networks (ANNs). Constr. Build. Mater. 2022, 325, 126839. [Google Scholar] [CrossRef]
- Pan, L.; Guo, Y.; Mu, B.; Shi, W.; Wei, X. Operation optimization of cement clinker production line based on neural network and genetic algorithm. Energy 2024, 303, 132016. [Google Scholar] [CrossRef]
- Coley, D.A. Genetic algorithms. Sci. Am. 1996, 37, 145–154. [Google Scholar] [CrossRef]
- Zhao, Z.; Bao, Y.; Gao, T.; An, Q. Optimization of GFRP-concrete-steel composite column based on genetic algorithm- artificial neural network. Appl. Ocean. Res. 2024, 143, 103881. [Google Scholar] [CrossRef]
- Owolabi, T.O. Modeling the magnetocaloric effect of manganite using hybrid genetic and support vector regression algorithms. Phys. Lett. A 2019, 383, 1782–1790. [Google Scholar] [CrossRef]
- Moein, M.M.; Saradar, A.; Rahmati, K.; Mousavinejad, S.H.G.; Bristow, J.; Aramali, V.; Karakouzian, M. Predictive models for concrete properties using machine learning and deep learning approaches: A review. J. Build. Eng. 2023, 63, 105444. [Google Scholar] [CrossRef]
- Firouzi, A.; Rahai, A. An integrated ANN-GA for reliability based inspection of concrete bridge decks considering extent of corrosion-induced cracks and life cycle costs. Sci. Iran. 2012, 19, 974–981. [Google Scholar] [CrossRef]
- Park, J.S.; Park, S.; Oh, B.K.; Hong, T.; Lee, D.-E.; Park, H.S. Estimation of concrete compressive strength from non-destructive tests using a customized neural network and genetic algorithm. Appl. Soft. Comput. 2024, 164, 111941. [Google Scholar] [CrossRef]
- Olivieri, A.C.; Goicoechea, H.C.; Iñón, F.A. MVC1: An integrated MatLab toolbox for first-order multivariate calibration. Chemometr. Intell. Lab. 2004, 73, 189–197. [Google Scholar] [CrossRef]
- Al-kahtani, M.S.M.; Zhu, H.; Ibrahim, Y.E.; Haruna, S.I.; Al-qahtani, S.S.M. Study on the Mechanical Properties of Polyurethane-Cement Mortar Containing Nanosilica: RSM and Machine Learning Approach. Appl. Sci. 2023, 13, 13348. [Google Scholar] [CrossRef]
- Kwan, A.K.H.; Fung, W.W.S. Roles of water film thickness and SP dosage in rheology and cohesiveness of mortar. Cem. Concr. Res. 2012, 34, 121–130. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, M.; Liu, R.; Li, X.; Liu, Y.; Jiang, P.; Yan, J.; Zhu, Z.; Chen, M. Rheological properties of cement-based slurry and evaluation of rheological model: Influence of particle size and shape. Constr. Build. Mater. 2023, 406, 133498. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, P.; Wang, T.; Zheng, Y.; Qiu, L.; Sun, S. Compressive strength and anti-chloride ion penetration assessment of geopolymer mortar merging PVA fiber and nano-SiO2 using RBF-BP composite neural network. Nanotechnol. Rev. 2022, 11, 1181–1192. [Google Scholar] [CrossRef]
- Ristic, N.; Petrovic, E.; Bijeljic, J.; Simonovic, M.; Grdic, D.; Nikolic, V.; Grdic, Z. Gaussian Regression Process for Prediction of Compressive Strength of Thermally Activated Geopolymer Mortars. Tehnički Vjesnik 2022, 29, 1833–1840. [Google Scholar]
- Huang, J.; Zhou, M.; Yuan, H.; Sabri, M.M.S.; Li, X. Prediction of the Compressive Strength for Cement-Based Materials with Metakaolin Based on the Hybrid Machine Learning Method. Materials 2022, 15, 3500. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Li, K.; Zhang, B.; Han, B. Effect of nano-SiO2 on mechanical properties, fluidity, and microstructure of superfine tailings cemented paste backfill. Mater. Today Sustain. 2023, 24, 100490. [Google Scholar] [CrossRef]
- Manikandan, P.; Selija, K.; Vasugi, V.; Kumar, V.P.; Natrayan, L.; Santhi, M.; Kumaran, G.S. An Artificial Neural Network Based Prediction of Mechanical and Durability Characteristics of Sustainable Geopolymer Composite. Adv. Civ. Eng. 2022, 2022, 9343330. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, P.; Wang, J.; Ling, Y. Compressive Strength Prediction of PVA Fiber-Reinforced Cementitious Composites Containing Nano-SiO2 Using BP Neural Network. Materials 2020, 13, 521. [Google Scholar] [CrossRef]

| Loss on Ignition (%) | pH | Stacking Density (g/cm3) | Nominal Particle Size (nm) | Specific Surface Area (m2/g) |
|---|---|---|---|---|
| 1.0 | 6.21 | 0.054 | 30 | 200 |
| Elongation at Fracture (%) | Filament Diameter (µm) | Fiber Length (mm) | Flexural |
|---|---|---|---|
| 6.5 | 40 | 12 | 1560 |
| Composition | Ingredient Contents(wt.%) | |||||||
|---|---|---|---|---|---|---|---|---|
| K2O | Al2O3 | Na2O | TiO2 | MgO | SiO2 | Fe2O3 | CaO | |
| MK | 0.26 | 43.52 | 0.18 | 0.06 | 0.35 | 54.34 | 1.17 | 0.42 |
| FA | 2.91 | 23.05 | 0.97 | 1.45 | 1.16 | 55.47 | 5.75 | 5.17 |
| Mix Number | NaOH | Water Glass | Fly Ash (FA) | Metakaolin (MK) | PVA Fiber | Nano Particle | Water Reducer | Static Yield Stress | Dynamic Yield Stress | Plastic Viscosity |
|---|---|---|---|---|---|---|---|---|---|---|
| kg/m3 | kg/m3 | kg/m3 | kg/m3 | % | % | kg/m3 | Pa | Pa | Pa·s | |
| M-0-0 | 71 | 445.4 | 184.1 | 429.5 | 0 | 0 | 3.07 | 350.72 | 577.6 | 42.8 |
| P-0.2-0 | 71 | 445.4 | 184.1 | 429.5 | 0.2 | 0 | 3.07 | 365.169 | 653.5 | 57.5 |
| P-0.4-0 | 71 | 445.4 | 184.1 | 429.5 | 0.4 | 0 | 3.07 | 404.755 | 759.5 | 65.4 |
| P-0.6-0 | 71 | 445.4 | 184.1 | 429.5 | 0.6 | 0 | 3.07 | 497.123 | 843.1 | 79.6 |
| P-0.8-0 | 71 | 445.4 | 184.1 | 429.5 | 0.8 | 0 | 3.07 | 513.444 | 912.3 | 84.1 |
| P-1.0-0 | 71 | 445.4 | 184.1 | 429.5 | 1.0 | 0 | 3.07 | 522.628 | 924.8 | 99.7 |
| P-1.2-0 | 71 | 445.4 | 183.1 | 427.2 | 1.2 | 0 | 3.07 | 547.441 | 950.9 | 111.9 |
| N-0-0.5 | 71 | 445.4 | 182.2 | 425 | 0 | 0.5 | 3.07 | 336.83 | 563.6 | 42.1 |
| N-0-1.0 | 71 | 445.4 | 181.2 | 422.7 | 0 | 1.0 | 3.07 | 296.202 | 472.8 | 40.9 |
| N-0-1.5 | 71 | 445.4 | 180.2 | 420.4 | 0 | 1.5 | 3.07 | 358.185 | 569.2 | 43.8 |
| N-0-2.0 | 71 | 445.4 | 182.2 | 425 | 0 | 2.0 | 3.07 | 372.596 | 634.1 | 47.1 |
| N-0-2.5 | 71 | 445.4 | 182.2 | 425 | 0 | 2.5 | 3.07 | 394.126 | 708.2 | 52.6 |
| PN-0.2-1.0 | 71 | 445.4 | 182.2 | 425 | 0.2 | 1.0 | 3.07 | 361.484 | 631.4 | 49.1 |
| PN-0.4-1.0 | 71 | 445.4 | 182.2 | 425 | 0.4 | 1.0 | 3.07 | 392.677 | 728.7 | 60.9 |
| PN-0.6-1.0 | 71 | 445.4 | 182.2 | 425 | 0.6 | 1.0 | 3.07 | 444.476 | 760.7 | 69.7 |
| PN-0.8-1.0 | 71 | 445.4 | 183.1 | 427.2 | 0.8 | 1.0 | 3.07 | 507.826 | 839.3 | 79.1 |
| PN-1.0-1.0 | 71 | 445.4 | 181.2 | 422.7 | 1.0 | 1.0 | 3.07 | 511.162 | 931.9 | 95.9 |
| PN-1.2-1.0 | 71 | 445.4 | 180.2 | 420.4 | 1.2 | 1.0 | 3.07 | 523.544 | 947.4 | 104.5 |
| PN-0.6-0.5 | 71 | 445.4 | 182.2 | 425 | 0.6 | 0.5 | 3.07 | 469.699 | 802.9 | 75.9 |
| PN-0.6-1.5 | 71 | 445.4 | 180.2 | 420.4 | 0.6 | 1.5 | 3.07 | 535.874 | 938.2 | 82.8 |
| PN-0.6-2.0 | 71 | 445.4 | 182.2 | 425 | 0.6 | 2.0 | 3.07 | 585.459 | 976.9 | 91.7 |
| PN-0.6-2.5 | 71 | 445.4 | 180.2 | 420.4 | 0.6 | 2.5 | 3.07 | 683.382 | 995.5 | 109.6 |
| Parameters | Output Layer Neurons | Output Layer Transfer Function | Hidden Layer Transfer Function | Hidden Layer Neurons | Input Layer Neurons |
|---|---|---|---|---|---|
| Value | 3 | Purelin | Tansig | 8 | 3 |
| Parameters | Number of Iterations | Mutation Probability | Individual Number | Crossover Probability |
|---|---|---|---|---|
| Value | 100 | 0.001 | 600 | 1 |
| Mix Number | Metakaolin (MK) | PVA Fiber | Nano Particle | Static Yield Stress | Dynamic Yield Stress | Plastic Viscosity |
|---|---|---|---|---|---|---|
| kg/m3 | % | % | Pa | Pa | Pa·s | |
| 1 | 425 | 0.2 | 1.0 | 361.484 | 631.4 | 49.1 |
| 2 | 425 | 0.4 | 1.0 | 392.677 | 728.7 | 60.9 |
| 3 | 425 | 0.6 | 1.0 | 444.476 | 760.7 | 69.7 |
| 4 | 427.2 | 0.8 | 1.0 | 507.826 | 839.3 | 79.1 |
| 5 | 422.7 | 1.0 | 1.0 | 511.162 | 931.9 | 95.9 |
| 6 | 420.4 | 1.2 | 1.0 | 523.544 | 947.4 | 104.5 |
| Rheological Parameters | Neural Network Models | R2 | RMSE | MAPE | MAE |
|---|---|---|---|---|---|
| Static yield stress | BP | 0.91 | 19.53 | 3.86% | 16.18 |
| GA–BP | 0.95 | 14.16 | 2.58% | 11.25 | |
| Dynamic yield stress | BP | 0.72 | 60.17 | 6.80% | 52.02 |
| GA–BP | 0.83 | 47.48 | 5.49% | 41.53 | |
| Plastic viscosity | BP | 0.94 | 4.61 | 5.88% | 4.07 |
| GA–BP | 0.96 | 3.64 | 4.77% | 3.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Zhang, P.; Wang, J.; Hu, S. Prediction of Rheological Properties of PVA Fiber and Nano-SiO2-Reinforced Geopolymer Mortar Based on Back Propagation Neural Network Model Optimized by Genetic Algorithm. Polymers 2025, 17, 1046. https://doi.org/10.3390/polym17081046
Zhang G, Zhang P, Wang J, Hu S. Prediction of Rheological Properties of PVA Fiber and Nano-SiO2-Reinforced Geopolymer Mortar Based on Back Propagation Neural Network Model Optimized by Genetic Algorithm. Polymers. 2025; 17(8):1046. https://doi.org/10.3390/polym17081046
Chicago/Turabian StyleZhang, Guo, Peng Zhang, Juan Wang, and Shaowei Hu. 2025. "Prediction of Rheological Properties of PVA Fiber and Nano-SiO2-Reinforced Geopolymer Mortar Based on Back Propagation Neural Network Model Optimized by Genetic Algorithm" Polymers 17, no. 8: 1046. https://doi.org/10.3390/polym17081046
APA StyleZhang, G., Zhang, P., Wang, J., & Hu, S. (2025). Prediction of Rheological Properties of PVA Fiber and Nano-SiO2-Reinforced Geopolymer Mortar Based on Back Propagation Neural Network Model Optimized by Genetic Algorithm. Polymers, 17(8), 1046. https://doi.org/10.3390/polym17081046







