Tailorable Energy Absorption During Quasi-Static Crush via Additively Manufactured Honeycomb
Abstract
:1. Introduction
2. Materials and Methods
2.1. Manufacturing and Testing
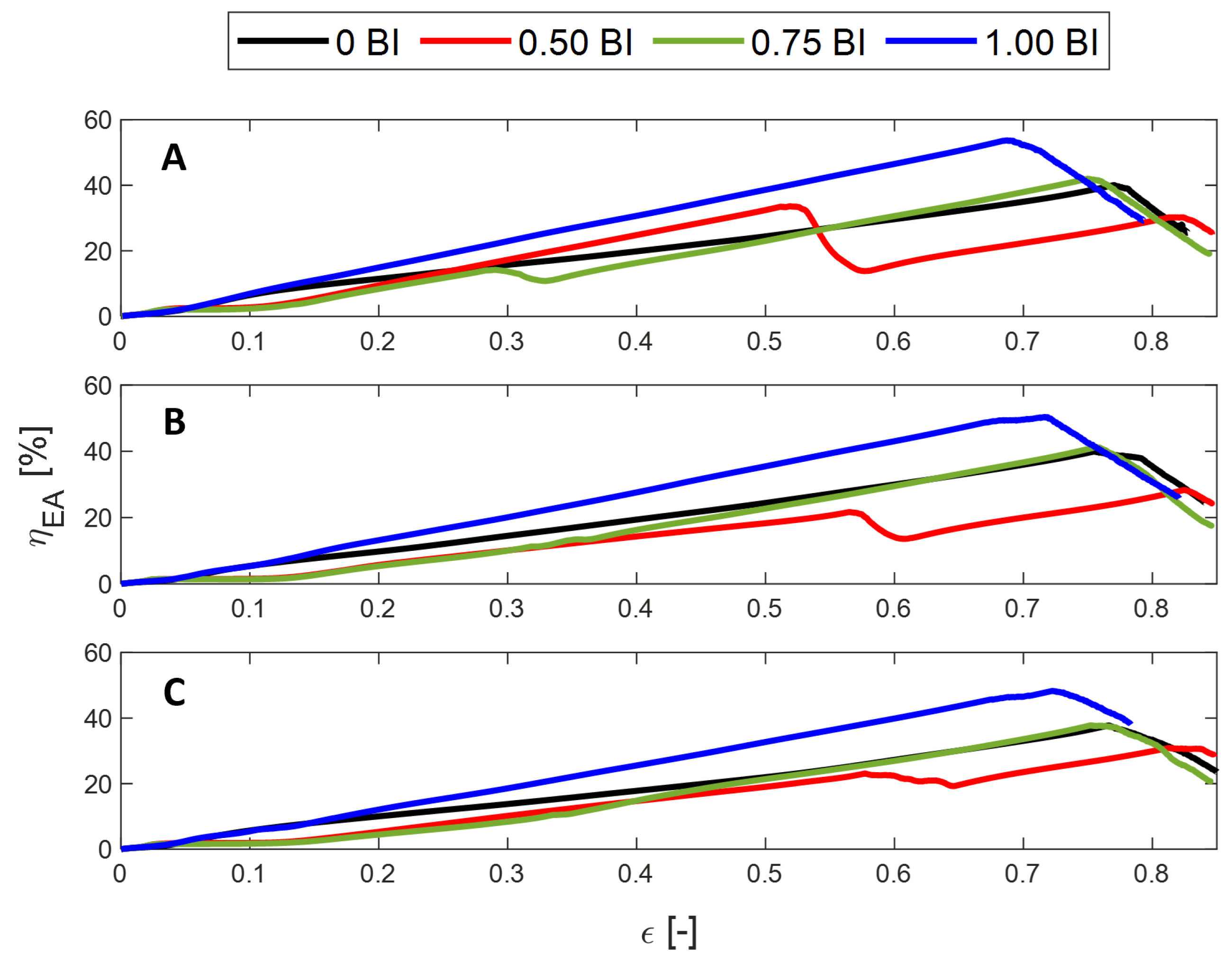
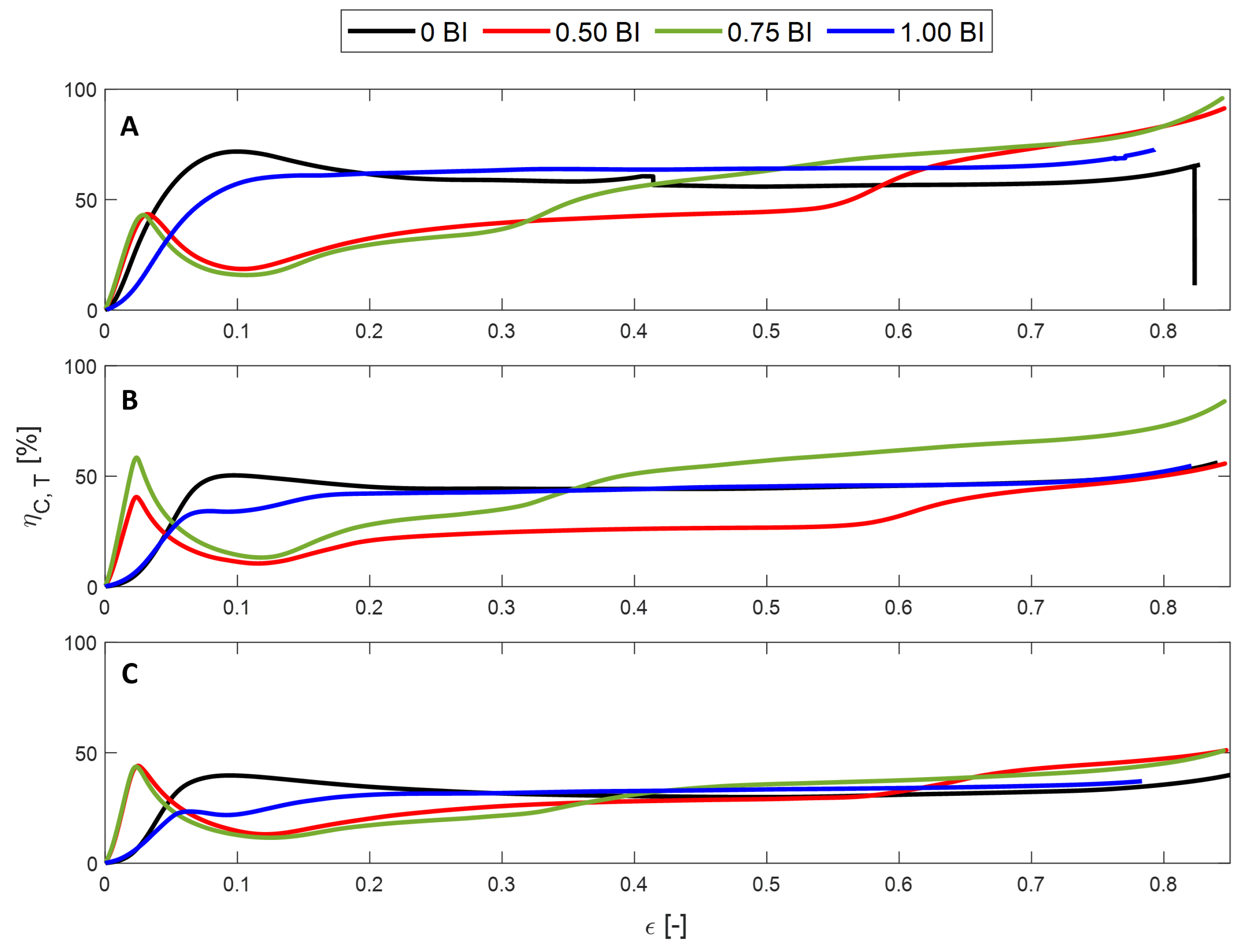
2.2. Metrics
2.3. Computational Analysis
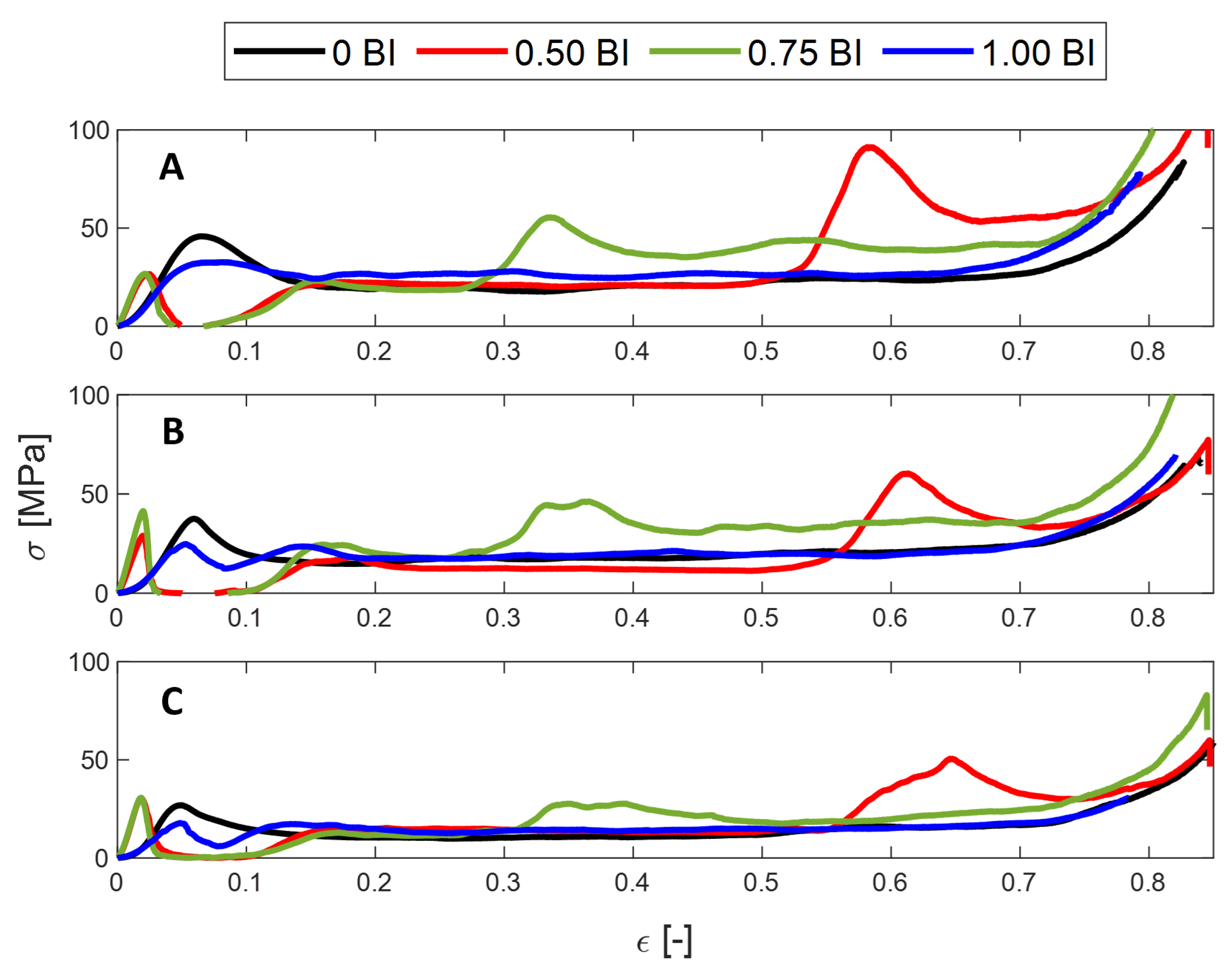
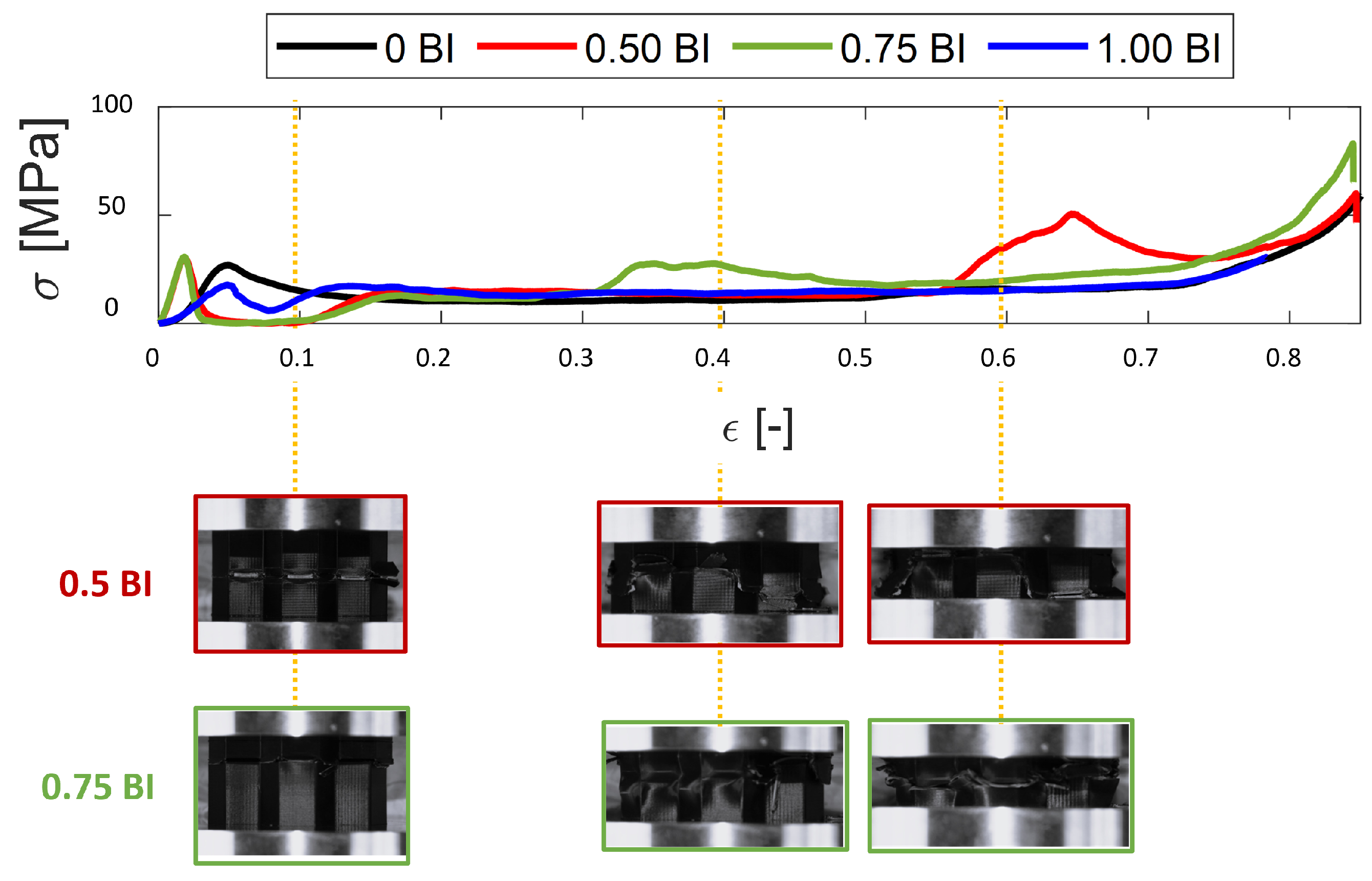
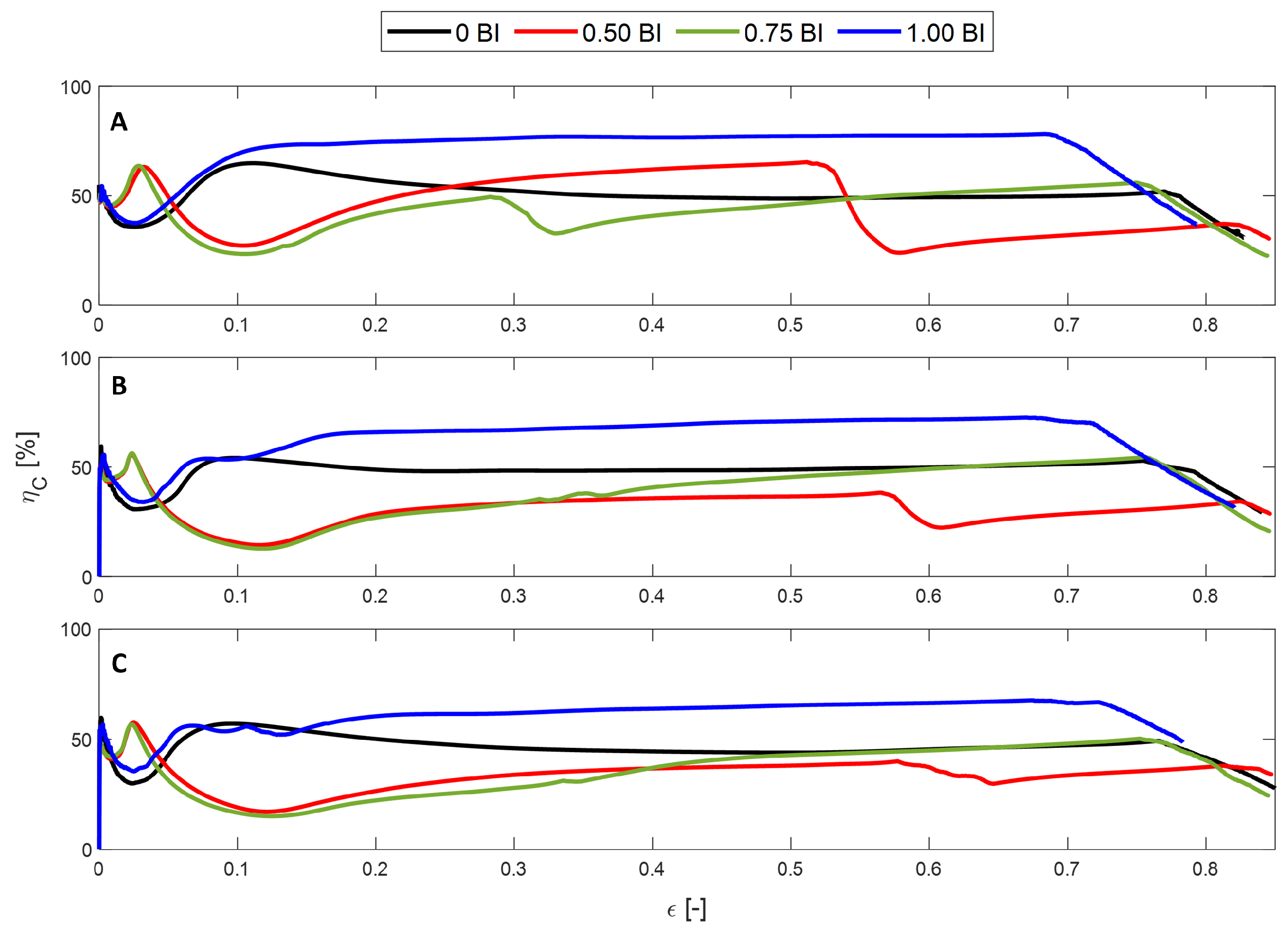
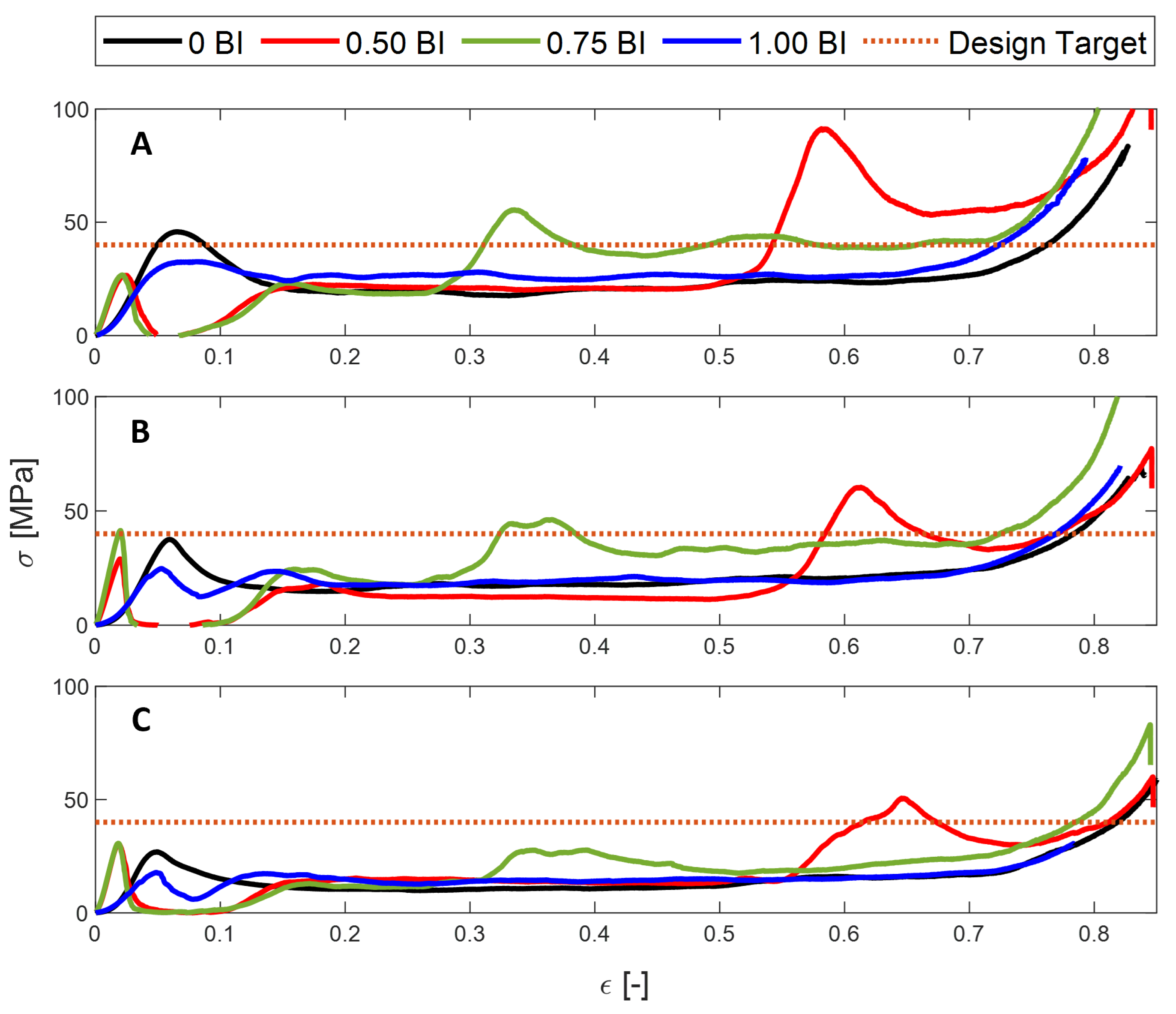
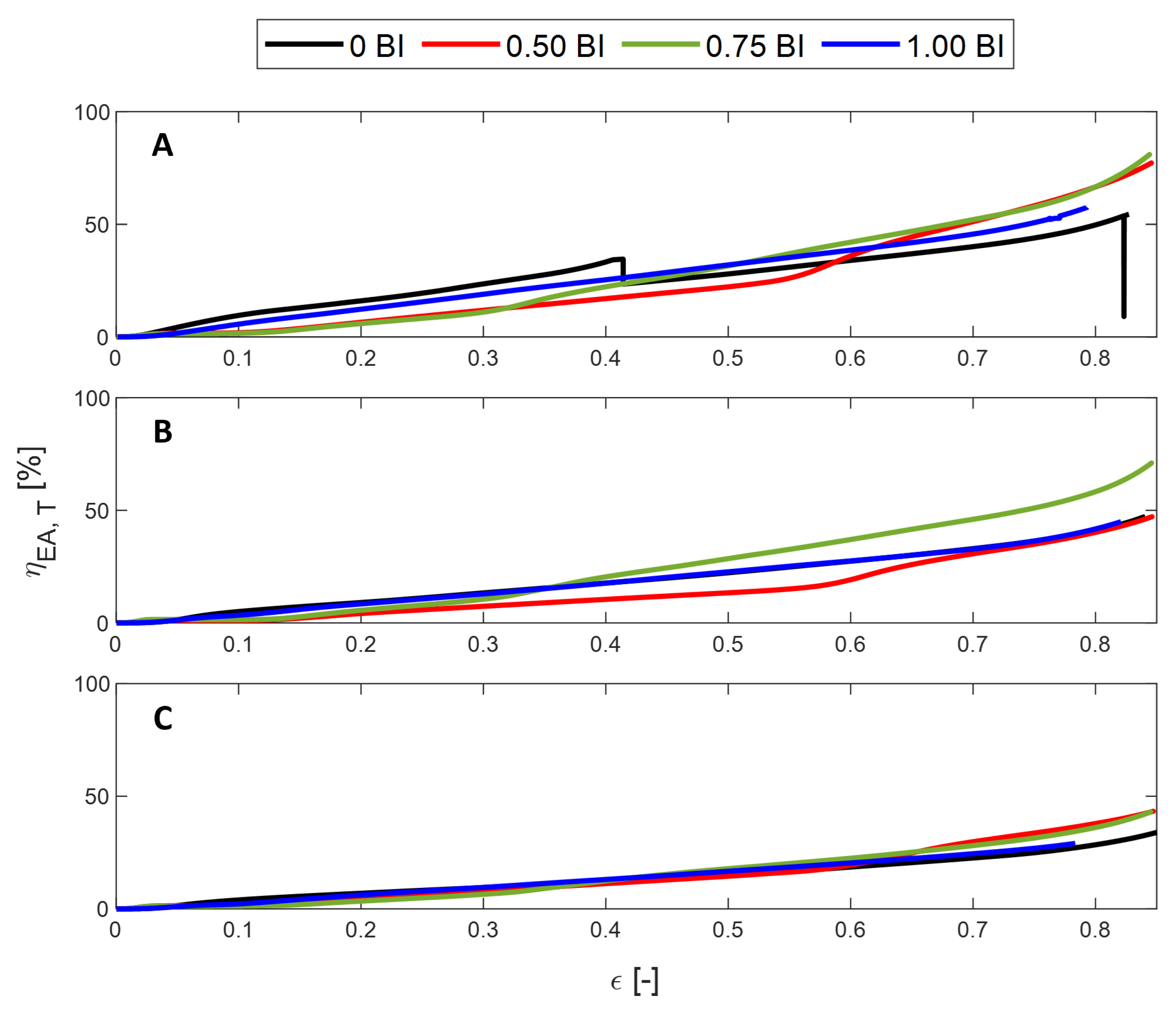
3. Results
3.1. Experimental Tests
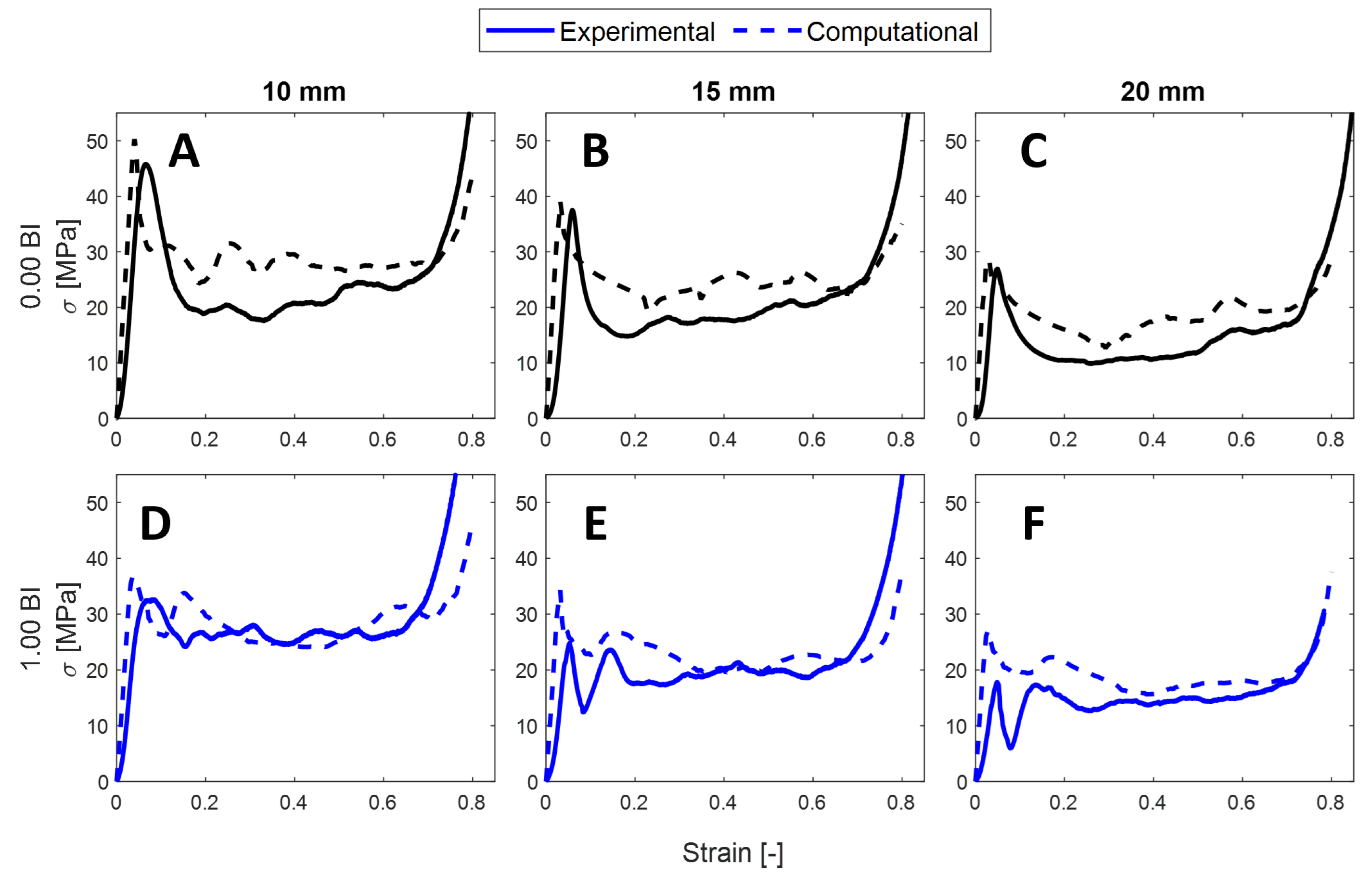
3.2. Validation of Results
3.2.1. FEM Analysis
3.2.2. Analytical Results
3.3. Tailoring to Safety Criteria
4. Discussion
5. Conclusions
- The peak stress and the mean crush stress will decrease with increasing inscribed diameter, regardless of the presence of buckling initiators. Similarly, the crush and energy absorbed efficiency will decrease as the inscribed diameter increases. For all metrics, except for the peak stress, the presence of buckling initiators will increase the performance compared to their counterparts. As mentioned above, the peak stress will decrease with the presence of buckling initiators.
- The performance of these samples was validated through the use of a finite element model in ABAQUS. The same trends are apparent: as the inscribed diameter increases, the peak and mean crush stress and energy absorbed and crush efficiencies will decrease regardless of the presence of buckling initiators.
- The analytical analysis validated the performance of the samples as well. The re-derived version of Roark’s equation allows the peak stress to be accurately predicted. The peak and mean crush stress decrease with increasing inscribed diameters.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AM | Additive Manufacturing |
| BI | Buckling Initiators |
| CE | Crush Efficiency |
| EA | Energy Absorption |
| FDM | Fused Deposition Modeling |
| HC | HoneyComb |
| HHC | Hexagonal HoneyComb |
| 0 BI | HHC sample with no buckling initiators |
| 0.5 BI | HHC sample with BI halfway up the sample |
| 0.75 BI | HHC sample with BI three quarters of the way up the sample |
| 1.0 BI | HHC sample with BI at the top of the sample |
Appendix A
| Diameter | Avg | |||||||
|---|---|---|---|---|---|---|---|---|
| (mm) | (MPa) | (MPa) | (%) | (%) | (%) | (-) | ||
| 10 | 0 BI | Measured | 8.00 | 5.28 | 41.35 | 1.86 | 50.90 | 0.0040 |
| Computed | 50.30 | 30.99 | 58.34 | 2.10 | 57.99 | 0.0005 | ||
| % Change | 528.8 | 998.3 | 41.08 | 12.90 | 13.93 | 87.5 | ||
| 1 BI | Measured | 5.93 | 5.01 | 60.01 | 47.79 | 72.84 | 0.0079 | |
| Computed | 36.73 | 28.96 | 72.39 | 54.96 | 74.17 | 0.0022 | ||
| % Change | 519.4 | 478.0 | 20.63 | 15.00 | 1.83 | 72.15 | ||
| 15 | 0 BI | Measured | 4.66 | 2.84 | 51.40 | 40.44 | 54.40 | 0.0026 |
| Computed | 39.13 | 27.13 | 67.82 | 49.41 | 63.32 | 0.0010 | ||
| % Change | 739.7 | 855.3 | 31.95 | 22.18 | 16.40 | 61.59 | ||
| 1 BI | Measured | 3.38 | 3.10 | 49.57 | 38.15 | 65.62 | 0.0072 | |
| Computed | 34.32 | 24.40 | 60.99 | 45.30 | 66.98 | 0.0011 | ||
| % Change | 915.4 | 687.1 | 23.04 | 18.43 | 2.07 | 84.72 | ||
| 20 | 0 BI | Measured | 2.92 | 1.77 | 40.37 | 30.20 | 46.87 | 0.0029 |
| Computed | 28.74 | 21.82 | 54.55 | 37.00 | 64.58 | 0.0026 | ||
| % Change | 884.2 | 1132 | 35.13 | 22.52 | 37.78 | 10.34 | ||
| 1 BI | Measured | 2.27 | 1.72 | 38.21 | 30.64 | 61.61 | 0.0041 | |
| Computed | 27.08 | 20.46 | 51.16 | 37.92 | 70.88 | 0.0012 | ||
| % Change | 1092 | 1089 | 33.89 | 23.76 | 15.05 | 70.73 |
References
- Mansour, M.T.; Tsongas, K.; Tzetzis, D. 3D Printed Hierarchical Honeycombs with Carbon Fiber and Carbon Nanotube Reinforced Acrylonitrile Butadiene Styrene. J. Compos. Sci. 2021, 5, 62. [Google Scholar] [CrossRef]
- Joseph, A.; Mahesh, V.; Mahesh, V. Effect of Loading Rates on the In-Plane Compressive Properties of Additively Manufactured ABS and PLA- Based Hexagonal Honeycomb Structures. J. Thermoplast. Compos. Mater. 2023, 36, 1113–1134. [Google Scholar] [CrossRef]
- Domingues-Rodriguez, G.; Ku-Herrera, J.; Hernandez-Perez, A. An Assesment of the Effect of Printing Orientation, Density, and Filler Pattern on the Compressive Performance of 3D Printed ABS Structures by Fuse Deposition. Int. J. Adv. Manuf. Technol. 2018, 95, 1685–1695. [Google Scholar] [CrossRef]
- Yavuz, G.; Kiral, B.; Hizarci, B.; Kiral, Z. Low- Velocity Single and Repeated Impact Behavior of 3D Printed Honeycomb Cellular Panels. Mater. Test. 2022, 64, 1420–1436. [Google Scholar] [CrossRef]
- Es-Said, O.; Foyos, J.; Noorani, R.; Mendelson, M.; Marloth, R.; Pregger, B. Effect of Layer Orientation on Mechanical Properties of Rapid Prototyped Samples. Mater. Manuf. Process. 2000, 15, 107–122. [Google Scholar] [CrossRef]
- Ozen, I.; Cava, K.; Gedikli, H.; Alver, U.; Aslan, M. Low-Energy Impact Response of Composite Sandwich Panels with Thermoplastic Honeycomb and Reentrant Cores. Thin-Walled Struct. 2020, 156, 106989. [Google Scholar] [CrossRef]
- Habib, F.; Iovenitti, P.; Masood, S.; Nikzad, M. Cell Geometry Effect on In-Plane Energy Absorption of Periodic Honeycomb Structures. Int. J. Adv. Manuf. Technol. 2018, 94, 2369–2380. [Google Scholar] [CrossRef]
- Menegozzo, M.; Cecchini, A.; Just-Agosot, F.; Acevedo, D.; Velez, O.; Acevedo-Figueroa, I.; Ruiz, J. A 3D Printed Honeycomb Cell Geometry Design with Enhaced Energy Absorption under Axial and Lateral Quasi-Static Compression Loads. Appl. Mech. 2022, 3, 296–312. [Google Scholar] [CrossRef]
- Gordelier, T.; Thies, P.; Turner, L.; Johanning, L. Optimising the FDM Additive Manufacturing Process to Achieve Maximum Tensile Strength: A State-of-the-Art Review. Rapid Prototyp. J. 2019, 25, 953–971. [Google Scholar] [CrossRef]
- Raut, S.; Jattie, V.; Khedkar, N.; Singh, T. Investigation of the Effect of Built Orientation on Mechanical Properties and Total Cost of FDM Parts. Procedia Mater. Sci. 2014, 6, 1625–1630. [Google Scholar] [CrossRef]
- Ivanez, I.; Fernandez-Canadas, L.; Sanchez-Saez, S. Compressive Deformation and Energy Absorption Capability of Ability of Aluminum Honeycomb Core. Compos. Struct. 2017, 174, 123–133. [Google Scholar] [CrossRef]
- Zhang, X.; Su, H.; Yu, T. Energy Absorption of an Axially Crushed Square Tube with a Buckling Initiator. Int. J. Impact Eng. 2009, 36, 402–427. [Google Scholar] [CrossRef]
- Nazir, A.; Arshad, A.B.; Lin, S.; Jeng, J. Mechanical Performance of Lightweight- Designed Honeycomb Structures Fabricated using Multijet Fusion Additive Manufacturing Technology. 3D Print. Addit. Manuf. 2022, 6. [Google Scholar] [CrossRef] [PubMed]
- Kim, H. New extruded multi-cell aluminum profile for maximum crash energy absorption and weight efficiency. Thin-Walled Struct. 2002, 40, 311–327. [Google Scholar] [CrossRef]
- Dionisius, F.; Istiyanto, J.; Sumarsono, D.A.; Prayogo, G.; Baskoro, A.S.; Malawat, M. Modeling of crashworthiness criteria based on variation of hole as crush initiator in thin-walled square. Int. J. Automot. Mech. Eng. 2022, 19, 9487–9497. [Google Scholar] [CrossRef]
- Cheng, Q.; Altenhof, W.; Li, L. Experimental investigations on the crush behaviour of AA6061-T6 aluminum square tubes with different types of through-hole discontinuities. Thin-Walled Struct. 2006, 44, 441–454. [Google Scholar] [CrossRef]
- Bhutada, S.; Goel, M.D. Progressive axial crushing behaviour of Al6061-T6 alloy tubes with geometrical modifications under impact loading. Thin-Walled Struct. 2023, 182, 110240. [Google Scholar] [CrossRef]
- Samer, F.; Tarlochan, F.; Samaka, H.; Khalid, K.; Abdulqadir, S. Improvement of Energy Asorption of Thin Walled Hexagonal Tube Made of Magnesium Alloy by Using Trigger Mechansims. Int. J. Res. Eng. Technol. 2013, 2, 173–180. [Google Scholar]
- Hongyong, J.; Yiru, R.; Binhua, G.; Jinqu, X.; Fuh-Gwo, Y. Design of Novel Plug-Type Triggers for Composite Square Tubes: Enhancement of Energy- Absorption Capacity and Inducing Failure Mechanisms. Int. J. Mech. Sci. 2017, 131, 113–136. [Google Scholar] [CrossRef]
- Ren, Y.; Jiang, H.; Liu, Z. Evaluation of Double- and Triple- Coupled Triggering Mechanisms to Improve Crashworthiness of Composite Tubes. Int. J. Mech. Sci. 2019, 157, 1–12. [Google Scholar] [CrossRef]
- Lau, S.; Said, M.; Yaakob, M. On the Effect of Geometrical Designs and Failure Modes in Composite Axial Crushing: A Literature Review. Compos. Struct. 2012, 94, 803–812. [Google Scholar] [CrossRef]
- Altenolf, B.A.W. Experimental observations on the crush characteristics of AA6061 T4 and T6 structural square tubes with and without circular discontinuities. Int. J. Crashworthiness 2010, 9, 73–87. [Google Scholar] [CrossRef]
- Reid, S.R. Metal Tubes as Impact Energy Absorbers. In Metal Forming and Impact Mechanics; Pergamon: Oxford, UK, 1985; pp. 249–269. [Google Scholar]
- Rezvani, M.; Jahan, A. Effect of Initiator, Design, and Material on Crashworthiness Performance of Thin-Walled Cylindrical Tubes: A Primary Multi-Criteria Analysis in Lightweight Design. Thin-Walled Struct. 2015, 96, 169–182. [Google Scholar] [CrossRef]
- Choi, Y.; Wereley, N. Energy Absorption Efficiencies of Honeycomb Structures with Buckling Initiators. In Proceedings of the AIAA SCITECH 2024 FORUM, Orlando, FL, USA, 8–12 January 2024. [Google Scholar] [CrossRef]
- Murray, C.; Wise, S.; Wereley, N. Electroplating Additively Manufactured Honeycomb Structures to Increase Energy Absorption Under Quasi-Static Crush. SAMPE J. 2024, 60, 38–45. [Google Scholar] [CrossRef]
- Murray, C.M.; Mao, M.; Park, J.; Howard, J.; Wereley, N.M. Visco-Elastic Honeycomb Structures with Increased Energy Absorption and Shape Recovery Performance Using Buckling Initiators. Polymers 2023, 15, 3350. [Google Scholar] [CrossRef]
- Timoshenko, S.; Gere, J. Theory of Elasticity Stability; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Roark, R.; Young, J. Formulas Stress and Strain; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Wierzbicki, T. Crushing Analysis of Metal Honeycombs. Int. J. Impact Eng. 1983, 1, 157–174. [Google Scholar] [CrossRef]
- Gibson, L.; Ashby, M. Cellular Solids: Structures and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
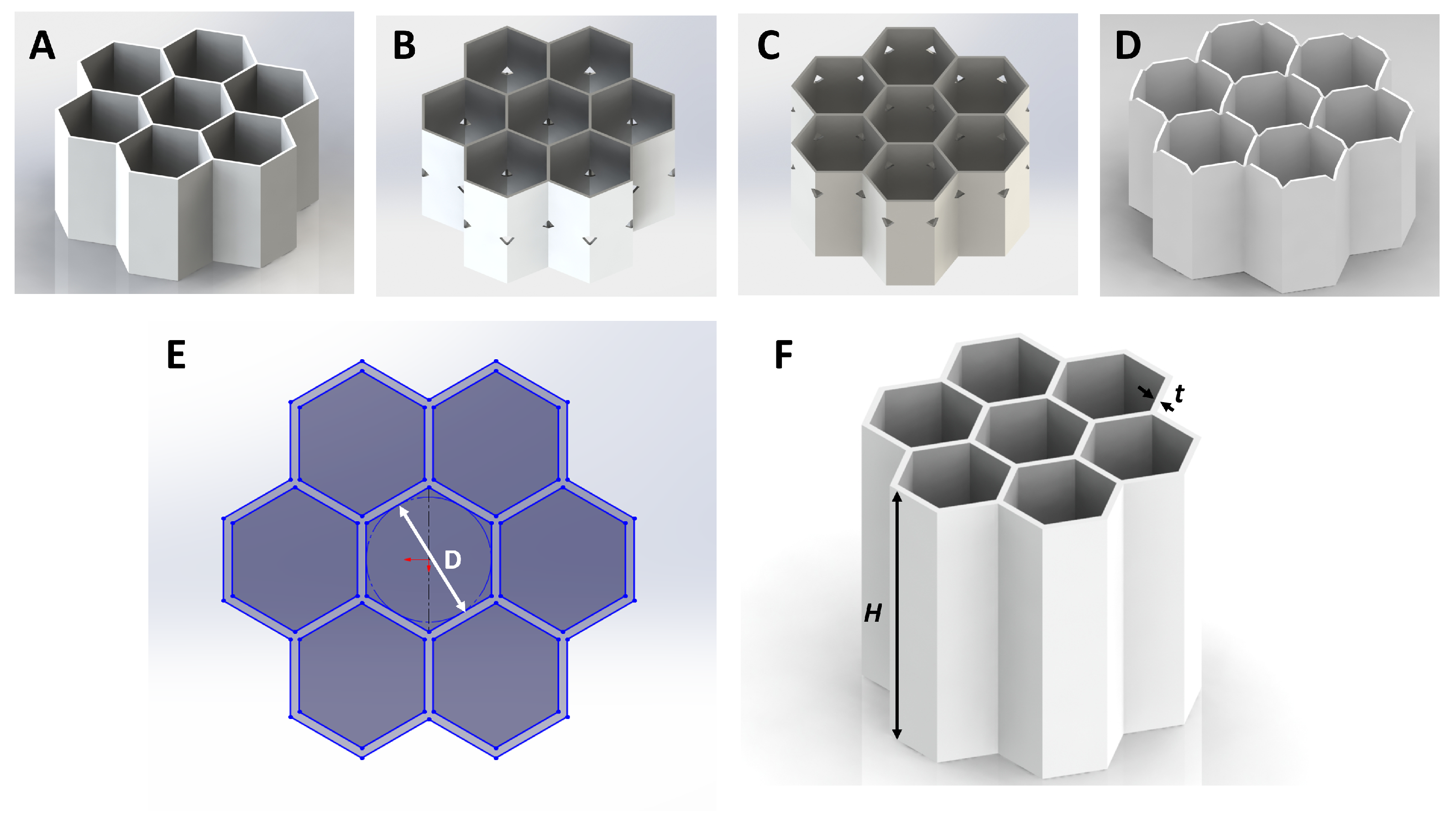




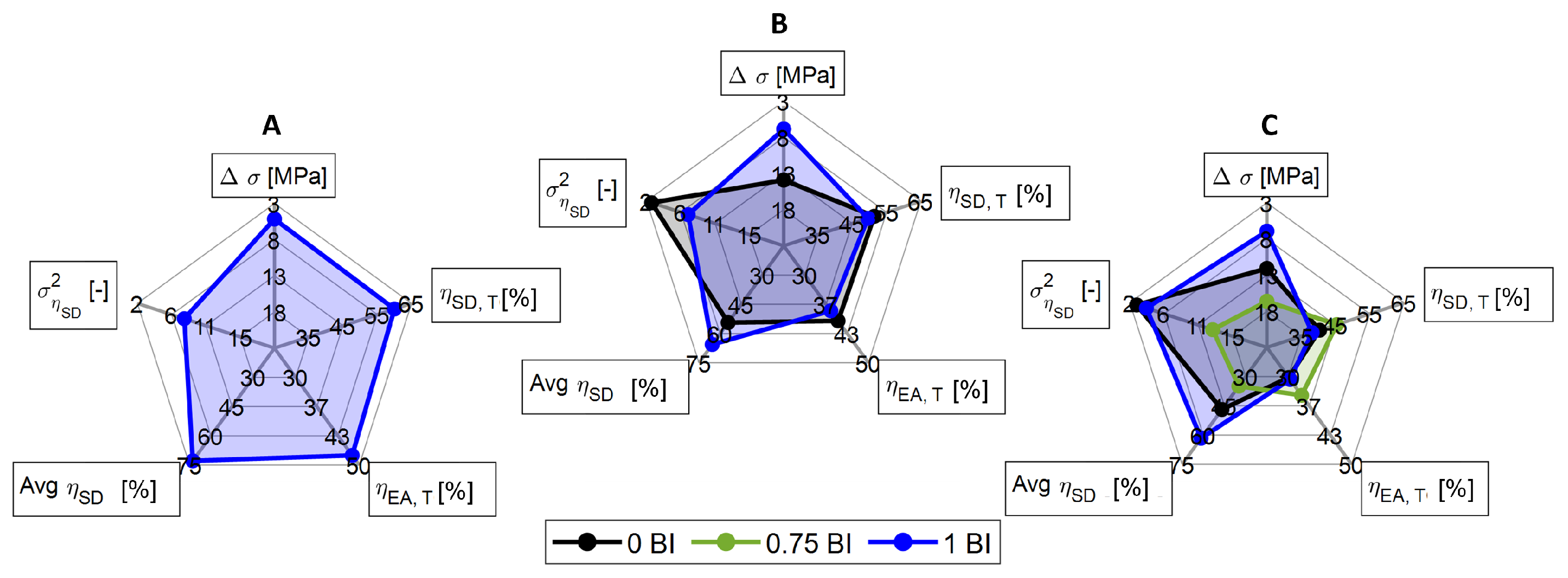
| D | BI | |||||
|---|---|---|---|---|---|---|
| [mm] | [-] | [MPa] | [MPa] | [MPa] | [%] | [%] |
| 10 | 0.00 | 47.09 | 31.09 | 16.00 | 72.37 | 40.10 |
| 0.50 | 91.62 | 34.66 | 56.96 | 65.96 | 34.49 | |
| 0.75 | 55.83 | 30.92 | 24.92 | 64.11 | 42.65 | |
| 1.00 | 33.26 | 28.11 | 5.15 | 78.57 | 54.64 | |
| 15 | 0.00 | 34.11 | 20.21 | 13.90 | 63.20 | 45.72 |
| 0.50 | 61.48 | 21.25 | 40.24 | 55.92 | 28.60 | |
| 0.75 | 49.92 | 27.47 | 22.45 | 57.77 | 41.62 | |
| 1.00 | 25.63 | 18.77 | 6.86 | 73.31 | 51.53 | |
| 20 | 0.00 | 28.10 | 16.02 | 12.08 | 65.92 | 38.97 |
| 0.50 | 50.94 | 20.63 | 29.32 | 57.83 | 34.31 | |
| 0.75 | 33.64 | 17.02 | 16.62 | 56.90 | 38.64 | |
| 1.00 | 21.24 | 14.31 | 6.93 | 73.40 | 49.82 |
| Diamater | Upper Bound | Analytical | Experimental | Lower Bound | |
|---|---|---|---|---|---|
| [mm] | [MPa] | [MPa] | [MPa] | [MPa] | |
| 10 | 22.05 | 20.38 | 8.00 | 0.31 | |
| 15 | 6.84 | 7.41 | 4.66 | 0.13 | |
| 20 | 3.33 | 1.92 | 2.92 | 0.05 | |
| 10 | - | 5.48 | 5.28 | - | |
| 15 | - | 2.99 | 2.56 | - | |
| 20 | - | 1.92 | 1.53 | - |
| Avg | |||||
|---|---|---|---|---|---|
| [MPa] | [%] | [%] | [%] | [-] | |
| Minimum | 3 | 35 | 30 | 30 | 2 |
| Maximum | 18 | 65 | 50 | 75 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murray, C.M.; Johnson, G.N.; Mao, M.; Wereley, N.M. Tailorable Energy Absorption During Quasi-Static Crush via Additively Manufactured Honeycomb. Polymers 2025, 17, 1050. https://doi.org/10.3390/polym17081050
Murray CM, Johnson GN, Mao M, Wereley NM. Tailorable Energy Absorption During Quasi-Static Crush via Additively Manufactured Honeycomb. Polymers. 2025; 17(8):1050. https://doi.org/10.3390/polym17081050
Chicago/Turabian StyleMurray, Colleen M., Grace N. Johnson, Min Mao, and Norman M. Wereley. 2025. "Tailorable Energy Absorption During Quasi-Static Crush via Additively Manufactured Honeycomb" Polymers 17, no. 8: 1050. https://doi.org/10.3390/polym17081050
APA StyleMurray, C. M., Johnson, G. N., Mao, M., & Wereley, N. M. (2025). Tailorable Energy Absorption During Quasi-Static Crush via Additively Manufactured Honeycomb. Polymers, 17(8), 1050. https://doi.org/10.3390/polym17081050







