Analyzing the Tensile Creep Behavior of Different Types of Polypropylenes Using a Simple Fractional Differential Viscoelastic Model
Abstract
1. Introduction
2. Experimental
2.1. Materials
2.2. Creep Test
3. Results and Discussion
3.1. Analysis from Primary to Secondary Creep
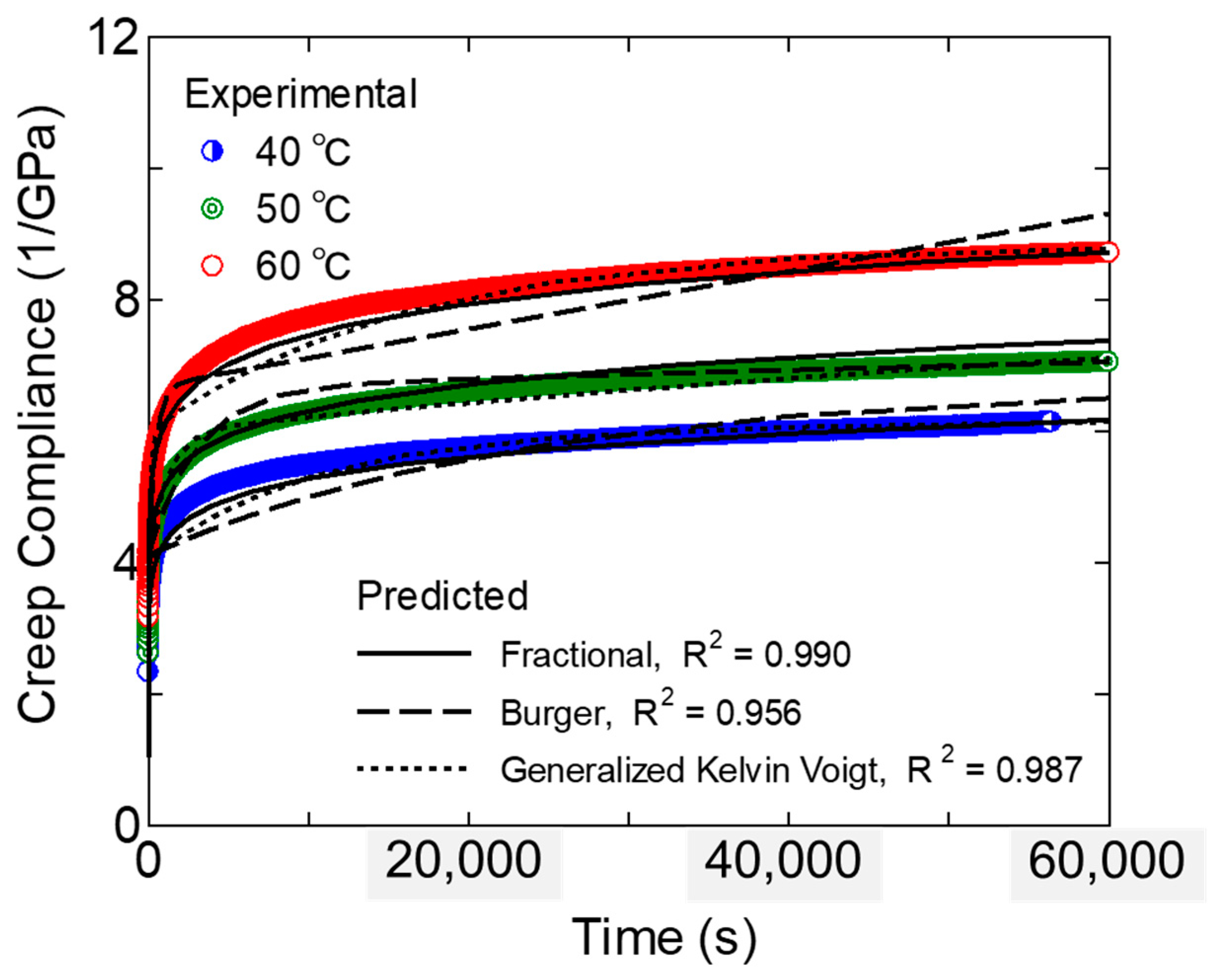
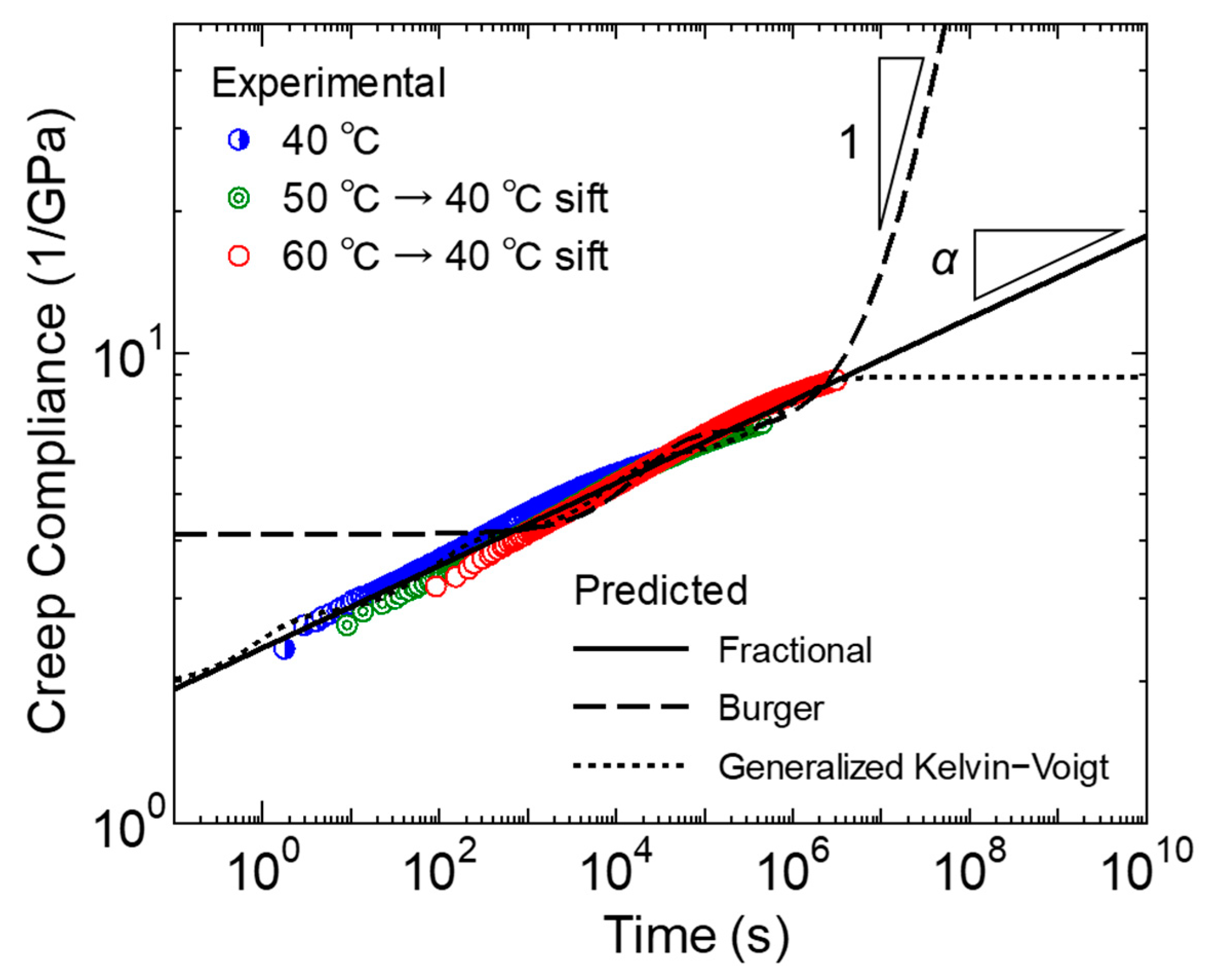
3.1.1. Experimental Results and Modeling Using Various Creep Models
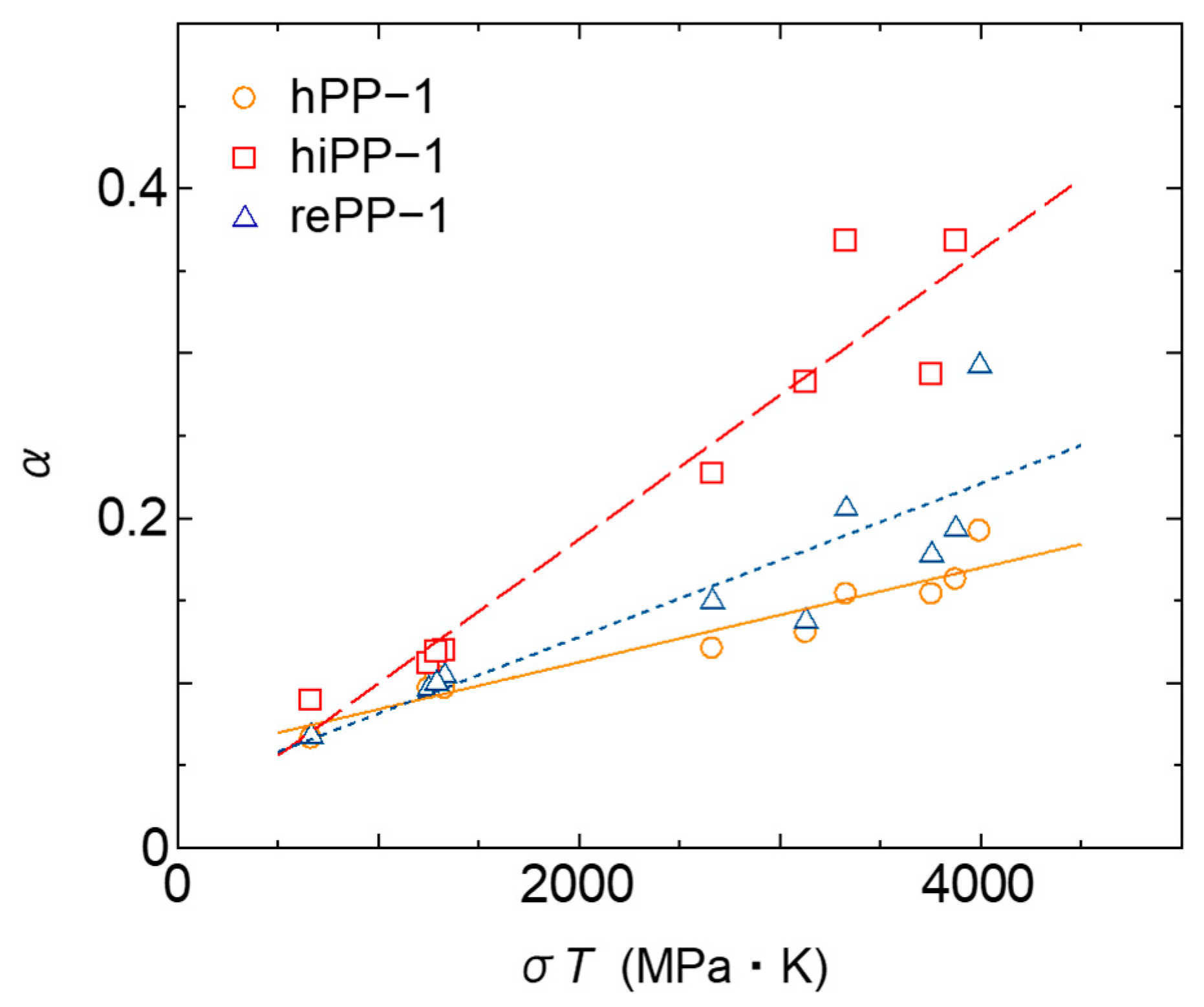
3.1.2. Temperature and Stress Dependence of Fractional Differential Order
3.2. Analysis of Tertiary Creep
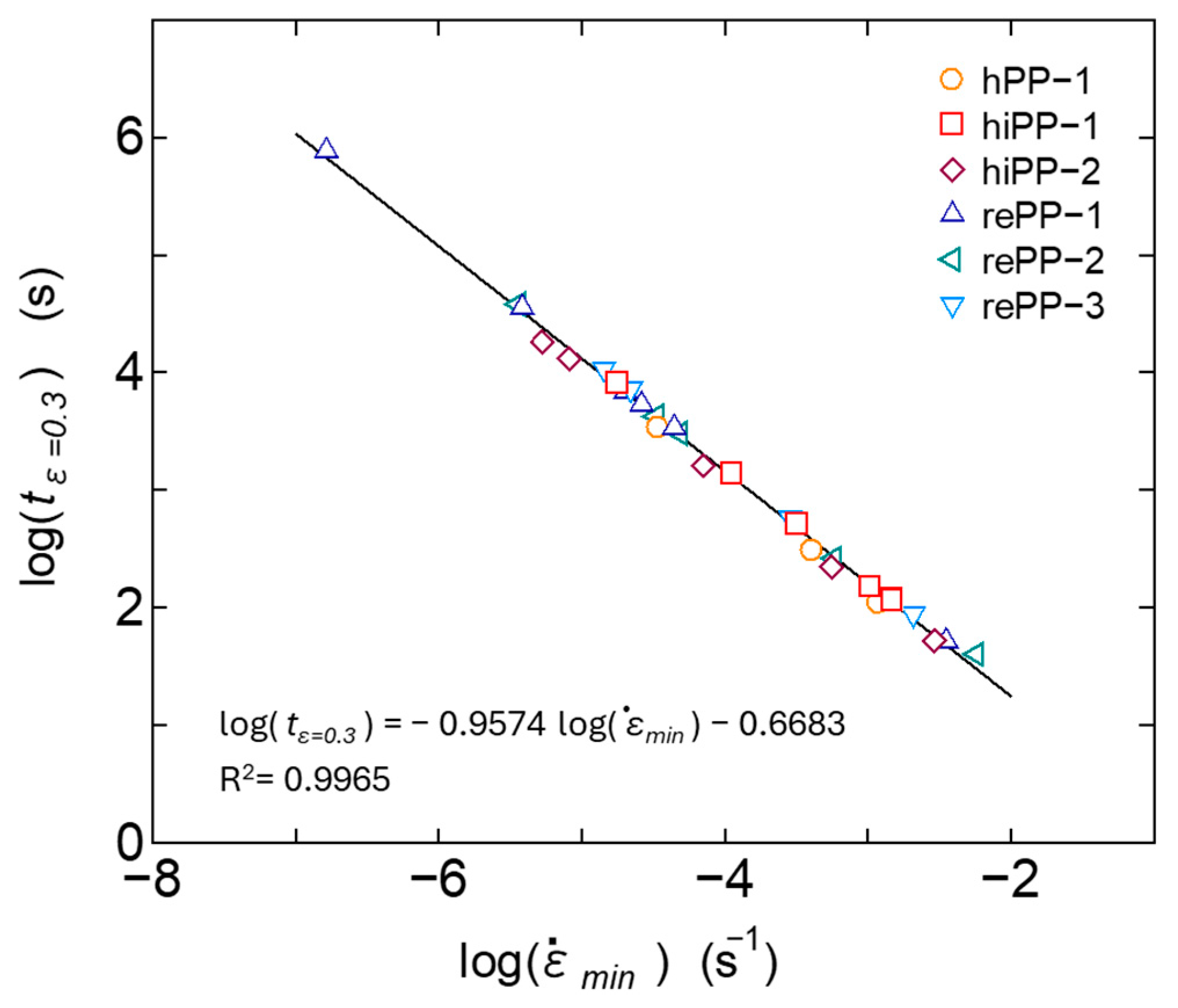
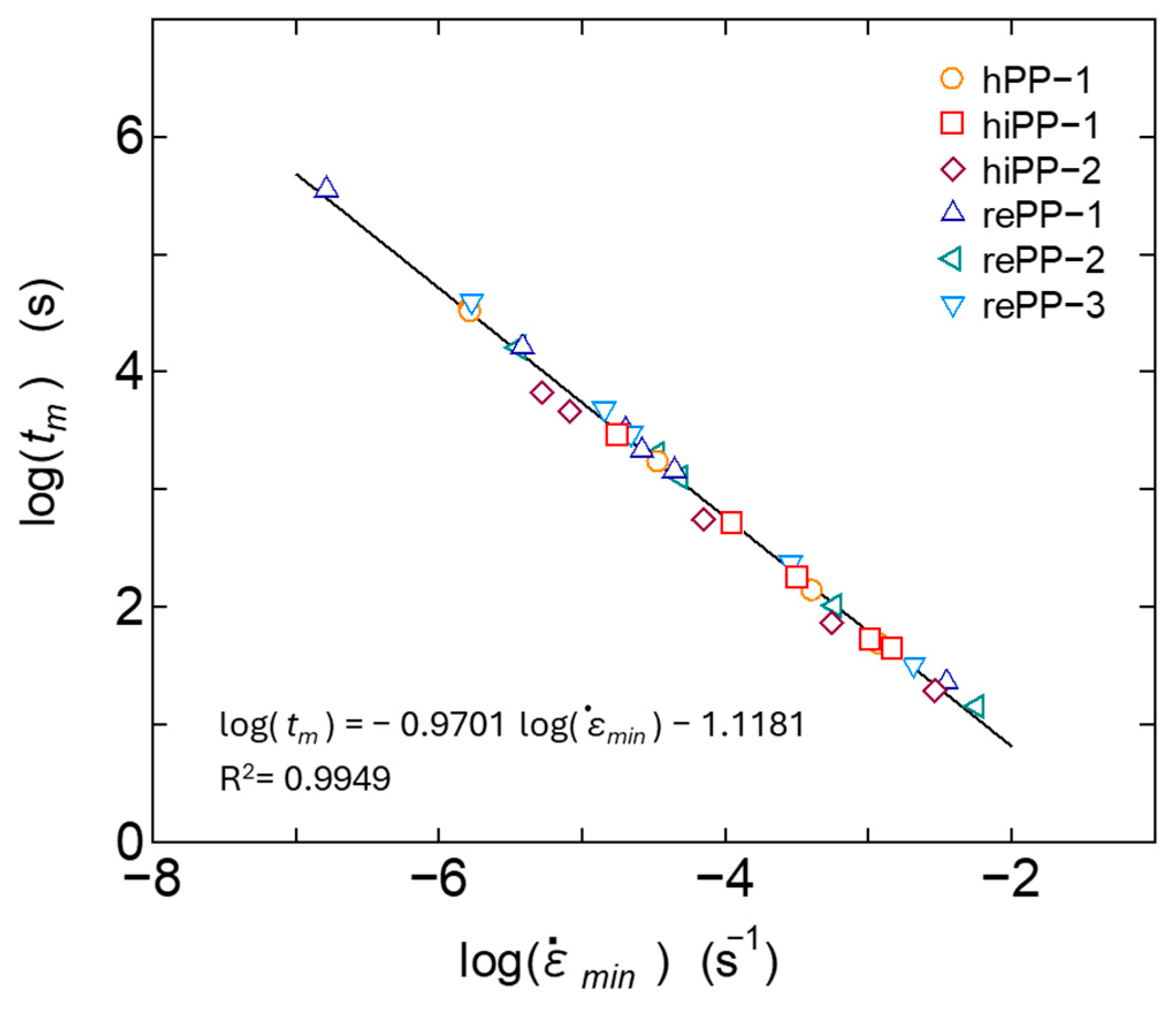
3.2.1. Application of the Monkman–Grant Law
3.2.2. Stress Dependence on Tertiary Creep
3.3. Prediction of the Overall Creep Behavior
3.3.1. Overall Creep Prediction Model
3.3.2. Parameter Identification and Material Property Analysis
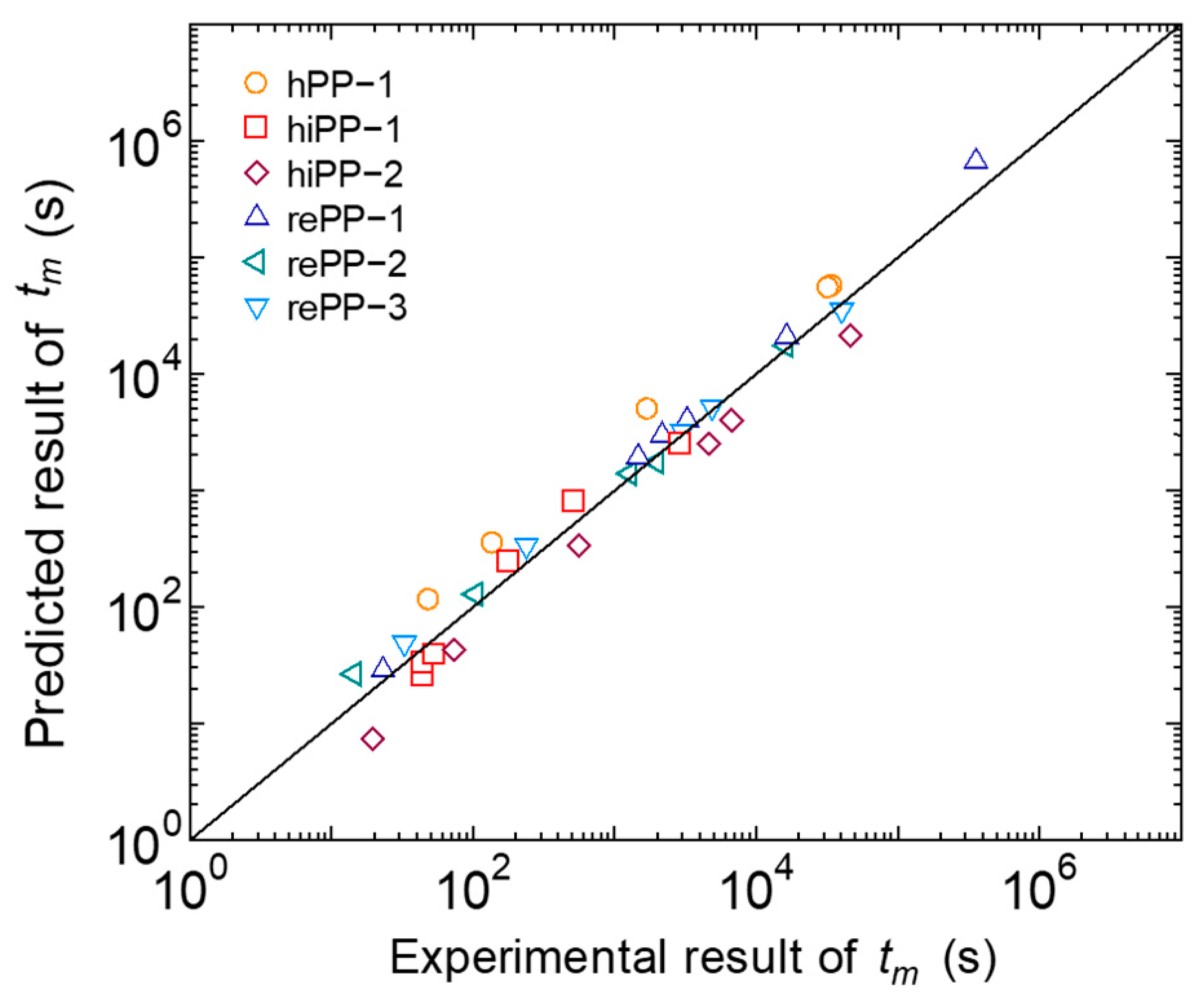
3.3.3. Application to Predict Rupture
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schyns, Z.O.; Shaver, M.P. Mechanical recycling of packaging plastics: A review. Macromol. Rapid Commun. 2021, 42, 200041. [Google Scholar] [CrossRef] [PubMed]
- Khalid, M.Y.; Arif, Z.U.; Ahmed, W.; Arshad, H. Recent trends in recycling and reusing techniques of different plastic polymers and their composite materials. Sustain. Mater. Technol. 2022, 31, e00382. [Google Scholar] [CrossRef]
- Nutting, P. A new general law of deformation. J. Franklin Inst. 1921, 191, 679–685. [Google Scholar] [CrossRef]
- Norton, F. The Creep of Steels at High Temperatures; Mc Graw Hill: New York, NY, USA, 1929; Volume 1, p. 90. [Google Scholar]
- Findley, W.N.; Lai, J.S.; Onaran, K. Creep and Relaxation of Nonlinear Viscoelastic Materials; Dover Publication: New York, NY, USA, 1989. [Google Scholar]
- Yao, H.T.; Xuan, F.; Wang, Z.; Tu, S.T. A review of creep analysis and design under multi-axial stress states. Nuclear Engng Design 2007, 237, 1969–1986. [Google Scholar] [CrossRef]
- Sattar, M.; Othman, A.; Kamaruddin, S.; Akhtar, M.; Khan, R. Limitations on the computational analysis of creep failure models: A review. Eng. Fail. Anal. 2022, 134, 105968. [Google Scholar] [CrossRef]
- Ward, I.M.; Sweeney, J. Mechanical Properties of Solid Polymers, 3rd ed.; John Wiley & Sons: Chichester, UK, 2013. [Google Scholar]
- Starkova, O.; Gagani, A.I.; Karl, C.W.; Rocha, I.; Burlakovs, J.; Krauklis, A.E. Modelling of Environmental Ageing of Polymers and Polymer Composites-Durability Prediction Methods. Polymers 2022, 14, 907. [Google Scholar] [CrossRef]
- Tschoegl, N.W. Phenomenological Theory of Linear Viscoelastic Behavior: An Introduction; Springer: New York, NY, USA, 1989. [Google Scholar]
- Otsuki, Y.; Kajiwara, T.; Funatsu, K. Numerical simulations of annular extrudate swell using various types of viscoelastic models. Polym. Eng. Sci. 1999, 39, 1969–1981. [Google Scholar] [CrossRef]
- Otsuki, Y.; Suzuki, M.; Kin, K.; Suzuki, M.; Kobayashi, Y.; Takarada, Y.; Kikutani, T. Transient Viscoelastic Flow Simulation of Film Blowing Process Incorporating Crystallization Model. Nihon Reoroji Gakkaishi (J. Soc. Rheol. Jpn.) 2022, 50, 197–217. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Otsuki, Y.; Kanno, H.; Sasakawa, T.; Hanamoto, Y.; Kanai, T. Crystallization of Polypropylene Near the Surface in Injection-Molded Plaques: A Comparison of Morphology and a Numerical Analysis. Polym. Eng. Sci. 2011, 51, 1236–1244. [Google Scholar] [CrossRef][Green Version]
- Gemant, A. A method of analyzing experimental results obtained from elastoviscous Bodies. Physics 1936, 7, 311–317. [Google Scholar] [CrossRef]
- Scott Blair, G.W.; Veinoglou, B.C.; Caffyn, J.E. Limitations of the Newtonian time scale in relation to non-equilibrium rheological states and a theory of quasi-properties. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1947, 189, 69–87. [Google Scholar]
- Smit, W.; De Vries, H. Rheological models containing fractional derivatives. Rheol. Acta 1970, 9, 525–534. [Google Scholar] [CrossRef]
- Koeller, R.C. Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity, An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]
- Schulte, U. A vision becomes true: 50 years of pipes made from High Density Polyethylene. In Proceedings of the of Plastic Pipes XIII, Washington, DC, USA, 2–5 October 2006. [Google Scholar]
- Dixon-Stubbs, P.J. Creep Behaviour of Polyethylene and Polypropylene. J. Mater. Sci. 1981, 16, 389–396. [Google Scholar] [CrossRef]
- Hellinckx, S. A quantitative model describing physical aging in isotactic polypropylenes. Colloid. Polym. Sci. 1995, 273, 130–137. [Google Scholar] [CrossRef]
- Tomlins, P.; Read, B. Creep and physical ageing of polypropylene: A comparison of models. Polymer 1998, 39, 355–367. [Google Scholar] [CrossRef]
- Dean, G.D.; Broughton, W. A model for non-linear creep in polypropylene. Polym. Test. 2007, 26, 1068–1081. [Google Scholar] [CrossRef]
- Alcock, B.; Cabrera, N.O.; Barkoula, N.-M.; Reynolds, C.T.; Govaert, L.E.; Peijs, T. The effect of temperature and strain rate on the mechanical properties of highly oriented polypropylene tapes and all-polypropylene composites. Compos. Sci. Technol. 2007, 67, 2061–2070. [Google Scholar] [CrossRef]
- Yamada, H.; Ikeda, M.; Shimbo, M.; Miyano, Y. Prediction Procedure of Creep Rupture of Polypropylene Resin based on Time-temperature Superposition Principle. Seikei-Kakou 2007, 19, 243–247. [Google Scholar] [CrossRef]
- Pedrazzoli, D.; Pegoretti, A. Long-term creep behavior of polypropylene/fumed silica nanocomposites estimated by time–temperature and time–strain superposition approaches. Polym. Bull. 2014, 71, 2247–2268. [Google Scholar] [CrossRef]
- Kolarik, J.; Pegoretti, A. Non-linear tensile creep of polypropylene: Time-strain superposition and creep prediction. Polymer 2006, 47, 346–356. [Google Scholar] [CrossRef]
- Houshyar, S.; Shanks, R.A.; Hodzic, A. Tensile Creep Behaviour of Polypropylene Fibre Reinforced Polypropylene Composites. Polym. Test. 2005, 24, 257–264. [Google Scholar] [CrossRef]
- Zhou, T.H.; Ruan, W.H.; Yang, J.L.; Rong, M.Z.; Zhang, M.Q.; Zhang, Z. A Novel Route for Improving Creep Resistance of Polymers Using Nanoparticles. Compos. Sci. Technol. 2007, 67, 2297–2302. [Google Scholar] [CrossRef]
- Ganß, M.; Satapathy, B.K.; Thunga, M.; Weidisch, R.; Pötschke, P.; Janke, A. Temperature dependence of creep behavior of PP-MWNT nanocomposites. Macromol. Rapid Commun. 2007, 28, 1624–1633. [Google Scholar] [CrossRef]
- Zhai, Z.Y.; Jiang, B.Y.; Drummer, D. Tensile Creep Behavior of Quasi-Unidirectional E-Glass Fabric Reinforced Polypropylene Composite. Polymers 2018, 10, 661. [Google Scholar] [CrossRef]
- Kyzy, B.K.; Lanzutti, A.; Magnan, M.; Rondinella, A.; Simonato, M.; Furlanetto, R.; Fedrizzi, L. Creep study of glass reinforced polypropylene: Effect of temperature and presence of notches. Eng. Fail. Anal. 2021, 128, 105624. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, J.; Huang, Y.; Li, G. Highly Improved Creep Resistance in Polypropylene Through Thermally Reduced Graphene Oxide and Its Creep Lifetime Prediction. Chin. J. Polym. Sci. 2024, 42, 256–266. [Google Scholar] [CrossRef]
- Bek, M.; Aulova, A.; Crešnar, K.P.; Matkovič, S.; Kalin, M.; Perše, L.S. Long-Term Creep Compliance of Wood Polymer Composites: Using Untreated Wood Fibers as a Filler in Recycled and Neat Polypropylene Matrix. Polymers 2022, 14, 2539. [Google Scholar] [CrossRef]
- Kolarik, J.; Pegoretti, A.; Fambri, L.; Penati, A. Non-linear long-term tensile creep of poly-(propylene)/cycloolefin copolymer blends with fibrous structure. Macromol. Mater. Eng. 2003, 288, 629–641. [Google Scholar] [CrossRef]
- Genovese, A.; Shanks, R.A. Time-Temperature Creep Behaviour of Poly(propylene) and Polar Ethylene Copolymer Blends. Macromol. Mater. Eng. 2007, 292, 184–196. [Google Scholar] [CrossRef]
- Kasgoz, A.; Tamer, M.; Kocyigit, C.; Durmus, A. Effect of the Comonomer Content on the Solid-State Mechanical and Viscoelastic Properties of Poly(Propylene-Co-1-Butene) Films. J. Appl. Polym. Sci. 2018, 135, 46350. [Google Scholar] [CrossRef]
- Drozdov, A.D. Creep rupture and viscoelastoplasticity of polypropylene. Eng. Fract. Mech. 2010, 77, 2277–2293. [Google Scholar] [CrossRef]
- Wu, C.; Wu, R.; Xia, W.; Tam, L.h. Understanding Creep Behavior of Semicrystalline Polymer via Coarse-Grained Modeling. J. Polym. Sci. Part B Polym. Phys. 2019, 57, 1779–1791. [Google Scholar] [CrossRef]
- Kasgoz, A.; Akın, D.; Durmus, A. Quantifying Structural and Solid-State Viscoelastic Properties of Poly(propylene) (PP)/Poly(oxymethylene) (POM) Blend Films. Macromol. Mater. Eng. 2016, 301, 1402–1414. [Google Scholar] [CrossRef]
- Kurt, G.; Kasgoz, A. Effects of molecular weight and molecular weight distribution on creep properties of polypropylene homopolymer. J. Appl. Polym. Sci. 2021, 138, 50722. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Z.; Schlarb, A.K.; Friedrich, K. On the characterization of tensile creep resistance of polyamide 66 nanocomposites. Part II: Modeling and prediction of long-term performance. Polymer 2006, 47, 6745–6758. [Google Scholar] [CrossRef]
- Slouf, M.; Steinhart, M.; Nemecek, P.; Gajdosova, V.; Hodan, J. Correlations between Microscale Indentation Creep and Macroscale Tensile Creep of Polymers. Materials 2023, 16, 834. [Google Scholar] [CrossRef]
- Gao, Y.; Zhao, B.; Yin, D. A general fractional model of creep response for polymer materials: Simulation and model comparison. J. Appl. Polym. Sci. 2022, 139, 51577. [Google Scholar] [CrossRef]
- Gao, Y.; Yin, D.; Zhao, B. A variable-order fractional constitutive model to characterize the rate-dependent mechanical behavior of soft materials. Fractal Fract. 2022, 6, 590. [Google Scholar] [CrossRef]
- Wang, P.; Cai, W.; Zhang, Y.; Wang, Z. A fractional rheological model for loading-dependent rheological behavior of polymers. Mech. Time Depend. Mater. 2023, 28, 1–12. [Google Scholar] [CrossRef]
- JIS K 7139; Plastics—Test specimens. Japanese Standards Association: Tokyo, Japan, 2009.
- Nuñez, A.J.; Marcovich, N.E.; Aranguren, M.I. Analysis of the creep behavior of polypropylene-woodflour composites. Polym. Eng. Sci. 2004, 44, 1594–1603. [Google Scholar] [CrossRef]
- Drozdov, A.D. Effect of temperature on the viscoelastic and viscoplastic behavior of polypropylene. Mech. Time-Depend. Mater. 2010, 14, 411–434. [Google Scholar] [CrossRef]
- Kosciuszko, A.; Marciniak, D.; Sykutera, D. Post-Processing Time Dependence of Shrinkage and Mechanical Properties of Injection-Molded Polypropylene. Materials 2021, 14, 22. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhang, J.; Wu, Q.; Petru, M. Fractional calculus-based creep model of HFRP double lap joint subjected to NaCl solution. Polym. Testing 2023, 126, 108166. [Google Scholar] [CrossRef]
- Ribeiro, J.G.T.; De Castro, J.T.P.; Meggiolaro, M.A. Modeling concrete and polymer creep using fractional calculus. J. Mater. Res. Technol. 2021, 12, 1184–1193. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X. A description of the isothermal ageing creep process in polymethyl methacrylate using fractional differential models. Polymers 2024, 16, 2725. [Google Scholar] [CrossRef]
- Cai, S.M.; Chen, Y.M.; Liu, Q.X. Development and validation of fractional constitutive models for viscoelastic-plastic creep in time-dependent materials: Rapid experimental data fitting. Appl. Math. Model. 2024, 132, 645–678. [Google Scholar] [CrossRef]
- Amjadi, M.; Fatemi, A. Creep behavior and modeling of high-density polyethylene (HDPE). Polym. Test. 2021, 94, 107031. [Google Scholar] [CrossRef]
- Jazouli, S.; Luo, W.; Bremand, F.; Vu-Khanh, T. Application of time–stress equivalence to nonlinear creep of polycarbonate. Polym. Test. 2005, 24, 463–467. [Google Scholar] [CrossRef]
- Gao, R.; Wu, F.; Li, C.; Jie, C. Intelligent parameter inversion of fractional-order model based on BP neural network. Lithosphere 2021, 2021, 9477507. [Google Scholar] [CrossRef]
- Wei, E.; Hu, B.; Li, J.; Cui, K.; Zhang, Z.; Cui, A.; Ma, L. Nonlinear Viscoelastic-Plastic Creep Model of Rock Based on Fractional Calculus. Adv. Civ. Eng. 2022, 2022, 3063972. [Google Scholar] [CrossRef]
- Gao, Y.H.; Zhou, Z.; Zhang, H.; Jin, S.; Yang, W.; Meng, Q.H. Viscoelastoplastic displacement solution for deep buried circular tunnel based on a fractional derivative creep model. Adv. Civ. Eng. 2021, 2021, 3664578. [Google Scholar] [CrossRef]
- Zhang, M.J.; Brinson, H.F. Cumulative creep damage for polycarbonate and polysulfone. Exp. Mech. 1986, 26, 155–162. [Google Scholar] [CrossRef]
- Kamdem, T.C.; Richard, K.G.; Béda, T. New description of the mechanical creep response of rocks by fractional derivative theory. Appl. Math. Model. 2022, 116, 624–635. [Google Scholar] [CrossRef]
- Wu, F.; Liu, J.F.; Wang, J. An improved maxwell creep model for rock based on variable-order fractional derivatives. Environ. Earth Sci. 2015, 73, 6965–6971. [Google Scholar] [CrossRef]
- Meng, R.; Yin, D.; Drapaca, C.S. A variable order fractional constitutive model of the viscoelastic behavior of polymers. Int. J. Nonlinear Mech. 2019, 113, 171–177. [Google Scholar] [CrossRef]
- Liu, X.L.; Li, D.J. Nonlinear damage creep model based on variable-order fractional theory for rock materials. SN App. Sci. 2020, 2, 1–11. [Google Scholar] [CrossRef]
- Cai, W.; Wang, P. Fractional modeling of temperature dependent mechanical behaviors for glassy polymers. Int. J. Mech. Sci. 2022, 232, 107607. [Google Scholar] [CrossRef]
- Sweeney, J.; Spares, R.; Woodhead, M. A constitutive model for large multiaxial deformations of solid polypropylene at high temperature. Polym. Eng. Sci. 2009, 49, 1902–1908. [Google Scholar] [CrossRef]
- Nitta, K. On a Thermodynamic Foundation of Eyring Rate Theory for Plastic Deformation of Polymer Solids. Philos. Mag. Lett. 2023, 103, 2186190. [Google Scholar] [CrossRef]








| Name | MFR/g/10 min (230 °C, 2.16 kg) | Tensile Modulus/MPa (50 mm/min) | Type |
|---|---|---|---|
| hPP-1 | 7.0 | 1150 | Homo PP |
| hiPP-1 | 3.1 | 800 | Ethylene copolymerized PP |
| hiPP-2 | 5.0 | 1250 | Ethylene copolymerized PP |
| rePP-1 | 5.7 | 950 | Recycled PP (PCR) |
| rePP-2 | 6.8 | 990 | Recycled PP (PCR) |
| rePP-3 | 4.0 | 1070 | Recycled PP (PCR) |
| EM/GPa | ηM/GPa·s | EK/GPa | ηK/GPa·s |
|---|---|---|---|
| 0.243 | 1,220,000 | 0.391 | 9290 |
| τi/s | Ei/GPa |
|---|---|
| 0.01 | 1.942 |
| 1 | 0.808 |
| 100 | 1.294 |
| 10,000 | 1.941 |
| 1,000,000 | 2.878 |
| Cα/GPa·s α | α |
|---|---|
| 0.443 | 0.0876 |
| Parameters | hPP-1 | hiPP-1 | hiPP-2 | rePP-1 | rePP-2 | rePP-3 | |
|---|---|---|---|---|---|---|---|
| Activation Energy | Ea/kJ/mol | 218.8 | 188.0 | 180.5 | 201.4 | 212.8 | 203.0 |
| Primary–Secondary Creep Parameters | |||||||
| Activation Volume | Va/nm3 | 2.977 | 3.328 | 1.349 | 2.402 | 3.646 | 2.268 |
| Elastic Modulus | E/GPa | 0.1211 | 0.09815 | 0.2129 | 0.1592 | 0.1039 | 0.1861 |
| Retardation Time | θ/s | 1.480 × 106 | 1.654 × 104 | 2.224 × 104 | 1.452 × 104 | 6.431 × 105 | 1.365 × 104 |
| Parameter determining fractional order α | A | 2.776 × 10−5 | 5.265 × 10−5 | 2.495 × 10−5 | 5.314 × 10−5 | 2.720 × 10−5 | 3.409 × 10−5 |
| B | 0.04898 | 0.04804 | 0.05419 | 0.007178 | 0.05706 | 0.04933 | |
| Tertiary Creep Parameters | |||||||
| Parameters of WLF type stress shift function | C1 | 60.94 | 39.79 | 52.41 | 57.90 | 45.25 | 70.32 |
| C2/MPa | 4.232 | 3.829 | 8.122 | 1.516 | 1.172 | 1.748 | |
| σ0/MPa | 2.369 | 2.456 | 0.005922 | 4.374 | 5.362 | 2.792 | |
| Viscosity | η0/GPa·s | 7.977 × 109 | 1.538 × 106 | 1.062 × 1010 | 8.866 × 108 | 1.403 × 108 | 2.63 × 108 |
| Damage Index | β | 0.1702 | 0.4357 | 0.5317 | 0.2729 | 0.1958 | 0.242 |
| Coefficient of Determination R2 | 0.995 | 0.991 | 0.997 | 0.995 | 0.999 | 0.990 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otsuki, Y.; Hashimoto, K.; Kobayashi, Y.; Nishitsuji, S.; Matsuno, H.; Ito, H. Analyzing the Tensile Creep Behavior of Different Types of Polypropylenes Using a Simple Fractional Differential Viscoelastic Model. Polymers 2025, 17, 1095. https://doi.org/10.3390/polym17081095
Otsuki Y, Hashimoto K, Kobayashi Y, Nishitsuji S, Matsuno H, Ito H. Analyzing the Tensile Creep Behavior of Different Types of Polypropylenes Using a Simple Fractional Differential Viscoelastic Model. Polymers. 2025; 17(8):1095. https://doi.org/10.3390/polym17081095
Chicago/Turabian StyleOtsuki, Yasuhiko, Kou Hashimoto, Yutaka Kobayashi, Shotaro Nishitsuji, Hisao Matsuno, and Hiroshi Ito. 2025. "Analyzing the Tensile Creep Behavior of Different Types of Polypropylenes Using a Simple Fractional Differential Viscoelastic Model" Polymers 17, no. 8: 1095. https://doi.org/10.3390/polym17081095
APA StyleOtsuki, Y., Hashimoto, K., Kobayashi, Y., Nishitsuji, S., Matsuno, H., & Ito, H. (2025). Analyzing the Tensile Creep Behavior of Different Types of Polypropylenes Using a Simple Fractional Differential Viscoelastic Model. Polymers, 17(8), 1095. https://doi.org/10.3390/polym17081095








