Thermo-Mechanical Properties of Cis-1,4-Polyisoprene: Influence of Temperature and Strain Rate on Mechanical Properties by Molecular Dynamic Simulations
Abstract
:1. Introduction
2. Theoretical Formulation and Methods
2.1. Green–Kubo Method and Force Field Representation
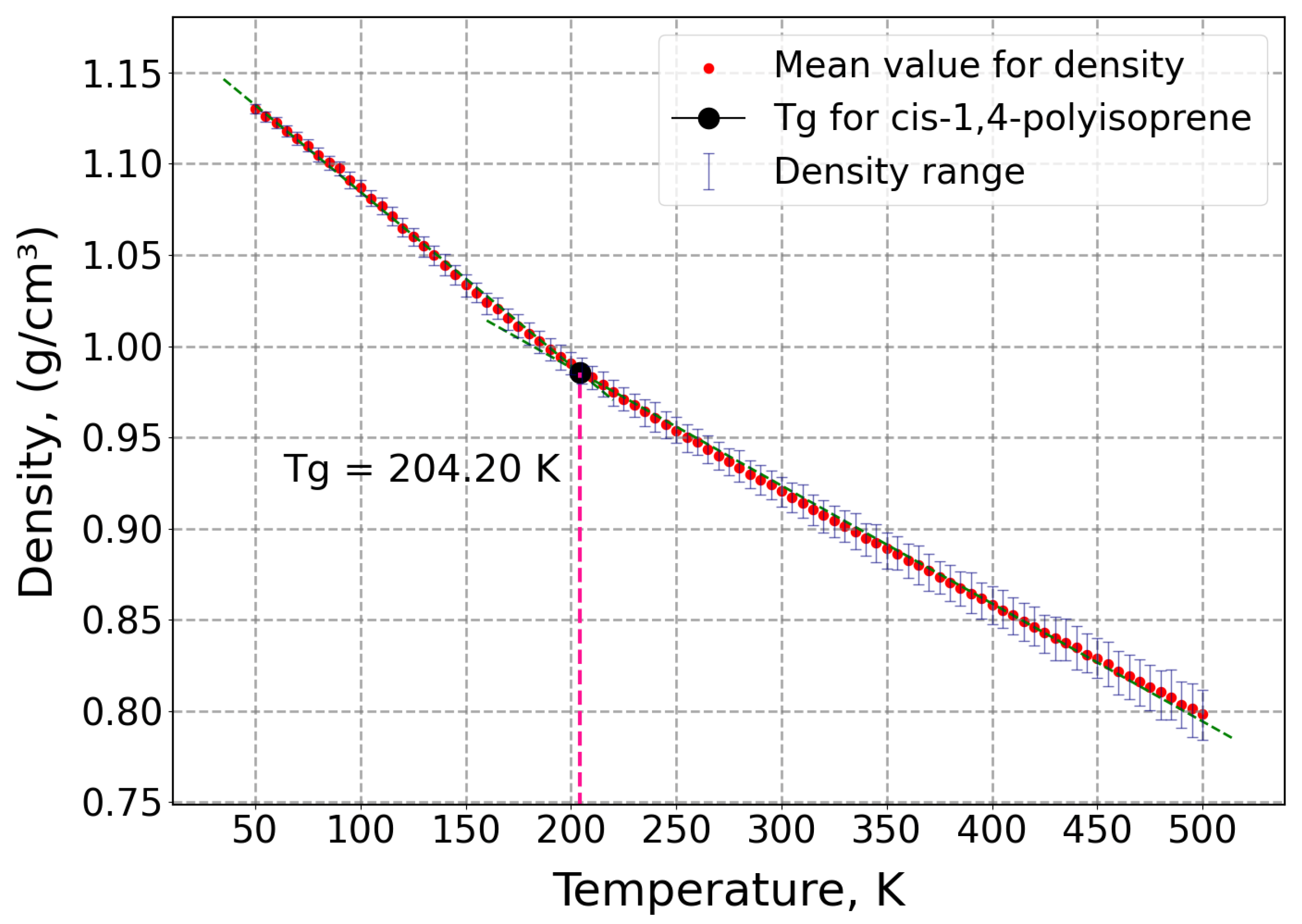
2.2. Glass Transition Temperature
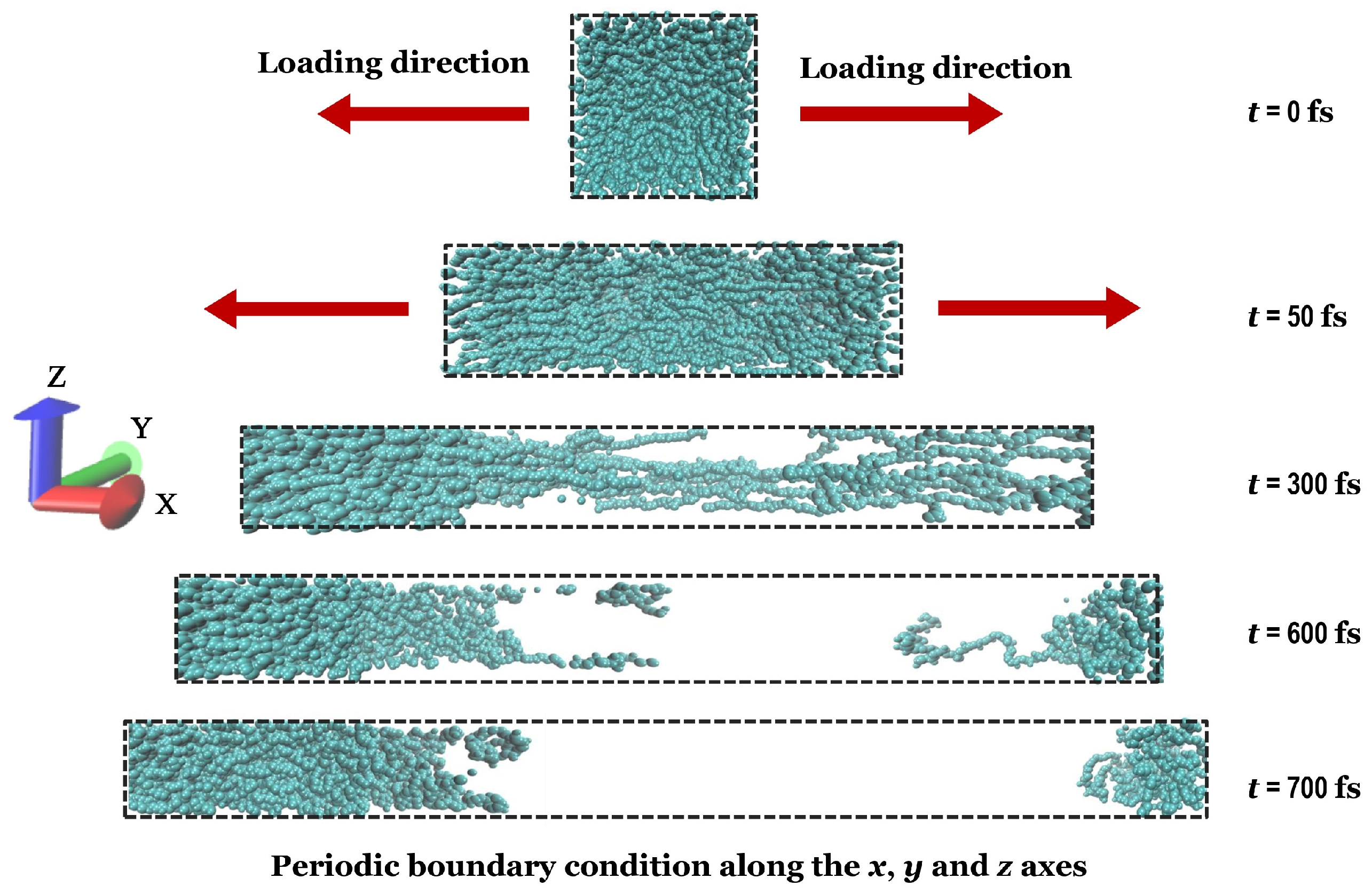
2.3. Uniaxial Tensile Simulation
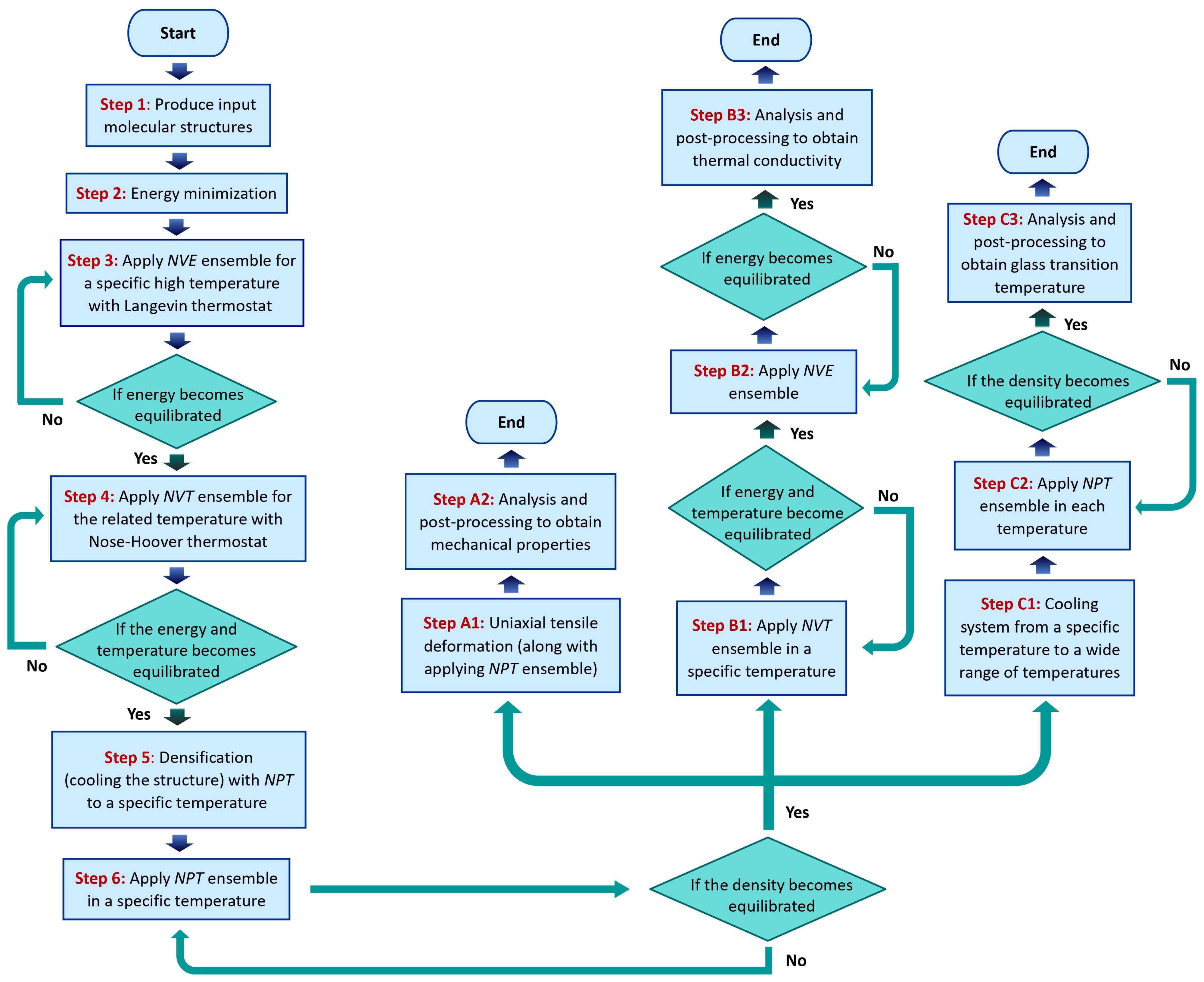
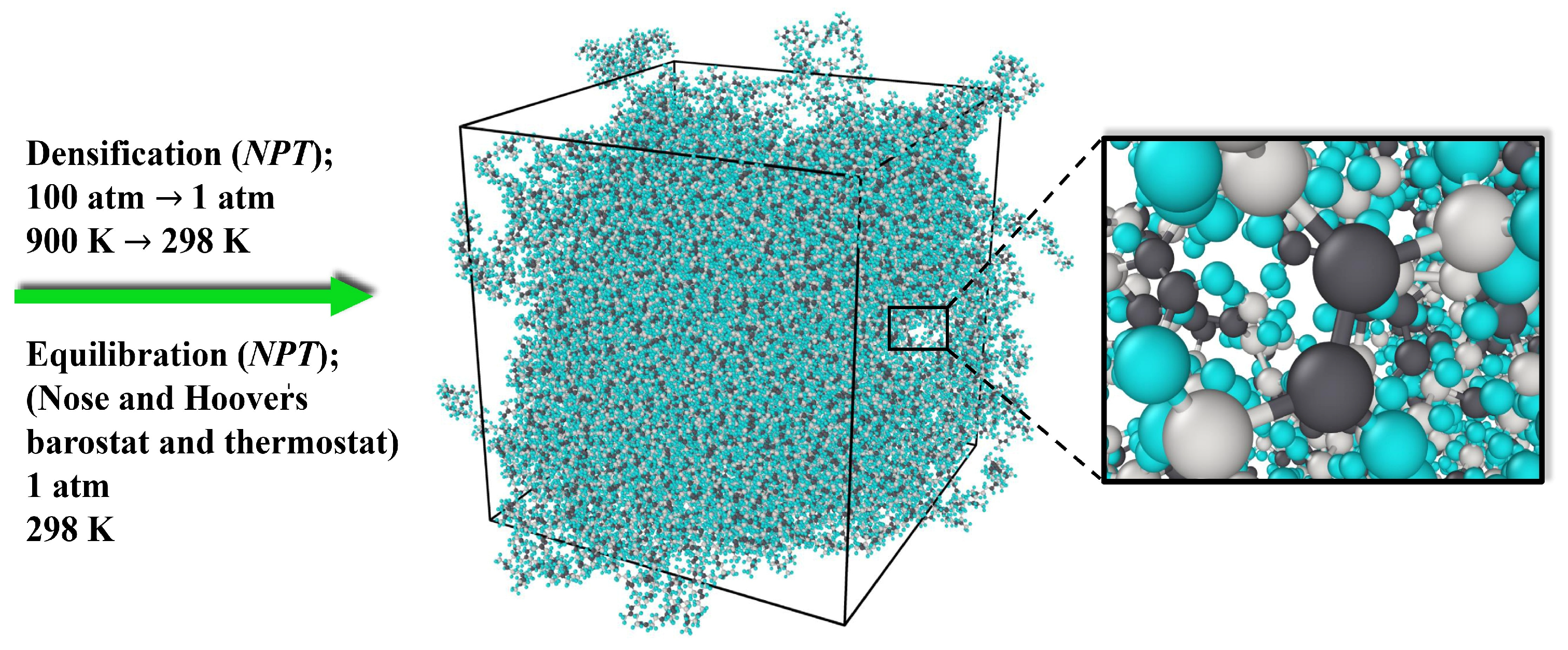
2.4. Set-Up of Simulation and Creation of Model
3. Results and Discussion
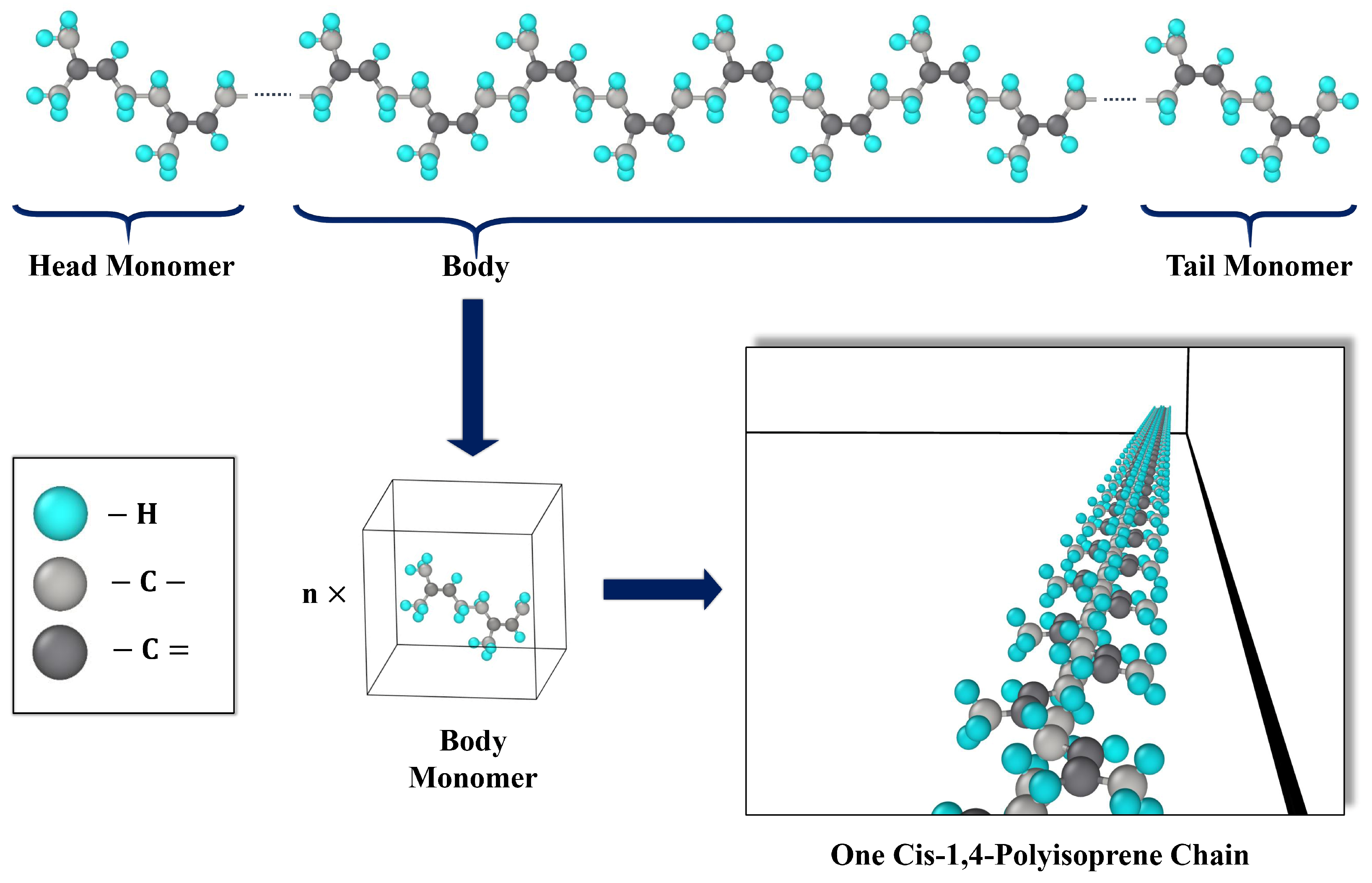
3.1. Representation of Cis-1,4-Polyisoprene in MD Simulations
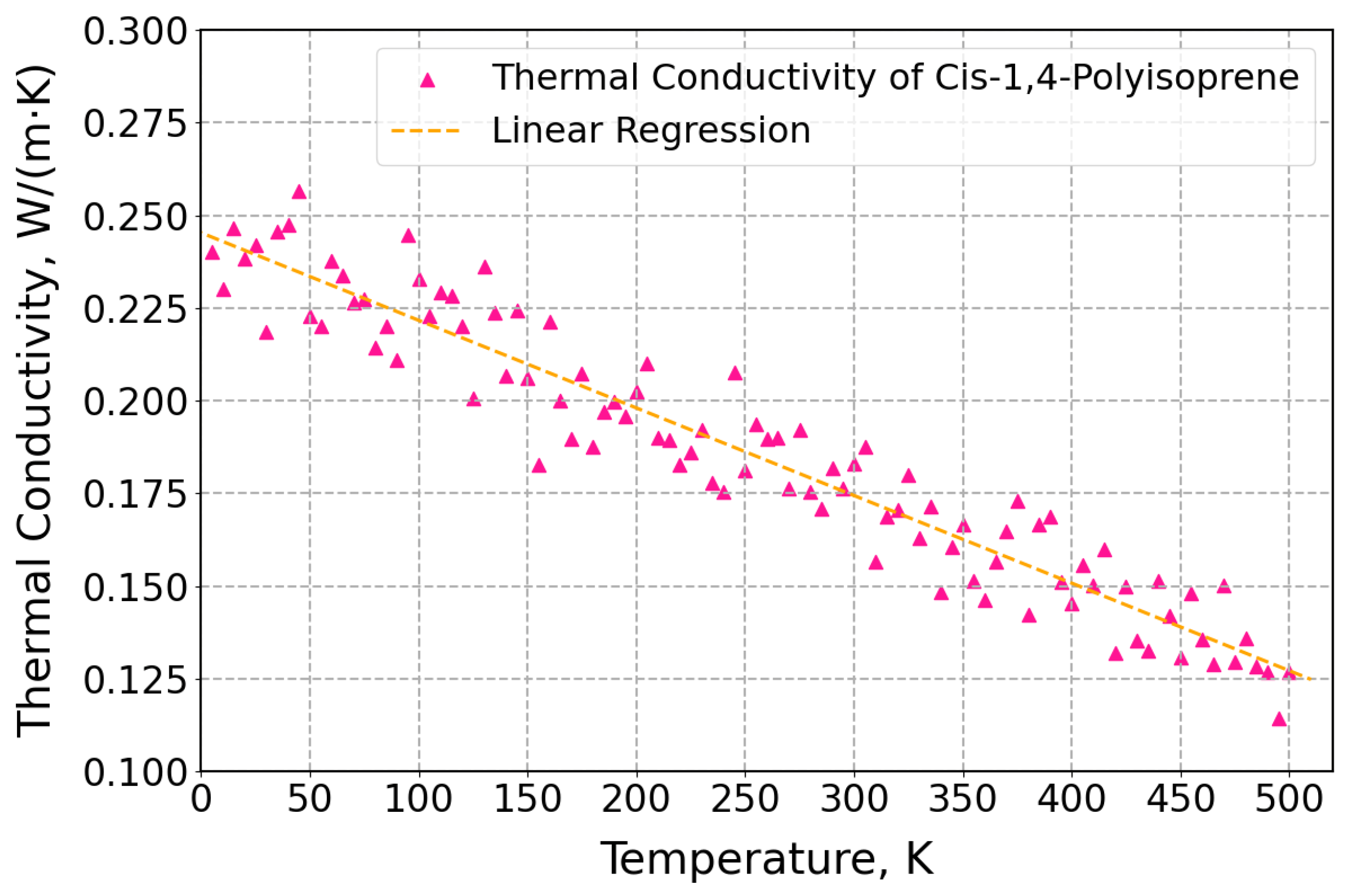
3.2. Thermal Properties of Cis-1,4-Polyisoprene with United-Atom Force Field in MD Simulations
3.3. Results and Analysis of Cis-1,4-Polyisoprene Tensile Simulation
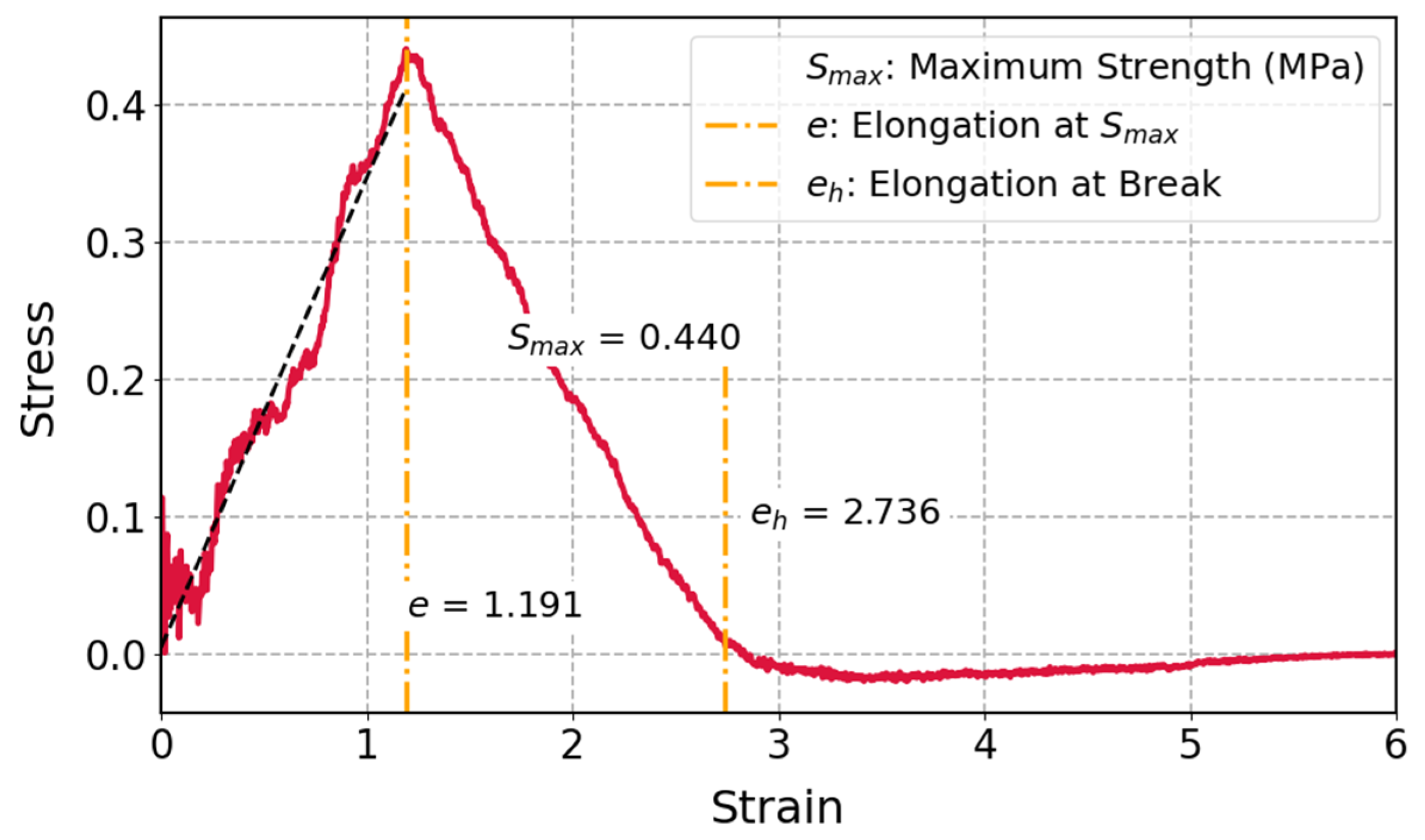
3.3.1. Tensile Test of Cis-1,4-Polyisoprene with All-Atom Force Field in MD Simulations
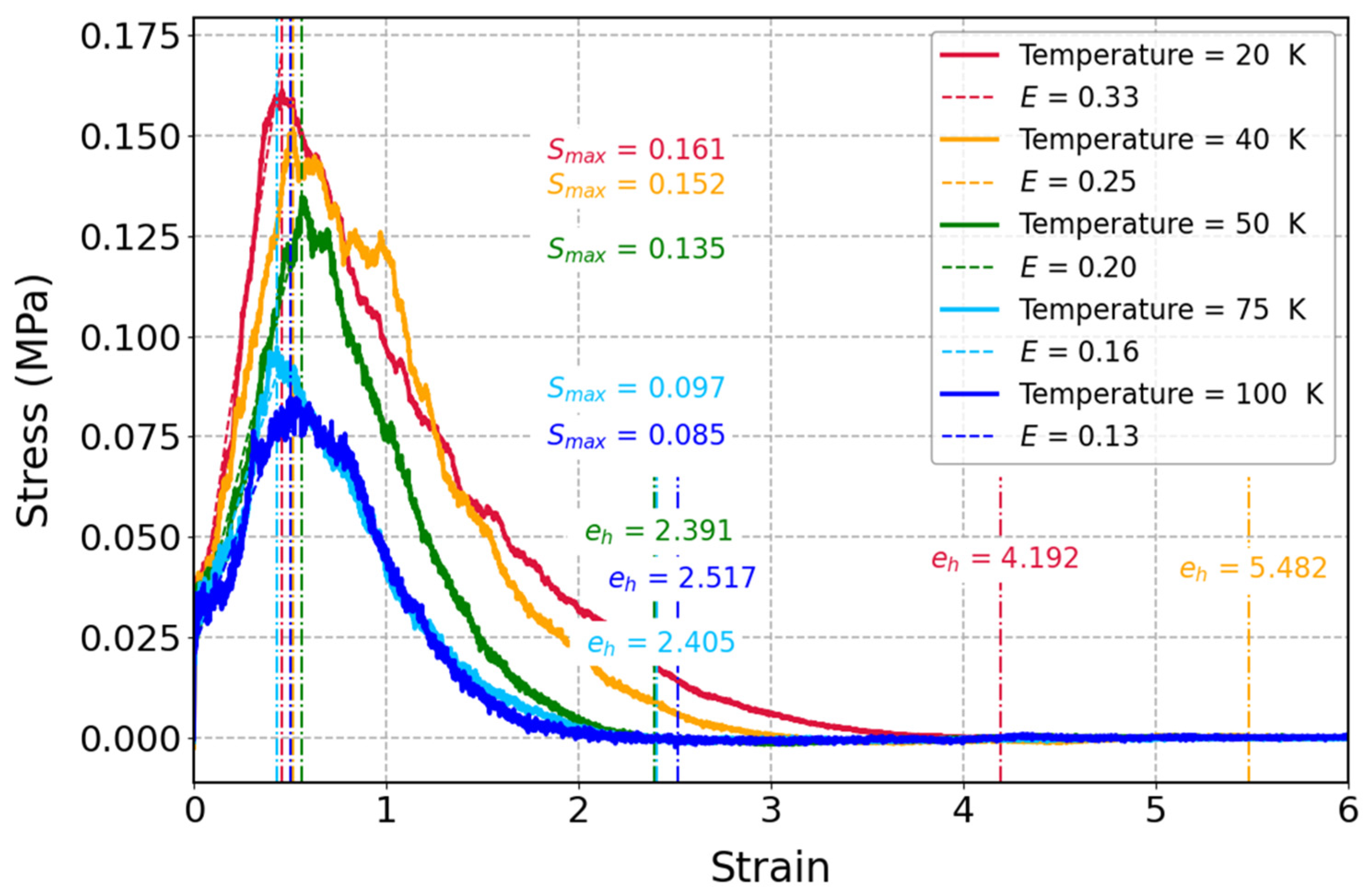
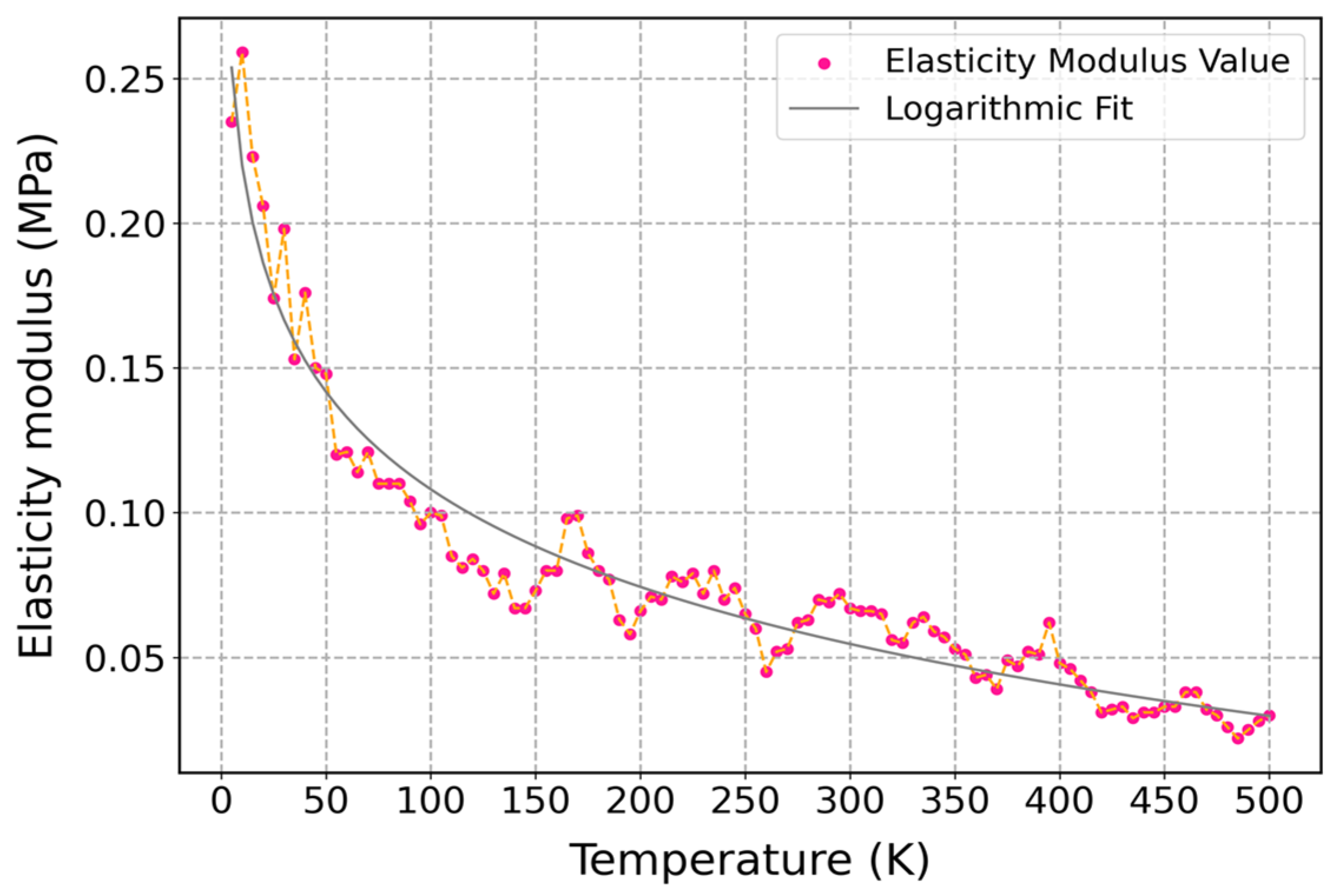
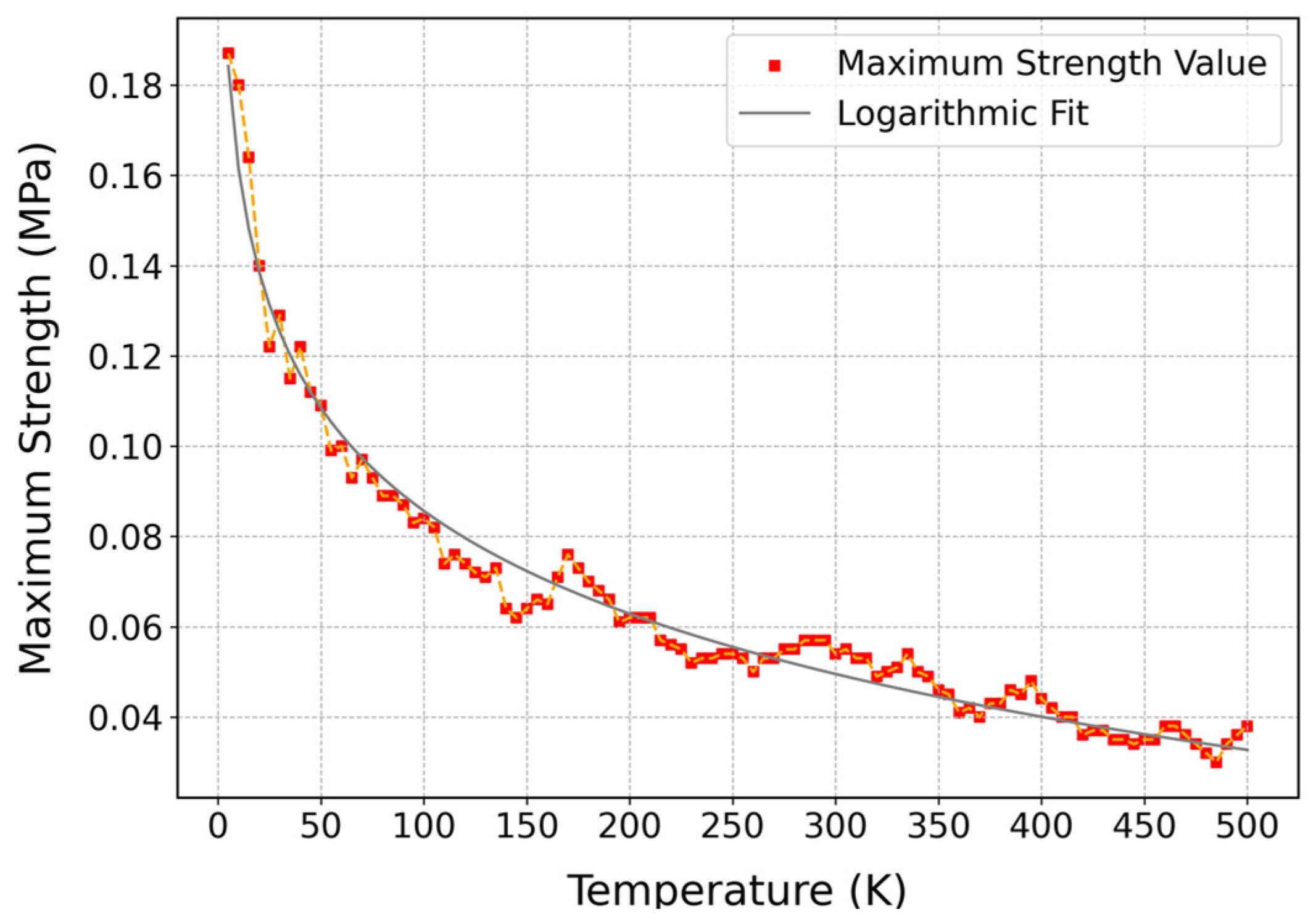
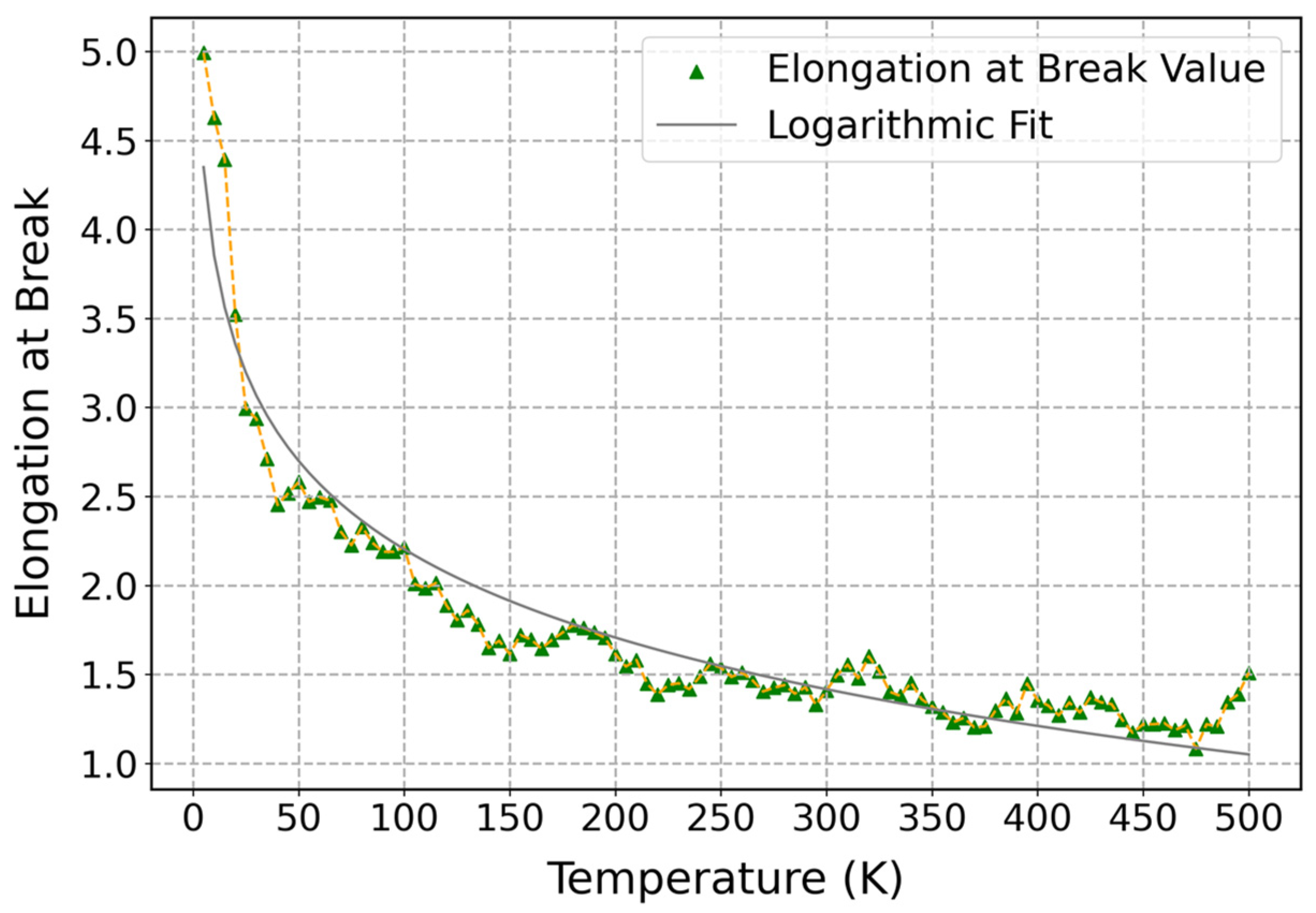
3.3.2. Influence of Temperature on Mechanical Properties of Cis-1,4-Polyisoprene with Constant Strain Rate
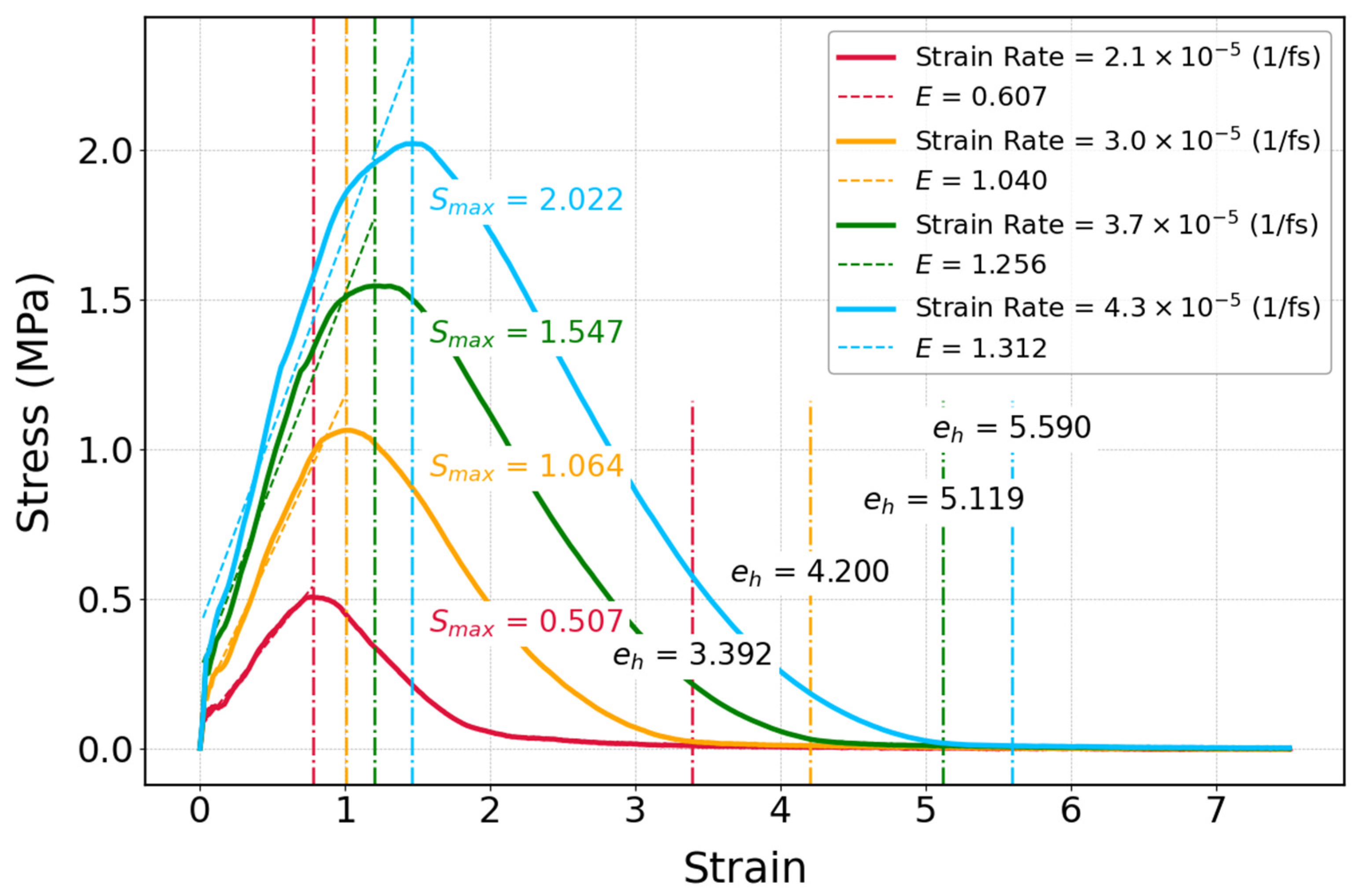
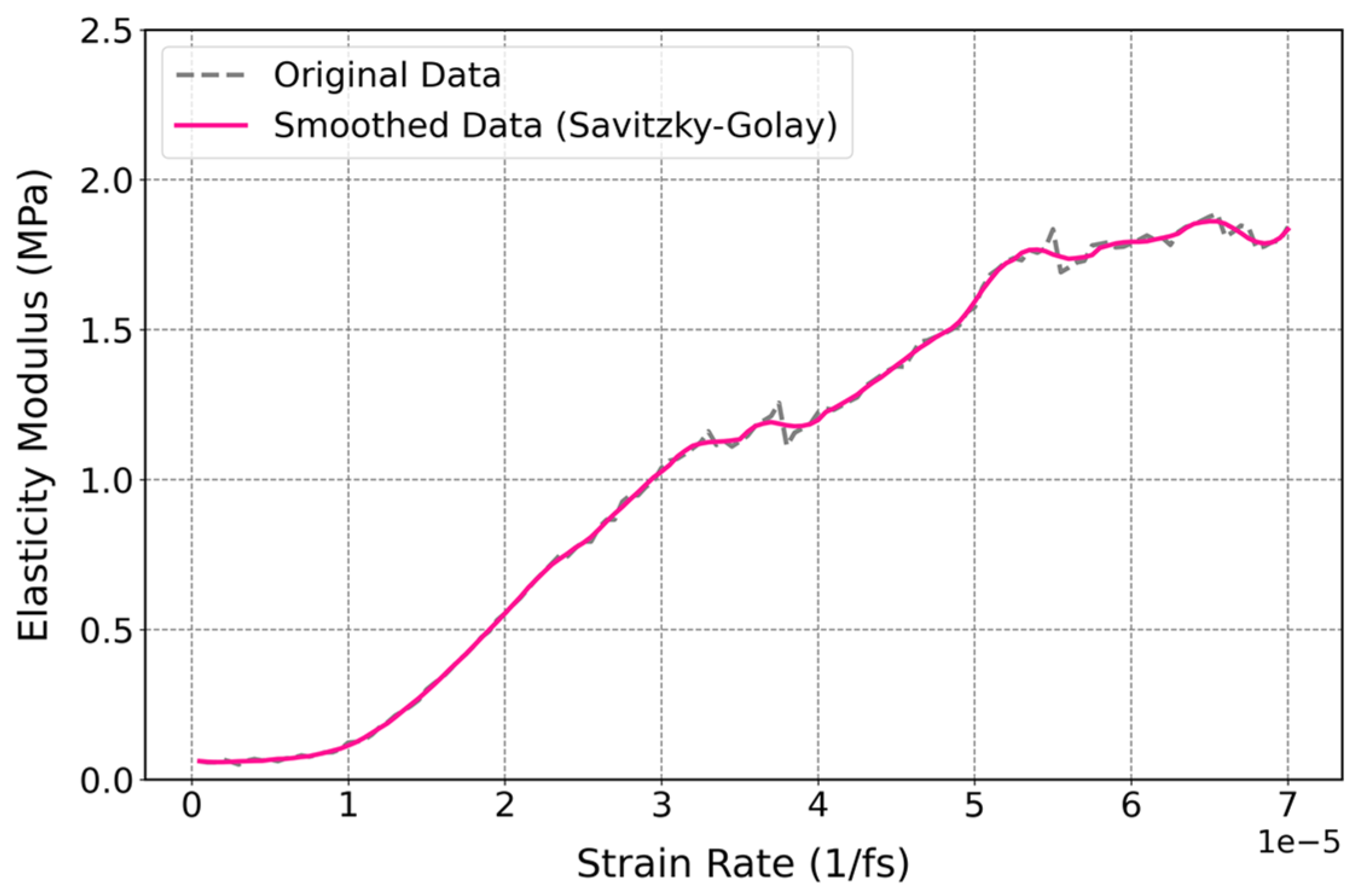
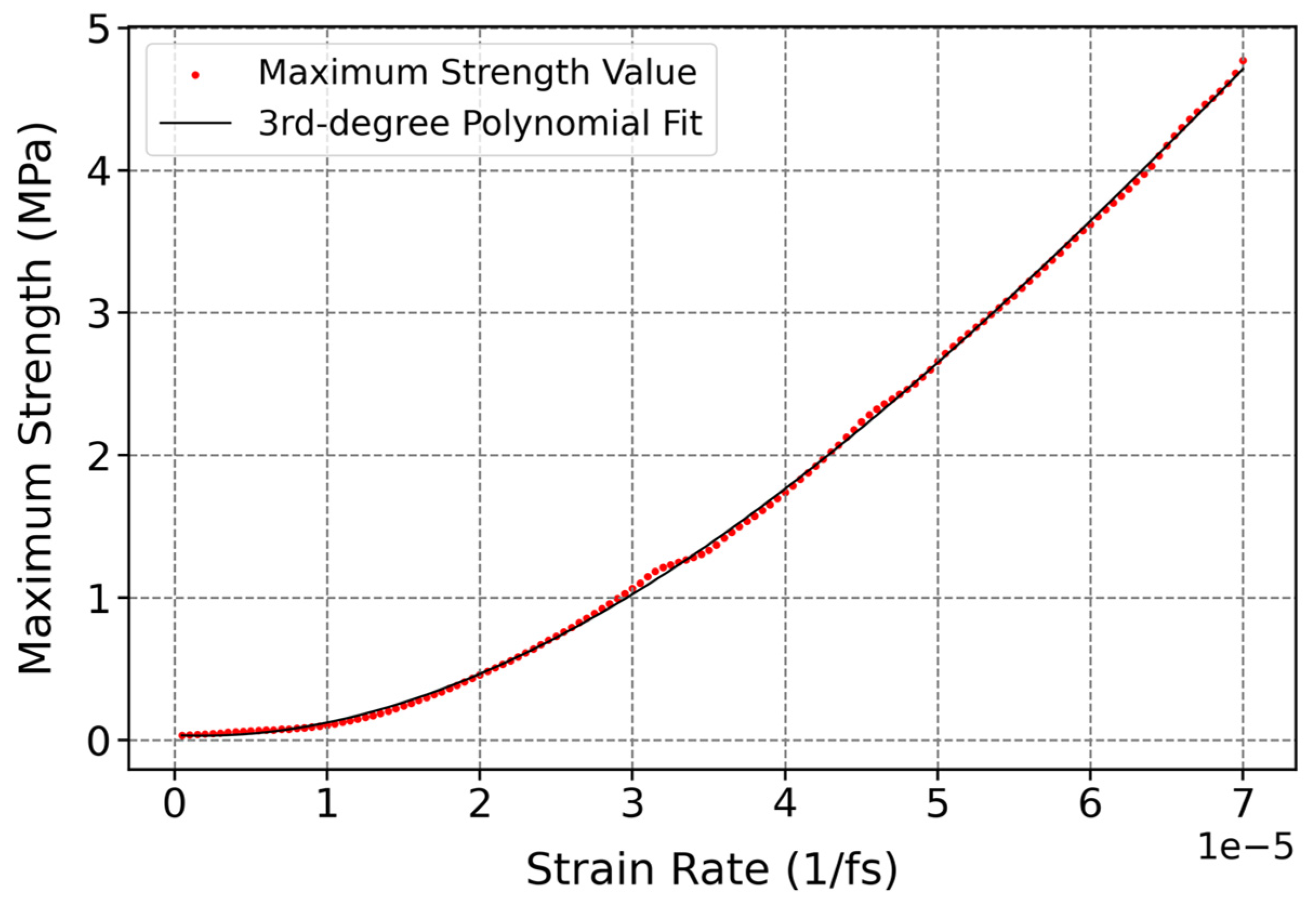
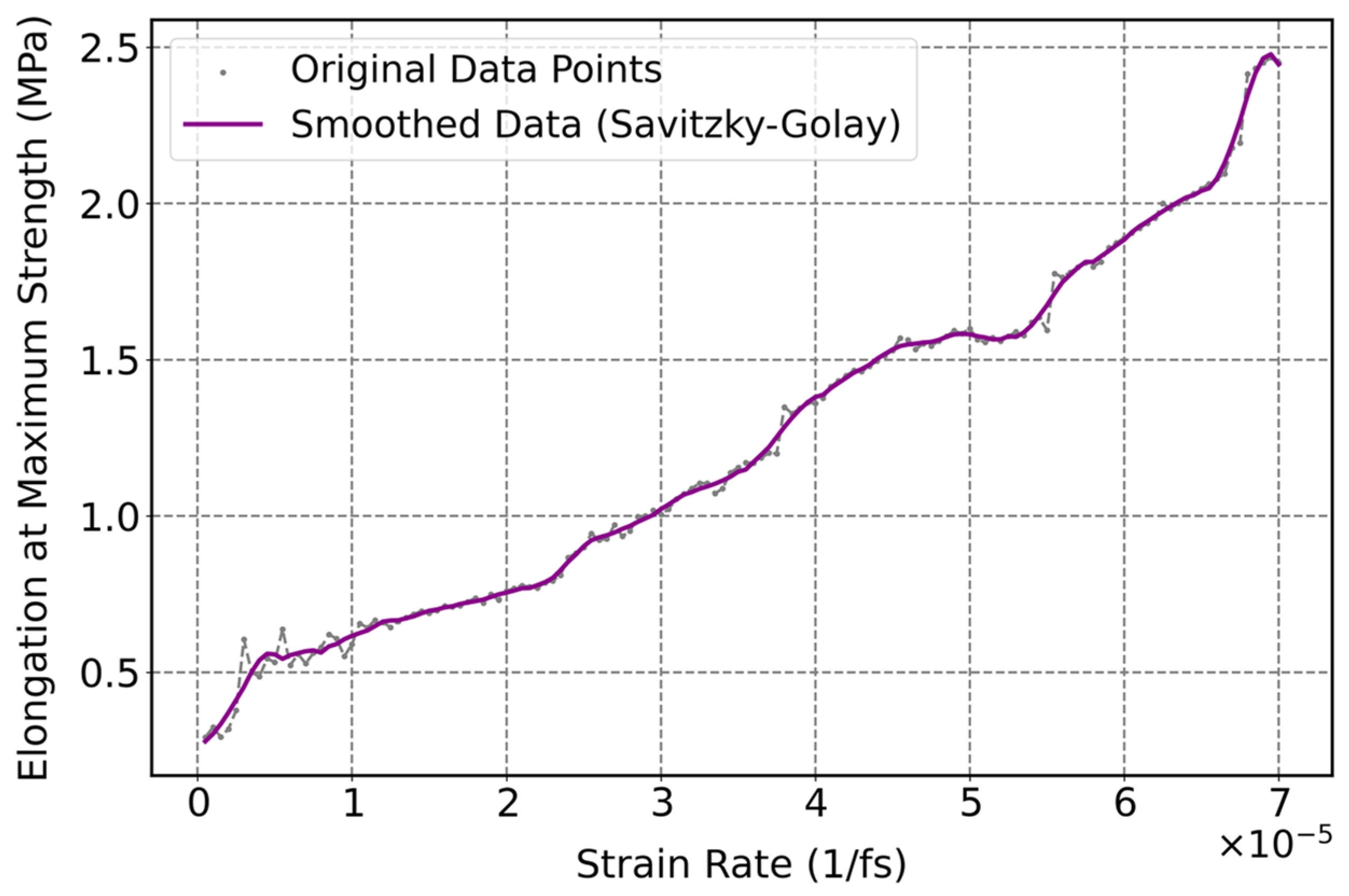
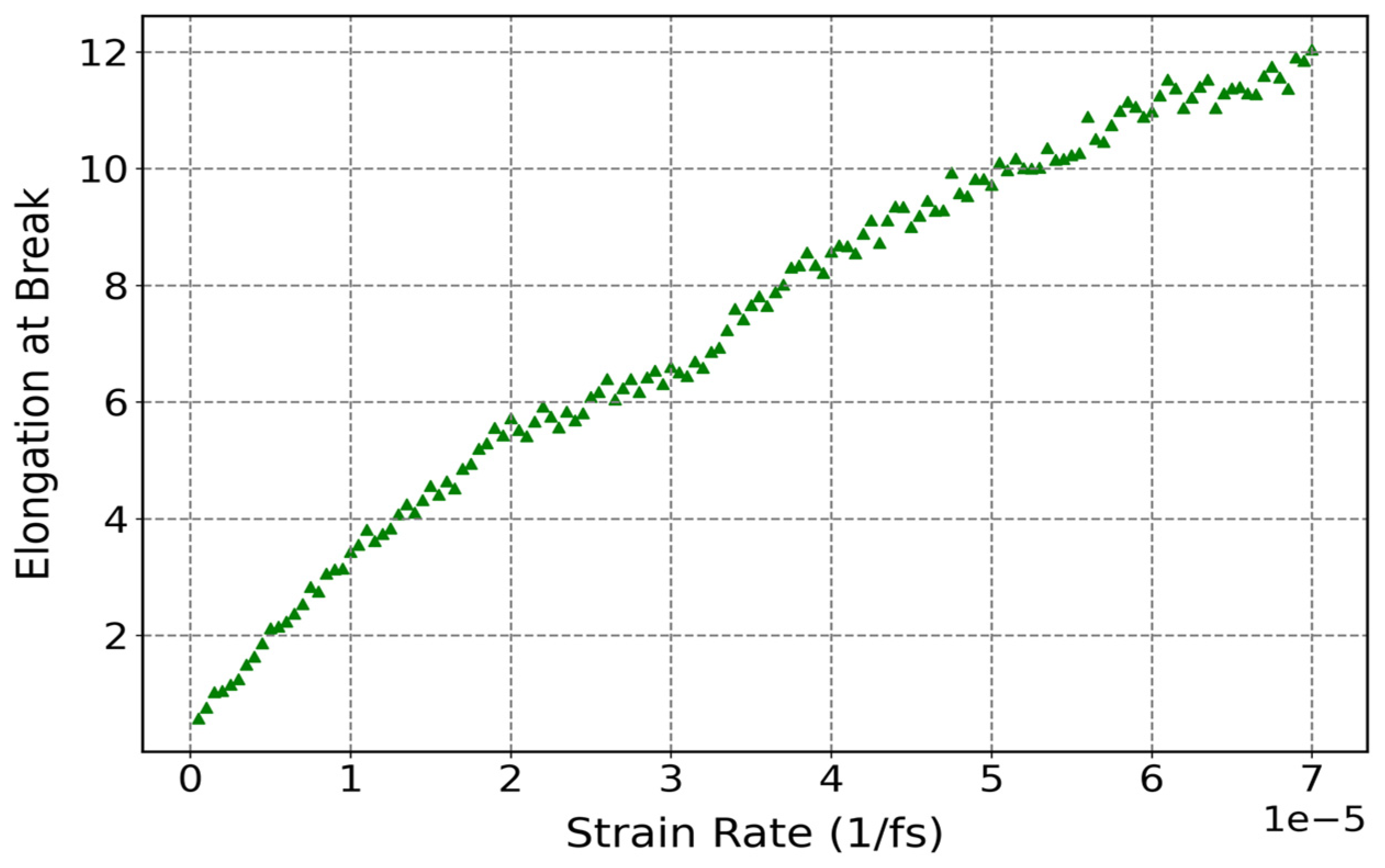
3.3.3. Influence of Strain Rate on Mechanical Properties of Cis-1,4-Polyisoprene with Constant Temperature
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schelling, P.K.; Phillpot, S.R.; Keblinski, P. Comparison of Atomic-Level Simulation Methods for Computing Thermal Conductivity. Phys. Rev. B 2002, 65, 144306. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press Inc.: San Diego, CA, USA, 1996; ISBN 978-0-12-267370-2. [Google Scholar]
- McGaughey, A.J.H.; Kaviany, M. Thermal Conductivity Decomposition and Analysis Using Molecular Dynamics Simulations. Part I. Lennard-Jones Argon. Int. J. Heat Mass Transf. 2004, 47, 1783–1798. [Google Scholar] [CrossRef]
- Henry, A.S.; Chen, G. Spectral Phonon Transport Properties of Silicon Based on Molecular Dynamics Simulations and Lattice Dynamics. J. Comput. Theor. Nanosci. 2008, 5, 141–152. [Google Scholar] [CrossRef]
- Henry, A.; Chen, G. High Thermal Conductivity of Single Polyethylene Chains Using Molecular Dynamics Simulations. Phys. Rev. Lett. 2008, 101, 235502. [Google Scholar] [CrossRef] [PubMed]
- Carbogno, C.; Ramprasad, R.; Scheffler, M. Ab Initio Green-Kubo Approach for the Thermal Conductivity of Solids. Phys. Rev. Lett. 2017, 118, 175901. [Google Scholar] [CrossRef]
- Koh, Y.K. Thermal Conductivity and Phonon Transport. In Encyclopedia of Nanotechnology; Bhushan, B., Ed.; Springer: Dordrecht, The Netherlands, 2012; pp. 2704–2711. ISBN 978-90-481-9751-4. [Google Scholar]
- Mehra, N.; Mu, L.; Ji, T.; Yang, X.; Kong, J.; Gu, J.; Zhu, J. Thermal Transport in Polymeric Materials and across Composite Interfaces. Appl. Mater. Today 2018, 12, 92–130. [Google Scholar] [CrossRef]
- Zhang, B.; Mao, P.; Liang, Y.; He, Y.; Liu, W.; Liu, Z. Modulating Thermal Transport in Polymers and Interfaces: Theories, Simulations, and Experiments. ES Energy Environ. 2019, 5, 37–55. [Google Scholar] [CrossRef]
- Chen, Z.; Tu, Q.; Fang, Z.; Shen, X.; Yin, Q.; Zhang, X.; Pan, M. Molecular Dynamics Studies of the Mechanical Behaviors and Thermal Conductivity of Polyisoprene with Different Degrees of Polymerization. Polymers 2022, 14, 4950. [Google Scholar] [CrossRef]
- Anderson, D.R. Thermal Conductivity of Polymers. Chem. Rev. 1966, 66, 677–690. [Google Scholar] [CrossRef]
- Dashora, P. A Study of Variation of Thermal Conductivity of Elastomers with Temperature. Phys. Scr. 1994, 49, 611. [Google Scholar] [CrossRef]
- He, Y.; Yin, Z.; Ma, L.X.; Song, J.P. Research of Thermal Conductivity and Tensile Strength of Carbon Black-Filled Nature Rubber. Adv. Mater. Res. 2010, 87–88, 200–205. [Google Scholar] [CrossRef]
- Ma, L.X.; Yan, H.Q.; Ke, J.N.; He, Y. Thermal Conductivity and Mechanical Properties of Natural Rubber Filled with Modified-Graphite. Key Eng. Mater. 2012, 501, 10–15. [Google Scholar] [CrossRef]
- Guevara-Carrion, G.; Nieto-Draghi, C.; Vrabec, J.; Hasse, H. Prediction of Transport Properties by Molecular Simulation: Methanol and Ethanol and Their Mixture. J. Phys. Chem. B 2008, 112, 16664–16674. [Google Scholar] [CrossRef] [PubMed]
- Nieto-Draghi, C.; Bonnaud, P.; Ungerer, P. Anisotropic United Atom Model Including the Electrostatic Interactions of Methylbenzenes. II. Transport Properties. J. Phys. Chem. C 2007, 111, 15942–15951. [Google Scholar] [CrossRef]
- Hummer, G.; Rasaiah, J.C.; Noworyta, J.P. Water Conduction through the Hydrophobic Channel of a Carbon Nanotube. Nature 2001, 414, 188–190. [Google Scholar] [CrossRef]
- Huxtable, S.T.; Cahill, D.G.; Shenogin, S.; Xue, L.; Ozisik, R.; Barone, P.; Usrey, M.; Strano, M.S.; Siddons, G.; Shim, M.; et al. Interfacial Heat Flow in Carbon Nanotube Suspensions. Nat. Mater. 2003, 2, 731–734. [Google Scholar] [CrossRef]
- Algaer, E.A.; Alaghemandi, M.; Böhm, M.C.; Müller-Plathe, F. Thermal Conductivity of Amorphous Polystyrene in Supercritical Carbon Dioxide Studied by Reverse Nonequilibrium Molecular Dynamics Simulations. J. Phys. Chem. A 2009, 113, 11487–11494. [Google Scholar] [CrossRef]
- Ni, B.; Watanabe, T.; Phillpot, S.R. Thermal Transport in Polyethylene and at Polyethylene–Diamond Interfaces Investigated Using Molecular Dynamics Simulation. J. Phys. Condens. Matter 2009, 21, 084219. [Google Scholar] [CrossRef]
- Varshney, V.; Patnaik, S.S.; Roy, A.K.; Farmer, B.L. A Molecular Dynamics Study of Epoxy-Based Networks: Cross-Linking Procedure and Prediction of Molecular and Material Properties. Macromolecules 2008, 41, 6837–6842. [Google Scholar] [CrossRef]
- Lussetti, E.; Terao, T.; Müller-Plathe, F. Nonequilibrium Molecular Dynamics Calculation of the Thermal Conductivity of Amorphous Polyamide-6,6. J. Phys. Chem. B 2007, 111, 11516–11523. [Google Scholar] [CrossRef]
- Greene, J.P. 3—Microstructures of Polymers. In Automotive Plastics and Composites; Greene, J.P., Ed.; William Andrew Publishing: Norwich, NY, USA, 2021; pp. 27–37. ISBN 978-0-12-818008-2. [Google Scholar]
- Bejagam, K.K.; Iverson, C.N.; Marrone, B.L.; Pilania, G. Molecular Dynamics Simulations for Glass Transition Temperature Predictions of Polyhydroxyalkanoate Biopolymers. Phys. Chem. Chem. Phys. 2020, 22, 17880–17889. [Google Scholar] [CrossRef] [PubMed]
- Gilman, J.W.; Jackson, C.L.; Morgan, A.B.; Harris, R.; Manias, E.; Giannelis, E.P.; Wuthenow, M.; Hilton, D.; Phillips, S.H. Flammability Properties of Polymer−Layered-Silicate Nanocomposites. Polypropylene and Polystyrene Nanocomposites. Chem. Mater. 2000, 12, 1866–1873. [Google Scholar] [CrossRef]
- Cao, F.; Jana, S.C. Nanoclay-Tethered Shape Memory Polyurethane Nanocomposites. Polymer 2007, 48, 3790–3800. [Google Scholar] [CrossRef]
- Liechty, W.B.; Kryscio, D.R.; Slaughter, B.V.; Peppas, N.A. Polymers for Drug Delivery Systems. Annu. Rev. Chem. Biomol. Eng. 2010, 1, 149–173. [Google Scholar] [CrossRef]
- Mayr, C.; Brütting, W. Control of Molecular Dye Orientation in Organic Luminescent Films by the Glass Transition Temperature of the Host Material. Chem. Mater. 2015, 27, 2759–2762. [Google Scholar] [CrossRef]
- Nicolas, J. Drug-Initiated Synthesis of Polymer Prodrugs: Combining Simplicity and Efficacy in Drug Delivery. Chem. Mater. 2016, 28, 1591–1606. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, Z.; Ahn, C.H.; Suo, Z. Conducting Polymer Coatings Prepared by Mixed Emulsions Are Highly Conductive and Stable in Water. Adv. Mater. 2024, 36, 2306960. [Google Scholar] [CrossRef]
- Heydari Gharahcheshmeh, M.; Dautel, B.; Chowdhury, K. Enhanced Carrier Mobility and Thermoelectric Performance by Nanostructure Engineering of PEDOT Thin Films Fabricated via the OCVD Method Using SbCl5 Oxidant. Adv. Funct. Mater. 2025, 35, 2418331. [Google Scholar] [CrossRef]
- Knauert, S.T.; Douglas, J.F.; Starr, F.W. The Effect of Nanoparticle Shape on Polymer-Nanocomposite Rheology and Tensile Strength. J. Polym. Sci. Part B Polym. Phys. 2007, 45, 1882–1897. [Google Scholar] [CrossRef]
- Kausch, H.H.; Michler, G.H. Effect of Nanoparticle Size and Size-Distribution on Mechanical Behavior of Filled Amorphous Thermoplastic Polymers. J. Appl. Polym. Sci. 2007, 105, 2577–2587. [Google Scholar] [CrossRef]
- Kim, S.Y.; Meyer, H.W.; Saalwächter, K.; Zukoski, C.F. Polymer Dynamics in PEG-Silica Nanocomposites: Effects of Polymer Molecular Weight, Temperature and Solvent Dilution. Macromolecules 2012, 45, 4225–4237. [Google Scholar] [CrossRef]
- Colmenero, J. Are Polymers Standard Glass-Forming Systems? The Role of Intramolecular Barriers on the Glass-Transition Phenomena of Glass-Forming Polymers. J. Phys. Condens. Matter 2015, 27, 103101. [Google Scholar] [CrossRef]
- Müller, C. On the Glass Transition of Polymer Semiconductors and Its Impact on Polymer Solar Cell Stability. Chem. Mater. 2015, 27, 2740–2754. [Google Scholar] [CrossRef]
- Rathod, V.T.; Kumar, J.S.; Jain, A. Polymer and Ceramic Nanocomposites for Aerospace Applications. Appl. Nanosci. 2017, 7, 519–548. [Google Scholar] [CrossRef]
- Fryer, D.S.; Nealey, P.F.; de Pablo, J.J. Thermal Probe Measurements of the Glass Transition Temperature for Ultrathin Polymer Films as a Function of Thickness. Macromolecules 2000, 33, 6439–6447. [Google Scholar] [CrossRef]
- Ediger, M.D.; Forrest, J.A. Dynamics near Free Surfaces and the Glass Transition in Thin Polymer Films: A View to the Future. Macromolecules 2014, 47, 471–478. [Google Scholar] [CrossRef]
- Dudowicz, J.; Freed, K.F.; Douglas, J.F. The Glass Transition Temperature of Polymer Melts. J. Phys. Chem. B 2005, 109, 21285–21292. [Google Scholar] [CrossRef]
- Lipson, J.E.G.; Milner, S.T. Local and Average Glass Transitions in Polymer Thin Films. Macromolecules 2010, 43, 9874–9880. [Google Scholar] [CrossRef]
- Binder, K.; Baschnagel, J.; Paul, W. Glass Transition of Polymer Melts: Test of Theoretical Concepts by Computer Simulation. Prog. Polym. Sci. 2003, 28, 115–172. [Google Scholar] [CrossRef]
- Baschnagel, J.; Varnik, F. Computer Simulations of Supercooled Polymer Melts in the Bulk and in Confined Geometry. J. Phys. Condens. Matter 2005, 17, R851. [Google Scholar] [CrossRef]
- Barrat, J.-L.; Baschnagel, J.; Lyulin, A. Molecular Dynamics Simulations of Glassy Polymers. Soft Matter 2010, 6, 3430–3446. [Google Scholar] [CrossRef]
- Hung, J.-H.; Patra, T.K.; Meenakshisundaram, V.; Mangalara, J.H.; Simmons, D.S. Universal Localization Transition Accompanying Glass Formation: Insights from Efficient Molecular Dynamics Simulations of Diverse Supercooled Liquids. Soft Matter 2019, 15, 1223–1242. [Google Scholar] [CrossRef]
- Xu, W.-S.; Douglas, J.F.; Sun, Z.-Y. Polymer Glass Formation: Role of Activation Free Energy, Configurational Entropy, and Collective Motion. Macromolecules 2021, 54, 3001–3033. [Google Scholar] [CrossRef]
- Harito, C.; Bavykin, D.V.; Yuliarto, B.; Dipojono, H.K.; Walsh, F.C. Polymer Nanocomposites Having a High Filler Content: Synthesis, Structures, Properties, and Applications. Nanoscale 2019, 11, 4653–4682. [Google Scholar] [CrossRef] [PubMed]
- de Oliveira, A.D.; Beatrice, C.A.G. Polymer Nanocomposites with Different Types of Nanofiller. In Nanocomposites—Recent Evolutions; IntechOpen: London, UK, 2018; ISBN 978-1-78985-012-3. [Google Scholar]
- Wang, K.; Ahzi, S.; Matadi Boumbimba, R.; Bahlouli, N.; Addiego, F.; Rémond, Y. Micromechanical Modeling of the Elastic Behavior of Polypropylene Based Organoclay Nanocomposites under a Wide Range of Temperatures and Strain Rates/Frequencies. Mech. Mater. 2013, 64, 56–68. [Google Scholar] [CrossRef]
- Konstantatos, G.; Howard, I.; Fischer, A.; Hoogland, S.; Clifford, J.; Klem, E.; Levina, L.; Sargent, E.H. Ultrasensitive Solution-Cast Quantum Dot Photodetectors. Nature 2006, 442, 180–183. [Google Scholar] [CrossRef]
- Mokhtari, A.; Tala-Ighil, N.; Masmoudi, Y.A. Nanoindentation to Determine Young’s Modulus for Thermoplastic Polymers. J. Mater. Eng. Perform 2022, 31, 2715–2722. [Google Scholar] [CrossRef]
- Grabbert, N.; Wang, B.; Avnon, A.; Zhuo, S.; Datsyuk, V.; Trotsenko, S.; Mackowiak, P.; Kaletta, K.; Lang, K.-D.; Ngo, H.-D. Mechanical Properties of Individual Composite Poly(Methyl-Methacrylate) -Multiwalled Carbon Nanotubes Nanofibers. IOP Conf. Ser. Mater. Sci. Eng. 2014, 64, 012005. [Google Scholar] [CrossRef]
- Alasfar, R.H.; Ahzi, S.; Barth, N.; Kochkodan, V.; Khraisheh, M.; Koç, M. A Review on the Modeling of the Elastic Modulus and Yield Stress of Polymers and Polymer Nanocomposites: Effect of Temperature, Loading Rate and Porosity. Polymers 2022, 14, 360. [Google Scholar] [CrossRef]
- Schodek, D.L.; Ferreira, P.; Ashby, M.F. Nanomaterials, Nanotechnologies and Design: An Introduction for Engineers and Architects; Butterworth-Heinemann: Oxford, UK, 2009; ISBN 978-0-7506-8149-0. [Google Scholar]
- Yoshimoto, K.; Jain, T.S.; Workum, K.V.; Nealey, P.F.; de Pablo, J.J. Mechanical Heterogeneities in Model Polymer Glasses at Small Length Scales. Phys. Rev. Lett. 2004, 93, 175501. [Google Scholar] [CrossRef]
- Quanguo, W.; Ke, Y.; Qingli, C. Molecular Simulation Investigations on the Interaction Properties of Graphene Oxide-Reinforced Polyurethane Nanocomposite toward the Improvement of Mechanical Properties. Mater. Today Commun. 2023, 35, 106404. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Z.; Korsunsky, A.M. Multiscale Stress and Strain Statistics in the Deformation of Polycrystalline Alloys. Int. J. Plast. 2022, 152, 103260. [Google Scholar] [CrossRef]
- Power, A.J.; Papananou, H.; Rissanou, A.N.; Labardi, M.; Chrissopoulou, K.; Harmandaris, V.; Anastasiadis, S.H. Dynamics of Polymer Chains in Poly(Ethylene Oxide)/Silica Nanocomposites via a Combined Computational and Experimental Approach. J. Phys. Chem. B 2022, 126, 7745–7760. [Google Scholar] [CrossRef] [PubMed]
- Hong, B.; Panagiotopoulos, A.Z. Molecular Dynamics Simulations of Silica Nanoparticles Grafted with Poly(Ethylene Oxide) Oligomer Chains. J. Phys. Chem. B 2012, 116, 2385–2395. [Google Scholar] [CrossRef]
- Rissanou, A.N.; Papananou, H.; Petrakis, V.S.; Doxastakis, M.; Andrikopoulos, K.S.; Voyiatzis, G.A.; Chrissopoulou, K.; Harmandaris, V.; Anastasiadis, S.H. Structural and Conformational Properties of Poly(Ethylene Oxide)/Silica Nanocomposites: Effect of Confinement. Macromolecules 2017, 50, 6273–6284. [Google Scholar] [CrossRef]
- Skountzos, E.N.; Tsalikis, D.G.; Stephanou, P.S.; Mavrantzas, V.G. Individual Contributions of Adsorbed and Free Chains to Microscopic Dynamics of Unentangled Poly(Ethylene Glycol)/Silica Nanocomposite Melts and the Important Role of End Groups: Theory and Simulation. Macromolecules 2021, 54, 4470–4487. [Google Scholar] [CrossRef]
- Kubo, R. The Fluctuation-Dissipation Theorem. Rep. Prog. Phys. 1966, 29, 255. [Google Scholar] [CrossRef]
- Kubo, R.; Toda, M.; Hashitsume, N. Statistical Physics II: Nonequilibrium Statistical Mechanics; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 978-3-642-96703-0. [Google Scholar]
- McQuarrie, D.A. Mathematical Methods for Scientists and Engineers; University Science Books: Herndon, VA, USA, 2003; ISBN 978-1891389290. [Google Scholar]
- Ladd, A.J.C.; Moran, B.; Hoover, W.G. Lattice Thermal Conductivity: A Comparison of Molecular Dynamics and Anharmonic Lattice Dynamics. Phys. Rev. B 1986, 34, 5058–5064. [Google Scholar] [CrossRef]
- Alamfard, T.; Lorenz, T.; Breitkopf, C. Glass Transition Temperatures and Thermal Conductivities of Polybutadiene Crosslinked with Randomly Distributed Sulfur Chains Using Molecular Dynamic Simulation. Polymers 2024, 16, 384. [Google Scholar] [CrossRef]
- Sambasivarao, S.V.; Acevedo, O. Development of OPLS-AA Force Field Parameters for 68 Unique Ionic Liquids. J. Chem. Theory Comput. 2009, 5, 1038–1050. [Google Scholar] [CrossRef]
- Doherty, B.; Zhong, X.; Gathiaka, S.; Li, B.; Acevedo, O. Revisiting OPLS Force Field Parameters for Ionic Liquid Simulations. J. Chem. Theory Comput. 2017, 13, 6131–6145. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Caleman, C.; van Maaren, P.J.; Hong, M.; Hub, J.S.; Costa, L.T.; van der Spoel, D. Force Field Benchmark of Organic Liquids: Density, Enthalpy of Vaporization, Heat Capacities, Surface Tension, Isothermal Compressibility, Volumetric Expansion Coefficient, and Dielectric Constant. J. Chem. Theory Comput. 2012, 8, 61–74. [Google Scholar] [CrossRef]
- Lyulin, A.V.; Balabaev, N.K.; Michels, M.A.J. Molecular-Weight and Cooling-Rate Dependence of Simulated T-g for Amorphous Polystyrene. Macromolecules 2003, 36, 8574–8575. [Google Scholar] [CrossRef]
- Li, C.; Strachan, A. Molecular Scale Simulations on Thermoset Polymers: A Review. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 103–122. [Google Scholar] [CrossRef]
- Hadipeykani, M.; Aghadavoudi, F.; Toghraie, D. A Molecular Dynamics Simulation of the Glass Transition Temperature and Volumetric Thermal Expansion Coefficient of Thermoset Polymer Based Epoxy Nanocomposite Reinforced by CNT: A Statistical Study. Phys. A Stat. Mech. Appl. 2020, 546, 123995. [Google Scholar] [CrossRef]
- Li, C.; Medvedev, G.A.; Lee, E.-W.; Kim, J.; Caruthers, J.M.; Strachan, A. Molecular Dynamics Simulations and Experimental Studies of the Thermomechanical Response of an Epoxy Thermoset Polymer. Polymer 2012, 53, 4222–4230. [Google Scholar] [CrossRef]
- Sahputra, I.H.; Alexiadis, A.; Adams, M.J. Temperature Dependence of the Young’s Modulus of Polymers Calculated Using a Hybrid Molecular Mechanics–Molecular Dynamics Method. J. Phys. Condens. Matter 2018, 30, 355901. [Google Scholar] [CrossRef]
- Alamfard, T.; Lorenz, T.; Breitkopf, C. Thermal Conductivities of Uniform and Random Sulfur Crosslinking in Polybutadiene by Molecular Dynamic Simulation. Polymers 2023, 15, 2058. [Google Scholar] [CrossRef]
- Dai, L.; Rutkevych, P.P.; Chakraborty, S.; Wu, G.; Ye, J.; Lau, Y.H.; Ramanarayan, H.; Wu, D.T. Molecular Dynamics Simulation of Octacosane for Phase Diagrams and Properties via the United-Atom Scheme. Phys. Chem. Chem. Phys. 2021, 23, 21262–21271. [Google Scholar] [CrossRef]
- Jewett, A.I.; Stelter, D.; Lambert, J.; Saladi, S.M.; Roscioni, O.M.; Ricci, M.; Autin, L.; Maritan, M.; Bashusqeh, S.M.; Keyes, T.; et al. Moltemplate: A Tool for Coarse-Grained Modeling of Complex Biological Matter and Soft Condensed Matter Physics. J. Mol. Biol. 2021, 433, 166841. [Google Scholar] [CrossRef] [PubMed]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Nosé, S. A Molecular Dynamics Method for Simulations in the Canonical Ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical Dynamics: Equilibrium Phase-Space Distributions. Phys. Rev. A Gen. Phys. 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Youssef, A.A.; Reda, H.; Harmandaris, V. Unraveling the Effect of Strain Rate and Temperature on the Heterogeneous Mechanical Behavior of Polymer Nanocomposites via Atomistic Simulations and Continuum Models. Polymers 2024, 16, 2530. [Google Scholar] [CrossRef]
- Kang, Y.; Zhou, D.; Wu, Q.; Duan, F.; Yao, R.; Cai, K. Fully Atomistic Molecular Dynamics Computation of Physico-Mechanical Properties of PB, PS, and SBS. Nanomaterials 2019, 9, 1088. [Google Scholar] [CrossRef]
- Sahputra, I.H.; Echtermeyer, A.T. Effects of Temperature and Strain Rate on the Deformation of Amorphous Polyethylene: A Comparison between Molecular Dynamics Simulations and Experimental Results. Model. Simul. Mater. Sci. Eng. 2013, 21, 065016. [Google Scholar] [CrossRef]
- Brandl, C.; Derlet, P.M.; Swygenhoven, H.V. Strain Rates in Molecular Dynamics Simulations of Nanocrystalline Metals. Philos. Mag. 2009, 89, 3465–3475. [Google Scholar] [CrossRef]
- Fu, X. Nanostructure, Plastic Deformation, and Influence of Strain Rate Concerning Ni/Al2O3 Interface System Using a Molecular Dynamic Study (LAMMPS). Nanomaterials 2023, 13, 641. [Google Scholar] [CrossRef]
- Vasilev, A.; Lorenz, T.; Breitkopf, C. Thermal Conductivity of Polyisoprene and Polybutadiene from Molecular Dynamics Simulations and Transient Measurements. Polymers 2020, 12, 1081. [Google Scholar] [CrossRef] [PubMed]
- Mukherji, D. Thermal Conductivity of Polymers: A Simple Matter Where Complexity Matters. Macromol. Rapid Commun. 2024, 45, 2400517. [Google Scholar] [CrossRef]
- Vasilev, A.; Lorenz, T.; Breitkopf, C. Thermal Conductivities of Crosslinked Polyisoprene and Polybutadiene from Molecular Dynamics Simulations. Polymers 2021, 13, 315. [Google Scholar] [CrossRef] [PubMed]
- Bai, L.; Zhao, X.; Bao, R.-Y.; Liu, Z.-Y.; Yang, M.-B.; Yang, W. Effect of Temperature, Crystallinity and Molecular Chain Orientation on the Thermal Conductivity of Polymers: A Case Study of PLLA. J Mater Sci 2018, 53, 10543–10553. [Google Scholar] [CrossRef]
- Makhiyanov, N.; Khasanov, M.N. Glass Transition Parameters of Polyisoprene Rubbers: Differential Scanning Calorimetry Study. Polym. Sci. Ser. A 2021, 63, 220–227. [Google Scholar] [CrossRef]
- Zhao, J.; Yu, P.; Dong, S. The Influence of Crosslink Density on the Failure Behavior in Amorphous Polymers by Molecular Dynamics Simulations. Materials 2016, 9, 234. [Google Scholar] [CrossRef]
- Zhang, Q.; Mortazavi, B.; Aldakheel, F. Molecular Dynamics Modeling of Mechanical Properties of Polymer Nanocomposites Reinforced by C7N6 Nanosheet. Surfaces 2021, 4, 240–254. [Google Scholar] [CrossRef]
- Baboo, M.; Dixit, M.; Sharma, K.; Saxena, N.S. Mechanical and Thermal Characterization of Cis-Polyisoprene and Trans-Polyisoprene Blends. Polym. Bull. 2011, 66, 661–672. [Google Scholar] [CrossRef]
- Diani, J.; Gilormini, P.; Fayolle, B. Study on the Temperature Dependence of the Bulk Modulus of Polyisoprene by Molecular Dynamics Simulations. Mol. Simul. 2008, 34, 1143–1148. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-Forming Liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Santangelo, P.G.; Roland, C.M. Temperature Dependence of Mechanical and Dielectric Relaxation in Cis-1,4-Polyisoprene. Macromolecules 1998, 31, 3715–3719. [Google Scholar] [CrossRef]
- Matsumiya, Y.; Watanabe, H.; Sukhonthamethirat, N.; Vao-soongnern, V. Viscoelastic and Dielectric Behavior of Polyisoprene Monofunctionally Head-Modified with Associative Metal-Carboxylate Group. Nihon Reoroji Gakk. 2021, 49, 189–197. [Google Scholar] [CrossRef]
- Persson, B.N.J. Influence of Temperature and Crack-Tip Speed on Crack Propagation in Elastic Solids. J. Chem. Phys. 2024, 161, 184704. [Google Scholar] [CrossRef] [PubMed]
- Candau, N.; Chazeau, L.; Chenal, J.-M.; Gauthier, C.; Munch, E. A Comparison of the Abilities of Natural Rubber (NR) and Synthetic Polyisoprene Cis-1,4 Rubber (IR) to Crystallize under Strain at High Strain Rates. Phys. Chem. Chem. Phys. 2016, 18, 3472–3481. [Google Scholar] [CrossRef] [PubMed]
- Siviour, C.R.; Jordan, J.L. High Strain Rate Mechanics of Polymers: A Review. J. Dyn. Behav. Mater. 2016, 2, 15–32. [Google Scholar] [CrossRef]
- Berto, P.; Grelier, S.; Peruch, F. Telechelic Polybutadienes or Polyisoprenes Precursors for Recyclable Elastomeric Networks. Macromol. Rapid Commun. 2017, 38, 1700475. [Google Scholar] [CrossRef]
- Harper, C.A. Handbook of Plastics, Elastomers, and Composites, 4th ed.; Harper, C.A., Ed.; McGraw-Hill Education: Noida, India, 2002; ISBN 978-0-07-138476-6. [Google Scholar]
- Akinay, A.E.; Tinçer, T. Preparation and Characterization of Ultrahigh Molecular Weight Polyethylene and Polyisoprene Solvent-Cast Blend Films. J. Appl. Polym. Sci. 1998, 67, 1619–1630. [Google Scholar] [CrossRef]
- Zhang, S.; Ocheje, M.U.; Luo, S.; Ehlenberg, D.; Appleby, B.; Weller, D.; Zhou, D.; Rondeau-Gagné, S.; Gu, X. Probing the Viscoelastic Property of Pseudo Free-Standing Conjugated Polymeric Thin Films. Macromol. Rapid Commun. 2018, 39, 1800092. [Google Scholar] [CrossRef]
- Jacob, G.C.; Starbuck, J.M.; Fellers, J.F.; Simunovic, S.; Boeman, R.G. Strain Rate Effects on the Mechanical Properties of Polymer Composite Materials. J. Appl. Polym. Sci. 2004, 94, 296–301. [Google Scholar] [CrossRef]


| Force Field Parameters for cis-1,4-Polyisoprene in All-Atom Model | ||||
|---|---|---|---|---|
| Atom Type | ||||
| 81, 81 | 0.066 | 3.5 | ||
| 80, 80 | 0.066 | 3.5 | ||
| 85, 85 | 0.030 | 2.5 | ||
| 86, 86 | 0.076 | 3.55 | ||
| 87, 87 | 0.076 | 3.55 | ||
| 89, 89 | 0.03 | 2.42 | ||
| 80, 89 | 0.044 | 2.910 | ||
| 81, 85 | 0.044 | 2.910 | ||
| 81, 86 | 0.071 | 3.525 | ||
| 81, 87 | 0.071 | 3.525 | ||
| 81, 89 | 0.044 | 2.910 | ||
| 85, 86 | 0.048 | 2.979 | ||
| 85, 87 | 0.048 | 2.979 | ||
| 85, 89 | 0.030 | 2.460 | ||
| 86, 87 | 0.076 | 3.550 | ||
| 86, 89 | 0.048 | 2.931 | ||
| 87, 89 | 0.048 | 2.979 | ||
| 81, 81 | 268.0 | 1.524 | ||
| 80, 85 | 340.0 | 1.09 | ||
| 81, 86 | 317.0 | 1.51 | ||
| 87, 89 | 340.0 | 1.08 | ||
| 86, 87 | 549.0 | 1.34 | ||
| 85, 81, 85 | 33.0 | 107.8 | ||
| 81, 81, 85 | 37.5 | 110.7 | ||
| 85, 81, 86 | 35.0 | 109.5 | ||
| 81, 81, 87 | 63.0 | 111.1 | ||
| 80, 86, 81 | 70.0 | 130.0 | ||
| 81, 87, 89 | 35.0 | 117.0 | ||
| 89, 87, 86 | 35.0 | 120.0 | ||
| 81, 86, 87 | 70.0 | 124.0 | ||
| 85, 80, 85 | 33.0 | 107.8 | ||
| 85, 81, 87 | 35.0 | 109.5 | ||
| 81, 87, 86 | 70.0 | 124.0 | ||
| 85, 81, 81, 85 | 0.0 | 0.0 | 0.3 | |
| 85, 81, 81, 87 | 0.0 | 0.0 | 0.366 | |
| 81, 81, 87, 89 | 0.0 | 0.0 | 0.468 | |
| 81, 81, 86, 80 | 2.817 | −0.169 | 0.543 | |
| 81, 81, 86, 87 | 0.346 | 0.405 | −0.904 | |
| 85, 80, 86, 81 | 0.0 | 0.0 | 0.3 | |
| 85, 81, 87, 89 | 0.0 | 0.0 | 0.318 | |
| 85, 81, 86, 87 | 0.0 | 0.0 | −0.372 | |
| 81, 87, 86, 80 | 0.0 | 14.0 | 0.0 | |
| 81, 86, 87, 89 | 0.0 | 14.0 | 0.0 | |
| 85, 81, 87, 89 | 0.0 | 0.0 | 0.318 | |
| 85, 81, 87, 86 | 0.0 | 0.0 | −0.372 | |
| 85, 80, 86, 87 | 15.0 | 180.0 | ||
| 85, 81, 86, 87 | 15.0 | 180.0 | ||
| 81, 81, 86, 87 | 15.0 | 180.0 | ||
| 81, 81, 86, 80 | 15.0 | 180.0 | ||
| 80, 86, 87, 89 | 15.0 | 180.0 | ||
| 81, 86, 87, 89 | 15.0 | 180.0 | ||
| 85, 81, 87, 86 | 15.0 | 180.0 | ||
| 81, 81, 87, 89 | 15.0 | 180.0 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alamfard, T.; Breitkopf, C. Thermo-Mechanical Properties of Cis-1,4-Polyisoprene: Influence of Temperature and Strain Rate on Mechanical Properties by Molecular Dynamic Simulations. Polymers 2025, 17, 1179. https://doi.org/10.3390/polym17091179
Alamfard T, Breitkopf C. Thermo-Mechanical Properties of Cis-1,4-Polyisoprene: Influence of Temperature and Strain Rate on Mechanical Properties by Molecular Dynamic Simulations. Polymers. 2025; 17(9):1179. https://doi.org/10.3390/polym17091179
Chicago/Turabian StyleAlamfard, Tannaz, and Cornelia Breitkopf. 2025. "Thermo-Mechanical Properties of Cis-1,4-Polyisoprene: Influence of Temperature and Strain Rate on Mechanical Properties by Molecular Dynamic Simulations" Polymers 17, no. 9: 1179. https://doi.org/10.3390/polym17091179
APA StyleAlamfard, T., & Breitkopf, C. (2025). Thermo-Mechanical Properties of Cis-1,4-Polyisoprene: Influence of Temperature and Strain Rate on Mechanical Properties by Molecular Dynamic Simulations. Polymers, 17(9), 1179. https://doi.org/10.3390/polym17091179







