Polymer and Water Dynamics in Poly(vinyl alcohol)/Poly(methacrylate) Networks. A Molecular Dynamics Simulation and Incoherent Neutron Scattering Investigation

Abstract

Chemically cross-linked polymer networks of poly(vinyl alcohol)/poly(methacrylate) form monolitic hydrogels and microgels suitable for biomedical applications, such as in situ tissue replacement and drug delivery. In this work, molecular dynamics (MD) simulation and incoherent neutron scattering methods are used to study the local polymer dynamics and the polymer induced modification of water properties in poly(vinyl alcohol)/poly(methacrylate) hydrogels. This information is particularly relevant when the diffusion of metabolites and drugs is a requirement for the polymer microgel functionality. MD simulations of an atomic detailed model of the junction domain at the experimental hydration degree were carried out at 283, 293 and 313 K. The polymer-water interaction, the polymer connectivity and the water dynamics were investigated as a function of temperature. Simulation results are compared with findings of elastic and quasi-elastic incoherent neutron scattering measurements, experimental approaches which sample the same space-time window of MD simulations. This combined analysis shows a supercooled water component and a temperature dependant increase of both hydrophilicity and mobility in these amphiphilic polymer networks.

1. Introduction

Chemically cross-linked polymer hydrogels form an important class of soft materials [1-6] which finds application in the agricultural, cosmetic, pharmaceutical and food industries. Several requirements have to be fulfilled by the polymer component when these systems are designed for biomedical applications. Besides biocompatibility, in the case of devices for tissue replacement and targeted drug delivery, a high water affinity is requested for a favorable interaction with tissues and cells. Hydrogel based on polysaccharides, such as dextran [7-12] and hyaluronan [13,14], display these characteristics and, in addition, are potentially biodegradable. Synthetic polypeptides are also used in synthesis of biodegradable hydrogels. Examples of such synthetic polypeptide hydrogels include poly(hydroxyl-L-glutamate), poly(L-or-oxinithine), poly(aspartic acid), poly(L-lysine) and poly-(L-glutamic acid) [15]. However, degradation is not always desirable depending on the time scale and location of the drug delivery or tissue replacement device. Therefore, scarcely degradable artificial macromolecules are also used to formulate chemically cross-linked hydrogel matrices for these applications. Poly(ethylene glycol), PEG, and poly(N-isopropylacrylamide), PNIPAAm, are only two examples of synthetic polymers extensively studied in recent years for the preparation of hydrogels for biomedical applications. PEG-based hydrogels are employed as multidimensional cell culture platforms in applications where the control of the microenvironment is requested [16]. The solution behavior of PNIPAAm, displaying a lower critical solution temperature in water, has been largely exploited to obtain reversible thermoresponsive polymer networks [17,18].

Poly(vinyl alcohol), PVA, is a biocompatible synthetic polymer suitable for the production of these networks, for its hydrophilic character and chemical versatility [19,20]. For a few years, we have been involved in the investigation of new hydrogels based on PVA for biomedical application [21-24]. Chemically cross-linked monolithic hydrogels and microgels of poly(vinyl alcohol)/poly(methacrylate), hereafter named PVAMA hydrogels, were recently prepared in our laboratory. PVAMA hydrogels and microgels displayed promising features for in situ tissue replacement [24,25] and controlled drug delivery applications [26], respectively. In PVAMA hydrogels the hydrophobic poly(methacrylate) chains are incorporated in the network to cross-link the PVA chains, imparting an amphiphilic character to the polymer matrix.

The characterization of these systems pertains to both structural and dynamical features of polymer and water. This information is requested to explain their behavior and to design improved systems. Between the structural characteristics, the degree of cross-linking, the pore size, the distribution of hydrophilic and hydrophobic domains affect the hydration, the permeability and the rheological properties. Between the dynamical features, the polymer and water mobility influences the permeability and biases the kinetics of loading and release of drugs [27].

An important aspect of the hydrogel characterization deals with the behavior of water, the major component of these matrices. It is known that the water behavior in confining media can be strongly modified. The interaction with hydrophilic matrices causes a slowing of the water dynamics, as reported for polysaccharide and polymer hydrogels [28,29]. The properties of water in a hydrophobic environment are differently affected depending on the dimension and the topology of the hydrophobic interface [30-32]. Therefore, the diffusion behavior of water in an amphipilic polymer network, such as PVAMA hydrogel, is an issue needing investigation.

Between the experimental techniques used for the characterization of polymer hydrogels, incoherent scattering of thermal neutrons allows us to explore a space-time window of Å-ps and it can be particularly useful to explore the polymer dynamics of matrices with a large H content [33-37]. Incoherent neutron scattering (INS) investigations described the local dynamics of polysaccharide [29,38] and vinyl [28,39-41] chains in hydrated networks and of lipids in self-assembling systems [42,43]. Quasi-elastic incoherent neutron scattering (QENS) experiments were carried out to study the structural dynamics of water, both in bulk phase [44] and in confining media [28,29,39].

The interpretation of neutron scattering data can become difficult for complex systems, such as polymer hydrogels. The combined use of QENS and molecular dynamics (MD) simulations, once validated by direct comparison with the experimental results, may help to clear the results' interpretation [45]. Fully-atomistic MD simulation studies of hydrated polymer systems appeared in the literature about ten years ago, when this method was already been largely exploited to study the dynamics of proteins. The first investigations modeled a relatively small portion of the system, with low hydration degrees [46-50]. Unlike the MD simulation studies of proteins, where the starting structure is available from crystallographic data, MD simulation studies of polymer networks need to build a model, corresponding to the experimental system at least in its more salient features. Efforts were made to increase the complexity and size of the model and to extend the simulation trajectory time [51-55], compatibly with the computing limits of the method. MD simulations of polymer networks using a coarse-grained representation of the repeating units can increase the space and time domains of the model; however, they do not provide information on the solvent features.

Neutron scattering experiments combined with MD simulations were used to study the segmental dynamics of polymer systems in bulk phase [56,57] and the collective dynamics of hydrated phospholipid bilayers [58]. A QENS-MD investigation of PVA networks at high hydration degree was recently reported by us [59].

In this work we use the combined approach of neutron scattering experiments and MD simulations for the investigation of a PVAMA hydrogel with low content of poly(methacrylate), hereafter named PVAMA1. The molar ratio between PMA and PVA residues in PVAMA1, equal to 1:100, is lower than the PMA/PVA residue molar ratio of PVAMA hydrogels previously studied [24-26], therefore a higher polymer mobility and lower confining of water should characterize these hydrogels. Elastic and quasi-elastic neutron scattering experiments were carried out to explore the local dynamics of polymer as a function of temperature. MD simulation technique was chosen to highlight at a molecular level the relationship between structural features and dynamical behavior of the network and to study the water properties in the hydrogel. The simulation model, built in agreement with the experimental residue composition and degree of hydration, focuses the junction domain, responsible of many peculiar properties of the system.

MD simulation study allows to analyze the network dynamics by separating the different polymer components, i.e., PVA and PMA chains, and to investigate the water behavior. However, the simulation work necessarily relies on a few assumptions about the network topology. Neutron scattering experiments provide a system averaged description of the characteristics of the local polymer mobility. The agreement between the findings of the two approaches validates the results of the simulation work and, in particular, a favorable comparison supports the model used to describe the hydrogel. Therefore, a more detailed description of the polymer network and of the permeating solvent is obtained by coupling MD simulations and neutron scattering measurements.

2. Experimental Section

2.1. Materials and Syntheses

Materials

4-(N,N-Dimethylamino)pyridine, DMAP, and glycidyl methacrylate, GMA, were Fluka products. Poly(vinyl alcohol) with nominal weight average molecular weight, M_w, of 35,000 g/mol (degree of deacetylation: 98%) was a Sigma product. The photoinitiator, 1-[4-(2-hydroxyethoxy)-phenyl]-2-hydroxy-2-methyl-1-propane-1-one, was supplied by Ciba. Dimethyl sulfoxide, DMSO, acetone, HCl, and NaOH were purchased from Carlo Erba. All chemicals were reagent grade and used without further purification. Water was Milli-Q purity grade (18.2 MΩ cm), produced with a deionization apparatus (PureLab) from USF. Dialysis membranes (cut off 12,000 g/mol) were purchased from Medicell International Ltd. and prepared according to standard procedure.

Synthesis of Poly(vinyl alcohol)-Methacrylate

PVA was grafted with a methacrylate moiety according to the procedure described by Hennink [60,61] and Anseth [62]. Typically, 10 g of PVA with M_w of 35,000 g/mol was dissolved in 250 mL of DMSO added with 5 g of DMAP. After displacement of oxygen by purging N₂ for 1 h, GMA was added in the 1:100 molar ratio with the polymer repeating units and left for 48 h under stirring in the darkness. DMAP was neutralized by the addition of concentrated hydrochloric acid to prevent alkaline hydrolysis of the methacrylic ester. Samples with stoichiometric degree of substitution, DS, of 1% were prepared.

After completion, the reaction mixture was dialyzed against water to purify the derivative of PVA and to exchange DMSO with water. The PVA-MA samples with DS lower than 2% are soluble in water. After dialysis the samples were precipitated very slowly by adding acetone up to a volume ratio of 50:50 (v/v). The precipitate was collected, finely broken up, and finally dried. The experimental DS value, determined by ¹H NMR [25], was 1.0 ± 0.1%.

Synthesis of the PVAMA1 Hydrogel

Typically a 9% (w/v) aqueous solution of PVA-MA was added with the photoinitiator at a concentration of 3 g/L. The mixture was irradiated in a photoreactor with a power of 12 Watt at 365 nm (Photochemical Multirays Reactor, Helios Italquarz) for 5 min. The system was left for 12 h at 25 °C. After this equilibration period, the gel was set, and extensive washings were carried out to remove the excess of reactants. Hydrogel samples were prepared in three replicas to average out possible differences and heterogeneities occurring in the gels. Polymer hydrogels at a working concentration of 8% (v/v) were transparent.

2.2. Neutron Scattering Experiments

2.2.1. Sample Preparation

Freeze-dried PVAMA1 hydrogels were re-hydrated with 99.9% pure D₂O (Aldrich) at the maximum swelling degree, corresponding to a polymer volume fraction, Φ₂, of 0.08 (v/v), by equilibrating the wet samples over-night in capped containers. For elastic neutron scattering experiments the D₂O hydration degree of the sample was 0.4 (w/w).

2.2.2. Elastic Neutron Scattering Measurements

Incoherent elastic neutron scattering experiments were carried out at the backscattering spectrometer IN13 [63] at the ILL facility. The instrumental resolution of 9 μeV was determined by calibrating the instrument with vanadium. Data were corrected for the absorption and normalized with respect to vanadium scattering, using the software package LAMP available at ILL. Measurements were performed at controlled temperature from 270 to 320 K in a range of scattering vectors, Q, from 0.2 to 4 Ǻ⁻¹. The thickness of the sample was 0.1 mm. At this level multiple scattering effects are deemed negligible.

The elastic incoherent neutron scattering was analyzed as a function of Q and temperature. At a particular temperature and in the Gaussian approximation, the Q-dependence of the elastic scattering law S(Q, ω = 0) is given by

$$S\left(\mathit{\text{Q}},\mathbf{0}\right)=K\cdot \mathbf{exp}(-\frac{\langle u^2\rangle \cdot {\mathit{\text{Q}}}^2}{\mathbf{6}})$$

(1)

where the mean-square amplitude <u²> is the full amplitude of the atomic displacements during the time resolution of the experiment, dominated by the values of the ¹H-atoms in the sample, and K is a constant. For the Gaussian approximation to be valid, either all ¹H-atoms must be dynamically equivalent and vibrate harmonically [64] or the values of Q should be

$$\mathit{\text{Q}}\cdot \sqrt{\frac{\langle u^2\rangle }{\mathbf{2}}}\le 1$$

(2)

We verified a posteriori that, for our systems, the condition of Equation 2 is fulfilled limiting the analysis at Q < 2 Ǻ⁻¹. The mean squared hydrogen displacement of the polymer moiety in the hydrogel was therefore obtained by Equation 3

$${\left(\frac{d\left\{\mathbf{\text{ln}}\left[S\left(\mathit{\text{Q}},\mathbf{0}\right)\right]\right\}}{d\left({\mathit{\text{Q}}}^2\right)}\right)}_{\mathit{\text{Q}}\to 0}=-\frac{\langle u^2\rangle }{\mathbf{6}}$$

(3)

derived from Equation 1, for Q values lower than 1.9 Ǻ⁻¹ [65].

2.2.3. Quasi-Elastic Neutron Scattering Measurements

QENS experiments were carried out at the ISIS pulsed neutron facility (Rutherford Appleton Laboratory, Chilton, UK) using the time-of-flight inverted-geometry backscattering spectrometer IRIS [66]. The instrument was operated in the 002 pyrolytic graphite configuration which provides a Q-range from 0.44 to 1.83 Ǻ⁻¹ with an energy window from −0.35 to 1.2 meV and an energy resolution of 17 μeV. Raw data were corrected for absorption and detector efficiencies and normalized using the standard software package GUIDE available from ISIS. Aluminium flat cells of 0.02 cm thickness were used for all measurements and corrections for multiple scattering were not applied since at this level multiple scattering effects are deemed negligible.

Measurements were performed at 283, 303 and 313 K. Samples were weighed before and after measurements and weight variations within 10% were observed. The instrumental resolution, R(Q,ω), was determined running a vanadium slab.

Assuming purely incoherent scattering, the experimental dynamical structure factor, S_exp(Q, ω), was fitted according to Equation 4

$$S_{exp}\left(\mathit{Q},\omega \right)=R\left(\mathit{\text{Q}},\omega \right)\otimes S_{\mathit{\text{inc}}}\left(\mathit{\text{Q}},\omega \right)+\mathit{\text{bkg}}$$

(4)

where the instrumental resolution is convoluted with the incoherent dynamical structure factor, S_inc(Q, ω), written as:

$$S_{\mathit{\text{inc}}}\left(\mathit{\text{Q}},\omega \right)=A\left(\mathit{\text{Q}}\right)\cdot \lfloor pt\cdot S_{\mathit{\text{inc}},\mathit{\text{pol}}}\left(\mathit{\text{Q}},\omega \right)+\left(1-pt\right)\cdot S_{\text{inc},D_{2}O}\left(\mathit{\text{Q}},\omega \right)\rfloor$$

(5)

with:

$$S_{\mathit{\text{inc}},\mathit{\text{pol}}}\left(\mathit{\text{Q}},\omega \right)=\left[\mathit{\text{EISF}}\left(\mathit{\text{Q}}\right)\cdot \delta \left(\omega \right)+\left(1-\mathit{\text{EISF}}\left(\mathit{\text{Q}}\right)\right)\cdot L_{\mathit{\text{pol}}}\left(\mathit{\text{Q}},\omega \right)\right]$$

(6)

and

$$S_{\mathit{\text{inc}},D_{2}O}\left(\mathit{\text{Q}},\omega \right)=\lfloor pa\left(\mathit{\text{Q}}\right)\cdot L_{D2O,1}\left(\mathit{\text{Q}},\omega \right)+\left(1-pa\left(\mathit{\text{Q}}\right)\right)\cdot L_{D2O,2}\left(\mathit{\text{Q}},\omega \right)\rfloor$$

(7)

The bkg term of Equation 4 is a background. The A(Q) term of Equation 5 accounts for an overall Debye-Waller behavior, assuming a common average Debye-Waller factor for all hydrogens in the sample [42]. In this model, Equation 5, the incoherent dynamical structure factor is described by a linear combination of polymer and solvent contributions, with weights given by pt and (1 − pt) factors, respectively. The pt factor resulted independent on Q and T in the fitting procedure, with a value of 0.72 ± 0.06. This value compares well with the stoichiometric polymer contribution to the cross section in the PVAMA hydrogel, pt_st. The fraction of the incoherent cross section due to the polymer in our sample, i.e., pt_st, is equal to 0.62, taking into account of the experimental hydration degree and of the residue composition of the polymer scaffold. The pt value, about 10% greater than pt_st, indicates that some solvent molecules are bound with the polymer and display a similar dynamics behavior. The polymer contribution to the dynamical structure factor, S_inc,_Pol(Q, ω), Equation 6, contains an elastic term, EISF, i.e., the elastic incoherent structure factor, and a quasi-elastic term, given by the Lorentzian function L_Pol. The purely elastic term accounts for the arrested dynamics of the polymer in the percolating network. The contribution of the solvent, S_inc,_D2O(Q, ω), Equation 7, is described by the Lorentzian functions L_D2O,1 and L_D2O,2, with Q-dependent weights pa and (1 − pa), respectively. This treatment of the quasielastic scattering of the solvent is in agreement with the results of QENS and MD simulations studies [44,67], indicating that QENS data of water can be analyzed in term of two motional components. The broader Lorentzian function, L_D2O,2, is related to local structural fluctuations within water clusters, the narrower Lorentzian function, L_D2O,1, accounts for the slower water diffusion. Assuming a random-jump diffusion motion of the solvent, the dependence on Q of the width of the narrower Lorentzian allows us to obtain a microscopic diffusion coefficient [68]. The value of the diffusion coefficient of the solvent, D, at the investigated temperatures is calculated by Equation 8

$${\Gamma }_{D_{2}O,1}=\frac{D{\mathit{\text{Q}}}^2}{1+D\mathit{\tau }{\mathit{\text{Q}}}^2}$$

(8)

where Γ_D2O,1 is the broadening of the Lorentzian L_D2O,1 and τ is the residence time between jumps. The diffusion coefficient values do not show differences respect to the corresponding values of the bulk solvent, within the accuracy of measurements. This result is in agreement with the finding of QENS measurements, carried out on PVAMA hydrogel microparticles, PVAMA5, synthesized from a PVA-MA polymer with a degree of substitution of methacryloyl groups equal to 5% [26]. The analysis of QENS spectra of PVAMA5 microparticles at the maximum degree of swelling in H₂O showed a limited influence on the dynamic behavior of bound water. The PVAMA1 hydrogel of this study, obtained from PVA-MA with a degree of substitution of 1%, has a polymer network with a lower degree of cross-linking in comparison to PVAMA5 hydrogel. Therefore, a lower effect on the dynamic behavior of bound water (and in the QENS spectrum) has to be expected for the PVAMA1 system. A deeper investigation of the solvent dynamics in the hydrogel needs the use of H₂O and deuterated polymer moiety. The work related to the synthesis of such hydrogels is in progress. In the present study we focus on the polymer component, performing the QENS experiments in D₂O.

2.3. Molecular Dynamics Simulations

2.3.1. Developing the Model

The PVAMA hydrogels are prepared by means a photoiniziated radical polymerization in aqueous solution of methacryloyl grafted PVA-MA chains. This reaction forms polymethacrylate (PMA) chains and generates a three-dimensional polymer network, since the PVA chains are inter-connected via PMA chains till to percolation. Chart 1 shows a scheme of junction in PVAMA networks.

Here we study a hydrogel system obtained by PVA-MA with M_w of 35,000 g/mol, corresponding to an average polymerization degree of about 800, and a degree of substitution of methacryloyl groups equal to 1%. Neutron scattering experiments were carried out on samples of this hydrogel and a corresponding molecular model was developed for the MD simulations.

The starting configuration consisted of a central PMA chain of eight residues, in an all-trans conformation, connecting seven looping PVA chains, each of 100 residues, and two PVA end chains of 50 residues, in an all-trans conformation. The model topology is shown in Chart 2.

An equal population of randomly distributed d and l enantiomers was used for PVA residues, in agreement with the atacticity of PVA. The polymer scaffold was then hydrated with a shell of water of thickness suited to introduce a solvent content corresponding to the experimental polymer volume fraction, Φ₂, of 0.08 and the system was compressed to the correct final density by means of a preliminary MD simulation applying a ‘pressure bath’ of 1 atm with the Berendsen's pressure coupling algorithm [69], a procedure already applied for the simulation of self cross-linked PVA hydrogel networks [52]. MD simulation runs at controlled pressure and at 313 K, using the Berendsen's temperature coupling algorithm [69], for 1 ns and then in the NVT ensemble for about 4 ns were performed to equilibrate the system. The following 1 ns trajectory of the NVT run was used for analysis. The equilibration of the system in the NVT MD run, at T = 313 K, was checked by following the time behavior of the root mean squared deviation of all N polymer atoms, RMSD:

$$\mathit{\text{RMSD}}\left(t+t_0\right)={\left[\frac{1}{M}\sum _{i=1}^N{m}_i{\Vert {\mathbf{\text{r}}}_i\left(t+t_0\right)-{\mathbf{\text{r}}}_i\left(t_0\right)\Vert }^2\right]}^{1/2}$$

(9)

The reference structure was the starting polymer configuration (t₀ = 0) of the NVT run. The RMSD was calculated after roto-translational fit on the backbone atoms of the PMA chain. In the trajectory interval used for analysis, the value of RMSD was stable, with a drift lower than 20% of the RMSD standard deviation.

During this equilibration phase, a few PVA chain formed entanglements with periodic images of other polymer sections, leading to the percolation of the network in one dimension.

The NVT MD run at 293 K was carried out after the NVT MD run at 313 K. The starting configuration at 293 K was the last configuration of the NVT MD run at 313 K. The RMSD for the MD run at 293 K was calculated using as reference structure the starting polymer configuration at 293 K. Finally, the NVT MD run at 283 K was carried out after the NVT MD run at 293 K. The starting configuration at 283 K was the last configuration of the NVT MD run at 293 K. The RMSD for the MD run at 283 K was calculated using as reference structure the starting polymer configuration at 283 K. The equilibration of the system in the NVT MD runs at 293 and 283 K required about 2 ns. The longer equilibration time of the run at 313 K was adopted due to a preliminary major rearrangement of the model. The following MD runs, at the lower temperatures, did not require this starting evolution, and had a shorter equilibration phase.

In the final configuration, the cubic simulation box (with size of 8.484 nm) contained a polymer network of 800 PVA and 8 PMA residues hydrated by 18,308 water molecules, for a polymer concentration of 9.9% (w/w).

2.3.2. Simulation Details

Calculations were carried out on the IBM Linux Cluster 1350 at the CINECA Supercomputing Center (Bologna, Italy). MD simulations were performed by GROMACS software, version 3.2.1 [70,71]. The GROMOS 45A3 force field [72,73] was used and the 45A4 ethanol model [74] was considered for the atomic partial charges of PVA residues. Water was simulated by the single-point charged (SPC) intermolecular potential model [75]. The same force field, using the united atom convention for CH and CH₂ groups, was selected in a previous MD simulation study of PVA hydrogels [55]. Production runs were carried out in the NVT ensemble, with the leap-frog integration algorithm [76] using a time step of 0.5 fs. Temperature was controlled at 313, 293 and 283 K by the Berendsen's temperature coupling algorithm [69]. Non-bonding interactions were treated as described in a previous work [59]. The total simulation time, including equilibration, was about 6 ns at 313 K, 3 ns at 293 K and 3 ns at 283 K. The configurations were saved every 0.1 ps.

MD simulations of a water box with the same size of the hydrogel model, containing 20,265 molecules, were carried out in the same simulation conditions to obtain the bulk water properties for a comparison. A trajectory of 400 ps for each temperature was calculated for the water box at 313, 293 and 283 K.

In the following of this Section we report some information about the procedures used for the trajectory analysis.

The hydrogen bond (HB) was studied by analyzing the trajectory for the occurrence of this interaction, adopting as geometric criteria an acceptor-donor distance (A…D) lower than 0.3 nm and an angle Θ (A…H-D) higher than 120°. The intramolecular HB was analyzed even by integration of the radial distribution function between the hydrogen and oxygen atoms of PVA, g_H-O(r), according to Equation 10

$$n_{HB}=\frac{N_{\text{o}}}{\text{V}}\underset{0}{\overset{R_{min}}{\int }}4\pi r^2{g}_{H-O}\left(r\right)dr$$

(10)

where n_HB, N_O, V are the average number of HB's per PVA residue, the total number of PVA residues and the volume of the simulation box, respectively. R_min is the first minimum distance of the gH-O(r). This procedure allowed us to separate the contribution to the intramolecular hydrogen bonding of near-neighboring and of more distant residues, by proper selection of the exclusion number in the calculation of the radial distribution function. The average number of HB's per PVA residue, calculated by means of Equation 10 including all residues, had the same value, within errors, as that obtained by direct trajectory analysis.

Polymer-water HB's formed by polymer OH group acting as a H acceptor and HB's formed by OH group acting as a H donor were separately evaluated by integration of the radial distribution functions between PVA oxygen and water hydrogen atoms, gO-HW(r), and between PVA hydrogen and water oxygen atoms, g_H-OW(r), respectively, according to Equations 11 and 12

$$n_{\mathit{\text{ACC}}}=\frac{N_{HW}}{V}\underset{0}{\overset{R_{min}}{\int }}4\pi r^2{g}_{O-HW}\left(r\right)dr$$

(11)

$$n_{DO}=\frac{N_{OW}}{V}\underset{0}{\overset{R_{min}}{\int }}4\pi r^2{g}_{O-OW}\left(r\right)dr$$

(12)

In Equations 11 and 12, n_ACC and n_DO are the average number of HB formed as acceptor and donor per PVA hydroxylic group, respectively. The total average number of HB's per water molecule, calculated as sum of n_ACC and n_DO, had the same value, within errors, than that obtained by direct trajectory analysis.

The coordination number of an atom X by atoms Y was evaluated by integration of the corresponding radial distribution function, Equation 13

$$n_{X-Y}=\frac{N_Y}{V}\underset{0}{\overset{R_{min}}{\int }}4\pi r^2{g}_{X-Y}\left(r\right)dr$$

(13)

where N_Y and R_min are the number of Y atoms in the simulation box of volume V and the first minimum distance in g_X-Y (r), respectively.

The dynamics of HB was evaluated by studying the normalized time autocorrelation function C_HB(t):

$$C_{HB}\left(t\right)=\frac{\langle S_{ij}(t_0)S_{ij}\left(t+t_0\right)\rangle }{\langle S_{ij}(t_0)S_{ij}\left(t_0\right)\rangle }$$

(14)

where the state variable s_ij has a value of 1 or 0 depending on the existence or nonexistence of an HB between a selected donor-acceptor pair ij. t₀ and t in Equation 14 range from 0 to half of the simulation time considered for analysis. The function s_ij(t + t₀) is set to 1 if the HB between ij is found to be present in the time steps t₀ and t₀ + t, even if the same HB can be interrupted in some intermediate time. This definition of C_HB(t) corresponds to the intermittent HB autocorrelation function, described by Rapaport [77] and Luzar [78], where the correlation of a particular donor-acceptor pair is evaluated irrespective of possible prior bond breaking and reforming events. With this choice the correlation time, τ_HB, estimates the average lifetime of interaction for the ensemble of HB pairs, within the time window of the analyzed trajectory time. The correlation time, τ_HB, was obtained by integration of C_HB(t) in a time window about 10 times τ_HB.

Water diffusion coefficient, D_W, was obtained from the long-time slope of the mean squared displacement, Equation 15

$$D_W=\frac{1}{6}\underset{t\to \infty }{\mathbf{lim}}\frac{d}{dt}\langle {\left|\mathbf{\text{r}}\left(t\right)-\mathbf{\text{r}}\left(0\right)\right|}^2\rangle$$

(15)

where r(t) and r(0) correspond to the position vector of the water oxygen at time t and 0, respectively, with an average performed over both time origins and water molecules. The mean squared displacement was calculated in a time-window equal to the average lifetime of the hydrogen bonds (HB) between PVA hydroxylic groups and water. The diffusion coefficient value was obtained from the slope of the mean squared displacement vs. time in the second half of the explored time window, when the double log plot of the mean squared displacement vs. time displayed a linear behavior with a slope of 1.

The <u>² value, obtained by elastic neutron scattering measurements as described in Section 2.2.2, was compared with the mean squared displacement (MSD) of the backbone carbon atoms calculated from the MD simulation trajectory according to Equation 16

$$\mathit{\text{MSD}}\left(t+t_0\right)={\langle {\Vert {\mathbf{\text{r}}}_i\left(t+t_0\right)-{\mathbf{\text{r}}}_i\left(t_0\right)\Vert }^2\rangle }_i$$

(16)

where i is a backbone carbon atom and the average is performed over all backbone carbon atoms of the model. The MSD was calculated for a t value equal to 70 ps, corresponding to the time resolution of the neutron scattering experiment. This MSD value is hereafter named MSD₇₀. The error of MSD₇₀ was estimated by the standard deviation of the ensemble average of carbon atoms. To increase the statistics, we sampled over 14 time intervals of 70 ps in the last ns trajectory. The final RMS₇₀ value is the average of these 14 values.

The graphic visualization was done using the molecular viewer software package VMD [79].

3. Results and Discussion

We report in this Section firstly the simulation results and then the findings of the neutron scattering measurements. The comparison between simulation and experimental results will be discussed during the presentation of the neutron scattering data.

A preliminary consideration has to be made about the solvent difference between neutron scattering experiments and MD simulations. We used D₂O in the experiments and H₂O (described by the SPC model) in the simulations. The differences in the behavior of macromolecular systems in H₂O and D₂O are important in systems where conformational transitions occur. An increase of the unfolding temperature in heavy water was found for some proteins [80-82]. The volume phase transition temperature of poly(N-isopropyl acrylamide) gel in D₂O is about 1 °C higher than that in water [83]. Larger effects were shown on the cooperative order-disorder transition in aqueous solution of Schizophyllan, a polysaccharide forming a triple helix complex [84]. However, the differences between the local structure and dynamics of the polymer in PVA based hydrogels, hydrated by H₂O or by D₂O, can be considered minor, due to the lacking of any cooperative process. These differences are negligible when QENS experiments are performed and in the data treatment the polymer contribution to QENS spectrum (obtained in an experiment in D₂O) is often used for the analysis of the corresponding QENS spectrum in H₂O [28]. Considering the approximations of our approach, the simplification of using the SPC model for the solvent description in the hydrogel is more important than the simplification to neglect the difference between H₂O and D₂O hydrated systems.

3.1. Simulation Results

3.1.1. Network Structure and Dynamics

One of the aims of the simulation study of polymer networks is to obtain a structural description of the system. By means of fully-atomistic molecular dynamics simulations we can focus the junction domain and include the inter- and intra-molecular interactions that influence its characteristics in the modeling.

In the PVAMA1 hydrogel, the DS of methacryloyl groups is very low, namely 1% of PVA residues, therefore the polymer component is mainly PVA. However, the particular junction topology of this system leads to a network structure different from that of PVA hydrogels obtained by self-crosslinking of telechelic PVA macromers [52]. In telechelic PVA hydrogels, the junction is strictly three-functional and the distribution of chains in the network can be quite homogeneous, even considering the chain end effects and the polydispersity of the starting macromers. The network structure in PVAMA hydrogels is based on 2N-functional junctions (see Chart 1) formed by PMA segments with N methacrylate residues, where N can assume several values since the polymerization degree of PMA chains is not controlled in the synthesis of the hydrogel [25].

In each 2N-functional junction, 2N PVA strands are connected and the network is formed when a same PVA chain participates to different junctions, thus jointing different cross-links. This kind of junction topology causes a large heterogeneity at a nanoscopic level in the chain density distribution, with a higher chain density in the surrounding of cross-links and a lower chain density in the regions including only PVA. The structural heterogeneity causes also a dynamical heterogeneity of the polymer network, as highlighted by the simulation. In this respect, even the different water affinity of PVA and PMA, hydrophilic and hydrophobic, respectively, contributes to increase the local heterogeneity of this hydrogel.

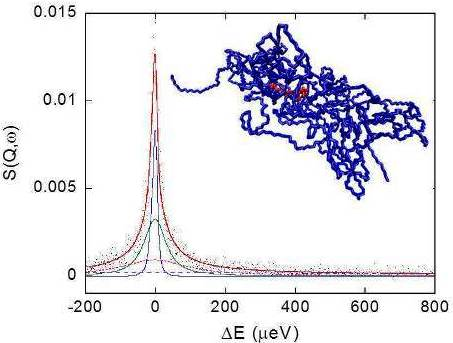
The picture of the junction domain obtained in the simulation study is reported in Figure 1, showing a snapshot of the MD trajectory at 313 K.

The PMA cross-linking chain, formed by eight PMA repeating units, is in the core of this structure and two PVA chains exit from each PMA residue, for a total of 800 PVA residues. This model describes a network portion in a surrounding of about 5 nm from the junction. The sterical development of the network in the hydrogel can be represented as an ensemble of elements similar to that shown in Figure 1, interconnected by means of one or more PVA chains.

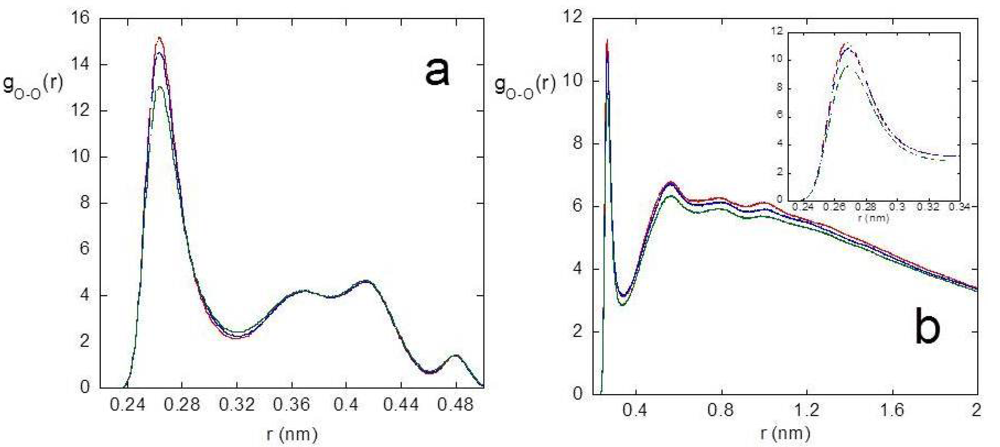
We investigated the intramolecular connectivity of the polymer system in the junction domain as a function of temperature, by selectively analyzing the radial distribution function between oxygen atoms of PVA, the major polymer component, and the intramolecular hydrogen bonding. [Figure 2(a)] reports the radial distribution function between PVA oxygen atoms, g_O-O(r), calculated including only the contribution of near neighboring residues, namely the radial distribution function between the oxygen atoms of the i and i + 1 residues of PVA.

The peak at about 0.27 nm shows the contribution to the first coordination shell of PVA oxygen atoms by adjacent residues and a decreasing of this contribution at increasing temperature is observed. The behavior of the g_O-O(r)s at higher distances seen in [Figure 2(a)], determined by the average conformational features and configuration constraints of adjacent residues, is not influenced by temperature, as reported for other vinyl polymers [85]. The temperature effect on the long range intramolecular connectivity is shown in [Figure 2(b)], where the radial distribution function between the oxygen atoms of i and i + j PVA residues, with j > 5, is reported. In this case, a lowering of the g_O-O(r) in the whole range of distances can be observed at increasing temperatures, denoting a relaxation and a loosening of the structure with temperature. The same kind of analysis was carried out on the radial distribution function between oxygen and hydrogen atoms of PVA hydroxyl groups, g_O-H(r), to investigate the intramolecular hydrogen bonding. By integration of the g_O-H(r), the average number of HBs per PVA residue was calculated, by distinguishing the contribution of near-neighboring and more distant residues. The results, reported in

Table 1. Intramolecular connectivity of PVA a.

T (K)	Average self-coordination number of PVA oxygen atoms b		Total average number of PVA-PVA hydrogen bonds per residue c	Average number of PVA-PVA HBs per residue d
	Contribution of near-neighboring residues	Contribution evaluated between i and (i + j) residues, with j> 5		Between near-neighboring residues	Between i and (i +j) residues, with j > 5
283	0.661	0.618	0.535	0.275	0.253
293	0.656	0.610	0.525	0.268	0.252
313	0.625	0.548	0.490	0.252	0.230

^aAnalysis performed over the last ns trajectory;^bCalculated by integration of the g_O-O(r)'s. R_min = 0.32 nm;^cCalculated analyzing the occurrence of hydrogen bond directly from trajectory;^dCalculated by integration of the g_O-H(r)'s. R_min = 0.24 nm.

together with the average self-coordination number of PVA oxygen atoms obtained from the g_O-O(r)s, indicate that the system evolves toward a less structured chain arrangement at increasing temperature.

The local mobility of the system in the surrounding of the junction was investigated by analyzing the torsional dynamics of the polymer backbone, governed by the possibility of transitions between different conformations of the chain dihedral angles. In a vinyl chain the dihedral angles defined by the backbone carbon atoms are all equivalent, therefore the description of the polymer conformation in the network can be performed in term of a single dihedral angle, θ, for PVA and for PMA, by considering two dihedrals per residue. The PVA and PMA components were separately analyzed and in the case of PVA the five residues nearest to the junction were excluded. We monitored the backbone dihedrals throughout the simulation to detect the transitions between rotational states. In PVA chains, the transitions occurred between the trans state (θ = 180°) and one of the gauche states (θ = ±70°), as the cis barrier was never crossed during the simulations.

The average lifetime of rotational state, <τ_rot>, was estimated by means of Equation 17

$$\langle {\tau }_{\mathit{\text{rot}}}\rangle =\frac{1}{N_{\mathit{\text{DIHE}}}}\sum _{i=1}^{N_{\mathit{\text{DIHE}}}}\frac{t_{\mathit{\text{SIM}}}}{\left(N_{\mathit{\text{TRANS}},i}+1\right)}$$

(17)

where N_DIHE, t_SIM and N_TRANS,i are the number of dihedral angles which perform transitions, the simulation time interval considered in the analysis and the number of transitions of the i-th dihedral angle, respectively. In Equation 17 the single term of the summation represents the time-average lifetime of rotational state for the i-th dihedral angle, τ_rot,i, then the average is performed on the mobile chain dihedral angles. The torsional dynamic behavior of PVA in the polymer network as a function of temperature is summarized in

Table 2. Backbone torsional dynamics of PVA and average root mean squared fluctuation of carbon atoms for whole system.

T(K)	Fraction of mobile dihedrals	Average lifetime of a torsional state a	Average RMSFb
	fDIHE	<trot> (ps)	(nm)
283	0.243	180 ± 50	0.23 ± 0.03
293	0.341	190 ± 40	0.26 ± 0.06
313	0.482	170 ± 30	0.28 ± 0.09

^aErrors estimated by the standard deviation of Equation 17;^bRMSF calculated over the last ns trajectory.

, where the fraction of mobile dihedrals, f_DIHE, and the <τ_rot> values are reported.

These findings show that the increase of temperature activates a higher number of dihedrals whereas the local torsional dynamics is, on average, less affected. By comparing the <τ_rot> values in Table 2 with the value of <τ_rot>, equal to 161 ps, obtained in the MD simulation of a telechelic PVA network at 323 K [52], we can conclude that, although the network structure is different, the local dynamics of the PVA component in these two hydrogels is quite similar.

The torsional mobility of the PMA chain is almost completely hindered and only the two external dihedrals can perform transitions, with τ_rot,i values of about 200 ps, irrespective of temperature. Therefore, the torsional dynamic behavior of the polymer in the surrounding of the junction of PVAMA1 hydrogel is strongly heterogeneous, with a very low mobility of the cross-linking chain and an activation effect by temperature acting only on the PVA moiety.

At the aim to evaluate the local dynamics of the polymer in the network, the root mean squared fluctuation (RMSF) of atomic positions for each backbone carbon atom was determined:

$$\mathit{\text{RMS}}{F}_i={\sqrt{\langle {\left({\mathbf{\text{r}}}_{\text{i}}\left(t\right)-\langle {\mathbf{\text{r}}}_i\rangle \right)}^2\rangle }}_t$$

(18)

The results are shown in Figure 3, where the RMSFs are reported as a function of the atom location in the polymer system (see Chart 2).

Empty squared symbols indicate atoms belonging to the PMA cross-linking chain. Figure 3 displays the dynamic heterogeneity of the junction domain. This heterogeneity is enhanced at the highest temperature. The system averaged RMSF increases at increasing temperature, as showed by values in the last column of Table 2.

3.1.2. Polymer-Water Interaction and Water Properties

We investigated the interaction between water and the two polymer components of the network, PVA and PMA, from both a structural and dynamic point of view. The analysis of polymer-water radial distribution functions and hydrogen bonding provided an averaged description of the network's hydration as a function of temperature. The study of polymer-water HB time autocorrelation function and of water mobility in the first hydration shell revealed the time scale of this interaction.

Figure 4 shows the radial distribution functions between hydroxyl PVA and water atoms, g_O-OW(r), g_H-OW(r), g_O-HW(r), at 283, 293 and 313 K. By integration of the g(r)s, as described in Section 2.3.2, we obtained the average water coordination number of PVA oxygen and the average HB capability of PVA with water.

The results, reported in

Table 3. PVA-water interaction: hydrogen bonding and water dynamics in the first hydration shell.

T (K)	Average water coordination number of PVA hydroxyl groups a	Average number of PVA-water HB's per PVA residue, with PVA acting as H acceptor b	Average number of PVA-water HBs per PVA residue, with PVA acting as H donor c	Average PVA-water HB lifetime d τHB(ps)	Halftime of desolvation in the 0.35 nm shell τ1/2 (ps)	Fraction of not exchangeable water in the 0.35 nm shell
283	1.32 ± 0.03	0.57 ± 0.01	0.46 ± 0.01	97 ± 17	101 ± 8	0.20 ± 0.02
293	1.39 ± 0.03	0.57 ± 0.01	0.46 ± 0.01	67 ± 13	80 ± 5	0.17 ± 0.01
313	1.48 ± 0.04	0.59 ± 0.02	0.49 ± 0.02	37 ± 3	62 ± 6	0.14 ± 0.01

^aCalculated by integration of the g_O-OW(r)'s. R_min = 0.34 nm;^bCalculated by integration of the g_O-HW(r)'s. R_min = 0.24 nm;^cCalculated by integration of the g_OW-H(r)'s. R_min = 0.24 nm;^dCalculated by integration of the PVA-water HB autocorrelation function.

, show a slightly increasing water affinity of PVA at increasing temperature.

The accessibility of water to the PMA cross-linking chain is described by Figure 5.

The radial distribution function between backbone carbon atoms of PMA and water oxygen atoms is reported in [Figure 5(a)]. From this curve we calculated the average number of water molecules per PMA residue inside a spherical domain of radius r centred on the PMA residue, N_OW(r), shown in [Figure 5(b)]. The results in [Figure 5(a,b)] indicate a swelling of the junction domain at increasing temperature. It is noteworthy that the temperature induced swelling effect begins at distances greater than about 0.9 nm. This result indicates that the low water affinity of the hydrophobic PMA residues is not affected by temperature, since at r > 0.9 nm from the PMA core only PVA residues are found. [Figure 5(c)], showing the radial distribution function between backbone carbon atoms of PMA and PVA, provides the complementary information to [Figure 5(a)]. In the distance range between about 0.8 and 2 nm the g(r)s of [Figure 5(a)] increase with temperature and, correspondingly, those in [Figure 5(c)] decrease; a behavior which describes the network swelling.

The polymer-water HB time autocorrelation function, C_HB(t), at the investigated temperatures is shown in [Figure 6(a)], together with the C_HB(t) of bulk water in the inset. The decay of the polymer-water C_HB(t) is strongly slowed, indicating a damping of water dynamics in the surrounding of PVA.

[Figure 6(b)] displays the results of an analysis of water mobility in the 0.35 nm thickness shell from the polymer. The solvent molecules included in this analysis correspond to the first hydration shell of polymer, since 0.35 nm is the distance of the first minimum in [Figure 4(a)]. We labeled the water molecules staying within a 0.35 nm distance from the polymer in the configuration at time t₀ and then we calculated the fraction of these water molecules, F_W0.35, jet residing inside the 0.35 nm shell at t > t₀. The F_W0.35(t) time decay, reported in [Figure 6(b)], is caused by the exchange of the water molecules in the first hydration shell with the more external water molecules, due to the diffusion motion of the solvent. The first information of [Figure 6(b)] is the kinetic effect of the temperature on water mobility, in agreement with the temperature behavior of the polymer-water hydrogen bond lifetime. In Table 3 we report the half-time of the hydration shell refresh, τ_1/2, obtained from the curves in [Figure 6(b)], and the average lifetime of PVA-water HB's, τ_HB, at the investigated temperatures. The increase of temperature enhances the water mobility in the surrounding of the polymer, with a decrease of both these times. The second information of [Figure 6(b)] is provided by the greater than 0 value of F_W0.35(t) at long times, indicating that some water molecules are confined within the first hydration shell. The fraction of these not exchangeable water molecules, reported in Table 3, decreases at increasing temperature. It is noteworthy that the value of τ_1/2 is always higher than the corresponding τ_HB (see Table 3) and that the C_HB(t) curves in [Figure 6(a)] can almost completely de-correlate in the investigated time window, whereas the corresponding F_W0.35(t) functions stabilize to a higher finite value. These findings indicate that a few water molecule moves along the polymer contour without leaving the shell. Indeed, such a dynamic behavior allows the de-correlation of C_HB(t), a function monitoring the HB between specific polymer-water pairs, but not the complete decay of the F_W0.35(t) function.

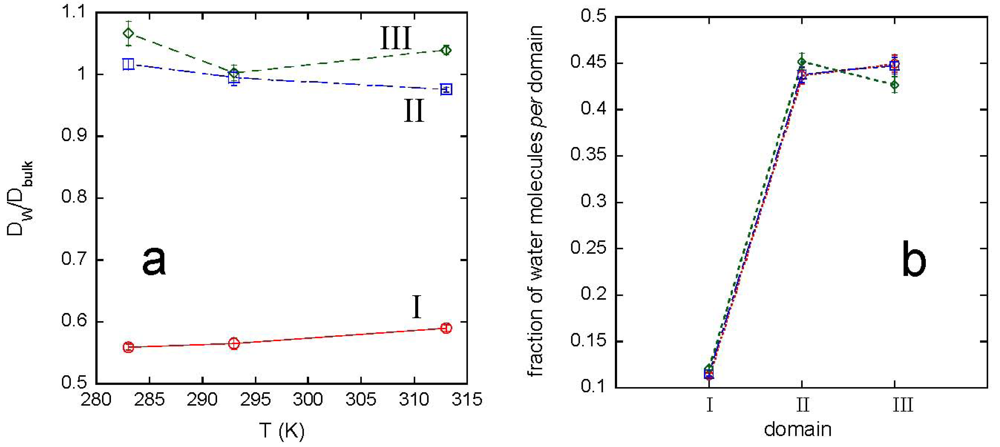
The interaction with the polymer network modifies the water dynamics, as shown by the behavior of the water diffusion coefficient, D_W, and of the hydrogen bonding between solvent molecules. The analysis of water properties was carried out by selecting the solvent molecules in different domains, depending on the distance from the polymer. The domain I includes water molecules within 0.6 nm, the distance corresponding to the second minimum of the g_O-OW(r), in [Figure 4(a)]. The domain II considers water molecules at distances from 0.6 to 2 nm. The remaining water molecules form the domain III. [Figure 7(a)] shows the ratio D_W/D_bulk for the three domains, being D_bulk the diffusion coefficient of bulk water, and Figure 7(b) reports the population of each water domain, as a function of temperature.

A supercooling effect on water molecules in domain I, including about 12% of total water, can be observed at each temperature. Moreover, the inversion of population of domain II over domain III at 313 K, shown in [Figure 7(b)], is in agreement with the network swelling at increasing temperature. The average lifetime of HBs between water molecules in the different domains, obtained by integration of the corresponding C_HB(t)s, is reported in

Table 4. Average lifetime of hydrogen bonds between water molecules of different domains a.

T (K)	τHB (ps)
	Domain I	Domain II	Domain III	Bulk water
283	5.68 ± 0.11	3.17 ± 0.03	3.11 ± 0.05	3.05 ± 0.02
303	4.85 ± 0.15	2.65 ± 0.03	2.60 ± 0.03	2.50 ± 0.04
313	3.32 ± 0.09	1.94 ± 0.01	1.91 ± 0.02	1.85 ± 0.03

^aCalculated by integration of the corresponding HB autocorrelation function.

, together with the values obtained for bulk water.

Data in Tables 3 and 4 indicate a polymer-induced slowing effect on the dynamics of the water. This effect involves solvent molecules which belong to the first and second coordination shell of the polymer, forming the domain I.

3.2. Neutron Scattering Experiments Results and Comparison with Simulation Findings

Figure 8 shows a typical QENS spectrum of PVAMA1 hydrogel at the maximum degree of swelling in D₂O, at 283 K and Q = 0.7751 Å⁻¹, together with the total fit curve and the single relaxation terms of Equations 6 and 7.

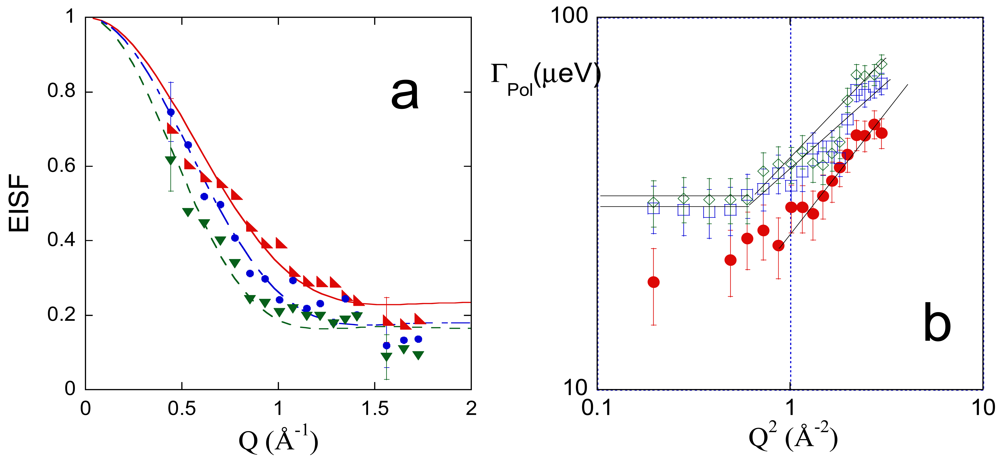
QENS spectra, acquired at 283, 303 and 313 K, were analyzed as a function of Q, as reported in Section 2.2.3. Figure 9(a,b) show the Q and temperature behavior of the terms related to the polymer dynamics, namely the EISF and the half width at half maximum of the L_pol relaxation function, Γ_Pol, respectively.

The Q-dependence of the EISF indicates a low confining regime for the polymer segmental dynamics, as previously observed in PVA hydrogels with low degree of cross-linking [28]. Curves in [Figure 9(b)] were fitted by Equation 19, according to the Volino-Dianoux model [86] which describes the confined motion of protons within a spherical potential of radius R

$$\mathit{\text{EISF}}=f+\left(1-f\right){\left[\frac{3_{j1}\left(\mathit{\text{Q}}R\right)}{\left(\mathit{\text{Q}}R\right)}\right]}^2$$

(19)

In Equation 19 j₁ is the first order spherical Bessel function and f is the fraction of “immobile” hydrogens that do not take part in the confined diffusion. The results of the fits, reported in

Table 5. Dynamical structural features of the polymer component by quasi-elastic neutron scattering.

T (K)	f	R (nm)	L (nm)
283	0.21 ± 0.02	0.29 ± 0.02
303	0.16 ± 0.01	0.31 ± 0.02	0.40 ± 0.05
313	0.15 ± 0.02	0.36 ± 0.02	0.41 ± 0.05

, show an increase of the confining length R and a decrease of the not diffusing hydrogen fraction f at increasing temperature.

The value of f could be interpreted assuming that the not mobile component of the network corresponds to the PMA cross-linking chains. In this hypothesis, the f value should be equal to 0.033, according to the 1% methacryloyl degree of substitution of PVA. The last value is considerably lower than the f values reported in Table 5. This consideration suggests that some PVA residues contribute to the fraction of “immobile” hydrogens, in agreement with the simulation findings, showing that the torsional dynamics of the PVA is precluded to some residues (see data in the second column of Table 2).

The results of the analysis of the EISF agree with the behavior of Γ_Pol as a function of Q, shown in [Figure 9(b)]. A low-Q plateau value is attained for measurements at 303 and 313 K, as expected for a confined diffusive dynamics [42,86-88]. Γ_Pol data at 283 K do not allow us to evaluate the low-Q limiting value due to large errors; however, we can assume a continuity in the dynamic behavior of the polymer in the investigated range of temperature. The low-Q plateau value is related to the local diffusion coefficient, D_Pol, within the confinement volume, according to Equation 20

$${\left({\Gamma }_{\mathit{\text{pol}}}\right)}_{\mathit{\text{Q}}\to 0}=\frac{D_{\mathit{\text{pol}}}{\pi }^2}{L^2}$$

(20)

where L is the radius of the confining domain. At higher Q-values, a departure from the constant limit value is expected since here the dynamics is probed over distances smaller than the confining ones. The departure point allows the estimate of L, according to QL = π. The value of L, reported in Table 5, is in satisfactory agreement with the value of R obtained from the EISF at the corresponding temperature. Using the L value and the asymptotic value of Γ_pol at low Q, the diffusion coefficient of the segmental motions of the chain was estimated according to Equation 20. The value of D_Pol at 303 K is 6 × 10⁻⁶ cm² s⁻¹, higher than that found for PVAMA5, equal to 1 × 10⁻⁶ cm² s⁻¹ [26]. This result shows that the polymer segmental mobility in PVAMA hydrogels is strongly affected by the degree of cross-linking.

The results of the QENS study can be compared with the findings on the polymer dynamics obtained in the MD simulations. The values of system averaged RMSFs, shown in the last column of Table 2, favorably compare with the corresponding values of R and L, reported in Table 5. The temperature influence on the polymer mobility is highlighted in the simulation by the behavior of RMSF of backbone carbon atoms, shown in Figure 3, and of the fraction of mobile dihedrals reported in Table 2. Simulation findings show the large dynamical heterogeneity of the network and the different effect of temperature on the dynamics of PMA and PVA chains.

The results of the incoherent elastic neutron scattering experiments on PVAMA1 hydrogel are reported in [Figure 10(a)] and the temperature behavior of the mean squared displacement of polymer hydrogen atoms, <u²>, is shown in [Figure 10(b)].

Figure 10(b) shows a rise of <u²> with the temperature, which is coherent with the increase of polymer mobility at increasing temperature found in QENS experiments and in MD simulations. The values of <u²>, obtained by means of Equation 3, describe the local polymer fluctuations in a time window of 70 ps, corresponding to instrumental resolution of the spectrometer in these experiments. Therefore, we compared the <u²> value with the value of the mean squared displacement of backbone carbon atoms calculated in trajectory intervals of 70 ps. The temperature behavior of <MSD₇₀>, calculated according to the procedure reported in Section 2.3.2, is shown in Figure 10(b). Each <MSD₇₀> value was obtained by averaging over all backbone carbon atoms. The large errors are due to the strong dynamical heterogeneity of the polymer network, showing a very low mobility in the surrounding of the junction and a higher mobility of some regions of the PVA chains. The <u²> and <MSD₇₀> values in Figure 10(b) are in satisfactory agreement, taking into account the complexity of the real system and the necessary approximations of the model.

4. Concluding Remarks

The properties of a hydrated polymer network are determined by: (i) chemical features of the constituting polymers, governing the solvent affinity and the intermolecular connectivity; (ii) structural factors, such as the degree of cross linking; (iii) dynamical factors, pertaining to both the matrix and the solvent. The double experimental and computational approach of this investigation, using incoherent neutron scattering and MD simulation, contributed to highlight the structural and dynamic features of PVAMA1 hydrogel in a space-time window of Å-ps.

The local polymer mobility in this network is enhanced by temperature, as shown by experimental and simulation findings. However, the network regions formed by PVA and PMA chains display a different dynamic behavior and temperature influence. The hydrophilic PVA chains show an increase of mobility with temperature. The hydrophobic PMA chain is very rigid and scarcely affected by temperature. The very low mobility of PMA is largely due to sterical effects and to the constraints of the cross-link. However, the lacking of a plasticizing effect from water molecules, which are excluded from the junction domain in a radius of about 0.9 nm, can increase the rigidity of PMA.

The peculiar contribution of the simulation study was to show how the different polymer moieties participate to the network mobility. Moreover, the MD simulations allowed us to study the polymer-water interaction, highlighting the heterogeneity in the solvent distribution and the swelling behavior of the network at increasing temperature. MD results indicate that the interaction with the polymer modifies the properties of a part of water molecules in the hydrogel, with a slowing of the solvent dynamics. This feature, not easy to experimentally prove in highly hydrated systems when the fraction of modified water is low, is relevant for the behavior of polymer macro- and micro-hydrogels in applications where the diffusion of permeating species, such as drugs and metabolites, is requested. Neutron scattering experiments of a deuterated polymer network in H₂O are planned, with the aim of deepening the study of the water dynamics in these hydrogels.