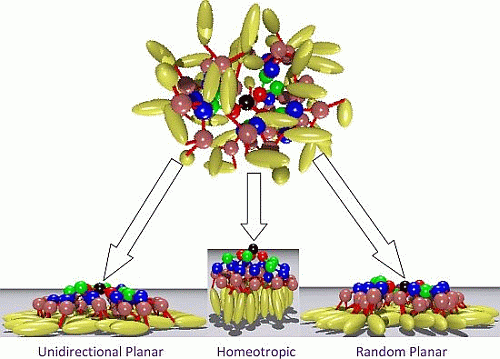
Surface-Induced Ordering on Model Liquid Crystalline Dendrimers
Abstract
:1. Introduction
2. Coarse Grain Modeling of LCDrs

| Parameter | Description | Values |
|---|---|---|
| D = σ0mm | diameter of mesogen | 1.0 (unit length) |
| L | length of mesogen | 3 D |
| σ0bb | diameter of bead | 1:2 D |
| σ0bm | mesogen-bead diameter | |
| σ0bw | bead-wall diameter | σ0bm |
| σ0mw | mesogen-wall diameter | σ0mm |
| ϵ0mm | energy unit | 1 |
| ϵ0bb | bead-bead interaction strength | 0.5 ϵ0mm |
| ϵ0bm | mesogen-bead interaction strength | |
| ϵ0bw | bead-wall interaction strength | ϵ0bm |
| ϵ0mw | mesogen-wall interaction strength | ϵ0mm |
| lmax | maximum bond length | 1:8 σ0mm |
| lmin | minimum bond length | 1:2 σ0mm |
3. Dendrimer-Substrate Interaction Potential

4. Simulation Details
5. Results and Discussion
5.1. Homeotropic Anchoring



5.2. Random Planar Anchoring



5.3. Unidirectional Planar Anchoring



6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Adroin, N.; Astruc, D. Molecular trees: From syntheses towards applications. Bull. Soc. Chem. Fr. 1995, 132, 875–909. [Google Scholar]
- Bosman, A.W.; Janssen, H.M.; Meijer, E.W. About dendrimers: Structure, physical properties, and applications. Chem. Rev. 1999, 99, 1665–1688. [Google Scholar] [CrossRef] [PubMed]
- Astruc, D.; Boisselier, E.; Ornelas, C. Dendrimers designed for functions: From physical, photophysical, and supramolecular properties to applications in sensing, catalysis, molecular electronics, photonics, and nanomedicine. Chem. Rev. 2010, 110, 1857–1959. [Google Scholar] [CrossRef] [PubMed]
- Astruc, D.; Chardac, F. Dendritic catalysts and dendrimers in catalysis. Chem. Rev. 2001, 101, 2991–3024. [Google Scholar] [CrossRef]
- Bronstein, L.M.; Shifrina, Z.B. Dendrimers as encapsulating, stabilizing, or directing agents for inorganic nanoparticles. Chem. Rev. 2011, 111, 5301–5344. [Google Scholar] [CrossRef] [PubMed]
- Tomalia, D.A.; Frechet, J.M.J. Introduction to the dendritic state. In Dendrimers and Other Dendritic Polymers; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Paez, J.I.; Martinelli, M.; Brunetti, V.; Strumia, M.C. Dendronization: A useful synthetic strategy to prepare multifunctional materials. Polymers 2012, 4, 355–395. [Google Scholar] [CrossRef]
- Goodby, J.W.; Mehl, G.H.; Saez, I.M.; Tuffin, R.P.; Mackenzie, G.; Auzély-Velty, R.; Benvegnu, T.; Plusquellec, D. Liquid crystals with restricted molecular topologies: Supermolecules and supramolecular assemblies. Chem. Commun. 1998, 1998, 2057–2070. [Google Scholar] [CrossRef]
- Marcos, M.; Martin-Rapun, R.; Omenat, A.; Serrano, J.L. Highly congested liquid crystal structures: Dendrimers, dendrons, dendronized and hyperbranched polymers. Chem. Soc. Rev. 2007, 36, 1889–1901. [Google Scholar] [CrossRef] [PubMed]
- Donnio, B.; Buathong, S.; Bury, I.; Guillon, D. Liquid crystalline dendrimers. Chem. Soc. Rev. 2007, 36, 1495–1513. [Google Scholar] [CrossRef] [PubMed]
- Rosen, B.M.; Wilson, C.J.; Wilson, D.A.; Peterca, M.; Imam, M.R.; Percec, V. Dendron-mediated self-assembly, disassembly, and self-organization of complex systems. Chem. Rev. 2009, 109, 6275–6540. [Google Scholar] [CrossRef] [PubMed]
- Tomalia, D.A.; Naylor, A.M.; Goddard, W.A. Starburst dendrimers: Molecular-level control of size, shape, surface chemistry, topology, and flexibility from atoms to macroscopic matter. Angew. Chem. Int. Ed. 1990, 29, 138–175. [Google Scholar] [CrossRef]
- Barbera, J.; Marcos, M.; Serrano, J.L. Dendromesogens: Liquid crystal organizations versus starburst structures. Chem. Eur. J. 1999, 5, 1834–1840. [Google Scholar] [CrossRef]
- Nardele, C.G.; Asha, S.K. Photoresponsive smectic liquid crystalline multipods and hyperbranched azo polymers. J. Phys. Chem. B 2014, 118, 1670–1684. [Google Scholar] [CrossRef] [PubMed]
- Marcos, M.; Gimenez, R.; Serrano, J.L.; Donnio, B.; Heinrich, B.; Guillon, D. Dendromesogens: Liquid crystal organizations of poly(amidoamine) dendrimers versus starburst structures. Chem. Eur. J. 2001, 7, 1006–1013. [Google Scholar] [PubMed]
- Hernandez-Ainsa, S.; Fedeli, E.; Barbera, J.; Marcos, M.; Sierra, T.; Serrano, J.L. Self-assembly modulation in ionic PAMAM derivatives. Soft Matter 2014, 10, 281–289. [Google Scholar]
- Buathong, S.; Gehringer, L.; Donnio, B.; Guillon, D. Supramolecular organization of dendritic supermolecules into liquid crystalline mesophases. Comptes Rendus Chim. 2009, 12, 138–162. [Google Scholar] [CrossRef]
- Donnio, B.; Barberá, J.; Giménez, R.; Guillon, D.; Marcos, M.; Serrano, J.L. Controlled molecular conformation and morphology in poly(amidoamine) (PAMAM) and poly(propyleneimine) (DAB) dendrimers. Macromolecules 2002, 35, 370–381. [Google Scholar] [CrossRef]
- Barbera, J.; Marcos, M.; Omenat, A.; Serrano, J.L.; Martinez, J.I.; Alonso, P.J. Copper-containing dendromesogens: The influence of the metal on the mesomorphism. Liq. Cryst. 2000, 27, 255–262. [Google Scholar] [CrossRef]
- Kim, Y.K.; Senyuk, B.; Shin, S.T.; Kohlmeier, A.; Mehl, G.H.; Lavrentovich, O.D. Surface alignment, anchoring transitions, optical properties, and topological defects in the thermotropic nematic phase of organo-siloxane tetrapodes. Soft Matter 2013, 10, 500–509. [Google Scholar] [CrossRef]
- Terzis, A.F.; Vanakaras, A.G.; Photinos, D.J. Conformational phase transitions and re-entrance phenomena in dendromesogens. Molec. Cryst. Liq. Crys. 2000, 352, 265–274. [Google Scholar] [CrossRef]
- Vanakaras, A.G.; Photinos, D.J. Ordered fluids of globular supermolecules. J. Mater. Chem. 2001, 11, 2832–2838. [Google Scholar] [CrossRef]
- Peroukidis, S.D.; Vanakaras, A.G.; Photinos, D.J. A simple theory of molecular organization in fullerene-containing liquid crystals. J. Chem. Phys. 2005, 123. [Google Scholar] [CrossRef]
- Vanakaras, A.G.; Photinos, D.J. Molecular theory of dendritic liquid crystals: Self-organization and phase transitions. J. Mater. Chem. 2005, 15, 2002–2012. [Google Scholar] [CrossRef]
- Richardson, R.M.; Hanna, S.; Brooks, N.J.; Gauthe, B.L.L.E.; Pizzey, C.; Agina, E.; Boiko, N.; Shibaev, V.P. Columnar phases in liquid crystal dendrimers: Variable pressure X-ray diffraction. Mol. Cryst. Liq. Cryst. 2011, 541, 177–187. [Google Scholar] [CrossRef]
- Ostrovskii, B.; Sulyanov, S.; Boiko, N.; Shibaev, V.; Astafev, S.; Yanusova, L.; Jeu, W. Order and frustration in liquid-crystalline dendrimers. Eur. Phys. J. E 2013, 36, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Hughes, Z.E.; Wilson, M.R.; Stimson, L.M. Coarse-grained simulation studies of a liquid crystal dendrimer: Towards computational predictions of nanoscale structure through microphase separation. Soft Matter 2005, 1, 436–443. [Google Scholar] [CrossRef]
- Ilnytskyi, J.; Lintuvuori, J.; Wilson, M. Simulation of bulk phases formed by polyphilic liquid crystal dendrimers. Condens. Matter Phys. 2010, 13, 33001–33016. [Google Scholar] [CrossRef]
- Wallace, E.J.; Buzza, D.M.A.; Read, D.J. Monte Carlo simulation scheme for dendrimers satisfying detailed balance. Macromolecules 2001, 34, 7140–7146. [Google Scholar] [CrossRef]
- Klos, J.S.; Sommer, J. Properties of dendrimers with flexible spacer-chains: A Monte Carlo study. Macromolecules 2009, 42, 4878–4886. [Google Scholar] [CrossRef]
- Gotze, I.O.; Likos, C.N. Conformations of flexible dendrimers: A simulation study. Macromolecules 2003, 36, 8189–8197. [Google Scholar] [CrossRef]
- Lenz, D.A.; Blaak, R.; Likos, C.N. Colloid-dendrimer complexation. Soft Matter 2009, 5, 4542–4548. [Google Scholar] [CrossRef]
- Lenz, D.A.; Blaak, R.; Likos, C.N. Adsorption characteristics of amphiphilic dendrimers. Soft Matter 2009, 5, 2905–2912. [Google Scholar] [CrossRef]
- Christopoulos, D.K.; Photinos, D.J.; Stimson, L.M.; Terzis, A.F.; Vanakaras, A.G. Structure and nanomechanics of linear dendronised polymers: A molecular simulation study. J. Mater. Chem. 2003, 13, 2756–2764. [Google Scholar] [CrossRef]
- Christopoulos, D.K.; Terzis, A.F.; Vanakaras, A.G.; Photinos, D.J. Helix formation in linear achiral dendronized polymers: A computer simulation study. J. Chem. Phys. 2006, 125. [Google Scholar] [CrossRef]
- Córdova-Mateo, E.; Bertran, O.; Zhang, B.; Vlassopoulos, D.; Pasquino, R.; Schlüter, A.D.; Kröger, M.; Alemán, C. Interactions in dendronized polymers: Intramolecular dominates intermolecular. Soft Matter 2014, 10, 1032–1044. [Google Scholar]
- Gay, J.G.; Berne, B.J. Modification of the overlap potential to mimic a linear site–site potential. J. Chem. Phys. 1981, 74, 3316–3319. [Google Scholar] [CrossRef]
- De Miguel, E.; Rull, L.F.; Chalam, M.K.; Gubbins, K.E. Liquid crystal phase diagram of the Gay-Berne fluid. Mol. Phys. 1991, 74, 405–424. [Google Scholar]
- Bates, M.; Luckhurst, G. Computer simulation of liquid crystal phases formed by Gay-Berne mesogens. In Liquid Crystals I: Structure and Bonding; Mingos, D., Ed.; Springer: Berlin, Germany, 1999; Volume 94, pp. 65–137. [Google Scholar]
- Luckhurst, G.R.; Stephens, R.A.; Phippen, R.W. The Gay-Berne mesogen: A paradigm shift? Liq. Cryst. 2006, 33, 1389–1405. [Google Scholar]
- Luckhurst, G.R.; Stephens, R.A.; Phippen, R.W. Computer simulation studies of anisotropic systems. XIX. Mesophases formed by the Gay-Berne model mesogen. Liq. Cryst. 1990, 8, 451–464. [Google Scholar]
- Chalam, M.K.; Gubbins, K.E.; Miguel, E.D.; Rull, L.F. A Molecular simulation of a liquid-crystal model. Mol. Simul. 1991, 7, 357–385. [Google Scholar] [CrossRef]
- De Miguel, E.; Vega, C. The global phase diagram of the Gay-Berne model. J. Chem. Phys. 2002, 117, 6313–6322. [Google Scholar]
- Gruhn, T.; Schoen, M. Microscopic structure of molecularly thin confined liquid-crystal films. Phys. Rev. E 1997, 55, 2861–2875. [Google Scholar] [CrossRef]
- Gruhn, T.; Schoen, M. Substrate-induced order in confined nematic liquid-crystal films. J. Chem. Phys. 1998, 108, 9124–9136. [Google Scholar] [CrossRef]
- Mima, T.; Yasuoka, K. Interfacial anisotropy in the transport of liquid crystals confined between flat, structureless walls: A molecular dynamics simulation approach. Phys. Rev. E 2008, 77. [Google Scholar] [CrossRef]
- Chiccoli, C.; Pasini, P.; Semeria, F.; Zannoni, C. A computer simulation of nematic droplets with radial boundary conditions. Phys. Lett. A 1990, 150, 311–314. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Workineh, Z.G.; Vanakaras, A.G. Surface-Induced Ordering on Model Liquid Crystalline Dendrimers. Polymers 2014, 6, 2082-2099. https://doi.org/10.3390/polym6082082
Workineh ZG, Vanakaras AG. Surface-Induced Ordering on Model Liquid Crystalline Dendrimers. Polymers. 2014; 6(8):2082-2099. https://doi.org/10.3390/polym6082082
Chicago/Turabian StyleWorkineh, Zerihun G., and Alexandros G. Vanakaras. 2014. "Surface-Induced Ordering on Model Liquid Crystalline Dendrimers" Polymers 6, no. 8: 2082-2099. https://doi.org/10.3390/polym6082082
APA StyleWorkineh, Z. G., & Vanakaras, A. G. (2014). Surface-Induced Ordering on Model Liquid Crystalline Dendrimers. Polymers, 6(8), 2082-2099. https://doi.org/10.3390/polym6082082