Performance Analysis of a Fiber Reinforced Plastic Oil Cooler Cover Considering the Anisotropic Behavior of the Fiber Reinforced PA66
Abstract
:1. Introduction
2. Elastic Constitutive Model of the Orthogonal Anisotropic Material
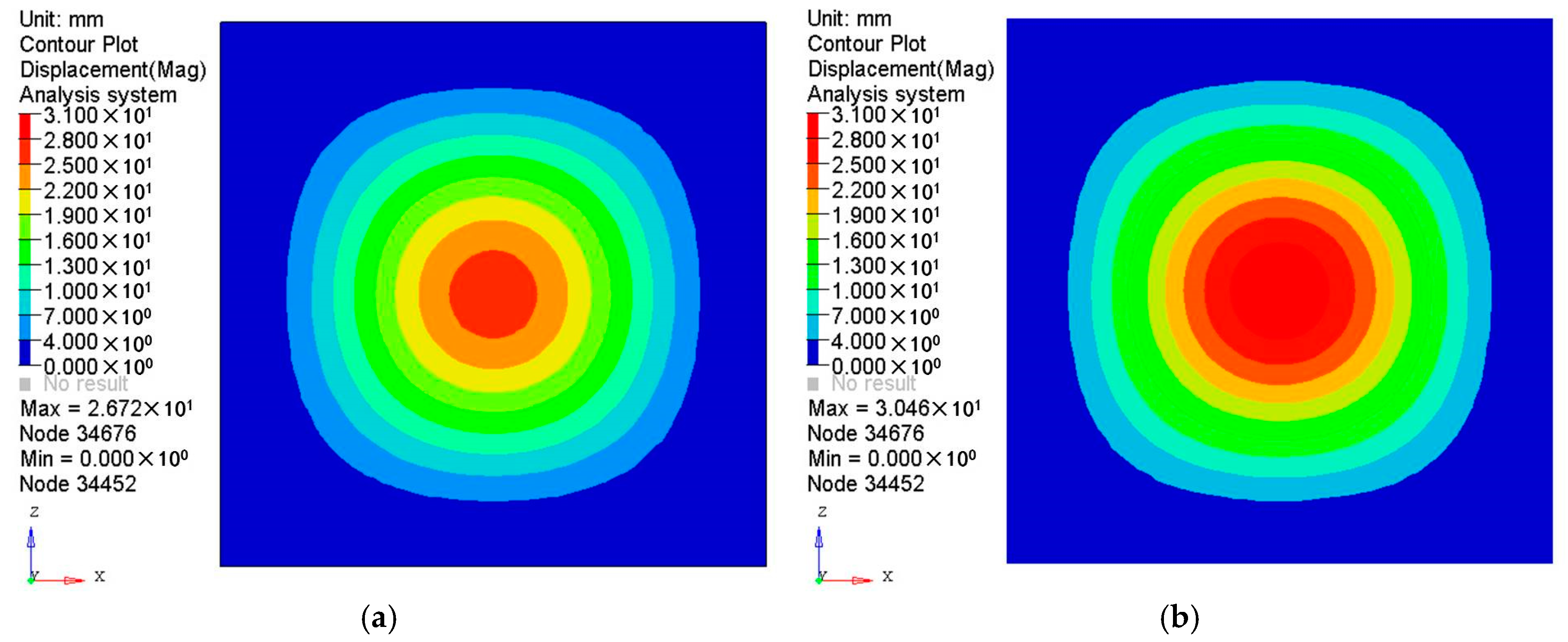
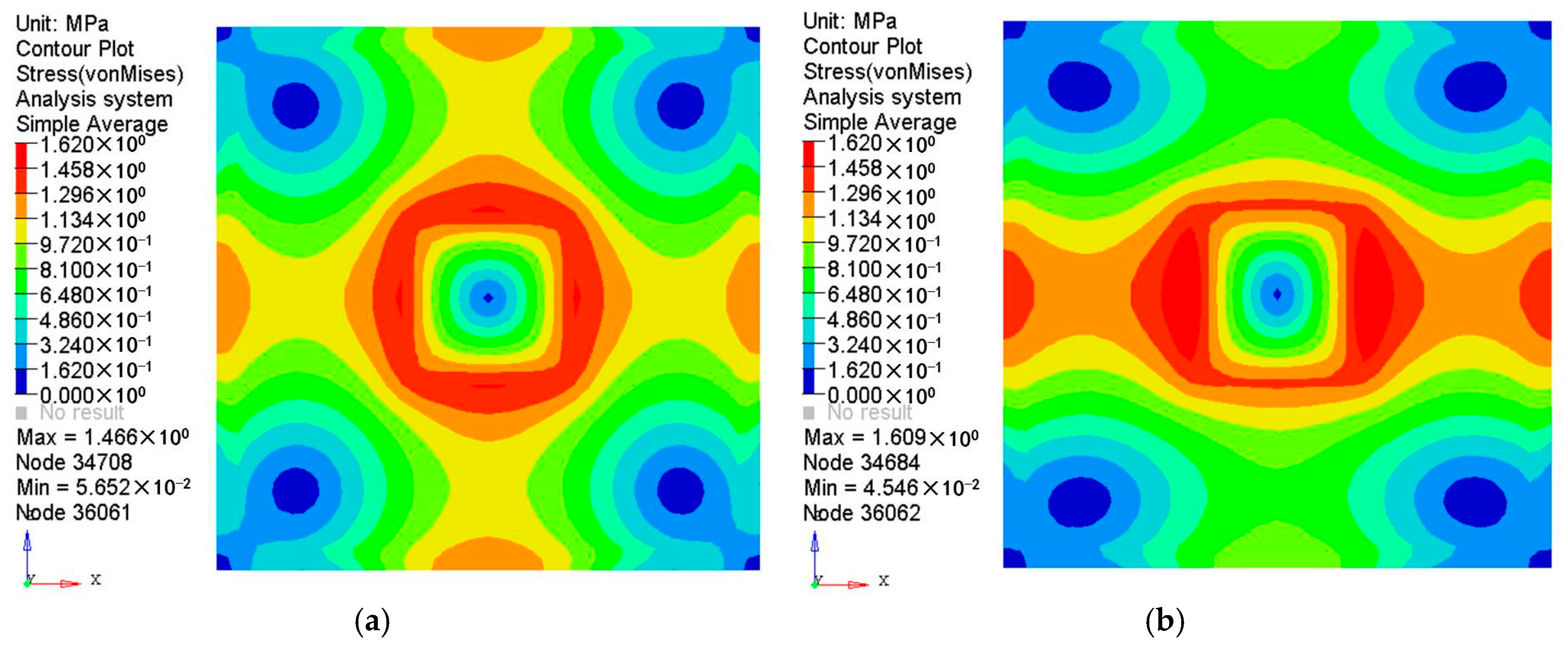
3. Comparison between Isotropic and Orthogonal Anisotropic Materials
3.1. Model and Material Properties
3.2. Comparison between Different Materials
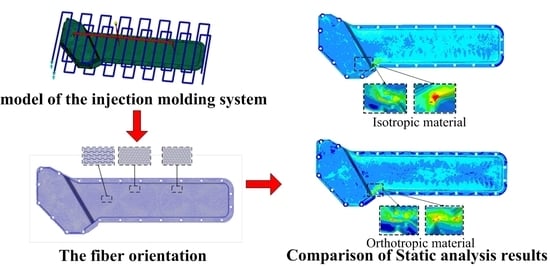
4. Performance Analysis of the Plastic Oil Cooler Cover
4.1. Model Information
4.1.1. Injection Model
4.1.2. Fluid Structure Coupled Model
- Cooling liquid:
- Gray cast iron:
- PA66 (GF 30%):
4.2. Static Analysis and Results
4.3. Dynamic Analysis and Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
References
- Ayadi, A.; Nouri, H.; Guessasma, S.; Roger, F. Determination of orthotropic properties of glass fibre reinforced thermoplastics using X-ray tomography and multiscale finite element computation. Compos. Struct. 2016, 136, 635–649. [Google Scholar] [CrossRef]
- Teixeira, D.; Giovanela, M.; Gonella, L.B.; Crespo, J.S. Influence of flow restriction on the microstructure and mechanical properties of long glass fiber-reinforced polyamide 6.6 composites for automotive applications. Mater. Des. 2013, 47, 287–294. [Google Scholar] [CrossRef]
- Thomason, J.L. The influence of fibre length, diameter and concentration on the impact performance of long glass-fibre reinforced polyamide 6,6. Compos. Part A Appl. Sci. Manuf. 2009, 40, 114–124. [Google Scholar] [CrossRef] [Green Version]
- Launay, A.; Maitournam, M.H.; Marco, Y.; Raoult, I.; Szmytka, F. Cyclic behaviour of short glass fibre reinforced polyamide: Experimental study and constitutive equations. Int. J. Plast. 2011, 27, 1267–1293. [Google Scholar] [CrossRef]
- Ku, H.; Wang, H.; Pattarachaiyakoop, N.; Trada, M. A review on the tensile properties of natural fiber reinforced polymer composites. Compos. Part B Eng. 2011, 42, 856–873. [Google Scholar] [CrossRef] [Green Version]
- AlMaadeed, M.A.; Kahraman, R.; Khanam, P.N.; Madi, N. Date palm wood flour/glass fibre reinforced hybrid composites of recycled polypropylene: Mechanical and thermal properties. Mater. Des. 2012, 42, 289–294. [Google Scholar] [CrossRef]
- Gupta, M.; Wang, K.K. Fiber orientation and mechanical properties of short-fiber-reinforced injection-molded composites: Simulated and experimental results. Polym. Compos. 1993, 14, 367–382. [Google Scholar] [CrossRef]
- Chung, S.T.; Kwon, T.H. Numerical simulation of fiber orientation in injection molding of short-fiber-reinforced thermoplastics. Polym. Eng. Sci. 1995, 35, 604–618. [Google Scholar] [CrossRef]
- Han, K.H.; Im, Y.T. Numerical simulation of three-dimensional fiber orientation in short-fiber-reinforced injection-molded parts. J. Mater. Process. Technol. 2002, 124, 366–371. [Google Scholar] [CrossRef]
- Thomason, J.L.; Vlug, M.A.; Schipper, G.; Krikor, H.G.L.T. Influence of fibre length and concentration on the properties of glass fibre-reinforced polypropylene: Part 3. Strength and strain at failure. Compos. Part A Appl. Sci. Manuf. 1996, 27, 1075–1084. [Google Scholar] [CrossRef]
- Thomason, J.L. Structure–property relationships in glass-reinforced polyamide, part 1: The effects of fiber content. Polym. Compos. 2006, 27, 552–562. [Google Scholar] [CrossRef] [Green Version]
- Thomason, J.L. Structure–property relationships in glass reinforced polyamide, Part 2: The effects of average fiber diameter and diameter distribution. Polym. Compos. 2007, 28, 331–343. [Google Scholar] [CrossRef] [Green Version]
- Bernasconi, A.; Rossin, D.; Armanni, C. Analysis of the effect of mechanical recycling upon tensile strength of a short glass fibre reinforced polyamide 6,6. Eng. Fract. Mech. 2007, 74, 627–641. [Google Scholar] [CrossRef]
- Bernasconi, A.; Cosmi, F. Analysis of the dependence of the tensile behaviour of a short fibre reinforced polyamide upon fibre volume fraction, length and orientation. Proc. Eng. 2011, 10, 2129–2134. [Google Scholar] [CrossRef]
- Bernasconi, A.; Conrado, E.; Hine, P. An experimental investigation of the combined influence of notch size and fibre orientation on the fatigue strength of a short glass fibre reinforced polyamide 6. Polym. Test. 2015, 47, 12–21. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, Y.; Mallick, P.K. Effects of temperature and strain rate on the tensile behavior of short fiber reinforced polyamide-6. Polym. Compos. 2002, 23, 858–871. [Google Scholar] [CrossRef]
- Zhou, Y.; Mallick, P.K. A non-linear damage model for the tensile behavior of an injection molded short E-glass fiber reinforced polyamide-6,6. Mater. Sci. Eng. A 2005, 393, 303–309. [Google Scholar] [CrossRef]
- De Monte, M.; Moosbrugger, E.; Quaresimin, M. Influence of temperature and thickness on the off-axis behavior of short glass fiber reinforced polyamide 6.6–Quasi-static loading. Compos. Part A Appl. Sci. Manuf. 2010, 41, 859–871. [Google Scholar] [CrossRef]
- Mortazavian, S.; Fatemi, A. Effects of fiber orientation and anisotropy on tensile strength and elastic modulus of short fiber reinforced polymer composites. Compos. Part B Eng. 2015, 72, 116–129. [Google Scholar] [CrossRef]
- Tezvergil, A.; Lassila, L.V.J.; Vallittu, P.K. The effect of fiber orientation on the thermal expansion coefficients of fiber-reinforced composites. Dent. Mater. 2003, 19, 471–477. [Google Scholar] [CrossRef]
- Heinle, M.; Drummer, D. Temperature-dependent coefficient of thermal expansion (CTE) of injection molded, short-glass-fiber-reinforced polymers. Polym. Eng. Sci. 2015, 55, 2661–2668. [Google Scholar] [CrossRef]
- Ding, X.; Liao, S.; Zhu, X.; Wang, H.M.; Zou, B.J. Effect of orthotropic material on finite element modeling of completely dentate mandible. Mater. Des. 2015, 84, 144–153. [Google Scholar] [CrossRef]
- Liao, S.H.; Zou, B.J.; Geng, J.P.; Wang, J.X.; Ding, X. Physical modeling with orthotropic material based on harmonic fields. Comput. Methods Prog. Biomed. 2012, 108, 536–547. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Liao, S.H.; Zhu, X.H.; Wang, H.M. Influence of orthotropy on biomechanics of peri-implant bone in complete mandible model with full dentition. Biomed. Res. Int. 2014, 2014. [Google Scholar] [CrossRef] [PubMed]
- Taylor, W.R.; Roland, E.; Ploeg, H.; Hertig, D.; Klabunde, R.; Warner, M.D.; Hobatho, M.C.; Rakotomanana, L.; Clift, S.E. Determination of orthotropic bone elastic constants using FEA and modal analysis. J. Biomech. 2002, 35, 767–773. [Google Scholar] [CrossRef]
- Advani, S.G.; Tucker, C.L., III. The use of tensors to describe and predict fiber orientation in short fiber composites. J. Rheol. 1987, 31, 751–784. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Jain, A.; Lomov, S.V.; Abdin, Y.; Verpoest, I.; Van Paepegem, W. Pseudo-grain discretization and full Mori Tanaka formulation for random heterogeneous media: Predictive abilities for stresses in individual inclusions and the matrix. Compos. Sci. Technol. 2013, 87, 86–93. [Google Scholar] [CrossRef]
- Jain, A.; Abdin, Y.; Van Paepegem, W.; Verpoest, I.; Lomov, S.V. Effective anisotropic stiffness of inclusions with debonded interface for Eshelby-based models. Compos. Struct. 2015, 131, 692–706. [Google Scholar] [CrossRef]
- Jain, A.; Veas, J.M.; Straesser, S.; Van Paepegem, W.; Verpoest, I.; Lomov, S.V. The Master SN curve approach—A hybrid multi-scale fatigue simulation of short fiber reinforced composites. Compos. Part A Appl. Sci. Manuf. 2015, in press. [Google Scholar] [CrossRef]
- Meraghni, F.; Benzeggagh, M.L. Micromechanical modelling of matrix degradation in randomly oriented discontinuous-fibre composites. Compos. Sci. Technol. 1995, 55, 171–186. [Google Scholar] [CrossRef]
- Brighenti, R.; Scorza, D. A micro-mechanical model for statistically unidirectional and randomly distributed fibre-reinforced solids. Math. Mech. Solids 2012, 17, 876–893. [Google Scholar] [CrossRef]
- Brighenti, R.; Scorza, D. Numerical modelling of the fracture behaviour of brittle materials reinforced with unidirectional or randomly distributed fibres. Mech. Mater. 2012, 52, 12–27. [Google Scholar] [CrossRef]
- Zhang, W.; Cai, C.S.; Pan, F. Finite element modeling of bridges with equivalent orthotropic material method for multi-scale dynamic loads. Eng. Struct. 2013, 54, 82–93. [Google Scholar] [CrossRef]
- Bikard, J.; Robert, G.; Moulinjeune, O. Multiscale modeling of the orthotropic behaviour of PA6-6 overmoulded composites using MMI approach. In Proceedings of the AIP Conference, Belfast, UK, 27–29 April 2011; pp. 726–731.
- Mouti, Z.; Westwood, K.; Long, D.; Njuguna, J. Finite element analysis of glass fiber-reinforced polyamide engine oil pan subjected to localized low velocity impact from flying projectiles. Steel Res. Int. 2012, 83, 957–963. [Google Scholar] [CrossRef] [Green Version]
- Mouti, Z.; Westwood, K.; Long, D.; Njuguna, J. An experimental investigation into localised low-velocity impact loading on glass fibre-reinforced polyamide automotive product. Compos. Struct. 2013, 104, 43–53. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef]
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Aboudi, J. Mechanics of Composite Materials: A Unified Micromechanical Approach; Elsevier: New York, NY, USA, 1991. [Google Scholar]
- Zhang, J.; Wang, J.; Lin, J.; Guo, Q.; Chen, K.; Ma, L. Multiobjective optimization of injection molding process parameters based on Opt LHD, EBFNN, and MOPSO. Int. J. Adv. Manuf. Technol. 2016, 85, 2857–2872. [Google Scholar] [CrossRef]

























| Properties | Values |
|---|---|
| Material structure | Crystalline |
| Glass fiber | 30% |
| Solid density (g/cm3) | 1.36 |
| Melt density (g/cm3) | 1.16 |
| E1 (MPa) | 10,300 |
| E2 E3 (MPa) | 6,800 |
| μ12,μ13 | 0.4 |
| G12 (MPa) | 1,910 |
| α1 (1/K) | 3 × 10−5 |
| α2 α3 (1/K) | 9 × 10−5 |
| Ejection temperature (°C) | 185 |
| Recommended mold temperature (°C) | 90 |
| Recommended melt temperature (°C) | 300 |
| Order | Isotropic (Hz) | Anisotropic (Hz) |
|---|---|---|
| 1 | 31.29 | 24.90 |
| 2 | 45.92 | 44.26 |
| 3 | 60.59 | 60.51 |
| 4 | 81.93 | 68.53 |
| 5 | 81.93 | 75.79 |
| Order | Test | Isotropic | Deviation (%) | Anisotropic | Deviation (%) |
|---|---|---|---|---|---|
| 1 | 32.78 | 40.14 | 22.45 | 34.15 | 4.18 |
| 2 | 47.72 | 55.05 | 15.36 | 51.04 | 6.95 |
| 3 | 98.95 | 109.90 | 11.07 | 96.25 | 2.73 |
| 4 | 122.02 | 137.10 | 12.36 | 126.25 | 3.46 |
| 5 | 169.37 | 184.00 | 8.64 | 165.50 | 2.28 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhang, J.; Lin, J.; Li, W.; Dai, H.; Hu, H. Performance Analysis of a Fiber Reinforced Plastic Oil Cooler Cover Considering the Anisotropic Behavior of the Fiber Reinforced PA66. Polymers 2016, 8, 312. https://doi.org/10.3390/polym8090312
Wang J, Zhang J, Lin J, Li W, Dai H, Hu H. Performance Analysis of a Fiber Reinforced Plastic Oil Cooler Cover Considering the Anisotropic Behavior of the Fiber Reinforced PA66. Polymers. 2016; 8(9):312. https://doi.org/10.3390/polym8090312
Chicago/Turabian StyleWang, Jian, Junhong Zhang, Jiewei Lin, Weidong Li, Huwei Dai, and Huan Hu. 2016. "Performance Analysis of a Fiber Reinforced Plastic Oil Cooler Cover Considering the Anisotropic Behavior of the Fiber Reinforced PA66" Polymers 8, no. 9: 312. https://doi.org/10.3390/polym8090312
APA StyleWang, J., Zhang, J., Lin, J., Li, W., Dai, H., & Hu, H. (2016). Performance Analysis of a Fiber Reinforced Plastic Oil Cooler Cover Considering the Anisotropic Behavior of the Fiber Reinforced PA66. Polymers, 8(9), 312. https://doi.org/10.3390/polym8090312