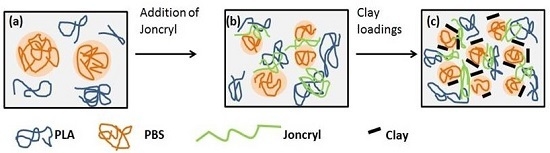
The Distribution of Nanoclay Particles at the Interface and Their Influence on the Microstructure Development and Rheological Properties of Reactively Processed Biodegradable Polylactide/Poly(butylene succinate) Blend Nanocomposites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Reactive Processing of Blends and Nanocomposites
2.3. Rheological Measurements
2.4. Morphological Analysis
2.5. SAXS Studies
3. Results and Discussion
3.1. Phase Morphology
3.2. Dispersion and Localization of Nanoclay Platelets
3.3. SAXS Analysis
3.4. Linear Rheological Analysis
3.5. Non-linear Rheological Analysis Based on LAOS Tests
FT-Rheology
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Babu, R.P.; O’Connor, K.; Seeram, R. Current progress on bio-based polymers and their future trends. Prog. Biomater. 2013, 2, 1–16. [Google Scholar] [CrossRef]
- Ojijo, V.; Ray, S.S. Processing strategies in bionanocomposites. Prog. Polym. Sci. 2013, 38, 1543–1589. [Google Scholar] [CrossRef]
- Ray, S.S. Environmentally Friendly Polymer Nanocomposites; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Odent, J.; Raquez, J.-M.; Leclère, P.; Lauro, F.; Dubois, P. Crystallization-induced toughness of rubber-modified polylactide: Combined effects of biodegradable impact modifier and effective nucleating agent. Polym. Adv. Technol. 2015, 26, 814–822. [Google Scholar] [CrossRef]
- Ojijo, V.; Ray, S.S. Super toughened biodegradable polylactide blends with non-linear copolymer interfacial architecture obtained via facile in situ reactive compatibilization. Polymer 2015, 80, 1–17. [Google Scholar] [CrossRef]
- Salehiyan, R.; Yussuf, A.A.; Hanani, N.F.; Hassan, A.; Akbari, A. Polylactic acid/polycaprolactone nanocomposite influence of montmorillonite and impact modifier on mechanical, thermal, and morphological properties. J. Elastom. Plast. 2015, 47, 69–87. [Google Scholar] [CrossRef]
- Jalali Dil, E.; Carreau, P.J.; Favis, B.D. Morphology, miscibility and continuity development in poly(lactic acid)/poly(butylene adipate-co-terephthalate) blends. Polymer 2015, 68, 202–212. [Google Scholar] [CrossRef]
- Ojijo, V.; Ray, S.S.; Sadiku, R. Toughening of biodegradable polylactide/poly(butylene succinate-co-adipate) blends via in situ reactive compatibilization. ACS Appl. Mater. Interfaces 2013, 5, 4266–4276. [Google Scholar] [CrossRef] [PubMed]
- Luzi, F.; Fortunati, E.; Jimenez, A.; Puglia, D.; Pezzolla, D.; Gigliotti, D.; Kenny, J.M.; Chiralt, A.; Torre, L. Production and characterization of PLA-PBS biodegradable blends reinforced with cellulose nanocrystals extracted from hemp fibres. Ind. Crop. Prod. 2016, 93, 276–289. [Google Scholar] [CrossRef]
- La Mantia, F.P.; Ceraulo, M.; Giacchi, G.; Mistretta, M.C.; Botta, L. Effect of a compatibilizer on the morphology and properties of polypropylene/polyethyleneterephthalate spun fibers. Polymers 2017, 9, 47. [Google Scholar] [CrossRef]
- Kumar, M.; Mohanty, S.; Nayak, S.K.; Parvaiz, M.R. Effect of glycidyl methacrylate (GMA) on the thermal, mechanical and morphological property of biodegradable PLA/PBAT blend and its nanocomposites. Bioresour. Technol. 2010, 101, 8406–8415. [Google Scholar] [CrossRef] [PubMed]
- Al-Itry, R.; Lamnawar, K.; Maazouz, A. Improvement of thermal stability, rheological and mechanical properties of PLA, PBAT and their blends by reactive extrusion with functionalized epoxy. Polym. Degrad. Stabil. 2012, 97, 1898–1914. [Google Scholar] [CrossRef]
- Ray, S.S.; Pouliot, S.; Bousmina, M.; Utracki, L.A. Role of organically modified layered Silicate as an active interfacial modifier in immiscible polystyrene/polypropylene blends. Polymer 2004, 45, 8403–8413. [Google Scholar]
- Trifkovic, M.; Hedegaard, A.T.; Sheikhzadeh, M.; Huang, S.; Macosko, C. Stabilization of PE/PEO cocontinuous blends by interfacial nanoclays. Macromolecules 2015, 48, 4631–4644. [Google Scholar] [CrossRef]
- Salehiyan, R.; Yoo, Y.; Choi, J.W.; Hyun, K. Characterization of morphologies of compatibilized polypropylene/polystyrene blends with nanoparticles via nonlinear Rheological properties from FT-rheology. Macromolecules 2014, 47, 4066–4076. [Google Scholar] [CrossRef]
- Salehiyan, R.; Song, H.Y.; Choi, W.J.; Hyun, K. Characterization of effects of silica nanoparticles on (80/20) PP/PS blends via nonlinear rheological properties from Fourier Transform rheology. Macromolecules 2015, 48, 4669–4679. [Google Scholar] [CrossRef]
- Sangroniz, L.; Moncerrate, M.A.; De Amicis, V.A.; Palacios, J.K.; Fernandez, M.; Santamaria, M.; Sanchez, J.J.; Laoutid, F.; Dubois, P.; Muller, A.J. The outstanding ability of nanosilica to stabilize dispersions of nylon 6 droplets in a polypropylene matrix. J. Polym. Sci Polym. Phys. 2015, 53, 1567–1579. [Google Scholar] [CrossRef]
- Cao, L.; Deng, S.; Lin, Z. Enhancement of carbon nanotube particle distribution in PPS/PEEK/Carbon nanotube ternary composites with sausage-like structure. Polymers 2016, 8, 50. [Google Scholar] [CrossRef]
- Bhatia, A.; Gupta, R.K.; Bhattacharya, S.N.; Choi, H.J. Effect of clay on thermal, mechanical and gas barrier properties of biodegradable poly(lactic acid)/poly(butylene succinate) (PLA/PBS) nanocomposites. Int. Polym. Proc. 2010, 25, 5–14. [Google Scholar] [CrossRef]
- Chen, G.X.; Kim, H.S.; Kim, E.S.; Yoon, J.S. Compatibilization-like effect of reactive organoclay on the poly(l-lactide)/poly(butylene succinate) blends. Polymer 2005, 46, 11829–11836. [Google Scholar] [CrossRef]
- La Mantia, F.P.; Mistretta, M.C.; Palermo, S.; Ceraulo, M. Morphology, rheology, and mechanical properties of a new nanobiocomposite. J. Appl. Polym. Sci. 2015, 132, 42128. [Google Scholar] [CrossRef]
- Coppola, B.; Scarfato, P.; Incarnato, L.; Di Maio, L. Morphology development and mechanical properties variation during cold-drawing of polyethylene-clay nanocomposite fibers. Polymers 2017, 9, 235. [Google Scholar]
- Palierne, J.F. Linear rheology of viscoelastic emulsions with interfacial tension. Rheol. Acta 1990, 29, 204–214. [Google Scholar] [CrossRef]
- Gramespacher, H.; Meissner, J. Interfacial tension between polymer melts measured by shear oscillations of their blends. J. Rheol. 1992, 36, 1127–1141. [Google Scholar] [CrossRef]
- Jacobs, U.; Fahrlander, M.; Winterhalter, J.; Friedrich, C. Analysis of Palierne’s emulsion model in the case of viscoelastic interfacial properties. J. Rheol. 1999, 43, 1495–1509. [Google Scholar] [CrossRef]
- Almusallam, A.C.; Larson, R.G.; Solomon, M.J. Comprehensive constitutive model for immiscible blends of Newtonian polymers. J. Rheol. 2004, 48, 319–348. [Google Scholar] [CrossRef]
- Hyun, K.; Wilhelm, M.; Klein, C.O.; Cho, K.S.; Nam, J.G.; Ahn, K.H.; Lee, S.J.; Ewoldt, R.H.; McKinley, G.H. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Prog. Polym. Sci. 2011, 36, 1697–1753. [Google Scholar] [CrossRef]
- Ewoldt, R.H. Defining nonlinear rheological material functions for oscillatory shear. J. Rheol. 2013, 57, 177–195. [Google Scholar] [CrossRef]
- Yazar, G.; Duvarci, O.C.; Tavman, S.; Kokini, J.L. Effect of mixing on LAOS properties of hard wheat flour dough. J. Food Eng. 2016, 190, 195–204. [Google Scholar] [CrossRef]
- Wilhelm, M.; Maring, D.; Spiess, H.-W. Fourier-transform rheology. Rheol. Acta 1998, 37, 399–405. [Google Scholar] [CrossRef]
- Wilhelm, M.; Reinheimer, P.; Ortseifer, M. High sensitivity Fourier-transform rheology. Rheol. Acta 1999, 38, 349–356. [Google Scholar] [CrossRef]
- Ock, H.G.; Ahn, K.H.; Lee, S.J.; Hyun, K. Characterization of compatibilizing effect of organoclay in poly (lactic acid) and natural rubber blends by FT-rheology. Macromolecules 2016, 49, 2832–2842. [Google Scholar] [CrossRef]
- Sangroniz, L.; Palacios, J.K.; Fernandez, M.; Eguiazabal, J.I.; Santamaria, A.; Muller, A.J. Linear and non-linear rheological behavior of polypropylene/polyamide blends modified with a compatibilizer agent and nanosilica and its relationship with the morphology. Eur. Polym. J. 2016, 83, 10–21. [Google Scholar] [CrossRef]
- Krevelen, D.W.V. Properties of Polymer; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Ojijo, V.; Ray, S.S.; Cele, H. Morphology and properties of polymer composites based on biodegradable polylactide/poly[(butylene succinate)-co-adipate] blend and nanoclay. Macromol. Mater. Eng. 2011, 296, 865–877. [Google Scholar] [CrossRef]
- Meng, Q.; Heuzey, M.C.; Carreaue, P.J. Control of thermal degradation of polylactide/clay nanocomposites during melt processing by chain extension reaction. Polym. Degrad. Stabil. 2012, 97, 2010–2020. [Google Scholar] [CrossRef]
- Chaiwutthinan, P.; Pimpan, V.; Chuayjuljit, S.; Leejarkpai, T. Biodegradable plastic prepared from poly(lactic acid), poly(butylene succinate) and microcrystalline cellulose extracted from waste-cotton fabric with a chain. J. Polym. Environ. 2015, 23, 114–125. [Google Scholar] [CrossRef]
- Van Puyvelde, P.; Velankar, S.; Moldenaers, P. Rheology and morphology of compatibilized polymer blends. Curr. Opin. Colloid Interface 2001, 6, 457–463. [Google Scholar] [CrossRef]
- Thareja, P.; Velankar, S. Rheology of immiscible blends with particle-induced drop clusters. Rheol. Acta 2008, 47, 189–200. [Google Scholar] [CrossRef]
- Thareja, P.; Moritz, K.; Velankar, S. Interfacially active particles in droplet/matrix blends of model immiscible homopolymers: Particles can increase or decrease drop size. Rheol. Acta 2010, 49, 285–298. [Google Scholar] [CrossRef]
- Bandyopadhyay, J.; Ray, S.S. The quantitative analysis of nano-clay dispersion in polymer nanocomposites by small angle X-ray scattering combined with electron microscopy. Polymer 2010, 51, 1437–1449. [Google Scholar] [CrossRef]
- Maani, A.; Heuzey, M.C.; Carreau, P.J. Coalescence in thermoplastic olefin (TPO) blends under shear flow. Rheol. Acta 2011, 50, 881–895. [Google Scholar] [CrossRef]
- Maani, A.; Blais, B.; Heuzey, M.C.; Carreau, P.J. Rheological and morphological properties of reactively compatibilized thermoplastic olefin (TPO) blends. J. Rheol. 2012, 56, 625–647. [Google Scholar] [CrossRef]
- Souza, A.M.C.; Demarquette, N.R. Influence of coalescence and interfacial tension on the morphology of PP/HDPE compatibilized blends. Polymer 2002, 43, 3959–3967. [Google Scholar] [CrossRef]
- Labaume, I.; Mederic, P.; Huitric, J.; Aubry, T. Comparative study of interphase viscoelastic properties in polyethylene/polyamide blends compatibilized with clay nanoparticles or with a graft copolymer. J. Rheol. 2013, 57, 377–392. [Google Scholar] [CrossRef]
- Salehiyan, R.; Song, H.Y.; Hyun, K. Nonlinear behavior of PP/PS blends with and without clay under large amplitude oscillatory shear (LAOS) flow. Korea Aust. Rheol. J. 2015, 27, 95–103. [Google Scholar] [CrossRef]
- Lim, H.T.; Ahn, K.H.; Hong, J.S.; Hyun, K. Nonlinear viscoelasticity of polymer nanocomposites under large amplitude oscillatory shear flow. J. Rheol. 2013, 57, 767–789. [Google Scholar] [CrossRef]
- Salehiyan, R.; Song, H.Y.; Kim, M.; Choi, W.J.; Hyun, K. Morphological evaluation of PP/PS blends filled with different types of clays by nonlinear rheological analysis. Macromolecules 2016, 49, 3148–3160. [Google Scholar] [CrossRef]
- Ziegler, V.; Wolf, B.A. Viscosity and morphology of the two-phase system PDMS/P(DMS-ran-MPS). J. Rheol. 1999, 43, 1033–1045. [Google Scholar] [CrossRef]
- Reinheimer, K.; Grosso, M.; Wilhelm, M. Fourier transform rheology as a universal non-linear mechanical characterization of droplet size and interfacial tension of dilute monodisperse emulsions. J. Colloid Interface Sci. 2011, 360, 818–825. [Google Scholar] [CrossRef] [PubMed]
- Wilhelm, M.; Reinheimer, K.; Kübel, J. Optimizing the sensitivity of FT-rheology to quantify and differentiate for the first time the nonlinear mechanical response of dispersed beer foams of light and dark Beer. Z. Phys. Chem. 2012, 226, 547–567. [Google Scholar] [CrossRef]
- Schwab, L.; Hojdis, N.; Lacayo, J.; Wilhelm, M. Fourier-transform rheology of unvulcanized, carbon black filled styrene butadiene rubber. Macromol. Mater. Eng. 2016, 301, 457–468. [Google Scholar] [CrossRef]
- Hyun, K.; Wilhelm, M. Establishing a new mechanical nonlinear coefficient Q from FT-rheology: First investigation of entangled linear and comb polymer model systems. Macromolecules 2009, 42, 411–422. [Google Scholar] [CrossRef]
- Vittorias, I.; Parkinson, M.; Klimke, K.; Debbaut, B.; Wilhelm, M. Detection and quantification of industrial polyethylene branching topologies via Fourier-transform rheology, NMR and simulation using the Pom-pom model. Rheol. Acta 2007, 46, 321–340. [Google Scholar] [CrossRef]
- Hyun, K.; Lim, H.T.; Ahn, K.H. Nonlinear response of polypropylene (PP)/clay nanocomposites under dynamic oscillatory shear flow. Korea Aust. Rheol. J. 2012, 24, 113–120. [Google Scholar] [CrossRef]
- Lee, C.J.; Salehiyan, R.; Ham, D.S.; Cho, S.K.; Lee, S.J.; Kim, K.J.; Yoo, Y.; Hyun, K.; Lee, J.H.; Choi, W.J. Influence of carbon nanotubes localization and transfer on electrical conductivity in PA66/(PS/PPE)/CNTs Nanocomposites. Polymer 2016, 84, 198–208. [Google Scholar] [CrossRef]
- Lee, S.H.; Song, H.Y.; Hyun, K. Effects of silica nanoparticles on copper nanowire dispersions in aqueous PVA solutions. Korea Aust. Rheol. J. 2016, 28, 111–120. [Google Scholar] [CrossRef]














| Parameter | Value |
|---|---|
| Specific gravity, 25 °C | 1.08 |
| Molecular weight, Mw | ~6800 g/mol |
| Number average molecular weight, Mn | 3000 |
| Glass transition temperature, °C | 54 |
| Epoxy equivalent weight | 285 g/mol |
| Sample | 2θ/Degree | d-Spacing/nm | rmax/nm | Distance (r/nm, Calculated from *.PDC Plots) to Find Neighbours | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2θ1 | 2θ2 | 2θ3 | d1 | d2 | d3 | ||||||
| PLA/PBS/J/1.5%C30B | 1.2 | 2.4 | 7.36 | 3.68 | 8.6 | 1.5 | 3.2 | 4.6 | 6.3 | ||
| PLA/PBS/J/3%C30B | 2.3 | 5.5 | 3.84 | 1.61 | 13 | 1.5 | 3.2 | 6.7 | |||
| PLA/PBS/J/5%C30B | 2.4 | 5.5 | 3.68 | 1.61 | 13 | 1.5 | 3.2 | 6.9 | |||
| PLA/PBS/J/1.5%BET | 2.3 | 4.6 | 3.84 | 16.2 | 3.7 | 7.5 | 11.0 | ||||
| PLA/PBS/J/3%/BET | 2.3 | 4.6 | 3.84 | 16 | 3.7 | 7.5 | 11.0 | ||||
| PLA/PBS/J/5%BET | 2.3 | 4.6 | 3.84 | 16 | 3.7 | 7.5 | 11.0 | ||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salehiyan, R.; Ray, S.S.; Bandyopadhyay, J.; Ojijo, V. The Distribution of Nanoclay Particles at the Interface and Their Influence on the Microstructure Development and Rheological Properties of Reactively Processed Biodegradable Polylactide/Poly(butylene succinate) Blend Nanocomposites. Polymers 2017, 9, 350. https://doi.org/10.3390/polym9080350
Salehiyan R, Ray SS, Bandyopadhyay J, Ojijo V. The Distribution of Nanoclay Particles at the Interface and Their Influence on the Microstructure Development and Rheological Properties of Reactively Processed Biodegradable Polylactide/Poly(butylene succinate) Blend Nanocomposites. Polymers. 2017; 9(8):350. https://doi.org/10.3390/polym9080350
Chicago/Turabian StyleSalehiyan, Reza, Suprakas Sinha Ray, Jayita Bandyopadhyay, and Vincent Ojijo. 2017. "The Distribution of Nanoclay Particles at the Interface and Their Influence on the Microstructure Development and Rheological Properties of Reactively Processed Biodegradable Polylactide/Poly(butylene succinate) Blend Nanocomposites" Polymers 9, no. 8: 350. https://doi.org/10.3390/polym9080350
APA StyleSalehiyan, R., Ray, S. S., Bandyopadhyay, J., & Ojijo, V. (2017). The Distribution of Nanoclay Particles at the Interface and Their Influence on the Microstructure Development and Rheological Properties of Reactively Processed Biodegradable Polylactide/Poly(butylene succinate) Blend Nanocomposites. Polymers, 9(8), 350. https://doi.org/10.3390/polym9080350