Assimilation of Sentinel-2 Estimated LAI into a Crop Model: Influence of Timing and Frequency of Acquisitions on Simulation of Water Stress and Biomass Production of Winter Wheat
Abstract
:1. Introduction
- The simulation of water stress (as the ratio between the actual and the potential crop transpiration) in the crop model for nine conventionally farmed fields in Germany and,
- The accuracy of winter wheat aboveground biomass predictions at harvest for those fields?
2. Materials and Methods
2.1. Field Data
2.2. Crop Model Setup
2.3. Sentinel-2 Leaf Area Index Estimations
2.4. Scenario Development
2.5. Model Run and LAI Assimilation
2.6. Evaluation of Model Performance
3. Results
3.1. Sentinel-2 LAI Estimations and Simulated LAI
3.2. Results for Simulation of Water Stress
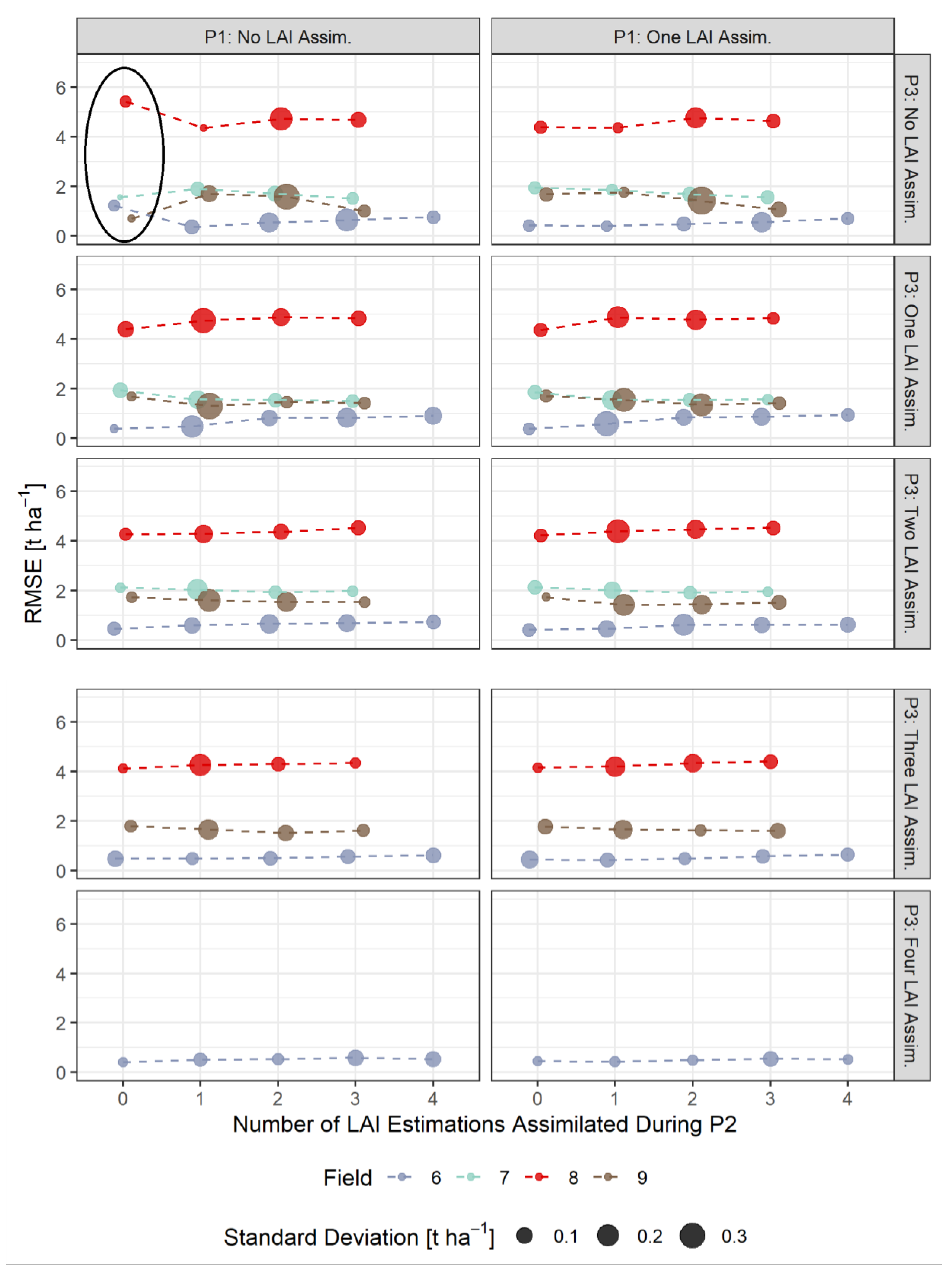
3.3. RMSE-Based Validation of Model Results
3.4. Bias-Based Validation of Model Results
4. Discussion
4.1. Sentinel-2 LAI Estimations
4.2. Impacts of Combinations of LAI Assimilation on Simulation Results
4.3. Limitations of Input and Validation Data
5. Conclusions
- The assimilation of a single Sentinel-2-estimated LAI value derived during an early stage of crop development (tillering phase) had positive effects on the accuracy of the simulation of total crop biomass at harvest. Compared to those results, updating LAI with a greater frequency and at later growing stages did not result in improvements of the predictions. LAI assimilation after the tillering phase is therefore not necessarily required, as it may not lead to the desired effect.
- The effects of LAI assimilation timing and frequency on water stress and biomass growth simulations might vary from site to site and season to season. We therefore encourage researchers to investigate and report those in detail, as to contribute to a better understanding of model responses.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A


References
- Eyshi Rezaei, E.; Siebert, S.; Ewert, F. Impact of data resolution on heat and drought stress simulated for winter wheat in Germany. Eur. J. Agron. 2015, 65, 69–82. [Google Scholar] [CrossRef]
- Maharjan, G.R.; Hoffmann, H.; Webber, H.; Srivastava, A.K.; Weihermüller, L.; Villa, A.; Coucheney, E.; Lewan, E.; Trombi, G.; Moriondo, M.; et al. Effects of input data aggregation on simulated crop yields in temperate and Mediterranean climates. Eur. J. Agron. 2019, 103, 32–46. [Google Scholar] [CrossRef]
- Mboh, C.M.; Srivastava, A.K.; Gaiser, T.; Ewert, F. Including root architecture in a crop model improves predictions of spring wheat grain yield and above-ground biomass under water limitations. J. Agron. Crop Sci. 2019, 205, 109–128. [Google Scholar] [CrossRef]
- Wallor, E.; Kersebaum, K.-C.; Ventrella, D.; Bindi, M.; Cammarano, D.; Coucheney, E.; Gaiser, T.; Garofalo, P.; Giglio, L.; Giola, P.; et al. The response of process-based agro-ecosystem models to within-field variability in site conditions. Field Crops Res. 2018, 228, 1–19. [Google Scholar] [CrossRef]
- Webber, H.; Gaiser, T.; Oomen, R.; Teixeira, E.; Zhao, G.; Wallach, D.; Zimmermann, A.; Ewert, F. Uncertainty in future irrigation water demand and risk of crop failure for maize in Europe. Environ. Res. Lett. 2016, 11, 074007. [Google Scholar] [CrossRef]
- Basso, B.; Ritchie, J.T.; Pierce, F.J.; Braga, R.P.; Jones, J.W. Spatial validation of crop models for precision agriculture. Agric. Syst. 2001, 68, 97–112. [Google Scholar] [CrossRef]
- Tewes, A.; Hoffmann, H.; Krauss, G.; Schäfer, F.; Kerkhoff, C.; Gaiser, T. New Approaches for the Assimilation of LAI Measurements into a Crop Model Ensemble to Improve Wheat Biomass Estimations. Agronomy 2020, 10, 446. [Google Scholar] [CrossRef] [Green Version]
- Waha, K.; Huth, N.; Carberry, P.; Wang, E. How model and input uncertainty impact maize yield simulations in West Africa. Environ. Res. Lett. 2015, 10, 024017. [Google Scholar] [CrossRef]
- Huang, J.; Gómez-Dans, J.L.; Huang, H.; Ma, H.; Wu, Q.; Lewis, P.E.; Liang, S.; Chen, Z.; Xue, J.-H.; Wu, Y.; et al. Assimilation of remote sensing into crop growth models: Current status and perspectives. Agric. For. Meteorol. 2019, 276–277, 107609. [Google Scholar] [CrossRef]
- Dong, T.; Shang, J.; Liu, J.; Qian, B.; Jing, Q.; Ma, B.; Huffman, T.; Geng, X.; Sow, A.; Shi, Y.; et al. Using RapidEye imagery to identify within-field variability of crop growth and yield in Ontario, Canada. Precis. Agric. 2019, 20, 1231–1250. [Google Scholar] [CrossRef]
- Kross, A.; McNairn, H.; Lapen, D.; Sunohara, M.; Champagne, C. Assessment of RapidEye vegetation indices for estimation of leaf area index and biomass in corn and soybean crops. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 235–248. [Google Scholar] [CrossRef] [Green Version]
- Wallach, D.; Makowski, D.; Jones, J.W.; Brun, F. Chapter 8-Data Assimilation for Dynamic Models. In Working with Dynamic Crop Models, 2nd ed.; Wallach, D., Makowski, D., Jones, J.W., Brun, F., Eds.; Academic Press: San Diego, CA, USA, 2014; pp. 311–343. ISBN 978-0-12-397008-4. [Google Scholar]
- Jin, X.; Li, Z.; Feng, H.; Ren, Z.; Li, S. Estimation of maize yield by assimilating biomass and canopy cover derived from hyperspectral data into the AquaCrop model. Agric. Water Manag. 2020, 227, 105846. [Google Scholar] [CrossRef]
- Silvestro, P.C.; Pignatti, S.; Pascucci, S.; Yang, H.; Li, Z.; Yang, G.; Huang, W.; Casa, R. Estimating Wheat Yield in China at the Field and District Scale from the Assimilation of Satellite Data into the Aquacrop and Simple Algorithm for Yield (SAFY) Models. Remote Sens. 2017, 9, 509. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zhang, Z.; Tao, F. Improving regional winter wheat yield estimation through assimilation of phenology and leaf area index from remote sensing data. Eur. J. Agron. 2018, 101, 163–173. [Google Scholar] [CrossRef]
- Zhou, G.; Liu, X.; Liu, M. Assimilating Remote Sensing Phenological Information into the WOFOST Model for Rice Growth Simulation. Remote Sens. 2019, 11, 268. [Google Scholar] [CrossRef] [Green Version]
- De Wit, A.J.W.; van Diepen, C.A. Crop model data assimilation with the Ensemble Kalman filter for improving regional crop yield forecasts. Agric. For. Meteorol. 2007, 146, 38–56. [Google Scholar] [CrossRef]
- Ines, A.V.M.; Das, N.N.; Hansen, J.W.; Njoku, E.G. Assimilation of remotely sensed soil moisture and vegetation with a crop simulation model for maize yield prediction. Remote Sens. Environ. 2013, 138, 149–164. [Google Scholar] [CrossRef] [Green Version]
- Pan, H.; Chen, Z.; de Wit, A.; Ren, J. Joint Assimilation of Leaf Area Index and Soil Moisture from Sentinel-1 and Sentinel-2 Data into the WOFOST Model for Winter Wheat Yield Estimation. Sensors 2019, 19, 3161. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Wang, P.; Bai, X.; Khan, J.; Zhang, S.; Li, L.; Wang, L. Assimilation of the leaf area index and vegetation temperature condition index for winter wheat yield estimation using Landsat imagery and the CERES-Wheat model. Agric. For. Meteorol. 2017, 246, 194–206. [Google Scholar] [CrossRef]
- Zhuo, W.; Huang, J.; Li, L.; Zhang, X.; Ma, H.; Gao, X.; Huang, H.; Xu, B.; Xiao, X. Assimilating Soil Moisture Retrieved from Sentinel-1 and Sentinel-2 Data into WOFOST Model to Improve Winter Wheat Yield Estimation. Remote Sens. 2019, 11, 1618. [Google Scholar] [CrossRef] [Green Version]
- Dong, T.; Liu, J.; Qian, B.; Zhao, T.; Jing, Q.; Geng, X.; Wang, J.; Huffman, T.; Shang, J. Estimating winter wheat biomass by assimilating leaf area index derived from fusion of Landsat-8 and MODIS data. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 63–74. [Google Scholar] [CrossRef]
- Gilardelli, C.; Stella, T.; Confalonieri, R.; Ranghetti, L.; Campos-Taberner, M.; García-Haro, F.J.; Boschetti, M. Downscaling rice yield simulation at sub-field scale using remotely sensed LAI data. Eur. J. Agron. 2019, 103, 108–116. [Google Scholar] [CrossRef]
- Huang, J.; Ma, H.; Su, W.; Zhang, X.; Huang, Y.; Fan, J.; Wu, W. Jointly Assimilating Modis LAI and ET Products Into the SWAP Model for Winter Wheat Yield Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4060–4071. [Google Scholar] [CrossRef]
- Huang, J.; Tian, L.; Liang, S.; Ma, H.; Becker-Reshef, I.; Huang, Y.; Su, W.; Zhang, X.; Zhu, D.; Wu, W. Improving winter wheat yield estimation by assimilation of the leaf area index from Landsat TM and MODIS data into the WOFOST model. Agric. For. Meteorol. 2015, 204, 106–121. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Chen, Z.; Liu, G.; Jiang, Z.; Huang, C. Improving Winter Wheat Yield Estimation from the CERES-Wheat Model to Assimilate Leaf Area Index with Different Assimilation Methods and Spatio-Temporal Scales. Remote Sens. 2017, 9, 190. [Google Scholar] [CrossRef] [Green Version]
- Mokhtari, A.; Noory, H.; Vazifedoust, M. Improving crop yield estimation by assimilating LAI and inputting satellite-based surface incoming solar radiation into SWAP model. Agric. For. Meteorol. 2018, 250–251, 159–170. [Google Scholar] [CrossRef]
- Novelli, F.; Spiegel, H.; Sandén, T.; Vuolo, F. Assimilation of Sentinel-2 Leaf Area Index Data into a Physically-Based Crop Growth Model for Yield Estimation. Agronomy 2019, 9, 255. [Google Scholar] [CrossRef] [Green Version]
- Tewes, A.; Hoffmann, H.; Nolte, M.; Krauss, G.; Schäfer, F.; Kerkhoff, C.; Gaiser, T. How Do Methods Assimilating Sentinel-2-Derived LAI Combined with Two Different Sources of Soil Input Data Affect the Crop Model-Based Estimation of Wheat Biomass at Sub-Field Level? Remote Sens. 2020, 12, 925. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Wang, P.; Sun, H.; Zhang, S.; Li, L. Assimilation of Leaf Area Index and Surface Soil Moisture With the CERES-Wheat Model for Winter Wheat Yield Estimation Using a Particle Filter Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1303–1316. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, S.; Shen, S. Assimilating remote sensing information with crop model using Ensemble Kalman Filter for improving LAI monitoring and yield estimation. Ecol. Model. 2013, 270, 30–42. [Google Scholar] [CrossRef]
- Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An Overview of Global Leaf Area Index (LAI): Methods, Products, Validation, and Applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Kooistra, L.; Van den Brande, M.M.M. Using Sentinel-2 Data for Retrieving LAI and Leaf and Canopy Chlorophyll Content of a Potato Crop. Remote Sens. 2017, 9, 405. [Google Scholar] [CrossRef] [Green Version]
- Pasqualotto, N.; Delegido, J.; Van Wittenberghe, S.; Rinaldi, M.; Moreno, J. Multi-Crop Green LAI Estimation with a New Simple Sentinel-2 LAI Index (SeLI). Sensors 2019, 19, 904. [Google Scholar] [CrossRef] [Green Version]
- Xie, Q.; Dash, J.; Huete, A.; Jiang, A.; Yin, G.; Ding, Y.; Peng, D.; Hall, C.C.; Brown, L.; Shi, Y.; et al. Retrieval of crop biophysical parameters from Sentinel-2 remote sensing imagery. Int. J. Appl. Earth Obs. Geoinformation 2019, 80, 187–195. [Google Scholar] [CrossRef]
- Fieuzal, R.; Bustillo, V.; Collado, D.; Dedieu, G. Combined Use of Multi-Temporal Landsat-8 and Sentinel-2 Images for Wheat Yield Estimates at the Intra-Plot Spatial Scale. Agronomy 2020, 10, 327. [Google Scholar] [CrossRef] [Green Version]
- Pause, M.; Raasch, F.; Marrs, C.; Csaplovics, E. Monitoring Glyphosate-Based Herbicide Treatment Using Sentinel-2 Time Series—A Proof-of-Principle. Remote Sens. 2019, 11, 2541. [Google Scholar] [CrossRef] [Green Version]
- Toscano, P.; Castrignanò, A.; Di Gennaro, S.F.; Vonella, A.V.; Ventrella, D.; Matese, A. A Precision Agriculture Approach for Durum Wheat Yield Assessment Using Remote Sensing Data and Yield Mapping. Agronomy 2019, 9, 437. [Google Scholar] [CrossRef] [Green Version]
- Vizzari, M.; Santaga, F.; Benincasa, P. Sentinel 2-Based Nitrogen VRT Fertilization in Wheat: Comparison between Traditional and Simple Precision Practices. Agronomy 2019, 9, 278. [Google Scholar] [CrossRef] [Green Version]
- Brogi, C.; Huisman, J.A.; Herbst, M.; Weihermüller, L.; Klosterhalfen, A.; Montzka, C.; Reichenau, T.G.; Vereecken, H. Simulation of spatial variability in crop leaf area index and yield using agroecosystem modeling and geophysics-based quantitative soil information. Vadose Zone J. 2020, 19. [Google Scholar] [CrossRef] [Green Version]
- Pätzold, S.; Mertens, F.M.; Bornemann, L.; Koleczek, B.; Franke, J.; Feilhauer, H.; Welp, G. Soil heterogeneity at the field scale: A challenge for precision crop protection. Precis. Agric. 2008, 9, 367–390. [Google Scholar] [CrossRef]
- Eckelmann, W.; Sponagel, H.; Grottenthaler, W.; Hartmann, K.-J.; Hartwich, R.; Janetzko, P.; Joisten, H.; Kühn, D.; Sabel, K.-J.; Traidl, R. Bodenkundliche Kartieranleitung. KA5; Bundesanstalt für Geowissenschaften und Rohstoffe, Ed.; Schweizerbart Science Publishers: Stuttgart, Germany, 2006; ISBN 978-3-510-95920-4. [Google Scholar]
- Enders, A.; Diekkrüger, B.; Laudien, R.; Gaiser, T.; Bareth, G. The IMPETUS Spatial Decision Support Systems. In Impacts of Global Change on the Hydrological Cycle in West and Northwest Africa; Speth, P., Christoph, M., Diekkrüger, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 360–393. ISBN 978-3-642-12957-5. [Google Scholar]
- Gaiser, T.; Perkons, U.; Küpper, P.M.; Kautz, T.; Uteau-Puschmann, D.; Ewert, F.; Enders, A.; Krauss, G. Modeling biopore effects on root growth and biomass production on soils with pronounced sub-soil clay accumulation. Ecol. Model. 2013, 256, 6–15. [Google Scholar] [CrossRef]
- Wolf, J. User Guide for LINTUL5: Simple Generic Model for Simulation of Crop Growth under Potential, Water Limited and Nitrogen, Phosphorus and Potassium Limited Conditions; Wageningen UR: Wageningen, The Netherlands, 2012. [Google Scholar]
- Faye, B.; Webber, H.; Diop, M.; Mbaye, M.L.; Owusu-Sekyere, J.D.; Naab, J.B.; Gaiser, T. Potential impact of climate change on peanut yield in Senegal, West Africa. Field Crop. Res. 2018, 219, 148–159. [Google Scholar] [CrossRef]
- Gabaldón-Leal, C.; Webber, H.; Otegui, M.E.; Slafer, G.A.; Ordóñez, R.A.; Gaiser, T.; Lorite, I.J.; Ruiz-Ramos, M.; Ewert, F. Modelling the impact of heat stress on maize yield formation. Field Crop. Res. 2016, 198, 226–237. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Ceglar, A.; Zeng, W.; Gaiser, T.; Mboh, C.M.; Ewert, F. The Implication of Different Sets of Climate Variables on Regional Maize Yield Simulations. Atmosphere 2020, 11, 180. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, A.K.; Mboh, C.M.; Gaiser, T.; Kuhn, A.; Ermias, E.; Ewert, F. Effect of mineral fertilizer on rain water and radiation use efficiencies for maize yield and stover biomass productivity in Ethiopia. Agric. Syst. 2019, 168, 88–100. [Google Scholar] [CrossRef]
- Webber, H.; Zhao, G.; Wolf, J.; Britz, W.; de Vries, W.; Gaiser, T.; Hoffmann, H.; Ewert, F. Climate change impacts on European crop yields: Do we need to consider nitrogen limitation? Eur. J. Agron. 2015, 71, 123–134. [Google Scholar] [CrossRef]
- Addiscott, T.M.; Whitmore, A.P. Simulation of solute leaching in soils of differing permeabilities. Soil Use Manag. 1991, 7, 94–102. [Google Scholar] [CrossRef]
- Wösten, J.H.M.; Lilly, A.; Nemes, A.; Le Bas, C. Development and use of a database of hydraulic properties of European soils. Geoderma 1999, 90, 169–185. [Google Scholar] [CrossRef]
- Main-Knorn, M.; Pflug, B.; Louis, J.; Debaecker, V.; Müller-Wilm, U.; Gascon, F. Sen2Cor for Sentinel-2. In Proceedings of the Image and Signal Processing for Remote Sensing XXIII, Warsaw, Poland, 11–13 September 2017; Bruzzone, L., Bovolo, F., Benediktsson, J.A., Eds.; SPIE: Warsaw, Poland, 2017; p. 3. [Google Scholar]
- Weiss, M.; Baret, F. S2ToolBox Level 2 Products: LAI, FAPAR, FCOVER. Sentinel-2 Algorithm Theoretical Based Document. Available online: http://step.esa.int/docs/extra/ATBD_S2ToolBox_L2B_V1.1.pdf (accessed on 13 August 2020).
- Hijmans, R.J. Raster: Geographic Data Analysis and Modeling; Scientific Research Publishing (SCIRP): Irvine, CA, USA, 2020. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Guo, C.; Tang, Y.; Lu, J.; Zhu, Y.; Cao, W.; Cheng, T.; Zhang, L.; Tian, Y. Predicting wheat productivity: Integrating time series of vegetation indices into crop modeling via sequential assimilation. Agric. For. Meteorol. 2019, 272–273, 69–80. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- Evensen, G. The Ensemble Kalman Filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Sieling, K.; Böttcher, U.; Kage, H. Dry matter partitioning and canopy traits in wheat and barley under varying N supply. Eur. J. Agron. 2016, 74, 1–8. [Google Scholar] [CrossRef]
- Djamai, N.; Fernandes, R.; Weiss, M.; McNairn, H.; Goïta, K. Validation of the Sentinel Simplified Level 2 Product Prototype Processor (SL2P) for mapping cropland biophysical variables using Sentinel-2/MSI and Landsat-8/OLI data. Remote Sens. Environ. 2019, 225, 416–430. [Google Scholar] [CrossRef]
- Pasqualotto, N.; Bolognesi, S.F.; Belfiore, O.R.; Delegido, J.; D’Urso, G.; Moreno, J. Canopy chlorophyll content and LAI estimation from Sentine1-2: Vegetation indices and Sentine1-2 Leve1-2A automatic products comparison. In Proceedings of the 2019 IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Portici, Italy, 24–26 October 2019; pp. 301–306. [Google Scholar]
- Upreti, D.; Huang, W.; Kong, W.; Pascucci, S.; Pignatti, S.; Zhou, X.; Ye, H.; Casa, R. A Comparison of Hybrid Machine Learning Algorithms for the Retrieval of Wheat Biophysical Variables from Sentinel-2. Remote Sens. 2019, 11, 481. [Google Scholar] [CrossRef] [Green Version]
- Nolte, M. Retrieval of Leaf Area Index for Field Crops with the Radiative Transfer Model PROSAIL. Master’s Thesis, University of Bonn, Bonn, Germany, 2019. [Google Scholar]
- Yan, G.; Hu, R.; Luo, J.; Weiss, M.; Jiang, H.; Mu, X.; Xie, D.; Zhang, W. Review of indirect optical measurements of leaf area index: Recent advances, challenges, and perspectives. Agric. For. Meteorol. 2019, 265, 390–411. [Google Scholar] [CrossRef]
- Montzka, C.; Herbst, M.; Weihermüller, L.; Verhoef, A.; Vereecken, H. A global data set of soil hydraulic properties and sub-grid variability of soil water retention and hydraulic conductivity curves. Earth Syst. Sci. Data 2017, 9, 529–543. [Google Scholar] [CrossRef] [Green Version]
- Tóth, B.; Weynants, M.; Pásztor, L.; Hengl, T. 3D soil hydraulic database of Europe at 250 m resolution. Hydrol. Process. 2017, 31, 2662–2666. [Google Scholar] [CrossRef] [Green Version]
- Tóth, B.; Weynants, M.; Nemes, A.; Makó, A.; Bilas, G.; Tóth, G. New generation of hydraulic pedotransfer functions for Europe: New hydraulic pedotransfer functions for Europe. Eur. J. Soil Sci. 2015, 66, 226–238. [Google Scholar] [CrossRef]

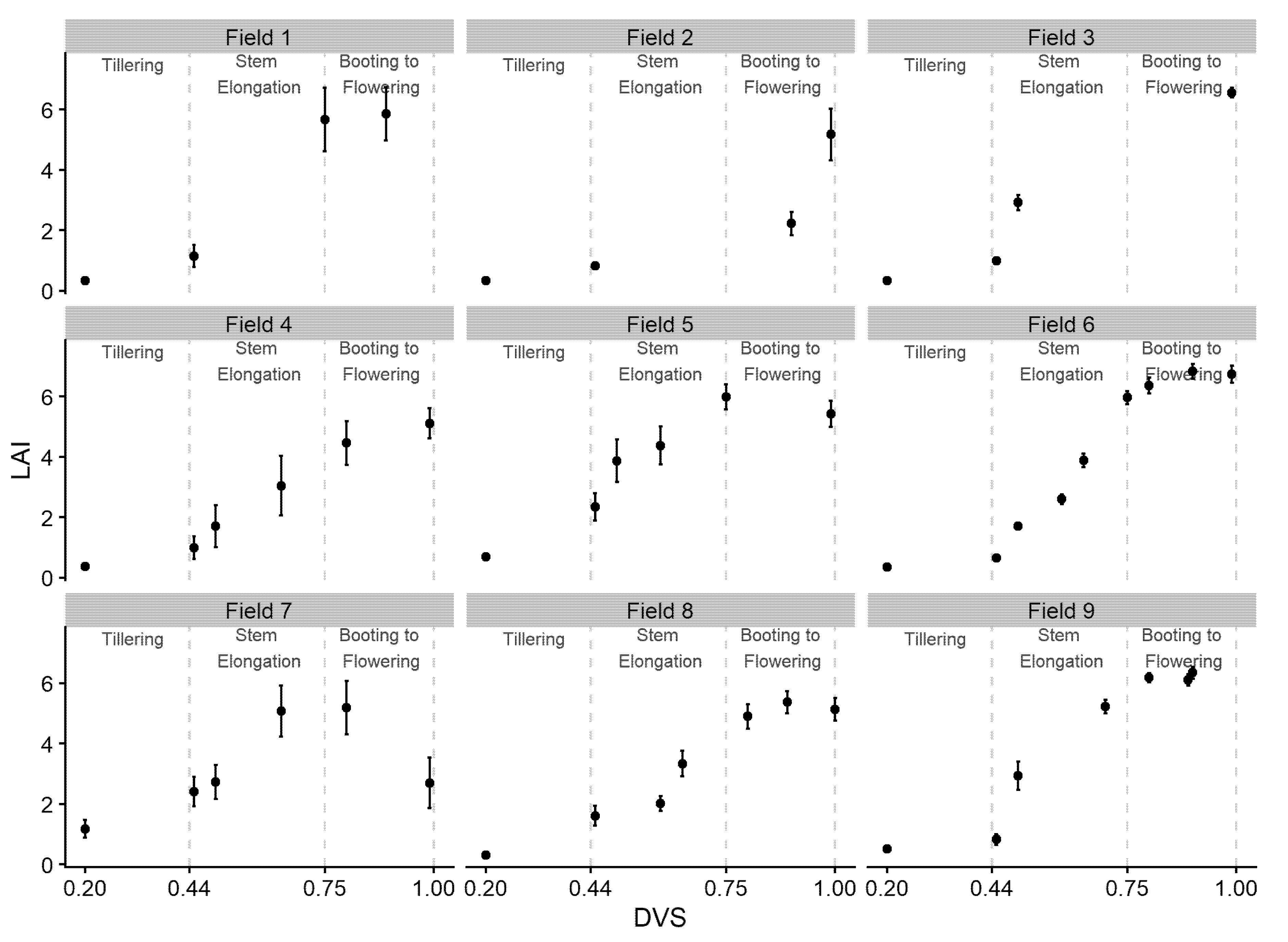




| Growing Season | Field | Location Within State | Name of Cultivar | Planting Date | BMY | GY | HI | No of Sampling Points | Sum Rainfall |
|---|---|---|---|---|---|---|---|---|---|
| 2016/2017 | 1 | SN | Benchmark | 30 November 2016 | 16.31 | 9.43 | 0.58 | 30 | 329 |
| 2016/2017 | 2 | NW | Jonny | 25 October 2016 | 14.51 | 5.96 | 0.41 | 29 | 393 |
| 2016/2017 | 3 | HE | Julius | 28 October 2016 | 19.34 | 9.85 | 0.51 | 20 | 496 |
| 2017/2018 | 4 | BY | RGT Reform | 3 November 2017 | 14.51 | 7.74 | 0.53 | 48 | 353 |
| 2017/2018 | 5 | BY | RGT Reform | 16 November 2017 | 16.41 | 8.09 | 0.49 | 44 | 324 |
| 2017/2018 | 6 | SN | RGT Reform | 16 October 2017 | 18.82 | 9.54 | 0.51 | 21 | 352 |
| 2017/2018 | 7 | TH | RGT Reform | 19 October 2017 | 12.13 | 5.18 | 0.43 | 38 | 214 |
| 2017/2018 | 8 | NI | RGT Reform | 3 November 2017 | 14.52 | 8.08 | 0.56 | 38 | 246 |
| 2017/2018 | 9 | RGT Reform | 17 October 2017 | 17.95 | 8.89 | 0.5 | 43 | 278 |
| Combination ID | P1 | P2 | P3 | Combination ID | P1 | P2 | P3 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 26 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 27 | 1 | 1 | 0 |
| 3 | 0 | 2 | 0 | 28 | 1 | 2 | 0 |
| 4 | 0 | 3 | 0 | 29 | 1 | 3 | 0 |
| 5 | 0 | 4 | 0 | 30 | 1 | 4 | 0 |
| 6 | 0 | 0 | 1 | 31 | 1 | 0 | 1 |
| 7 | 0 | 1 | 1 | 32 | 1 | 1 | 1 |
| 8 | 0 | 2 | 1 | 33 | 1 | 2 | 1 |
| 9 | 0 | 3 | 1 | 34 | 1 | 3 | 1 |
| 10 | 0 | 4 | 1 | 35 | 1 | 4 | 1 |
| 11 | 0 | 0 | 2 | 36 | 1 | 0 | 2 |
| 12 | 0 | 1 | 2 | 37 | 1 | 1 | 2 |
| 13 | 0 | 2 | 2 | 38 | 1 | 2 | 2 |
| 14 | 0 | 3 | 2 | 39 | 1 | 3 | 2 |
| 15 | 0 | 4 | 2 | 40 | 1 | 4 | 2 |
| 16 | 0 | 0 | 3 | 41 | 1 | 0 | 3 |
| 17 | 0 | 1 | 3 | 42 | 1 | 1 | 3 |
| 18 | 0 | 2 | 3 | 43 | 1 | 2 | 3 |
| 19 | 0 | 3 | 3 | 44 | 1 | 3 | 3 |
| 20 | 0 | 4 | 3 | 45 | 1 | 4 | 3 |
| 21 | 0 | 0 | 4 | 46 | 1 | 0 | 4 |
| 22 | 0 | 1 | 4 | 47 | 1 | 1 | 4 |
| 23 | 0 | 2 | 4 | 48 | 1 | 2 | 4 |
| 24 | 0 | 3 | 4 | 49 | 1 | 3 | 4 |
| 25 | 0 | 4 | 4 | 50 | 1 | 4 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tewes, A.; Montzka, C.; Nolte, M.; Krauss, G.; Hoffmann, H.; Gaiser, T. Assimilation of Sentinel-2 Estimated LAI into a Crop Model: Influence of Timing and Frequency of Acquisitions on Simulation of Water Stress and Biomass Production of Winter Wheat. Agronomy 2020, 10, 1813. https://doi.org/10.3390/agronomy10111813
Tewes A, Montzka C, Nolte M, Krauss G, Hoffmann H, Gaiser T. Assimilation of Sentinel-2 Estimated LAI into a Crop Model: Influence of Timing and Frequency of Acquisitions on Simulation of Water Stress and Biomass Production of Winter Wheat. Agronomy. 2020; 10(11):1813. https://doi.org/10.3390/agronomy10111813
Chicago/Turabian StyleTewes, Andreas, Carsten Montzka, Manuel Nolte, Gunther Krauss, Holger Hoffmann, and Thomas Gaiser. 2020. "Assimilation of Sentinel-2 Estimated LAI into a Crop Model: Influence of Timing and Frequency of Acquisitions on Simulation of Water Stress and Biomass Production of Winter Wheat" Agronomy 10, no. 11: 1813. https://doi.org/10.3390/agronomy10111813
APA StyleTewes, A., Montzka, C., Nolte, M., Krauss, G., Hoffmann, H., & Gaiser, T. (2020). Assimilation of Sentinel-2 Estimated LAI into a Crop Model: Influence of Timing and Frequency of Acquisitions on Simulation of Water Stress and Biomass Production of Winter Wheat. Agronomy, 10(11), 1813. https://doi.org/10.3390/agronomy10111813






