Impact Analysis of Environmental Conditions on Odour Dispersion Emitted from Pig House with Complex Terrain Using CFD
Abstract
1. Introduction
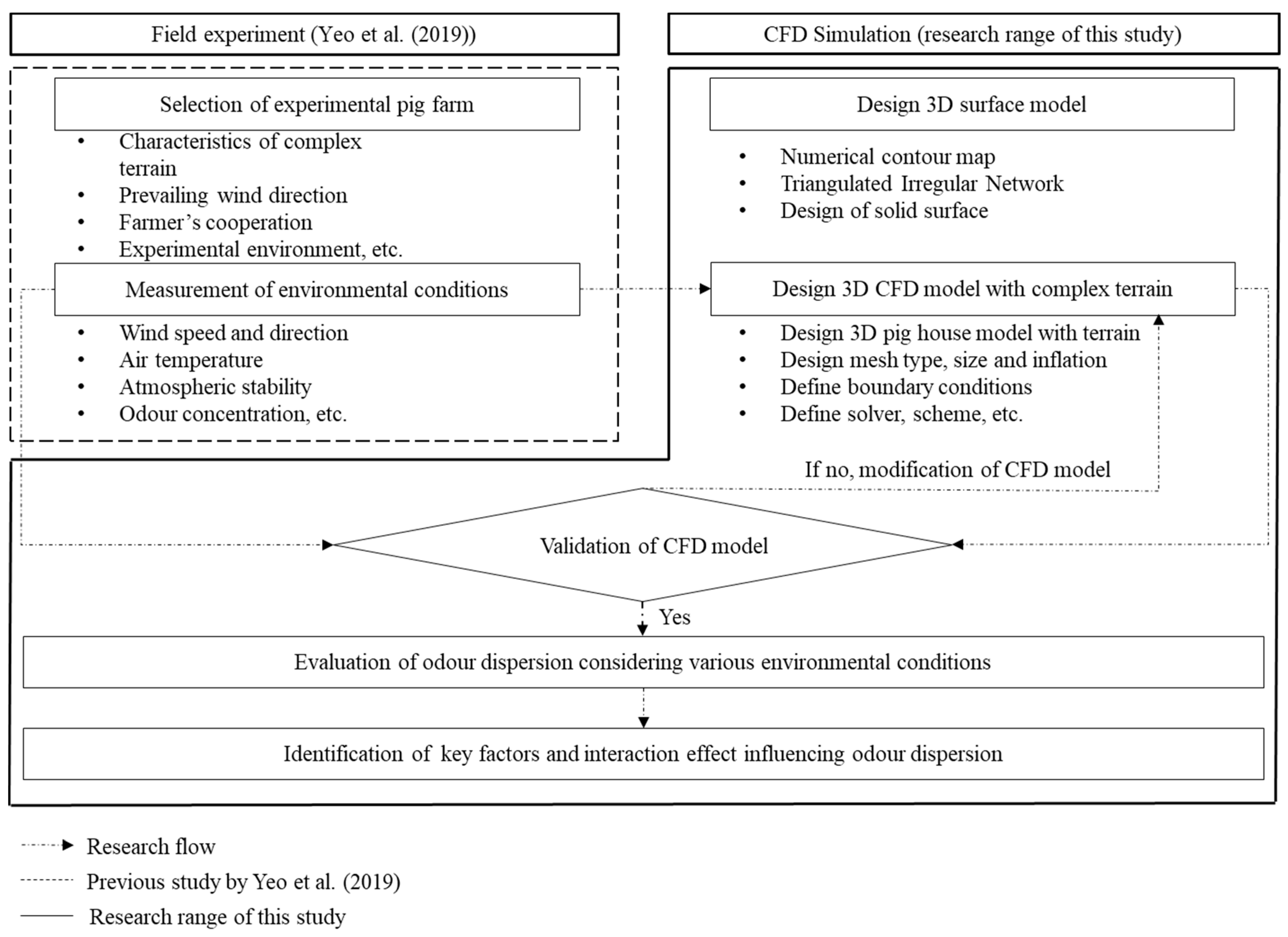
2. Materials and Methods
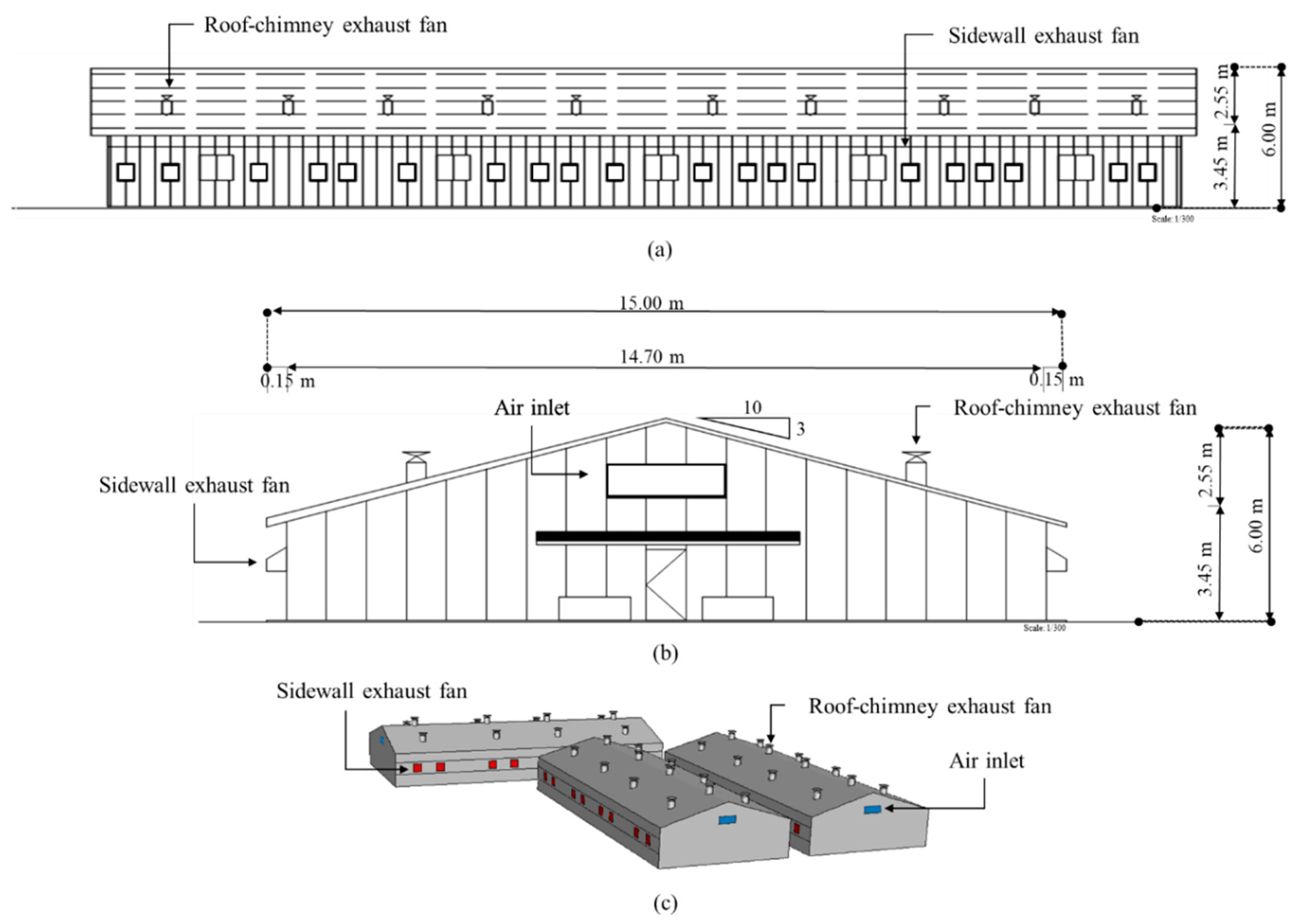
2.1. Farm Description
2.2. Korean Standard Pig House
2.3. Design Tool for Numerical Analysis
2.4. Description of Experimental Procedures
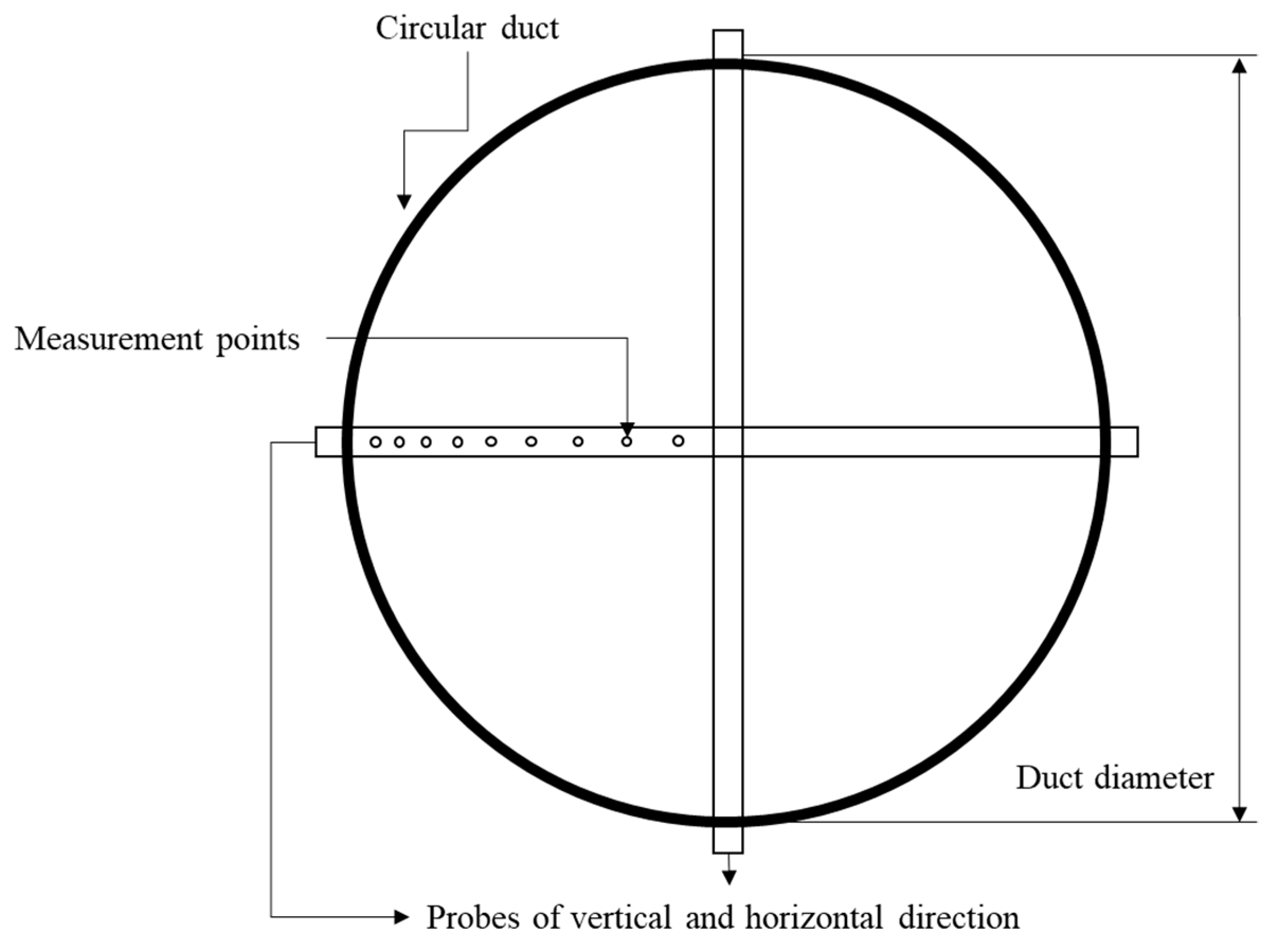
2.4.1. Field Experiment for CFD Model Design and Validation
2.4.2. Design, Validation, and Case Study Using the CFD Model
2.5. Statistical Analysis for Identifying Key Factors Influencing Odour Dispersion
3. Results
3.1. Field Experiment Results (Yeo et al., 2019)
3.2. Validation of the CFD Simulation Model
3.3. Case Study of Odour Dispersion
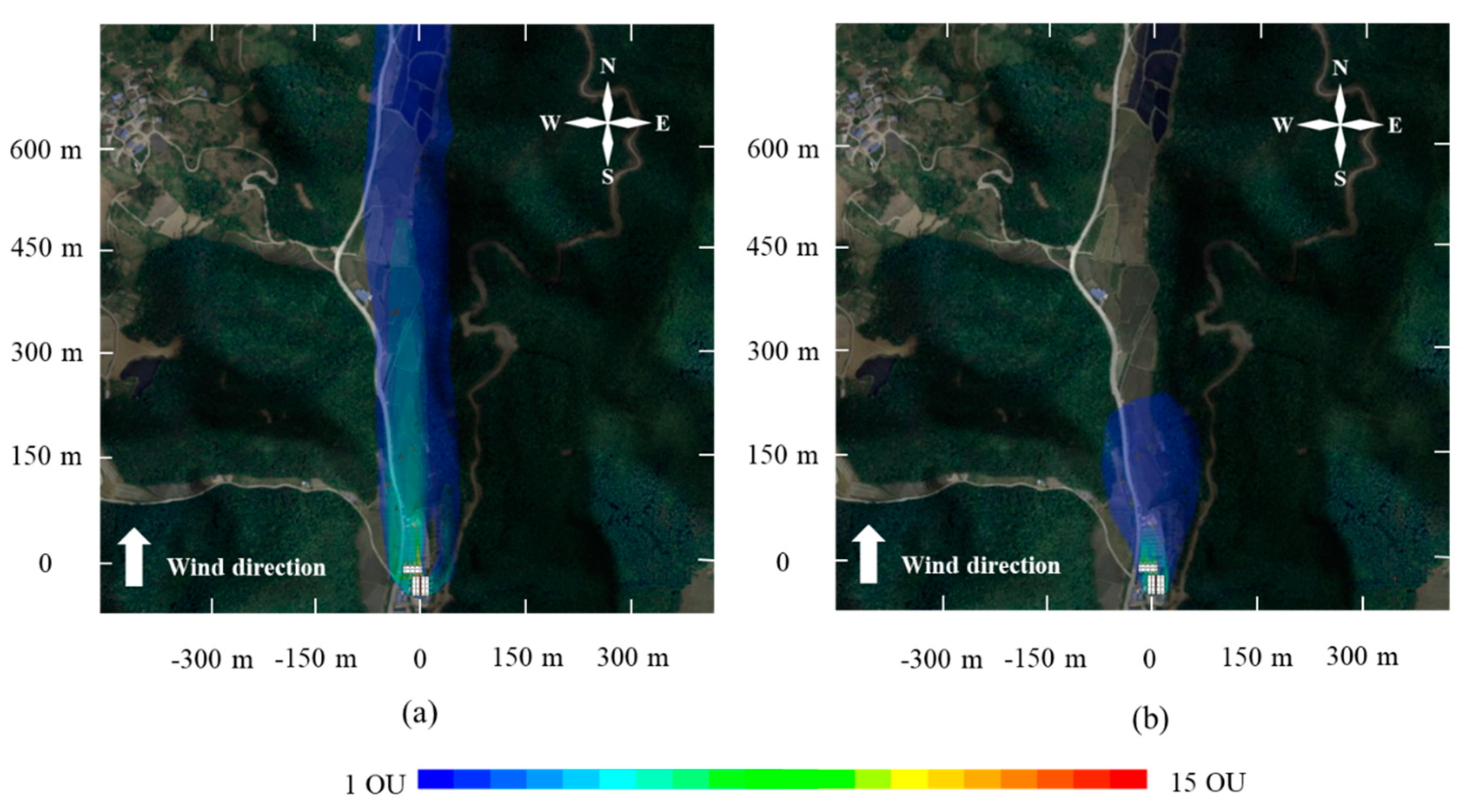
3.3.1. Effect of Ventilation Types on Odour Dispersion
3.3.2. Effect of Atmospheric Stability in Odour Dispersion
3.3.3. Effect of Wind Speed in Odour Dispersion
3.3.4. Effect of Wind Direction in Odour Dispersion
3.4. Statistical Analysis for Odour Dispersion
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Statistics Korea. 2020. Available online: http://kostat.go.kr (accessed on 3 January 2020).
- Statistics Korea. 2019. Available online: http://kostat.go.kr (accessed on 21 November 2019).
- Ministry of Environment. Available online: https://eng.me.go.kr (accessed on 12 November 2019).
- Bottcher, R.; Munilla, R.; Baughman, G.; Keener, K. Designs for windbreak walls for mitigating dust and odor emissions from tunnel ventilated swine buildings. In Proceedings of the Swine Housing Conference, Des Moines, IA, USA, 9–11 October 2000; p. 1. [Google Scholar]
- Colletti, J.; Hoff, S.; Thompson, J.; Tyndall, J. Vegetative environmental buffers to mitigate odor and aerosol pollutants emitted from poultry production sites. In Proceedings of the Workshop on Agricultural Air Quality: State of Science, Potomac, MD, USA, 4–8 June 2006; pp. 5–8. [Google Scholar]
- Rzeźnik, W.; Mielcarek-Bocheńska, P. Effect of the slurry application method on odour Emissions: A pilot study. Pol. J. Environ. Stud. 2020, 29, 1503–1509. [Google Scholar] [CrossRef]
- Choi, E.; Kim, J.; Choi, I.; Ahn, H.; Dong, J.I.; Kim, H. Microbial additives in controlling odors from stored swine slurry. Water Air Soil Pollut. 2015, 226, 104. [Google Scholar] [CrossRef]
- Ha, D.-M.; Kim, D.-H. Effects of the Liquid Manure Circulation System on the Environmental Improvement of Swine Farm. J. Environ. Sci. Int. 2019, 28, 137–145. [Google Scholar]
- Hartung, E.; Jungbluth, T.; Bascher, W. Reduction of ammonia and odor emissions from a piggery with biofilters. Trans. ASAE 2001, 44, 113. [Google Scholar] [CrossRef]
- Lim, T.-T.; Jin, Y.; Ni, J.-Q.; Heber, A.J. Field evaluation of biofilters in reducing aerial pollutant emissions from a commercial pig finishing building. Biosyst. Eng. 2012, 112, 192–201. [Google Scholar] [CrossRef]
- McCrory, D.F.; Hobbs, P. Additives to Reduce Ammonia and Odor Emissions from Livestock Wastes: A Review. J. Environ. Qual. 2001, 30, 345–355. [Google Scholar] [CrossRef]
- Melse, R.W.; Hol, J.M. Biofiltration of exhaust air from animal houses: Evaluation of removal efficiencies and practical experiences with biobeds at three field sites. Biosyst. Eng. 2017, 159, 59–69. [Google Scholar] [CrossRef]
- Hong, S.; Lee, E. Study on the reduction of livestock malodor using microbial agents-focusing on swine facilities. J. Odor Indoor Environ. 2018, 17, 85–94. [Google Scholar] [CrossRef]
- Yoo, J.; Suh, J.; Lee, E. Study on the Reduction of Malodor Produced from Pig Excreata using Microbial Agents. Korean J. Odor Res. Eng. 2010, 9, 203–207. [Google Scholar]
- Zhao, Y.; Aarnink, A.; De Jong, M.; Ogink, N.; Koerkamp, P. Effectiveness of multi-stage scrubbers in reducing emissions of air pollutants from pig houses. Trans. ASABE 2011, 54, 285–293. [Google Scholar] [CrossRef]
- National Institute of Environment Research (NEIR). Available online: https://www.nier.go.kr (accessed on 21 December 2019).
- Ambient Air-Determination of Odour in Ambient Air by Using Field Inspection-Part 1: Grid Method, EN 16841-1; European Committee for Standardization CEN: Brussels, Belgium, 2016.
- Yeo, U.-H.; Lee, I.-B.; Ha, T.-H.; Decano, C.; Kim, R.-W.; Lee, S.-Y.; Kim, J.-G.; Choi, Y.-B.; Park, Y.-M. Evaluation of Odor Dispersion from Livestock Building through Field Experiment. Korean Soc. Agric. Eng. 2019, 61, 21–30. [Google Scholar]
- Sironi, S.; Capelli, L.; Céntola, P.; Del Rosso, R.; Pierucci, S. Odour impact assessment by means of dynamic olfactometry, dispersion modelling and social participation. Atmos. Environ. 2010, 44, 354–360. [Google Scholar] [CrossRef]
- Hong, S.; Lee, I.; Hwang, H.; Seo, I.; Bitog, J.; Kwon, K.; Song, J.; Moon, O.; Kim, K.; Ko, H. CFD modelling of livestock odour dispersion over complex terrain, part II: Dispersion modelling. Biosyst. Eng. 2011, 108, 265–279. [Google Scholar] [CrossRef]
- Guo, H.; Yu, Z.; Lague, C. Livestock odour dispersion modeling: A review. In Proceedings of the 2006 ASAE Annual Meeting, Edmonton, AB, Canada, 16–19 July 2006; p. 1. [Google Scholar]
- Chastain, J.P.; Wolak, F.J. Application of a Gaussian plume model of odor dispersion to select a site for livestock facilities. In Proceedings of the Odors and VOC Emissions 2000 Conference, Cincinnati, OH, USA, 16–19 April 2000; pp. 745–758. [Google Scholar]
- Carlson, J.; Arndt, D.S. The Oklahoma Dispersion Model: Using the Gaussian plume model as an operational management tool for determining near-surface dispersion conditions across Oklahoma. J. Appl. Meteorol. Climatol. 2008, 47, 462–474. [Google Scholar] [CrossRef]
- Schulte, D.D.; Modi, M.R.; Henry, C.G.; Billesbach, D.P.; Stowell, R.R.; Hoff, S.J.; Jacobson, L.D. Modeling odor dispersion from a swine facility using AERMOD. In Proceedings of the International Symposium on Air Quality and Waste Management for Agriculture, Broomfield, CO, USA, 16–19 September 2007; p. 64. [Google Scholar]
- Busini, V.; Capelli, L.; Sironi, S.; Nano, G.; Rossi, A.N.; Bonati, S. Comparison of CALPUFF and AERMOD models for odour dispersion simulation. Chem. Eng. Trans. 2012, 30, 1–6. [Google Scholar]
- Sheridan, B.; Hayes, E.; Curran, T.; Dodd, V. A dispersion modelling approach to determining the odour impact of intensive pig production units in Ireland. Bioresour. Technol. 2004, 91, 145–152. [Google Scholar] [CrossRef]
- Zhu, J.; Jacobson, L.D.; Schmidt, D.R.; Nicolai, R. Evaluation of INPUFF-2 model for predicting downwind odors from animal production facilities. Appl. Eng. Agric. 2000, 16, 159–164. [Google Scholar] [CrossRef]
- Capelli, L.; Sironi, S.; Del Rosso, R.; Guillot, J.-M. Measuring odours in the environment vs. dispersion modelling: A review. Atmos. Environ. 2013, 79, 731–743. [Google Scholar] [CrossRef]
- Lin, X.-J.; Barrington, S.; Nicell, J.; Choiniere, D.; Vezina, A. Influence of windbreaks on livestock odour dispersion plume in the field. Agric. Ecosyst. Environ. 2006, 116, 263–272. [Google Scholar] [CrossRef]
- Chastain, J.P. Air quality and odor control from swine production facilities. In Confined Animal Manure Managers Certification Program Manual; Clemson University: Clemson, SC, USA, 1999; pp. 9.1–9.11. [Google Scholar]
- Stockie, J.M.J.S.R. The mathematics of atmospheric dispersion modeling. SIAM Rev. 2011, 53, 349–372. [Google Scholar] [CrossRef]
- Sánchez-Sosa, J.E.; Castillo-Mixcóatl, J.; Beltrán-Pérez, G.; Muñoz-Aguirre, S. An Application of the Gaussian Plume Model to Localization of an Indoor Gas Source with a Mobile Robot. Sensors 2018, 18, 4375. [Google Scholar]
- Conti, C.; Guarino, M.; Bacenetti, J. Measurements techniques and models to assess odor annoyance: A review. Environ. Int. 2020, 134, 105261. [Google Scholar] [CrossRef] [PubMed]
- Cao, S. CFD applications in structural wind engineering. In Advanced Structural Wind Engineering; Springer: Heidelberg, Germany, 2013; pp. 301–324. [Google Scholar]
- Stergiannis, N.; Lacor, C.; Beeck, J.; Donnelly, R. CFD modelling approaches against single wind turbine wake measurements using RANS. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Brussel, Belgium, 2016; Volume 753, p. 032062. [Google Scholar]
- Vilag, V.; Vilag, J.; Carlanescu, R.; Mangra, A.; Florean, F. CFD Application for Gas Turbine Combustion Simulations. In Computational Fluid Dynamics Simulations; IntechOpen: London, UK, 2019. [Google Scholar]
- Ardejani, F.D.; Baafi, E.; Panahi, K.S.; Singh, R.N.; Shokri, B.J. Application of Computational Fluid Dynamics (CFD) for simulation of acid mine drainage generation and subsequent pollutants transportation through groundwater flow systems and rivers. In Computational Fluid Dynamics Technologies and Applications; IntechOpen: London, UK, 2011; pp. 123–160. [Google Scholar]
- Modenesi, K.; Furlan, L.; Tomaz, E.; Guirardello, R.; Núnez, J. A CFD model for pollutant dispersion in rivers. Braz. J. Chem. Eng. 2004, 21, 557–568. [Google Scholar] [CrossRef][Green Version]
- Zárate, L.G.; Uribe, S.; Cordero, M.E. Applications of CFD for Process Safety. In Computational Fluid Dynamics-Basic Instruments and Applications in Science; IntechOpen: London, UK, 2017. [Google Scholar]
- Selmi, M.; Belmabrouk, H.; Bajahzar, A. Numerical Study of the Blood Flow in a Deformable Human Aorta. Appl. Sci. 2019, 9, 1216. [Google Scholar] [CrossRef]
- Shin, E.; Kim, J.J.; Lee, S.; Ko, K.S.; Rhee, B.D.; Han, J.; Kim, N. Hemodynamics in diabetic human aorta using computational fluid dynamics. PLoS ONE 2018, 13, e0202671. [Google Scholar] [CrossRef]
- Suzelle, B.; Jun, L.X.; Denis, C. Simulating Odour Dispersion about Natural Windbreaks. Comput. Fluid Dyn. Technol. Appl. 2011, 181, 182–215. [Google Scholar]
- Bjerg, B.; Kai, P.; Morsing, S.; Takai, H. CFD analysis to predict close range spreading of ventilation air from livestock buildings. Agric. Eng. Int.: CIGR J. 2004, 6, 1–12. [Google Scholar]
- Bonifacio, H.F.; Maghirang, R.G.; Glasgow, L.A. Numerical simulation of transport of particles emitted from ground-level area source using AERMOD and CFD. Eng. Appl. Comput. Fluid Mech. 2014, 8, 488–502. [Google Scholar] [CrossRef]
- Li, Y.; Guo, H. Comparison of odor dispersion predictions between CFD and CALPUFF models. Trans. ASABE 2006, 49, 1915–1926. [Google Scholar] [CrossRef]
- Lin, X.-J.; Barrington, S.; Choiniere, D.; Prasher, S. Effect of weather conditions on windbreak odour dispersion. J. Wind. Eng. Ind. Aerodyn. 2009, 97, 487–496. [Google Scholar] [CrossRef]
- Riddle, A.; Carruthers, D.; Sharpe, A.; McHugh, C.; Stocker, J. Comparisons between FLUENT and ADMS for atmospheric dispersion modelling. Atmos. Environ. 2004, 38, 1029–1038. [Google Scholar] [CrossRef]
- Diego, I.; Pelegry, A.; Torno, S.; Toraño, J.; Menendez, M. Simultaneous CFD evaluation of wind flow and dust emission in open storage piles. Appl. Math. Model. 2009, 33, 3197–3207. [Google Scholar] [CrossRef]
- Katsanis, S. Numerical Modelling of Wind Borne Pollution Dispersion from Open Windrow Compost Sites. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 23 March 2014. [Google Scholar]
- Úbeda Sánchez, Y.; López Jiménez, P.A.; Nicolas, J.; Calvet Sanz, S. Strategies to control odours in livestock facilities: A critical review. Span. J. Agric. Res. 2013, 11, 1004–1015. [Google Scholar] [CrossRef]
- Hong, S.-W.; Lee, I.-B.; Seo, I.-H.; Bitog, J.; Kwon, K.-S. Prediction of livestock odour dispersion over complex terrain using CFD technology: Review and simulation study. In Proceedings of the Ist International Symposium on CFD Applications in Agriculture, Valencia, Spain, 9–10 July 2012; pp. 29–36. [Google Scholar]
- Appropriate Livestock Raising Standard per Unit Area of Livestock Raising Facility. Available online: http://www.law.go.kr (accessed on 2 March 2020).
- Jang, J.; Jin, X.; Hong, J.; Kim, Y. Effects of different space allowances on growth performance, blood profile and pork quality in a grow-to-finish production system. Asian-Australas. J. Anim. Sci. 2017, 30, 1796–1802. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Agriculture, Food and Rural Affairs (MAFRA). Available online: http://www.mafra.go.kr (accessed on 2 March 2020).
- ANSYS Fluent Tutorial Guide 18; ANSYS Inc.: Canonsburg, PA, USA, 2018; pp. 724–746.
- Dyer, A.; Hicks, B. Flux-gradient relationships in the constant flux layer. Q. J. R. Meteorol. Soc. 1970, 96, 715–721. [Google Scholar] [CrossRef]
- Hicks, B. Wind profile relationships from the ‘Wangara’ experiment. Q. J. R. Meteorol. Soc. 1976, 102, 535–551. [Google Scholar]
- Bache, D.H.; Johnstone, D.R. Microclimate and Spray Dispersion; Ellis Horwood: West Sussex, UK, 1992. [Google Scholar]
- ASHRAE. Standard 62-1989, Ventilation for Acceptable Indoor Air Quality; American Society of Heating, Refrigeration, and Air Conditioning Engineers: Atlanta, GA, USA, 1989. [Google Scholar]
- Power, V.; Stafford, T. Odour Impacts and Odour Emission Control Measures for Intensive Agriculture; EPA: Wexford, Ireland, 2001.
- Tonidandel, S.; LeBreton, J.M. Relative importance analysis: A useful supplement to regression analysis. J. Bus. Psychol. 2011, 26, 1–9. [Google Scholar] [CrossRef]
- Guo, H.; Jacobson, L.D.; Schmidt, D.R.; Janni, K. Simulation of Odor Dispersions as Impacted by Weather Conditions. In Proceedings of the Livestock Environment VI: Proceedings of the 6th International Symposium 2001, Louisville, KY, USA, 21–23 May 2001; pp. 687–695. [Google Scholar]
- Xing, Y.; Guo, H.; Feddes, J.; Yu, Z.; Shewchuck, S.; Predicala, B. Sensitivities of four air dispersion models to climatic parameters for swine odor dispersion. Trans. ASABE 2007, 50, 1007–1017. [Google Scholar] [CrossRef]
- Heinemann, P.; Wahanik, D. Modeling the generation and dispersion of odors from mushroom composting facilities. Trans. ASAE 1998, 41, 437–446. [Google Scholar] [CrossRef]









| Main Parameter | Input Values | ||||
|---|---|---|---|---|---|
| Model for Validation * | Model for Case Study ** | ||||
| Sidewall Exhaust Fan | Roof-Chimney Exhaust Fan | Sidewall + Roof-Chimney Exhaust Fan | |||
| Wind speed of fans | P1 | 8.94 m s−1 | 6.8 m s−1 | 11.59 m s−1 | 5.5 m s−1 (sidewall) 5.37 m s−1 (roof-chimney) |
| P2 | 3.84 m s−1, 7.08 m s−1 | ||||
| P3 | 6.38 m s−1 | ||||
| Odour concentration | P1 | 100 OU m−3 | 577.5 OU m−3 | ||
| P2 | 64.3 OU m−3 | ||||
| P3 | 448 OU m−3 | ||||
| Wind Speed | 0.5 m s−1 | 0.5, 1.5, 2.5 m s−1 | |||
| Atmospheric stability | stable | stable, neutral, unstable | |||
| Convergence criteria | |||||
| Temperature | 299.45 K | ||||
| Density of air | 1.225 kg m−3 | ||||
| Gravitational acceleration of air | 9.81 m s−2 | ||||
| Atmospheric pressure | 101,325 Pa | ||||
| Wind speed | 0.5, 1.5, 2.5 m s−1 | ||||
| Grid size | selected from the grid independence test (4.0, 10.0, 20.0, and 40.0 m) | ||||
| Time step | selected from the time step test (1, 5, 10, 20 s) | ||||
| Turbulence models | selected from the validation test (Standard k–ε, RNG k–ε, Realisable k–ε, LES) | ||||
| Date | Air Temperature (°C) | Odour Concentration (OU m−3) | ||||||
|---|---|---|---|---|---|---|---|---|
| PS1 | PS2 | PS3 | S1 | S2 | S3 | S4 | ||
| 8 August * (a.m.) | 26.3 | 44.8 | 5.5 | 20.8 | 4.6 | 2.1 | 1.4 | 3.0 |
| 8 August * (p.m.) | 33.5 | 11.8 | 5.5 | 5.5 | 2.1 | 1.0 | 1.4 | 3.1 |
| 6 September * (a.m.) | 15.7 | 311.0 | 44.8 | 30.0 | 1.7 | 3.1 | 2.1 | 1.4 |
| 6 September * (p.m.) | 26.2 | 448.1 | 100 | 64.6 | 6.7 | 2.5 | 1.4 | 1.2 |
| Grid Size | Number of Elements (Million) | Odour Concentration (OU m−3) | |||||
|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | R2 | RMSE | ||
| Field experiment | - | 6.7 | 2.5 | 1.4 | 1.2 | - | - |
| 4.0 m | 8.73 | 7.40 | 1.75 | 0.04 | 0.00 | 0.999 | 1.06 |
| 10.0 m | 5.16 | 6.79 | 1.33 | 0.03 | 0.00 | 0.998 | 1.09 |
| 20.0 m | 3.98 | 14.97 | 2.00 | 0.09 | 0.00 | 0.991 | 4.24 |
| 40.0 m | 3.76 | 9.79 | 1.68 | 0.09 | 0.00 | 0.996 | 1.84 |
| Time Step | Odour Concentration (OU m−3) | |||||
|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | R2 | RMSE | |
| Field experiment | 6.7 | 2.5 | 1.4 | 1.2 | - | - |
| 1 s | 7.69 | 1.40 | 0.20 | 0.23 | 0.994 | 1.083 |
| 5 s | 6.79 | 1.33 | 0.03 | 0.00 | 0.998 | 1.093 |
| 10 s | 16.56 | 1.96 | 0.04 | 0.01 | 0.988 | 5.027 |
| 20 s | 25.99 | 1.31 | 0.04 | 0.02 | 0.969 | 9.711 |
| Odour Concentration (OU m−3) | ||||||
|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | R2 | RMSE | |
| Measured | 6.7 | 2.5 | 1.4 | 1.2 | - | - |
| Standard k-ε | 6.79 | 1.33 | 0.03 | 0.00 | 0.998 | 1.09 |
| RNG k-ε | 7.26 | 0.54 | 0.00 | 0.00 | 0.977 | 1.39 |
| Standard k-ω | 5.18 | 0.11 | 0.00 | 0.00 | 0.960 | 1.70 |
| LES | 3.49 | 0.26 | 0.00 | 0.00 | 0.977 | 2.17 |
| Ventilation Type | Speed | Atmospheric Condition | Dispersion Distance (m) | |||
|---|---|---|---|---|---|---|
| Northerly Wind | Easterly Wind | Southerly Wind | Westerly Wind | |||
| Sidewall exhaust | 0.5 m s−1 | Stable | 1081.3 | 541.3 | 1427.4 | 567.7 |
| Neutral | 782.9 | 401.7 | 1488.1 | 478.0 | ||
| Unstable | 349.6 | 346.0 | 485.3 | 304.3 | ||
| 1.5 m s−1 | Stable | 640.4 | 213.6 | 653.4 | 332.7 | |
| Neutral | 470.7 | 213.4 | 564.8 | 277.4 | ||
| Unstable | 230.4 | 168.3 | 231.7 | 182.9 | ||
| 2.5 m s−1 | Stable | 479.6 | 186.7 | 573.5 | 256.9 | |
| Neutral | 273.3 | 153.6 | 491.8 | 301.8 | ||
| Unstable | 182.1 | 147.8 | 186.4 | 151.9 | ||
| Roof-chimney exhaust | 0.5 m s−1 | Stable | 595.1 | 207.2 | 817.6 | 352.4 |
| Neutral | 651.2 | 293.7 | 900.6 | 295.9 | ||
| Unstable | 224.0 | 154.9 | 235.2 | 220.6 | ||
| 1.5 m s−1 | Stable | 256.2 | 144.4 | 309.9 | 148.4 | |
| Neutral | 267.9 | 149.0 | 304.2 | 218.9 | ||
| Unstable | 169.8 | 107.8 | 165.3 | 118.2 | ||
| 2.5 m s−1 | Stable | 221.5 | 130.7 | 227.6 | 112.3 | |
| Neutral | 151.7 | 106.7 | 230.6 | 120.6 | ||
| Unstable | 129.7 | 91.0 | 114.4 | 78.9 | ||
| Sidewall + Roof-chimney exhaust | 0.5 m s−1 | Stable | 579.4 | 300.5 | 652.2 | 392.9 |
| Neutral | 614.4 | 311.7 | 928.2 | 410.0 | ||
| Unstable | 293.0 | 194.4 | 318.3 | 210.7 | ||
| 1.5 m s−1 | Stable | 256.1 | 146.6 | 323.2 | 157.5 | |
| Neutral | 255.7 | 151.6 | 309.9 | 164.6 | ||
| Unstable | 178.4 | 110.1 | 168.4 | 142.9 | ||
| 2.5 m s−1 | Stable | 228.5 | 136.8 | 238.0 | 126.5 | |
| Neutral | 256.7 | 138.2 | 239.5 | 131.1 | ||
| Unstable | 142.4 | 94.0 | 117.6 | 92.0 | ||
| Model | Independent Variable | R | R2 | Adjusted R2 |
|---|---|---|---|---|
| 1 | speed, dummy variable d | 0.508 | 0.259 | 0.252 |
| 2 | speed, dummy variable d, f | 0.622 | 0.386 | 0.375 |
| 3 | speed, dummy variable d, f, a | 0.712 | 0.507 | 0.493 |
| 4 | speed, dummy variable d, f, a, b | 0.736 | 0.542 | 0.524 |
| 5 | speed, dummy variable d, f, a, b, e | 0.789 | 0.622 | 0.603 |
| 6 | speed, dummy variable d, f, a, b, e, | 0.806 | 0.650 | 0.629 |
| 7 | speed, dummy variable d, f, a, b, e, g | 0.828 | 0.685 | 0.663 |
| Odour Dispersion Distance | Unstandardized Coefficients | Standardized Coefficients | t-Value | p-Value | |
|---|---|---|---|---|---|
| Coefficient | Std. Error | Coefficient | |||
| (Intercept) | 791.108 | 44.718 | 17.691 | 1.46 × 10−32 | |
| Speed | −157.849 | 17.428 | −0.508 | −9.057 | 1.15 × 10−14 |
| dummy variable a | −188.733 | 34.857 | −0.351 | −5.415 | 4.23 × 10−7 |
| dummy variable b | −175.188 | 34.857 | −0.326 | −5.026 | 2.20 × 10−6 |
| dummy variable d | −192.199 | 30.187 | −0.357 | −6.367 | 5.90 × 10−9 |
| dummy variable e | −171.123 | 40.249 | −0.292 | −4.252 | 4.78 × 10−5 |
| dummy variable f | 101.513 | 40.249 | 0.173 | 2.522 | 0.0013 |
| dummy variable g | −133.853 | 40.249 | −0.229 | −3.326 | 0.001 |
| Variable | Raw Relative Weight | Rescaled Relative Weight (%) |
|---|---|---|
| ventilation type | 0.080 | 17.91 |
| atmospheric stability | 0.103 | 23.20 |
| wind speed | 0.259 | 58.17 |
| direction | 0.003 | 0.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeo, U.-H.; Decano-Valentin, C.; Ha, T.; Lee, I.-B.; Kim, R.-W.; Lee, S.-Y.; Kim, J.-G. Impact Analysis of Environmental Conditions on Odour Dispersion Emitted from Pig House with Complex Terrain Using CFD. Agronomy 2020, 10, 1828. https://doi.org/10.3390/agronomy10111828
Yeo U-H, Decano-Valentin C, Ha T, Lee I-B, Kim R-W, Lee S-Y, Kim J-G. Impact Analysis of Environmental Conditions on Odour Dispersion Emitted from Pig House with Complex Terrain Using CFD. Agronomy. 2020; 10(11):1828. https://doi.org/10.3390/agronomy10111828
Chicago/Turabian StyleYeo, Uk-Hyeon, Cristina Decano-Valentin, Taehwan Ha, In-Bok Lee, Rack-Woo Kim, Sang-Yeon Lee, and Jun-Gyu Kim. 2020. "Impact Analysis of Environmental Conditions on Odour Dispersion Emitted from Pig House with Complex Terrain Using CFD" Agronomy 10, no. 11: 1828. https://doi.org/10.3390/agronomy10111828
APA StyleYeo, U.-H., Decano-Valentin, C., Ha, T., Lee, I.-B., Kim, R.-W., Lee, S.-Y., & Kim, J.-G. (2020). Impact Analysis of Environmental Conditions on Odour Dispersion Emitted from Pig House with Complex Terrain Using CFD. Agronomy, 10(11), 1828. https://doi.org/10.3390/agronomy10111828






