The Adaptability of APSIM-Wheat Model in the Middle and Lower Reaches of the Yangtze River Plain of China: A Case Study of Winter Wheat in Hubei Province
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Site
2.2. Data Source
2.3. APSIM-Wheat Model
2.4. Calibration and Validation of the APSIM-Wheat Model
2.5. Evaluation of the Model’s Performance
2.6. Statistical Analysis of the Data
3. Results
3.1. Genetic Parameters of Each Variety for the APSIM-Wheat Model
3.2. Performance of the Calibrated APSIM-Wheat Model
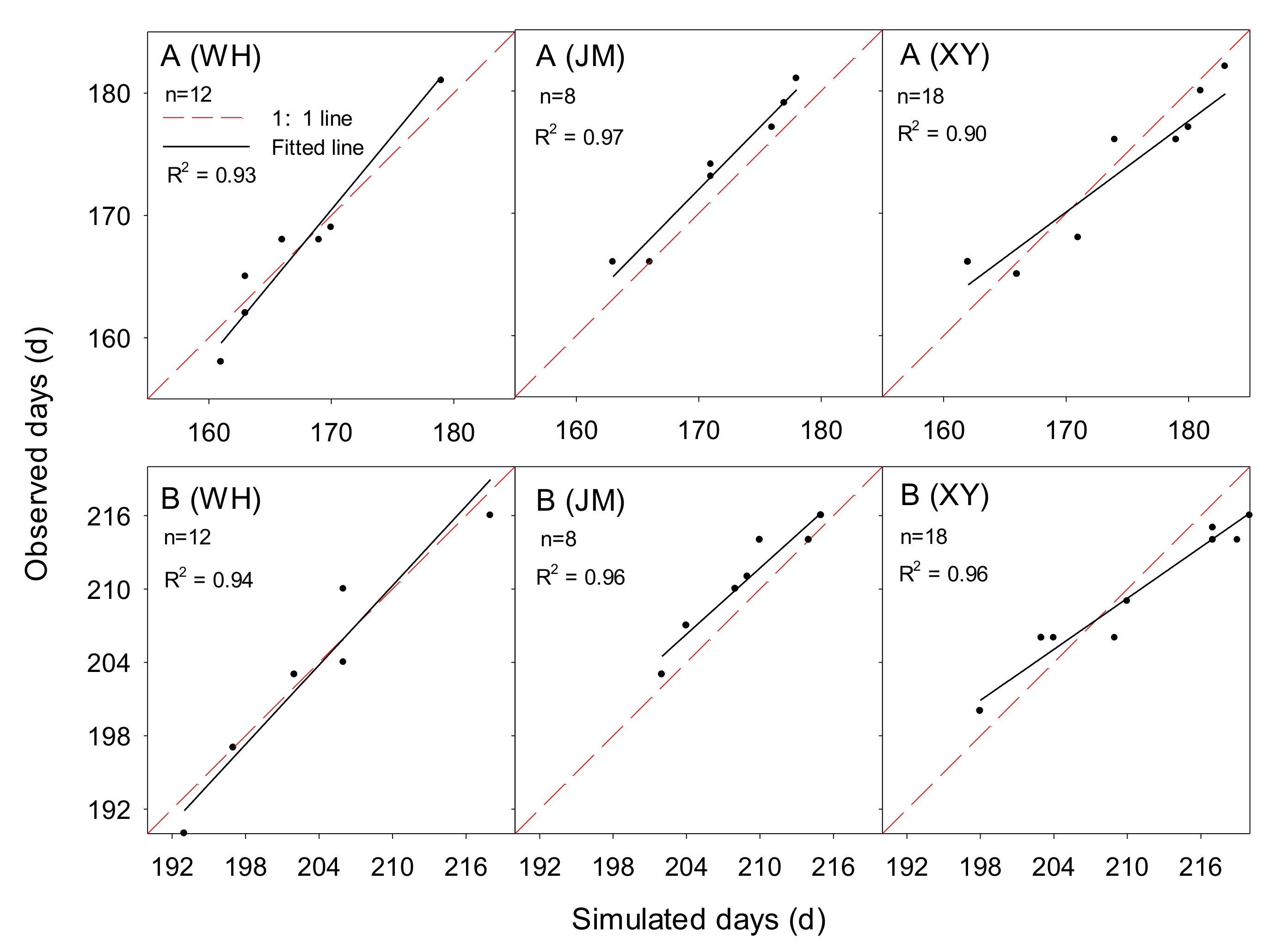
3.2.1. Wheat Growth Duration
3.2.2. Grain Yield and Above-Ground Biomass
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, X.; Chen, F.; Lin, X.; Liu, Z.; Zhang, H.-L.; Zhao, J.; Li, K.; Ye, Q.; Li, Y.; Lv, S.; et al. Potential benefits of climate change for crop productivity in China. Agric. For. Meteorol. 2015, 208, 76–84. [Google Scholar] [CrossRef]
- Qin, X.; Zhang, F.; Liu, C.; Yu, H.; Cao, B.; Tian, S.; Liao, Y.; Siddique, K.H. Wheat yield improvements in China: Past trends and future directions. Field Crop. Res. 2015, 177, 117–124. [Google Scholar] [CrossRef]
- Li, H.; Liu, L.; Wang, Z.; Yang, J.; Zhang, J. Agronomic and physiological performance of high-yielding wheat and rice in the lower reaches of Yangtze River of China. Field Crop. Res. 2012, 133, 119–129. [Google Scholar] [CrossRef]
- Yi, Q.; He, P.; Zhang, X.Z.; Yang, L.; Xiong, G.Y. Optimizing Fertilizer Nitrogen for Winter Wheat Production in Yangtze River Region in China. J. Plant Nutr. 2015, 38, 1639–1655. [Google Scholar] [CrossRef]
- National Bureau of Statistics of China (NBSC). Agriculture, National Data; National Bureau of Statistics of China: Beijing, China, 2019. Available online: http://www.stats.gov.cn/tjsj/ndsj/2019/indexeh.htm (accessed on 15 February 2020).
- Tian, Z.; Jing, Q.; Dai, T.; Jiang, D.; Cao, W. Effects of genetic improvements on grain yield and agronomic traits of winter wheat in the Yangtze River Basin of China. Field Crop. Res. 2011, 124, 417–425. [Google Scholar] [CrossRef]
- Shi, Z.; Li, D.; Jing, Q.; Cai, J.; Jiang, N.; Cao, W.; Dai, T. Effects of nitrogen applications on soil nitrogen balance and nitrogen utilization of winter wheat in a rice–wheat rotation. Field Crop. Res. 2012, 127, 241–247. [Google Scholar] [CrossRef]
- Fan, Y.; Tian, M.; Jing, Q.; Tian, Z.; Han, H.; Jiang, N.; Cao, W.; Dai, T. Winter night warming improves pre-anthesis crop growth and post-anthesis photosynthesis involved in grain yield of winter wheat (Triticum aestivum L.). Field Crop. Res. 2015, 178, 100–108. [Google Scholar] [CrossRef]
- Ding, J.F.; Cheng, Y.M.; Huang, Z.J.; Li, C.Y.; Guo, W.S.; Zhu, X.K. Analysis of post-flowering material production and senescence characteristics of different nitrogen efficiency groups in rice stubble wheat. J. Integr. Agric. 2015, 48, 1063–1073. [Google Scholar]
- McCown, R.; Hammer, G.; Hargreaves, J.; Holzworth, D.; Freebairn, D. APSIM: A novel software system for model development, model testing and simulation in agricultural systems research. Agric. Syst. 1996, 50, 255–271. [Google Scholar] [CrossRef]
- Ahmed, M.; Akram, M.N.; Asim, M.; Aslam, M.; Hassan, F.-U.; Higgins, S.; Stöckle, C.O.; Hoogenboom, G. Calibration and validation of APSIM-Wheat and CERES-Wheat for spring wheat under rainfed conditions: Models evaluation and application. Comput. Electron. Agric. 2016, 123, 384–401. [Google Scholar] [CrossRef]
- Keating, B.; Carberry, P.; Hammer, G.; Probert, M.; Robertson, M.; Holzworth, D.; Huth, N.; Hargreaves, J.; Meinke, H.; Hochman, Z.; et al. An overview of APSIM, a model designed for farming systems simulation. Eur. J. Agron. 2003, 18, 267–288. [Google Scholar] [CrossRef] [Green Version]
- Asseng, S.; Fillery, I.R.P.; Dunin, F.X.; Keating, B.A.; Meinke, H. Potential deep drainage under wheat crops in a Mediterranean climate. I. Temporal and spatial variability. Aust. J. Agric. Res. 2001, 52, 45–56. [Google Scholar] [CrossRef]
- Hammer, G.; Van Oosterom, E.; McLean, G.; Chapman, S.C.; Broad, I.; Harland, P.; Muchow, R.C. Adapting APSIM to model the physiology and genetics of complex adaptive traits in field crops. J. Exp. Bot. 2010, 61, 2185–2202. [Google Scholar] [CrossRef] [Green Version]
- Yu, Q.; Li, L.; Braunack, M.; Eamus, D.; Xu, S.; Chen, C.; Wang, E.; Liu, J.; Nielsen, D. Year patterns of climate impact on wheat yields. Int. J. Clim. 2013, 34, 518–528. [Google Scholar] [CrossRef]
- Nelson, R.A.; Dimes, J.P.; Paningbatan, E.P.; Silburn, D.M. Erosion/productivity modelling of maize farming in the Philippine uplands: Part I: Parameterising the agricultural production systems simulator. Agric. Syst. 1998, 58, 29–33. [Google Scholar] [CrossRef]
- Xiao, D.; Bai, H.; Liu, D.L. Impact of Future Climate Change on Wheat Production: A Simulated Case for China’s Wheat System. Sustainability 2018, 10, 1277. [Google Scholar] [CrossRef] [Green Version]
- Sun, S.; Yang, X.; Lin, X.; Sassenrath, G.F.; Li, K. Winter Wheat Yield Gaps and Patterns in China. Agron. J. 2018, 110, 319–330. [Google Scholar] [CrossRef]
- Wu, L.; Feng, L.; Li, Y.; Wang, J.; Wu, L. A Yield-Related Agricultural Drought Index Reveals Spatio-Temporal Characteristics of Droughts in Southwestern China. Sustainability 2019, 11, 714. [Google Scholar] [CrossRef] [Green Version]
- Jones, H. Plants and Microclimate: A Quantitative Approach to Environmental Plant Physiology; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Tao, F.; Yokozawa, M.; Xu, Y.; Hayashi, Y.; Zhang, Z. Climate changes and trends in phenology and yields of field crops in China, 1981–2000. Agric. For. Meteorol. 2006, 138, 82–92. [Google Scholar] [CrossRef]
- Sun, S. Study on Yield Potential and Resource Utilization Efficiency of Winter Wheat in Different Regions of China. Ph.D. Thesis, China Agricultural University, Beijing, China, 2018. [Google Scholar]
- Zhang, Y.Q.; Huang, R.H.; Zhuang, Z.Y.; Gao, C.B. High-yield population structure and cultivation techniques of Zhengmai 9023. Hubei Agric. Sci. 2005, 3, 33–34. [Google Scholar]
- Xu, F.C.; Li, M.F.; Dong, J.; Qin, D.D. Studies on planting performance of wheat varieties in different ecological areas in Hubei province. Mod. Agric. Sci. Technol. 2014, 24, 69–70. [Google Scholar]
- Dong, J.; Li, M.; Xu, F.; Ge, S.T.; Wang, X.Z.; Li, L.F. Effects of planting density sowing time and on population traits and grain yield of new wheat cultivar Emai596. Hubei Agric. Sci. 2010, 49, 1563–1566. [Google Scholar]
- Liu, Y.K.; Yan, J.; Zhang, Y.; Gao, C. Breeding and cultivation techniques of new wheat variety Emai170. Hubei Agric. Sci. 2015, 24, 6191–6192. [Google Scholar]
- Guan, S.H.; Yang, W.B.; Zou, J.L.; Li, H.B.; Fu, X.Q.; Li, Q. An analysis of the benefits of wheat “3414” fertilizer in Zhongxiang City. China Agric. Technol. Ext. 2015, 3, 51–53. [Google Scholar]
- Ruan, J.Z.; Wang, W.J.; Ren, S.Z.; Shi, Y.D.; Kuang, H.Q.; Liu, H.W.; Sun, F.S.; Xu, Y.Z.; Guo, G.L.; Zhu, Z.W.; et al. Studies on main technical measures for wheat yielding above 7500 kg/hm2 in highland area in Northern Hubei provinceI. Analysis on the causes of wheat high yield in highland area in Northern Hubei province. Hubei Agric. Sci. 2013, 23, 5690–5692. [Google Scholar]
- Guan, W.; Li, M.F.; Ge, S. Characteristics and cultivation techniques of middle gluten wheat variety Emai18. Hubei Agric. Sci. 2005, 5, 33–34. [Google Scholar]
- Wang, P.; Zhang, G.; Chen, B.; Peng, C.; Zhu, Z.; Gao, C.; Zhu, W. Research on fertilizer demand of wheat variety Emai596. Hubei Agric. Sci. 2016, 55, 303–305, 313. [Google Scholar]
- Xiong, Y.S.; Yuan, J.F.; Hao, F.X.; Ruan, J.Z.; Zhao, S.; Wang, C.; Peng, C.; Xu, X. Yield change and accumulation regular pattern of nitrogen nutrient for Emai18 under different level of nitrogen. Hubei Agric. Sci. 2009, 48, 2391–2394. [Google Scholar]
- Ming, C.F. High yield cultivation technique for wheat variety Emai18. China Agric. Technol. Ext. 2005, 3, 27. [Google Scholar]
- Birch, C.; Hammer, G.; Rickert, K.G. Improved methods for predicting individual leaf area and leaf senescence in maize (Zea mays). Aust. J. Agric. Res. 1998, 49, 249. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Matsuura, K. A refined index of model performance. Int. J. Clim. 2011, 32, 2088–2094. [Google Scholar] [CrossRef]
- Ali, H.; Abustan, I. A new novel index for evaluating model performance. J. Nat. Resour. Dev. 2014, 4, 1–9. [Google Scholar] [CrossRef]
- Seyoum, S.; Rachaputi, R.; Chauhan, Y.; Prasanna, B.; Fekybelu, S. Application of the APSIM model to exploit G × E × M interactions for maize improvement in Ethiopia. Field Crop. Res. 2018, 217, 113–124. [Google Scholar] [CrossRef]
- Makowski, D.; Naud, C.; Jeuffroy, M.-H.; Barbottin, A.; Monod, H. Global sensitivity analysis for calculating the contribution of genetic parameters to the variance of crop model prediction. Reliab. Eng. Syst. Saf. 2006, 91, 1142–1147. [Google Scholar] [CrossRef]
- Chen, C.; Wang, E.; Yu, Q. Modeling Wheat and Maize Productivity as Affected by Climate Variation and Irrigation Supply in North China Plain. Agron. J. 2010, 102, 1037–1049. [Google Scholar] [CrossRef] [Green Version]
- Li, K.; Yang, X.; Liu, Z.; Zhang, T.; Lu, S.; Liu, Y. Low yield gap of winter wheat in the North China Plain. Eur. J. Agron. 2014, 59, 1–12. [Google Scholar] [CrossRef]
- Archontoulis, S.V.; Miguez, F.; Moore, K.J. A methodology and an optimization tool to calibrate phenology of short-day species included in the APSIM PLANT model: Application to soybean. Environ. Model. Softw. 2014, 62, 465–477. [Google Scholar] [CrossRef]
- Ceglar, A.; Črepinšek, Z.; KAJFEŽ-BOGATAJ, L.; POGAČAR, T. The simulation of phenological development in dynamic crop model: The Bayesian comparison of different methods. Agric. For. Meteorol. 2011, 151, 101–115. [Google Scholar] [CrossRef]
- Arora, V.; Singh, H.; Singh, B. Analyzing wheat productivity responses to climatic, irrigation and fertilizer-nitrogen regimes in a semi-arid sub-tropical environment using the CERES-Wheat model. Agric. Water Manag. 2007, 94, 22–30. [Google Scholar] [CrossRef]
- Fox, D.G. Judging air quality model performance: A summary of the AMS Workshop on Dispersion Model Performance. Bull. Am. Meteorol. Soc. 1981, 62, 599–609. [Google Scholar] [CrossRef] [Green Version]
- Tang, L.; Zhu, Y.; Hannaway, D.; Meng, Y.; Liu, L.; Chen, L.; Cao, W. RiceGrow: A rice growth and productivity model. NJAS Wagening. J. Life Sci. 2009, 57, 83–92. [Google Scholar] [CrossRef] [Green Version]
- Zheng, B.Y.; Chen, U.K.; Doherty, A.; Chapman, S. The APSIM-Wheat Module (7.5 R3008) Documentation; APSRU: Toowoomba, Australia, 2014; pp. 20–25. [Google Scholar]
- Zhang, Y.; Feng, L.; Wang, E.; Wang, J.; Li, B. Evaluation of the APSIM-Wheat model in terms of different cultivars, management regimes and environmental conditions. Can. J. Plant Sci. 2012, 92, 937–949. [Google Scholar] [CrossRef] [Green Version]
- Nie, Z.; Li, G.; Wang, J.; Ma, W.; Luo, C.; Dong, L.; Lu, Y. Parameter optimization for the simulation of leaf area index of dryland wheat with the APSIM model. Sci. Agric. Sin. 2019, 52, 2056–2068. [Google Scholar]
- Asseng, S.; Turner, N.C.; Botwright, T.; Condon, A.G. Evaluating the Impact of a Trait for Increased Specific Leaf Area on Wheat Yields Using a Crop Simulation Model. Agron. J. 2003, 95, 10. [Google Scholar] [CrossRef]


| Region | Cultivar | Dataset | |||
|---|---|---|---|---|---|
| Calibration | Validation | ||||
| Experimental Year | Data Source | Experimental Year | Data Source | ||
| Wuhan | Zhengmai 9023 | 1999–2000 | Zhang et al. [23] | 2013–2014 | Xu et al. [24] |
| 2008–2009 | ATEC of Hubei province ‡ | 2014–2015, 2015–2016 | Unpublished data | ||
| Emai596 | 2009–2010 | Dong et al. [25] | 2009–2010 | Dong et al. [25] | |
| Emai170 | 2012–2013 | Liu et al. [26] | 2013–2014 | Liu et al. [26] | |
| 2015–2016 | Unpublished data § | 2015–2016 | Unpublished data | ||
| Jingmen | Zhengmai 9023 | 1999–2000 | Zhang et al. [23] | 2000–2001 | Zhang et al. [23] |
| 2010–2011 | ATEC of Jingmen | 2013–2014 | Guan et al. [27] | ||
| Emai596 | 2010–2011 | ATEC of Jingmen | 2012–2013 | Ruan et al. [28] | |
| – † | – | 2015–2016 | Unpublished data | ||
| Emai170 | – | – | 2015–2016 | Unpublished data | |
| Emai18 | 2008–2009 | ATEC of Jingmen | 2002–2003 | Guan et al. [29] | |
| – | – | 2015–2016 | Unpublished data | ||
| Xiangyang | Zhengmai 9023 | 2001–2002 | ATEC of Xiangyang | 1999–2000 | Zhang et al. [23] |
| 2010–2011 | ATEC of Xiangyang | 2011–2012 | Ruan et al. [28] | ||
| – | – | 2013–2014 | Xu et al. [24] | ||
| – | – | 2015–2016 | Unpublished data | ||
| Emai596 | 2013–2014 | Wang et al. [30] | 2013–2014 | Wang et al. [30] | |
| – | – | 2015–2016 | Unpublished data | ||
| Emai170 | 2012–2013 | ATEC of Xiangyang | 2015–2016 | Unpublished data | |
| Emai18 | 2007–2008 | Xiong et al. [31] | 2002–2003 | Ming et al. [32] | |
| – | – | 2007–2008 | Xiong et al. [31] | ||
| – | – | 2010–2011 | ATEC of Xiangyang | ||
| Corp Module | Parameter Type | Genetic Parameters | Description |
|---|---|---|---|
| APSIM-wheat | Phenology control parameters | vern_sens | Sensitivity to vernalization |
| photop_sens | Sensitivity to photoperiod | ||
| tt_startgf_to_mat | The thermal time required from grain filling to maturity (°C d) | ||
| Yield control parameters | grain_per_gram_stem | Numbers of grain per gram stem (kernel (g stem)−1) | |
| potential_grain_filling_Rate | Potential grain filling rate (g grain−1 d−1) | ||
| Leaf area control parameters | sla-max | Maximum specific leaf area of ΔLAI † (mm−2 g−1) |
| PMARE Value (%) | Model Rating |
|---|---|
| 0–5 | Excellent |
| 5–10 | Very good |
| 10–15 | Good |
| 15–20 | Fair |
| 20–25 | Moderate |
| >25 | Unsatisfactory |
| Variety | STV | STP | TTRGM (°C d) | NGS | PGFR (g Grain−1 d−1) | MSLA (mm2 g−1) | |
|---|---|---|---|---|---|---|---|
| x-lai = 0 | x-lai = 5 | ||||||
| Zhengmai9023 | 3.5 | 3.6 | 650 | 30.5 | 0.0018 | 21,000 | 18,000 |
| Emai596 | 2.5 | 2.8 | 520 | 28.5 | 0.0031 | 25,000 | 23,000 |
| Emai18 | 2.4 | 2.5 | 610 | 38.5 | 0.0028 | 24,000 | 23,000 |
| Emai170 | 3.0 | 3.1 | 620 | 39.6 | 0.0027 | 23,000 | 20,000 |
| Growth Duration | Region | Linear Regression Equation | F–Value | p–Value | R2 | NRMSE (%) | dr-Values | PMARE (%) |
|---|---|---|---|---|---|---|---|---|
| Sowing to anthesis | WH | y = 1.21x − 35.4 | 139.67 | <0.0001 | 0.93 | 1.2 | 0.81 | 1.1 |
| JM | y = 1.02x − 1.1 | 172.5 | <0.0001 | 0.97 | 1.3 | 0.78 | 1.1 | |
| XY | y = 0.74x + 43.6 | 142.8 | <0.0001 | 0.90 | 1.6 | 0.79 | 1.4 | |
| Sowing to maturity | WH | y = 1.08x − 17.1 | 144.4 | <0.0001 | 0.94 | 1.1 | 0.87 | 0.8 |
| JM | y = 0.90x + 22.4 | 75.59 | <0.0001 | 0.93 | 1.0 | 0.76 | 0.8 | |
| XY | y = 0.70x + 63.1 | 359.7 | <0.0001 | 0.96 | 1.3 | 0.74 | 1.3 |
| Model Traits | WH | JM | XY | |||
|---|---|---|---|---|---|---|
| Observed (Mean) | Simulated (Mean) | Observed (Mean) | Simulated (Mean) | Observed (Mean) | Observed (Mean) | |
| STA (d) | 158–181 (164.9) | 161–179 (165.4) | 166–181 (174.4) | 163–178 (171.8) | 165–182 (170.4) | 166–186 (170.4) |
| STM (d) | 190–216 (200.0) | 193–218 (200.5) | 203–216 (211.4) | 202–215 (208.9) | 200–216 (207.4) | 198–220 (207.3) |
| GY (kg ha−1) | 3637–9328 (5593) | 4935–7550 (5372) | 1283–6563 (4520) | 1303–6199 (4726) | 1789–7936 (5796) | 1525–8021 (5240) |
| AGB (kg ha−1) | 7688–20,730 (11,444) | 8180–17,471 (11,854) | 2895–13,775 (9861) | 4829–13,896 (11,185) | 3370–19,520 (12,211) | 4930–18,104 (12,237) |
| Model Attribute | Region | Linear Regression Equation | F-Value | p-Value | R2 | NRMSE (%) | dr-Values | PMARE (%) |
|---|---|---|---|---|---|---|---|---|
| Yield | WH | y = 0.97x + 295.2 | 29.4 | 0.0003 | 0.75 | 13.0 | 0.73 | 11.9 |
| JM | y = 0.93x + 122.2 | 20.3 | 0.0041 | 0.77 | 18.1 | 0.78 | 13.6 | |
| XY | y = 0.89x + 1022.7 | 55.9 | <0.0001 | 0.78 | 17.1 | 0.71 | 14.6 | |
| Above-ground biomass | WH | y = 1.25x − 3316.8 | 65.1 | <0.0001 | 0.87 | 13.5 | 0.80 | 10.6 |
| JM | y = 1.02x − 1600.5 | 40.9 | 0.0007 | 0.87 | 17.7 | 0.71 | 19.9 | |
| XY | y = 0.98x + 560.0 | 41.0 | <0.0001 | 0.72 | 19.8 | 0.72 | 18.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, P.; Zhou, Y.; Li, F.; Ling, X.; Deng, N.; Peng, S.; Man, J. The Adaptability of APSIM-Wheat Model in the Middle and Lower Reaches of the Yangtze River Plain of China: A Case Study of Winter Wheat in Hubei Province. Agronomy 2020, 10, 981. https://doi.org/10.3390/agronomy10070981
Zhao P, Zhou Y, Li F, Ling X, Deng N, Peng S, Man J. The Adaptability of APSIM-Wheat Model in the Middle and Lower Reaches of the Yangtze River Plain of China: A Case Study of Winter Wheat in Hubei Province. Agronomy. 2020; 10(7):981. https://doi.org/10.3390/agronomy10070981
Chicago/Turabian StyleZhao, Panpan, Yang Zhou, Fengfeng Li, Xiaoxia Ling, Nanyan Deng, Shaobing Peng, and Jianguo Man. 2020. "The Adaptability of APSIM-Wheat Model in the Middle and Lower Reaches of the Yangtze River Plain of China: A Case Study of Winter Wheat in Hubei Province" Agronomy 10, no. 7: 981. https://doi.org/10.3390/agronomy10070981





